感知器的训练算法实例

感知器的训练算法
已知两个训练模式集分别属于ω1类和ω2类，权向量的初始值为w(1)，可任意取值。

若0x )k (w ,x k T 1k >∈ω，若0x )k (w ,x k T 2k ≤∈ω，则在用全部训练模式集进行迭代训练时，第k 次的训练步骤为：
- 若1k x ω∈且0x )k (w k T ≤，则分类器对第k 个模式x k 做了错误分类，此时应校正权向量，使得w(k+1) = w(k) + Cx k ，其中C 为一个校正增量。

- 若2k x ω∈且0x )k (w k T >，同样分类器分类错误，则权向量应校正如下：w(k+1) = w(k) - Cx k
- 若以上情况不符合，则表明该模式样本在第k 次中分类正确，因此权向量不变，即：w(k+1) = w(k)
若对2x ω∈的模式样本乘以(-1)，则有：
0x )k (w k T ≤时，w(k+1) = w(k) + Cx k
此时，感知器算法可统一写成：
⎩⎨⎧≤+>=+0
x )k (w if Cx )k (w 0x )k (w if )k (w )1k (w k T k k T。

多层感知器--MLP神经⽹络算法提到⼈⼯智能(Artificial Intelligence,AI),⼤家都不会陌⽣,在现今⾏业领起风潮,各⾏各业⽆不趋之若鹜,作为技术使⽤者,到底什么是AI,我们要有⾃⼰的理解.⽬前,在⼈⼯智能中,⽆可争议的是深度学习占据了统治地位,,其在图像识别,语⾳识别,⾃然语⾔处理,⽆⼈驾驶领域应⽤⼴泛.如此,我们要如何使⽤这门技术呢?下⾯我们来⼀起了解"多层感知器",即MLP算法,泛称为神经⽹络.神经⽹络顾名思义,就像我们⼈脑中的神经元⼀样,为了让机器来模拟⼈脑,我们在算法中设置⼀个个节点,在训练模型时,输⼊的特征与预测的结果⽤节点来表⽰,系数w(⼜称为"权重")⽤来连接节点,神经⽹络模型的学习就是⼀个调整权重的过程,训练模型⼀步步达到我们想要的效果.理解了原理,下⾯来上代码直观看⼀下:1.神经⽹络中的⾮线性矫正每个输⼊数据与输出数据之间都有⼀个或多个隐藏层,每个隐藏层包含多个隐藏单元.在输⼊数据和隐藏单元之间或隐藏单元和输出数据之间都有⼀个系数(权重).计算⼀系列的加权求和和计算单⼀的加权求和和普通的线性模型差不多.线性模型的⼀般公式:y = w[0]▪x[0]+w[1]▪x[1] + ▪▪▪ + w[p]▪x[p] + b为了使得模型⽐普通线性模型更强⼤,所以我们要进⾏⼀些处理,即⾮线性矫正(rectifying nonlinearity),简称为(rectified linear unit,relu).或是进⾏双曲正切处理(tangens hyperbolicus,tanh)############################# 神经⽹络中的⾮线性矫正 ########################################导⼊numpyimport numpy as np#导⼊画图⼯具import matplotlib.pyplot as plt#导⼊numpyimport numpy as py#导⼊画图⼯具import matplotlib.pyplot as plt#⽣成⼀个等差数列line = np.linspace(-5,5,200)#画出⾮线性矫正的图形表⽰plt.plot(line,np.tanh(line),label='tanh')plt.plot(line,np.maximum(line,0),label='relu')#设置图注位置plt.legend(loc='best')#设置横纵轴标题plt.xlabel('x')plt.ylabel('relu(x) and tanh(x)')#显⽰图形plt.show()tanh函数吧特征X的值压缩进-1到1的区间内,-1代表的是X中较⼩的数值,⽽1代表X中较⼤的数值.relu函数把⼩于0的X值全部去掉,⽤0来代替2.神经⽹络的参数设置#导⼊MLP神经⽹络from sklearn.neural_network import MLPClassifier#导⼊红酒数据集from sklearn.datasets import load_wine#导⼊数据集拆分⼯具from sklearn.model_selection import train_test_splitwine = load_wine()X = wine.data[:,:2]y = wine.target#下⾯我们拆分数据集X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)#接下来定义分类器mlp = MLPClassifier(solver='lbfgs')mlp.fit(X_train,y_train)MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,beta_2=0.999, early_stopping=False, epsilon=1e-08,hidden_layer_sizes=(100,), learning_rate='constant',learning_rate_init=0.001, max_iter=200, momentum=0.9,n_iter_no_change=10, nesterovs_momentum=True, power_t=0.5,random_state=None, shuffle=True, solver='lbfgs', tol=0.0001,validation_fraction=0.1, verbose=False, warm_start=False)identity对样本特征不做处理,返回值是f(x) = xlogistic返回的结果会是f(x)=1/[1 + exp(-x)],其和tanh类似,但是经过处理后的特征值会在0和1之间#导⼊画图⼯具import matplotlib.pyplot as pltfrom matplotlib.colors import ListedColormap#定义图像中分区的颜⾊和散点的颜⾊cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF'])cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])#分别⽤样本的两个特征值创建图像和横轴和纵轴x_min,x_max = X_train[:, 0].min() - 1,X_train[:, 0].max() + 1y_min,y_max = X_train[:, 1].min() - 1,X_train[:, 1].max() + 1xx,yy = np.meshgrid(np.arange(x_min,x_max, .02),np.arange(y_min,y_max, .02))Z = mlp.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z = Z.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:solver=lbfgs")plt.show()(1)设置隐藏层中节点数为10#设置隐藏层中节点数为10mlp_20 = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10])mlp_20.fit(X_train,y_train)Z1 = mlp_20.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z1 = Z1.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z1, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:nodes=10")plt.show()(2)设置神经⽹络有两个节点数为10的隐藏层#设置神经⽹络2个节点数为10的隐藏层mlp_2L = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10])mlp_2L.fit(X_train,y_train)ZL = mlp_2L.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊ZL = ZL.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, ZL, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:2layers")plt.show()(3)设置激活函数为tanh#设置激活函数为tanhmlp_tanh = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10],activation='tanh')mlp_tanh.fit(X_train,y_train)Z2 = mlp_tanh.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z2 = Z2.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z2, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:2layers with tanh")plt.show()(4)修改模型的alpha参数#修改模型的alpha参数mlp_alpha = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10],activation='tanh',alpha=1)mlp_alpha.fit(X_train,y_train)Z3 = mlp_alpha.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z3 = Z3.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z3, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:alpha=1")plt.show()总结: 如此,我们有4种⽅法可以调节模型的复杂程度: 第⼀种,调整神经⽹络每⼀个隐藏层上的节点数 第⼆种,调节神经⽹络隐藏层的层数 第三种,调节activation的⽅式 第四种,通过调整alpha值来改变模型正则化的过程 对于特征类型⽐较单⼀的数据集来说,神经⽹络的表现还是不错的,但是如果数据集中的特征类型差异⽐较⼤的话,随机森林或梯度上升随机决策树等基于决策树的算法的表现会更好⼀点. 神经⽹络模型中的参数调节⾄关重要,尤其是隐藏层的数量和隐藏层中的节点数. 这⾥给出⼀个参考原则:神经⽹络中的隐藏层的节点数约等于训练数据集的特征数量,但⼀般不超过500. 如果想对庞⼤复杂⾼维的数据集做处理与分析,建议往深度学习发展,这⾥介绍两个流⾏的python深度学习库:keras,tensor-flow⽂章引⾃ : 《深⼊浅出python机器学习》。

零基础⼊门深度学习（1）-感知器⽆论即将到来的是⼤数据时代还是⼈⼯智能时代，亦或是传统⾏业使⽤⼈⼯智能在云上处理⼤数据的时代，作为⼀个有理想有追求的程序员，不懂深度学习（Deep Learning）这个超热的技术，会不会感觉马上就out了？现在救命稻草来了，《零基础⼊门深度学习》系列⽂章旨在讲帮助爱编程的你从零基础达到⼊门级⽔平。

零基础意味着你不需要太多的数学知识，只要会写程序就⾏了，没错，这是专门为程序员写的⽂章。

虽然⽂中会有很多公式你也许看不懂，但同时也会有更多的代码，程序员的你⼀定能看懂的（我周围是⼀群狂热的Clean Code程序员，所以我写的代码也不会很差）。

⽂章列表深度学习是啥在⼈⼯智能领域，有⼀个⽅法叫机器学习。

在机器学习这个⽅法⾥，有⼀类算法叫神经⽹络。

神经⽹络如下图所⽰：上图中每个圆圈都是⼀个神经元，每条线表⽰神经元之间的连接。

我们可以看到，上⾯的神经元被分成了多层，层与层之间的神经元有连接，⽽层内之间的神经元没有连接。

最左边的层叫做输⼊层，这层负责接收输⼊数据；最右边的层叫输出层，我们可以从这层获取神经⽹络输出数据。

输⼊层和输出层之间的层叫做隐藏层。

隐藏层⽐较多（⼤于2）的神经⽹络叫做深度神经⽹络。

⽽深度学习，就是使⽤深层架构（⽐如，深度神经⽹络）的机器学习⽅法。

那么深层⽹络和浅层⽹络相⽐有什么优势呢？简单来说深层⽹络能够表达⼒更强。

事实上，⼀个仅有⼀个隐藏层的神经⽹络就能拟合任何⼀个函数，但是它需要很多很多的神经元。

⽽深层⽹络⽤少得多的神经元就能拟合同样的函数。

也就是为了拟合⼀个函数，要么使⽤⼀个浅⽽宽的⽹络，要么使⽤⼀个深⽽窄的⽹络。

⽽后者往往更节约资源。

深层⽹络也有劣势，就是它不太容易训练。

简单的说，你需要⼤量的数据，很多的技巧才能训练好⼀个深层⽹络。

这是个⼿艺活。

感知器看到这⾥，如果你还是⼀头雾⽔，那也是很正常的。

为了理解神经⽹络，我们应该先理解神经⽹络的组成单元——神经元。

多层感知机例题
多层感知机是一种前馈神经网络，它由多个感知器组成，可以用于分类和回归等任务。

下面是一个简单的多层感知机示例，用于解决二分类问题。

假设我们有一些数据点，每个数据点都有两个特征，我们想要根据这两个特征将数据点分为两类。

我们可以使用一个多层感知机来解决这个问题。

具体来说，我们可以定义一个多层感知机，其中输入层有两个神经元，隐藏层有两个神经元，输出层有一个神经元。

我们使用sigmoid激活函数作为隐藏层和输出层的激活函数。

我们可以通过以下步骤来训练这个多层感知机：
1. 初始化权重和偏置项。

2. 对于每个训练样本(x1, x2, y)，计算隐藏层的输出和输出层的输出。

3. 根据输出层的输出和真实标签计算损失函数。

4. 反向传播，根据损失函数计算梯度。

5. 更新权重和偏置项。

6. 重复步骤2-5，直到达到预设的迭代次数或损失函数达到预设的值。

训练完成后，我们可以使用训练好的权重和偏置项来预测新数据点的类别。

具体来说，对于每个新数据点(x1, x2)，我们首先计算隐藏层的输出和输出
层的输出，然后根据输出层的输出判断该数据点属于哪一类。

以上是一个简单的多层感知机示例，实际上多层感知机可以包含多个隐藏层，每个隐藏层可以包含多个神经元。

此外，还可以使用不同的激活函数和优化算法来提高多层感知机的性能。

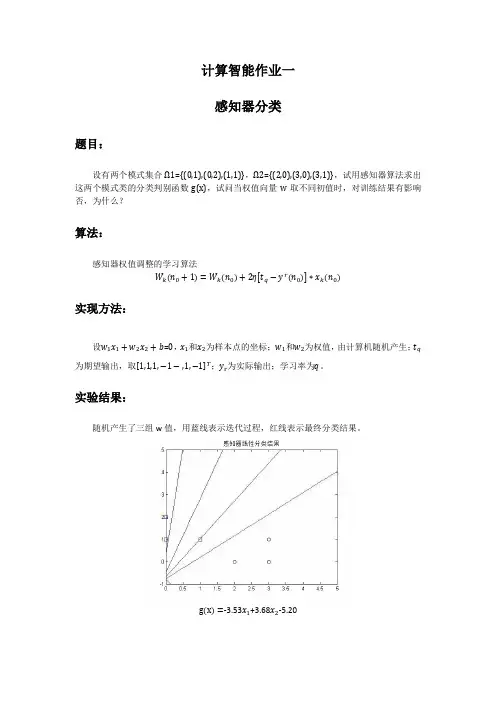
计算智能作业一感知器分类题目：设有两个模式集合Ω1={(0,1),(0,2),(1,1)}，Ω2={(2,0),(3,0),(3,1)}，试用感知器算法求出这两个模式类的分类判别函数g(x)，试问当权值向量w取不同初值时，对训练结果有影响否，为什么？算法：感知器权值调整的学习算法W k n0+1=W k n0+2ηt q−y r n0∗x k n0实现方法：设w1x1+w2x2+b=0，x1和x2为样本点的坐标；w1和w2为权值，由计算机随机产生；t q 为期望输出，取1,1,1,−1−,1,−1T；y r为实际输出；学习率为q。

实验结果：随机产生了三组w值，用蓝线表示迭代过程，红线表示最终分类结果。

g x=-3.53x1+3.68x2-5.20g x=-5.65x1-2.01x2+8.05g x=-2.48x1-7.28x2-1.37 实验代码：%感知器先行分类问题程序代码x=[0,0,1,2,3,3];y=[1,2,1,0,0,1];w=10*(2*rand(1,3)-1);b=w(3); %w1,w2,b取-10到10之间的随机数q=1;%学习率设为1t=[1,1,1,-1,-1,-1];%期待输出，1为一类，-1为另一类syms p;syms l;for j=1:3%画出一个样本中三个待分类的点plot(x(j),y(j),'sb');hold on;endfor j=4:6%画出另一个样本中三个待分类的点plot(x(j),y(j),'ok');hold on;endwhile (p~=w(1)||l~=w(2))p=w(1);l=w(2);for i=1:6z=t(i)*(x(i)*w(1)+y(i)*w(2)+b);if z<=0w(1)=w(1)+q*x(i)*t(i);%¸感知器学习算法w(2)=w(2)+q*y(i)*t(i);b=b+t(i);endtitle('感知器线性分类结果');axis([0,5,-1,5]);h=[-1:0.1:5];g=[0:0.1:5];k=-w(1)/w(2);m=-b/w(2);h=k*g+m;line(g,h); hold on;%将每一次迭代的直线都画出来endendplot(g,h,'r'); hold on;%将最终分类结果用红色表示结论分析：实验中权值由计算机随机生成，初始权值越接近最终分类的结果，则训练次数越少。

感知机的实验报告感知机是一种基本的二分类线性模型，可以用于解决二分类问题。

本实验主要目的是通过编程实现感知机算法，并使用UCI数据集对算法进行测试和评估。

1. 实验原理感知机是一种基于误分类驱动的在线学习算法。

算法的基本原理是，通过不断调整超平面的参数，使得对于给定的输入样本能够正确地分类。

感知机算法通过迭代的方式更新模型参数，直到所有样本能够正确分类或达到最大迭代次数。

2. 实验步骤（1）建立感知机模型的类结构。

包括初始化参数、计算预测值、参数更新等函数。

（2）读取UCI数据集。

本实验选择了Iris鸢尾花数据集作为测试数据集。

（3）将数据集随机打乱，并将数据集划分为训练集和测试集。

（4）调用感知机模型进行训练，并输出训练结果。

（5）使用测试集评估模型的性能，并输出测试结果。

3. 实验结果与分析本实验使用了UCI数据集中的Iris鸢尾花数据集进行实验。

对于该数据集，我们选择了两个特征作为输入，并将其中两类作为正例，另一类作为反例。

训练集包含80%的样本，测试集包含剩下的20%。

在实验中，我们设置了最大迭代次数为1000次。

经过多次实验，发现在该数据集上，平均只需60次迭代就能够得到一个准确率较高的感知机模型。

在测试集上的分类准确率可以达到96%左右。

通过实验结果分析，感知机算法具有较好的二分类能力。

通过对输入样本的不断学习和调整，感知机能够逐步提升分类准确率。

然而，由于感知机算法在参数更新时是根据单个样本进行调整，对于不线性可分的数据集，感知机算法可能无法达到100%的分类准确率。

4. 实验总结与改进本实验通过实现感知机算法并对UCI数据集进行测试，验证了感知机算法的有效性。

感知机算法在二分类问题上具有较好的性能，可以在较短的迭代次数内得到一个准确率较高的模型。

然而，在实际应用中，感知机算法往往受到数据线性可分性的限制。

对于不线性可分的数据集，感知机算法可能无法收敛或得到较低的分类准确率。

为了提升感知机算法的性能，可以考虑使用核函数将输入特征映射到高维空间，或者使用非线性模型。

机器学习算法--Perceptron（感知器）算法概括Perceptron(感知器)是⼀个⼆分类线性模型，其输⼊的是特征向量，输出的是类别。

Perceptron的作⽤即将数据分成正负两类的超平⾯。

可以说是机器学习中最基本的分类器。

模型Perceptron ⼀样属于线性分类器。

对于向量X=x1,x2,...x n，对于权重向量（w）相乘，加上偏移（b），于是有：f(x)=N∑i=1w i x i+b设置阈值threshold之后，可以的到如果f(x)>threshold,则y(标签)设为1如果f(x)<threshold,则y(标签)设为0即，可以把其表⽰为：y=sign(w T x+b)参数学习我们已经知道模型是什么样，也知道Preceptron有两个参数，那么如何更新这两个参数呢？⾸先，我们先Preceptron的更新策略：1. 初始化参数2. 对所有数据进⾏判断，超平⾯是否可以把正实例点和负实例点完成正确分开。

3. 如果不⾏，更新w，b。

4. 重复执⾏2，3步，直到数据被分开，或者迭代次数到达上限。

那么如何更新w，b呢？我们知道在任何时候，学习是朝着损失最⼩的地⽅，也就是说，我的下⼀步更新的策略是使当前点到超平⾯的损失函数极⼩化。

在超平⾯中，我们定义⼀个点到超平⾯的距离为：(具体如何得出，可以⾃⾏百度~~~ )，此外其中1|w|是L2范数。

意思可表⽰全部w向量的平⽅和的开⽅。

1‖w‖w T x+b 这⾥假设有M个点是误差点，那么损失函数可以是：L(w,b)=−1‖w‖∑x i∈M yi(w T x+b)当然，为了简便计算，这⾥忽略1|w|。

1|w|不影响-y(w,x+b)正负的判断，即不影响学习算法的中间过程。

因为感知机学习算法最终的终⽌条件是所有的输⼊都被正确分类，即不存在误分类的点。

则此时损失函数为0，则可以看出1|w|对最终结果也⽆影响。

既然没有影响，为了简便计算，直接忽略1|w|。

1、用感知器算法求解向量,训练样本为:(1) ω1}(1,1,0),(1,0,1),(1,0,0),{(0,0,0):TT T T (2) ω2:}(1,1,1),(0,1,0),(0,1,1),{(0,0,1)T T T T（1）训练样本分量增广化及符号规范化。

)10,0,0(1'=，x )10,0,1(2'=，x )11,0,1(3'=，x )10,1,1(4'=，x )1-1-,0,0(5'=，x )1-1-,1-,0(6'=，x )1-0,1-,0(7'=，x )1-1-,1-,1-(8'=，x （2）运用感知器训练算法，任意给增广权矢量赋初值：)111,1()1(w '=， 取增量1=ρ则： )10,0,0(1'=，x )10,0,1(2'=，x )11,0,1(3'=，x )10,1,1(4'=，x )1-1-,0,0(5'=，x)1-1-,1-,0(6'=，x)1-0,1-,0(7'=，x)1-1-,1-,1-(8'=，x)111,1()1(w '=，)1()2(,01)()(,,11w w x k w x d x x k k k k=>='=== )2()3(,02)()(,,22w w x k w x d x x k k k k=>='=== )3()4(,03)()(,,33w w x k w x d x x k k k k=>='=== )4()5(,03)()(,,44w w x k w x d x x k k k k=>='===)00,1,1()5()6(,02)()(,,555'=+=<-='===，x w w x k w x d x x k k k k)1-1-,0,1()6()7(,01)()(,,666'=+=<-='===，x w w x k w x d x x k k k k)7()8(,01)()(,,77w w x k w x d x x k k k k=>='=== )8()9(,01)()(,,88w w x k w x d x x k k k k=>='===)01-,0,1()9()10(,01)()(,,911'=+=<-='===，x w w x k w x d x x k k k k)10()11(,01)()(,,102w w x k w x d x x k k k k=>='===)0,1,0,2()11()12(,0)()(,,1133'=+=='===，x w w x k w x d x x k k k k)12()13(,03)()(,,124w w x k w x d x x k k k k=>='===)01-,0,2()13()14(,01)()(,,1355'=+=<-='===，x w w x k w x d x x k k k k)14()15(,01)()(,,146w w x k w x d x x k k k k=>='===)1-1-,1,2()15()16(,0)()(,,1577'-=+=='===，x w w x k w x d x x k k k k)16()17(,01)()(,,168w w x k w x d x x k k k k=>='===)0,1,1,2()17()18(,01)()(,,1711'--=+=<-='===x w w x k w x d x x k k k k)18()19(,02)()(,,182w w x k w x d x x k k k k=>='=== )19()20(,01)()(,,193w w x k w x d x x k k k k=>='=== )20()21(,01)()(,,204w w x k w x d x x k k k k=>='=== )21()22(,01)()(,,215w w x k w x d x x k k k k=>='=== )22()23(,02)()(,,226w w x k w x d x x k k k k=>='=== )23()24(,01)()(,,237w w x k w x d x x k k k k=>='===)1,2,2,1()24()25(,0)()(,,2488'---=+=='===x w w x k w x d x x k k k k)02-,2,1()25()26(,01)()(,,2511'-=+=<-='===，x w w x k w x d x x k k k k)26()27(,01)()(,,262w w x k w x d x x k k k k=>='===)1,1,2,2()27()28(,01)()(,,2733'--=+=<-='===x w w x k w x d x x k k k k)28()29(,01)()(,,284w w x k w x d x x k k k k=>='===)0,2,2,2()29()30(,0)()(,,2955'--=+=='===x w w x k w x d x x k k k k)30()31(,04)()(,,306w w x k w x d x x k k k k=>='=== )31()32(,02)()(,,317w w x k w x d x x k k k k=>='=== )32()33(,02)()(,,328w w x k w x d x x k k k k=>='===)1,2,2,2()33()34(,0)()(,,3311'--=+=='===x w w x k w x d x x k k k k)34()35(,03)()(,,342w w x k w x d x x k k k k=>='===)35()36(,01)()(,,353w w x k w x d x x k k k k=>='===)36()37(,01)()(,,364w w x k w x d x x k k k k=>='=== )37()38(,01)()(,,375w w x k w x d x x k k k k=>='=== )38()39(,03)()(,,386w w x k w x d x x k k k k=>='=== )39()40(,01)()(,,397w w x k w x d x x k k k k=>='=== )40()41(,01)()(,,408w w x k w x d x x k k k k=>='=== )41()42(,01)()(,,411w w x k w x d x x k k k k=>='===由上边结果可以看出，经过，，，，，，，，87654321x x x x x x x x一轮迭代后表明使用)34(w异能对所有样本正确分类，增广权矢量的值不再变化，所以算法收敛于)34(w ，)34(w 就是所求的解向量，即)1,2,2,2()34(*'--=w。

第4章感知器（Perceptron）感知器是由美国计算机科学家罗森布拉特（F.Roseblatt）于1957年提出的。

单层感知器神经元模型图：图4．1 感知器神经元模型F.Roseblatt已经证明，如果两类模式是线性可分的（指存在一个超平面将它们分开），则算法一定收敛。

感知器特别适用于简单的模式分类问题，也可用于基于模式分类的学习控制中。

本节中所说的感知器是指单层的感知器。

多层网络因为要用到后面将要介绍的反向传播法进行权值修正，所以把它们均归类为反向传播网络之中。

4．1 感知器的网络结构根据网络结构，可以写出第i个输出神经元(i＝1，2，…，s)的加权输入和ni 及其输出ai为：感知器的输出值是通过测试加权输入和值落在阈值函数的左右来进行分类的，即有：阈值激活函数如图4．3所示。

4．2 感知器的图形解释由感知器的网络结构，我们可以看出感知器的基本功能是将输入矢量转化成0或1的输出。

这一功能可以通过在输人矢量空间里的作图来加以解释。

感知器权值参数的设计目的，就是根据学习法则设计一条W*P+b＝0的轨迹，使其对输入矢量能够达到期望位置的划分。

以输入矢量r＝2为例，对于选定的权值w1、w2和b，可以在以p1和p2分别作为横、纵坐标的输入平面内画出W*P+b＝w1p1十w2p2十b＝0的轨迹，它是一条直线，此直线上的及其线以上部分的所有p1、p2值均使w1p1十w2p2十b＞0，这些点若通过由w1、w2和b构成的感知器则使其输出为1；该直线以下部分的点则使感知器的输出为0。

所以当采用感知器对不同的输入矢量进行期望输出为0或1的分类时，其问题可转化为：对于已知输入矢量在输入空间形成的不同点的位置，设计感知器的权值W和b，将由W*P+b＝0的直线放置在适当的位置上使输入矢量按期望输出值进行上下分类。

图4．4 输入矢量平面图（此图横坐标有问题）4．3 感知器的学习规则学习规则是用来计算新的权值矩阵W及新的偏差B的算法。

3.5 感知器算法对于线性判别函数，当模式的维数已知时判别函数的形式实际上就已经定了下来，如二维 121122T()x x d w x w x w ==++（,），X X三维123112233T,()+x x x d w x w x w x w==++（,），X X剩下的问题也就是确定权向量W ，只要求出权向量，分类器的设计即告完成。

非线性判别函数也有类似的问题。

本章的后续部分将主要讨论一些基本的训练权向量的算法，或者说学习权向量的算法，它们都是都是用于设计确定性分类器的迭代算法。

1. 概念理解在学习感知器算法之前，首先要明确几个概念。

1）训练与学习训练是指利用已知类别的模式样本指导机器对分类规则进行反复修改，最终使分类结果与已知类别信息完全相同的过程。

从分类器的角度来说，就是学习的过程。

学习分为监督学习和非监督学习两大类。

非监督学习主要用于学习聚类规则，没有先验知识或仅有极少的先验知识可供利用，通过多次学习和反复评价，结果合理即可。

监督学习主要用于学习判别函数，判别函数的形式已知时，学习判别函数的有关参数；判别函数的形式未知时，则直接学习判别函数。

训练与监督学习方法相对应，需要掌握足够的与模式类别有关的先验信息，这些先验信息主要通过一定数量的已知类别的模式样本提供，这些样本常称作训练样本集。

用训练样本集对分类器训练成功后，得到了合适的判别函数，才能用于分类。

前面在介绍线性判别函数的同时，已经讨论了如何利用判别函数的性质进行分类，当然，前提是假定判别函数已知。

2）这种分类器只能处理确定可分的情况，包括线性可分和非线性可分。

只要找到一个用于分离的判别函数就可以进行分类。

由于模式在空间位置上的分布是可分离的，可以通过几何方法把特征空间分解为对应不同类别的子空间，故又称为几何分类器。

当不同类别的样本聚集的空间发生重叠现象时，这种分类器寻找分离函数的迭代过程将加长，甚至振荡，也就是说不收敛，这时需要用第4章将要介绍的以概率分类法为基础的概率分类器进行分类。

感知器算法的基本步骤嘿，咱今儿个就来聊聊感知器算法的那些事儿哈！你知道不，这感知器算法就像是一个神奇的魔法盒子，里面装着好多奇妙的步骤呢！首先啊，得有一堆数据，就好像是一堆五颜六色的糖果，每颗糖果都有它独特的味道和特征。

然后呢，就要开始给这些数据分分类啦！这就好比把不同口味的糖果放进不同的小盒子里。

怎么分呢？这就得靠感知器算法的魔力啦！它会先观察这些数据，就像我们仔细观察糖果的颜色、形状一样。

接着，它会试着找到一些规律，一些能把这些数据区分开来的关键之处。

这可不是一件容易的事儿啊，就好像在一堆乱糟糟的东西里找线索一样。

找到规律后，它就开始行动啦！它会根据这些规律来判断新的数据该归到哪一类。

这就好像来了一颗新糖果，它能马上判断出这颗糖果该放进哪个小盒子里。

你说神奇不神奇？而且哦，这个过程就像是一场有趣的游戏，不断地尝试、调整，直到找到最合适的分类方法。

想象一下，如果没有这个神奇的感知器算法，那我们面对那么多复杂的数据该咋办呀？不就像无头苍蝇一样乱撞啦！它的基本步骤虽然听起来简单，可实际操作起来可不容易呢！得小心翼翼地处理每一个数据，就像对待珍贵的宝贝一样。

在这个过程中，可能会遇到各种问题呢。

有时候会发现分错类啦，那就得赶紧调整策略，重新再来。

有时候数据太多太复杂啦，就好像走进了一个巨大的迷宫，得慢慢摸索着找到出口。

但正是因为有了这些挑战，才让感知器算法变得更加有趣和有意义呀！它就像是一个勇敢的探险家，在数据的海洋里不断探索、前行。

总之呢，感知器算法的基本步骤就像是搭积木一样，一块一块地堆积起来，最后建成一座坚固的城堡。

虽然过程中会有困难，但只要我们用心去理解、去实践，就一定能掌握这个神奇的算法，让它为我们服务呀！所以，还等什么呢，赶紧去探索感知器算法的奥秘吧！。

感知器的训练算法实例将属于ω2的训练样本乘以(-1),并写成增广向量的形式。

x①=(0 0 1)T, x②=(0 1 1)T, x③=(-1 0 -1)T, x④=(-1 -1 -1)T第一轮迭代:取C=1,w(1)= (0 0 0)T因w T(1)x①=(0 0 0)(0 0 1)T=0≯0,故w(2)=w(1)+x①=(0 0 1)T 因wT(2)x②=(0 0 1)(0 1 1)T=1>0,故w(3)=w(2)=(0 0 1)T因w T(3)x③=(0 0 1)(-1 0 -1)T=-1≯0,故w(4)=w(3)+x③=(-1 0 0)T 因w T(4)x④=(-1 0 0)(-1 -1 -1)T=1>0,故w(5)=w(4)=(-1 0 0)T 这里,第1步和第3步为错误分类,应“罚”。

因为只有对全部模式都能正确判别的权向量才是正确的解,因此需进行第二轮迭代。

第二轮迭代:因w T(5)x①=(-1 0 0)(0 0 1)T=0≯0,故w(6)=w(5)+x①=(-1 0 1)T 因w T(6)x②=(-1 0 1)(0 1 1)T=1>0,故w(7)=w(6)=(-1 0 1)T因w T(7)x③=(-1 0 1)(-1 0 -1)T=0≯0,故w(8)=w(7)+x③=(-2 0 0)T 因w T(8)x④=(-2 0 0)(-1 -1 -1)T=2>0,故w(9)=w(8)=(-2 0 0)T 需进行第三轮迭代。

第三轮迭代:因w T(9)x①=(-2 0 0)(0 0 1)T=0≯0,故w(10)=w(9)+x①=(-2 0 1)T因w T(10)x②=(-2 0 1)(0 1 1)T=1>0,故w(11)=w(10)=(-2 0 1)T 因wT(11)x③=(-2 0 1)(-1 0 -1)T=1>0,故w(12)=w(11)=(-2 0 1)T 因w T(12)x④=(-2 0 1)(-1 -1 -1)T=1>0,故w(13)=w(12)=(-2 0 1)T 需进行第四轮迭代。