感知器算法实验1

一、实验背景感知器算法是一种简单的线性二分类模型，由Frank Rosenblatt于1957年提出。

它是一种基于误分类项进行学习，以调整权重来拟合数据集的算法。

感知器算法适用于线性可分的数据集，能够将数据集中的样本正确分类。

本次实验旨在通过编程实现感知器算法，并使用iris数据集进行验证。

通过实验，我们能够熟悉感知器算法的基本原理，了解其优缺点，并掌握其在实际应用中的使用方法。

二、实验目的1. 理解感知器算法的基本原理；2. 编程实现感知器算法；3. 使用iris数据集验证感知器算法的性能；4. 分析感知器算法的优缺点。

三、实验环境1. 操作系统：Windows 102. 编程语言：Python3. 机器学习库：Scipy、Numpy、Matplotlib、sklearn四、实验步骤1. 导入必要的库```pythonimport numpy as npimport matplotlib.pyplot as pltfrom sklearn import datasetsfrom sklearn.model_selection import train_test_split```2. 读取iris数据集```pythoniris = datasets.load_iris()X = iris.datay = iris.target```3. 将数据集划分为训练集和测试集```pythonX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)```4. 编写感知器算法```pythondef perceptron(X, y, w, b, learning_rate):for i in range(len(X)):if np.dot(X[i], w) + b <= 0:w += learning_rate y[i] X[i]b += learning_rate y[i]return w, b```5. 训练感知器模型```pythonlearning_rate = 0.1max_iter = 100w = np.zeros(X.shape[1])b = 0for _ in range(max_iter):w, b = perceptron(X_train, y_train, w, b, learning_rate)```6. 评估感知器模型```pythondef predict(X, w, b):return np.sign(np.dot(X, w) + b)y_pred = predict(X_test, w, b)accuracy = np.mean(y_pred == y_test)print("感知器算法的准确率：", accuracy)```7. 可视化感知器模型```pythondef plot_decision_boundary(X, y, w, b):plt.figure(figsize=(8, 6))plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired,edgecolors='k', marker='o')x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1), np.arange(y_min, y_max, 0.1))Z = np.dot(np.c_[xx.ravel(), yy.ravel()], w) + bZ = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, alpha=0.4)plt.xlabel("Sepal length (cm)")plt.ylabel("Sepal width (cm)")plt.title("Perceptron Decision Boundary")plt.show()plot_decision_boundary(X_train, y_train, w, b)```五、实验结果与分析1. 感知器算法的准确率为约0.9，说明感知器算法在iris数据集上表现良好。

Percept1（简单分类问题）：设计单一感知器神经元来解决一个简单的分类问题：将4个输入向量分为两类，其中两个输入向量对应的目标值为1，另两个对应的目标值为0.输入向量为：P=[-1 -0.5 0.3 -0.1;-0.5 0.5 -0.5 1.0]目标向量为：T=[1 1 0 0]P=[-1 -0.5 0.3 -0.1 50;-0.5 0.5 -0.5 1.0 35];T=[1 1 0 0 0];plotpv(P,T);pause;net=newp([-1 50; -1 40],1);watchon;cla;plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});E=1;net=init(net);linehandle=plotpc(net.IW{1},net.b{1});while(sse(E))[net,Y,E]=adapt(net,P,T);linehandle=plotpc(net.IW{1},net.b{1});drawnow;end;pause;watchoff;p=[0.7;1.2];a=sim(net,p);plotpv(p,a);ThePoint=findobj(gca,'type','line');set(ThePoint,'Color','red');hold on;plotpv(P,T);plotpc(net.IW{1},net.b{1});hold off;disp('End of percept1');Percept2（多个感知器神经元的分类问题）：将上例的输入向量扩充为10组，将输入向量分为4类，即输入向量为：P=[0.1 0.7 0.8 0.8 1.0 0.3 0.0 -0.3 -0.5 -1.5;1.2 1.8 1.6 0.6 0.8 0.5 0.2 0.8 -1.5 -1.3]输出向量为：T=[1 1 1 0 0 1 1 1 0 0;0 0 0 0 0 1 1 1 1 1]P=[0.1 0.7 0.8 0.8 1.0 0.3 0.0 -0.3 -0.5 -1.5;1.2 1.8 1.6 0.6 0.8 0.5 0.2 0.8 -1.5 -1.3];T=[1 1 1 0 0 1 1 1 0 0;0 0 0 0 0 1 1 1 1 1];plotpv(P,T);net=newp([-1.5 1;-1.5 1],2);figure;watchon;cla;plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});E=1;net=init(net);linehandle=plotpc(net.IW{1},net.b{1});while(sse(E))[net,Y,E]=adapt(net,P,T);linehandle=plotpc(net.IW{1},net.b{1},linehandle);drawnow;end;watchoff;figure;p=[1.7;-1.2];a=sim(net,p);plotpv(p,a);ThePoint=findobj(gca,'type','line');set(ThePoint,'Color','red');hold on;plotpv(P,T);plotpc(net.IW{1},net.b{1});hold off;disp('End of percept2');Percept3（输入奇异样本对网络训练的影响）当网络的输入样本中存在奇异样本时（即该样本向量相对其他所有样本向量特别大或特别小），此时网络训练时间将大大增加，如：输入向量为：P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50];输出向量为：T=[1 1 0 0 1];P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50];T=[1 1 0 0 1];plotpv(P,T);net=newp([-40 1; -1 50],1);pause;plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});cla;plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});E=1;net.adaptParam.passes=1net=init(net);linehandle=plotpc(net.IW{1},net.b{1});while(sse(E))[net,Y,E]=adapt(net,P,T);linehandle=plotpc(net.IW{1},net.b{1},linehandle);drawnow;end;pause;p=[0.7;1.2];a=sim(net,p);plotpv(p,a);ThePoint=findobj(gca,'type','line');set(ThePoint,'Color','red');hold on;plotpv(P,T);plotpc(net.IW{1},net.b{1});hold off;pause;axis([-2 2 -2 2]);disp('End of percept3');解决此问题只需用标准化感知器学习规则训练即可大大缩短训练时间原始感知器学习规则的权值调整为：T T ep p a t w =-=∆)(标准化感知器学习规则的权值调整为：p p e p p a t w TT=-=∆)(，由函数learnpn()实现见Percept4P=[-0.5 -0.5 0.3 -0.1 -40;-0.5 0.5 -0.5 1.0 50];T=[1 1 0 0 1];plotpv(P,T);pause;net=newp([-40 1; -1 50],1,'hardlim','learnpn');cla;plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});E=1;net.adaptParam.passes=1;net=init(net);linehandle=plotpc(net.IW{1},net.b{1});while(sse(E))[net,Y,E]=adapt(net,P,T);linehandle=plotpc(net.IW{1},net.b{1},linehandle);drawnow;end;pause;p=[0.7;1.2];a=sim(net,p);plotpv(p,a);ThePoint=findobj(gca,'type','line');set(ThePoint,'Color','red');hold on;plotpv(P,T);plotpc(net.IW{1},net.b{1});hold off;pause;axis([-2 2 -2 2]);disp('End of percept4');Percept5（线性不可分的输入向量）定义向量P=[-0.5 -0.5 0.3 -0.1 -0.8;-0.5 0.5 -0.5 1.0 0.0];T=[1 1 0 0 0];用感知器对其分类实验练习：1、设计一个matlab程序实现教材p25例3.12、即输入向量为：P=[0.1 0.7 0.8 0.8 1.0 0.3 0.0 -0.3 -0.5 -1.5;1.2 1.8 1.6 0.6 0.8 0.5 0.2 0.8 -1.5 -1.3]输出向量为：T=[1 1 1 0 0 1 1 1 0 0]对其进行分类P=[-0.5 -0.5 0.3 -0.1 -0.8;-0.5 0.5 -0.5 1.0 0.0];T=[1 1 0 0 0];plotpv(P,T);net=newp([-1 1; -1 1],1);plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});pause;for a=1:25[net,Y,E]=adapt(net,P,T);linehandle=plotpc(net.IW{1},net.b{1},linehandle);drawnow;end;。

感知机的实验报告感知机是一种基本的二分类线性模型，可以用于解决二分类问题。

本实验主要目的是通过编程实现感知机算法，并使用UCI数据集对算法进行测试和评估。

1. 实验原理感知机是一种基于误分类驱动的在线学习算法。

算法的基本原理是，通过不断调整超平面的参数，使得对于给定的输入样本能够正确地分类。

感知机算法通过迭代的方式更新模型参数，直到所有样本能够正确分类或达到最大迭代次数。

2. 实验步骤（1）建立感知机模型的类结构。

包括初始化参数、计算预测值、参数更新等函数。

（2）读取UCI数据集。

本实验选择了Iris鸢尾花数据集作为测试数据集。

（3）将数据集随机打乱，并将数据集划分为训练集和测试集。

（4）调用感知机模型进行训练，并输出训练结果。

（5）使用测试集评估模型的性能，并输出测试结果。

3. 实验结果与分析本实验使用了UCI数据集中的Iris鸢尾花数据集进行实验。

对于该数据集，我们选择了两个特征作为输入，并将其中两类作为正例，另一类作为反例。

训练集包含80%的样本，测试集包含剩下的20%。

在实验中，我们设置了最大迭代次数为1000次。

经过多次实验，发现在该数据集上，平均只需60次迭代就能够得到一个准确率较高的感知机模型。

在测试集上的分类准确率可以达到96%左右。

通过实验结果分析，感知机算法具有较好的二分类能力。

通过对输入样本的不断学习和调整，感知机能够逐步提升分类准确率。

然而，由于感知机算法在参数更新时是根据单个样本进行调整，对于不线性可分的数据集，感知机算法可能无法达到100%的分类准确率。

4. 实验总结与改进本实验通过实现感知机算法并对UCI数据集进行测试，验证了感知机算法的有效性。

感知机算法在二分类问题上具有较好的性能，可以在较短的迭代次数内得到一个准确率较高的模型。

然而，在实际应用中，感知机算法往往受到数据线性可分性的限制。

对于不线性可分的数据集，感知机算法可能无法收敛或得到较低的分类准确率。

为了提升感知机算法的性能，可以考虑使用核函数将输入特征映射到高维空间，或者使用非线性模型。

3.5 感知器算法对于线性判别函数，当模式的维数已知时判别函数的形式实际上就已经定了下来，如二维 121122T()x x d w x w x w ==++（,），X X三维123112233T,()+x x x d w x w x w x w==++（,），X X剩下的问题也就是确定权向量W ，只要求出权向量，分类器的设计即告完成。

非线性判别函数也有类似的问题。

本章的后续部分将主要讨论一些基本的训练权向量的算法，或者说学习权向量的算法，它们都是都是用于设计确定性分类器的迭代算法。

1. 概念理解在学习感知器算法之前，首先要明确几个概念。

1）训练与学习训练是指利用已知类别的模式样本指导机器对分类规则进行反复修改，最终使分类结果与已知类别信息完全相同的过程。

从分类器的角度来说，就是学习的过程。

学习分为监督学习和非监督学习两大类。

非监督学习主要用于学习聚类规则，没有先验知识或仅有极少的先验知识可供利用，通过多次学习和反复评价，结果合理即可。

监督学习主要用于学习判别函数，判别函数的形式已知时，学习判别函数的有关参数；判别函数的形式未知时，则直接学习判别函数。

训练与监督学习方法相对应，需要掌握足够的与模式类别有关的先验信息，这些先验信息主要通过一定数量的已知类别的模式样本提供，这些样本常称作训练样本集。

用训练样本集对分类器训练成功后，得到了合适的判别函数，才能用于分类。

前面在介绍线性判别函数的同时，已经讨论了如何利用判别函数的性质进行分类，当然，前提是假定判别函数已知。

2）这种分类器只能处理确定可分的情况，包括线性可分和非线性可分。

只要找到一个用于分离的判别函数就可以进行分类。

由于模式在空间位置上的分布是可分离的，可以通过几何方法把特征空间分解为对应不同类别的子空间，故又称为几何分类器。

当不同类别的样本聚集的空间发生重叠现象时，这种分类器寻找分离函数的迭代过程将加长，甚至振荡，也就是说不收敛，这时需要用第4章将要介绍的以概率分类法为基础的概率分类器进行分类。

感知器算法寻找估计参数的方法引言感知器算法是一种基本的机器学习算法，用于分类和模式识别问题。

它使用线性模型和阈值函数来对输入数据进行分类。

在这篇文章中，我们将深入探讨感知器算法中寻找估计参数的方法。

什么是感知器算法？感知器算法是一种二分类线性模型，可以将输入数据进行二分。

它的基本思想是根据输入数据的特征和权重，通过阈值函数进行判断，并输出预测结果。

感知器算法的核心就是通过迭代调整权重和阈值，使得算法能够逐渐逼近真实模型的参数，从而实现对未知数据的分类。

感知器算法的原理感知器算法的原理非常简单：对于一个输入向量X和权重向量W，感知器算法的输出可以表示为：y = sign(W * X + b)其中，sign函数是一个阈值函数，当输入大于等于0时输出1，小于0时输出-1。

W和b是感知器的参数，通过迭代调整可以优化预测效果。

具体来说，感知器算法通过以下步骤进行迭代： 1. 初始化W和b，可以使用随机值或者其他启发式方法。

2. 对于每个输入样本X，计算感知器的输出y。

3. 如果y与期望输出不一致，根据差异调整W和b的值。

4. 重复步骤2和3，直到感知器的输出与期望输出一致或者达到预定的迭代次数。

感知器算法中寻找估计参数的方法为了找到最优的参数W和b，使得感知器算法能够对输入数据进行准确的分类，我们需要使用一种方法来调整参数值。

下面介绍几种常见的方法：1. 原始感知器算法原始感知器算法是感知器算法最早的一种形式。

它使用了简单的梯度下降法来更新参数值。

具体来说，对于错误分类的样本，我们可以这样更新参数值：W_new = W + α * y * Xb_new = b + α * y其中，α是学习率，用于控制每次更新的幅度。

通过迭代计算，不断更新参数值，最终可以找到使感知器算法最优的参数。

2. 对偶感知器算法对偶感知器算法是对原始感知器算法的改进。

它使用了对偶形式的学习算法，从而避免了对每个样本进行更新参数值的操作。

(完整)感知器算法作业编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整)感知器算法作业）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整)感知器算法作业的全部内容。

感知器算法 作业：图为二维平面中的4个点，x 1, x 2∈ω1 ,x 3,x 4∈ω2 ，设计使用感知器算法的线性分类器，步长参数设为1.解:由题知：所有样本写成增广向量形式，进行规范化处理，属于的样本乘以-1步长c=1，任取第一轮迭代：，故 ，故,故，故第二轮迭代：，故 ，故112:[1,0][0,1]T T X X ω=-=234:[01][10]T T X X ω=-=，，2ω12[1,0,1][0,1,1]T T X X =-=34[011][101]T T X X =-=--，，，，(1)[0,0,0]T W =11(1)[0,0,0]0=001T W X -⎡⎤⎢⎥=≤⎢⎥⎢⎥⎣⎦，1(2)(1)[1,0,1]T W W X =+=-20(2)[1,0,1]1=101T W X ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，>(3)(2)[1,0,1]T WW ==-30(3)[1,0,1]1=101T W X ⎡⎤⎢⎥=--≤⎢⎥⎢⎥-⎣⎦，3(4)(3)[1,1,0]T W W X =+=-41(4)[1,1,0]0=101T W X -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦，>(5)(4)[1,1,0]T WW ==-11(5)[1,1,0]0=101T W X -⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，>(6)(5)[1,1,0]T WW ==-20(6)[1,1,0]1=101T W X ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，>(7)(6)[1,1,0]T WW ==- 4x 1x 3x 2x，故，故该轮迭代的分类结果全部正确，故解向量相应的判别函数为function Perceptron%UNTITLED Summary of this function goes here% Detailed explanation goes hereX=[-1 0 0 —1；0 1 1 0；1 1 —1 —1]；W1=[0 0 0］’；t=0；s=1;while s 〉0s=0;for i=1:4if W1’＊X(:，i ）<=0；W1=W1+X （:,i);s=s+1;else W1=W1+0;s=s+0；endendt=t+1;endfprintf('迭代次数为’，t)fprintf （'解向量为\nW='）disp （W1）x1=［-1 0］；x2=［0 1］;plot(x1,x2，'*')hold onx1=[0 1]；x2=［-1 0];plot （x1,x2，’o’）hold onezplot （'—x1+x2’)axis （[—2 2 —2 2])end程序运行结果:30(7)[1,1,0]1=101T W X ⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦，>(8)(7)[1,1,0]T WW ==-41(8)[1,1,0]0=101T W X -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦，>(9)(8)[1,1,0]T WW ==-[1,1,0]T W =-12()dXx x =-+〉> Perceptron 迭代次数为2解向量为W= -11。

实验二感知器准则算法实验一、实验目的贝叶斯分类方法是基于后验概率的大小进行分类的方法，有时需要进行概率密度函数的估计，而概率密度函数的估计通常需要大量样本才能进行，随着特征空间维数的增加，这种估计所需要的样本数急剧增加，使计算量大增。

在实际问题中，人们可以不去估计概率密度，而直接通过与样本和类别标号有关的判别函数来直接将未知样本进行分类。

这种思路就是判别函数法，最简单的判别函数是线性判别函数。

采用判别函数法的关键在于利用样本找到判别函数的系数，模式识别课程中的感知器算法是一种求解判别函数系数的有效方法。

本实验的目的是通过编制程序，实现感知器准则算法，并实现线性可分样本的分类。

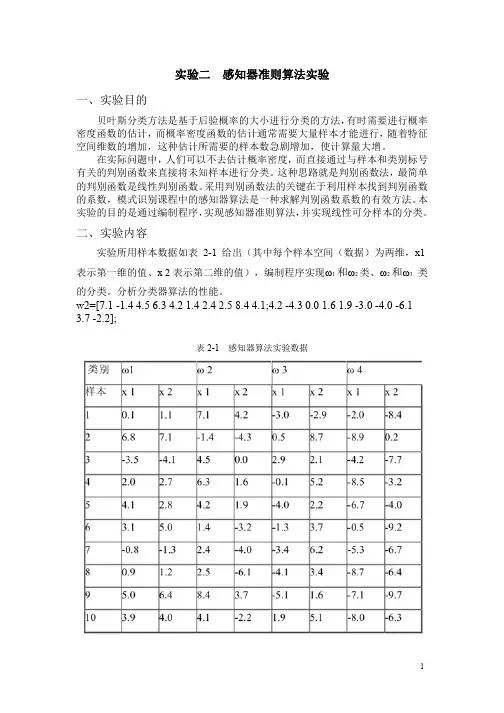
二、实验内容实验所用样本数据如表2-1给出（其中每个样本空间（数据）为两维，x1表示第一维的值、x2表示第二维的值），编制程序实现ω1和ω2类、ω2和ω3类的分类。

分析分类器算法的性能。

w2=[7.1-1.44.56.34.21.42.42.58.44.1;4.2-4.30.01.61.9-3.0-4.0-6.1 3.7-2.2];表2-1感知器算法实验数据三、具体要求1、复习感知器算法；2、写出实现批处理感知器算法的程序1）从v=0开始，将你的程序应用在ω1和ω2的训练数据上。

记下收敛的步数。

2）将你的程序应用在ω2和ω3类上，同样记下收敛的步数。

3）试解释它们收敛步数的差别。

3、提高部分：ω3和ω4的前5个点不是线性可分的，请手工构造非线性映射，使这些点在映射后的特征空间中是线性可分的，并对它们训练一个感知器分类器。

分析这个分类器对剩下的（变换后的）点分类效果如何？四、参考例程及其说明针对ω1、ω2和ω3的分类程序如下：clear%original data%产生第一类、第二类和第三类原始数据，分别赋给w1、w2和w3变量w1=[0.16.8-3.52.04.13.1-0.80.95.03.9;1.17.1-4.12.72.85.0-1.31.2 6.44.0];w2=[7.1-1.44.56.34.21.42.42.58.44.1;4.2-4.30.01.61.9-3.0-6.13.7-2.2];w3=[-3.00.52.9-0.1-4.0-1.3-3.4-4.1-5.11.9;-2.98.72.15.22.23.76.23.4 1.65.1];%normalized%分别产生第一类、第二类和第三类增广样本向量集ww1、ww2和ww3ww1=[ones(1,size(w1,2));w1];ww2=[ones(1,size(w2,2));w2];ww3=[ones(1,size(w3,2));w3];%产生第一类和第二类样本向量的规范化增广样本向量集w12w12=[ww1,-ww2];%%w13=[ww1,-ww3];%%w23=[ww2,-ww3];y=zeros(1,size(w12,2));%产生1x20的行向量，赋给y，初值全为0v=[1;1;1];%给权向量v赋初值k=0;%k为迭代次数，v(0)=[1;1;1]while any(y<=0)for i=1:size(y,2)y(i)=v'*w12(:,i);endv=v+(sum((w12(:,find(y<=0)))'))';k=k+1;endv%显示最终求得的权向量v的值k%迭代次数值figure(1)plot(w1(1,:),w1(2,:),'r.')hold onplot(w2(1,:),w2(2,:),'*')xmin=min(min(w1(1,:)),min(w2(1,:)));xmax=max(max(w1(1,:)),max(w2(1,:)));ymin=min(min(w1(2,:)),min(w2(2,:)));ymax=max(max(w1(2,:)),max(w2(2,:)));xindex=xmin-1:(xmax-xmin)/100:xmax+1;yindex=-v(2)*xindex/v(3)-v(1)/v(3);plot(xindex,yindex)%写出实现批处理感知器算法的程序，从v=0开始，将程序应用在ω2和ω3类上，同样记下收敛的步数。

智能信息技术处理技术实验学生姓名XX班级电信093学号094012003XX成绩指导教师XXX电气与信息工程学院2013年1 月5日实验一感知器实验（1）熟悉感知器网络及相关知识。

（2）熟悉matlab相关的知识。

（3）学会利用matlab实现感知器网络，并将输入样本线性划分。

二、实验要求（1）复习人工智能神经网络中感知器网络的相关内容。

（2）掌握感知器网络的学习算法。

（3）利用matlab建立感知器网络。

三、内容及步骤设计单一感知器神经元来解决一个简单的分类问题：将4个输入向量分为两类，其中两个输入向量对应的目标值为1，另两个对应的目标值为0。

主要程序程序如下：P=[-1 -0.5 0.3 -0.1 50;-0.5 0.5 -0.5 1.0 35];T=[1 1 0 0 0];plotpv(P,T);pause;net=newp([-1 50; -1 40],1);watchon;cla;plotpv(P,T);linehandle=plotpc(net.IW{1},net.b{1});E=1;net=init(net);linehandle=plotpc(net.IW{1},net.b{1});while(sse(E))[net,Y,E]=adapt(net,P,T);linehandle=plotpc(net.IW{1},net.b{1});drawnow;end;pause;watchoff;p=[0.7;1.2];a=sim(net,p);plotpv(p,a);ThePoint=findobj(gca,'type','line');set(ThePoint,'Color','red');hold on;plotpv(P,T);plotpc(net.IW{1},net.b{1});hold off;disp('End of percept1');End of percept1通过实验程序导入后，可得到以下结果：按任意键！再按任意键！就得出了结果。

实验⼀感知器及其应⽤1. 实验⽬的理解感知器算法原理，能实现感知器算法；掌握机器学习算法的度量指标；掌握最⼩⼆乘法进⾏参数估计基本原理；针对特定应⽤场景及数据，能构建感知器模型并进⾏预测。

2. 实验内容安装Pycharm，注册学⽣版。

安装常见的机器学习库，如Scipy、Numpy、Pandas、Matplotlib，sklearn等。

编程实现感知器算法。

熟悉iris数据集，并能使⽤感知器算法对该数据集构建模型并应⽤。

3. 实验报告要求按实验内容撰写实验过程；报告中涉及到的代码，每⼀⾏需要有详细的注释；按⾃⼰的理解重新组织，禁⽌粘贴复制实验内容！4. 作业信息这个作业属于哪个课程这个作业要求在哪学号3180701101 5. 代码#导⼊包import pandas as pdimport numpy as npfrom sklearn.datasets import load_irisimport matplotlib.pyplot as plt%matplotlib inline# load data,下载数据iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)#⽣成表格df['label'] = iris.target# 统计鸢尾花的种类与个数df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']bel.value_counts() # value_counts() 函数可以对df⾥⾯label每个值进⾏计数并且排序，默认是降序结果：2 501 500 50Name: label, dtype: int64#画数据的散点图plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')#将数据的前50个数据绘制散点图plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')#将数据的50-100之间的数据绘制成散点图plt.xlabel('sepal length')#给x坐标命名plt.ylabel('sepal width')#给y坐标命名plt.legend()结果：#对数据进⾏预处理data = np.array(df.iloc[:100, [0, 1, -1]])#iloc函数：通过⾏号来取⾏数据,读取数据前100⾏的第0,1列和最后⼀列X, y = data[:,:-1], data[:,-1]#X为data数据中除去最后⼀列的数据，y为data数据的最后⼀列(y中有两类0和1)y = np.array([1 if i == 1 else -1 for i in y])#将y中的两类（0和1）改为（-1和1）两类# 定义算法# 此处为⼀元⼀次线性⽅程class Model:def __init__(self):self.w = np.ones(len(data[0])-1, dtype=np.float32) #初始w的值self.b = 0 #初始b的值为0self.l_rate = 0.1 #步长为0.1# self.data = datadef sign(self, x, w, b):y = np.dot(x, w) + b #dot进⾏矩阵的乘法运算，y=w*x+breturn y#随机梯度下降法def fit(self, X_train, y_train):is_wrong = False #初始假设有误分点while not is_wrong:wrong_count = 0 #误分点个数初始为0for d in range(len(X_train)):X = X_train[d] #取X_train⼀组及⼀⾏数据y = y_train[d] #取y_train⼀组及⼀⾏数据if y * self.sign(X, self.w, self.b) <= 0: #为误分点self.w = self.w + self.l_rate*np.dot(y, X) #对w和b进⾏更新self.b = self.b + self.l_rate*ywrong_count += 1 #误分点个数加1if wrong_count == 0: #误分点个数为0，算法结束is_wrong = Truereturn 'Perceptron Model!'def score(self):passperceptron = Model()#⽣成⼀个算法对象perceptron.fit(X, y)#将测试数据代⼊算法中结果：'Perceptron Model!'#画出超平⾯x_points = np.linspace(4, 7,10) #⽤于产⽣4,7之间的10点⾏⽮量。

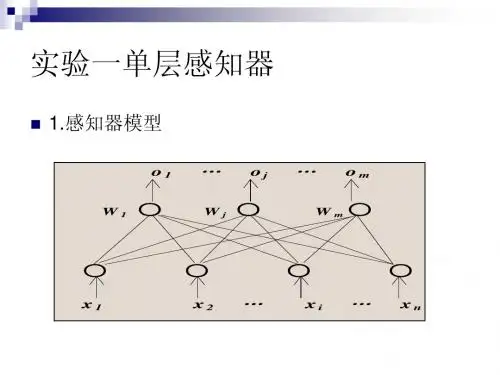
感知器的学习算法1．离散单输出感知器训练算法设网络输入为n 维向量()110-=n x x x ,,, X ，网络权值向量为()110-=n ωωω,,, W ，样本集为(){}i i d ,X ，神经元激活函数为f ，神经元的理想输出为d ，实际输出为y 。

算法如下：Step1：初始化网络权值向量W ；Step2：重复下列过程，直到训练完成：（2.1）对样本集中的每个样本()d ,X ，重复如下过程：（2.1.1）将X 输入网络；（2.1.2）计算)(T =WX f y ；（2.1.3）若d y ≠，则当0=y 时，X W W ⋅+=α；否则X W W ⋅-=α。

2．离散多输出感知器训练算法设网络的n 维输入向量为()110-=n x x x ,,, X ，网络权值矩阵为{}ji n m ω=⨯W ，网络理想输出向量为m 维，即()110-=m d d d ,,, D ，样本集为(){}i i D X ,，神经元激活函数为f ，网络的实际输出向量为()110-=m y y y ,,, Y 。

算法如下：Step1：初始化网络权值矩阵W ；Step2：重复下列过程，直到训练完成：（2.1）对样本集中的每个样本()D X ,，重复如下过程：（2.1.1）将X 输入网络；（2.1.2）计算)(T =XW Y f ；（2.1.3）对于输出层各神经元j （110-=m j ,,, ）执行如下操作： 若j j d y ≠，则当0=j y 时，i ji ji x ⋅+=αωω，110-=n i ,,, ； 否则i ji ji x ⋅-=αωω，110-=n i ,,, 。

3．连续多输出感知器训练算法设网络的n 维输入向量为()110-=n x x x ,,, X ，网络权值矩阵为{}ji n m ω=⨯W ，网络理想输出向量为m 维，即()110-=m d d d ,,, D ，实际输出向量()110-=m y y y ,,, Y ，样本集为(){}i i D X ,，神经元激活函数为f ，ε为训练的精度要求。

感知器算法求判别函数一、 实验目的掌握判别函数的概念和性质，并熟悉判别函数的分类方法，通过实验更深入的了解判别函数及感知器算法用于多类的情况，为以后更好的学习模式识别打下基础。

二、 实验内容学习判别函数及感知器算法原理，在MA TLAB 平台设计一个基于感知器算法进行训练得到三类分布于二维空间的线性可分模式的样本判别函数的实验，并画出判决面，分析实验结果并做出总结。

三、 实验原理3.1 判别函数概念直接用来对模式进行分类的准则函数。

若分属于ω1，ω2的两类模式可用一方程d (X ) =0来划分，那么称d (X ) 为判别函数，或称判决函数、决策函数。

如，一个二维的两类判别问题，模式分布如图示，这些分属于ω1，ω2两类的模式可用一直线方程 d (X )=0来划分。

其中0)(32211=++=w x w x w d X (1) 21,x x 为坐标变量。

将某一未知模式 X 代入（1）中：若0)(>X d ，则1ω∈X 类；若0)(<X d ，则2ω∈X 类；若0)(=X d ，则21ωω∈∈X X 或或拒绝维数=3时：判别边界为一平面。

维数>3时：判别边界为一超平面[1]。

3.2 感知器算法1958年，(美)F.Rosenblatt 提出，适于简单的模式分类问题。

感知器算法是对一种分类学习机模型的称呼，属于有关机器学习的仿生学领域中的问题，由于无法实现非线性分类而下马。

但“赏罚概念（ reward-punishment concept ）” 得到广泛应用，感知器算法就是一种赏罚过程[2]。

两类线性可分的模式类 21,ωω，设X W X d T )(=其中，[]T 121,,,,+=n n w w w w W ，[]T211,,,,n x x x =X 应具有性质（2）对样本进行规范化处理，即ω2类样本全部乘以(－1)，则有：（3）感知器算法通过对已知类别的训练样本集的学习，寻找一个满足上式的权向量。

感知器学习算法感知器的学习是一种有教师的学习方式，其学习规则称之为delta 规则。

若以t表示目标输出，a表示实际输出，则e=t-a网络训练的目的就是要使t a。

当e=0时，得到最优的网络权值和阈值；当e>0时，实际输出小于目标输出，应加大网络权值和阈值；当e<0时，实际输出大于目标输出，就减小网络权值和阈值；其权值阈值学习算法为：W(k+1)=W(k)+ep Tb(k+1)=b(k)+e式中：e----误差向量，e=t-aW---权值向量b----阈值向量p----输入向量k-----表示第k步学习过程例1.1 感知器学习算法（1）构建一个如图的感知器网络，在Matlab中输入命令如下：clear all; % 清空所有变量pr = [-2 2; -2 2; -2 2]; % 输入变量的取值范围net = newp(pr,1); % 生成感知器网络（2）将网络的权值和阈值修改为指定的权值和阈值，命令如下：net.IW{1,1} = [ -1 0 1 ]; % 修改成指定的权值net.b{1} = [ 1 ]; % 修改成指定的阈值（3）给定输入向量P＝[1;2;－1]，目标向量T＝[1]，对网络进行一次调整训练，命令如下：P = [ 1; 2; -1 ]; % 输入向量T = [ 1 ]; % 目标向量net.trainParam.epochs = 1; % 只训练一步net = train(net,P,T); % 训练网络net.IW{1,1} % 查看调整后的权值net.b{1} % 查看调整后的阈值（4）结果分析可以看到新的权值为：0 2 0新的阈值为：2分析：当输入P＝[1 2 －1]时计算a=hardlim(WP+b)a=hardlim(WP+b)=hardlim([-1 0 1]*[1;2;-1]+1)=hardlim(-1*1+0*2+1*(-1)+1)=hardlim(-1)=0而此时目标向量t=1，故误差为e=t－a=1－0=1，由权值调整算法公式：W(k+1)＝W(k)+ep TW(1)＝W(0)+ ep T＝[－1 0 1]+1*[1；2；－1]T＝[－1 0 1]+[1 2 －1]＝[0 2 0]由阈值调整算法公式：b(k+1)＝b(k)+eb(1)＝b(0)+e＝1+1＝2此程序的完整程序，参见perceptron.m----------------------- perceptron.m----------------------- % 感知器学习算法研究用例clear all; % 清空所有变量pr = [-2 2; -2 2; -2 2]; % 输入变量的取值范围net = newp(pr,1); % 生成感知器网络net.IW{1,1} = [ -1 0 1 ]; % 修改成指定的权值net.b{1} = [ 1 ]; % 修改成指定的阈值P = [ 1; 2; -1 ]; % 输入向量T = [ 1 ]; % 目标向量net.trainParam.epochs = 1; % 只训练一步net = train(net,P,T); % 训练网络net.IW{1,1} % 查看调整后的权值net.b{1} % 查看调整后的阈值。

感知器的训练算法实例将属于ω2的训练样本乘以(-1),并写成增广向量的形式。

x①=(0 0 1)T, x②=(0 1 1)T, x③=(-1 0 -1)T, x④=(-1 -1 -1)T第一轮迭代:取C=1,w(1)= (0 0 0)T因w T(1)x①=(0 0 0)(0 0 1)T=0≯0,故w(2)=w(1)+x①=(0 0 1)T 因wT(2)x②=(0 0 1)(0 1 1)T=1>0,故w(3)=w(2)=(0 0 1)T因w T(3)x③=(0 0 1)(-1 0 -1)T=-1≯0,故w(4)=w(3)+x③=(-1 0 0)T 因w T(4)x④=(-1 0 0)(-1 -1 -1)T=1>0,故w(5)=w(4)=(-1 0 0)T 这里,第1步和第3步为错误分类,应“罚”。

因为只有对全部模式都能正确判别的权向量才是正确的解,因此需进行第二轮迭代。

第二轮迭代:因w T(5)x①=(-1 0 0)(0 0 1)T=0≯0,故w(6)=w(5)+x①=(-1 0 1)T 因w T(6)x②=(-1 0 1)(0 1 1)T=1>0,故w(7)=w(6)=(-1 0 1)T因w T(7)x③=(-1 0 1)(-1 0 -1)T=0≯0,故w(8)=w(7)+x③=(-2 0 0)T 因w T(8)x④=(-2 0 0)(-1 -1 -1)T=2>0,故w(9)=w(8)=(-2 0 0)T 需进行第三轮迭代。

第三轮迭代:因w T(9)x①=(-2 0 0)(0 0 1)T=0≯0,故w(10)=w(9)+x①=(-2 0 1)T因w T(10)x②=(-2 0 1)(0 1 1)T=1>0,故w(11)=w(10)=(-2 0 1)T 因wT(11)x③=(-2 0 1)(-1 0 -1)T=1>0,故w(12)=w(11)=(-2 0 1)T 因w T(12)x④=(-2 0 1)(-1 -1 -1)T=1>0,故w(13)=w(12)=(-2 0 1)T 需进行第四轮迭代。

北华大学开放实验报告实验名称：实验一基于感知器的线性分类器设计所属课程：模式识别班级：信息10—1学号：36*名：**实验一、基于感知器算法的线性分类器设计一、实验目的：1. 熟悉感知器算法。

2. 掌握感知准则函数分类器设计方法。

3. 掌握感知器算法，利用它对输入的数据进行分类。

二、实验原理：感知机算法线性分类器的第一个迭代算法是1956年由Frank Rosenblatt提出的，即具有自学习能力的感知器（Perceptron）神经网络模型，用来模拟动物或者人脑的感知和学习能力。

这个算法被提出后，受到了很大的关注。

感知器在神经网络发展的历史上占据着特殊的位置：它是第一个从算法上完整描述的神经网络，是一种具有分层神经网络结构、神经元之间有自适应权相连接的神经网络的一个基本网络。

感知器的学习过程是不断改变权向量的输入，更新结构中的可变参数，最后实现在有限次迭代之后的收敛。

感知器的基本模型结构如图1所示：图1 感知器基本模型其中，X输入，Xi表示的是第i个输入；Y表示输出；W表示权向量；w0是阈值，f是一个阶跃函数。

感知器实现样本的线性分类主要过程是：特征向量的元素x1，x2，……，xk是网络的输入元素，每一个元素与相应的权wi相乘。

，乘积相加后再与阈值w0相加，结果通过f函数执行激活功能，f为系统的激活函数。

因为f是一个阶跃函数，故当自变量小于0时，f= -1；当自变量大于0时，f= 1。

这样，根据输出信号Y，把相应的特征向量分到为两类。

然而，权向量w 并不是一个已知的参数，故感知器算法很重要的一个步骤即是寻找一个合理的决策超平面。

故设这个超平面为w ，满足：12*0,*0,T Tw x x w x x ωω>∀∈<∀∈ （1）引入一个代价函数，定义为：()**T x x YJ w w xδ∈=∑ （2）其中，Y 是权向量w 定义的超平面错误分类的训练向量的子集。

变量x δ定义为：当1x ω∈时，x δ= -1；当2x ω∈时，x δ= +1。