直线和平面的位置关系及平面与平面的平行关系测试题

专题1.4.1 用空间向量研究直线、平面的位置关系4种常见考法归类（80题）题型一 求直线的方向向量题型二 求平面的法向量题型三 用空间向量证明平行问题（一）判断直线、平面的位置关系（二）已知直线、平面的平行关系求参数（三）证明直线、平面的平行问题（1）利用向量方法证明线线平行（2）利用向量方法证明线面平行（3）利用向量方法证明面面平行（4）与平行有关的探索性问题题型四 利用空间向量证明垂直问题（一）判断直线、平面的位置关系（二）已知直线、平面的垂直关系求参数（三）证明直线、平面的垂直问题（1）利用向量方法证明线线垂直（2）利用向量方法证明线面垂直（3）利用向量方法证明面面垂直（4）与垂直有关的探索性问题在空间中,我们取一定点O 作为基点,那么空间中任意一点P 就可以用向量OP 表示.我们把向量OP称为点P 的位置向量.如图.注：线段中点的向量表达式：对于AP → ＝tAB →，当t ＝12时，我们就得到线段中点的向量表达式．设点M 是线段AB 的中点，则OM → ＝12(OA → ＋OB →)，这就是线段AB 中点的向量表达式．2、直线的方向向量如图①,a 是直线l 的方向向量,在直线l 上取AB a =,设P 是直线l上的任意一点,则点P 在直线l 上的充要条件是存在实数t ,使得AP ta = ，即AP t AB=3、空间直线的向量表示式如图②,取定空间中的任意一点O ,可以得到点P 在直线l 上的充要条件是存在实数t ,使OP OA ta =+ ①或OP OA t AB =+ ②①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.4、用向量表示空间平面的位置根据平面向量基本定理，存在唯一实数对(,)x y ，使得AP xa yb =+，如图；取定空间任意一点O ，空间一点P 位于平面ABC 内的充要条件是存在实数x ，y ，使OP OA xAB y AC =++ .5.直线的方向向量若A 、B 是直线上的任意两点，则为直线的一个方向向量；与平行的任意非零向量也是直线的方向向量．【注意】①在直线上取有向线段表示的向量，或在与它平行的直线上取有向线段表示的向量，均为直线的方向向量；②在解具体立体几何题时，直线的方向向量一般不再叙述而直接应用，可以参与向量运算或向量的坐标运算．6.平面的法向量定义：AB l ABl直线l ⊥α，取直线l 的方向向量a ，我们称向量a 为平面α的法向量.给定一个点A 和一个向量a ，那么过点A ，且以向量a.注：一个平面的法向量不是唯一的，在应用时，可适当取平面的一个法向量.已知一平面内两条相交直线的方向向量，可求出该平面的一个法向量.7.平面法向量的性质（1）平面a 的一个法向量垂直于平面a 内的所有向量；（2）一个平面的法向量有无限多个，它们互相平行．8.平面的法向量的求法求一个平面的法向量时，通常采用待定系数法，其一般步骤如下:设向量：设平面a 的法向量为(,,)n x y z =选向量：选取两不共线向量,AB AC列方程组：由00n AB n AC ì×=ïí×=ïî列出方程组解方程组：解方程组00n AB n AC ì×=ïí×=ïî赋非零值：取其中一个为非零值（常取±1)得结论：得到平面的一个法向量.题型一 求直线的方向向量解题策略：1、理解直线方向向量的概念(1)直线上任意两个不同的点都可构成直线的方向向量．(2)直线的方向向量不唯一．（空间中一条直线的方向向量有无数个）．2.求直线的方向向量，首先是找到直线上两点，然后用坐标表示以这两点为起点和终点的向量，该向量就是直线的一个方向向量．1.（23-24高二下·江苏扬州·期末）已知一直线经过点()()2,3,2,1,0,1A B --，下列向量中是该直线的方向向量的为（ ）A ．()1,1,1a =-B ．()1,1,1a =-C ．()1,1,1a =-D ．()1,1,1a =2．【多选】（2024·湖北十堰·高二校联考阶段练习）如图，在正方体1111ABCD A B C D -中，E 为棱1CC上不与1C ，C 重合的任意一点，则能作为直线1AA 的方向向量的是（ ）A ．1AAB ．1C EC ．ABD ．1A A3．（2024·高二课时练习）如图，在四棱锥P －ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD的中点，AB ＝AP ＝1，AD PC 的一个方向向量．4．（2024·高二课时练习）已知直线1l 的一个方向向量为()5,3,2-，另一个方向向量为(),,8x y ，则x =________，y = ________.5．（2024·江苏常州·高二校联考期中）已知直线l 的一个方向向量()2,1,3m =-，且直线l 过A (0，y ，3)和B (－1，2，z )两点，则y －z 等于（ ）A ．0B ．1C ．2D ．36.（23-24高二上·江西赣州·期中）已知直线1l 的方向向量是()2,2,a x =-，直线2l 的方向向量是()2,,2b y =-，若3a = ，且12l l ^，则x y -的值是（ ）A ．-4或0B ．4或1C ．-4D ．07.（23-24高二上·湖北武汉·期中）两条不同直线1l ，2l 的方向向量分别为()1,1,2m =-，()2,2,1n =- ，则这两条直线（ ）A ．相交或异面B ．相交C ．异面D ．平行题型二 求平面的法向量解题策略:1.求平面法向量的方法①设出平面的法向量为n ＝(x ，y ，z )；②找出(或求出)平面内的两个不共线的向量的坐标：a ＝(a 1，a 2，a 3)，b ＝(b 1，b 2，b 3)；③依据法向量的定义建立关于x ，y ，z 的方程组00{=×=×b n a n ④解方程组，取其中的一个解，即得法向量，由于一个平面的法向量有无数多个，故可在方程组的解中取一个最简单的作为平面的法向量．注：利用待定系数法求平面的法向量，求出向量的横、纵、竖坐标是具有某种关系的，而不是具体的值，可设定某个坐标为常数，再表示其他坐标．2.求平面法向量的三个注意点（1）选向量：在选取平面内的向量时，要选取不共线的两个向量（2）取特值：在求n 的坐标时，可令x ，y ，z 中一个为一特殊值得另两个值，就是平面的一个法向量（3）注意0：提前假定法向量n ＝(x ，y ，z )的某个坐标为某特定值时一定要注意这个坐标不为08.【多选】（23-24高二上·浙江绍兴·期中）直线l 的方向向量是(1,2,0)a =，若l a ^，则平面a 的法向量可以是（ ）A ．()1,2,0n = B ．()2,4,0n =--C ．()2,1,0n =-D ．()2,1,2n =-9.（2024·江苏淮安·高二校考阶段练习）空间直角坐标系O xyz -中，已知点()2,0,2A ，()2,1,0B ，()0,2,0C ，则平面ABC 的一个法向量可以是（ ）．A ．()2,1,2B ．()1,2,1-C ．()2,4,2D ．()2,1,2-10．（2024·高二课时练习）已知()()()1,1,0,1,0,1,0,1,1A B C ，则平面ABC 的一个单位法向量是（ ）A ．()1,1,1B ．C ．111(,,)333D ．11.（2023秋·湖北荆州·高二沙市中学校考期末）已知正方体1111ABCD A B C D -的棱长为 1， 以D 为原点， {}1,,DA DC DD为单位正交基底， 建立空间直角坐标系， 则平面1AB C 的一个法向量是（ ）A ．(1,1,1)B ．(1,1,1)-C ．(1,1,1)-D ．(1,1,1)-12．（2024·高二课时练习）在如图所示的坐标系中，1111ABCD A B C D -为正方体，给出下列结论：①直线1DD 的一个方向向量为(0,0,1)；②直线1BC 的一个方向向量为(0,1,1)；③平面11ABB A 的一个法向量为(0,1,0)；④平面1B CD 的一个法向量为(1,1,1).其中正确的个数为（ ）A ．1个B ．2个C ．3个D ．4个13.（2023春·高二课时练习）已知四边形ABCD 是直角梯形，90ABC ∠= ，SA ^平面ABCD ，1SA AB BC ===，12A D =，求平面SCD 的一个法向量．14．（2024·高二课时练习）在棱长为2的正方体1111ABCD A B C D -中，E ，F 分别为棱1111,A D A B 的中点，在如图所示的空间直角坐标系中，求：(1)平面11BDD B 的一个法向量；(2)平面BDEF 的一个法向量.15．（2024·福建龙岩·高二校联考期中）《九章算术》中，将四个面都为直角三角形的四面体称为鳖臑.在鳖臑A BCD -中，AB ^平面BCD ，=90BDC ∠°，BD AB CD ==.若建立如图所示的“空间直角坐标系，则平面ACD 的一个法向量为（ ）A ．()0,1,0B ．()0,1,1C ．()1,1,1D ．()1,1,016．（2024·全国·高三专题练习）放置于空间直角坐标系中的棱长为2的正四面体ABCD 中，H 是底面中心，DH ^平面ABC ，写出：平面BHD 的一个法向量___________；17.（2023春·高二课时练习）如图的空间直角坐标系中，PD 垂直于正方形ABCD 所在平面，2,AB PB =与平面xDy 的所成角为4p，E 为PB 中点，则平面ABE 的单位法向量0n =______．（用坐标表示）18．【多选】（2024·福建宁德·高二校联考期中）已知空间中三个向量()2,1,0AB =，()1,2,1AC =- ，()3,1,1BC =-，则下列说法正确的是（ ）A ．AB与AC 是共线向量B ．与AB同向的单位向量是ö÷÷øC ．BC 在AB方向上的投影向量是()2,1,0--D ．平面ABC 的一个法向量是()1,2,5-19．（2024·四川成都·高二成都市锦江区嘉祥外国语高级中学校考期中）已知()2,0,2a =，()3,0,0= b 分别是平面a ，b 的法向量，则平面a ，b 交线的方向向量可以是（ ）A ．()1,0,0B ．()0,1,0C ．()0,0,1D ．()1,1,120．（2024·湖北·高二校联考阶段练习）已知点()2,6,2A -在平面a 内，()3,1,2=n 是平面a 的一个法向量，则下列点P 中，在平面a 内的是（ ）A ．()1,1,1P -B ．31,3,2P æöç÷èøC ．31,3,2P æö-ç÷èøD ．31,3,4P æö---ç÷èø(1)线线平行的向量表示：设u 1，u 2分别是直线l 1，l 2的方向向量，则l 1∥l 2⇔u 1∥u 2⇔∃λ∈R ，使得u 1＝λu 2.(2)线面平行的向量表示：设u 是直线 l 的方向向量，n 是平面α的法向量，l ⊄α，则l ∥α⇔u ⊥n ⇔u ·n ＝0.注：（1）在平面a 内取一个非零向量a ，若存在实数x ，使得u xa =，且l a Ë，则//l a ．（2）在平面a 内取两个不共线向量,a b ，若存在实数,x y ，使得u xa yb =+，且l a Ë，则//l a ．(3)面面平行的向量表示：设n 1 ，n 2 分别是平面α，β的法向量，则α∥β⇔n 1∥n 2⇔∃λ∈R ，使得n 1＝λn 2 .2．利用向量证明线线平行的思路：证明线线平行只需证明两条直线的方向向量共线即可．3．证明线面平行问题的方法：(1)证明直线的方向向量与平面内的某一向量是共线向量且直线不在平面内；(2)证明直线的方向向量可以用平面内两个不共线向量表示且直线不在平面内；(3)证明直线的方向向量与平面的法向量垂直且直线不在平面内．4．证明面面平行问题的方法：(1)利用空间向量证明面面平行，通常是证明两平面的法向量平行．(2)将面面平行转化为线线平行然后用向量共线进行证明．题型三 用空间向量证明平行问题（一）判断直线、平面的位置关系21．（2024·湖北黄石·高二校考阶段练习）若直线l 的一个方向向量为()257，，a =，平面α的一个法向量为()111，，u ®=-，则（ ）A ．l ∥α或l ⊂αB ．l ⊥αC ．l ⊂αD ．l 与α斜交22．（2024·高二单元测试）若平面a 与b 的法向量分别是()1,0,2a =- ，()1,0,2b =-r，则平面a 与b 的位置关系是（ ）A ．平行B ．垂直C ．相交不垂直D ．无法判断23．（2024·山东菏泽·高二统考期末）已知平面a 与平面ABC 是不重合的两个平面，若平面α的法向量为(2,1,4)m =-，且(2,0,1)AB =- ，(1,6,1)AC = ，则平面a 与平面ABC 的位置关系是________.24．（2024·陕西宝鸡·高二统考期末）在长方体ABCD A B C D -¢¢¢¢中，222AA AB AD ¢===，以点D 为坐标原点，以,,DA DC DD ¢分别为x 轴，y 轴，z 轴建立空间直角坐标系，设对角面ACD ¢所在法向量为(,,)x y z ，则::x y z =__________．25．【多选】（2024·甘肃张掖·高二高台县第一中学校考期中）下列利用方向向量、法向量判断线、面位置关系的结论中正确的是（ ）A ．若两条不重合直线1l ，2l 的方向向量分别是()2,3,1a =- ，()2,3,1b =--，则12//l l B ．若直线l 的方向向量()0,3,0a = ，平面a 的法向量是()0,5,0m =-，则l //a C ．若两个不同平面a ，b 的法向量分别为()12,1,0n =- ，()24,2,0n =-，则//a bD ．若平面a 经过三点()1,0,1A -，()0,1,0B ，()1,2,0C -，向量()11,,n u t =是平面a 的法向量，则1u t +=（二）已知直线、平面的平行关系求参数26.（2023春·四川成都·高二四川省成都市新都一中校联考期中）已知直线l 的方向向量为1,2,4)m (-=，平面a 的法向量为,1,2)n x =(-，若直线l 与平面a 平行，则实数x 的值为（ ）A ．12B ．12-C ．10D ．10-27．（2024·广东广州·高二广州市第九十七中学校考阶段练习）直线l 的方向向量是()1,1,1s =-，平面a 的法向量()222,,n x x x =+- ，若直线//l 平面a ，则x =______．28．（2024·上海浦东新·高二上海南汇中学校考期末）已知直线l 的一个方向向量为(1,2,1)d =-，平面a 的一个法向量(,4,2)n x =-，若//l a ，则实数x =_______．29．（2024·天津蓟州·高二校考期中）直线l 的方向向量是()1,1,1s ®=，平面a 的法向量()21,,n x x x ®=--，若直线l a ∥，则x =___________.30.（2023·全国·高三专题练习）在长方体1111ABCD A B C D -中，E 是1BB 的中点，111B F B D l =，且//EF 平面1ACD ，则实数l 的值为（ ）A ．15B ．14C ．13D ．1231.【多选】（2023春·高二课时练习）在正方体1111ABCD A B C D -中，E 为1AA 中点，若直线//EF 平面11A BC ，则点F 的位置可能是（ ）A ．线段1CC 中点B ．线段BC 中点C ．线段CD 中点D ．线段11C D 中点32．（2024·上海·高二校联考阶段练习）已知平面a 的一个法向量为()11,2,3n =-，平面b 的一个法向量为()22,4,n k =--，若//a b ，则k 的值为______（三）证明直线、平面的平行问题（1）利用向量方法证明线线平行解题策略：向量法证明两条直线平行的方法：两直线的方向向量共线时，两直线平行或共线，否则两直线相交或异面．33.（2023·江苏·高二专题练习）在正方体1111ABCD A B C D -中，点P 在线段1A D 上，点Q 在线段AC 上，线段PQ 与直线1A D 和AC 都垂直，求证：1PQ BD .34.（2023·江苏·高二专题练习）已知长方体1111ABCD A B C D -中，4AB =，3AD =，13AA =，点S 、P 在棱1CC 、1AA 上，且112CS SC =，12AP PA =，点R 、Q 分别为AB 、11D C 的中点．求证：直线PQ ∥直线RS ．35.（2023·江苏·高二专题练习）已知在正四棱柱1111ABCD A B C D -中，1AB =,12AA =，点E 为1CC 的中点，点F 为1BD 的中点．(1)求证：1EF BD ^ 且1EF CC ^ ；(2)求证：EF AC ∥．（2）利用向量方法证明线面平行解题策略：1.利用向量法证明平行问题的两种途径(1)利用三角形法则、平行四边形法则和空间向量基本定理实现向量间的相互转化，得到向量的共线关系．(2)通过建立空间直角坐标系，借助直线的方向向量和平面的法向量进行平行关系的证明．2.利用向量法证明线面平行的三种思路（1）与法向量垂直：设直线l 的方向向量是a ,平面α的法向量是u , 则要证明l //α,只需证明u a ^,即0=×u a .（2）与平面内一个向量平行：在平面内找一个向量与已知直线的方向向量是共线向量即可.（3）用平面内两个不共线向量线性表示：证明这条直线的方向向量能够用平面内两个不共线向量线性表示即可.注：证明直线与平面平行，只需证明直线的方向向量与平面的法向量的数量积为零，或证直线的方向向量与平面内的两个不共线的向量共面，或证直线的方向向量与平面内某直线的方向向量共线，再说明直线在平面外即可．这样就把几何的证明问题转化为向量的运算．36．（2022春·江苏镇江·高二江苏省镇江第一中学校联考期末）如图，三棱柱11ABC AB C -中侧棱与底面垂直，且AB ＝AC ＝2，AA 1＝4，AB ⊥AC ，M ，N ，P ，D 分别为CC 1，BC ，AB ，11B C 的中点．求证：PN ∥面ACC 1A 1；37．（2024·湖北黄冈·浠水县第一中学校考模拟预测）如图，在三棱柱111ABC A B C -中，1BB ^平面ABC ，D ，E 分别为棱AB ，11B C 的中点，2BC =，AB =114A C =.证明：//DE 平面11ACC A ；38.（2023春·高二课时练习）如图，在四面体A BCD -中，AD ^平面BCD ，BC CD ^，2AD =，BD =．M 是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且3AQ QC =．证明：PQ 平面BCD ；39.（2023·全国·高二专题练习）如图，在四棱锥P ABCD -中，底面ABCD 为直角梯形，其中//AD BC .,3,2,AD AB AD AB BC PA ^===^平面ABCD ，且3PA =，点M 在棱PD 上，点N 为BC 中点.若2DM MP =，证明：直线//MN 平面PAB .40．（2024·天津和平·耀华中学校考二模）如图，四棱锥P ABCD -中，侧面PAD 为等边三角形，线段AD 的中点为O 且PO ^底面ABCD ，112AB BC AD ===，π2BAD ABC ∠==∠，E 是PD 的中点．证明：CE ∥平面PAB ；41．（2024·江苏盐城·高二盐城市大丰区南阳中学校考阶段练习）如图，在三棱锥-P ABC 中，PA ^底面ABC ，90BAC ∠=°．点D ，E ，N 分别为棱PA ，PC ，BC 的中点，M 是线段AD 的中点，2PA AC ==，1AB =．求证：//MN 平面BDE ；42．（2024·天津南开·南开中学校考模拟预测）在四棱锥P ABCD -中，PA ^底面ABCD ，且2PA =，四边形ABCD 是直角梯形，且AB AD ^，//BC AD ，2AD AB ==，4BC =，M 为PC 中点，E 在线段BC 上，且1BE =.求证：//DM 平面PAB ；43.（2024·高二课时练习）如图所示，在直角梯形ABCP 中，AP BC ∥，AP AB ^，122AB BC AP ===，D 是AP 的中点，,,E F G 分别为,,PC PD CB 的中点，将PCD V 沿CD 折起，使得PD ^平面ABCD ，试用向量方法证明AP 平面EFG .（3）利用向量方法证明面面平行解题策略：(1)由面面平行的判定定理，要证明面面平行，只要转化为证明相应的线面平行、线线平行即可；(2)若能求出平面b a ，的法向量υm ，,则要证明b a //,只需证明υm //.值得注意的是，虽然空间向量的坐标运算比线性运 算更为简单，但法向量的求解有时比较烦琐，有时在 平面内找与直线平行的向量也不直观，因此求解时，需要灵活选择解题方法.44．（2024·高二课时练习）如图，在长方体1111ABCD A B C D -中，点E ，F ，G 分别在棱1A A ，11A B ，11A D 上，1111A E A F A G ===；点P ，Q ，R 分别在棱1CC ，CD ，CB 上，1CP CQ CR ===．求证：平面//EFG 平面PQR ．45．（2024·上海普陀·曹杨二中校考模拟预测）如图所示，正四棱柱ABCD ﹣A 1B 1C 1D 1的底面边长1，侧棱长4，AA 1中点为E ，CC 1中点为F ．求证：平面BDE ∥平面B 1D 1F ；46.（2023春·高二课时练习）如图所示，平面PAD ^平面ABCD ，四边形ABCD 为正方形，PAD ∆是直角三角形，且2PA AD ==，E ，F ，G 分别是线段PA ，PD ，CD 的中点，求证：平面EFG 平面PBC ．47.（23-24高二上·新疆·期末）已知正方体1111ABCD A B C D -的棱长为a ，M ，N ，E ，F 分别是棱11A D ，11A B ，11D C ，11B C 的中点．求证：平面//AMN 平面BDEF ．（4）与平行有关的探索性问题解题策略：平行关系中的探究性问题探究点的位置时，可先设出对应点的坐标，然后根据面面平行的判定定理转化为向量共线问题或者利用两个平面的法向量共线，建立与所求点的坐标有关的方程，通过解方程可得点的坐标．48.（2023秋·高二课时练习）如图，已知空间几何体P ABCD -的底面ABCD 是一个直角梯形，其中90BAD ∠=,//AD BC ,BA BC a ==,2AD a =，且PA ^底面ABCD ，PD 与底面成30 角．(1)若8BC PD ×= ，求该几何体的体积；(2)若AE 垂直PD 于E ，证明：BE PD ^；(3)在（2）的条件下，PB 上是否存在点F ，使得//EF BD ，若存在，求出该点的坐标；若不存在，请说明理由．49.（2023·全国·高三专题练习）如图，在斜三棱柱111ABC A B C - 中，已知ABC ∆为正三角形，四边形11ACC A 是菱形，D ，E 分别是AC ，1CC 的中点，平面11ACC A ⊥平面ABC .(1)求证：1A C ^平面BDE ；(2)若160C CA ∠= ，在线段1DB 上是否存在点M ，使得//AM 平面BDE ？若存在，求1DM DB 的值，若不存在，请说明理由．50.（2023·江苏·高二专题练习）如图所示，在直三棱柱111ABC A B C -中，3AC =，4BC =，5AB =，14AA =.(1)求证：1AC BC ^；(2)在AB 上是否存在点D ，使得1//AC 平面1CDB ，若存在，确定D 点位置并说明理由，若不存在，说明理由．51.（2022·高二课时练习）如图，在正方体1111ABCD A B C D -中，O 为底面ABCD 的中心，P 是1DD 的中点．在棱1CC 上是否存在一点Q ，使得平面1//D BQ 平面PAO ？若存在，指出点Q 的位置；若不存在，请说明理由．(1)线线垂直的向量表示：设 u 1，u 2 分别是直线 l 1 , l 2 的方向向量，则l 1⊥l 2⇔u 1⊥u 2⇔u 1·u 2＝0.(2)线面垂直的向量表示：设u 是直线 l 的方向向量，n 是平面α的法向量， l ⊄α，则l ⊥α⇔u ∥n ⇔∃λ∈R ，使得u ＝λn .注：在平面a 内取两个不共线向量,a b ，若0a u b u ×=×= .则l a ^．(3)面面垂直的向量表示：设n 1，n 2 分别是平面α，β的法向量，则α⊥β⇔n 1⊥n 2⇔n 1·n 2＝0.2.利用向量法证明空间中的平行、垂直可以通过建立空间直角坐标系，把要证的空间中的平行与垂直问题转化为证明空间向量之间的平行和垂直问题．破解此类题的关键点如下：①合理建系，抓住空间几何体的结构特征，充分利用图形中的垂直关系(或在图形中构造垂直关系)建立空间直角坐标系．②确定坐标，利用题设条件写出相关点的坐标，进而获得相关向量的坐标．③准确运算，验证两向量平行或垂直的条件成立．④得出结论，由运算结果说明原问题得证．题型四 利用空间向量证明垂直问题（一）判断直线、平面的位置关系52．（2021秋·北京·高二校考期中）直线12,l l 的方向向量分别为(1,3,1),(8,2,2)a b =--= ，则（ ）A ．12l l ^B ．1l ∥2lC ．1l 与2l 相交不平行D ．1l 与2l 重合53．（2024·北京·高二校考阶段练习）若直线l 的方向向量为e (2,3,1)=- ，平面a 的法向量为311,,22n æö=--ç÷èø ，则直线l 和平面a 位置关系是（ ）A ．l a ^B ．//l a C ．l a ÌD ．不确定54．【多选】（2024·广东珠海·高二珠海市斗门区第一中学校考期末）已知v 为直线l 的方向向量,12,n n 分别为平面a ,b 的法向量（a ,b 不重合）,那么下列说法中正确的有（ ）．A ．12n n a bÛ∥∥ B ．12n n a b ^Û^ C ．1v n l Û a ∥∥D ．1v n l ^Û^ a55.（23-24高二上·浙江·期中）如图，在正方体1111ABCD A B C D -中，不能互相垂直的两条直线是（ ）A ．1AB 和1AC B ．1A B 和1CD C ．1C D 和1B C D ．1A B 和11B C 56．（2024·江苏·高二南师大二附中校联考阶段练习）下列利用方向向量､法向量判断线､面位置关系的结论中，正确的是（ ）A ．两条不重合直线12,l l 的方向向量分别是()()2,3,1,2,3,1a b =-=-- ，则12l l ∥B ．直线l 的方向向量()112a ,,=- ，平面a 的法向量是()6,4,1u =- ，则l a^C ．两个不同的平面,a b 的法向量分别是()()2,2,1,3,4,2u v =-=- ，则a b^D ．直线l 的方向向量()0,3,0a = ，平面a 的法向量是()0,5,0u =- ，则l a∥57．【多选】（2024·高二课时练习）下列命题是真命题的有( )A ．A ，B ，M ，N 是空间四点，若,,BA BM BN 不能构成空间的一个基底，那么A ，B ，M ，N 共面B ．直线l 的方向向量为()1,1,2a =- ，直线m 的方向向量12,1,2b æö=-ç÷èør 为，则l 与m 垂直C ．直线l 的方向向量为()1,1,2a =- ，平面α的法向量为10,1,2n æö=ç÷èø ，则l ⊥αD ．平面α经过三点()()()1,0,1,0,1,0,1,2,0A B C --，()1,,=r n u t 是平面α的法向量，则u +t ＝1（二）已知直线、平面的垂直关系求参数58.（2023·全国·高三专题练习）设直线12,l l 的方向向量分别为(1,2,2),(2,3,)a b m =-=- ，若12l l ^，则实数m等于（）A ．1B ．2C ．3D ．459．（2024·北京海淀·高二中央民族大学附属中学校考开学考试）已知平面a 的法向量为()1,2,0n = ，直线l的方向向量为v ，则下列选项中使得l a ^的是（ ）A ．()2,1,0v =- B ．()2,1,0v = C ．()2,4,0v = D ．()1,2,0v =- 60．（江苏省扬州市2023-2024学年高二下学期6月期末数学试题）已知直线l 的方向向量为()2,1,2e =- ，平面a 的法向量为()()2,,,n a b a b a b =--+ÎR .若l a ^，则3a b +的值为（ ）A ．5-B ．2-C ．1D ．461．（2024·高二课时练习）已知()()3,,,R u a b a b a b =-+Î 是直线l 的方向向量，()1,2,4n =r 是平面a 的法向量．若l a ^，则ab =______．62．（2024·广东珠海·高二珠海市实验中学校考阶段练习）若直线l 方向向量为()2,1,m ，平面a 的法向量为11,,22æöç÷èø，且l a ^，则m 为（ ）A ．1B ．2C ．4D ．54-63.（2023秋·北京石景山·高二统考期末）已知(2,,)(,)=-+-Î m a b a b a b R 是直线l 的方向向量，(2,1,2)=- n 是平面a 的法向量．若l a ^，则下列选项正确的是（ ）A ．340a b --=B ．350a b --=C ．13,22a b =-=D ．13,22a b ==-64．（2024·江苏盐城·高二江苏省响水中学校考阶段练习）如图，在正三棱锥D -ABC 中，AB =2DA =，O 为底面ABC 的中心，点P 在线段DO 上，且PO DO l =uuu r uuu r ，若PA ^平面PBC ，则实数l =（ ）A ．12B ．13-C D 65.（2023春·高二课时练习）如图，在棱长为2的正方体1111ABCD A B C D -中，,E F 分别为棱11B C ，1BB 的中点，G 为面对角线1A D 上的一点，且1(01)DG DA l l =££ ,若1A C ^平面EFG ，则l =（ ）A ．14B ．13C D ．1266.（2023·江苏·高二专题练习）如图，在四棱锥E ABCD -中，平面ADE ^平面ABCD ，O ，M 分别为AD ，DE 的中点，四边形BCDO 是边长为1的正方形，AE DE =，AE DE ^．点N 在直线AD 上，若平面BMN ^平面ABE ，则线段AN 的长为_________．（三）证明直线、平面的垂直问题（1）利用向量方法证明线线垂直解题策略：利用空间向量证明两直线垂直的常用方法及步骤(1)基向量法：①选取三个不共面的已知向量(通常是它们的模及其两两夹角为已知)为空间的一个基底；②把两直线的方向向量用基底表示；③利用向量的数量积运算，计算出两直线的方向向量的数量积为0；④由方向向量垂直得到两直线垂直．(2)坐标法：①根据已知条件和图形特征，建立适当的空间直角坐标系，正确地写出各点的坐标；②根据所求出点的坐标求出两直线方向向量的坐标；③计算两直线方向向量的数量积为0；④由方向向量垂直得到两直线垂直．67.【多选】（2023春·江苏盐城·高二盐城中学校考期中）点P 在正方体1111ABCD A B C D -的侧面11CDD C 及其边界上运动，并保持1BP A C ^，若正方体边长为，则1A P 的可能取值是（ ）A B C D 68.（2023秋·高二课时练习）如图，在棱长为1的正方体1111ABCD A B C D -中，,E F 分别是1DD BD 、的中点，建立适当的空间直角坐标系，证明：1EF B C ^．69.（2023·江苏·高二专题练习）如图，在直棱柱111ABC A B C -中，12AA AB AC ===，π2BAC ∠=，,,D E F 分别是11A B ，1CC ，BC 的中点．求证：AE DF ^；70.（2023·四川雅安·统考模拟预测）已知下面给出的四个图都是各棱长均相等的直三棱柱，A 为一个顶点，D ，E ，F 分别是所在棱的中点．则满足直线AD EF ^的图形个数是（ ）A ．1B ．2C ．3D ．4（2）利用向量方法证明线面垂直解题策略：向量法证明线面垂直的两种思路(1)根据线面垂直的判定定理证明：求出直线的方向向量，在平面内找两条相交直线，并分别求出表示它们的方向向量，计算两组向量的数量积为0，得到该直线与平面内的两条相交直线都垂直．(2)法向量法：求出直线的方向向量与平面的法向量，用向量法判断直线的方向向量与平面的法向量平行．71．（2024·高二课时练习）如图，在三棱锥P －ABC 中，AB ＝AC ，D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．已知BC ＝8，PO ＝4，AO ＝3，OD ＝2.(1)证明：AP ⊥BC ；(2)若点M 是线段AP 上一点，且AM ＝3，试证明AM ⊥平面BMC .72.（2023春·高二课时练习）如图所示，正三棱柱111ABC A B C -的所有棱长都为2，D 为1CC 的中点．求证：1AB ^平面1A BD .73．（2024·安徽合肥·合肥市第八中学校考模拟预测）如图，在三棱柱111ABC A B C -中，底面ABC V 是等腰三角形，且π,26ACB AB AC ∠===，又侧棱1BB =面对角线116A C A B ==，点,D F 分别是棱11,A B CB 的中点，11344AE AC AC =+ .证明：1B E ^平面AEF ；74．（2024·河北唐山·唐山市第十中学校考模拟预测）如图，在四棱台1111ABCD A B C D -中，平面11ADD A ^平面ABCD ，底面ABCD 为正方形，2AD =，11111DD D A A A ===.求证：1AD ^平面11CDD C .（3）利用向量方法证明面面垂直解题策略：证明面面垂直的两种方法(1)常规法：利用面面垂直的判定定理转化为线面垂直、线线垂直去证明．(2)向量法：证明两个平面的法向量互相垂直．75．（2024秋·广东深圳·高二深圳外国语学校校考期末）已知：在四棱锥P ABCD -中，底面ABCD 为正方形，侧棱PA ^平面ABCD ，点M 为PD 中点，1PA AD ==．求证：平面MAC ^平面PCD ；76．（2024·高二课时练习）如图所示，△ABC 是一个正三角形，EC ⊥平面ABC ，BD ∥CE ，且CE ＝CA ＝2BD .求证：平面DEA ⊥平面ECA .77．（2024·全国·高二专题练习）如图，在四棱锥P ABCD -中，PA ^平面ABCD ，底面ABCD 是梯形，点E 在BC 上，,,22248AD BC AB AD BC AB AD AP BE ^=====∥．求证：平面PDE ^平面PAC ；（4）与垂直有关的探索性问题解题策略：解决立体几何中探索性问题的基本方法(1)通常假设题中的数学对象存在(或结论成立)，然后在这个前提下进行逻辑推理．(2)探索性问题的关键是设点：①空间中的点可设为(x ，y ，z )；②坐标平面内的点其中一个坐标为0，如xOy 面上的点为(x ，y,0)；③坐标轴上的点两个坐标为0，如z 轴上的点为(0,0，z )；④直线(线段)AB 上的点P ，可设为AP → ＝λAB →，表示出点P 的坐标，或直接利用向量运算．78．（2024·江苏连云港·高二统考期中）如图，在多面体ABCDE 中，ABC V ，BCD △，CDE V 都是边长为2的等边三角形，平面ABC ^平面BCD ，平面CDE ^平面BCD ．(1)判断A ，B ，D ，E 四点是否共面，并说明理由；(2)在ABC V 中，试在边BC 的中线上确定一点Q ，使得DQ ^平面BCE ．79.（2023春·广东汕尾·高二陆丰市龙山中学校考阶段练习）如图，在四棱锥P ABCD -中，PA ^平面ABCD ，正方形ABCD 的边长为2，E 是PA 的中点．(1)求证：//PC 平面BDE ．(2)若2PA =，线段PC 上是否存在一点F ，使AF ^平面BDE ？若存在，求出PF 的长度；若不存在，请说明理由．80.（2023春·高二课时练习）如图1，在边长为2的菱形ABCD 中，60,BAD DE AB ∠=^ 于点E ，将ADE △沿DE 折起到1A DE △的位置，使1A D BE ^，如图2．(1)求证：1A E ^平面BCDE ；(2)在线段BD 上是否存在点P ，使平面1A EP ^平面1A BD ？若存在，求BP BD 的值；若不存在，说明理由．。

直线与平面平行的判定和性质年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共26题，题分合计130分)1.直线a //平面M ,直线b ⊂/M ,那么a //b 是b //M 的 条件. A.充分而不必要 B.必要而不充分 C.充要 D.不充分也不必要2.已知l 、m 、n 为两两垂直且异面的三条直线，过l 作平面α与m 垂直，则直线n 与平面α的关系是A.n //αB.n //α或n ⊂αC.n ⊂α或n 不平行于αD.n ⊂α3.能保证直线a 与平面α平行的条件是A.b a b a //，，αα⊂⊄B.b a b //，α⊂C.c a b a c b //////，，，αα⊂D.b D b C a B a A b ∈∈∈∈⊂，，，，α且BD AC =4.如果直线a 平行于平面α,则A.平面α内有且只有一直线与a 平行B.平面α内无数条直线与a 平行C.平面α内不存在与a 平行的直线D.平面α内的任意直线与直线a 都平行5.如果两直线a ∥b ,且a ∥平面α,则b 与α的位置关系A.相交B.α//bC.α⊂bD.α//b 或α⊂b6.下列命题正确的个数是（1）若直线l 上有无数个点不在平面α内,则l ∥α（2）若直线l 与平面α平行,则l 与平面α内的任意一直线平行（3）两条平行线中的一条直线与一个平面平行,那么另一条也与这个平面平行 （4）若一直线a 和平面α内一直线b 平行,则a ∥α A.0个 B.1个 C.2个 D.3个7.若直线a ⊥b ,且a ∥平面α,则直线b 与平面α的位置关系是A.b ⊂αB.b ∥αC.b ⊂α或b ∥αD.b 与α相交或b ∥α或b ⊂α都有可能8.已知α､β是两个不同的平面,在下列条件中,可判断平面α与平面β平行的是A.α､β都垂直于平面γB.a ､b 是α内两条直线,且a ∥β,b ∥βC.α内不共线的三个点到β的距离相等D.a ､b 为异面直线,且a ∥α,b ∥α,a ∥β,b ∥β9.下列命题正确的个数是①若直线l 上有无数个点不在平面α内，则l ∥α②若直线l 与平面α平行，则l 与平面α内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行，那么另一条直线也与这个平面平行 ④若直线l 与平面α平行，则l 与平面α内的任意一条直线都没有公共点 A.0个 B.1个 C.2个 D.3个10.b 是平面α外的一条直线，下列条件中可得出b ∥α是A.b 与α内的一条直线不相交B.b 与α内的两条直线不相交C.b 与α内的无数条直线不相交D.b 与α内的所有直线不相交11.已知直线l 1、l 2，平面α，l 1∥l 2,l 1∥α，则l 2与α的位置关系是A.l 2∥αB.l 2⊂αC.l 2∥α或l 2⊂αD.l 2与α相交12.已知两条相交直线a 、b ，a ∥平面α，则b 与α的位置关系A.b ∥αB.b 与α相交C.b ⊂αD.b ∥α或b 与α相交13.下列命题中正确的是①过一点，一定存在和两条异面直线都平行的平面②垂直于同一条直线的一条直线和一个平面平行③若两条直线没有公共点，则过其中一条直线一定有一个平面与另一条直线平行 A.① B.③ C.①③ D.①②③14.a、b为平面M外的两条直线，在a∥M的前提下，a∥b是b∥M的A.充要条件B.充分条件C.必要条件D.以上情况都不15.α和β是两个不重合的平面,在下列条件中可判定平面α与β平行的是A.α､β都垂直于平面γB.α内不共线的三点到β的距离相等C.l,m是α平面内的直线,且l∥β,m∥βD.l､m是两条异面直线且l∥α,m∥α,m∥β,l∥β16.在空间中，下述命题正确的A.若直线a∥平面M，直线b⊥直线a，则直线b⊥平面MB.若平面M∥平面N，则平面M内任意一条直线a∥平面NC.若平面M与平面N的交线为a，平面M内的直线b⊥直线a，则直线b⊥平面ND.若平面N内的两条直线都平行于平面M，则平面N∥平面M17.设直线a在平面M内，则直线M平行于平面N是直线a平行于平面N的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件18.设a、b是平面α外的任意两条直线，则"a、b长相等"是"a、b在平面α内的射影长相等"的A.既不充分也不必要条件B.充分必要条件C.必要但不充分条件D.充分但不必要条件19.如果平面α和直线l满足l和α内两条平行直线垂直,则A.l αB.l∥αC.l与α相交D.以上都不对20.如果一条直线和一个平面平行，为了使夹在它们之间的两条线段的长相等，以下结论正确的是A.其充分条件是这两条线段平行B.其必要条件是这两条线段平行C.其充要条件是这两条线段平行D.其必要条件是这两条线段平行21.直线a∥平面α,平面α内有n条直线交于一点,那么这几条直线中与直线a平行的A.至少有一条B.至多有一条C.有且只有一条D.不可能有22.若直线m平面α,则“平面α∥平面β”是“直线m∥平面β”的A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件23.平行于同一个平面的两条直线的位置关系是A.平行B.相交C.异面D.平行或相交或异面24.下列四个命题中假命题的个数是①两条直线都和同一个平面平行，则这两条直线平行②两条直线没有公共点，则这两条直线平行③两条直线都和第三条直线垂直，则这两条直线平行④一条直线和一个平面内无数条直线没有公共点，则这条直线和这个平面平行A.4B.3C.2D.125.如果一条直线和一个平面平行,为了使夹在它们之间的两条线段的长相等,以下结论正确的是A.其充分条件是这两条线段平行B.其必要条件是这两条线段平行C.其充要条件是这两条线段平行D.其必要条件是这两条线段平行26.直线与平面平行的充要条件是这条直线与平面内的A.一条直线不相交B.两条直线不相交C.任意一条直线都不相交D.无数条直线不相交二、填空题(共6题，题分合计25分)1.如图，空间四边形ABCD 中，E 、H 分别是AB 、AD 的中点，F 、G 分别是CB 、CD 上的点.且32==CD CG CB CF ,若BD =6 cm ，梯形EFGH 的面积为28 cm 2，则平行线EH 与FG 间的距离为_______.2.一条直线与平面α相交于点A ，在平面α内不过A 点的直线与这条直线所成角的最大值为_________.3.正方体ABCD -A 1B 1C 1D 1中，E 为DD 1的中点，则BD 1与过点A 、E 、C 的平面的位置关系是__________.4.几何体ABCD -A 1B 1C 1D 1是棱长为A 的正方体，M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点，P 是上底面的棱AD 上的一点，AP ＝31a ，过P 、M 、N 的平面交上底面于PQ ，Q 在CD 上，则PQ ＝___________.5.如果两条直线a 与b 互相平行，且a ∥平面α，那么b 与α的位置关系是 ．6.直线a ∥平面α，直线b 、c 都在α 内且a ∥b ∥c ，若a 到b ， c 的距离分别为d 1、d 2，且d 1＞d 2，则直线a 到α 的距离d 的取值范围是___________.三、解答题(共12题，题分合计112分)1.求证:若直线l与平面α有一个公共点,且l平行于α内的一条直线,则l α..2.如图，P是△ABC所在平面外一点，M∈PB，试过AM作一平面平行于BC，并说明画法的理论依据Array3.设AB、CD为夹在两个平行平面α、β之间线段,且直线AB、CD为异面直线,М、P分别为AB、CD的中点,求证:MP ∥α.4.ABCD-A1B1C1D1是棱长为a的正方体，(1)画出过A、C、B1的平面与下底面的交线l；(2)求l与直线AC的距离.5.正方体ABCD-A1B1C1D1中，侧面对角线AB1、BC1分别有E、F，且B1E=C1F，求证：EF∥平面ABCD.6.平面外的两条平行直线中的一条平行于这个平面，那么另一条直线也平行于这个平面.7.设a、b是异面直线，自AB的中点O作平面α与a、ｂ分别平行，M、N分别是a、b上的任意两点，MN与α交于点P，求证：P是MN的中点.8.求证：如果一条直线和两个相交的平面都平行，那么这条直线和它们的交线平行.9.α∩β=c,α∩γ=b,β∩γ=a,若直线a∥直线b,你能得到什么结论?10.如图，正方体ABCD-A1B1C1D1中，E在AB1上，F在BD上，且B1E＝BF.求证：EF∥平面BB1C1C.11.如图，在正方体ABCD-A1B1C1D1中，点N在BD上，点M在B1C上，并且CM=DN.求证:MN∥平面AA1B1B.12.如图，平面EFGH分别平行于CD、AB，E、F、G、H分别在BD、BC、AC、AD上，且CD＝a，AB＝b，CD⊥AB.(1)求证：EFGH是矩形.(2)点E在什么位置时，EFGH的面积最大.直线与平面平行的判定和性质答案一、选择题(共26题，合计130分)1.答案：A2.答案：A3.答案：A4.答案：B5.答案：D6.答案：A7.答案：D8.答案：B9.答案：B10.答案：D11.答案：C12.答案：D13.答案：B14.答案：B15.答案：D16.答案：B17.答案：A18.答案：A19.答案：D20.答案：A21.答案：B22.答案：A23.答案：D24.答案：A25.答案：A26.答案：C二、填空题(共6题，合计25分)1.答案：8 cm2.答案：90°3.答案：BD1∥平面AEC4.答案：a2 325.答案：b∥α或b α6.答案：) ,0(2 d三、解答题(共12题，合计112分)1.答案：见注释2.答案：见注释3.答案：见注释4.答案：. 26 a5.答案：见注释6.答案：见注释7.答案：见注释8.答案：见注释9.答案：见注释10.答案：见注释11.答案：见注释12.答案：（1）见注释（2）E为BD的中点时。

第二章综合素能检测本试卷分第Ⅰ卷（选择题)和第Ⅱ卷(非选择题）两部分．满分150分．考试时间120分钟．第Ⅰ卷（选择题共60分）一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．直线l1∥l2，在l1上取3个点，在l2上取2个点，由这5个点能确定平面的个数为错误!（）A．5B．4C．9D．1［答案] D[解析］由经过两条平行直线有且只有一个平面可知分别在两平行直线上的5个点只能确定一个平面．2．教室内有一直尺，无论怎样放置，在地面总有这样的直线，使得它与直尺所在直线错误!（)A．平行B．垂直C．相交D．异面[答案] B[解析］当直尺垂直于地面时，A不对;当直尺平行于地面时,C不对；当直尺位于地面上时，D不对．3．已知m、n是两条不同直线，α、β是两个不同平面，则下列命题正确的是错误!(）A．若α、β垂直于同一平面，则α与β平行B．若m、n平行于同一平面，则m与n平行C．若α、β不平行．．．与β平行的直线．．．,则在α内不存在D．若m、n不平行．．．垂直于同一平面．．．，则m与n不可能[答案］ D［解析]A项，α、β可能相交，故错误；B项，直线m、n的位置关系不确定，可能相交、平行或异面,故错误；C项，若m⊂α，α∩β＝n,m∥n，则m∥β，故错误;D项，假设m、n垂直于同一平面,则必有m∥n，所以原命题正确，故D项正确．4．已知α、β是两个平面,直线l⊄α，l⊄β,若以①l⊥α；②l∥β；③α⊥β中两个为条件,另一个为结论构成三个命题，则其中正确的命题有错误!（)A．①③⇒②；①②⇒③B．①③⇒②；②③⇒①C．①②⇒③；②③⇒①D．①③⇒②；①②⇒③;②③⇒①［答案] A［解析]因为α⊥β，所以在β内找到一条直线m，使m⊥α，又因为l⊥α,所以l∥m.又因为l⊄β，所以l∥β,即①③⇒②；因为l∥β，所以过l可作一平面γ∩β＝n，所以l∥n，又因为l⊥α，所以n⊥α，又因为n⊂β，所以α⊥β，即①②⇒③.5．如图，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，BC1⊥AC，若过C1作C1H⊥平面ABC，垂足为H，则点H一定在导学号 92180601（)A．直线AC上B．直线AB上C．直线BC上D．△ABC的内部[答案] B[解析］∵∠BAC＝90°,∴BA⊥AC．又∵BC1⊥AC,∴AC⊥平面ABC1，∴平面ABC⊥平面ABC1.∵平面ABC∩平面ABC1＝AB，∴C1在面ABC上的射影在直线AB上．6．设直线l⊂平面α，过平面α外一点A与l，α都成30°角的直线有错误!（) A．1条B．2条C．3条D．4条[答案] B［解析］如图，和α成30°角的直线一定是以A为顶点的圆锥的母线所在直线,当∠ABC＝∠ACB＝30°且BC∥l时，直线AC，AB都满足条件，故选B．7．（2016·浙江文）已知互相垂直的平面α、β交于直线l.若直线m、n满足m∥α，n⊥β，则错误!(）A．m∥l B．m∥nC．n⊥l D．m⊥n[答案］ C[解析]选项A，只有当m∥β或m⊂β时,m∥l；选项B,只有当m⊥β时,m∥n；选项C,由于l⊂β,∴n⊥l；选项D，只有当m∥β或m⊂β时，m⊥n,故选C．8．（2016·南安一中高一检测)如图，在正方体ABCD－A1B1C1D1中，M、N分别为棱BC 和棱CC1的中点，则异面直线AC与MN所成的角为错误!（）A．30°B．45°C．60°D．90°[答案] C[解析］如图，连接A1C1、BC1、A1B．∵M、N分别为棱BC和棱CC1的中点，∴MN∥BC1。

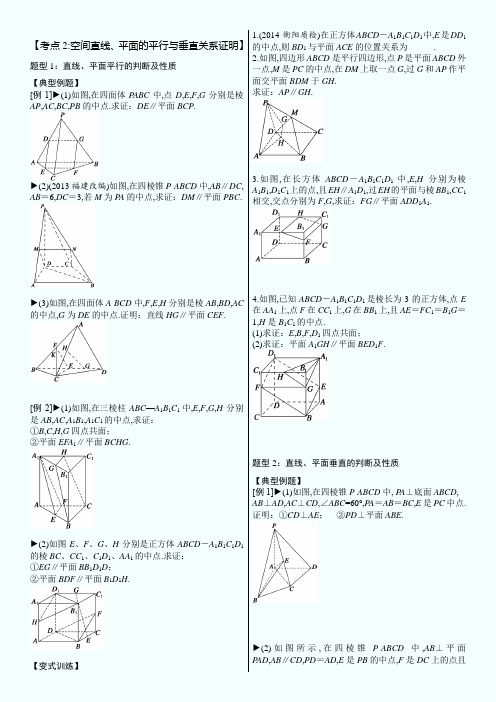
【考点2:空间直线、平面的平行与垂直关系证明】题型1：直线、平面平行的判断及性质【典型例题】[例1]►(1)如图,在四面体P ABC中,点D,E,F,G分别是棱AP,AC,BC,PB的中点.求证：DE∥平面BCP .►(2)(2013福建改编)如图,在四棱锥P-ABCD中,AB∥DC, AB＝6,DC＝3,若M为P A的中点,求证：DM∥平面PBC . ►(3)如图,在四面体A-BCD中,F,E,H分别是棱AB,BD,AC 的中点,G为DE的中点.证明：直线HG∥平面CEF .[例2]►(1)如图,在三棱柱ABC—A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点,求证：①B,C,H,G四点共面；②平面EF A1∥平面BCHG .►(2)如图E、F、G、H分别是正方体ABCD－A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证：①EG∥平面BB1D1D；②平面BDF∥平面B1D1H .【变式训练】1.(2014·衡阳质检)在正方体ABCD－A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为______.2.如图,四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证：AP∥GH .3.如图,在长方体ABCD－A1B1C1D1中,E,H分别为棱A1B1,D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G,求证：FG∥平面ADD1A1.4.如图,已知ABCD－A1B1C1D1是棱长为3的正方体,点E 在AA1上,点F在CC1上,G在BB1上,且AE＝FC1＝B1G＝1,H是B1C1的中点.(1)求证：E,B,F,D1四点共面；(2)求证：平面A1GH∥平面BED1F .题型2：直线、平面垂直的判断及性质【典型例题】[例1]►(1)如图,在四棱锥P-ABCD中, P A⊥底面ABCD, AB⊥AD,AC⊥CD,∠ABC=60°,P A＝AB＝BC,E是PC中点. 证明：①CD⊥AE；②PD⊥平面ABE .►(2)如图所示,在四棱锥P-ABCD中,AB⊥平面P AD,AB∥CD,PD＝AD,E是PB的中点,F是DC上的点且DF＝12AB,PH为△P AD中AD边上的高.①证明：PH⊥平面ABCD；②证明：EF⊥平面P AB.[例2]►(1)[2014·辽宁文]如图所示,△ABC和△BCD所在平面互相垂直,且AB＝BC＝BD＝2,∠ABC＝∠DBC＝120°,E,F,G分别为AC,DC,AD的中点.(I)求证：EF⊥平面BCG；(II)求三棱锥D -BCG的体积.►(2)(2012·课标全国)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB＝90°,AC＝BC＝12AA1,D是棱AA1的中点.(I)证明：平面BDC1⊥平面BDC；(II)平面BDC1分此棱柱为两部分,求这两部分体积的比.►(3)(2015·大庆质检) 如图,四棱锥P-ABCD中,PD⊥平面ABCD,PD＝DC＝BC＝1,AB＝2,AB∥DC,∠BCD＝90°.①求证：PC⊥BC；②求点A到平面PBC的距离.【变式训练】1.如图,四棱锥P—ABCD中,P A⊥底面ABCD,AB⊥AD,点E 在线段AD上,且CE∥AB. (1)求证：CE⊥平面P AD；(2)若P A=AB=1,AD=3,CD=2,∠CDA=45°,求四棱锥P-ABCD的体积.2.[2014·福建文]如图所示,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD.(1)求证：CD⊥平面ABD；(2)若AB=BD=CD=1,M为AD中点,求三棱锥A -MBC的体积.3.(2015·唐山统考)如图,在三棱锥P-ABC中,P A＝PB＝AB ＝BC,∠PBC＝90°,D为AC的中点,AB⊥PD.(1)求证：平面P AB⊥平面ABC；(2)如果三棱锥P-BCD的体积为3,求P A.4.[2014·课标Ⅰ文]如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.(1)证明：B1C⊥AB；(2)若AC⊥AB1,∠CBB1＝60°,BC＝1,求三棱柱ABC-A1B1C1的高.☆题型3：直线、平面平行与垂直关系的综合【典型例题】[例1]►(1)已知l,m是两条不同的直线,α,β是两个不同的平面,下列命题中真命题是(写出序号).①若l⊂α,m⊂α,l∥β,m∥β,则α∥β；②若l⊂α,l∥β,α∩β＝m,则l∥m；③若α∥β,l∥α,则l∥β；④若l⊥α,m∥l,α∥β,则m⊥β.►(2)(2014·辽宁)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥nB.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α►(3)(2015·江西七校联考)已知直线a和平面α,β,α∩β＝l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面►(4)(2013·课标Ⅱ)已知m,n为异面直线,m⊥平面α,n⊥平面β,直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l►(5)(2016·课标Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题：①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有________.(填写所有正确命题的编号) [例2]►(1)(2014·北京)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1＝AC＝2,BC＝1,E,F分别为A1C1,BC的中点.(I)求证：平面ABE⊥平面B1BCC1；(II)求证：C1F∥平面ABE；(III)求三棱锥E-ABC的体积.►(2)[2014江苏文]如图,三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知P A⊥AC,P A＝6,BC＝8,DF＝5. 求证：(I)直线P A∥平面DEF；(II)平面BDE⊥平面ABC.[例3]►(1)[2014·陕西文]四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.(I)求四面体ABCD的体积；(II)证明：四边形EFGH是矩形.►(2)(2012·北京)如图1,在Rt△ABC中,∠C＝90°,D,E分别为AC,AB的中点,点F为线段CD上的一点.将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图2.(I)求证：DE∥平面A1CB；(II)求证：A1F⊥BE；(III)线段A1B上是否存在点Q,使A1C⊥平面DEQ？说明理由.【变式训练】1.(2016·浙江联考)已知a,b,c为三条不同的直线,α,β是空间两个平面,且a⊂α,b⊂β,α∩β＝c.给出下列命题：①若a与b是异面直线,则c至少与a,b中的一条相交；②若a不垂直于c,则a与b一定不垂直；③若a∥b,则必有a∥c；④若a⊥b,a⊥c,则必有α⊥β. 其中正确命题的个数是()A.0B.1C.2D.32.(2012·四川)下列命题正确的是()A.若两直线和同一平面所成的角相等,则这两条直线平行B.若一平面内有三点到另一平面的距离相等,则这两平面平行C.若一直线平行于两相交平面,则这条直线与这两平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行3.(2015·福建)若l,m是两条不同的直线,m垂直于平面α,则“l⊥m”是“l∥α”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.(2016·山东济南一模)设m,n是两条不同的直线,α,β是两个不同的平面.()A.若m⊥n,n∥α,则m⊥αB.若m∥β,β⊥α,则m⊥αC.若m⊥β,n⊥β,n⊥α,则m⊥αD.若m⊥n,n⊥β,β⊥α,则m⊥α5.(2016·浙江温州联考)关于直线a,b,l及平面α,β,下列命题中正确的是()A.若a∥α,b∥α,则a∥bB.若a∥α,b⊥a,则b⊥αC.若a ⊂α,b ⊂α,且l ⊥a ,l ⊥b ,则l ⊥αD.若a ⊥α,a ∥β,则α⊥β 6.(2015·山东二模)设m ,n 是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是( ) A.当n ⊥α时,“n ⊥β”是“α∥β”的充要条件B.当m ⊂α时,“m ⊥β”是“α⊥β”的充分不必要条件C.当m ⊂α时,“n ∥α”是“m ∥n ”的必要不充分条件D.当m ⊂α时,“n ⊥α”是“m ⊥n ”的充分不必要条件 7.(2016·浙江)已知互相垂直的平面α,β交于直线l ,若直线m ,n 满足m ∥α,n ⊥β,则( )A.m ∥lB.m ∥nC.n ⊥lD.m ⊥n 8.(2013北京)如图,四棱锥P -ABCD 中,AB ∥CD ,AB ⊥AD ,CD ＝2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD .E 和F 分别是CD 和PC 的中点.求证： (1)P A ⊥底面ABCD ； (2)BE ∥平面P AD ；(3)平面BEF ⊥平面PCD .9.[2014·山东文]如图,四棱锥P -ABCD 中,AP ⊥平面PCD , AD ∥BC ,AB ＝BC＝12AD ,E ,F 分别为线段AD ,PC 的中点. (1)求证：AP ∥平面BEF ； (2)求证：BE ⊥平面P AC .10.(2013全国Ⅱ文)如图,直三棱柱ABC －A 1B 1C 1中,D ,E 分别是AB ,BB 1的中点.(Ⅰ)证明：BC 1∥平面A 1CD ；(Ⅱ)设AA 1=AC =CB =2,AB =22,求三棱锥C -A 1DE 的体积.11.(2013·辽宁)如图,AB 是圆O 的直径,P A 垂直圆O 所在的平面,C 是圆O 上的点. (1)求证：BC ⊥平面P AC ； (2)设Q 为P A 的中点,G 为△AOC 的重心,求证：QG ∥平面PBC .12.[2014·课标Ⅱ文]如图,四棱锥P -ABCD 中,底面ABCD 为矩形,P A ⊥平面ABCD ,E 为PD 的中点. (1)证明：PB ∥平面AEC ；(2)设AP ＝1,AD ＝3,三棱锥P - ABD 的体积V ＝34,求A到平面PBC 的距离.13.(2015江苏)如图,在直三棱柱ABC -A 1B 1C 1中,已知AC ⊥BC ,BC ＝CC 1.设AB 1的中点为D ,B 1C ∩BC 1＝E . 求证：(1)DE ∥平面AA 1C 1C ； (2)BC 1⊥AB 1.14.(2015广东文)如图,三角形PDC 所在的平面与长方形ABCD 所在的平面垂直,PD =PC ＝4,AB ＝6,BC ＝3. (1)证明：BC ∥平面PDA ； (2)证明：BC ⊥PD ；(3)求点C 到平面PDA 的距离.15.(2015课标Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1中,AB ＝16, BC =10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E =D 1F =4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形．(1)在图中画出这个正方形(不必说明画法和理由)； (2)求平面α把该长方体分成的两部分体积的比值．16.(2015陕西)如图,直角梯形ABCD 中,AD ∥B C,∠BAD =π2, AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点．将△ABE 沿BE 折起到如图2中△A 1BE 的位置,得到四棱锥A 1﹣BCDE ． (Ⅰ)证明：CD ⊥平面A 1OC ；(Ⅱ)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1﹣BCDE 的体积为362,求a 的值．17.(2016·课标Ⅱ文)如图,菱形ABCD 的对角线AC 与BD 交于点O ,点E ,F 分别在AD ,CD 上,AE ＝CF ,EF 交BD 于点H ,将△DEF 沿EF 折到△D ′EF 的位置． (1)证明：AC ⊥HD ′(2)若AB =5,AC =6,AE =54,OD ′=22,求五棱锥D ′­ABCFE 的体积．18.(2016·课标Ⅲ文)如图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AB ＝AD ＝AC ＝3,P A ＝BC ＝4,M 为线段AD 上一点,AM ＝2MD ,N 为PC 的中点． (1)证明MN ∥平面P AB ；(2)求四面体N -BCM 的体积．19.[2017全国I 文]如图,在四棱锥P-ABCD 中,AB//CD ,且∠BAP ＝∠CDP ＝90°.(1)证明：平面PAB ⊥平面PAD ； (2)若PA =PD =AB =DC ,∠ADP ＝90°,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.20.[2017全国II 文]如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB =BC =12AD , ∠BAD =∠ABC =90°.(1)证明：直线BC ∥平面PAD ;(2)若△PCD 面积为27,求四棱锥P-ABCD 的体积.21.[2017全国III 文]在正方体ABCD-A 1B 1C 1D 1中,E 为棱CD 的中点,则( )A.A 1E ⊥DC 1B.A 1E ⊥BDC.A 1E ⊥BC 1D.A 1E ⊥AC22.[2017全国III 文]如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明：AC ⊥BD ；(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.。

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

简记为：线线平行，则线面平行。

符号表示：a αb β => a∥αa∥b●知能训练一．选择题1．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n2．若直线l不平行于平面α，且l⊄α，则（）A．α内存在直线与l异面B．α内存在与l平行的直线C．α内存在唯一的直线与l平行D．α内的直线与l都相交3．如图，M是正方体ABCD-A1B1C1D1的棱DD1的中点，给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交；②过M点有且只有一条直线与直线AB、B1C1都垂直；③过M点有且只有一个平面与直线AB、B1C1都相交；④过M点有且只有一个平面与直线AB、B1C1都平行．其中真命题是（）A．②③④B．①③④C．①②④D．①②③4．正方体ABCD-A1B1C1D1中M，N，Q分别是棱D1C1，A1D1，BC的中点．P在对角线BD1上，且BP＝BD1，给出下面四个命题：（1）MN∥面APC；（2）C1Q∥面APC；（3）A，P，M三点共线；（4）面MNQ∥面APC．正确的序号为（）A．（1）（2）B．（1）（4）C．（2）（3）D．（3）（4）5．在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中，任取两点连成直线，所连的直线中与A1BC1平行的直线共有（）A．12条B．18条C．21条D．24条6．直线a∥平面α，P∈α，那么过P且平行于a的直线（）A．只有一条，不在平面α内B．有无数条，不一定在平面α内C．只有一条，且在平面α内D．有无数条，一定在平面α内7．如果直线a∥平面α，那么直线a与平面α内的（）A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线不相交8．如图在正方体ABCD-A1B1C1D1中，与平面AB1C平行的直线是（）A．DD1B．A1D1C．C1D1D．A1D9．如图，在三棱柱ABC-A1B1C1中，点D为AC的中点，点D1是A1C1上的一点，若BC1∥平面AB1D1，则等于（）A．1/2B．1 C．2 D．310．下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（）A．①②B．①④C．②③D．③④11．如图，正方体的棱长为1，线段B′D′上有两个动点E，F，EF=，则下列结论中错误的是（）A．AC⊥BEB．EF∥平面ABCDC．三棱锥A-BEF的体积为定值D．异面直线AE，BF所成的角为定值二．填空题12．如图，在正方体ABCD-A1B1C1D1中，E，F，G，H，M分别是棱AD，DD1，D1A1，A1A，AB的中点，点N在四边形EFGH的四边及其内部运动，则当N只需满足条件时，就有MN⊥A1C1；当N只需满足条件时，就有MN∥平面B1D1C．13．如图，正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于．三．解答题14．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．（1）求证：AB 1∥平面BC1D；（2）若BC=3，求三棱锥D-BC1C的体积．2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。

空间角和距离一、选择题（本大题共10个小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．直线m 与平面α间距离为d ，那么到m 与α距离都等于2d 的点的集合是（ ）A ．一个平面B ．一条直线C ．两条直线D ．空集 2．异面直线a 、b 所成的角为θ，a 、b 与平面α都平行，b ⊥平面β，则直线a与平面β所成的角（ ）A ．与θ相等B ．与θ互余C ．与θ互补 D ．与θ不能相等．3．在正方体ABCD —A 'B 'C 'D '中，BC '与截面BB 'D 'D 所成的角为（ ） A ．3πB ．4π C ．6πD ．arctan24．在正方形SG 1G 2G 3中，E ，F 分别是G 1G 2及G 2G 3的中点，D是EF 的中点，现在沿SE ，SF 及EF 把这个正方形折成一个四面体，使G 1，G 2，G 3三点重合，重合后的点记为G ，那么，在四面体S －EFG中必有（ ）A ．SG ⊥△EFG 所在平面B ．SD ⊥△EFG 所在平面C ．GF ⊥△SEF 所在平面D ．GD ⊥△SEF 所在平面 5．有一山坡，它的倾斜角为30°，山坡上有一条小路与斜坡底线成45°角，某人沿这条小路向上走了200米，则他升高了（ ）A ．1002米 B ．502米 C ．256米D ．506米6．已知三棱锥D －ABC 的三个侧面与底面全等，且AB ＝AC ＝3，BC ＝2，则以BC 为棱，以面BCD 与面BCA 为面的二面角的大小为 （ ）A ．arccos33 B ．arccos 31 C ．2π D ．32π7．正四面体A —BCD 中E 、F 分别是棱BC 和AD 之中点，则EF 和AB 所成的角 （ ） A ．45︒ B ．60︒ C．90︒D ．30︒8．把∠A =60°，边长为a 的菱形ABCD 沿对角线BD 折成60°的二面角，则AC 与BD 的距离为（ ）A ．43aB ．43 a C ．23 aD ．46 a9．若正三棱锥的侧面均为直角三角形，侧面与底面所成的角为α，则下列各等式中成立的是（ ）A ．0＜α＜6πB ．6π＜α＜4πC ．4π＜α＜3πD ．3π＜α＜2π10．已知A （1，1，1），B （－1，0 ，4），C （2 ，－2，3），则〈AB ，CA〉的大小为（ ）A ．6πB ．65π C ．3πD ．32π二、填空题（本大题共4小题，每小题6分，共24分）11．从平面α外一点P 引斜线段PA 和PB ，它们与α分别成45︒和30︒角，则∠APB 的最大值是______最小值是_______12．∆ABC 中∠ACB=90︒，PA ⊥平面ABC ，PA=2，AC=2 3 ，则平面PBC 与平面PAC ，平面ABC 所成的二角的大小分别是______、_________．13．在三棱锥Ｐ－ＡＢＣ中，90=∠ABC，30=∠BAC，ＢＣ＝５，又ＰＡ＝ＰＢ＝ＰＣ＝ＡＣ，则点Ｐ到平面ＡＢＣ的距离是 ．14．球的半径为8，经过球面上一点作一个平面，使它与经过这点的半径成45°角，则这个平面截球的截面面积为 ． 三、解答题（共计76分）15．（本小题满分12分）已知SA ⊥平面ABC ，SA=AB ，AB ⊥BC ，SB=BC ，E 是SC 的中点，DE ⊥SC 交AC 于D ． （1） 求证：SC ⊥面BDE ；（2）求二面角E —BD —C 的大小．16．（本小题满分12分）如图，点P 为斜三棱柱111C B A ABC -的侧棱1BB 上一点，1BB PM⊥交1AA 于点M，1BB PN ⊥交1CC 于点N．(1) 求证：MN CC ⊥1； (2) 在任意DEF ∆中有余弦定理：DFEEF DF EFDFDE∠⋅-+=cos 2222．拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明．17．（本小题满分12分）如图，四棱锥S—ABCD的底面是边长为1的正方形，SD垂直于底面ABCD，SB=3．（1）求证BC SC；（2）求面ASD与面BSC所成二面角的大小；（3）设棱SA的中点为M，求异面直线DM与SB所成角的大小．18．（本小题满分12分）在直角梯形ABCD中，∠D=∠BAD=90︒,AD=DC=1AB=a,(如图一)将△ADC 沿AC折起，使2D到D'．记面AC D'为α,面ABC为β．面BC D'为γ．（1）若二面角α-AC-β为直二面角（如图二），求二面角β-BC-γ的大小;（2）若二面角α-AC-β为60︒（如图三），求三棱锥D'-ABC的体积．19．（本小题满分14分）如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=2，AF=1，M是线段EF的中点．（1）求证AM//平面BDE；（2）求二面角A-DF-B的大小；（3）试在线段AC上确定一点P，使得PF与BC所成的角是60︒．20．（本题满分14分）如图，正方形ABCD、ABEF的边长都是1，而且平面ABCD、ABEF互相垂直．点M在AC上移动，点N在BF上移动，若a=)BNCM=<a．20(<（1）求MN的长；（2）当a为何值时，MN的长最小；（3）当MN长最小时，求面MNA与面MNB所成的二面角α的大小．参考答案一．选择题（本大题共10小题，每小题5分，共50分）二．填空题（本大题共4小题，每小题6分，共24分） 11．750 ,150 12．900 ,300 13．35 14．π32三、解答题（本大题共6题，共76分）15．(12分) （1）证明：（1）∵SB=BC E 是SC 的中点 ∴BE ⊥SC ∵DE ⊥SC ∴SC ⊥面BDE（2）解：由（1）SC ⊥BD ∵SA ⊥面ABC ∴SA ⊥BD ∴BD ⊥面SAC ∴∠EDC 为二面角E-BD-C 的平面角设SA=AB=a,则SB=BC=a2．,2,a SC SBC Rt =∆∴中在,30,0=∠∆∴DCESAC Rt 中在60,=∠∆∴EDC DEC Rt 中在．16．(12分) (1) 证：MNCC PMN CC PN CC PM CC BB CC ⊥⇒⊥∴⊥⊥⇒111111,,//平面 ； (2)解：在斜三棱柱111C B A ABC -中，有αcos 21111111111222A ACCB BCCA ACCB BCCA ABBS S S S S ⋅-+=，其中α为 平面B B CC 11与平面A A CC 11所组成的二面角．∴⊥,1PMN CC 平面 上述的二面角为MNP ∠,在PMN ∆中，cos 2222⇒∠⋅-+=MNP MN PN MNPNPMMNPCC MN CC PN CCMN CC PN CCPM ∠⋅⋅⋅-+=cos )()(211111222222， 由于111111111,,BB PM S CCMN S CCPN S A ABBA ACCB BCC⋅=⋅=⋅=，∴有αcos 21111111111222A ACCB BCCA ACCB BCCA ABBS S S S S ⋅-+=．17．(12分) （1）证法一：如，∵底面ABCD 是正方形， ∴BC ⊥DC ．∵SD ⊥底面ABCD ，∴DC 是SC 在平面ABCD 上的射影， 由三垂线定理得BC ⊥SC ．证法二：如图1，∵底面ABCD 是正方形， ∴BC ⊥DC ．∵SD ⊥底面ABCD ，∴SD ⊥BC ，又DC ∩SD=D ，∴BC ⊥平面SDC ，∴BC ⊥SC ．（2）解：如图2，过点S 作直线,//AD l l ∴在面ASD 上，∵底面ABCD 为正方形，l BC AD l ∴∴,////在面BSC 上，l ∴为面ASD 与面BSC 的交线．l ∴,,,,SC l SD l SC BC AD SD ⊥⊥∴⊥⊥∴∠CSD 为面ASD 与面BSC 所成二面角的平面角．（以下同解法一） （3）解1：如图2，∵SD=AD=1，∠SDA=90°， ∴△SDA 是等腰直角三角形．又M 是斜边SA 的中点，∴DM ⊥SA ．∵BA ⊥AD ，BA ⊥SD ，AD ∩SD=D ，∴BA ⊥面ASD ，SA 是SB 在面ASD 上的射影．由三垂线定理得DM ⊥SB ．∴异面直线DM 与SB 所成的角为90°．图1图2解2：如图3，取AB 中点P ，连结MP ，DP ．在△ABS 中，由中位线定理得 MP//SB ，DMP ∠∴是异面直线DM 与SB 所成的角．2321==SB MP，又,25)21(1,222=+==DP DM∴在△DMP 中，有DP 2=MP 2+DM 2，︒=∠∴90DMP∴异面直线DM 与SB 所成的角为90°．18．(12分) 解：（1）在直角梯形ABCD 中， 由已知∆DAC 为等腰直角三角形， ∴45,2=∠=CAB a AC , 过C 作CH ⊥AB ，由AB=2a ，可推得 AC=BC=.2a∴ AC ⊥BC ．取 AC 的中点E ，连结ED '，则 ED '⊥AC 又 ∵ 二面角β--AC a 为直二面角，∴ED '⊥β 又 ∵ ⊂BC 平面β ∴ BC ⊥E D ' ∴ BC ⊥a ，而a C D ⊂'，∴ BC ⊥C D ' ∴ CAD '∠为二面角γβ--BC 的平面角．由于45='∠CAD ， ∴二面角γβ--BC 为 45．（2）取AC 的中点E ，连结E D '，再过D '作β⊥'O D ，垂足为O ，连结OE ．∵ AC ⊥E D '， ∴ AC ⊥OE ∴ EOD '∠为二面角β--ACa 的平面角， ∴ EO D '∠60=． 在OE D Rt '∆中，aACE D 2221=='，∴O D S V ABC ABC D '⋅=∆-'31O D BC AC '⋅⋅⨯=2131a a a 462261⨯⨯⨯=.1263a =19．（14分）解法一: (1)记AC 与BD 的交点为O,连接OE, ∵O 、M 分别是AC 、EF 的中点，图3ACEF 是矩形，∴四边形AOEM 是平行四边形， ∴AM ∥OE ．∵⊂OE平面BDE ，⊄AM 平面BDE ，∴AM ∥平面BDE ．(2)在平面AFD 中过A 作AS ⊥DF 于S ，连结BS ，∵AB ⊥AF ， AB ⊥AD ， ,A AF AD = ∴AB ⊥平面ADF ，∴AS 是BS 在平面ADF 上的射影，由三垂线定理得BS ⊥DF ．∴∠BSA 是二面角A —DF —B 的平面角． 在RtΔASB 中，,2,36==AB AS∴,60,3tan ︒=∠=∠ASB ASB∴二面角A —DF —B 的大小为60º．（3）设CP=t （0≤t≤2）,作PQ ⊥AB 于Q ，则PQ ∥AD ， ∵PQ ⊥AB ，PQ ⊥AF ，A AFAB = ，∴PQ ⊥平面ABF ，⊂QE平面ABF ，∴PQ ⊥QF ．在RtΔPQF 中，∠FPQ=60º，PF=2PQ ． ∵ΔPAQ 为等腰直角三角形，∴).2(22t PQ -=又∵ΔPAF 为直角三角形，∴1)2(2+-=t PF，∴).2(2221)2(2t t -⋅=+-所以t=1或t=3(舍去),即点P是AC 的中点．解法二： （1）建立如图所示的空间直角坐标系． 设NBD AC = ，连接NE ， 则点N 、E 的坐标分别是（)0,22,22、（0,0,1）,∴)1,22,22(--=NE, 又点A 、M 的坐标分别是)0,2,2(,（)1,22,22∴AM =（)1,22,22--∴AMNE =且NE与AM 不共线，∴NE ∥AM ．又∵⊂NE 平面BDE ， ⊄AM 平面BDE ，∴AM ∥平面BDF ．（2）∵AF ⊥AB ，AB ⊥AD ，AF ,A AD = ∴AB ⊥平面ADF ．∴AB)0,0,2(-=为平面DAF 的法向量．∵DBNE ⋅=（)1,22,22--·)0,2,2(-=0， ∴NFNE⋅=（)1,22,22--·)0,2,2(=0得DBNE ⊥，NFNE⋅，∴NE 为平面BDF 的法向量．∴cos<>⋅NE AB =21∴AB 与NE 的夹角是60º．即所求二面角A —DF —B的大小是60º． （3）设P(t,t,0)(0≤t≤2)得PF),1,2,2(t t --=∴BC =（2，0，0）又∵PF 和BC 所成的角是60º．∴21)2()2(2)2(60cos 22⋅+-+-⋅-=︒t t t解得22=t 或223=t （舍去），即点P 是AC 的中点．20．(14分) 解：（1）作MP ∥AB 交BC 于点P NQ∥AB 交BE 于点Q ，连结PQ ，依题意可得MP ∥NQ ，且MP =NQ，即MNQP 是平行四边形∴MN =PQ由已知a BN CM ==，1===BE AB CB∴2==BF AC 又21a CP =，21a BQ =，即2a BQ CP ==∴MN=PQ =22)1(BQCP +-=22)2()21(a a +-=21)22(2+-a )20(<<a（2）由（Ⅰ），MN=21)22(2+-a ,所以，当22=a 时，MN=22即M 、N 分别移动到AC 、BF 的中点时，MN 的长最小，最小值为22．（3）取MN 的中点G ，连结AG 、BG ，∵ANAM =，BNBM=，G 为MN的中点 ∴AG⊥MN，BG ⊥MN，∠A G B即为二面角α的平面角,又AG =BG 46=，所以，由余弦定理有314646214646cos 22-=⋅⋅-⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛=α, 故所求二面角⎪⎭⎫⎝⎛-=31arccos α。

【考点梳理】一、考试内容1.平面。

平面的基本性质。

平面图形直观图的画法。

2.两条直线的位置关系。

平行于同一条直线的两条直线互相平行。

对应边分别平行的角。

异面直线所成的角。

两条异面直线互相垂直的概念。

异面直线的公垂线及距离。

3.直线和平面的位置关系。

直线和平面平行的判定与性质。

直线和平面垂直的判定与性质。

点到平面的距离。

斜线在平面上的射影。

直线和平面所成的角。

三垂线定理及其逆定理。

4.两个平面的位置关系。

平面平行的判定与性质。

平行平面间的距离。

二面角及其平面角。

两个平面垂直的判定与性质。

二、考试要求1.掌握平面的基本性质，空间两条直线、直线与平面、平面与平面的位置关系（特别是平行和垂直关系）以及它们所成的角与距离的概念。

对于异面直线的距离，只要求会计算已给出公垂线时的距离。

2.能运用上述概念以及有关两条直线、直线和平面、两个平面的平行和垂直关系的性质与判定，进行论证和解决有关问题。

对于异面直线上两点的距离公式不要求记忆。

3.会用斜二测画法画水平放置的平面图形（特别是正三角形、正四边形、正五边形、正六边形）的直观图。

能够画出空间两条直线、两个平面、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。

4.理解用反证法证明命题的思路，会用反证法证明一些简单的问题。

三、考点简析1.空间元素的位置关系2.平行、垂直位置关系的转化3.空间元素间的数量关系（1）角①相交直线所成的角；②异面直线所成的角——转化为相交直线所成的角；③直线与平面所成的角——斜线与斜线在平面内射影所成的角；④二面角——用二面角的平面角来度量。

（2）距离①两点之间的距离——连接两点的线段长；②点线距离——点到垂足的距离；③点面距离——点到垂足的距离；④平行线间的距离——平行线上一点到另一直线的距离；⑤异面直线间的距离——公垂线在两条异面直线间的线段长；⑥线面距离——平行线上一点到平面的距离；⑦面面距离——平面上一点到另一平面的距离；⑧球面上两点距离——球面上经过两点的大圆中的劣弧的长度。

//a α//a b点线面位置关系总复习知识梳理一、直线与平面平行 1.判定方法（1）定义法：直线与平面无公共点。

（2）判定定理：（3）其他方法：//a αββ⊂2.性质定理：//a a bαβαβ⊂⋂=二、平面与平面平行 1.判定方法（1）定义法：两平面无公共点。

（2）判定定理：////a b a b a b Pββαα⊂⊂⋂= //αβ（3）其他方法：a a αβ⊥⊥ //αβ; ////a γβγ//αβ 2.性质定理：//a bαβγαγβ⋂=⋂=三、直线与平面垂直（1）定义：如果一条直线与一个平面内的所有直线都垂直，则这条直线和这个平面垂直。

（2）判定方法 ① 用定义.//a b a b αα⊄⊂//a α//a b//a b ② 判定定理:a ba cb c A b c αα⊥⊥⋂=⊂⊂ a α⊥③ 推论://a a bα⊥ b α⊥ （3）性质 ①a b αα⊥⊂ a b ⊥ ②a b αα⊥⊥四、平面与平面垂直（1）定义：两个平面相交，如果它们所成的二面角是直线二面角，就说这两个平面互相垂直。

（2）判定定理a a αβ⊂⊥ αβ⊥ （3）性质①性质定理la a lαβαβα⊥⋂=⊂⊥ αβ⊥② l P P A A αβαβαβ⊥⋂=∈⊥垂足为 A l ∈④ l P PA αβαβαβ⊥⋂=∈⊥ PA α⊂“转化思想”面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O，在两半平面内分别作射线OA⊥l，OB⊥l，则∠AOB叫做二面角的平面角例1．如图，在三棱锥S-ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC，且分别交AC于D，交SC于E，又SA=AB，SB=BC，求以BD为棱，以BDE和BDC为面的二面角的度数。

●求线面夹角定义：斜线和它在平面内的射影的夹角叫做斜线和平面所成的角（或斜线和平面的夹角）方法：作直线上任意一点到面的垂线，与线面交点相连，利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。

直线、平面平行的判定及其性质 测试题〔有详解〕A一、选择题1．以下条件中,能判断两个平面平行的是( )A ．一个平面的一条直线平行于另一个平面;B ．一个平面的两条直线平行于另一个平面C ．一个平面有无数条直线平行于另一个平面D ．一个平面任何一条直线都平行于另一个平面2．E ，F ，G 分别是四面体ABCD 的棱BC ，CD ，DA 的中点，则此四面体中与过E ，F ，G 的截面平行的棱的条数是A ．0B ．1C ．2D ．33． 直线,a b c ，及平面αβ，，使//a b 成立的条件是〔 〕A ．//,a b αα⊂B ．//,//a b ααC ．//,//a c b cD ．//,a b ααβ=4．假设直线m 不平行于平面α，且m ⊄α，则以下结论成立的是〔 〕A ．α的所有直线与m 异面B ．α不存在与m 平行的直线C ．α存在唯一的直线与m 平行D ．α的直线与m 都相交5．以下命题中，假命题的个数是〔 〕① 一条直线平行于一个平面，这条直线就和这个平面的任何直线不相交；② 过平面外一点有且只有一条直线和这个平面平行；③ 过直线外一点有且只有一个平面和这条直线平行；④ 平行于同一条直线的两条直线和同一平面平行；⑤a 和b 异面，则经过b 存在唯一一个平面与α平行A ．4B ．3C ．2D ．16．空间四边形ABCD 中，,M N 分别是,AB CD 的中点，则以下判断正确的选项是〔 〕A ．()12MN AC BC ≥+B ．()12MN AC BC ≤+ C ．()12MN AC BC =+ D ．()12MN AC BC <+ 二、填空题7．在四面体ABCD 中，M ，N 分别是面△ACD ，△BCD 的重心，则四面体的四个面中与MN 平行的是________.8．如以下图所示，四个正方体中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，能得到AB//面MNP 的图形的序号的是①②③④9．正方体ABCD -A 1B 1C 1D 1中，E 为DD 1中点，则BD 1和平面ACE 位置关系是．三、解答题10.如图，正三棱柱111C B A ABC -的底面边长是2，侧棱长是3，D 是AC 的中点.求证：//1C B 平面BD A 1.11.如图，在平行六面体ABCD -A 1B 1C 1D 1中，E ，M ，N ，G 分别是AA 1，CD ，CB ，CC 1的中点， 求证：〔1〕MN //B 1D 1；〔2〕AC 1//平面EB 1D 1；〔3〕平面EB 1D 1//平面BDG . B一、选择题1．α，β是两个不重合的平面，a ，b 是两条不同直线，在以下条件下，可判定α∥β的是〔 〕A ．α，β都平行于直线a ，bB ．α有三个不共线点到β的距离相等C ．a ，b 是α两条直线，且a ∥β，b ∥βD ．a ，b 是两条异面直线且a ∥α，b ∥α，a ∥β，b ∥β2．两条直线a ，b 满足a ∥b ，b α，则a 与平面α的关系是〔 〕A ．a ∥αB ．a 与α相交C ．a 与α不相交D ．a α3．设,a b 表示直线，,αβ表示平面，P 是空间一点，下面命题中正确的选项是〔 〕A ．a α⊄，则//a αB ．//a α，b α⊂，则//a bC ．//,,a b αβαβ⊂⊂，则//a bD ．,,//,//P a P a βααβ∈∈，则a β⊂4．一条直线假设同时平行于两个相交平面，则这条直线与这两个平面的交线的位置关系是〔 〕A.异面B.相交C.平行D.不能确定5.以下四个命题中，正确的选项是〔 〕①夹在两条平行线间的平行线段相等；②夹在两条平行线间的相等线段平行；③如果一条直线和一个平面平行，则夹在这条直线和平面间的平行线段相等；④如果一条直线和一个平面平行，则夹在这条直线和平面间的相等线段平行A ．①③B ．①②C ．②③D ．③④6．a ，b 是两条异面直线，A 是不在a ，b 上的点，则以下结论成立的是A ．过A 有且只有一个平面平行于a ，bB ．过A 至少有一个平面平行于a ，bC ．过A 有无数个平面平行于a ，bD ．过A 且平行a ，b 的平面可能不存在二、填空题7．a ，b ，ｃ为三条不重合的直线，α，β，γ为三个不重合的平面，直线均不在平面，给出六个命题：其中正确的命题是________________.〔将正确的序号都填上〕8．设平面α∥β，A ，C ∈α，B ，D ∈β，直线AB 与CD 交于S ，假设AS =18，BS =9，CD =34，则CS =_____________.9．如图，正四棱柱ABCD-A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，DD 1，DC 中点，N 是BC 中点，点M 在四边形EFGH 及其部运动，则M 满足时，有MN ∥平面B 1BD D 1．三、解答题10.如图，在正四棱锥P ABCD -中，PA AB a ==,点E 在棱PC 上． 问点E 在何处时，//PA EBD 平面，并加以证明.11.如以下图，设P 为长方形ABCD 所在平面外一点，M ，N 分别为AB ，PD 上的点，且MB AM =NPDN ，求证：直线MN ∥平面PBC . C1.平面两正方形ABCD 与ABEF ，点M ，N 分别在对角线AC ,FB 上，且AM:MC=FN:NB ，沿AB 折起，使得∠DAF =900(1)证明：折叠后MN//平面CBE ；〔2〕假设AM:MC =2：3，在线段AB 上是否存在一点G ，使平面MGN //平面CBE "假设存在，试确定点G 的位置.2.设平面α∥平面β，AB 、CD 是两条异面直线，M ，N 分别是AB ，CD 的中点，且A ，C ∈α，B ，D ∈β，求证：MN ∥平面α.参考答案A一、选择题1．D【提示】当l =⋂βα时，α有无数多条直线与交线l 平行，同时这些直线也与平面β平行.故A ，B ，C 均是错误的2．C【提示】棱AC ，BD 与平面EFG 平行，共2条.3．C【提示】//,,a b αα⊂则//a b 或,a b 异面；所以A 错误；//,//,a b αα则//a b 或,a b 异面或,a b 相交，所以B 错误；//,,a b ααβ=则//a b 或,a b 异面，所以D 错误；//,//a c b c ，则//a b ，这是公理4，所以C 正确.4．B【提示】假设直线m 不平行于平面α，且m ⊄α，则直线m 于平面α相交，α不存在与m 平行的直线.5．B【提示】②③④错误.②过平面外一点有且只有一个平面和这个平面平行，有无数多条直线与它平行.③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上.6. D【提示】此题可利用空间中的平行关系，构造三角形的两边之和大于第三边.二、填空题7．平面ABC ，平面ABD【提示】连接AM 并延长，交CD 于E ，连结BN 并延长交CD 于F ，由重心性质可知，E 、F 重合为一点，且该点为CD 的中点E ，由MA EM =NB EN =21得MN ∥AB .因此，MN ∥平面ABC 且MN ∥平面ABD . 8.①③【提示】对于①，面MNP//面AB,故AB//面MNP.对于③，MP//AB,故AB//面MNP,对于②④，过AB 找一个平面与平面MNP 相交，AB 与交线显然不平行，故②④不能推证AB//面MNP.9．平行【提示】连接BD 交AC 于O ，连OE ，∴OE ∥B D 1，OEC 平面ACE ，∴B D 1∥平面ACE.三、解答题10.证明：设1AB 与B A 1相交于点P ，连接PD ，则P 为1AB 中点，D 为AC 中点，∴PD//C B 1.又 PD ⊂平面B A 1D ，∴C B 1//平面B A 1 D11.证明：〔1〕 M 、N 分别是CD 、CB 的中点，∴MN//BD又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形.所以BD//B 1D 1.又MN//BD ，从而MN//B 1D 1〔2〕〔法1〕连A 1C 1，A 1C 1交B 1D 1与O 点四边形A 1B 1C 1D 1为平行四边形，则O 点是A 1C 1的中点E 是AA 1的中点，∴EO 是∆AA 1C 1的中位线，EO//AC 1.AC 1⊄面EB 1D 1 ，EO ⊂面EB 1D 1，所以AC 1//面EB 1D 1〔法2〕作BB 1中点为H 点，连接AH 、C 1H ，E 、H 点为AA 1、BB 1中点，所以EH //C 1D 1，则四边形EHC 1D 1是平行四边形，所以ED 1//HC 1又因为EA //B 1H ，则四边形EAHB 1是平行四边形，所以EB 1//AHAH ⋂HC 1=H ，∴面AHC 1//面EB 1D 1.而AC 1⊂面AHC 1，所以AC 1//面EB 1D 1 〔3〕因为EA //B 1H ，则四边形EAHB 1是平行四边形，所以EB 1//AH因为AD //HG ，则四边形ADGH 是平行四边形，所以DG//AH ，所以EB 1//DG 又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形. 所以BD//B 1D 1.BD ⋂DG=G ，∴面EB 1D 1//面BDGB一、选择题1．D【提示】A 错，假设a ∥b ，则不能断定α∥β；B 错，假设A ，B ，C 三点不在β的同一侧，则不能断定α∥β；C 错，假设a∥b，则不能断定α∥β；D 正确.2．C【提示】假设直线a ，b 满足a ∥b ，b α，则a ∥α或a α3．D【提示】根据面面平行的性质定理可推证之.4．C【提示】设α∩β=l ，a ∥α，a ∥β，过直线a 作与α、β都相交的平面γ，记α∩γ=b ，β∩γ=c ，则a ∥b 且a ∥c ，∴b ∥c .又b ⊂α，α∩β=l ，∴b ∥l .∴a ∥l .5．A【提示】6． D【提示】过点A 可作直线a ′∥a ，b ′∥b ，则a ′∩b ′=A ，∴a ′，b ′可确定一个平面，记为α.如果a ⊄α，b ⊄α，则a ∥α，b ∥α.由于平面α可能过直线a 、b 之一，因此，过A 且平行于a 、b 的平面可能不存在.二、填空题7.①④⑤⑥8.68或368 【提示】如图〔1〕，由α∥β可知BD ∥AC ，∴SA SB =SC SD ，即189=SC SC 34-，∴SC =68. 如图〔2〕，由α∥β知AC ∥BD ，∴SB SA =SD SC =SC CD SC -，即918=SCSC -34. ∴SC =368. 9．M ∈HF【提示】易证平面NHF ∥平面BD D 1B 1，M 为两平面的公共点，应在交线HF 上.三、解答题 10．解：当E 为PC 中点时，//PA EBD 平面．证明：连接AC ，且AC BD O =，由于四边形ABCD 为正方形，∴O 为AC 的中点，又E 为中点，∴OE 为△ACP 的中位线，∴//PA EO ，又PA EBD ⊄平面，∴//PA EBD 平面.11．证法一：过N 作NR ∥DC 交PC 于点R ，连接RB ，依题意得NR NR DC -=NP DN =MBAM =MB MB AB -=MB MB DC -⇒NR =MB .∵NR ∥DC ∥AB ，∴四边形MNRB 是平行四边形.∴MN ∥RB .又∵RB 平面PBC ，∴直线MN ∥平面PBC . 证法二：过N 作NQ ∥AD 交PA 于点Q ，连接QM ，∵MB AM =NP DN =QPAQ ，∴QM ∥PB .又NQ ∥AD ∥BC ，∴平面MQN ∥平面PBC .∴直线MN ∥平面PBC .C1.〔1〕证明：设直线AN 与BE 交与点H ，连接CH ，ANF ∆ ∽HNB ∆,∴NHAN NB FN =. 又NB FN MC AM =,则NH AN =MCAM ，∴MN//CH. 又CBE CBE MN 平面，平面⊂⊄CH ,∴MN//平面CBE.(2)解：存在，过M 作MG ⊥AB,垂足为G ，则MG//BC, ∴MG//平面CBE,又MN//平面CBE ，M MN MG =⋂,平面MGN//平面CBE.即G 在AB 线上，且AG:GB=AM:MC=2：32.证明：连接BC ，AD ，取BC 的中点E ，连接ME 、NE ，则ME 是△BAC 的中位线，故ME ∥AC.ME ⊄α，∴ME ∥α.同理可证，NE ∥BD.又α∥β，设CB 与DC 确定的平面BCD 与平面α交于直线CF ，则CF ∥BD ，∴NE ∥CF. 而NE ⊄平面α，CF ⊂α，∴NE ∥α.O F A B CD P E又ME ∩NE=E ，∴平面MNE ∥α，而MN ⊂平面MNE ，∴MN ∥平面α.一、选择题1．以下条件中,能判断两个平面平行的是( )A ．一个平面的一条直线平行于另一个平面;B ．一个平面的两条直线平行于另一个平面C ．一个平面有无数条直线平行于另一个平面D ．一个平面任何一条直线都平行于另一个平面2．E ，F ，G 分别是四面体ABCD 的棱BC ，CD ，DA 的中点，则此四面体中与过E ，F ，G 的截面平行的棱的条数是A ．0B ．1C ．2D ．33． 直线,a b c ，及平面αβ，，使//a b 成立的条件是〔 〕A ．//,a b αα⊂B ．//,//a b ααC ．//,//a c b cD ．//,a b ααβ=4．假设直线m 不平行于平面α，且m ⊄α，则以下结论成立的是〔 〕A ．α的所有直线与m 异面B ．α不存在与m 平行的直线C ．α存在唯一的直线与m 平行D ．α的直线与m 都相交5．以下命题中，假命题的个数是〔 〕① 一条直线平行于一个平面，这条直线就和这个平面的任何直线不相交；② 过平面外一点有且只有一条直线和这个平面平行；③ 过直线外一点有且只有一个平面和这条直线平行；④ 平行于同一条直线的两条直线和同一平面平行；⑤a 和b 异面，则经过b 存在唯一一个平面与α平行A ．4B ．3C ．2D ．16．空间四边形ABCD 中，,M N 分别是,AB CD 的中点，则以下判断正确的选项是〔 〕A ．()12MN AC BC ≥+B ．()12MN AC BC ≤+ C ．()12MN AC BC =+ D ．()12MN AC BC <+ 二、填空题7．在四面体ABCD 中，M ，N 分别是面△ACD ，△BCD 的重心，则四面体的四个面中与MN 平行的是________.8．如以下图所示，四个正方体中，A ，B 为正方体的两个顶点，M ，N ，P 分别为其所在棱的中点，能得到AB//面MNP 的图形的序号的是①②③④9．正方体ABCD -A 1B 1C 1D 1中，E 为DD 1中点，则BD 1和平面ACE 位置关系是．三、解答题10.如图，正三棱柱111C B A ABC -的底面边长是2，侧棱长是3，D 是AC 的中点.求证：//1C B 平面BD A 1.11.如图，在平行六面体ABCD -A 1B 1C 1D 1中，E ，M ，N ，G 分别是AA 1，CD ，CB ，CC 1的中点， 求证：〔1〕MN //B 1D 1；〔2〕AC 1//平面EB 1D 1；〔3〕平面EB 1D 1//平面BDG .B一、选择题1．α，β是两个不重合的平面，a ，b 是两条不同直线，在以下条件下，可判定α∥β的是〔 〕A ．α，β都平行于直线a ，bB ．α有三个不共线点到β的距离相等C ．a ，b 是α两条直线，且a ∥β，b ∥βD ．a ，b 是两条异面直线且a ∥α，b ∥α，a ∥β，b ∥β2．两条直线a ，b 满足a ∥b ，b α，则a 与平面α的关系是〔 〕A ．a ∥αB ．a 与α相交C ．a 与α不相交D ．a α3．设,a b 表示直线，,αβ表示平面，P 是空间一点，下面命题中正确的选项是〔 〕A ．a α⊄，则//a αB ．//a α，b α⊂，则//a bC ．//,,a b αβαβ⊂⊂，则//a bD ．,,//,//P a P a βααβ∈∈，则a β⊂4．一条直线假设同时平行于两个相交平面，则这条直线与这两个平面的交线的位置关系是〔 〕A.异面B.相交C.平行D.不能确定5.以下四个命题中，正确的选项是〔 〕①夹在两条平行线间的平行线段相等；②夹在两条平行线间的相等线段平行；③如果一条直线和一个平面平行，则夹在这条直线和平面间的平行线段相等；④如果一条直线和一个平面平行，则夹在这条直线和平面间的相等线段平行A ．①③B ．①②C ．②③D ．③④6．a ，b 是两条异面直线，A 是不在a ，b 上的点，则以下结论成立的是A ．过A 有且只有一个平面平行于a ，bB ．过A 至少有一个平面平行于a ，bC ．过A 有无数个平面平行于a ，bD ．过A 且平行a ，b 的平面可能不存在二、填空题7．a ，b ，ｃ为三条不重合的直线，α，β，γ为三个不重合的平面，直线均不在平面，给出六个命题：其中正确的命题是________________.〔将正确的序号都填上〕8．设平面α∥β，A ，C ∈α，B ，D ∈β，直线AB 与CD 交于S ，假设AS =18，BS =9，CD =34，则CS =_____________.9．如图，正四棱柱ABCD-A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，DD 1，DC 中点，N 是BC 中点，点M 在四边形EFGH 及其部运动，则M 满足时，有MN ∥平面B 1BD D 1．三、解答题10.如图，在正四棱锥P ABCD -中，PA AB a ==,点E 在棱PC上． 问点E 在何处时，//PA EBD 平面，并加以证明.11.如以下图，设P 为长方形ABCD 所在平面外一点，M ，N 分别为AB ，PD 上的点，且MB AM =NP DN，求证：直线MN ∥平面PBC .C1.平面两正方形ABCD 与ABEF ，点M ，N 分别在对角线AC ,FB 上，且AM:MC=FN:NB ，沿AB 折起，使得∠DAF =900(1)证明：折叠后MN//平面CBE ；〔2〕假设AM:MC =2：3，在线段AB 上是否存在一点G ，使平面MGN //平面CBE "假设存在，试确定点G 的位置.2.设平面α∥平面β，AB 、CD 是两条异面直线，M ，N 分别是AB ，CD 的中点，且A ，C ∈α，B ，D ∈β，求证：MN ∥平面α.参考答案A一、选择题1．D【提示】当l =⋂βα时，α有无数多条直线与交线l 平行，同时这些直线也与平面β平行.故A ，B ，C 均是错误的2．C【提示】棱AC ，BD 与平面EFG 平行，共2条.3．C【提示】//,,a b αα⊂则//a b 或,a b 异面；所以A 错误；//,//,a b αα则//a b 或,a b 异面或,a b 相交，所以B 错误；//,,a b ααβ=则//a b 或,a b 异面，所以D 错误；//,//a c b c ，则//a b ，这是公理4，所以C 正确.4．B【提示】假设直线m 不平行于平面α，且m ⊄α，则直线m 于平面α相交，α不存在与m 平行的直线.5．B【提示】②③④错误.②过平面外一点有且只有一个平面和这个平面平行，有无数多条直线与它平行.③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上.6. D【提示】此题可利用空间中的平行关系，构造三角形的两边之和大于第三边.二、填空题7．平面ABC ，平面ABD【提示】连接AM 并延长，交CD 于E ，连结BN 并延长交CD 于F ，由重心性质可知，E 、F 重合为一点，且该点为CD 的中点E ，由MA EM =NB EN =21得MN ∥AB .因此，MN ∥平面ABC 且MN ∥平面ABD . 8.①③【提示】对于①，面MNP//面AB,故AB//面MNP.对于③，MP//AB,故AB//面MNP,对于②④，过AB 找一个平面与平面MNP 相交，AB 与交线显然不平行，故②④不能推证AB//面MNP.9．平行【提示】连接BD 交AC 于O ，连OE ，∴OE ∥B D 1，OEC 平面ACE ，∴B D 1∥平面ACE.三、解答题10.证明：设1AB 与B A 1相交于点P ，连接PD ，则P 为1AB 中点，D 为AC 中点，∴PD//C B 1.又 PD ⊂平面B A 1D ，∴C B 1//平面B A 1 D11.证明：〔1〕 M 、N 分别是CD 、CB 的中点，∴MN//BD又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形.所以BD//B 1D 1.又MN//BD ，从而MN//B 1D 1〔2〕〔法1〕连A 1C 1，A 1C 1交B 1D 1与O 点四边形A 1B 1C 1D 1为平行四边形，则O 点是A 1C 1的中点E 是AA 1的中点，∴EO 是∆AA 1C 1的中位线，EO//AC 1.AC 1⊄面EB 1D 1 ，EO ⊂面EB 1D 1，所以AC 1//面EB 1D 1〔法2〕作BB 1中点为H 点，连接AH 、C 1H ，E 、H 点为AA 1、BB 1中点，所以EH //C 1D 1，则四边形EHC 1D 1是平行四边形，所以ED 1//HC 1又因为EA //B 1H ，则四边形EAHB 1是平行四边形，所以EB 1//AHAH ⋂HC 1=H ，∴面AHC 1//面EB 1D 1.而AC 1⊂面AHC 1，所以AC 1//面EB 1D 1 〔3〕因为EA //B 1H ，则四边形EAHB 1是平行四边形，所以EB 1//AH因为AD //HG ，则四边形ADGH 是平行四边形，所以DG//AH ，所以EB 1//DG 又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形. 所以BD//B 1D 1.BD ⋂DG=G ，∴面EB 1D 1//面BDGB一、选择题1．D【提示】A 错，假设a ∥b ，则不能断定α∥β；B 错，假设A ，B ，C 三点不在β的同一侧，则不能断定α∥β；C 错，假设a∥b，则不能断定α∥β；D 正确.2．C【提示】假设直线a ，b 满足a ∥b ，b α，则a ∥α或a α3．D【提示】根据面面平行的性质定理可推证之.4．C【提示】设α∩β=l ，a ∥α，a ∥β，过直线a 作与α、β都相交的平面γ，记α∩γ=b ，β∩γ=c ，则a ∥b 且a ∥c ，∴b ∥c .又b ⊂α，α∩β=l ，∴b ∥l .∴a ∥l .5．A【提示】6． D【提示】过点A 可作直线a ′∥a ，b ′∥b ，则a ′∩b ′=A ，∴a ′，b ′可确定一个平面，记为α.如果a ⊄α，b ⊄α，则a ∥α，b ∥α.由于平面α可能过直线a 、b 之一，因此，过A 且平行于a 、b 的平面可能不存在.二、填空题7.①④⑤⑥8.68或368 【提示】如图〔1〕，由α∥β可知BD ∥AC ，∴SA SB =SC SD ，即189=SC SC 34-，∴SC =68. 如图〔2〕，由α∥β知AC ∥BD ，∴SB SA =SD SC =SC CD SC -，即918=SCSC -34. ∴SC =368. 9．M ∈HF【提示】易证平面NHF ∥平面BD D 1B 1，M 为两平面的公共点，应在交线HF 上.三、解答题 10．解：当E 为PC 中点时，//PA EBD 平面．证明：连接AC ，且AC BD O =，由于四边形ABCD 为正方形，∴O 为AC 的中点，又E 为中点，∴OE 为△ACP 的中位线，∴//PA EO ，又PA EBD ⊄平面，∴//PA EBD 平面.11．证法一：过N 作NR ∥DC 交PC 于点R ，连接RB ，依题意得NR NR DC -=NP DN =MBAM =MB MB AB -=MB MB DC -⇒NR =MB .∵NR ∥DC ∥AB ，∴四边形MNRB 是平行四边形.∴MN ∥RB .又∵RB 平面PBC ，∴直线MN ∥平面PBC . 证法二：过N 作NQ ∥AD 交PA 于点Q ，连接QM ，∵MB AM =NP DN =QPAQ ，∴QM ∥PB .又NQ ∥AD ∥BC ，∴平面MQN ∥平面PBC .∴直线MN ∥平面PBC .C1.〔1〕证明：设直线AN 与BE 交与点H ，连接CH ，ANF ∆ ∽HNB ∆,∴NHAN NB FN =. 又NB FN MC AM =,则NH AN =MCAM ，∴MN//CH. 又CBE CBE MN 平面，平面⊂⊄CH ,∴MN//平面CBE.(2)解：存在，过M 作MG ⊥AB,垂足为G ，则MG//BC, ∴MG//平面CBE,又MN//平面CBE ，M MN MG =⋂,平面MGN//平面CBE.即G 在AB 线上，且AG:GB=AM:MC=2：32.证明：连接BC ，AD ，取BC 的中点E ，连接ME 、NE ，则ME 是△BAC 的中位线，故ME ∥AC.ME ⊄α，∴ME ∥α.同理可证，NE ∥BD.又α∥β，设CB 与DC 确定的平面BCD 与平面α交于直线CF ，则CF ∥BD ，∴NE ∥CF. 而NE ⊄平面α，CF ⊂α，∴NE ∥α.O F A B CD P E又ME∩NE=E，∴平面MNE∥α，而MN⊂平面MNE，∴MN∥平面α.。

1.点A 在直线上,记作 ；点A 在平面α内,记作 ；直线α在平面α内,记作 .2.平面基本性质即三条公理的“文字语言”、“符号语言”、“图形语言”列表如下：3.公理的作用：（1）公理1作用：判断直线是否在平面内；（2）公理2作用：确定一个平面的依据；（3）公理3作用：判定两个平面是否相交的依据. 4. 空间两条直线的位置关系：5. 等角定理：6. 已知两条异面直线，经过空间任一点作直线，把所成的锐角（或直角）叫异面直线所成的角（或夹角）. 所成的角的大小与点的选择无关，为了简便，点通常取在异面直线的一条上；异面直线所成的角的范围为，如果两条异面直线所成的角是直角，则叫两条异面直线垂直，记作. 求两条异面直线所成角的步骤可以归纳为四步：选点→平移→定角→计算.7. 公理4：8. 公理4作用：判断空间两条直线 的依据.9.直线与平面有三种位置关系：（1） —— 有无数个公共点（2）——有且只有一个公共点（3）——没有公共点10. 两个平面之间有两种位置关系：（1）——没有公共点（2）——有且只有一条公共直线2.2 直线、平面平行的判定及其性质11.判定定理的符号表示为：.12. 证明线面平行的根本问题是要在平面内找一直线与已知直线平行，此时常用中位线定理、成比例线段、射影法、平行移动、补形等方法，具体用何种方法要视条件而定.13.面面平行判定定理：．用符号表示为：.14. 垂直于同一条直线的两个平面平行.15. 平面α上有不在同一直线上的三点到平面β的距离相等，则α与β的位置关系是.16.线面平行的性质定理：符号语言：18. 面面平行的性质：. 用符号语言表示为：.19. 其它性质：①；②；③夹在平行平面间的平行线段相等.1．四面体ABCD中，AB＝CD＝2，E、F分别是AC、BD的中点，且EF＝3，则AB与CD所成的角为__________．3 / 72．在空间四边形ABCD 中，已知AD ＝1，BC ＝3，且AD ⊥BC ，对角线BD ＝213，AC ＝23，求AC 和BD 所成的角．3．已知E 、F 、G 、H 分别是空间四边形ABCD 各边AB 、AD 、CB 、CD 上的点，并且有GB CG EB AB ＝，HD CH FD AF ＝，试证EF 、GH 、BD 共点或两两平行．4 已知异面直线a 、b 所成的角为60°，在过空间一定点P 的直线中，与a ，b 所成的角均为60°的直线有多少条？过P 与a 、b 所成角均为50°，或均为70°的直线又各有多少呢？希望读者通过对上述三个具体问题的求解，总结解题方法，然后再探讨关于与异面直线成等角的直线的存在性问题的一般性情况：已知异面直线a ，b 所成的角为θ0且θ0＜90°，过空间一点P 的直线中与a ，b 所成的角均为θ的直线有多少条？5．已知长方体1111D C B A ABCD -中，M 、N 分别是1BB 和BC 的中点，AB=4，AD=2，1521=BB ，求异面直线D B 1与MN 所成角的余弦值。