用图象法求一元二次方程的根

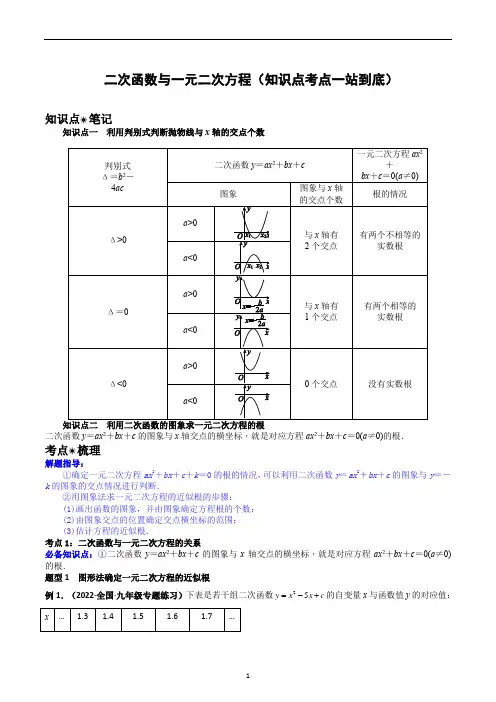
二次函数与一元二次方程（知识点考点一站到底）知识点☀笔记知识点一 利用判别式判断抛物线与x 轴的交点个数判别式 Δ＝b 2－ 4ac二次函数y ＝ax 2＋bx ＋c 一元二次方程ax 2＋bx ＋c ＝0(a ≠0)图象图象与x 轴 的交点个数根的情况Δ>0a >0与x 轴有 2个交点有两个不相等的实数根a <0Δ＝0a >0与x 轴有 1个交点有两个相等的 实数根a <0Δ<0a >00个交点没有实数根a <0二次函数y ＝ax 2＋bx ＋c 的图象与x 轴交点的横坐标，就是对应方程ax 2＋bx ＋c ＝0(a ≠0)的根．考点☀梳理解题指导：①确定一元二次方程ax 2＋bx ＋c ＋k ＝0的根的情况，可以利用二次函数y ＝ax 2＋bx ＋c 的图象与y ＝－k 的图象的交点情况进行判断．②用图象法求一元二次方程的近似根的步骤：(1)画出函数的图象，并由图象确定方程根的个数； (2)由图象交点的位置确定交点横坐标的范围； (3)估计方程的近似根．考点1：二次函数与一元二次方程的关系必备知识点：①二次函数y ＝ax 2＋bx ＋c 的图象与x 轴交点的横坐标，就是对应方程ax 2＋bx ＋c ＝0(a ≠0)的根．题型1 图形法确定一元二次方程的近似根例1．（2022·全国·九年级专题练习）下表是若干组二次函数25y x x c =-+的自变量x 与函数值y 的对应值： x …1.31.41.51.61.7…y … 0.36 0.13 ﹣0.08 ﹣0.27 ﹣0.44 … 那么方程x 2﹣5x +c ＝0的一个近似根（精确到0.1）是（ ）A ．3.4 B ．3.5 C ．3.6 D ．3.7【答案】B【分析】观察表格可得-0.08更接近于0，得到方程的一个近似根（精确到0.1）是1.5，再由25y x x c =-+的对称轴为x =52得到方程250x x c -+=的另一个近似根（精确到0.1）是3.5【详解】解：∵二次函数25y x x c =-+， ∵对称轴为直线x ＝52，观察表格得：方程250x x c -+=的一个近似根（精确到0.1）是1.5， ∵另一个近似根m 满足 1.52m +＝52， ∵m ＝3.5， 故选：B.【点睛】此题考查了图象法求一元二次方程的近似根，弄清表格中的数据是解本题的关键．＝ax 2+bx +c 的图象，并求得一个近似根为x ＝﹣4.3，则方程的另一个近似根为（ ）（精确到0.1）A ．x ＝4.3B ．x ＝3.3C ．x ＝2.3D ．x ＝1.3【答案】C【分析】根据抛物线与x 轴的一个交点为（﹣4.3，0），又抛物线的对称轴为：x ＝﹣1，即可求解． 【详解】解：∵抛物线与x 轴的一个交点为（﹣4.3，0），又抛物线的对称轴为：x ＝﹣1， ∵另一个交点坐标为：（2.3，0）， 则方程的另一个近似根为x ＝2.3，故选：C ．【点睛】本题考查了根据二次函数图象求方程的近似根，掌握抛物线的对称性是解题的关键．练习1．（2022·全国·九年级专题练习）根据表格中二次函数y ＝ax 2+bx +c 的自变量x 与函数值y 的对应值，可以判断方程 ax 2+bx +c ＝0的一个解x 的范围是（ ）x 00.5 1 1.5 2 y ＝ax 2+bx +c 1-0.5-13.57A ．0＜x ＜0.5B ．0.5＜x ＜1C ．1＜x ＜1.5D ．1.5＜x ＜2【答案】B【分析】利用二次函数和一元二次方程的性质．【详解】解：观察表格可知：当x =0.5时，y =-0.5；当x =1时，y =1， ∵方程ax 2+bx +c =0（a ≠0，a ，b ，c 为常数）的一个解x 的范围是0.5＜x ＜1． 故选：B ．【点睛】本题考查了用图象法求一元二次方程的近似根，解题的关键是找到y 由正变为负时，自变量的取值即可．练习2．（2022.浙江湖州.九年级期末）在二次函数y ＝ax 2+bx +c 中，函数y 与自变量x 的部分对应值如表，则方程ax 2+bx +c ＝0的一个解x 的范围是（ ） x (1)1.11.2 1.3 1.4 … y …-1-0.490.040.591.16…A ．1＜x ＜1.1B ．1.1＜x ＜1.2C ．1.2＜x ＜1.3D ．1.3＜x ＜1.4【答案】B【分析】根据表格中自变量与函数的值的变化情况得出当y =0时相应的自变量的取值范围即可． 【详解】由表格中数据可知，当x ＝1.1时，y ＝－0.49. 当x ＝1.2时，y ＝0.04于是可得，当y ＝0时，相应的自变量x 的取值范围为1.1＜x ＜1.2 故选B【点睛】本题考查了用图像法求一元二次方程的近似根，解题的关键是找到y 由正变为负时自变量的取值即可．练习2．（2022·全国·九年级课时练习）如表，是二次函数()y f x =的自变量x 与函数值y 的几组对应值．那么方程()0f x =的一个近似解是（ ）x 0.9 1 1.1 1.2 1.3 1.4 y -1.49-1-0.490.040.591.16A ．1B ．1.1C ．1.2D ．1.3【答案】C【分析】由表格可得抛物线与x 轴的一个交点在(1.1,0)和(1.2,0)之间且距离(1.2,0)较近，进而求解． 【详解】解：由表格可得 1.1x =时，0y <， 1.2x =时，0y >，()0f x ∴=的一个解在1.1与1.2之间， |0.49|0.04>，()0f x ∴=的一个近似解是1.2，故选：C ．【点睛】本题考查二次函数图象上点的坐标特征，解题的关键是掌握二次函数与方程的关系．练习4．（2022·江苏·九年级专题练习）观察下列表格，估计一元二次方程2350x x +-=的正数解在（ ）x－1 0 1 2 3 425x x +- －7 －5 －1 5 13 23A ．－1和0之间B ．0和1之间C ．1和2之间D ．2和3之间【答案】C【分析】令y =x 2＋3x －5根据x =﹣1和x =5时的函数值，即可得到答案． 【详解】解：令y =x 2＋3x －5， 当1x =时，10y =-<， 当2x =时，50y =>，∴x 2＋3x －5=0的一个正数x 的取值范围为1＜x ＜2，故选C ．【点睛】本题考查二次函数的与坐标轴的交点问题，掌握二次函数的性质是解题关键． 例1．（2022·吉林省实验中学九年级阶段练习）抛物线253y x x =-+-与y 轴的交点坐标是（ ） A ．()0,3 B ．()0,3-C ．()0,5-D ．()0,5【答案】B【分析】把x ＝0代入253y x x =-+-求得y 的值，即可得到答案． 【详解】解：∵当x ＝0时，253y x x =-+-＝﹣3， ∵抛物线253y x x =-+-与y 轴的交点坐标是（0，﹣3）．故选：B例2．（2022·全国·九年级专题练习）已知二次函数y ＝x 2﹣6x +5．函数图象与x 轴交点坐标为_____，与y 轴的交点坐标为__________；【答案】 （5，0），（1，0） （0，5）【分析】利用y =0解方程得到图象与轴的交点，利用x =0求图象与y 轴的交点即可． 【详解】把y ＝0代入y ＝x 2﹣6x +5得0＝x 2﹣6x +5， 解得x 1＝5，x 2＝1，∵抛物线与x 轴交点坐标为（5，0），（1，0）， 把x ＝0代入y ＝x 2﹣6x +5得y ＝5， ∵抛物线与y 轴交点坐标为（0，5）， 故答案为：（5，0），（1，0）；（0，5）．【点睛】此题考查了二次函数图象与坐标轴的交点坐标，解一元二次方程，正确掌握计算方法是解题的关键．练习1．（2021·江苏·南通市八一中学九年级阶段练习）抛物线y ＝23x +4x +2与x 轴的交点个数是_____． 【答案】0【分析】先计算判别式的值，然后根据判别式的意义进行判断． 【详解】解：∵Δ=24-4×3×2=-8＜0， ∵抛物线与x 轴没有交点． 故答案为：0．【点睛】本题考查了抛物线与x 轴的交点，解题关键是把求二次函数y =2ax +bx +c (a ，b ，c 是常数，a ≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程的根的判别式的应用进行解决． 练习2．（2022·浙江温州·九年级期中）已知二次函数1y x k =--+的图象过点0,3．(1)求该二次函数的表达式．(2)求该二次函数图象与x 轴的交点坐标． 【答案】(1)()214y x =--+ (2)()1,0-，()3,0【分析】（1）把点()0,3代入函数解析式，求出k 的值即可得到函数表达式； （2）取y ＝0，得到()2140x --+=，求出x 的值，即可得到答案． （1）解：把()0,3代入()21y x k =--+得：()2013k --+=，解得：4k =，∵该二次函数的表达式是()214y x =--+； （2）当0y =时，()2140x --+=， 解得：11x =-或23x =，∵该二次函数图象与x 轴的交点坐标是()1,0-，()3,0．【点睛】此题考查了待定系数法求二次函数的表达式、二次函数图象与x 轴的交点等知识，熟练掌握方法是解题的关键．练习3．（2022·全国·九年级专题练习）如图，已知二次函数223y ax x ++＝的图象与x 轴交于点A （﹣1，0）和点B ，与y 轴交于点C .(1)求二次函数的解析式和点B 的坐标； (2)直接写出y 的最大值为 .【答案】(1)2y x 2x 3=-++；B （3，0）； (2)4【分析】（1）运用待定系数法即可求得二次函数的解析式，令y ＝0，解一元二次方程即可求得点B 的坐标； （2）运用配方法将二次函数解析式化为顶点式，即可得出答案． （1）∵抛物线223y ax x ++＝经过点A （﹣1，0）， ∵a ﹣2+3＝0， 解得：a ＝﹣1，∵二次函数的解析式为2y x 2x 3=-++， 令y ＝0，得2230x x -++=， 解得：13x =，21x =- ∵B （3，0）； （2）∵()222314y x x x =-++=--+， ∵当x ＝1时，4y =最大值． 故答案为：4．【点睛】本题考查了待定系数法求函数解析式，抛物线与x 轴交点坐标，二次函数最值等，难度较小，是常见的基础题．练习4．（2021·江西上饶·九年级阶段练习）如图，抛物线23y ax bx ++＝（a ≠0）与x 轴交于点A （1，0）和点B （﹣3，0），与y 轴交于点C ，连接BC ，与抛物线的对称轴交于点E ，顶点为点D ．(1)求抛物线的解析式； (2)求∵BOC 的面积． 【答案】(1)223y x x --+＝ (2)92【分析】（1）根据抛物线23y ax bx ++＝（a ≠0）与x 轴交于点A （1，0）和点B （﹣3，0），即可得到关于a 、b 的方程，从而可以求得a 、b 的值，然后即可写出抛物线的解析式；（2）根据（1）中抛物线的解析式，可以写出点C 的坐标，然后再根据点B 的坐标，即可得到OC 和OB 的长，再根据三角形面积公式，即可求得∵BOC 的面积． （1）解：∵抛物线23y ax bx ++＝（a ≠0）与x 轴交于点A （1，0）和点B （﹣3，0），∵309330a b a b ++=⎧⎨-+=⎩， 解得12a b =-⎧⎨=-⎩，∵抛物线的解析式为223y x x --+＝． （2）解：由（1）知，223y x x --+＝，∵点C 的坐标为（0，3）， ∵OC ＝3，∵点B 的坐标为（﹣3，0）， ∵OB ＝3， ∵∵BOC ＝90°， ∵∵BOC 的面积是2OB OC ⋅＝33922⨯=． 【点睛】本题主要考查抛物线与x 轴的交点、待定系数法求二次函数解析式、二次函数的性质、三角形的面积，解答本题的关键是明确二次函数的性质，利用数形结合的思想解答． 例1．（2022·福建省长汀县第二中学九年级阶段练习）定义：min{a ，b }＝(),().a a b b a b ⎧≤⎨>⎩若函数y ＝min{x ＋1，223x x -++ }，则该函数的最大值为___________.【答案】3【分析】根据定义画出函数图象，设直线y =x +1，抛物线2y x 2x 3=-++，联立直线与抛物线方程得抛物线与直线交点坐标，结合图象求解．【详解】解：依题意，设直线y =x +1，抛物线2y x 2x 3=-++， 联立直线与抛物线方程得2123y x y x x =+⎧⎨=-++⎩， 解得23x y =⎧⎨=⎩或10x y =-⎧⎨=⎩，∵直线与抛物线交点坐标为（-1，0），（2，3）， 如图，∵x ≤-1时，y =223x x -++，函数最大值为y =0，-1＜x ≤2时，y =x +1，函数最大值为y =3， 当x ＞2时，y =223x x -++，y ＜3， ∵x =2时，函数取最大值为3， 故答案为：3．【点睛】本题考查二次函数的性质，解题关键是掌握函数与方程及不等式的关系．通过数形结合求解． 例2．（2022·全国·九年级课时练习）抛物线223y x x =-，当1y =-时，自变量的值为_________． 【答案】1或12【分析】把y =1代入解析式中得到关于x 的方程，解方程即可 【详解】解：223y x x =-， 当1y =-时，2231x x -=-， 解得11x =，212x =， 故答案为：1或12．【点睛】本题考查函数值以及自变量，解题的关键是掌握函数值的计算方法．练习．（全国八年级课时练习）已知，当时，的值为；当时，y 的值等于9． 【答案】 3 0或6【分析】令y =0即可得到关于x 的一元二次方程，求出x 的值即可；令y =9即可得到关于x 的一元二次方程，求出x 的值即可．【详解】解：∵y =x 2-6x +9中的值为0， ∵令x 2-6x +9=0，解得x =3； ∵y =x 2-6x +9中的值为9， ∵令x 2-6x +9=9，即x 2-6x =0， 解得1206x x ==，． 故答案为：3；0或6．【点睛】本题考查了二次函数与一元二次方程，根据函数值得到关于x 的元二次方程，求出x 的值是解答此题的关键．练习．（全国九年级课时练习）如图，抛物线与轴交于、两点，且点、B 都在原点右侧，抛物线的顶点为点P ，当ABP △为直角三角形时，m 的值为________．【答案】2【分析】设点A （x 1，y 1），B （x 2，y 2），则AB =｜x 2-x 1｜，求出点P （m ，-（m -1）2），由抛物线的对称性知∵ABP 为等腰直角三角形，建立方程｜x 2-x 1｜=2（m -1）2，根据根与系数关系可求得m 值． 【详解】解：设点A （x 1，y 1），B （x 2，y 2），则AB =｜x 2-x 1｜， 令y =0得22210x mx m -+-=，∵x 1+x 2=2m ，x 1·x 2=2m -1，则｜x 2-x 1｜2=4m 2-8m +4=4（m -1）2，由抛物线2221y x mx m =-+-=（x -m ）2－（m -1）2得顶点坐标为P （m ，-（m -1）2）， 抛物线的对称性知∵ABP 为等腰直角三角形， ∵｜x 2-x 1｜=2（m -1）2， 即4（m -1）2=4（m -1）4， 解得：m =2或m =0或m =1，∵抛物线2221y x mx m =-+-与x 轴交于A 、B 两点，且点A 、B 都在原点右侧， ∵2m ＞0且m ≠1且2m -1＞0，即m ＞12且m ≠1， ∵m =2， 故答案为：2．【点睛】本题考查二次函数的图象与性质、等腰直角三角形的判定与性质、根与系数的关系、解高次方程等知识，熟练掌握二次函数的性质是解答的关键．意创造非凡、探索未来．某商店准备用2400元购进一批冰墩墩钥匙扣出售．假如每个钥匙扣的进价降低20%，则可以多买50个．(1)求每个冰墩墩钥匙扣的进价；(2)市场调查发现：当每个冰墩墩钥匙扣的售价是20元时，每周可以销售200个；每涨价1元，每周少销售10个．设每个冰墩墩钥匙扣的售价是x 元（x 是大于20的正整数），每周总利润是w 元． ①求w 与x 的函数关系，并求每周总利润的最大值；②当每周总利润大于1870元时，直接写出每个冰墩墩钥匙扣的售价． 【答案】(1)每个冰墩墩钥匙扣的进价为12元(2)①2105204800w x x =-+-，最大值为1960元；②每个冰墩墩钥匙扣的售价为24元或25元或26元或27元或28元【分析】（1）设每个冰墩墩钥匙扣的进价为x 元，根据题意列出分式方程，进而计算求解即可；（2）①根据题意列出二次函数关系，根据二次函数的性质求得最大利润即可；②根据题意列出方程，根据二次函数的性质求得x 的范围，根据题意取整数解即可．(1)设每个冰墩墩钥匙扣的进价为x 元，由题意得：()2400240050120%x x +=-，解得12x =，经检验，12x =是原方程的解且符合题意，答：每个冰墩墩钥匙扣的进价为12元；(2)①()()122001020w x x =---⎡⎤⎣⎦2105204800x x =-+-()210261960x =--+ ∵0a <且x 是大于20的正整数∵当26x =时，w 有最大值，最大值为1960元②由题意得，21052048001870x x -+-=，解得23x =或29∵抛物线开口向下，x 是大于20的正整数∵当2329x <<时，每周总利润大于1870元，∵售价为24元或25元或26元或27元或28元．【点睛】本题考查了分式方程的应用，二次函数的应用，一次函数的应用，根据题意列出方程或关系式是解题的关键．练习．（全国九年级课时练习）如图，已知二次函数的图象经过点．(1)求a 的值和图象的顶点坐标；(2)点(,)Q m n 在该二次函数图象上；①当11n =时，求m 的值，②当m ＜x ＜m -3时，该二次函数有最小值2，请直接写出m 的取值范围． 【答案】(1)2a =；()1,2-(2)①4m =-或2；②41m -<-【分析】（1）将点P 的坐标代入二次函数解析式可得关于a 的方程，再解方程即可得出a 的值．将二次函数的解析式进行配方，即可得到图象的顶点坐标；（2）①将点Q 的坐标代入二次函数解析式，求解方程即可得到m 的值；②根据当1x =-时，二次函数取最小值为2，得出13m m -≤+＜，解关于m 的不等式组即可．（1）解：∵二次函数21y x ax a =+++的图象经过点()2,3P -，∵()()23221a a =-+⨯-++．解得：a =2；∵二次函数的解析式为()222312y x x x =++=++．∵图象的顶点坐标是()1,2-．（2）①∵点(),Q m n 在该二次函数图象上，且n =11，∵21123m m =++．解得14m =-，22m =，∵m 的值为-4或2；②∵二次函数()222312y x x x =++=++的最小值为2，∵13m m -≤+＜，解得：41m -≤-＜，∵m 的取值范围是41m -≤-＜．【点睛】本题考查了二次函数的图象和性质，解一元二次方程，二次函数的最值，能够正确应用数形结合思想是解题关键．题型4 根据二次函数系数求对应方程根的情况或与x 轴交点情况例1．（2022·全国·九年级专题练习）如图，抛物线2y ax =与直线y bx c =+的两个交点坐标分别为(2,4)A -，(1,1)B ，则方程2ax bx c =+的解是________________.【答案】12x =-，21x =【分析】二次函数图象与一次函数图象交点的横坐标即为2ax bx c =+的解：12x =-，21x =.【详解】解：抛物线 2y ax =与直线y bx c =+的两个交点坐标分别为 ()2,4A - ， ()1,1B ，∴方程组2y ax y bx c ⎧=⎨=+⎩的解为1124x y =-⎧⎨=⎩ ，2211x y =⎧⎨=⎩ ， 即关于x 的方程 20ax bx c --=的解为12x =-，21x =，所以方程2ax bx c =+ 的解是 12x =-，21x =，故答案为： 12x =-，21x =．【点睛】本题考查了函数图象与方程的解的关系，函数与方程是密不可分的，方程的根的个数问题，往往可以转化为两个函数图象的交点问题．例2．（2022·福建南平·九年级期末）如图，抛物线2y ax bx c =++的对称轴为1x =，点P 是抛物线与x 轴的一个交点，若点P 的坐标为()4,0，则关于x 的一元二次方程20ax bx c ++=的解为__________．【答案】124,2x x ==-【分析】根据函数的对称轴和点P 的坐标可以得出与x 轴的另一交点坐标，从而得出结论．【详解】解：∵抛物线2y ax bx c =++的对称轴为x ＝1，点P 是抛物线与x 轴的一个交点，坐标为（4，0），∵抛物线与x 轴的另一个交点坐标为（−2，0），∵关于x 的一元二次方程20ax bx c ++=的解为：124,2x x ==-．故答案为：124,2x x ==-．【点睛】本题考查抛物线与x 轴的交点问题，关键是对二次函数性质的掌握和运用．练习1．（2022·全国·九年级课时练习）已知抛物线2y x bx c =++的部分图像如图所示，则方程20x bx c ++=的解是___________【答案】11x =-或23x =【分析】根据抛物线的轴对称性即可求得抛物线与x 轴的另一个交点的坐标，这两个交点的横坐标就是方程20x bx c ++=的解．【详解】解：由图像可知抛物线与x 轴的一个交点坐标为(1,0)-，对称轴为直线1x =，设抛物线与x 轴的另一个交点为2(,0)x ，则2112x -+=， 解得：23x =．∵方程20x bx c ++=的解为11x =-或23x =．故答案为：11x =-或23x =【点睛】本题考查的是利用二次函数的图像求解一元二次方程，以及抛物线的对称性问题，正确理解抛物线与x 轴的交点的横坐标与相应的一元二次方程的根之间的关系是解题的关键．练习2．（2021·湖北·武汉二中广雅中学九年级阶段练习）如图，已知抛物线223y x x =--与x 轴交于A 、B 两点，与y 轴交于点C ，直线25y kx k =-+与它有三个公共点时，则k 值为______．【答案】222-+或53【分析】先确定A 、B 、C 三点坐标，y =kx -2k +5=k （x -2）+5，可得直线经过定点（2，5）画出图形，分别找到两个极限位置，求出k 的值．【详解】解：∵223y x x =--∵当y =0时，解得x =-1或x =3；当x =0时，解得y =3∵A （-1,0），B （3,0），C （0，3）∵y =kx -2k +5=k （x -2）+5∵直线25y kx k =-+必过定点（2，5）要使直线y =kx -2k +5与图像有三个公共点，则可得到如图所示的两个极限位置，①直线经过A 、N ，此时将点A （-1，0）代入可得：0=-k -2k +5，解得：k =53②直线经过点N 与抛物线相切时，由题意可得：22325x x kx k -++=-+整理得：2(2)220x k x k +--+=2(2)4(22)0k k ∆=---+=，解得222k =-±由图像可知，k ＞0，则222k =-+综上可知，25y kx k =-+与223y x x =--有三个公共点时，则k 值为222-+或53． 故答案为222-+或53．【点睛】本题主要考查了一次函数与抛物线的交点问题，根据题意找到恰好有3个公共点的位置以及数形结合思想的运用是解答本题的关键．练习3．（2020·北京房山·九年级期中）若二次函数23y kx x =--的图象与轴有交点，则k 的取值范围是_______．【答案】13k ≥-且0k ≠##k ≠0且k ≥13- 【分析】根据二次函数的定义可知0k ≠，由题意令0y =，得出一元二次方程，根据一元二次方程根的判别式大于或等于0，解不等式即可求解．【详解】解：∵二次函数223y kx x =--的图象与x 轴有交点，令0y =，则2230kx x --=，∵4120k =+≥且0k ≠，解得13k ≥-且0k ≠． 故答案为：13k ≥-且0k ≠． 【点睛】本题考查了二次函数的定义以及二次函数与x 轴交点问题，转为一元二次方程根的判别式是解题的关键，注意不要漏掉0k ≠．练习．（全国九年级专题练习）已知抛物线与轴的一个交点为，则代数式2225m m -+=_____________． 【答案】15【分析】把点(,0)m 代入二次函数解析式可得25m m -=，然后问题可求解．【详解】解：把点(,0)m 代入二次函数解析式得：250m m --=，则有25m m -=，∵()222252515m m m m -+=-+=； 故答案为15．【点睛】本题主要考查二次函数的图象与性质，熟练掌握二次函数的图象与性质是解题的关键．。

一元二次不等式的解法在数学中，一元二次不等式是指形如ax^2+bx+c>0或ax^2+bx+c<0的二次不等式。

解一元二次不等式的方法可以通过图像法、代入法和判别法来实现。

本文将介绍这三种解法，并通过实例来说明其具体步骤。

图像法图像法是解一元二次不等式最直观的方法之一，它通过绘制一元二次函数的图像来找到不等式的解集。

下面以一元二次不等式x^2-4x+3>0为例来说明图像法的解题步骤：首先，将不等式转化为方程x^2-4x+3=0，求出方程的根。

我们可以通过求解x的一元二次方程来得到根，即使用求根公式x = (-b±√(b^2-4ac))/(2a)。

将方程x^2-4x+3=0代入求根公式中，得到x=1和x=3。

其次，在数轴上绘制一元二次函数y=x^2-4x+3的图像。

根据函数的开口方向和图像的凹凸性，我们可以确定函数在x<1和x>3的区间上为正值，即图像在该区间上位于x轴之上。

最后，根据不等式的正号，我们可以得出一元二次不等式x^2-4x+3>0的解集为x<1或x>3。

代入法代入法是通过代入特定的数值来判断一元二次不等式的真假。

下面以一元二次不等式x^2-4x+3>0为例来说明代入法的解题步骤：首先，将不等式转化为方程x^2-4x+3=0，求出方程的根。

我们可以使用同样的方法得到x=1和x=3。

其次，选择一些特定的数值，代入一元二次不等式中，判断不等式的真假。

例如，选择x=0、x=2和x=4来代入不等式。

计算得到代入x=0时，不等式为3>0，代入x=2时，不等式为-1>0，代入x=4时，不等式为3>0。

根据计算结果，我们可以确定不等式在x<1和x>3的区间上为真。

最后，根据不等式的真假，我们可以得出一元二次不等式x^2-4x+3>0的解集为x<1或x>3。

判别法判别法是解一元二次不等式的一种常用方法，它利用一元二次不等式的判别式来确定不等式的解集。

初中数学如何求解一元二次方程的小数解要求解一元二次方程的小数解，我们可以使用配方法、求根公式或图像法。

下面将详细介绍这三种方法的步骤和应用。

方法一：配方法配方法是一种通过变换方程的形式来求解一元二次方程的方法。

它的基本思想是将方程转化为完全平方形式，然后求解。

步骤：1. 将方程表示成标准形式：ax² + bx + c = 0，其中a，b和c是已知的实数常数，且a ≠ 0。

2. 如果方程的系数a不为1，则将方程两边都除以a，使得方程的首项系数为1。

3. 将方程的常数项c分解为两个数的乘积，这两个数的和等于方程的一次项系数b。

假设这两个数为m和n。

4. 重新排列方程，将一次项bx拆分为mx + nx。

5. 将方程按照完全平方的形式进行重新组合，即(x + m)(x + n) = 0。

6. 使用零乘法，将方程拆分为两个线性因式，即x + m = 0和x + n = 0。

7. 解这两个方程，得到x的值。

这些值即为方程的小数解。

举例来说，考虑方程2x² + 5x - 3 = 0。

1. 将方程表示成标准形式，得到2x² + 5x - 3 = 0。

2. 系数a为2，不为1，所以我们将方程两边都除以2，得到x² + (5/2)x - 3/2 = 0。

3. 将常数项-3/2分解为两个数的乘积，这两个数的和等于5/2。

我们可以将-3/2分解为1/2和-2，因为1/2 + (-2) = 5/2。

4. 重新排列方程，得到x² + (1/2)x - 2x - 3/2 = 0。

5. 将方程按照完全平方的形式进行重新组合，即(x + 1/2)(x - 2) = 0。

6. 使用零乘法，将方程拆分为两个线性因式，即x + 1/2 = 0和x - 2 = 0。

7. 解这两个方程，得到x = -1/2和x = 2。

这两个值即为方程的小数解。

方法二：求根公式求根公式是一种通过直接计算方程的根的公式来求解一元二次方程的方法。

21.3 二次函数与一元二次方程（第二课时）实验中学-余志高一、教材分析：《利用二次函数的图像解一元二次方程》选自义务教育课程教科书《数学》（沪科版）九年级上册第21章第3节，这节课是在学生学习了二次函数与一元二次方程的关系，知道二次函数的图像与x 轴交点个数的不同对应了一元二次方程有两个不等实根、有两个相等实根、没有实根的三种情况下继续经历用图象法求一元二次方程的近似根的过程，获得用图象法求方程近似根的体验及了解一元二次不等式的解集.．这也突出了课标的要求：注重数形结合。

二、教学目标【知识与技能】掌握二次函数y=ax2+bx+c的图象与x轴的交点个数与一元二次方程ax2+bx+c=0的解的情况之间的关系,会用二次函数的图象求一元二次方程的近似解以及一元二次不等式的解集.经历用图象法求一元二次方程的近似根的过程，获得用图象法求方程近似根的体验．【过程与方法】经历探究二次函数与一元二次方程、一元二次不等式关系的过程,体会函数、方程、不等式之间的联系.利用图象法求一元二次方程的近似根，重要的是让学生懂得这种求解方程的思路，体验数形结合思想．【情感、态度与价值观】进一步培养学生的综合解题能力,掌握解决问题的方法,培养探究精神.重点难点【重点】用函数图象求一元二次方程的近似解及一元二次不等式的解集.【难点】利用二次函数的图象求一元二次方程的近似根【教学方法】学生合作交流学习法三、教学过程Ⅰ．创设问题情境，引入新课[师]上节课我们学习了二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴的交点坐标和一元二次方程ax2＋bx＋c＝0(a≠0)的根的关系，懂得了二次函数图象与x轴交点的横坐标，就是y＝0时的一元二次方程的根，于是，我们在不解方程的情况下，只要知道二次函数与x轴交点的横坐标即可．但是在图象上我们很难准确地求出方程的解，所以要进行估算．本节课我们将学习利用二次函数的图象估计一元二次方程的根．Ⅱ．讲授新课【例】用图象法求一元二次方程x2+2x-1=0的近似解(精确到0.1).解:画出函数y=x2+2x-1的图象,如图.由图象可知,方程有两个实数根,一个在-3和-2之间,另一个在0和1之间.先求位于-3和-2之间的根.由图象可估计这个根是-2.5或-2.4,利用计算器进行探索,见下观察上表可以发现,当x分别取-2.5和-2.4时,对应的y由正变负,可见在-2.5与-2.4之间肯定有一个x使y=0,即有方程x2+2x-1=0的一个根.题目只要求精确到0.1,这时取x=-2.5或x=-2.4作为根都符合要求.但当x=-2.4时,y=-0.04比y=0.25(x=-2.5)更接近0,故选x=-2.4.同理,可求出方程x2+2x-1=0在0和1之间精确到0.1的另一个根.方程x2+2x-1=0的近似解还可以这样求:分别画出函数y=x2和y=-2x+1的图象,如图,它们的交点A、B的横坐标就是方程x2+2x-1=0的根.函数图象求一元二次不等式的解集.：画出函数y=ax2+bx+c(a≠0）的图象，不等式ax2+bx+c>0的解集为图象在x轴上方的点所对应的x值所组成的集合，不等式ax2+bx+c<0的解集为图象在x轴下方的点所对应的x值所组成的集合.如下表：ax2+bx+c>0(a>0)的解集是x<x1或x>x2ax2+bx+c<0(a>0)的解集是x1<x<x2ax2+bx+c>0(a<0)的解集是x1<x<x2ax2+bx+c<0(a<0)的解集是x<x1或x>x2Ⅲ．课堂练习P34随堂练习Ⅳ．课时小结本节课学习的内容：1．经历了探索二次函数与一元二次方程的关系的过程，体会了方程与函数之间的联系；2．经历了用图象法求一元二次方程的近似根的过程，获得了用图象法求方程近似根的体验．3．了解一元二次方程不等式的解集可由二次函数图象直接得出结论。

浅谈用图像法解一元二次方程高一12班 薛雨晴现在有这样一个题目，设关于x 的方程2kx 2+2x-3k-2=0的两根一个大于1，一个小于1，求k 的取值范围。

通常看到这类题目，我们会有韦达定理来求出答案，过程是这样的 方程可变成x 2+ x+ =0设二次函数为y=x 2+ x+ △>0设方程两根为x1,x2. (x1-1)(x2-1)<0→…… k >0可见解题过程繁琐。

但是，换一个角度，用图像法更加方便直观。

一、何为图像法:顾名思义就是用画图的方法直观地解题。

二、在一元二次方程中图像法的使用方法在研究一元二次方程根的分布情况时，我们可以使用图像法。

在运用图像法时，我们要从四个方面考虑：1.开口方向 2.根的多少 3.对称轴分布 4.分界点。

考虑了这几方面，这类题目的解题时就会明朗很多。

我们再回头看开篇的那道题目。

2 2k -3k-2 2k2 2k -3k-2 2k（图像法）从图像中可以看出，开口向上，对称轴没有范围，有两个根。

另外当x=1时，y <0 答案是k >0相比之下，图像法明显简单了许多。

三、图像法思考能训练我们的思维相比繁琐的代数解题方法，图像法更加直观易懂。

图像法更加可以培养空间想象力，开阔思维性，敏捷性。

学数学靠的是对题目的理解和做题时的一种直觉。

图像法能够提高综合运用数学知识的能力。

在一些抽象的数学题目面前，图像法能够使题目具体化。

多掌握一种数学解题方法，对数学的认识也会更深一步。

正如萧伯纳所说的：你有一个苹果，我有一个苹果，彼此交换一下，我们彼此仍然是各有一个苹果；但你有一种思想，我有一种思想，彼此交换，我们就都有了两种思想，甚至更多。

如何求解一元二次方程的根一元二次方程是数学中常见的一种方程形式，它的一般形式为ax^2 + bx + c = 0，其中a、b、c为已知常数，x为未知数。

求解一元二次方程的根是数学学习中的基本内容之一，下面将介绍一些常见的求解方法。

一、因式分解法当一元二次方程可以被因式分解为两个一次因式相乘的形式时，我们可以通过因式分解法求解方程的根。

例如，对于方程x^2 - 5x + 6 = 0，我们可以将其分解为(x - 2)(x - 3) = 0，从而得到x = 2和x = 3两个根。

二、配方法对于一些无法直接因式分解的一元二次方程，我们可以通过配方法来求解其根。

配方法的基本思想是通过添加适当的常数使得方程可以被因式分解。

例如，对于方程x^2 + 6x + 8 = 0，我们可以通过添加一个恰当的常数使得方程可以被因式分解为(x + 2)(x + 4) = 0，从而得到x = -2和x = -4两个根。

三、求根公式求根公式是求解一元二次方程的一种常用方法。

对于一元二次方程ax^2 + bx + c = 0，其根可以通过求根公式x = (-b ± √(b^2 - 4ac))/(2a)来得到。

其中，±表示两个根，√表示平方根。

通过求根公式，我们可以得到一元二次方程的解。

四、图像法图像法是一种直观的求解一元二次方程根的方法。

我们可以通过绘制一元二次方程的图像来观察其根的情况。

对于一元二次方程ax^2 + bx + c = 0，我们可以绘制出其对应的抛物线图像，并通过观察图像与x轴的交点来得到方程的根。

这种方法在直观上帮助我们理解方程根的性质。

五、完全平方差公式完全平方差公式是一种求解一元二次方程根的特殊方法。

对于一元二次方程ax^2 + bx + c = 0，如果其可以写成(x + p)^2 = q的形式，那么方程的根可以通过求解x + p = ±√q来得到。

这种方法在某些特殊情况下能够简化方程的求解过程。

一元二次方程求根方法一元二次方程是初中数学中的重要内容，也是学生们常常遇到的问题之一。

在解一元二次方程时，我们可以运用不同的方法来求根，本文将介绍几种常见的求根方法，并通过具体例子进行说明。

首先，我们来讨论一元二次方程的标准形式：ax² + bx + c = 0。

其中，a、b、c 为已知实数，且a ≠ 0。

求解一元二次方程的根，可以运用以下几种方法。

一、因式分解法当一元二次方程可以因式分解时，我们可以利用因式分解法来求解。

例如，考虑方程x² - 5x + 6 = 0。

我们可以将方程进行因式分解，得到(x - 2)(x - 3) = 0。

由此可知，方程的两个根分别为x = 2和x = 3。

二、配方法当一元二次方程无法直接因式分解时，我们可以运用配方法来求解。

例如，考虑方程x² - 6x + 8 = 0。

我们可以通过配方法将方程转化为完全平方的形式，即(x - 3)² - 1 = 0。

进一步化简，得到(x - 3)² = 1。

通过开平方运算，我们可以得到方程的两个根分别为x = 2和x = 4。

三、求根公式求根公式是解一元二次方程的常用方法之一。

对于一元二次方程ax² + bx + c = 0，其根可以通过求根公式x = (-b ± √(b² - 4ac)) / (2a)来得到。

例如，考虑方程x² - 4x - 5 = 0。

我们可以根据求根公式计算出方程的两个根分别为x = 5和x = -1。

四、图像法图像法是一种直观且易于理解的求解一元二次方程的方法。

我们可以通过绘制一元二次方程的图像，来观察方程的根。

例如，考虑方程x² - 2x - 3 = 0。

我们可以绘制出该方程的图像，发现方程的两个根分别为x = 3和x = -1。

五、因子法当一元二次方程的系数为整数时，我们可以通过因子法来求解。

例如，考虑方程x² - 7x + 10 = 0。

图像法解一元二次方程浅析教学目标(1) 会求出二次函数与坐标轴的交点坐标；(2) 会利用二次函数的图象求一元二次方程的近似解。

(3) 总结出二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系，表述何时方程有两个不等的实根、两个相等的实根和没有实根。

重点和难点：重点：(1)会求出二次函数与坐标轴的交点坐标；(2)总结出二次函数与x轴交点的个数与一元二次方程的根的个数之间的关系，表述何时方程有两个不等的实根、两个相等的实根和没有实根。

难点：一元二次方程的图象解法一、预习交流：画出函数y x22x 3的图象，根据图象回答下列问题.⑴翻线与渐几个公共点?交点的坐标分别是什么？⑵ 条取何值时，函数广火-2广3的值是0?（3）一元二次方程x2-2v-3 = 0有没有极？如果有根,它的根是什么？（4）-元二舫散：-21-3=0 wiftgy寸-小3乐输佛筋鼬标轴么好？（5）傩鼬项□炫桂冰+加+c=瞰敏拥日通绑=ar+版+c 乐敝决辅掀甄的关勰？小结：二次函数与一元二次方程有密切的联系，二次函数与x轴的两个交点的横坐标即是对应的一元二次方程的两根，根的判别式决定着二次函数与x轴交点的个数和一元二次方程根的情况。

二.例题欣赏：例1 用图象法讨论一元二次方程x^-3x-2 = 0的根(精确到0.1 )分析：先画图像，再观察图像，找出图像与x轴的公共点，最后再求出方程的根的近似值。

解(1)画抛物线y^x2 ~3x~ 2(图5-27 ).(2 )观察图象找出图象与*轴的公共点，可以发现，在-1与0之间以及3与4之间各有一个根.为求-1和。

之间的根，可分别计算尸0,》=-由于当x=T时，当工= -0.5时，i <0tTORO-1»-0.5ZR.可再的和也力耽为5靴够分点枷氏利册辩求顺褪艇数底歹惕可师由我个根在-0,6和-03丽,由于槌蔓端蒯0』,晒可将-0.6或-05看作二次方爵』-2 = 0 .同舰,可以黜-亡次方程F项- X 0的另-㈱的顾值.赚得批荆见洲眼5粉询翩破翻如春忙l2tt§rJx-2=0«ffi(W10J),(2)由于图象乐猿有公共点，所以-元二次方程f d + 3=0没有实数根例3 用图象法讨论一元二次方程F r十｝ = 0的根.解（1 ）画出抛物线广寸- l 土（图5-29 ）,|¥1 5-29、课堂小结：二次函数y=ax2+bx+c的图象和x轴交点的三种情况与一元二次方程根的关系:四、当堂达标：1 .如果关于x的一元二次方程x2— 2x+n= 0有两个相等的实数根, 则n=，此时抛物线y=x2— 2x+m与x轴有个交点.2. 已知抛物线y=x2- 8x + c的顶点在x轴上，贝U c =.3. 抛物线y=2x2 - 3x — 5与y轴交于点,与x轴交于点.4. 一元二次方程3 x2+x- 10=0的两个根是x i=—2 , X2=5,那么二次32函数y= 3x +x —10与x轴的父点坐标是.五、课外作业：1、必做题：习题5.9 A组1—— 3.2、选做题：习题5.9 B组.。

一元二次不等式及其解法知识点：1、一元二次不等式：只含有一个未知数，并且未知数的最高次数是2的不等式．同步练习：1、不等式2654x x +<的解集为（ ） A ．41,,32⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ B ．41,32⎛⎫- ⎪⎝⎭C ．14,,23⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭ D ．14,23⎛⎫- ⎪⎝⎭3、若不等式210x mx ++>的解集为R ，则m 的取值范围是（ ） A ．RB ．()2,2-C ．()(),22,-∞-+∞D ．[]2,2-4、设一元二次不等式210ax bx ++>的解集为113x x ⎧⎫-<<⎨⎬⎩⎭，则ab 的值是（ ）A ．6-B ．5-C ．6D ．55、不等式()221200x ax a a --<<的解集是（ ）A ．()3,4a a -B ．()4,3a a -C ．()3,4-D ．()2,6a a 6、不等式220ax bx ++>的解集是1123x x ⎧⎫-<<⎨⎬⎩⎭，则a b -=（ ） A ．14- B ．14 C ．10- D ．107、不等式222693191122x x x x -+++⎛⎫⎛⎫≤⎪ ⎪⎝⎭⎝⎭的解集是（ ）A ．[]1,10-B ．()[),110,-∞-+∞C ．RD ．(][),110,-∞-+∞ 8、不等式()()120x x --≥的解集是（ ）A ．{}12x x ≤≤B ．{}12x x x ≥≤或C ．{}12x x <<D ．{}12x x x ><或 9、不等式()20ax bx c a ++<≠的解集为∅，那么（ ）A ．0a <，0∆>B ．0a <，0∆≤C ．0a >，0∆≤D ．0a >，0∆≥11、若01a <<，则不等式()10a x x a ⎛⎫--> ⎪⎝⎭的解是（ ） A ．1a x a<<B ．1x a a<< C ．x a <或1x a>D ．1x a<或x a >12、不等式()130x x ->的解集是（ ） A ．1,3⎛⎫-∞ ⎪⎝⎭B ．()1,00,3⎛⎫-∞ ⎪⎝⎭C ．1,3⎛⎫+∞ ⎪⎝⎭D ．10,3⎛⎫ ⎪⎝⎭13、二次函数()2y ax bx c x R =++∈的部分对应值如下表：则不等式20ax bx c ++>的解集是____________________________．14、若0a b >>，则()()0a bx ax b --≤的解集是_____________________________．15、不等式20ax bx c ++>的解集为{}23x x <<，则不等式20ax bx c -+>的解集是________________________．16、不等式2230x x -->的解集是___________________________． 17、不等式2560x x -++≥的解集是______________________________． 18、()21680k x x --+<的解集是425x x x ⎧⎫<->⎨⎬⎩⎭或，则k =_________． 19、已知不等式20x px q ++<的解集是{}32x x -<<，则p q +=________． 20、求下列不等式的解集：⑴ ()()410x x +--<； ⑵ 232x x -+>； ⑶ 24410x x -+>．22、已知不等式220ax bx ++>的解集为1123x x ⎧⎫-<<⎨⎬⎩⎭，求a 、b 的值．23、已知集合{}290x x A =-≤，{}2430x x x B =-+>，求A B ，A B ．。

求解一元二次方程根的方法一元二次方程是指具有形如ax^2+bx+c=0的方程，其中a、b、c 是已知常数，x是未知数。

求解一元二次方程的根是数学中的一个重要问题，下面将介绍几种常见的方法。

一、因式分解法对于一元二次方程ax^2+bx+c=0，如果可以将其因式分解为(a_1x+b_1)(a_2x+b_2)=0的形式，那么方程的根就是方程(a_1x+b_1)=0和(a_2x+b_2)=0的根。

通过因式分解法，可以将一元二次方程转化为一次方程，进而求得方程的根。

二、配方法配方法是指通过添加或减去适当的常数，将一元二次方程转化为完全平方形式的方程，进而求得方程的根。

具体步骤如下：1. 若方程的二次项系数a不为1，可通过除以a将其化为1；2. 将方程的一次项系数b除以2，并将结果的平方加减到方程两边；3. 将方程右边的常数项c移到方程左边，形成完全平方形式的方程；4. 对方程两边开平方，得到方程的解。

三、求根公式法求根公式法是指通过求解一元二次方程的根的公式，直接求得方程的根。

一元二次方程的根的公式为：x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}根据该公式，我们可以直接计算出方程的根。

四、图像法图像法是指通过绘制方程的图像，观察图像与x轴的交点来求解方程的根。

具体步骤如下：1. 绘制方程的函数图像，横轴表示x，纵轴表示方程的值y；2. 观察图像与x轴的交点，即为方程的根。

需要注意的是，图像法只适用于观察方程在图像上的根的个数和大致位置，无法精确求解根的值。

求解一元二次方程的根可以通过因式分解法、配方法、求根公式法和图像法等多种方法进行。

在实际问题中，我们可以根据具体情况选择合适的方法来求解方程的根。

同时，要注意方程的根可能有一个、两个或无解的情况，需要综合考虑方程的系数和常数项来判断方程的解的情况。