周周清(2)第二章:不等式与不等式组习题精美课件
- 格式:ppt
- 大小:407.50 KB
- 文档页数:6

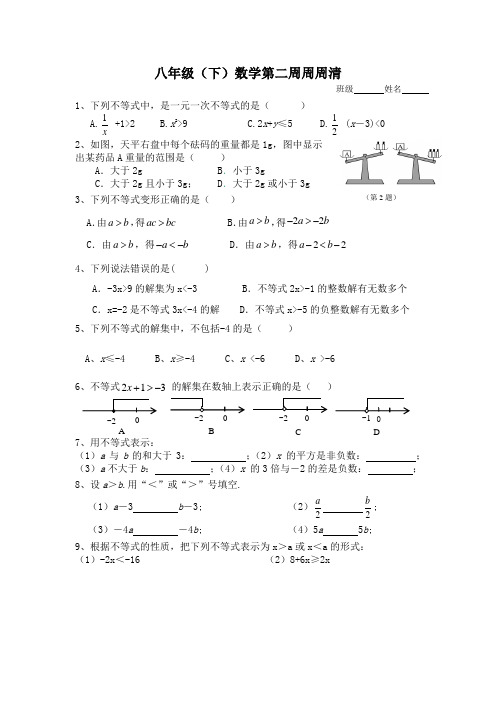
1、下列不等式中,是一元一次不等式的是( )A.x 1 +1>2B.x 2>9C.2x+y ≤5 D.21 (x -3)<0 2、如图,天平右盘中每个砝码的重量都是1g ,图中显示出某药品A 重量的范围是( )A.大于2g B .小于3gC .大于2g 且小于3g ; D.大于2g 或小于3g3、下列不等式变形正确的是( )A .由a b >,得a c b c >B .由a b >,得22a b ->-C .由a b >,得a b -<-D .由a b >,得22a b -<-4、下列说法错误的是( )A .-3x>9的解集为x<-3B .不等式2x>-1的整数解有无数多个C .x=-2是不等式3x<-4的解D .不等式x>-5的负整数解有无数多个5、下列不等式的解集中,不包括-4的是( )A 、x ≤-4B 、x ≥-4C 、x <-6D 、x >-66、不等式312->+x 的解集在数轴上表示正确的是( )7、用不等式表示:(1)a 与b 的和大于3: ;(2)x 的平方是非负数: ;(3)a 不大于b : ;(4)x 的3倍与-2的差是负数: ;8、设a >b .用“<”或“>”号填空.(1)a -3 b -3; (2)2a 2b ; (3)-4a -4b ; (4)5a 5b ;9、根据不等式的性质,把下列不等式表示为x >a 或x <a 的形式:(1)-2x <-16 (2)8+6x ≥2x(第2题) -2A B C D10、解下列不等式,并把解集在数轴上表示出来:(1)3(x+1)<4(x+2)-3 (2)215132x x-+-≤1。


《高三数学周周清》(02)一选择题:(每小题5分,共60分)1、已知集合{}(){},2lg |,0,2|2x x y x N x y y M x -==>== 则N M ⋂为( ) A 、(1,2) B 、(1,+∞) C 、[)+∞,2 D 、[)+∞,12、集合{}{},10|,20|<≤=≤≤=x x B x x A 下列表示从A 到B 的函数是( ) A 、x y x f 31:=→ B 、x y x f 2:=→ C 、x y x f 21:=→ D 、x y x f =→: 3、已知集合{},02|2>+-=a x x x A ,且1,A ∉则实数a 的取值范围是( ) A 、(]1,∞- B 、[)+∞,1 C 、[)+∞,0 D 、()1,-∞- 4、已知函数()()()⎩⎨⎧>≤+=,02,03x x x x f x则()[]2-f f 的值为( )A 、-1B 、41C 、2D 、4 5、已知函数(),12-+=x x x f 集合(){},|x f x x M ==(){}x f y y N ==|,则( ) A 、N M = B 、N M ⊃ C 、φ=⋂N M D 、N N M =⋃ 6、若集合{},2|>=x x P {},13|>=x x Q 则()()Q P C C RR⋂等于( )A 、()0,∞-B 、(]2,∞-C 、 []0,2-D 、[]2,2-7、设P 与Q 是两个集合,定义集合{},|Q x P x x Q P ∉∈=-且 若{}{},12|,1log |2<-=<=x x Q x x P 则Q P -=( )A 、{}10|<<x x B 、{}10|≤<x x C 、{}21|≤≤x x D 、{}32|<≤x x 8、已知全集{},0145|2≤--=x x x A {}121|-<<+=m x m x B ,且,φ≠B若,A B A =⋃则( )A 、43≤≤-mB 、43<<-mC 、42<<mD 、42≤<m9、下列函数中,在其定义域内既是增函数又是奇函数的是( ) A 、()0log 2>-=x x y B 、()R x x x y ∈+=3 C 、()R x y x ∈=3 D 、()01≠=x xy 10、已知函数()[)()⎪⎩⎪⎨⎧∞-∈+-++∞∈=0,,23,0,232x a a x x x x f 在区间()+∞∞-,是增函数,则常数a 的取值范围是( )A 、21≤≤aB 、21≥≤a a 或C 、21<<aD 、21><a a 或11、设函数()x f 是定义在R 上的以5为周期的奇函数,若(),12>f (),3332-++=a a a f 则a 的取值范围是( )A 、()()302,,⋃-∞-B 、()()∞+⋃-,,302C 、()()∞+⋃-∞-,,02D 、()()∞+⋃∞-,,3012、已知()x f y =是定义在R 上的奇函数,当0>x 时,(),2-=x x f 则不等式()21<x f 的解集是( ) A 、⎭⎬⎫⎩⎨⎧<<250|x x B 、⎭⎬⎫⎩⎨⎧<<-023|x x C 、⎭⎬⎫⎩⎨⎧<≤<<-250023|x x x 或 D 、⎭⎬⎫⎩⎨⎧<≤-<25023|x x x 或 二、填空题(每小题4分,共16分)13、已知集合{}{},12,3,1,,32--==m B m A 若,B A ⊆则实数m 的值为 .14、已知函数(),tan 1x x f +=若(),3=a f 则()=-a f .15、定义在[]11,-的偶函数()x f ,当[]1,0∈x 时为减函数,则不等式:()x f x f <⎪⎭⎫⎝⎛-21的解集为 .16、若函数()()2122+-+=x a x x f 在区间(]4,∞-上是减函数,那么实数a 的取值范围是 .《高三数学周周清》(02)姓名: 分数:一、选择题;1-5: ;6-10 : ;11-12: 。


检测内容:2.1~2.2得分________卷后分________评价________一、选择题(每小题3分,共24分)1.(-8)+(+5)=( B )A.3 B.-3 C.13 D.-132.某日,北京的最低气温是-11 ℃,嘉兴的最低气温是-1 ℃,则这日北京的最低气温比嘉兴的最低气温低( C )A.-12 ℃B.-10 ℃C.10 ℃D.12 ℃3.下列各式结果等于3的是( C )A.(-2)-(-9)+(+3)-(-1)B.0-1+2-3+4-5C.4.5-2.3+2.5-3.7+2D.-2-(-7)+(-6)+0+(+3)4.绝对值小于2 018的所有整数的和为( C )A.3 B.4 C.0 D.75.若x是3的相反数,|y|=4,则x-y的值是( D )A.-7 B.1C.-1或7 D.1或-76.如图,数轴上A,B两点所对应的数分别为a,b,则下列结论正确的是( B )A.a+b>0 B.b-a<0C.a-b<0 D.(-a)+(-b)<07.一个病人每天下午需要测量血压,下表是该病人这周一到周五与前一天相比较收缩压变化情况:A.100单位B.110单位C.120单位D.130单位王博在做课外习题时遇到如图所示的一道题,其中●是被污损而看不清的一个数,它翻看答案后得知该题的计算结果为15,则●表示的数是( D )A.10 B.-4 C.-10 D.10或-4二、填空题(每小题4分,共20分)9.(2018·德州)计算:|-2+3|=__1__.10.某公交车原坐有22人,经过4个站点时上下车情况如下(上车为正,下车为负):(+4,-8),(-5,6),(-3,2),(1,-7),则车上还有__12__人.11.分别输入-1,-2,按如图所示的程序运算,则输出的结果的和是__1__.12.已知有理数-1,+11,-2,-8,请你通过有理数的加减混合运算,使运算结果最大,最大结果为__22__.○13读一读:式子“1+2+3+4+…+100”表示从1开始的100个连续自然数的和,由于式子比较长,书写不方便,为了简便起见,我们将其表示为错误!错误!=__错误!__.三、解答题(共56分) 14.(15分)计算:(1)7-(-4)+(-5); 解:原式=7+4-5 =6.(2)12-(-18)+(-7)-15; 解:原式=12+18-7-15 =30-22 =8.(3)-12+11-8+39;解:原式=(-12-8)+(11+39) =-20+50 =30.(4)-7.2-0.8-5.6+11.6;解:原式=(-7.2-0.8-5.6)+11.6 =-13.6+11.6 =-2.(5)(-37)+56-(-217)+(-56).解:原式=(-37+157)+(56-56)=127.15.(12分)某检修小组从A 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,该检修小组一天中七次行驶的记录如下表:(单位: km)(1)在第__五__次记录时距A 地最远;(2)求收工时距A 地有多远,在A 地的什么方向上; (3)若每千米耗油0.4升,问共耗油多少升? 解:(2)-3+7-8+10+2-6-4=-2, ∴收工时在A 的西面,距A 地2千米. (3)(3+7+8+10+2+6+4)×0.4=16(升) ∴共耗油16升.16.(10分)一场游戏规则如下:(1)每人每次抽4张卡片,如果抽到形如的卡片,那么加上卡片上的数字,如果抽到形如的卡片,那么减去卡片上的数字;(2)比较两人所抽到的4张卡片的计算结果,结果大的为胜者. 请你通过计算(要求有计算过程)回答本次游戏获胜的是谁. 小亮抽到的卡片如图所示:小丽抽到的卡片如图所示:解:小亮所抽卡片上的数的计算结果为 12-(-32)+(-5)-4=-7; 小丽所抽卡片上的数的计算结果为 -2-(-13)+5-(-14)=3712,∵-7<3712,∴本次游戏获胜的是小丽.17.(9分)已知|-a|=21,|+b|=21,且|a +b|=-(a +b),求a -b 的值. 解:∵|-a|=21,|+b|=21, ∴a =±21,b =±21, ∵|a +b|=-(a +b), ∴a +b ≤0,∴a =-21,b =-21或a =-21,b =21或a =21,b =-21. 当a =-21,b =-21时,a -b =0; 当a =-21,b =21时,a -b =-42; 当a =21,b =-21时,a -b =42. ∴a -b 的值为0或-42或42.(10分)阅读第(1)小题的计算方法,再用这种方法计算第(2)小题. (1)计算: -556+(-923)+1734+(-312);解:原式=⎣⎡⎦⎤(-5)+(-56)+⎣⎡⎦⎤(-9)+(-23)+(17+34)+⎣⎡⎦⎤(-3)+(-12) =[(-5)+(-9)+17+(-3)]+⎣⎡⎦⎤(-56)+(-23)+34+(-12) =0+(-54)=-114.上面这种解题方法叫做拆项法.(2)计算: (-2 00056)+(-1 99923)+4 00023+(-112).解:原式=(-2 000-56)+(-1999-23)+(4 000+23)+(-1-12)=(-2 000-1 999+4 000-1)+(-56-12)+(-23+23)=0-43+0=-113.。