当前位置：文档之家 › 第二章 线性规划习题课

第二章 线性规划习题课

  • 格式：ppt
  • 大小：397.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

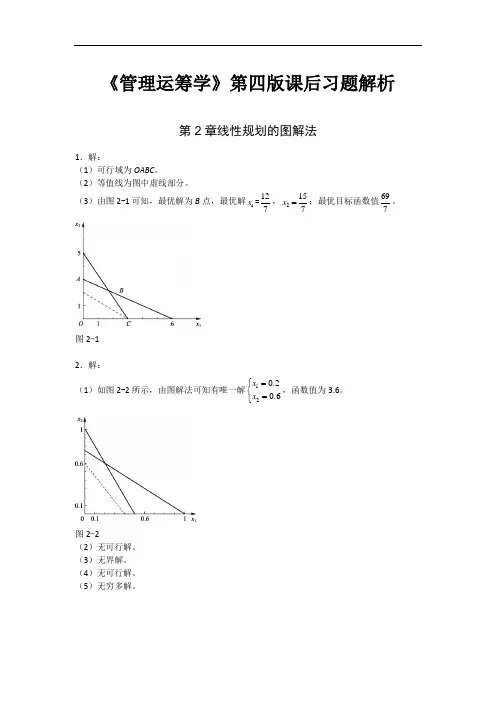
《管理运筹学》第四版 第2章 线性规划的图解法 课后习题解析

《管理运筹学》第四版 第2章 线性规划的图解法 课后习题解析

《管理运筹学》第四版课后习题解析第2章线性规划的图解法1．解：（1）可行域为OABC 。

（2）等值线为图中虚线部分。

（3）由图2-1可知，最优解为B 点，最优解1x =127，2157x =；最优目标函数值697。

图2-12．解：（1）如图2-2所示，由图解法可知有唯一解120.20.6x x =⎧⎨=⎩，函数值为3.6。

图2-2（2）无可行解。

（3）无界解。

（4）无可行解。

（5）无穷多解。

（6）有唯一解1220383x x ⎧=⎪⎪⎨⎪=⎪⎩，函数值为923。

3．解：（1）标准形式12123max 32000f x x s s s =++++1211221231212392303213229,,,,0x x s x x s x x s x x s s s ++=++=++=≥（2）标准形式1212min 4600f x x s s =+++12112212121236210764,,,0x x s x x s x x x x s s --=++=-=≥（3）标准形式12212min 2200f x x x s s ''''=-+++ 1221122122212212355702555032230,,,,0x x x s x x x x x x s x x x s s '''-+-+=''''-+=''''+--=''''≥4．解： 标准形式1212max 10500z x x s s =+++1211221212349528,,,0x x s x x s x x s s ++=++=≥ 松弛变量（0，0） 最优解为1x =1，x 2=3/2。

5．解：标准形式12123min 118000f x x s s s =++++121122123121231022033184936,,,,0x x s x x s x x s x x s s s +-=+-=+-=≥剩余变量（0, 0, 13） 最优解为x 1=1，x 2=5。

北航刘红英数学规划教材课后习题参考答案

北航刘红英数学规划教材课后习题参考答案


ri(x)∇ri(x)
=
2A(x)T r(x),
∇2f (x)
= =
2 2
∑m ∑mi=1
i=1
ri(x)∇2ri(x) ri(x)∇2ri(x)
+ +
2
∑n
i=1
∇ri
(x)(∇ri
(x))T
2A(x)T A(x).
1.6 考虑向量值函数 f (x) : Rn → Rm ，设 f 的每个分量函数 fi(x) 在 x′ 都可微. 写出 f 在 x′ 的Taylor展式，请用 A(x)T 表示 ∇f (x)T (= [∇f1(x), · · · , ∇fm(x)]).
maximize 200x + 60y + 206z
subject to 3x + y + 5z ≤ 8000000
5x + y + 3z ≤ 5000000
x, y, z ≥ 0, 且 x, y, z 是整数.
忽略掉整性要求后，调用 Matlab 中的 linprog.m 函数求解，得最优解 x = 0, y = 500000, z = 1500000，自动满足整性要求.
的最优值相同，将这个问题的最优解投影到 (x, y, z) 所在的空间可以得到原问题的解. 这个问题可以写成线性规划问题：
minimize t1 + t2 + t3 subject to x + y ≤ 1,
2x + z = 3, −t1 ≤ x ≤ t1, −t2 ≤ y ≤ t2, −t3 ≤ z ≤ t3.
解:
(a) ∇f (x) = a, ∇2f (x) = 0n×n; (b) ∇f (x) = (A + AT )x, ∇2f (x) = A + AT ;
第二章 线性规划(管理运筹学,李军)

第二章 线性规划(管理运筹学,李军)

2014-1-28
5
构建线性规划数学模型
习题1：人力资源规划问题 2：00~ 6：00 2名； 6：00~10：00 12名； 10：00~14：00 20名； 14：00~18：00 6名； 18：00~22：00 26名； 22：00~ 2：00 4名。
2014-1-28
6
构建线性规划数学模型：习题1
2014-1-28
2
资源合理利用问题：第5页例2-1
1. 决策变量：x1和x2 2. 目标函数：max Z = 2 x1+3 x2 3. 约束条件： x1+2 x2 8 s.t. 4 x1 16 4 x2 12 x 1， x 2 0
2014-1-28
3
质量检验问题：第6页例2-2
③ ①
1 2 3 4 5 6 7 8
x1
25
图解法求解线性规划
1. 决策变量：x1和x2 2. 目标函数：max Z = 2 x1+4 x2 3. 约束条件： x1+2 x2 8 s.t. 4 x1 16 4 x2 12 x1，x2 0
2014-1-28
26
图解法求解线性规划:习题1
时间段 2：00~ 6：00 6：00~10：00 10：00~14：00 14：00~18：00 18：00~22：00 22：00~ 2：00
2014-1-28
需要人数 2名 12名 20名 6名 26名 4名
上班人数 X1 X2 X3 X4 X5 X6
7
构建线性规划数学模型：习题1
min Z = X1 + X2 +X3+ X4 + X5 + X6 X6 + X1 ≥ 2 X1 + X2 ≥ 12 s.t. X2 + X3 ≥ 20 X3 + X4 ≥ 6 X4 + X5 ≥ 26 X5 + X6 ≥ 4 X1,X2,X3,X4, X5,X6≥ 0
2线性规划的图解法

2线性规划的图解法


16
建模练习
P25,T7(1)建立线性规划模型
17
图解法
目标函数：max Z=50x1+100x2 满足约束条件：x1 +x2≤300
2 x1+x2≤400 x2≤250 x1≥0, x2≥0
18
问题1 ，即不等式组，由于只包含两个决策变量，
可以用图解法来求解。多于两个决策变量不能用图 解法解。 图解法.首先把每个约束条件（代表一个平面） 画在二维坐标轴上。
9
常见的线性规划问题
管理上有很多问题可建立线性规划模型来解决，如 合理利用线材问题。现有一批长度一定的钢管，由于 生产的需要，要求截出不同规格的钢管若干。试问应 如何下料，既满足了生产的需要，又使得使用的原材 料钢管的数量最少。 配料问题。用若干种不同价格不同成分含量的原料， 用不同的配比混合调配出一些不同价格不同规格的产 品，在原料供应量的限制和保证产品成分的含量的前 提下，如何获取最大的利润。
松弛变量和线性规划标准化
为了把一个线性规划标准化，需要有代表没使用的
资源或能力的变量，称之为松弛变量，记为Si。显 然这些松弛变量对目标函数不会产生影响，可以在 目标函数中把这些松弛变量的系数看成零，加了松 弛变量后我们得到如下的例1的数学模型： 目标函数： max Z=50x1+100x2+0s1+0s2+0s3， 约束条件： x1+x2+s1=300, 2x1+x2+s2=400, x2+s3=250, x1,x2,s1,s2,s3≥0
x1 X1+X2=300
100
300
x1 X1+X2=300
21
2，即线 性规划问 题，其解 与问题1 的解有什 么关系？
运筹学课件 第二章线性规划

运筹学课件 第二章线性规划


2020/11/23
广东工业大学管理学院
10
配料问题：由若干种不同价格、不同成分含量的原料，用 不同的配比混合调配出一些不同规格的产品，在原料的供 应量限制和保证产品成分含量的前提下，如何进行配料来 获取最大利润或使总成本最低。
投资问题：如何从不同的投资项目中选出一个投资方案， 使得投资的回报达到最大。
甲
乙
丙
A B C 加工费
x11 60%以上 x12 20%以下 x13 0.50
x21 15%以上 x22 60%以下 x23 0.40
x31 x32 50%以下 x33 0.30
售价
3.40
2.85
2.25
原料成本 2.00 1.50 1.00
限制用量 2000 2500 1200
设该厂每月生产甲品牌糖果(x11 x12 x13)千克，其中用原料A x11千克，用原料B x12千克，用原料C x13千克; 生产乙品牌糖果(x21 x22 x23)千克，其中用原料A x21千克，用原料B x22千克，用原料C x23千克; 生产丙品牌糖果(x31 x32 x33)千克，其中用原料A x31千克，用原料B x32千克，用原料C x33千克。
设一共植了y棵树，男生中有x1人挖坑, x2人栽树, x3人浇水； 女生中有x4人挖坑, x5人栽树, x6人浇水.
max z y
20x1 10x4 y 0 30x2 20x5 y 0
s.t.
25x3
x1
x2
15x6 x3
y 30
0
x4
x5
x6
20
x1, x2 , x3 , x4 , x5 , x6 , y 0
松弛变量
xs 2 (2x1 3x2 x3)
线性规划习题课

线性规划习题课

车间3：设车间3的能力增加10单位，即第三个约束条件为
2x1 + 2x2≤ 450 此时，最优解变为：x1** = 150 x2** = 75 最大值：z** = 105000(元) 车间3的对偶价格为(105000-103000)/10=200
Solution
(5)从（2）中的图可以看出，目标函数的斜率在约束1和约束3的直线斜率
500
如果产品II的利润为400不变，有 即当产品I的利润取值范围为[400,∞]；
c1 400
1
400
c1
习题
1.用单纯形法求解
目标函数 约束条件
max z x1 2x2 x3 x1 x2 x3 12, 2x1 x2 x3 6, x1 3x2 9, x1, x2 , x3 0.
由此可知：车间2的能力还有剩余，剩余540-210=330； 车间4的能力也有剩余，剩余300-285=15；
在这个线性规划中称为松弛变量。
Solution
(4)车间2和车间4的能力有剩余，对偶价格为0；
车间1：设车间1的能力增加10单位，即第一个约束条件为
2x1≤ 310 此时，最优解变为：x1** = 155 x2** = 65 最大值：z** = 103500(元) 车间1的对偶价格为(103500-103000)/10=50
车间
ⅠⅡ
限制
1
2
0
300
2
0
3
540
3
2
2
440
4
1.2 1.5
300
利润 500 400
Solution
解：产品Ⅰ生产x1件，产品Ⅱ生产x2件。z为利润函数，建立线性规划模型 目标函数： max z = 500x1 + 400x2 约束条件： 2x1≤ 300 3x2≤ 540 2x1 + 2x2≤ 440 1.2x1+1.5x2≤ 300 x1,x2 ≥ 0 每个约束条件上加上一个松弛变量si，此线性规划模型的标准型为： 目标函数： max z = 500x1 + 400x2+ 0s1+0s2+0s3+0s4 约束条件： 2x1+s1=300 3x2+s2=540 2x1+2x2+s3=440 1.2x1+1.5x2+s4=300 x1,x2,s1,s2,s3,s4 ≥ 0
第二章 线性规划习题课

第二章 线性规划习题课


单位成本
甲 乙 丙 丁
1 2 1 1
(元／吨) 5 6 7 8
3. 约束条件：
x1 + 2x2 + x3 + x4 ≥160 2x1 +4 x0单位；B种药物恰好200单 位，C种药物不超过180单位， 且使原料总成本最小。
3x1 ＋ x2 + x3 +2 x4 ≤180 x1、x2 、x3 、x4 ≥0
解：设总利润为z，
max z = 4 x1 + 10 x2 + 3 x3 － 2 x4 2 x1 + 3x2 ≤ 12 3x1 + 4x2 ≤ 24 －4x2 +x3 + x4 = 0 x3 ≤5 x1、x2 、x3 、x4≥ 0
A、B产品销量为x1、x2，
产品C的销售量为x3 ， 报废量为x4，则：
0 x 7 0 x 8 100 1 x 7 0 x 8 100 3 x 7 4 x 8 100 0
Ⅵ Ⅶ Ⅷ
方
案 长度m 2.9 2.1 1.5 合计
Ⅰ
Ⅱ
Ⅲ
Ⅳ
Ⅴ
x1
x2
x3
x4
x5
x6
x7
x8
2 0 1
7.3 0.1
1 2 0
1 1 1
1 0 3
7.4 0.0
0 3 0
x1 +
2x1
x2 + 2x3 +
+ 2x3
x4≤ 30
≤ 34
4x2 + 4x3 + 4x4 ≤ 52 25x1 + 20x2 ＝ 200 40x3 + 20x4＝ 400
运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案 (2)

运筹学第三版课后习题答案第一章：引论1.1 课后习题习题1a)运筹学是一门应用数学的学科，旨在解决实际问题中的决策和优化问题。

它包括数学模型的建立、问题求解方法的设计等方面。

b)运筹学可以应用于各个领域，如物流管理、生产计划、流程优化等。

它可以帮助组织提高效率、降低成本、优化资源分配等。

c)运筹学主要包括线性规划、整数规划、指派问题等方法。

习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。

它可以帮助制定最佳的生产计划，优化供应链管理，提高运输效率等。

运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题，优化医疗资源分配等。

1.2 课后习题习题1运筹学方法可以应用于各个领域，如物流管理、生产计划、供应链管理、流程优化等。

在物流管理中，可以使用运筹学方法优化仓储和运输的布局，提高货物的运输效率。

在生产计划中，可以使用运筹学方法优化产品的生产数量和生产周期，降低生产成本。

在供应链管理中，可以使用运筹学方法优化订单配送和库存管理，提高供应链的效率。

在流程优化中，可以使用运筹学方法优化业务流程，提高整体效率。

习题2在物流管理中，可以使用运筹学方法优化车辆的调度和路线规划，以提高运输效率和降低成本。

在生产计划中，可以使用运筹学方法优化生产线的安排和产品的生产量，以降低生产成本和提高产能利用率。

在供应链管理中，可以使用运筹学方法优化供应链各个环节的协调和调度，以提高整体效率和减少库存成本。

在流程优化中，可以使用运筹学方法优化业务流程的排布和资源的分配，以提高流程效率和客户满意度。

第二章：线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法，用于解决包含线性约束和线性目标函数的优化问题。

其一般形式为：max c^T*xs.t. Ax <= bx >= 0其中，c是目标函数的系数向量，x是决策变量向量，A是约束矩阵，b是约束向量。

习题2使用线性规划方法可以解决许多实际问题，如生产计划、供应链管理、资源分配等。

第二章 线性规划习题(附答案)

第二章 线性规划习题(附答案)

z
x1
x2
x3
x4
x5
x6
RHS
z
1
0
2
0
1/5
3/5
-1/5
27
x1
3
1
-1/3
0
1/3
-1/3
2
5
x3
4
0
1
1
-1/5
2/5
-4/5
3
由于增加决策变量 后求得的最优单纯形表为：
z
x1
x2
x3
x4
x5
x6
RHS
z
1
1/10
89/30
0
7/30
17/30
0
55/2
x6
3
1/2
-1/6
0
1/6
-1/6
习题
2-1判断下列说法是否正确：
（1）任何线性规划问题存在并具有惟一的对偶问题；
（2）对偶问题的对偶问题一定是原问题；
（3）根据对偶问题的性质，当原问题为无界解时，其对偶问题无可行解，反之，当对偶问题无可行解时，其原问题具有无界解；
（4）若线性规划的原问题有无穷多最优解，则其对偶问题也一定具有无穷多最优解；
（8）已知yi为线性规划的对偶问题的最优解，若yi>0，说明在最优生产计划中第i种资源已经完全耗尽；若yi=0，说明在最优生产计划中的第i种资源一定有剩余。
2-2将下述线性规划问题化成标准形式。
解：(1)令 ，增加松弛变量 ，剩余变量 ，则该问题的标准形式如下所示：
(2)令 ， ， ，增加松弛变量 ，则该问题的标准形式如下所示：
则可知，最优解变为 ，最优值变为27。
（3）先将原问题最优解变量值代入，因有
运筹学--第二章 线性规划的对偶问题

运筹学--第二章 线性规划的对偶问题

习题二2.1 写出下列线性规划问题的对偶问题(1) max z ＝10x1＋x2＋2x3(2) max z ＝2x1＋x2＋3x3＋x4st. x1＋x2＋2 x3≤10 st. x1＋x2＋x3 ＋x4≤54x1＋x2＋x3≤20 2x1－x2＋3x3＝－4x j≥0 （j＝1,2,3）x1－x3＋x4≥1x1，x3≥0，x2，x4无约束(3) min z ＝3x1＋2 x2－3x3＋4x4(4) min z ＝－5 x1－6x2－7x3st. x1－2x2＋3x3＋4x4≤3 st. －x1＋5x2－3x3≥15x2＋3x3＋4x4≥－5 －5x1－6x2＋10x3≤202x1－3x2－7x3 －4x4＝2＝x1－x2－x3＝－5 x1≥0，x4≤0，x2，，x3无约束x1≤0，x2≥0，x3无约束2.2 已知线性规划问题max z＝CX，AX=b，X≥0。

分别说明发生下列情况时，其对偶问题的解的变化：（1）问题的第k个约束条件乘上常数λ（λ≠0）；（2）将第k个约束条件乘上常数λ（λ≠0）后加到第r个约束条件上；（3）目标函数改变为max z＝λCX（λ≠0）；'x代换。

（4）模型中全部x1用312.3 已知线性规划问题min z＝8x1＋6x2＋3x3＋6x4st. x1＋2x2＋x4≥33x1＋x2＋x3＋x4≥6x3 ＋x4＝2x1 ＋x3 ≥2x j≥0（j＝1,2,3,4）(1) 写出其对偶问题；(2) 已知原问题最优解为x*＝（1，1，2，0），试根据对偶理论，直接求出对偶问题的最优解。

2.4 已知线性规划问题min z＝2x1＋x2＋5x3＋6x4 对偶变量st. 2x1 ＋x3＋x4≤8 y12x1＋2x2＋x3＋2x4≤12 y2x j≥0（j＝1,2,3,4）对偶问题的最优解y1*=4；y2*=1，试对偶问题的性质，求出原问题的最优解。

2.5 考虑线性规划问题max z＝2x1＋4x2＋3x3st. 3x1＋4 x2＋2x3≤602x1＋x2＋2x3≤40x1＋3x2＋2x3≤80x j≥0 （j＝1,2,3）４７４８（1）写出其对偶问题（2）用单纯形法求解原问题，列出每步迭代计算得到的原问题的解与互补的对偶问题的解；（3）用对偶单纯形法求解其对偶问题，并列出每步迭代计算得到的对偶问题解及与其互补的对偶问题的解；（4）比较（2）和（3）计算结果。

《运筹学》 习题 线性规划部分练习题及 答案

《运筹学》 习题 线性规划部分练习题及 答案

《运筹学》线性规划部分练习题 一、思考题 1． 什么是线性规划模型，在模型中各系数的经济意义是什么？ 2． 线性规划问题的一般形式有何特征？ 3． 建立一个实际问题的数学模型一般要几步？ 4． 两个变量的线性规划问题的图解法的一般步骤是什么？ 5． 求解线性规划问题时可能出现几种结果，那种结果反映建模时有错误？ 6． 什么是线性规划的标准型，如何把一个非标准形式的线性规划问题转化成标准形式。

7． 试述线性规划问题的可行解、基础解、基础可行解、最优解、最优基础解的概念及它们之间的相互关系。

8． 试述单纯形法的计算步骤，如何在单纯形表上判别问题具有唯一最优解、有无穷多个最优解、无界解或无可行解。

9． 在什么样的情况下采用人工变量法，人工变量法包括哪两种解法？10．大M 法中，M 的作用是什么？对最小化问题，在目标函数中人工变量的系数取什么？最大化问题呢？11．什么是单纯形法的两阶段法？两阶段法的第一段是为了解决什么问题？在怎样的情况下，继续第二阶段？ 二、判断下列说法是否正确。

1． 线性规划问题的最优解一定在可行域的顶点达到。

2． 线性规划的可行解集是凸集。

3． 如果一个线性规划问题有两个不同的最优解，则它有无穷多个最优解。

4． 线性规划模型中增加一个约束条件，可行域的范围一般将缩小，减少一个约束条件，可行域的范围一般将扩大。

5． 线性规划问题的每一个基本解对应可行域的一个顶点。

6． 如果一个线性规划问题有可行解，那么它必有最优解。

7． 用单纯形法求解标准形式（求最小值）的线性规划问题时，与0>j σ对应的变量都可以被选作换入变量。

8． 单纯形法计算中，如不按最小非负比值原则选出换出变量，则在下一个解中至少有一个基变量的值是负的。

9． 单纯形法计算中，选取最大正检验数k σ对应的变量k x 作为换入变量，可使目 标函数值得到最快的减少。

10． 一旦一个人工变量在迭代中变为非基变量后，该变量及相应列的数字可以从单纯形表中删除，而不影响计算结果。

线性规划习题课教案

线性规划习题课教案第一章：线性规划基础1.1 线性规划的定义与意义解释线性规划的概念说明线性规划在实际生活中的应用1.2 线性规划模型介绍线性规划的基本模型解释目标函数和约束条件1.3 图形解法学习利用图形方法求解线性规划问题掌握图形解法的步骤和技巧第二章：线性规划的单纯形法2.1 单纯形法的原理解释单纯形法的运作机制理解单纯形法的目标是最优解2.2 单纯形法的步骤学习单纯形法的具体步骤掌握转轴步骤和迭代过程2.3 单纯形法的应用利用单纯形法解决实际问题分析单纯形法的适用范围和限制第三章：线性规划的对偶理论3.1 对偶理论的基本概念解释对偶理论的定义和意义说明对偶问题的关系与转化3.2 对偶理论的应用学习如何利用对偶理论解决线性规划问题掌握对偶理论在实际问题中的应用3.3 对偶理论的扩展探索对偶理论的进一步应用和发展了解对偶理论与其他数学规划方法的关系第四章：线性规划的灵敏度分析4.1 灵敏度分析的概念解释灵敏度分析的目的和意义说明灵敏度分析在实际问题中的应用4.2 灵敏度分析的步骤学习灵敏度分析的具体步骤掌握目标函数和约束条件的灵敏度分析方法4.3 灵敏度分析的应用利用灵敏度分析解决实际问题分析灵敏度分析的局限性和改进方向第五章：线性规划的其他方法5.1 分支定界法介绍分支定界法的原理和步骤学习分支定界法在解决实际问题中的应用5.2 内点法解释内点法的概念和原理掌握内点法的步骤和技巧5.3 启发式算法介绍启发式算法在线性规划中的应用学习启发式算法的优势和局限性第六章：线性规划的解法实践6.1 解法实践概述解释解法实践的意义和目的强调解法实践在加深理解线性规划方法的重要性6.2 标准形和简化形学习如何将线性规划问题转换为标准形和简化形掌握简化形的求解技巧6.3 解法实践案例通过具体案例进行线性规划问题的求解练习应用各种解法解决实际问题第七章：线性规划软件应用7.1 线性规划软件介绍介绍常见的线性规划软件及其功能解释如何选择合适的线性规划软件7.2 软件操作演示演示如何使用线性规划软件解决问题学习软件操作的基本步骤和技巧7.3 软件应用案例通过实际案例练习使用线性规划软件分析软件应用的优势和局限性第八章：线性规划在经济管理中的应用8.1 线性规划在经济管理中的应用概述解释线性规划在经济管理领域的重要性讨论线性规划在决策支持中的作用8.2 生产计划与调度学习线性规划在生产计划与调度中的应用练习解决生产优化问题8.3 物流与配送探讨线性规划在物流与配送中的应用分析线性规划在优化物流成本和效率中的作用第九章：线性规划在工程中的应用9.1 线性规划在工程中的应用概述讨论线性规划在工程技术领域的应用强调线性规划在资源优化和决策中的价值9.2 网络流和运输问题介绍线性规划在网络流和运输问题中的应用学习求解运输问题和最大流问题的方法9.3 项目管理解释线性规划在项目管理中的应用练习使用线性规划优化项目资源分配第十章：线性规划在其他领域的应用10.1 线性规划在生物医学中的应用探讨线性规划在生物医学研究中的应用分析线性规划在药物配方和医疗资源分配中的作用10.2 线性规划在通信领域的应用介绍线性规划在通信网络设计和优化中的应用学习如何使用线性规划提高通信系统的效率10.3 线性规划在其他领域的应用讨论线性规划在其他学科和行业中的应用案例强调线性规划作为一种通用优化工具的广泛价值第十一章：线性规划的综合应用案例分析11.1 综合应用案例介绍分析复杂线性规划问题的实际案例强调综合应用各种方法和技巧解决问题的重要性11.2 案例分析过程详细解析典型线性规划案例的求解过程学习如何将理论方法应用于实际问题11.3 案例研究通过深入研究具体案例，提高解决实际问题的能力讨论案例中的难点和解决策略第十二章：线性规划与其它数学规划方法的比较12.1 与其他数学规划方法的比较介绍线性规划与其他数学规划方法（如非线性规划、整数规划等）的区别和联系分析不同规划方法在不同问题上的适用性12.2 混合整数线性规划解释混合整数线性规划的概念和特点学习混合整数线性规划的求解方法12.3 随机线性规划介绍随机线性规划的基本原理探讨随机线性规划在处理不确定性问题中的应用第十三章：线性规划问题的扩展与挑战13.1 扩展问题介绍探讨线性规划问题的扩展形式，如多目标线性规划、动态线性规划等分析这些扩展问题的特点和求解方法13.2 挑战性问题讨论线性规划在实际应用中面临的挑战性问题探索解决这些问题的潜在方法和研究方向13.3 研究趋势与展望了解线性规划领域的研究趋势和未来发展激发学生对线性规划问题研究的兴趣和热情第十四章：线性规划习题训练与解答14.1 习题训练提供一系列线性规划习题供学生训练强调习题训练在提高解题能力的重要性14.2 习题解答与解析给出习题的详细解答和解析帮助学生巩固所学知识和提高解题技巧14.3 习题讨论与交流鼓励学生进行习题讨论和交流促进学生之间的学习与合作第十五章：线性规划课程总结与拓展阅读15.1 课程总结总结线性规划课程的主要内容和知识点强调线性规划在实际问题中的应用价值15.2 拓展阅读推荐提供一系列拓展阅读材料，供学生进一步深入学习引导学生探索线性规划领域的最新研究成果和应用案例重点和难点解析重点：1. 线性规划的基本概念和模型建立；2. 线性规划的求解方法，包括单纯形法、对偶理论、灵敏度分析等；3. 线性规划在不同领域的应用，如经济管理、工程、生物医学等；4. 线性规划软件的应用和实践案例分析；5. 线性规划问题的扩展形式和挑战性问题。

交通分析习题课（运筹学）

习 题第二章 线性规划习题2－1 某桥梁工地需集合料3万立方米，集合料含量为：粘土含量不大于0.8％，细沙含量在5％～8％之间，粗沙含量在60％～70％之间，砾石含量在20％～30％之间，现有材料数量及单价如下表所示。

问如何配料才能使集合料的总成本费用最低？（试列出数学模型）。

2—2 将下列线性规划问题化成标准型：① 42154m ax x x x S ++=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≥+-≤-+≤+++=+0,,,843104480334304432143432432121x x x x x x x x x x x x x x x② 4321343m in x x x x S --+=s.t.⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≥≤+-≥++=-+≤+0,0,8434040403213242132141x x x x x x x x x x x x x 2—3 用图解法求解下列线性规划问题：2152m ax x x S +=s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤≤0,8234212121x x x x x x（答案：19=*S ，()T X 3,2=*。

）2—4 用单纯形法求解下列线性规划问题 ① 321834m in x x x S ++=s.t.⎪⎩⎪⎨⎧≥≥+≤+0,,5223213231x x x x x x x（答案：15=*S ，T X ),0,5,0(=*。

） ② 432132m ax x x x x S -++=s.t. ⎪⎪⎩⎪⎪⎨⎧≥=+++=++=++0,,,1022052153243214321321321x x x x x x x x x x x x x x （答案：15=*S ，T X )0,2/5,2/5,2/5(=*。

）第三章 特殊类型的线性规划习题3－1用表上作业法求解以下运输问题。

3－2某市区交通愿望图有三个始点和三个终点，始点发生的出行交通量a i ，终点吸引的交通量b j 及始终点之间的旅行费用如下所示。

线性规划习题(课堂PPT)


• 约束条件
4
x
5
x7
2 x8
2 x9
0
x j 0 , j 1, 2 ,L , 9
返回
线性规划的一般模型：
假设线性规划模型中，有m个约束条件，有n个 决策变量xj(j=1,2, …,n),目标函数的变量系数用Cj表示, Cj
称为价值系数。约束条件的变量系数用aij 表示， aij称为工 艺系数。约束条件右端的常数用bi表示， bi称为资源限量。 则线性规划数学模型的一般表达式可写为：
到 第 六 年 实 有 资 金 总 额 为 ： x 9 2 x 7 返回
原问题可化为:
maxz2x7x9
• 目标函数
x1 x2 2 0 0
x1
2 x2
2 x3
2 x4
0
s.t .
4 x1 x3 2 x 4 2 x5 2 x 6 0
4
x
3
x5
2 x6
2 x7
2 x8
0
xj 0, j 1,2,L ,n
返回
线性规划的一般模型可简记为：
n
max(min)z cjxj j1
• 目标函数
s.t.
n
aijxj
(或， ）bii1,2,L,m
j1 xj 0,j1,2,L,n
•
约束条件
返回
讨论下列问题
1、在例一中，假设企业一周内工作5天，每天8小时， 企业设备A有5台，利用率为0.8，设备B有7台，利 用率为0.85，其它条件不变，数学模型怎样变化？
m i n z 0 . 3 x 2 0 . 5 x 3 0 . 1 x 4 0 . 4 x 5 0 . 3 x 7 0 . 6 x 8 0 . 9 x 2 0 . 5 x 1 0

运筹学第三版_刁在筠课后答案(2-4章)


−1
0
4
22
2
wx 1
1
−3 2
−1 2
0
1 2
0
1
w x6
0
−1 2
−1 -1
2
1 2
1
4
所以，辅助问题的最优解为 x* = (1, 0, 0, 0, 0, 4)T ，其最优值为 g* = 4 > 0 .因此，原问题没有
可行解.
运筹学作业参考解答
⎧max z = 2x1 − 4x2 + 5x3 − 6x4
注（零行元素的获得）：先将目标函 数化成求最小值的形式，再把所有变
⎪ ⎪
x1 + x2 − x3 ≤ 20
量移到等式左边，常数移到等式右 边。则变量前的系数为零行对应的元
⎪⎩ x j ≥ 0, j = 1, 2, 3
素.
解：将此问题化成标准形式
⎧min
m ⎪⎪⎪s.t.
⎨
z = −2x1 − x2 + x3 3x1 + x2 + x3 + x4 x1 − x2 + 2x3 + x5
3
3
z
-1
0
0
4
2
4
2
g
−3 0
4
−3
0
0
0
2
2
x4
1 8
1 −1 1
24
1 8
0
1 4
x6
−3 2
0
4
−1
0
1
2
0
m 以 x3 为进基变量， x6 为离基变量旋转得
o x1 x2 x3 x4 x5 x6 RHS
c 65

《运筹学教学课件》第二章 线性规划应用举例

备的费用如下表，要求安排最优的生产计划，使该厂利润最大。
2.21 某公司在第一年有 100 万元资金。每年 都有以下的投资方案可供考虑采纳：“假如 今年投入一笔资金，明年又继续投入此资金 的 50%，那么到后年就可收回今年初投入资 金的两倍金额。”该公司要如何决定最优投 资策略才可使第六年拥有的资金最多。
上机求解的结果是：
即每天用475公斤原料A，725公斤原料B，500公斤原料C，800 公斤原料D来生产2500公斤产品1；以及用525公斤原料A，275 公斤原料B，250公斤原料C来生产1 050公斤产品2，可获得最大 利润为13825元。
例15（多阶段投资问题） 某公司有100万元用于投资，可选择的投资项目如下所示： 项目A：从第一年到第四年每年年初都可投资，并于次年末回 收本利110%，规定每年的最低投资额为10万元； 项目B：第二年初可以投资，到第五年年末能收回本利135%， 规定投资额不超过20万元； 项目C：第三年初可以投资，到第五年末回收本利125%，规定 最低投资额为20万元，最高投资额为40万元； 项目D：五年内每年初都可投资，年末回收本利104%。 问该公司应如何确定给这些项目每年的投资额，使到第五年末 回收资金的本利总额为最大？
到第五年末该公司回收资金的本利总额为132.88（万元），即盈利32.88%。
本例的另一个最优解（单位：万元）为：
例18（餐巾供应问题） 某饭店筵席部预计一周每天接待的客人数如下表所示：
规定每位客人每天用餐巾一条。所用餐巾中可购买新的，每条成本6元，或 用已经洗净的餐巾。附近有两家洗衣店：甲店洗净一条餐巾收费3元，隔一天后 送还；乙店洗净一条收费2元，隔两天后送还。假定第7天后餐巾应换新的，且每 周开始时没有旧餐巾。问饭店后勤部应如何安排各天餐巾的供应，以使总成本最 低？

3.3.3线性规划习题课


(1) , ;(2)0, 4
A5, B0, 50
湖南省长沙市一中卫星远程学校
2 2
0 x 2 5 D {( x , y ) | 0 y }上的函数，则 2 y x 1 ( 2, 13] 函数f ( x )值域是________.
湖南省长沙市一中卫星远程学校
y 0 2.若实数x、y满足不等式 x y 0 , 2 x y 2 0 1 ( ,1] y 1 则z= 的取值范围是________. 2 x 1
第六步：求出目标函数的最大值或最小值，然后作答.
制—设—列—确—作—移—找—求—答
湖南省长沙市一中卫星远程学校
例题精讲
x y 1 例1.设变量x、y满足约束条件 x y 1 , 3 x y 3 求下列函数的最大、最小值. （1)z=2x +y； (2)z=x +2y； (3)z=2x y； (4)z=y 2 x.
湖南省长沙市一中卫星远程学校
例题精讲
x y 1 x y 1 3 x y 3 （1)z=2x +y； (2)z=x +2y； (3)z=2x y； (4)z=y 2 x.
A(0,1)
y
C (2, 3)
o
B(1,0)
x
湖南省长沙市一中卫星远程学校
x y 1 1.设变量x,y满足条件 x y 1 , 则目标函数 3 x y 3
1 . 所形成的平面区域的面积等于___
湖南省长沙市一中卫星远程学校
【例4】某人有楼房一幢，室内面积共计 180m2,拟分割成两类房间作为旅游客房。大 房间每间面积 为18m2,可住游客5名，每名游 客每天住宿费40元；小房间每间面积15m2, 可住游客3名，每名游客每天50元；装修大房 间每间需要1000元,装修小房间每间需要600 元.如果他只能筹款8000元用于装修，且游客 能住满房间，他应隔出大房间和小房间各多 少间才能获得最大利益？
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
min z = 5 x1 + 6 x2 + 7 x3 + 8 x4 3. 约束条件：
丙 141 7 丁 122 8
要求：生产A种药物至少 160单位；B种药物恰好200单 位，C种药物不超过180单位， 且使原料总成本最小。
x1 + 2x2 + x3 + x4 ≥160
2x1
+4 x3 +2 x4 ＝200
j 1，2，3，4，5
例6 某厂生产三种药物， 解：
这些药物可以从四种不同的 原料中提取。下表给出了单 位原料可提取的药物量
1. 决策变量：设四种原料的使
用量分别为：x1、x2 、x3 、x4
药物
单位成本
原料
A B C (元／吨)
甲 123 5
乙 201 6
2. 目标函数：设总成本为z， 则有：
线性规划问题求解程序设计要求
1. 线性规划问题的数学模型
max(min) z c1 x1 c2 x2 cn xn
a11 x1 a12 x2 a1n xn ( ，)b1
a21 x1 a22 x2 a2n xn ( ，)b2
am1 x1
例3 合理利用线材问题
现要做100套钢架，每套用长2.9m，2.1m，1.5m， 的圆钢各一根。已知原料长7.4m，问应如何下料，使用 的原材料最省？
解：所有下料方案如下表：
方 案 长度m
2.9 2.1 1.5 合计 料头
ⅠⅡ Ⅲ ⅣⅤ Ⅵ ⅦⅧ
x1 x2 x3 x4 x5 x6 x7 x8
2 1 11 00 00 0 2 10 32 10 1 0 13 02 34
a11 x1 a12 x2 a1n xn ( ，) b1
a21 x1 a22 x2 a2n xn ( ，) b2

am1 x1 am2 x2 amn xn ( ，) bm
x1
，x2
， ，xn
产品名称
规格要求
单价（元/kg）
A
C不少于50%，P不超过25%
50
B
C不少于25%，P不超过50%
35
D
不限
25
原材料名称
C P H
每天最多供应量（kg） 单价（元/kg）
100
65
100
25
60
35
解： 原料
产品
C
P
H 单价
x1 A x2 B x3 D
x AC x AP x AH
50
xBC xBP xBH
项目D， 5年内每年初可购买公债，与当年末归还， 并加利息6%。
该部门现有资金10万元，问他应如何确定给这些项 目每年的投资额，使到五年末拥有资金的本利总额为最 大？
解： 确定决策变量如下表：
年份
项目
1
2
3
4
5 5年末
A
x A1
xA2
x A3
x A4
1.15 x A4
B
xB3
1.25 x B 3
C
2 x1 + 3x2
≤ 12
3x1 + 4x2
≤ 24
－4x2 +x3 + x4 = 0
x3 ≤ 5
x1、x2 、x3 、x4≥ 0
例2 某航运局现有船只种类、数量以及计划期内各 条航线的货运量、货运成本如下表所示：问：应如何 编队，才能既完成合同任务，又使总货运成本为最小？
航线 船队 号 类型
1 1
x1 x2 x3 x4 x5 x6 x7 x8
2 1 11 00 00 0 2 10 32 10 1 0 13 02 34
7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0
0.1 0.3 0.9 0.0 1.1 0.2 0.8 1.4
例4 配料问题。
某工厂要用三种原材料C、P、H混合调配出三种 不同规格的产品A、B、D。已知产品的规格要求，产 品单价，每天供应的原材料数量及原材料单价如下表， 该厂应如何安排生产，使利润收入为最大？
min z = 36x1 + 36x2 + 72x3 + 27x4
x1 + x2 + 2x3 + x4≤ 30
2x1
+ 2x3
≤ 34
4x2 + 4x3 + 4x4 ≤ 52
25x1 + 20x2
＝ 200
40x3 + 20x4＝ 400
xj ≥ 0 j = 1,2,3,4
用单纯形法可求得：x1 = 8，x2 = 0 ，x3 = 7， x4 = 6 最优值：z = 954，即：四种船队类型的队数分别是8、 0、7、6，此时可使总货运成本为最小，为954千元。
2 找出所有限定条件：即决策变量受到的所有 的约束；
3 写出目标函数：即问题所要达到的目标，并 明确是max 还是 min。
三、建 模 案 例
例1 某工厂生产A、B两种产品，有关资料如下表所示：
工序 产品
A
C
工时限
B
销售 报废
制
工序 1 2
3
—
—
12
工序 2 3
4
—
—
24
单位利润生产单位产品 B 可得到 4 单位副产品 C， 据预测，市场上产品 C 的最大销量为 5 单位，若
产品 C 销售不出去，则报废。
解：设总利润为z， max z = 4 x1 + 10 x2 + 3 x3 － 2 x4
A、B产品销量为x1、x2， 产 品 C 的 销 售 量 为 x3 ， 报废量为x4，则：
am2 x2
amn xn
( ，)bm
x1，x2， ，xn 0 (无约束)
2. 线性规划问题的求解方法 采用两阶段法求解
3. 求解程序的输入与输出
变量个数n= ( ) 约束条件个数m= ( )
max(min) z c1 x1 c2 x2 cn xn
0
x1 x1

2x2 0x2

x3 x3

0x4 3x4

3x5 0x5

2x6 2x6

1x7 3x7
0x8 4x8

100 100
x1，x2，x3，x4，x5，x6，x7，x8 0
方 案 长度m
2.9 2.1 1.5 合计
ⅠⅡ Ⅲ ⅣⅤ Ⅵ ⅦⅧ
2 3 2 4
编队形式
拖轮
A型 驳船
B型 驳船
1
2
—
1
—
4
2
2
4
1
—
4
货运成本 （千元／队）
36 36 72 27
货运量 （千吨）
25 20 40 20
船只种类 拖轮 A型驳船 B型驳船
船只数 30 34 52
航线号 1 2
合同货运量 200 400
解：设 xj 为第 j 号类型船队的队数( j = 1,2,3,4 ), z 为总货运成本,则：
35
xDC xDP xDH
25
单 价 65 25
35 max z 15xAC 25xAP 15xAH 30xBC 10xBP 0xBH 40xDC 0xDP 10xDH
xAC 0.50( xAC xAP xAH )

xAP 0.25( xAC xAP xAH )
xC 2
1.40xC 2
D
xD1
xD2
xD3
xD4
x D5 1.06x D5
年初拥有 10 1.06xD1 1.06xD2 1.06xD3 1.06xD4
资金
1.15xA1 1.15xA2 1.15xA3
max z 1.15xA4 1.25xB3 1.40xC 2 1.06xD5

3x1 ＋ x2 + x3 +2 x4 ≤180
x1、x2 、x3 、x4 ≥0
线性规划研究的主要问题
一类是已有一定数量的资源（人力、物质、 时间等），研究如何充分合理地使用它们，才能 使完成的任务量为最大。
另一类是当一项任务确定以后，研究如何统 筹安排，才能使完成任务所耗费的资源量为最少。
—— 实际上，上述两类问题是一个问题的两个不同 的方面，都是求问题的最优解（ max 或 min ）。
(1) 线性规划问题的标准型 (2) 第一阶段的所有单纯形表( ) (3) 第二阶段的所有单纯形表( )

xBP 0.50( xBC xBP xBH )

xBC 0.25( xBC xBP xBH )
xAC xBC xDC 100 xAP xBP xCP 100 xAH xBH xDH 60
xij 0 i A, B, D J C , P, H
7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0
0.1 0.3 0.9 0.0 1.1 0.2 0.8 1.4
min z 0.1x1 0.3x2 0.9x3 0x4 1.1x5 0.2x6 0.8x7 1.4x8
2x1 x2 x3 x4 0x5 0x6 0x7 0x8 100
xA1 xD1 10
xA2 xC 2 xD2 1.06xD1

xA3

xB3

xD3

1.06 x D 2
1.15xA1