下载文档原格式
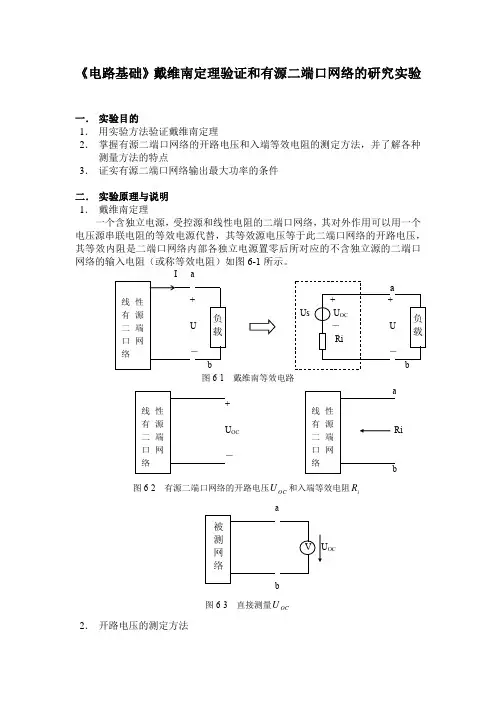
《电路基础》戴维南定理验证和有源二端口网络的研究实验一． 实验目的1． 用实验方法验证戴维南定理2． 掌握有源二端口网络的开路电压和入端等效电阻的测定方法，并了解各种测量方法的特点3． 证实有源二端口网络输出最大功率的条件二． 实验原理与说明 1． 戴维南定理一个含独立电源，受控源和线性电阻的二端口网络，其对外作用可以用一个电压源串联电阻的等效电源代替，其等效源电压等于此二端口网络的开路电压，其等效内阻是二端口网络内部各独立电源置零后所对应的不含独立源的二端口网络的输入电阻（或称等效电阻）如图6-1所示。
图6-1 戴维南等效电路OC图6-2 有源二端口网络的开路电压OC U 和入端等效电阻i RU OC图6-3 直接测量OC U2． 开路电压的测定方法（1） 直接测量法当有源二端口网络的入端等效电阻i R 与万用表电压档的内阻V R 相比可以忽略不计时，可以用电压表直接测量该网络的开路电压OC U 。
如图6-3所示。
（2） 补偿法当有源二端口网络的入端电阻i R 较大时，用电压表直接测量开路电压的误差较大，这时采用补偿法测量开路电压则较为准确。
图6-4中虚线框内为补偿电路，'S U 为另一个直流电压源，可变电阻器P R 接成分压器使用，G 为检流计。
当需要测量网络A 、B 两端的开路电压时，将补偿电路'A 、'B 端分别与A 、B 两端短接，调节分压器的输出电压，使检流计的指示为零，被测网络即相当于开路，此时电压表所测得的电压就是该网络的开路电压OC U 。
由于这时被测网络不输出电流，网络内部无电压降测得的开路电压数值较前一种方法准确。
图6-4 补偿法测量开路电压3． 入端等效电阻i R 的测定方法（1） 外加电源法将有源二端口网络内部的独立电压源Us 处短接，独立电流源Is 处开路，被测网络成为无独立源的二端口网络，然后在端口上加一给定的电源电压"S U ，测量流入网络的电流I ，如图6-5所示。
186第10章 二端口网络网络按其引出端子的数目可分为二端网络、三端网络及四端网络等，如果一个二端网络满足从一个端子流入的电流等于另一个端子上流出的电流时，就可称为一端口网络，如果电路中有两个一端口网络时就构成了一个二端口网络。
本章是把二端口网络当作一个整体，不研究其内部电路的工作状态，只研究端口电流、电压之间的关系，即端口的外特性。
联系这些关系的是一些参数。
这些参数只取决于网络本身的元件参数和各元件之间连接的结构形式。
一旦求出表征这个二端口网络的参数，就可以确定二端口网络各端口之间电流、电压的关系，进而对二端口网络的传输特性进行分析。
本章主要解决的问题是找出表征二端口网络的参数及由这些参数联系着的端口电流、电压方程，并在此基础上分析双口网络的电路。
本章教学要求理解二端口网络的概念，掌握二端口网络的特点，熟悉二端口网络的方程及参数，能较为熟练地计算参数，理解二端口网络等效的概念掌握其等效计算的方法，理解二端口网络的输入电阻、输出电阻及特性阻抗的定义及计算方法。
通过实验环节进一步加深理解二端口网络的基本概念和基本理论，掌握直流二端口网络传输参数的测量技术。
10.1 二端口网络的一般概念学习目标：熟悉二端口网络的判定，了解无源、有源、线性、非线性二端口网络在组成上的不同点。
在对直流电路的分析过程中，我们通过戴维南定理讲述了具有两个引线端的电路的分析方法，这种具有两个引线端的电路称为一端口网络，如图10.1（a ）所示。
一个一端口网络，不论其内部电路简单或复杂，就其外特性来说，可以用一个具有一定内阻的电源进行置换，以便在分析某个局部电路工作关系时，使分析过程得到简化。
当一个电路有四个外引线端子，如图10.1（b ）所示，其中左、右两对端子都满足：从一个引线端流入电路的电流与另一个引线端流出电路的电流相等的条件，这样组成的电路可称为二端口网络（或称为双口网络）。
（a ）一端口网络 （b ）二端口网络图10.1 端口网络2U ＋_ _187当一个二端口网络的端口处电流与电压满足线性关系时，则该二端口网络称为线性二端口网络。
电路基础原理二端口网络的特性与参数分析在电路领域中，二端口网络是一个非常重要的概念。
二端口网络是指具有两个输入端口和两个输出端口的电路系统。
它可以用于各种电子设备和通信系统中，包括滤波器、放大器和传输线等。
二端口网络的特性可以通过参数来描述。
这些参数包括传输参数、散射参数、喉参数和混合参数。
传输参数描述了输入和输出之间的关系，散射参数描述了输入和输出之间的散射特性，喉参数描述了输入和输出之间的传输特性，混合参数描述了输入和输出之间的相互作用。
传输参数是描述输入和输出之间关系的一类参数。
它们包括传输增益、电压传输、电流传输和功率传输等。
传输增益是指输出电压与输入电压之间的比例关系，电压传输是指输入电压与输出电流之间的比例关系，电流传输是指输入电流与输出电压之间的比例关系，功率传输是指输入功率与输出功率之间的比例关系。
散射参数是描述输入和输出之间散射特性的一类参数。
它们包括散射系数、反射系数和传输系数等。
散射系数是指从输入端口到输出端口的散射功率与输入功率之间的比例关系，反射系数是指从输出端口返回到输入端口的反射功率与输入功率之间的比例关系，传输系数是指从输入端口到输出端口的传输功率与输入功率之间的比例关系。
喉参数是描述输入和输出之间传输特性的一类参数。
它们包括输入阻抗、输出阻抗、输入导纳和输出导纳等。
输入阻抗是指输入端口的阻抗与输入电压和输入电流之间的关系，输出阻抗是指输出端口的阻抗与输出电压和输出电流之间的关系，输入导纳是指输入端口的导纳与输入电压和输入电流之间的关系，输出导纳是指输出端口的导纳与输出电压和输出电流之间的关系。
混合参数是描述输入和输出之间相互作用的一类参数。
它们包括互阻、互导和互传等。
互阻是指输入电流与输出电压之间的关系，互导是指输入电压与输出电流之间的关系，互传是指输入功率与输出功率之间的关系。
通过对二端口网络的特性和参数进行分析，可以更好地了解电路的传输、散射、传输和相互作用特性。
186第10章 二端口网络网络按其引出端子的数目可分为二端网络、三端网络及四端网络等，如果一个二端网络满足从一个端子流入的电流等于另一个端子上流出的电流时，就可称为一端口网络，如果电路中有两个一端口网络时就构成了一个二端口网络。
本章是把二端口网络当作一个整体，不研究其内部电路的工作状态，只研究端口电流、电压之间的关系，即端口的外特性。
联系这些关系的是一些参数。
这些参数只取决于网络本身的元件参数和各元件之间连接的结构形式。
一旦求出表征这个二端口网络的参数，就可以确定二端口网络各端口之间电流、电压的关系，进而对二端口网络的传输特性进行分析。
本章主要解决的问题是找出表征二端口网络的参数及由这些参数联系着的端口电流、电压方程，并在此基础上分析双口网络的电路。
本章教学要求理解二端口网络的概念，掌握二端口网络的特点，熟悉二端口网络的方程及参数，能较为熟练地计算参数，理解二端口网络等效的概念掌握其等效计算的方法，理解二端口网络的输入电阻、输出电阻及特性阻抗的定义及计算方法。
通过实验环节进一步加深理解二端口网络的基本概念和基本理论，掌握直流二端口网络传输参数的测量技术。
10.1 二端口网络的一般概念学习目标：熟悉二端口网络的判定，了解无源、有源、线性、非线性二端口网络在组成上的不同点。
在对直流电路的分析过程中，我们通过戴维南定理讲述了具有两个引线端的电路的分析方法，这种具有两个引线端的电路称为一端口网络，如图10.1（a ）所示。
一个一端口网络，不论其内部电路简单或复杂，就其外特性来说，可以用一个具有一定内阻的电源进行置换，以便在分析某个局部电路工作关系时，使分析过程得到简化。
当一个电路有四个外引线端子，如图10.1（b ）所示，其中左、右两对端子都满足：从一个引线端流入电路的电流与另一个引线端流出电路的电流相等的条件，这样组成的电路可称为二端口网络（或称为双口网络）。
（a ）一端口网络 （b ）二端口网络图10.1 端口网络2U ＋_ _187当一个二端口网络的端口处电流与电压满足线性关系时，则该二端口网络称为线性二端口网络。
通常线性二端口网络内的所有元件都是线性元件，如：电阻、电容、电感等。
否则二端口网络为非线性网络。
如果一个二端口网络内部不含有任何独立电源和受控源，则称其为无源二端口网络，否则称为有源二端口网络，如图10.2所示。
本章只介绍无源线性二端口网络。
检验学习结果：10.1.1 什么是二端口网络？ 10.1.2 什么是无源线性二端口网络？10.2 二端口网络的基本方程和参数学习目标：熟悉表征二端口网络参数的不同形式，能够写出由这些参数联系着的端口电流、电压方程，并在此基础上分析双口网络的电路。
熟悉表征二端口网络不同参数之间的关系。
在实际应用过程中，不少电路（如集成电路）制作完成后就被封装起来，无法看到具体的结构。
在分析这类电路时，只能通过其引线端或端口处电压与电流的相互关系，来表征电路的功能。
而这种相互关系，可以用一些参数来表示，这些参数只决定于网络本身的结构和内部元件，一但表征这个端口网络的参数确定之后，当一个端口的电压和电流发生变化时，利用网络参数，就可以很容易找出另一个端口的电压和电流。
利用这些参数，还可以比较不同网络在传递电能和信号方面的性能，从而评价端口网络的质量。
一个二端口网络输入端口和输出端口的电压和电流共有四个，即1U 、1I 、2U 、2I 。
在分析二端口网络时，通常是已知其中的两个电量，求出另外两个电量。
因此由这四个物理量构成的组合，共有六组关系式，其中四组为常用关系式。
10.2.1阻抗方程和Z 参数在图10.3所示的无源线性二端口网络中，已知电流1I 和2I ，求端口电压1U 和2U ，这时I（a ）无源二端口网络 （b ）有源二端口网络图10.2 二端口网络188如何列写其关系式呢？我们以图10.3（b ）电路为例，列写其关系式。
根据基尔霍夫第二定律，列写出的两个回路电压方程如下：()()232132231311I Z Z I Z U I Z I Z Z U ++=++=令：Z 11＝Z 1+Z 3 Z 12＝Z 3Z 21＝Z 3 Z 22＝Z 2+Z 3将它们代入上式，得阻抗方程的一般表示形式 22212122121111I Z I Z U I Z I Z U +=+= （10.1）式10.1虽然是由T 型二端口网络推导出来的，但具有一般形式。
可以证明式（10.1）适合任何无源线性二端口网络。
式中的系数Z 11、Z 12、Z 21、Z 22具有阻抗性质，所以式（10.1）称为阻抗方程或Z 方程。
由上述例子可以看出，无源二端口网络的Z 参数，仅与网络的内部结构、元件参数、工作频率有关，而与输入信号的振幅、负载的情况无关。
因此，这些参数描述了二端口网络本身的电特性。
二端口网络Z 参数的物理意义，可由式（10.1）推导而得。
当输出端口开路时，2I ＝0，这时有011112==I IU Z （10.2a ）即Z 11是输出端口开路时在输入端口处的输入阻抗，称为开路输入阻抗。
而012212==I IU Z （10.2b ）即Z 21是输出端口开路时的转移阻抗，称为开路转移阻抗。
转移阻抗是一个端口的电压与另一个端口的电流之比。
同理，当输入端口开路时，1I ＝0，这时有022221==I IU Z （10.2c ）2 I （a ） （b ）图10.3 无源线性二端口网络＋ _189即Z 22是输入端口开路时在输出端口处的输出阻抗，称为开路输出阻抗。
而021121==I I U Z （10.2d ）即Z 12是输入端口开路时的转移阻抗，称为开路转移阻抗。
以上四个阻抗的单位都是【Ω】。
对于无源线性二端口网络利用互易定理可以得到证明，即输入和输出互换位置时，不会改变由同一激励所产生的响应。
由此得出Z 12＝Z 21 （10.3a ）的结论。
即在Z 参数中，只有三个参数是独立的。
如果二端口网络是对称的，则输出端口和输入端口互换位置后，电压和电流均不改变，表明Z 11＝Z 22 （10.3b ）无源线性二端口网络如果同时满足式（10.3）时，则Z 参数中只有两个参数是独立的。
10.2.2 导纳方程与Y 参数当已知一个无源二端口网络输入电压和输出电压的值，要求解出输入电流和输出电流时，我们可以利用式（10.1）写出1I 和2I 的表示式2211222111112112221121222112221112121122211221U Z Z Z Z Z U Z Z Z Z Z I U Z Z Z Z Z U Z Z Z Z Z I -+--=--+-=由此得到导纳方程的一般表示形式22212122121111U Y U Y I U Y U Y I +=+= （10.4）二端口网络Y 参数的物理意义，可由式（10.4）推导得到。
当输出端口短路时，2U ＝0，这时有011112==U UI Y （10.5a ）即Y 11是输出端口短路时在输入端口处的输入导纳，称为短路输入导纳。
012212==U UI Y （10.5b ）Y 21是输出端口短路时的转移导纳，称为出端短路转移导纳。
当输入端口短路时，1U＝0，这时有190022221==U UY （10.5c ）Y 22是输入端口短路时在输出端口处的输出导纳，称为短路输出导纳。
021121==U UI Y （10.5d ）Y 12是输入端口短路时的转移导纳，称为入端短路转移导纳。
Y 参数的单位是西门子。
同样可以证明，对于无源线性二端口网络Y 12＝Y 21。
对称二端口网络有Y 11＝Y 22。
例10.1 写出图10.4电路的Z 参数方程。
解：根据Z 参数的定义，将输出端22´开路得011112==I IU Z ＝()()()Ω=+++⨯=+8121212121212//321R R R 012212==I IU Z ＝Ω=⨯+=+4812121211322Z R R R因为该电路是对称无源线性二端口网络，所以Z 22＝Z 11，Z 12＝Z 21，图10.4电路的Z 参数方程为2122118448I I U I I U +=+=10.2.3 传输方程和A 参数在已知二端口网络的输出电压2U 和电流2I ，求解二端口网络的输入电压1U 和电流1I 的情况下，用A 参数建立输出信号与输入信号之间的关系。
当选择电流的参考方向为流入二端口网络时，A 参数方程的一般形式为 ()()22222112122111IA U A I I A U A U -+=-+= （10.6）若选择输出电流的参考方向为流出二端口网络时，方程中电流2I 符号为“＋”。
当二端口网络为无源线性网络时，A 11A 22－A 12A 21＝1，A 参数中有三个是独立的。
如果网络是对称的，则A 11＝A 22，这时A 参数中只有二个是独立的。
A 参数的意义可以这样来理解。
当输出端口开路时，有021112==I UUA （10.7a ）021212==I UI A （10.7b ）当输出端口短路时，有1 22·图10.4 例10.1电路19102222=-=U IA （10.7c ） 021122=-=U I UA （10.7d ）由A 参数建立的方程主要用于研究网络传输问题。
10.2.4 混合方程与h 参数在已知二端口网络的输出电压2U 和输入电流1I ，求解二端口网络的输入电压1U 和输出电流2I 时，用h 参数建立信号之间的关系。
当选择电流的参考方向为流入二端口网络时，h 参数方程的一般形式为22212122121111Uh I h I U h I h U +=+= （10.8）当二端口网络为无源线性网络时，h 参数之间有h 12＝－h 21成立，h 参数中有三个是独立的。
如果网络是对称的，则h 11h 22－h 12h 21＝1，这时h 参数中只有二个是独立的。
h 参数的意义可以这样来理解。
当输出端口短路时，有011112==U IU h （10.9a ） 012212==U II h （10.9b ）当输入端口开路时，有 021121==I UUh （10.9c ）022221==I UI h （10.9d ）由h 参数建立的方程主要用于晶体管低频放大电路的分析。
10.2.5 二端口网络参数之间的关系对于一个无源线性二端口网络，我们可以根据对电路不同的分析要求，选择不同的参数来描述，达到简化分析过程的目的。
当采用不同的参数表示同一个二端口网络时，各参数之间必然存在一定的关系，可以相互换算。
各参数之间的相互表示关系见表10.1。
192表中：|Z |＝Z 11Z 22－Z 12Z 21； |Y |＝Y 11Y 22－Y 12Y 21； |A |＝A 11A 22－A 12A 21； |h |＝h 11h 22－h 12h 2110.2.6 实验参数无源线性二端口网络除了采用上述四种参数描述之外，还可以采用网络的开路阻抗和短路阻抗描述。
