第十六章(二端口网络)习题
- 格式:doc
- 大小:527.00 KB
- 文档页数:3


电路习题解答第一章 电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得 U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上 式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=; ⑴ KCL :43211-=I I ;I 185=A ;U I I S =-⨯=218511V 或16.V ;或I I 12=-。
⑵ KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章电阻电路的等效变换【题1】:[解答]I=-+9473A=0.5A;U Ia b.=+=9485V;IU162125=-=a b.A;P=⨯6125.W=7.5W;吸收功率7.5W。
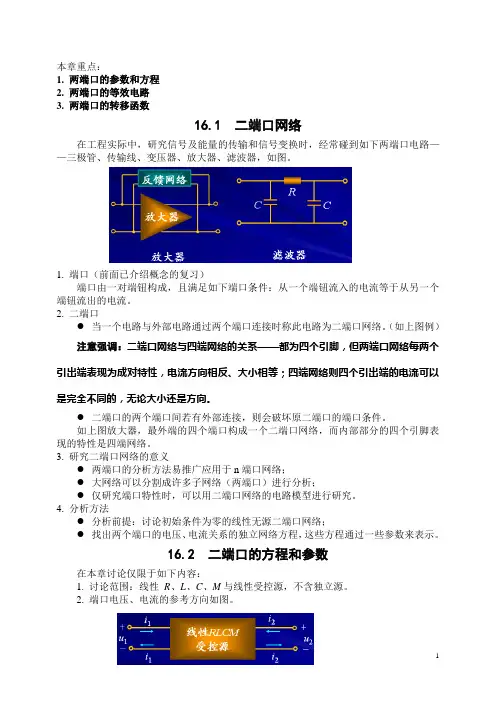
本章重点:1. 两端口的参数和方程2. 两端口的等效电路3. 两端口的转移函数16.1 二端口网络在工程实际中,研究信号及能量的传输和信号变换时,经常碰到如下两端口电路——三极管、传输线、变压器、放大器、滤波器,如图。
1. 端口(前面已介绍概念的复习)端口由一对端钮构成,且满足如下端口条件:从一个端钮流入的电流等于从另一个端钮流出的电流。
2. 二端口●当一个电路与外部电路通过两个端口连接时称此电路为二端口网络。
(如上图例)注意强调:二端口网络与四端网络的关系——都为四个引脚,但两端口网络每两个引出端表现为成对特性,电流方向相反、大小相等;四端网络则四个引出端的电流可以是完全不同的,无论大小还是方向。
●二端口的两个端口间若有外部连接,则会破坏原二端口的端口条件。
如上图放大器,最外端的四个端口构成一个二端口网络,而内部部分的四个引脚表现的特性是四端网络。
3. 研究二端口网络的意义●两端口的分析方法易推广应用于n端口网络;●大网络可以分割成许多子网络(两端口)进行分析;●仅研究端口特性时,可以用二端口网络的电路模型进行研究。
4. 分析方法●分析前提:讨论初始条件为零的线性无源二端口网络;●找出两个端口的电压、电流关系的独立网络方程,这些方程通过一些参数来表示。
16.2 二端口的方程和参数在本章讨论仅限于如下内容:1. 讨论范围:线性R、L、C、M与线性受控源,不含独立源。
2. 端口电压、电流的参考方向如图。
针对上图,可以看到:⏹ 端口物理量4个:i1、i2、u1、u2⏹ 端口电压电流有六种不同的方程来表示,即可用六套(三组)参数描述二端口网络。
2121u u i i ⇔;2211i u i u ⇔;2121u i i u ⇔;1. Y 参数和方程● Y 参数方程(Y → 短路导纳参数) 采用相量形式(正弦稳态)。
将两个端口各施加一电压源,则端口电流可视为电压源单独作用时产生的电流之和。
即:⎪⎩⎪⎨⎧+=+=22212122121111U Y U Y I U Y U Y I写成矩阵形式为:⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡212221121121U U Y Y Y Y I I Y 参数矩阵:⎥⎦⎤⎢⎣⎡=22211211Y Y Y Y ][Y 注意:Y 参数值由内部元件参数及连接关系决定。

《电路分析》习题册班级学号姓名中国地质大学(武汉)电子信息工程系注意事项:1. 习题册请用A4纸双面打印,装订成册,填好相关信息;2. 每章习题均来自课本中的课后习题,不清楚的地方可以参看教材。
这里挑选出来整理成册,方便大家使用;3. 后附有两套模拟试题,供考前进行模拟测试;4. 册内带两张空白的课堂测试答题纸,不要损坏。
通知课堂测试的时候再使用。
第一章电路模型与电路定律1-1 求解电路以后,校核所得结果的方法之一是核对电路中所有元件的功率平衡,即一部分元件发出的总功率应等于其他元件吸收的总功率。
试校核图1-1电路所得解答是否正确。
图1-11-2 电路如图1-2所示,试求:(1) 图(a)中,i1与u ab;(2) 图(b)中,u cb。
图1-21-3 对图1-3所示的电路,若:(1) R1、R2、R3不定;(2)R1 = R2 = R3。
在以上两种情况下,尽可能地确定各电阻中的未知电流。
图1-31-4 电路如题1-4图所示,试求每个元件发出和吸收的功率。
图1-41-5 试求图1-5所示电路中控制量I1及电压U o。
图1-5第二章电阻电路的等效变换2-1 电路如题2-1图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压u2和电流i2;(2)若电阻R1增大,对哪些元件的电压、电流有影响?影响如何?图2-1 2-2 求图2-2所示电路中对角线电压U及总电压U ab。
图2-22-3 利用电源的等效变换,求图2-3所示电路的电流i。
图2-32-4 利用电源的等效变换,求图2-4所示电路中电压比u o/u s。
已知R1 = R2 = 2Ω,R3 = R4 = 1Ω。
图2-42-5 试求图2-5(a)和(b)的输入电阻R i。
图2-5第三章电阻电路的一般分析3-1 用网孔电流法求解图3-1所示电路中电流I a及电压U o 。
图3-1 3-2 用网孔电流法求解图3-2所示电路中I x以及CCVS的功率。


答案第一章【1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【2】:D 。
【3】:300;-100。
【4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得 U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上 式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=; ⑴ KCL :43211-=I I ;I 185=A ;U I I S =-⨯=218511V 或16.V ;或I I 12=-。
⑵ KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章【题1】:[解答]I=-+94 73A=0.5A;U Ia b.=+=9485V;I U162125=-=a b.A;P=⨯6125.W=7.5W;吸收功率7.5W。


第一章“电路模型和电路定律”练习题1-1说明题1-1图(a )、(b )中:(1)u 、i 的参考方向是否关联?(2)ui 乘积表示什么功率?(3)如果在图(a )中u >0、i <0;图(b )中u >0、i >0,元件实际发出还是吸收功率?(a ) (b )题1-1图1-4 在指定的电压u 和电流i 的参考方向下,写出题1-4图所示各元件的u 和i 的约束方程(即VCR )。
(a ) (b ) (c )(d ) (e ) (f )题1-4图1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率(须说明是吸收还是发出)。
(a ) (b ) (c )题1-5图1-16 电路如题1-161(a ) (b )题1-16图 1-20 试求题1-20图所示电路中控制量u 1及电压u 。
题1-20图第二章“电阻电路的等效变换”练习题2-1电路如题2-1图所示,已知u S =100V ,R 1=2k ?,R 2=8k ?。
试求以下3种情况下的电压u 2和电流i 2、i 3:(1)R 3=8k ?;(2)R 3=?(R 3处开路);(3)R 3=0(R 3处短路)。
题2-1图2-5用△—Y 等效变换法求题2-5图中a 、b 端的等效电阻:(1)将结点①、②、③之间的三个9?电阻构成的△形变换为Y 形;(2)将结点①、③、④与作为内部公共结点的②之间的三个9?电阻构成的Y 形变换为△形。
题2-52-11 利用电源的等效变换,求题2-11图所示电路的电流i 。
题2-11图2-13 题2-13图所示电路中431R R R ==,122R R =,CCVS 的电压11c 4i R u =,利用电源的等效变换求电压10u 。
题2-13图2-14 试求题2-14图(a )、(b )的输入电阻ab R 。
(a ) (b )题2-14图 第三章“电阻电路的一般分析”练习题3-1 在以下两种情况下,画出题3-1图所示电路的图,并说明其结点数和支路数:(1)每个元件作为一条支路处理;(2)电压源(独立或受控)和电阻的串联组合,电流源和电阻的并联组合作为一条支路处理。

二端口网络一、填空题〔建议较易填空每空0.5分,较难填空每空1分〕1、一个二端口网络输入端口和输出端口的端口变量共有4个,它们分别是U1、I1、U2和I2。
2、二端口网络的根本方程共有6种,各方程对应的系数是二端口网络的根本参数,经常使用的参数是Z参数、Y参数、A参数和h参数。
3、描述无源线性二端口网络的4个参数中,只有3个是独立的,当无源线性二端口网络为对称网络时,只有2个参数是独立的。
4、对无源线性二端口网络用任意参数表示网络性能时,其最简电路形式为π形网络结构和T形网络结构两种。
5、输出端口的响应信号与输入端口的鼓励信号之比,称为二端口网络的传输函数。
该函数模的大小表示信号经二端口网络后幅度变化的关系,通常称为幅频特性。
其幅角表示信号传输前后相位变化的关系,通常称为相频特性。
6、两个二端口网络串联时,参数之间的关系为Z=Z A+Z B;两个二端口网络并联时,参数之间的关系为Y=Y A+Y B;两个二端口网络级联时,参数之间的关系为A=A A A B。
7、二端口网络工作在匹配状态下,对信号的传输能力可用传输常数γ表示,其中的α称为衰减常数,β称为相移常数。
8、结构特点为串联臂是LC并联谐振电路,并联臂是LC串联谐振电路的是带阻滤波器。
9、LC高通滤波器的结构特点是:串联臂是电容,并联臂是电感。
10、相移器电抗元件在传输信号时,本身不消耗能量,所以传输过程中无衰减,网络的衰减常数α= 0,传输常数γ= jβ。
二、判断以下说法的正确与错误〔建议每题1分〕1、线性二端口网络是指端口处电流与电压均满足线性关系的二端口网络。
〔∨〕2、一个二端口网络的输入端口和输出端口的电压和电流共有6个。
〔×〕3、无源二端口网络的Z参数仅与网络元件参数有关,与网络内部结构无关。
〔×〕4、无论二端口网络是否对称,Z参数中只有2个参数是独立的。
〔×〕5、如果二端口网络对称,那么A参数中就有2个是独立的。
Chapter 16 二端口网络习题精选一、填空题1. 如果一对端子,在所有时刻都满足 这一条件,则可称为一端口网络。
2. 对任何一个无源线性二端口,只要 个独立的参数就足以表征它的外特性。
3. 二端口的对称有两种形式: 和 ,对于对称二端口的Y 参数,只有 个是独立的。
4. 有两个线性无源二端口1P 和2P , 它们的传输参数矩阵分别为1T 和2T ,它们按级联方式连接后的新二端口的传输矩阵T = 。
5. 两个线性无源二端口1P 和2P ,它们的导纳参数矩阵分别为1Y 和2Y ,它们的阻抗参数矩阵分别为1Z 和2Z 。
当1P 和2P 并联连接后的新二端口的导纳矩阵Y , 则Y = ; 当1P 和2P 串联连接后的新二端口的阻抗矩阵Z , 则Z = 。
6. 对于内部无独立源和附加电源的线性无源二端口,其转移函数(或称传递函数)就是用 表示的输出电压或电流与输入电压或电流之比。
7. 对于所有时间t ,通过回转器的两个端口的功率之和等于 。
8. 回转器具有把一个端口上的 “回转”为另一端口上的 或相反过程的性质。
正是这一性质,使回转器具有把电容回转为一个 的功能。
9. 负阻抗变换器具有 的功能,从而为电路设计 实现提供了可能性。
10. 在一个回转系数为r =20Ω的回转器的负载端,接以10Ω的电阻,则回转器的输入端等效电阻 。
11. 有些端口网络不可能用短路参数矩阵Y 表示,试举一例: 。
12. 有些端口网络不可能用开路参数矩阵Z 表示,试举一例: 。
二、选择题1. 回转器如图16-1所示,回转常数为r ,则回转器的Z 参数矩阵为( )。
A . ⎥⎦⎤⎢⎣⎡-00r rB .⎥⎦⎤⎢⎣⎡-r r 00C .⎥⎦⎤⎢⎣⎡-00r rD .⎥⎦⎤⎢⎣⎡-r r 002. 如图16-2所示电路,回转器的回转常数为r ,则从端口1-1’看进去的输入阻抗in Z =( )。
A . sC r 2B . sC r 2- C . sC r /2D . 2/r sC3. 有一电流反向型负阻抗变换器(NIC )如图16-3所示,已知1I (s)=2kI (s),在端口2-2’接阻抗2Z ,则从1-1’看进去的输入阻抗1Z =( ).A .kZ 2 B . kZ2- C . 2kZ D . 2kZ -4.电路如图16-4所示,此二端口的导纳矩阵为( )。
电路邱关源《电路》第五版课后习题答案第一章 电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得 U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上 式,得U A C =-7V 。
【题18】:P P I I 12122222==;故I I 1222=;I I 12=; ⑴ KCL :43211-=I I ;I 185=A ;U I I S =-⨯=218511V 或16.V ;或I I 12=-。
⑵ KCL :43211-=-I I ;I 18=-A ;U S =-24V 。
第二章 电阻电路的等效变换【题1】:[解答]I =-+9473 A =0.5 A ;U I a b .=+=9485V ; I U 162125=-=a b .A ;P =⨯6125. W =7.5 W;吸收功率7.5W 。
第十六章(二端口网络)习题一、选择题二、填空题1.图16—3(a )所示二端口电路的Y 参数矩阵为Y = ,图16—3(b )所示二端口的Z 参数矩阵为Z = 。
2.图16—4所示二端口网络的Y 参数矩阵是Y = 。
3.图16—5所示回转器的T 参数矩阵为 。
4.图16—6所示的二端口网络中,设子二端口网络1N 的传输参数矩阵为⎥⎦⎤⎢⎣⎡D C B A ,则复合二端口网络的传输参数矩阵为 。
5.图16—7所示二端口网络的Y 参数矩阵为 。
6.描述无源线性二端口网络的4个参数中,只有 个是独立的,当无源线性二端口网络为对称网络时,只有 个参数是独立的。
三、计算题1.图16—8所示二端口网络的Z 参数是Ω=1011Z 、Ω=1512Z 、Ω=521Z ,Ω=2022Z 。
试求s U U 2。
2.求图16—11所示二端口网络的T 参数。
3.图示电路中,二端口网络N 的传输参数矩阵为 2.560.5 1.6T S Ω⎡⎤=⎢⎥⎣⎦, 求(1)L R 等于多少时其吸收功率最大?(2)若9V S U =,求L R 所吸收的最大功率max P ,以及此时网络N 吸收的功率N P4.图示电路中,直流电源U S =10 V ,网络N 的传输参数矩阵为⎥⎦⎤⎢⎣⎡=11.0102][T ,t <0时电路处于稳态,t =0时开关S 由a 打向b 。
求t >0时的响应u (t )。
0.01F7.已知图示电路中,二端口网络N 的传输参数矩阵为 1.52.50.5 1.5T SΩ⎡⎤=⎢⎥⎣⎦,t=0时闭合开关k 。
求零状态响应()C i t8.电路如图所示,N 不含独立电源,25202020Z ⎛⎫=Ω ⎪⎝⎭,原电路已处于稳态,今于0t =时闭合S ,求0t >时的()c u t 。
u i本章作业:计算题的3、4、7、8小题。
二端口网络练习题及答案二端口网络是电子电路中的一个重要概念,它由两个端口组成,可以是输入端口和输出端口。
在电路分析中,二端口网络通常用来描述电路元件的电气特性,如电阻、电感和电容。
以下是一些关于二端口网络的练习题及答案:练习题1:二端口网络参数定义1. 什么是二端口网络的Z参数矩阵?2. 什么是二端口网络的Y参数矩阵?3. 什么是二端口网络的h参数矩阵?答案1:1. Z参数矩阵,也称为阻抗参数矩阵,是一个2x2的矩阵,用于描述二端口网络的输入和输出阻抗。
2. Y参数矩阵,也称为导纳参数矩阵,是一个2x2的矩阵,用于描述二端口网络的输入和输出导纳。
3. h参数矩阵,也称为混合参数矩阵,是一个2x2的矩阵,用于描述二端口网络的输入和输出混合参数。
练习题2:二端口网络参数转换1. 如何从Z参数矩阵转换到Y参数矩阵?2. 如何从Y参数矩阵转换到Z参数矩阵?答案2:1. 从Z参数矩阵转换到Y参数矩阵,可以使用以下公式:\[ Y =Z^{-1} \] 其中Z^{-1}表示Z矩阵的逆矩阵。
2. 从Y参数矩阵转换到Z参数矩阵,可以使用以下公式:\[ Z =Y^{-1} \]练习题3:二端口网络的等效电路1. 如何使用Z参数矩阵构建二端口网络的等效电路?2. 如何使用Y参数矩阵构建二端口网络的等效电路?答案3:1. 使用Z参数矩阵构建二端口网络的等效电路,可以通过将Z参数矩阵的元素视为电路元件的阻抗值来实现。
2. 使用Y参数矩阵构建二端口网络的等效电路,可以通过将Y参数矩阵的元素视为电路元件的导纳值来实现。
练习题4:二端口网络的串联和并联1. 两个二端口网络串联时,它们的Z参数矩阵如何计算?2. 两个二端口网络并联时,它们的Y参数矩阵如何计算?答案4:1. 两个二端口网络串联时,它们的Z参数矩阵可以通过矩阵加法来计算,即:\[ Z_{total} = Z_1 + Z_2 \] 其中Z_1和Z_2分别是两个二端口网络的Z参数矩阵。
第十六章(二端口网络)习题
一、选择题
1.二端口电路的H 参数方程是 。
a .⎩⎨⎧+=+=22212122121111U H I H I U H I H U
b . ⎩⎨⎧+=+=2221212
2
121111I H U H U I H U H I
c .⎩⎨⎧+=+=2
2222112
122111U H I H U U H I H I d . ⎩⎨⎧+=+=22212112121112I H U H I I H U H U
2.图16—1所示二端口网络的Z 参数方程为 。
a .⎥⎦⎤⎢⎣⎡---+j1j4j4j43;
b .⎥⎦
⎤⎢⎣⎡----j1j4j4j43;
c .⎥⎦⎤⎢⎣⎡--j1j4j4j43;
d .⎥⎦
⎤⎢⎣⎡--+j1j4j4j43
3.无任何电源的线性二端口电路的T 参数应满足 。
a .D A =
b .C B =
c .1=-AD BC
d .1=-BC AD
4.两个二端口 联接,其端口条件总是满足的。
a .串联
b .并联
c .级联
d .a 、b 、c 三种
5.图16—2所示理想变压器的各电压、电流之间满足的关系为 。
a .
n u u 121=,n i i =2
1
; b .n u u =21,n i i
121-=;
c .
n u u 121-=,n i i
=2
1;
d .
n u u =21,n
i i
121=; 二、填空题
1.图16—3(a )所示二端口电路的Y 参数矩阵为Y = 。
图16—3(b )所
示二端口的Z 参数矩阵为Z = 。
2.图16—4所示二端口网络的Y 参数矩阵是Y = 。
3.图16—5所示回转器的T 参数矩阵为 。
4.图16—6所示的二端口网络中,设子二端口网络1N 的传输参数矩阵为⎥⎦
⎤
⎢⎣⎡D C B A ,
则复合二端口网络的传输参数矩阵为 。
5.图16—7所示二端口网络的Y 参数矩阵为 。
式中 。
三、计算题
1.图16—8所示二端口网络的Z 参数是Ω=1011Z 、Ω=1512Z 、Ω=521Z ,
Ω=2022Z 。
试求s U U 2。
2.已知某二端口的Y 参数矩阵为Y ⎥
⎦
⎤
⎢⎣⎡--=3225S ,求其π形等效电路(如图16—9所示)中的1Y 、2Y 、3Y 。
3.已知图16—10所示二端口S N 的Z 参数为Ω=10011Z ,Ω-=50012Z ,
Ω=32110Z ,Ω=1022Z ,求:L Z 等于多少时其吸收功率最大。
4.求图16—11所示二端口网络的T 参数。
5.电路如图16—12所示,试求用H 参数表示的双端接二端口电压转移函数s
U U
2。