前方交会计算公式

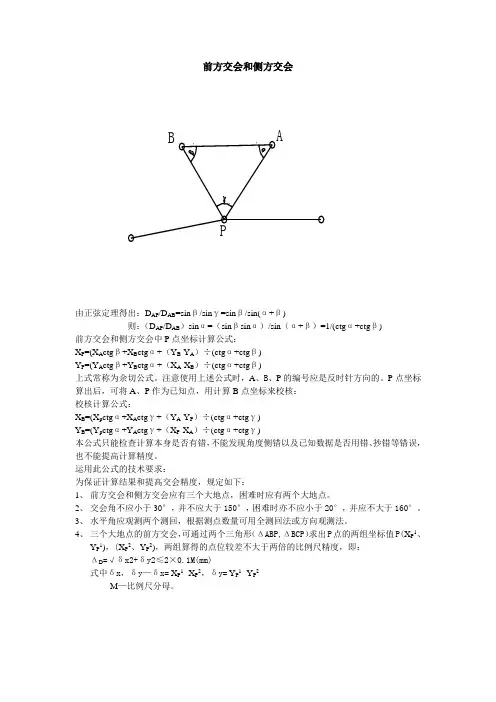
前方交会和侧方交会由正弦定理得出：D AP/D AB=sinβ/sinγ=sinβ/sin(α+β)则：（D AP/D AB）sinα=（sinβsinα）/sin（α+β）=1/(ctgα+ctgβ)前方交会和侧方交会中P点坐标计算公式：X P=(X A ctgβ+X B ctgα+（Y B-Y A）÷(ctgα+ctgβ)Y P=(Y A ctgβ+Y B ctgα+（X A-X B）÷(ctgα+ctgβ)上式常称为余切公式。

注意使用上述公式时，A、B、P的编号应是反时针方向的。

P点坐标算出后，可将A、P作为已知点，用计算B点坐标来校核：校核计算公式：X B=(X p ctgα+X A ctgγ+（Y A-Y P）÷(ctgα+ctgγ)Y B=(Y p ctgα+Y A ctgγ+（X P-X A）÷(ctgα+ctgγ)本公式只能检查计算本身是否有错，不能发现角度侧错以及已知数据是否用错、抄错等错误，也不能提高计算精度。

运用此公式的技术要求：为保证计算结果和提高交会精度，规定如下：1、前方交会和侧方交会应有三个大地点，困难时应有两个大地点。

2、交会角不应小于30°，并不应大于150°，困难时亦不应小于20°，并应不大于160°。

3、水平角应观测两个测回，根据测点数量可用全测回法或方向观测法。

4、三个大地点的前方交会，可通过两个三角形（ΔABP,ΔBCP）求出P点的两组坐标值P(X P1、Y P1)，(X P2、Y P2)，两组算得的点位较差不大于两倍的比例尺精度，即：ΔD=√δx2+δy2≤2×0.1M(mm)式中δx，δy—δx= X P1- X P2，δy= Y P1 -Y P2M—比例尺分母。

后方交会B如图所示，A、B、C是已知三角点，P点是导线点，将仪器安置在P点上，观测P至A、B、C各个方向之间的水平夹角α、β，然后根据已知三角点的坐标，可解算P点坐标。

深基坑水平位移监测测量深基坑水平位移可采用视准线法、小角度法、投点法、前方交会法、自由设站法、极坐标法等。

本节简要叙述常用的小角度法、极坐标法及前方交汇法。

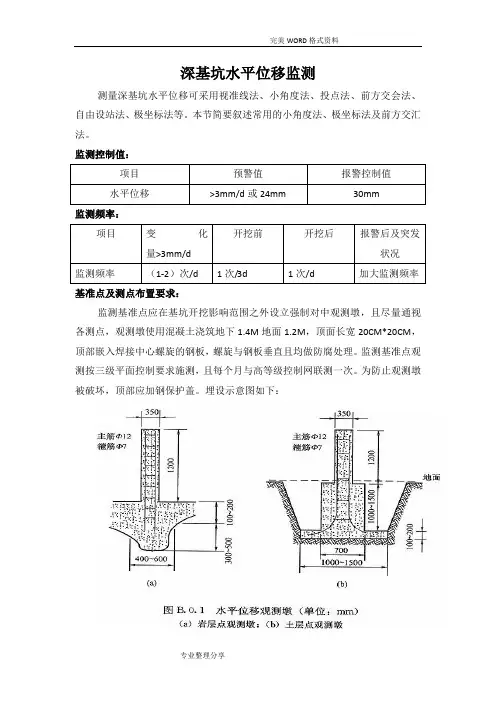
监测控制值：项目预警值报警控制值水平位移>3mm/d或24mm 30mm监测频率：项目变化量>3mm/d 开挖前开挖后报警后及突发状况监测频率（1-2）次/d 1次/3d 1次/d 加大监测频率基准点及测点布置要求：监测基准点应在基坑开挖影响范围之外设立强制对中观测墩，且尽量通视各测点，观测墩使用混凝土浇筑地下1.4M地面1.2M，顶面长宽20CM*20CM，顶部嵌入焊接中心螺旋的钢板，螺旋与钢板垂直且均做防腐处理。

监测基准点观测按三级平面控制要求施测，且每个月与高等级控制网联测一次。

为防止观测墩被破坏，顶部应加钢保护盖。

埋设示意图如下：当采用精密的光学对中装置时，对中误差不宜大于0.5mm，且尽量通视测点。

在混凝土支撑、连续墙顶等混凝土结构上安装水平位移桩，可直接在结构上用冲击钻成孔插入水平位移桩，垂直放置，缝隙使用锚固剂填充，容易受施工破坏的地方应加保护装置。

在土体等松软结构埋设水平位移测点应采用混凝土桩顶插入水平位移桩的形式，混凝土桩采用直径10CM地下50CＭ地面10CM，中心用钢筋加固。

如有需要应加保护装置，并设置醒目标志。

实物图如下：仪器架设：到达测量现场后打开仪器箱一段时间，使仪器温度与周围环境温度相适应，消除由环境温度带来的误差。

检查设备是否完整，配件是否齐全，电源电力是否充足等。

仪器架设时应注意仪器安全，在光滑的地面上架设全站仪时须在脚架上套绳索，防止脚架滑落损坏仪器。

全站仪脚架高度与观测者肩高齐平，拧紧脚架螺旋，将脚架均匀架设在基准点上。

取出仪器一手提全站仪手提柄，一手拧紧中心螺旋，将全站仪平稳架设在脚架上。

对中整平：在有强制对中装置的观测墩上架设全站仪时，应一手提全站仪手提柄，另一只手旋转基座使仪器牢固地固定在观测墩上。

角度前方交会法原理角度前方交会法是一种基本的测量方法，主要用于确定某一点的位置，特别是在野外测量和工程建设中。

该方法利用三角形相似性原理，将测量和计算过程分解为若干个简单的步骤，从而得到准确的测量结果。

本文将对角度前方交会法的原理、步骤和应用进行详细讲解。

角度前方交会法的原理角度前方交会法是基于三角形相似性原理的建立的。

三角形相似性原理指的是两个三角形的对应角度相等，对应边成比例关系。

在以下的图形中，三角形 ABC 和 DEF 相似，因为∠ABC =∠DEF，∠ACB =∠DFE和∠BAC =∠EDF。

与BC、AC、DC、EF、DF和DE相似的边成比例，即，BC/EF = AC/DF = DC/DE利用三角形相似性原理，可以得到角度前方交会法的基本原理：在已知两个点的位置和与这些点的连线所成夹角的情况下，可以测量出另外一个点的位置。

角度前方交会法的步骤角度前方交会法的测量可以分为以下步骤：第一步：在地面上确定两点的位置，并测量两点之间的距离。

这些点可以是明显的位置、桩点、或者标志物。

必须确认这些点的位置是精确的，以确保后续步骤的准确性。

第二步：测量这两点之间的夹角（或者方位角）。

这可以通过使用方位仪或者经纬仪测量得出。

如果使用经纬仪，则需要确定两点之间的经度和纬度，并计算方位角。

第三步：在第一点位置处测量与第一条线相交的第二条线的夹角（或者方位角），并测量与第二点位置的连线所成的夹角（或者方位角）。

记住将仪器调整到正确的方向上，确保夹角或者方位角的准确性。

第四步：从两个已知点的位置向前方测量出第三条线。

可以使用三角板或者望远镜或者其他测量仪器来测量这条线。

第五步：将第三条线的长度和与前两条线相交的夹角输入计算器。

计算器将使用三角形相似性原理来计算出第三条线相对于第一个点的位置。

确定了第三条线的位置之后，就可以测量和计算与该点相交的其他线。

角度前方交会法的应用角度前方交会法主要应用于建筑、土木工程和地理学中。

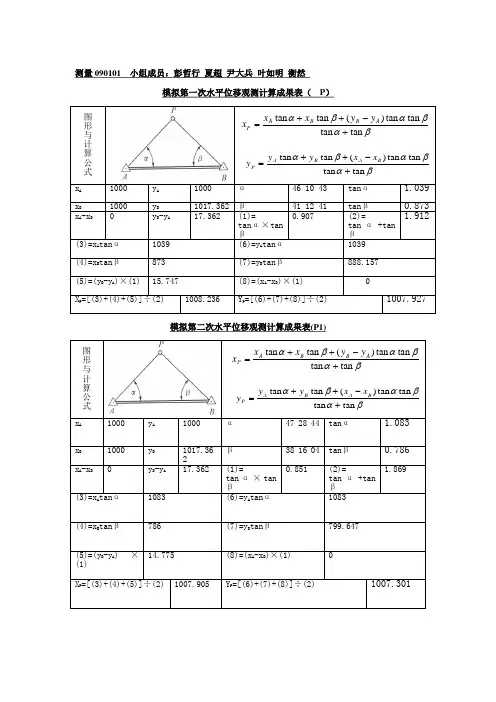
前方交会法1.前方交会法定义自两已知坐标之三角点上，观测一欲测点之水平角，以推算其坐标位置，称之前方交会法。

图-1，前方交会法。

图-2，前方交会点。

图-1 前方交会法图-2 前方交会点2.前方交会点此种补点（前方交会点），通常为无法设置仪器之测点，如塔尖、避雷针、烟囱等等。

3.前方交会法适用场合：A.具两已知三角点。

B.三点（两已知点及欲测点）间可以通视。

C.两已知点可以架设仪器，但欲测点不方便架设仪器。

D.有数个欲测点待测定时。

图-3，为数个欲测点图-3 数个欲测点4.前方交会法施作步骤：A.经纬仪分别整置于A、B 两三角点上。

B.照准P 点，分别测得α、β两水平角。

C.以计算方法，求P 点坐标。

图-4，为量测角度。

图-4 量测角度5.已知、量测、计算之数据：A.已知：xA、yA、xB、yB。

B.量测：α、β。

C.计算：xP、yP。

图-5，为前方交会法相关角度位置图-5 前方交会法相关角度位置6.限制：α、β、γ三内角均必须介于30°～120°之间。

图-6 ，为角度限制。

图-6 为角度限制7.计算法前方交会法计算方法有三种：A.三角形法; B.角度法; C.方位角法8.三角形法19()()3891802890--++=---= βφφαφφABBP AB AP ()()()()()689cos sin cos 589sin cos sin 48922222---=-==---=-==---+-=∆+∆= ABAB AB AB AB AB A B AB A B A B y y AB ABy y x x AB ABx x y y x x AB y x AB φθφφθφ()()789sin sin sin sin sin sin --+===βαβγβγβAB AB AP ABAP γβαABP AB AB y y y -=∆ABNB.求方位角ψAP 、ψBP ：C.求各邊邊長：①AB 邊長：有三種方法可求得②AP 邊長：()[](βαβαγγβα+=+-==++sin 180sin sin 180γβαsin sin sin AB AP BP ==20()()1289cos 1189sin --+=--+= BPB P BP B P BP y y BP x x φφ()()889sin sin sin sin sin sin --+===βααγαγαAB AB BP ABBP ()()1089cos 989sin --+=--+= APA P AP A P AP y y AP x x φφAPAP l φcos A Py yPBy y BPy y l y BP x x l x yy y x x x BP BP BP B P BP BP B P B P -=∆==-=∆=-=∆+=∆+=φφφφcos cos sin sin ③BP 邊長：D.求P 座標x P 、y P ：①由A 點求P 點②由B 點求P 點9.角度法A.由上法直接代入：將(9-8-2)式與(9-8-7)式代入(9-8-9)式中，可得：yy y x x x A P A P ∆+=∆+=APy y l y AP x x l x AP AP AP AP AP AP -=∆=-=∆=φφcos sin21()()()1389sin sin sin sin ---++=+= αφβαβφAB A APA P AB x AP x x ()αφαφαφsin cos cos sin sin AB AB AB -=-()()()1489cos sin sin cos ---++=+= αφβαβφAB A APA P AB y AP y y ()αααφsin cos sin ABy y AB x x AB A B AB ---=-()()()()()1589sin sin sin sin sin cos --+--+-+= βαβαβαβαA B A B A P y y x x x x ()()()()()1789cot cot cot sin cos sin 1689tan tan tan sin cos sin 1cot cot 1tan tan sin cos sin cos cos sin sin cos sin --+=+--+=++=+=+=+ αβαβαβαββαβαβααββαβαβαβαβαβα或將(9-8-2)式與(9-8-7)式代入(9-8-9)式中，可得：B.化簡x P ：由和差化積公式：將(9-8-5)式與(9-8-6)式代入，可得：再之代入(9-8-13)式中，可得：由和差化積公式：化簡下式，可得：()βαβαβαcos cos cos sin sin +=+22()2289cot cot cot cot --++-+=βααβBA B A P x x y y y ()()()()ABPB PA APBA BP A B A P APA B A P y y y y y y x x φφφφφφφcos sin cos sin tan ---+=-+=()()()()2089tan tan tan tan tan tan tan tan tan tan tan tan tan --+--+=+--+-+= βαβαβαβαβαβαβA B B A P A B A B A P y y x x x y y x x x x ()()()()()1989cot cot sin sin sin 1889tan tan tan tan sin sin sin tan 1tan 1sin sin sin cos cos sin sin sin sin --+=+--+=++=+=+ βαβαβαβαβαβαβααββαβαβαβαβα或()()()2189cot cot cot cot cot cot 1cot cot cot --+-++=+--+-+= βααββαβααBA B A P A B A B A P y y x x x y y x x x x 同理，化簡下式，可得：將(9-8-16)式與(9-8-18)式代入(9-8-15)式中，可得：或將(9-8-17)式與(9-8-19)式代入(9-8-15)式中，可得：C.化簡y P ：（推演過程省略）D.角度法所得公式(9-18-21)式與(9-18-22)式，適於計算機使用，唯應注意：左A ，右B ；左α，右β。