角度前方交会计算表(Word)

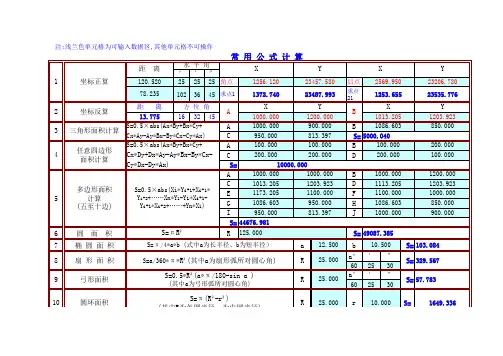
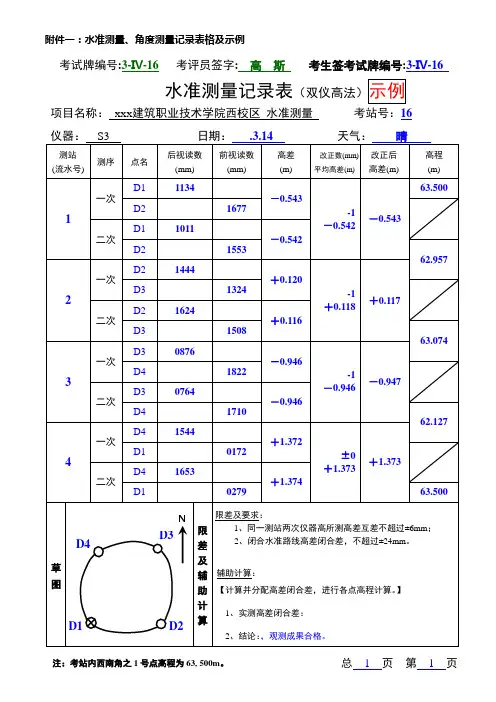
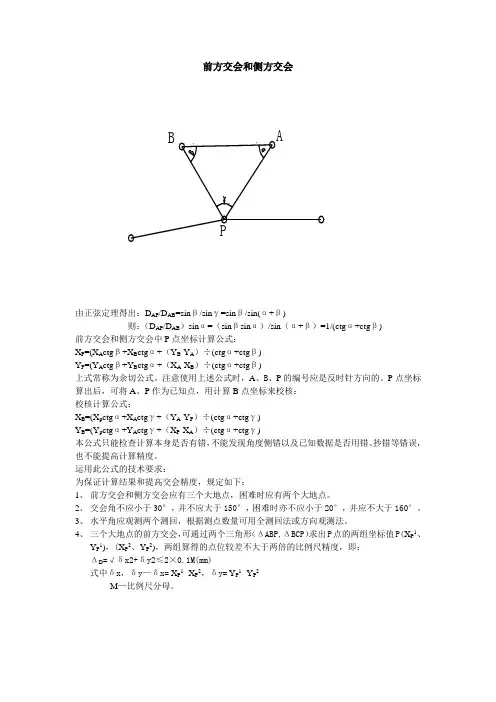
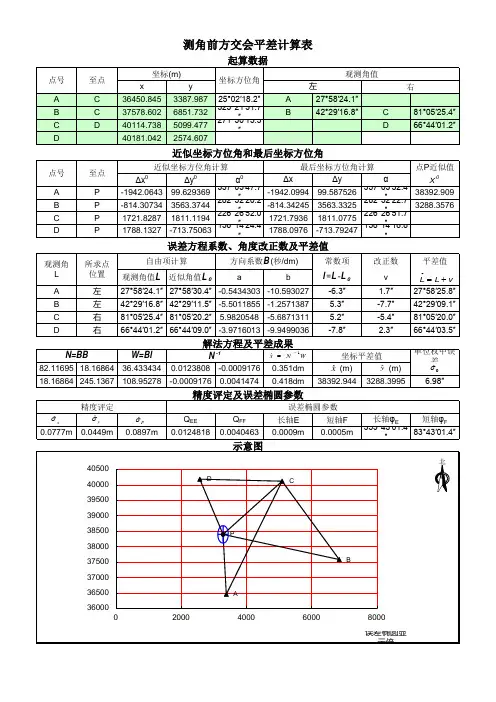
前方交会和侧方交会由正弦定理得出：D AP/D AB=sinβ/sinγ=sinβ/sin(α+β)则：（D AP/D AB）sinα=（sinβsinα）/sin（α+β）=1/(ctgα+ctgβ)前方交会和侧方交会中P点坐标计算公式：X P=(X A ctgβ+X B ctgα+（Y B-Y A）÷(ctgα+ctgβ)Y P=(Y A ctgβ+Y B ctgα+（X A-X B）÷(ctgα+ctgβ)上式常称为余切公式。

注意使用上述公式时，A、B、P的编号应是反时针方向的。

P点坐标算出后，可将A、P作为已知点，用计算B点坐标来校核：校核计算公式：X B=(X p ctgα+X A ctgγ+（Y A-Y P）÷(ctgα+ctgγ)Y B=(Y p ctgα+Y A ctgγ+（X P-X A）÷(ctgα+ctgγ)本公式只能检查计算本身是否有错，不能发现角度侧错以及已知数据是否用错、抄错等错误，也不能提高计算精度。

运用此公式的技术要求：为保证计算结果和提高交会精度，规定如下：1、前方交会和侧方交会应有三个大地点，困难时应有两个大地点。

2、交会角不应小于30°，并不应大于150°，困难时亦不应小于20°，并应不大于160°。

3、水平角应观测两个测回，根据测点数量可用全测回法或方向观测法。

4、三个大地点的前方交会，可通过两个三角形（ΔABP,ΔBCP）求出P点的两组坐标值P(X P1、Y P1)，(X P2、Y P2)，两组算得的点位较差不大于两倍的比例尺精度，即：ΔD=√δx2+δy2≤2×0.1M(mm)式中δx，δy—δx= X P1- X P2，δy= Y P1 -Y P2M—比例尺分母。

后方交会B如图所示，A、B、C是已知三角点，P点是导线点，将仪器安置在P点上，观测P至A、B、C各个方向之间的水平夹角α、β，然后根据已知三角点的坐标，可解算P点坐标。

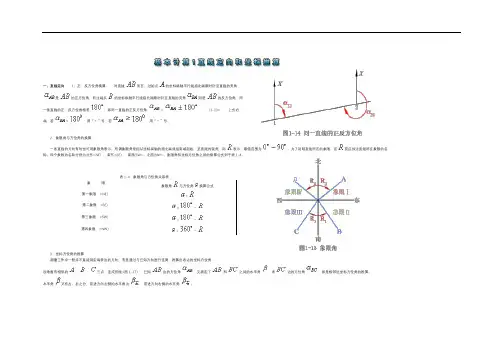
一、直线定向1、正、反方位角换算对直线而言，过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角，而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角，同一条直线的正、反方位角相差，即同一直线的正反方位角＝ (1-13> 上式右端，若<，用“＋”号，若，用“－”号。

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东<NE）、南东<SE）、南西(SW>、北西(NW>。

象限角和坐标方位角之间的换算公式列于表1-4。

象限角与方位角换算公式==－=＋=－3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线<图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

设三点相关位置如图1-17(>所示，应有＝＋＋ (1-14>设三点相关位置如图1-17(>所示，应有＝＋＋－＝＋－ (1-15>若按折线前进方向将视为后边，视为前边，综合上二式即得相邻边坐标方位角推算的通式：＝＋(1-16>显然，如果测定的是和之间的前进方向右侧水平角，因为有＝－，代入上式即得通式＝－ (1-17>上二式右端，若前两项计算结果<，前面用“＋”号，否则前面用“－”号。

二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

如图1所示，设直线AB的边长DAB和一个端点A的坐标XA、YA为已知，则直线另一个端点B的坐标为：XB=XA+ΔXABYB=YA+ΔYAB式中，ΔXAB、ΔYAB称为坐标增量，也就是直线两端点A、B的坐标值之差。

一、直线定向1、正、反方位角换算对直线而言，过始点的坐标纵轴平行线指北端顺时针至直线的夹角是的正方位角，而过端点的坐标纵轴平行线指北端顺时针至直线的夹角则是的反方位角，同一条直线的正、反方位角相差，即同一直线的正反方位角＝ (1-13)上式右端，若<，用“＋”号，若，用“－”号。

2、象限角与方位角的换算一条直线的方向有时也可用象限角表示。

所谓象限角是指从坐标纵轴的指北端或指南端起始，至直线的锐角，用表示，取值范围为。

为了说明直线所在的象限，在前应加注直线所在象限的名称。

四个象限的名称分别为北东（NE）、南东（SE）、南西(SW)、北西(NW)。

象限角和坐标方位角之间的换算公式列于表1-4。

表1-4 象限角与方位角关系表象限象限角与方位角换算公式第一象限（NE）=第二象限（SE）=－第三象限（SW）=＋第四象限（NW）=－3、坐标方位角的推算测量工作中一般并不直接测定每条边的方向，而是通过与已知方向进行连测，推算出各边的坐标方位角。

设地面有相邻的、、三点，连成折线（图1-17），已知边的方位角，又测定了和之间的水平角，求边的方位角，即是相邻边坐标方位角的推算。

水平角又有左、右之分，前进方向左侧的水平角为，前进方向右侧的水平角。

设三点相关位置如图1-17()所示，应有＝＋＋ (1-14)设三点相关位置如图1-17()所示，应有＝＋＋－＝＋－ (1-15)若按折线前进方向将视为后边，视为前边，综合上二式即得相邻边坐标方位角推算的通式：＝＋(1-16)显然，如果测定的是和之间的前进方向右侧水平角，因为有＝－，代入上式即得通式＝－ (1-17)上二式右端，若前两项计算结果<，前面用“＋”号，否则前面用“－”号。

二、坐标推算1、坐标的正算地面点的坐标推算包括坐标正算和坐标反算。

坐标正算，就是根据直线的边长、坐标方位角和一个端点的坐标，计算直线另一个端点的坐标的工作。

如图1所示，设直线AB的边长DAB和一个端点A的坐标XA、YA为已知，则直线另一个端点B的坐标为：XB=XA+ΔXABYB=YA+ΔYAB式中，ΔXAB、ΔYAB称为坐标增量，也就是直线两端点A、B的坐标值之差。

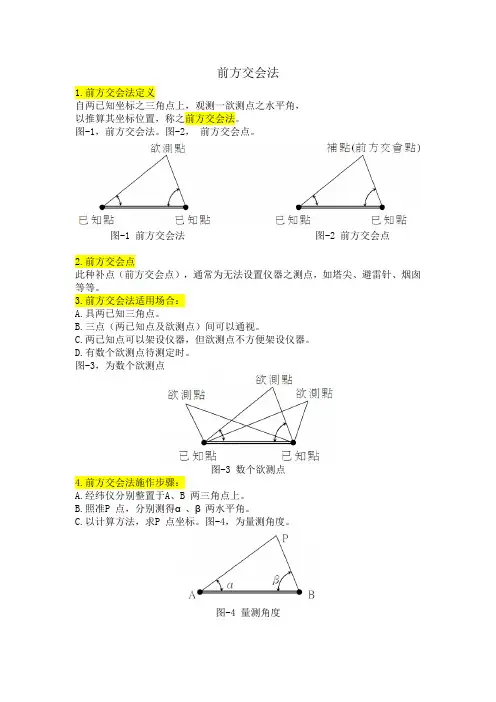
前方交会法1.前方交会法定义自两已知坐标之三角点上，观测一欲测点之水平角，以推算其坐标位置，称之前方交会法。

图-1，前方交会法。

图-2，前方交会点。

图-1 前方交会法图-2 前方交会点2.前方交会点此种补点（前方交会点），通常为无法设置仪器之测点，如塔尖、避雷针、烟囱等等。

3.前方交会法适用场合：A.具两已知三角点。

B.三点（两已知点及欲测点）间可以通视。

C.两已知点可以架设仪器，但欲测点不方便架设仪器。

D.有数个欲测点待测定时。

图-3，为数个欲测点图-3 数个欲测点4.前方交会法施作步骤：A.经纬仪分别整置于A、B 两三角点上。

B.照准P 点，分别测得α、β两水平角。

C.以计算方法，求P 点坐标。

图-4，为量测角度。

图-4 量测角度5.已知、量测、计算之数据：A.已知：xA、yA、xB、yB。

B.量测：α、β。

C.计算：xP、yP。

图-5，为前方交会法相关角度位置图-5 前方交会法相关角度位置6.限制：α、β、γ三内角均必须介于30°～120°之间。

图-6 ，为角度限制。

图-6 为角度限制7.计算法前方交会法计算方法有三种：A.三角形法; B.角度法; C.方位角法8.三角形法19()()3891802890--++=---= βφφαφφABBP AB AP ()()()()()689cos sin cos 589sin cos sin 48922222---=-==---=-==---+-=∆+∆= ABAB AB AB AB AB A B AB A B A B y y AB ABy y x x AB ABx x y y x x AB y x AB φθφφθφ()()789sin sin sin sin sin sin --+===βαβγβγβAB AB AP ABAP γβαABP AB AB y y y -=∆ABNB.求方位角ψAP 、ψBP ：C.求各邊邊長：①AB 邊長：有三種方法可求得②AP 邊長：()[](βαβαγγβα+=+-==++sin 180sin sin 180γβαsin sin sin AB AP BP ==20()()1289cos 1189sin --+=--+= BPB P BP B P BP y y BP x x φφ()()889sin sin sin sin sin sin --+===βααγαγαAB AB BP ABBP ()()1089cos 989sin --+=--+= APA P AP A P AP y y AP x x φφAPAP l φcos A Py yPBy y BPy y l y BP x x l x yy y x x x BP BP BP B P BP BP B P B P -=∆==-=∆=-=∆+=∆+=φφφφcos cos sin sin ③BP 邊長：D.求P 座標x P 、y P ：①由A 點求P 點②由B 點求P 點9.角度法A.由上法直接代入：將(9-8-2)式與(9-8-7)式代入(9-8-9)式中，可得：yy y x x x A P A P ∆+=∆+=APy y l y AP x x l x AP AP AP AP AP AP -=∆=-=∆=φφcos sin21()()()1389sin sin sin sin ---++=+= αφβαβφAB A APA P AB x AP x x ()αφαφαφsin cos cos sin sin AB AB AB -=-()()()1489cos sin sin cos ---++=+= αφβαβφAB A APA P AB y AP y y ()αααφsin cos sin ABy y AB x x AB A B AB ---=-()()()()()1589sin sin sin sin sin cos --+--+-+= βαβαβαβαA B A B A P y y x x x x ()()()()()1789cot cot cot sin cos sin 1689tan tan tan sin cos sin 1cot cot 1tan tan sin cos sin cos cos sin sin cos sin --+=+--+=++=+=+=+ αβαβαβαββαβαβααββαβαβαβαβαβα或將(9-8-2)式與(9-8-7)式代入(9-8-9)式中，可得：B.化簡x P ：由和差化積公式：將(9-8-5)式與(9-8-6)式代入，可得：再之代入(9-8-13)式中，可得：由和差化積公式：化簡下式，可得：()βαβαβαcos cos cos sin sin +=+22()2289cot cot cot cot --++-+=βααβBA B A P x x y y y ()()()()ABPB PA APBA BP A B A P APA B A P y y y y y y x x φφφφφφφcos sin cos sin tan ---+=-+=()()()()2089tan tan tan tan tan tan tan tan tan tan tan tan tan --+--+=+--+-+= βαβαβαβαβαβαβA B B A P A B A B A P y y x x x y y x x x x ()()()()()1989cot cot sin sin sin 1889tan tan tan tan sin sin sin tan 1tan 1sin sin sin cos cos sin sin sin sin --+=+--+=++=+=+ βαβαβαβαβαβαβααββαβαβαβαβα或()()()2189cot cot cot cot cot cot 1cot cot cot --+-++=+--+-+= βααββαβααBA B A P A B A B A P y y x x x y y x x x x 同理，化簡下式，可得：將(9-8-16)式與(9-8-18)式代入(9-8-15)式中，可得：或將(9-8-17)式與(9-8-19)式代入(9-8-15)式中，可得：C.化簡y P ：（推演過程省略）D.角度法所得公式(9-18-21)式與(9-18-22)式，適於計算機使用，唯應注意：左A ，右B ；左α，右β。