有序数图形练习题

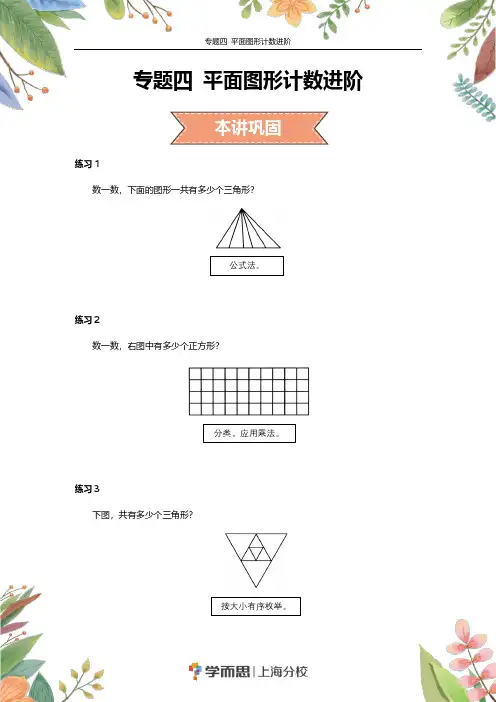
专题四 平面图形计数进阶练习1数一数，下面的图形一共有多少个三角形？练习2数一数，右图中有多少个正方形？练习3下图，共有多少个三角形？下图含有多少个三角形？练习5下图有多少个三角形？练习6只含有一个○的正方形的个数为________?乐乐老师今天要在数学课上教大家认识图形，大家都觉的很简单，可乐乐老师笑着说：“没那么简单哦”！请同学们看下图有多少个三角形？练习8大家被刚才的题目难住了，乐乐老师接着说下面的这个会简单一些，下图中长方形的个数是多少个？练习9乐乐老师看大家都答出了题目，然后在地上画了几个长方形，中间放了一个草莓，包含草莓的长方形的个数为________？牛牛说，我也给大家出一道这样的题目吧，数数看，这幅图一共有多少个三角形？练习11大家很快的答出了丁丁的题目，田田说我也来一道吧。

下图中三角形的个数为________？练习12最后丁丁也加入了进来，说这一道题不简单，谁可以解答出来呢？数数下图一共有多少个三角形？小朋友们来数数下图中一共有多少个正方形？练习1：15个。

【解析】找到基本三角形，按顺序，标序号，添“+”号。

列式：1234515++++=（个）。

练习2：90个。

【解析】10493827190⨯+⨯+⨯+⨯=（个）。

练习3：9个。

【解析】独立的三角形有7个，由4个三角形组成的三角形有1个，由7个三角形组成的三角形有1个。

因此共有7119++=个三角形。

练习4：8个。

【解析】如图：标上序号后，按图形大小分类，由1个三角形组成的有4个，由2个组成的有（1，2），（2，3），（3，4），（4，1）4个，共有8个。

练习5：8个。

【解析】6个小三角形，2个大三角形，一共有8个三角形。

练习6：10个。

【解析】分类枚举，由11⨯的正方形有2个，22⨯的正方形有6个，33⨯的正方形有2个，一共有26210++=（个）。

练习7：28个。

【解析】由一个三角形组成的：12个；由两个三角形组成的：6个；由三个三角形组成的：8个；由六个三角形组成的：2个；共有1268228+++=个。

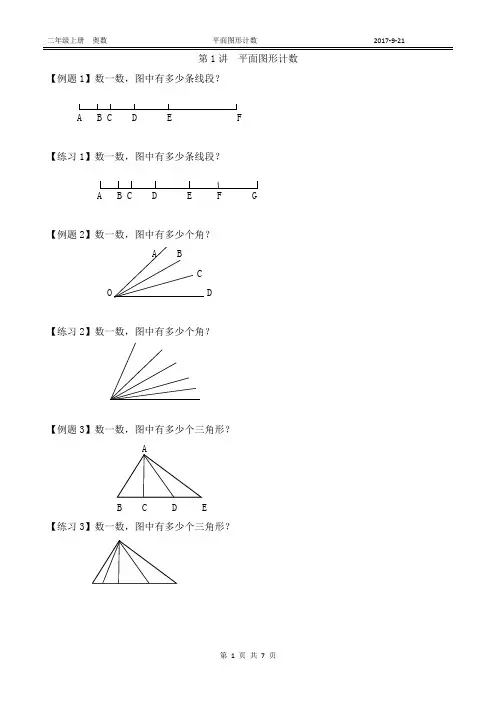
第1讲平面图形计数【例题1】数一数，图中有多少条线段？A B C D E F【练习1】数一数，图中有多少条线段？A B C D E F G【例题2】数一数，图中有多少个角？A BCO D【练习2】数一数，图中有多少个角？【例题3】数一数，图中有多少个三角形？B C D E【练习3】数一数，图中有多少个三角形？【例题4】数一数，图中共有多少个长方形？（1）（2【练习4】下图中共有多少个长方形？【例题5】数一数，图中共有多少个正方形？【练习5】数一数图中含有@的正方形有几个？自我能力提升1.下图中共有多少条线段？2.数一数，每个图形中共有多少个三角形？图（1）图（2）3.下图中共有多少个三角形？4.数一数图中共有多少个三角形？5.数一数图中共有多少个正方形？学霸挑战1.下面各图中各有多少个正方形？（1）2.图中有几个含★的正方形？几个含★的三角形？3.图中共有多少个三角形？4.图中共有多少个三角形？答案：【例题1】5+4+3+2+1=15（条）解析：按左端点有序地数。

（1）以A为左端点：AB,AC,AD,AE,AF 共5条。

（2）以B为左端点：BC,BD,BE,BF 共4条。

（3）以C为左端点：CD,CE,CF 共3条。

（4）以D为左端点：DE,DF 共2条。

（5）以E为左端点：EF 共1条。

【练习1】6+5+4+3+2+1=21(条）【例题2】3+2+1=6(个）解析：（1）以OA为一边的角：∠AOB,∠AOC,∠AOD, 共3个（2）以OB为一边的角(∠AOB除外）：∠BOC,∠BOD, 共2个(3)以OC为一边的角（∠AOC,∠BOC除外）：∠COD, 共1个【练习2】5+4+3+2+1=15（个）【例题3】3+2+1=6(个）解析：以BC,BD,BE,CD,CE,DE为一边的三角形各有1个。

【练习3】4+3+2+1=10（个）【例题4】（1）4+3+2+1=10（个）（2）（4+3+2+1）×（2+1）=30（个）【练习4】（3+2+1）×（3+2+1）=36（个）【例题5】16+9+4+1=30（个）解析：边长为1的：4×4=16（个）；边长为2的：3×3=9（个）边长为3的：2×2=4（个）；边长为4的：1（个）【练习5】1+4+2=7（个）解析：边长为1的：1（个）；边长为2的：4（个）边长为3的：2（个）；1.（3+2+1）+（4+3+2+1）=16（条）2.（1）20 （2）24解析：（1）将大三角形分层：上面一层小三角形里有10个，整个大三角形里有10个，总共有20个。

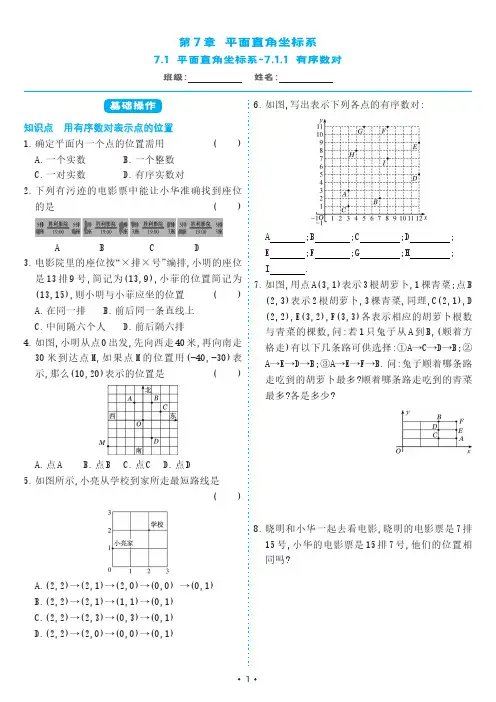
第7章平面直角坐标系7.1平面直角坐标系-7.1.1有序数对班级：姓名：知识点用有序数对表示点的位置1.确定平面内一个点的位置需用()A.一个实数B.一个整数C.一对实数D.有序实数对2.下列有污迹的电影票中能让小华准确找到座位的是()A B C D3.电影院里的座位按“×排×号”编排,小明的座位是13排9号,简记为(13,9),小菲的位置简记为(13,15),则小明与小菲应坐的位置()A.在同一排B.前后同一条直线上C.中间隔六个人D.前后隔六排4.如图,小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,那么(10,20)表示的位置是()A.点AB.点BC.点CD.点D5.如图所示,小亮从学校到家所走最短路线是()A.(2,2)→(2,1)→(2,0)→(0,0)→(0,1)B.(2,2)→(2,1)→(1,1)→(0,1)C.(2,2)→(2,3)→(0,3)→(0,1)D.(2,2)→(2,0)→(0,0)→(0,1)6.如图,写出表示下列各点的有序数对:A;B;C;D;E;F;G;H;I.7.如图,用点A(3,1)表示3根胡萝卜,1棵青菜;点B(2,3)表示2根胡萝卜,3棵青菜,同理,C(2,1),D (2,2),E(3,2),F(3,3)各表示相应的胡萝卜根数与青菜的棵数,问:若1只兔子从A到B,(顺着方格走)有以下几条路可供选择:①A→C→D→B;②A→E→D→B;③A→E→F→B.问:兔子顺着哪条路走吃到的胡萝卜最多?顺着哪条路走吃到的青菜最多?各是多少?8.晓明和小华一起去看电影,晓明的电影票是7排15号,小华的电影票是15排7号,他们的位置相同吗?9.七年级(1)班的小芳家、小明家、小亮家、小新家位置如下图,若一个小正方形的边长表示1km,试用有序数对表示小芳家、小明家、小亮家、小新家的位置.10.如图是阳光小区内的一幢商品房的示意图,若小亿家所在的位置用(2,4)表示.(1)用有序数对表示小雪、小明家的位置;(2)(4,5),(3,2)分别表示谁家所在的位置?综合点学科间综合11.如图,雷达探测器测得六个目标A,B,C,D,E,F 出现.按照规定的目标表示方法,目标C,F 的位置表示为C(6,120°),F(5,210°).按照此方法在表示目标A,B,D,E 的位置时,其中表示不正确的是()A.A(5,30°)B.B(2,90°)C.D(4,240°)D.E(3,60°)12.在中国地图上找出北京、济南、上海的位置,并用有序数对分别写出其经纬度(经度写在前边).拓展训练拓展点生活中的有序数对13.如图,小海龟位于图中点A(2,1)处,按下述路线移动:(2,1)→(2,4)→(7,4)→(7,7)→(1,7)→(1,1)→(2,1).用粗线将小海龟经过的路线描出来,看一看是什么图形.14.象棋盘上有一只(如图).问:它跳五步能回到原来的位置上吗?第7章平面直角坐标系7.1平面直角坐标系-7.1.1有序数对答案与点拨1.D(点拨:确定平面内一个点的位置需用一对有序实数,即有序实数对,故选D.)2.D(点拨:能让小华准确找到座位的必须是排数、座位号均清晰的.分析可知只有D符合,故选D.)3.A(点拨:∵13排9号简记为(13,9),∴(13,15)表示13排15号,∴小明(13,9)与小菲(13,15)应坐的位置在同一排,中间隔5人.故选A.)4.B(点拨:根据题意可得:小明从点O出发,先向西走40米,再向南走30米到达点M,如果点M的位置用(-40,-30)表示,即向西走为横线负方向,向南走为纵线负方向,则(10,20)表示的位置是向东走10米,向北走20米,即点B所在位置.)5.B(点拨:由图可知小亮从学校到家所走最短路线是(2,2)→(2,1)→(1,1)→(0,1)(或(2,2)→(1,2)→(0,2)→(0,1)),故选B.)6.根据图形可得各点表示为:A(3,3);B(7,2);C(3,1);D(12,5);E(12,9);F(8,11);G(5,11);H(4,8);I(8,7).7.按①走吃到胡萝卜的根数为3+2+2+2=9(根),青菜的棵数为1+1+2+3=7(棵);按②走吃到胡萝卜的根数为3+3+2+2=10(根),青菜的棵数为1+2+2+3=8(棵);按③走吃到胡萝卜的根数为3+3+3+2=11(根),青菜的棵数为1+2+3+3=9(棵);故按③走吃到的胡萝卜和青菜都是最多的,吃到胡萝卜11根,青菜9棵.8.不相同.9.小芳家(2,2),小明家(5,2),小亮家(5,5),小新家(8,6).10.(1)小雪家的位置为(1,3),小明家的位置为(5,1);(2)(4,5)表示小马家所在的位置,(3,2)表示小亮家所在的位置.11.D(点拨:由题意可知A,B,D,E的坐标分别可表示为:A(5,30°),故A正确;B(2,90°),故B正确;D(4,240°),故C正确;E(3,300°),故D错误,故选D.)12.略(点拨:可参考相关地理知识.)13.如图,像一面旗子.14.跳五步不能回到原位.。

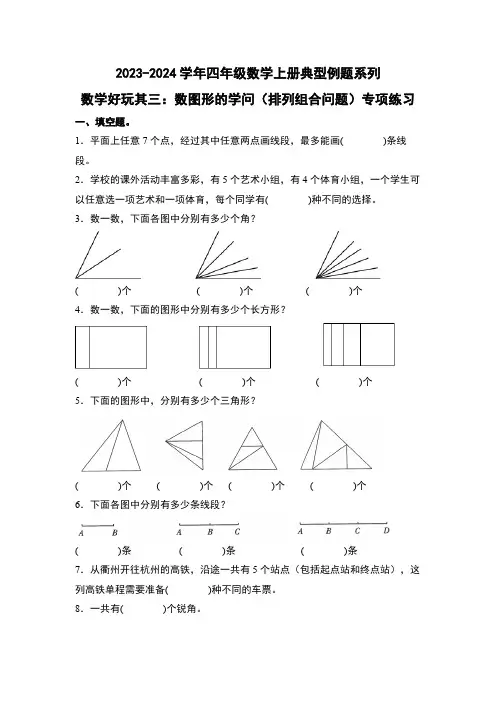
2023-2024学年四年级数学上册典型例题系列数学好玩其三：数图形的学问（排列组合问题）专项练习一、填空题。

1．平面上任意7个点，经过其中任意两点画线段，最多能画( )条线段。

2．学校的课外活动丰富多彩，有5个艺术小组，有4个体育小组，一个学生可以任意选一项艺术和一项体育，每个同学有( )种不同的选择。

3．数一数，下面各图中分别有多少个角？( )个( )个( )个4．数一数，下面的图形中分别有多少个长方形？( )个( )个( )个5．下面的图形中，分别有多少个三角形？( )个( )个( )个( )个6．下面各图中分别有多少条线段？( )条( )条( )条7．从衢州开往杭州的高铁，沿途一共有5个站点（包括起点站和终点站），这列高铁单程需要准备( )种不同的车票。

8．一共有( )个锐角。

13．有6位羽毛球运动员进行单环赛，每两个活动员都要赛一场，一共需要赛( )场。

14．某校初三年级共有8个班进行辩论赛，规定单循环比赛（两个班之间赛一场）问初三年级的比赛是进行( )场。

15．从深圳到北京的高铁，沿途一共有7个站点（包括起点站和终点站），这列高铁单程需要准备( )种不同的车票。

二、解答题。

16．新年到了，小强、小刚、小芳、小东4个人，互相寄一张贺卡，一共寄了几张贺卡？17．体操表演队为联络方便，设计了一种联系方式。

一旦有事，先由教练同时通知两位队长，这两位队长再分别同时通知两名同学，依此类推，每人再同时通知两个人。

如果每同时通知两个人共需1分钟，6分钟可以通知到多少名同学？18．某校从10名候选人中选2名参加区“少代会”，有多少种不同的选法？19．暑假里，小明，小华、小亮、小丽、小红5个人，每两人通一次电话，一共通了几次电话？20．你能把四张数字卡片按要求组数吗？（按从小到大的顺序依次填写）（1）最大的四位数是多少？最小的四位数是多少？（2）只读一个零的四位数有哪些？一个零也不读的四位数有哪些？2023-2024学年四年级数学上册典型例题系列数学好玩其三：数图形的学问（排列组合问题）专项练习一、填空题。

有序地数图形一、知识点解读有序地数图形的方法（掌握运用）知识点：数图形的个数时，要仔细观察，按顺序分类数，先数基本图形，再数由基本图形组成的组合图形，最后相加，求出图形的总个数，做到不重复、不遗漏。

例：图中有几个长方形先数基本图形，有3个；再数由两个基本图形组成的组合图形，有2个；最后数由三个基本图形组成的组合图形，有1个；所以，图中的长方形一共有3+2+1=6个。

像这样分类，有顺序地去数，就能做到不重复、不遗漏。

教学要求：教学这部分内容，要给学生留出充足的时间和空间，让学生自己去观察、去数，多次实践发现规律。

通过摆学具或者画图做标记的方法独立探索，然后组织交流。

交流时，要重点关注学生数的过程。

在学生交流完可能出现的情况后，再组织学生讨论怎样数才能既不重复又不遗漏，让学生进一步体会有序思考的过程，使学生从中感悟到：有顺序地数，能做到不重复、不遗漏。

无论是数线段，数角还是数三角形，练习时要注意沟通它们之间的联系，交流时重点引导学生体会到有序思考的优越性。

二、知识拓展1.运用分类法解决数图形的问题：解决稍复杂的数图形问题时，可以先分类数，再求出图形的总个数。

2.运用有序法解决数线段的问题：数线段的条数时，可以先数出基本线段的条数，然后依次加比前面少1的数，加到1为止；也可以先数出线段上的端点数，用（端点数-1）+（端点数-2）+（端点数-3）+^……+1来求。

3.数有特殊标记的图形，例如：图中包含五角星的正方形有几个？解决这类问题时，结合前面的知识点，要有序，做到不重不漏。

三、知识点训练基础训练1. 数一数下面的图形中各有多少条线段。

（）条（）条（）条2. 数一数下面图形中各有多少个长方形。

（）个（）个（）个3. 在下图中的每两点之间画一条线段，一共可以画多少条线段？4. 请同学们数一数，下图中共有多少个长方形?5.数一数下图中有多少个平行四边形？能力提升1. 数一数，下面图形中共有多少个三角形？（）个（）个（）个（）个2. 数一数。