当前位置：文档之家 › 受冲击荷载作用时构件的应力和变形计算优秀课件

受冲击荷载作用时构件的应力和变形计算优秀课件

  • 格式：ppt
  • 大小：1.33 MB
  • 文档页数：50

下载文档原格式

  / 50

合集下载

11动载荷_2冲击载荷

11动载荷_2冲击载荷

所以，此时轴内的最大扭转切应力
d max
Td Wt

JGIp Wt 2l
1057 MPa
◆ 相较前例，最大切应力增大了约 395 倍。在这种情况下，早 已超过了材料的许用切应力。因此，为了保证转轴的安全，在停 车时应尽量避免急刹车。
1.8 MPa
梁内的动荷最大弯曲正应力
d max Kd st max 71.7 1.8 MPa = 129.1 MPa
[例4] 如图，钢丝绳的下端悬挂一重为 P 的重物，以速度 v 匀速下 降，当钢丝绳长度为 l 时，滑轮突然被卡住，试求钢丝绳内的动荷 应力。已知钢丝绳的横截面面积为 A，弹性模量为 E，滑轮与钢丝 绳的质量均忽略不计 。
垂直冲击，冲击物的初速为 v0 ，冲击物与被冲击构件的 相对高度为 h
动荷因数：
h
P
d
st
Kd 1
1 2h v02
st
g
式中，st 为冲击物自重以静荷方式作用引起的冲击点沿冲击方向
的静位移
◆ 对于突加载荷，动荷系数 Kd = 2
四、水平冲击的动荷因数
水平冲击，冲击物的初速为 v0 动荷因数：
解： 1）计算静荷位移
P
h
s t

Pl
3103 6
EA 10 109 π 0.32
0.0255 mm
4
l
2）计算动荷因数
d
Kd 1
1 2h 1
st
1 2 200 mm 126.2 0.0255 mm
Kd 126.2
3）计算静荷应力
st

P A
Kd
v02 g
st

受冲击荷载作用时构件的应力和变形计算概要课件

受冲击荷载作用时构件的应力和变形计算概要课件
优化结构设计
通过计算，可以了解构件在冲击荷载 作用下的性能表现，为结构优化设计 提供依据。
02
CATALOGUE
冲击荷载作用下构件的应力计算
应力计算的基本原理
01
02
03
平衡方程
根据力的平衡原理，建立 平衡方程，求解构件在冲 击荷载作用下的应力分布 。
应力的定义与分类
根据材料的力学性质，将 应力分为拉应力和压应力 ，并了解其特点。
VS
变形计算
根据冲击荷载的大小和持续时间，计算出 构件的变形量、变形形态以及与应力的相 互关系。
案例中的稳定性分析
静态稳定性分析
分析构件在冲击荷载作用下是否会发生整体倾覆或失稳。
动态稳定性分析
分析构件在冲击荷载作用下是否会发生共振或振动失稳。
06
CATALOGUE
结论与展望
对冲击荷载作用下构件应力和变形的认识
冲击荷载作用下构件的应力分布
在冲击荷载作用下，构件的应力分布呈现出明显的非线性特征，高应力区域集中在冲击点附近，并随着距离的增 加而迅速减小。
冲击荷载作用下构件的变形规律
在冲击荷载作用下，构件的变形呈现出动态变化的特性，变形量随冲击能量的增加而增大，同时与材料的弹性模 量、泊松比等力学性能有关。
对未来研究的建议与展望
05
CATALOGUE
工程实例分析
实际工程中的冲击荷载案例
桥梁工程
桥梁在车辆突然撞击、地震等情况下，会受到冲 击荷载。
建筑结构
高层建筑在风载、人为撞击等情况下，也会受到 冲击荷载。
机械系统
机械设备在突然启动、停止或遇到突发性故障时 ，相关构件也会受到冲击荷载。
案例中的应力与变形计算

材料力学PPT课件11-第十一讲-冲击应力

材料力学PPT课件11-第十一讲-冲击应力

冲击过程演示
冲击变形最大位置
回弹静平衡位置
冲击末－变形最大位置
冲击、回弹全过程
静平衡位置
冲击应力分析（工程方法）
假设 分析
冲击物为刚体，且与被冲击物接触后，始终保持 接触；
被冲击构件的质量（惯性）忽略不计，冲击变形 在瞬间传遍全场；
冲击过程中的能量损失忽略不计。 冲击变形最大时，冲击物的速度为零
解：
DE DVε
Dd Dst 1 v
EA gPl
Pd
P
Dst
Dd
P1
v
EA gPl
d
Pd A
P A
1
v
EA gPl
讨论：
可否建立如下“能量守恒”关系？
Pv 2 2g
PDd
1 2
kD
2 d
吊绳产生静变形的过程非冲击过程， 载荷是缓慢施加的。
自由落体冲击分析
P(h
Dd
)
kD2d
2
单位状态：施加与D对应的单位载荷，确定内力
D l F N ( x)d T ( x)d M y( x)d y M z ( x)dz
D －广义位移，施加相应单位广义载荷
当所得位移为正，则位移与所加单位载荷同向
单位载荷法
D l F N( x)d T ( x)d M y( x)dy M z ( x)dz
对于线弹性杆或杆系：
D
l
F
N
(
x )FN EA
(
x
)
dx
T
(
x )T GI t
(
x
)
dx
M
y( x)M y( x) dx EI y
M
z

构件受冲击时的应力和变形

构件受冲击时的应力和变形

T V Ud
1 P v2 1 d2 P
2g
2 j
由此求得
d
v2
g j
j
Kd j
式中， Kd 为动荷因数，且有
v2 Kd g j
与自由落体冲击时的动荷因数相比可以发现，冲击形式不同，其动荷因 数也会不同。
下面计算三种情况下的杆内动应力，列于表 13-1 中。
表 13-1
情况 （a）
静应力（ j ）
图13-7
从冲击物与弹簧开始接触到弹簧变形到最低位置，其动能由 T 变为零，
变化量 T Gv2 ，其中 v 2g
2gh ；重量为 G 的重物向下移动的距离为 d 。将
冲击后的位置取作势能零点，势能的变化量V Gd 。
由于不计冲击过程中的能量损失，根据机械守恒定律，冲击系统的动能和
势能的变化应等于弹簧的变形能，若以Ud 表示弹簧的变形能，即
j
Pl3 48EI
150 13 12 48 200 109 (50 103)4
m
30 106
m
自由落体冲击时的动荷因数为
2h
2 75 103
Kd 1
1 1 j
1
30 106
71.7
对于情况二，梁跨度中点的变形由梁的弯曲和弹簧的缩短两部分组成，其变
形量为
j
Pl3 48EI
P 2k
30 106
（a） （b）
（c）
图 13-9
解 首先应用能量守恒定律求出水平冲击时杆的动变形 d 。由于是水平 冲击，冲击过程中系统的势能不变，故重物损失的势能V 0 。因冲击物与杆端 接触时的速度为 v ，所以重物损失的动能T 为
T 1 P v2 2g

工程力学课件 第11章 动载荷、冲击载荷、交变应力简介

工程力学课件 第11章 动载荷、冲击载荷、交变应力简介
1.1.1 电路பைடு நூலகம்组成
交变应力的变化特点可用最小应力与最大应力的比值r表示， 称为循环特征（应力比）即
它的可能取值范围为
在五个特征量
中，只有两个是独立的，即只要已知其中的任意两个特征量， 就可求出其他的量。如果
工程力学
12
称为脉动循环交变应力，其循环特征r＝0。 当
1.1.1 电路的组成
r＝1 交变应力统称为非对称循环交变应力。
对于以等加速度作直线运动构件，只要确定其上各点的加速度a, 就可以应用达朗贝尔原理施加惯性力，如果为集中质量m，则惯性力 为集中力。
如果是连续分布质量，则作用在质量微元上的惯性力为
工程力学
2
然后，按照弹性 静力学中的方法对构
1.件1进.1行电应力路分的析和组强成 度与刚度的计算。以 图中的起重机起吊重 物为例，在开始吊起 重物的瞬时，重物具 有向上的加速度a，重 物上便有方向向下的 惯性力，如式(11-1) 所示。
其中
分别称为静应力(staticsstress)和动应力(dynamicsstress)。
工程力学
4
第二节 冲击载荷
一、基本假定 1.1.1具电有一路定的速度组的成运动物体，向着静止的构件冲击时，冲击物的
速度在很短的时间内发生了很大变化，即：冲击物得到了很大的负 值加速度。这表明，冲击物受到与其运动方向相反的很大的力作用。 同时，冲击物也将很大的力施加于被冲击的构件上，这种力在工程 上称为“冲击力”或“冲击载荷”。
③假设冲击过程中没有其他形式的能量转换，机械能量守恒定 理仍成立。
工程力学
5
二、自由落体冲击 1.1.1设电一简路支的梁(组线弹成性体)受自由落体冲击如图11.3所示，试分析

材料力学11动载荷_2冲击载荷

材料力学11动载荷_2冲击载荷

st
P
[例5] 如图，在转轴 AB 的B 端有一个质量很大的飞轮，在 A 端有 制动装置。若在飞轮转速 n = 100 r/min 时突然在 A 端急刹车，瞬 间停止转动，试求轴内的最大切应力。 已知轴的长度 l = 1 m，直 径 d = 100 mm ，切变模量 G = 80 GPa，飞轮对轴的转动惯量 J = 500 kg·m2 ，轴的质量可以忽略不计。
1.8 MPa
梁内的动荷最大弯曲正应力
d max Kd st max 71.7 1.8 MPa = 129.1 MPa
[例4] 如图，钢丝绳的下端悬挂一重为 P 的重物，以速度 v 匀速下 降，当钢丝绳长度为 l 时，滑轮突然被卡住，试求钢丝绳内的动荷 应力。已知钢丝绳的横截面面积为 A，弹性模量为 E，滑轮与钢丝 绳的质量均忽略不计 。
2）重物落在弹簧上 此时的静荷位移
st

Pl EA

ห้องสมุดไป่ตู้
P k

7.074 106
m + 500106
m
=
507.074 106
m
2）重物落在弹簧上
静荷位移
st 507.074106 m
动荷因数
2h
Kd 1
1 15.08
st
杆内的动荷应力
d Kdst 15.08 0.7074 MPa = 10.7 MPa
4
P
hP
l
d
4）计算动荷应力
d Kdst 126.2 0.0424 MPa = 5.35 MPa
◆ 此时的动荷应力是静荷应力的126.2倍，可见，冲击载荷是 非常大的。
[例2] 钢制圆截面杆如图，其上端固定，下端固连一无重刚性托盘 以承接落下的环形重物。已知杆的长度 l = 2 m ，直径 d = 30 mm ， 弹性模量 E = 200 GPa。若环形重物的重力 P = 500 N，自相对高度 h = 50 mm 处自由落下，使杆受到冲击。试求在下列两种情况下， 杆内的动荷应力：（1）重物直接落在刚性托盘上；（2）托盘上放 一刚度系数量 k = 1 MN/m的弹簧，环形重物落在弹簧上。

第6章构建受力变形及其应力分析.ppt

材料力学
材料力学的任务 静力学：受力平衡（刚体）；
材料力学：构件强度、刚度、稳定性。（变形体）
构件：工程结构或机械的各组成部分。
构件分类：
板
壳
杆
件
6.1 概述 6.1.1 强度、刚度、稳定性的基本参数
1、强度 : 构件在外载作用下，抵抗破坏的能力。 （煤气罐爆炸、钢丝绳断）
2、刚度 :构件在外载作用下，抵抗变形的能力。 （机械传动装置中传动轴过大弯曲变形， 轴承、齿轮加剧磨损）
L
L
线应变：单位长度的变形量。
6.5.2 杆的横向变形 1、横向绝对变形
Δb b1 b
2、横向相对变形（横向线应变）
ε' Δb b1 b
b
b
6.5.3 泊松比
ε
ε
或：ε νε
6.5.4 胡克定律 (弹性范围内)
1、拉压杆的胡克定律
ΔL PL NL EA EA
1
P
N
P1
+
P x
P吴书104例4-1（bc）
6.4 截面上的应力
6.4.1 应力的概念
问题提出：（材料相同粗细不同）
P
P
P
P
分析结果：（内力相同，但是细杆易断裂）
结论：1. 内力大小不能衡量构件强度的大小。 2. 内力在截面分布集度应力；
1. 应力定义：由外力引起的（构件某截面上一点处） 内力集度。

6.6.3 材料在压缩时的力学性能
P谢140 图14-26 14-27
可看出低钢在拉伸压缩时弹性阶段和屈服阶段曲线基 本重合 铸铁的抗压强度σbc远大于抗拉强度σb ，所以脆性材 料宜做受压构件
例1 图示杆的A、B、C、D点分别作用着5P、8P、4P、 P的力，方向如图，试画出杆的轴力图。

受冲击荷载作用时构件的应力和变形计算共51页


谢谢！
ห้องสมุดไป่ตู้
36、自己的鞋子，自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢，但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何，且尽全力做你应该做的事吧。——美华纳
受冲击荷载作用时构件的应力和变形 计算
6、法律的基础有两个，而且只有两个……公平和实用。——伯克 7、有两种和平的暴力，那就是法律和礼节。——歌德
8、法律就是秩序，有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起，可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的，因为好人用不着它们，而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
40、学而不思则罔，思而不学则殆。——孔子

构件受冲击时的应力和变形

st
1 2h )
st
Fd P
d st
Kd
d Kd st
Fd Kd P
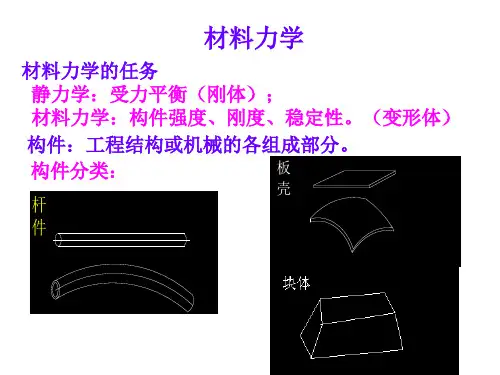
例题7 一重量为P的重物由高度为h的位置自由下落,与一块和直
杆AB 相连的平板发生冲击. 杆的横截面面积为A, 求杆的冲击应力.
重物是冲击物,
A
A
杆 AB（包括圆盘）是被冲击物.
P
冲击物减少的势能 V P(h d )
Vεd
1 2
Fd d
Δd
所以
P(h
d
)
1 2
Fd d
Fd d P st
Fd
d st
P
P(h
Δd
)
1 2
Δd Δst
P Δd
d2 2 st d 2h st 0
d 2 st
42st
2
8h st
st (1
d st ( 1
1
2h
st
)
Kd st
其中 Kd 1
1 2h 为动荷因数
Kd 1
1 2h 2
st
P
由此可见,突加载荷的动荷因数是2,这时所引
h
起的荷应力和变形的2倍.
（2）若已知冲击开始瞬间冲击物与被冲击 物接触时的速度为v,则
v2 h
2g
Kd 1
1 2h 1 Δst
1 v2
g st
（3）若已知冲击物自高度 h 处以初速度v0 下落,则
v2 v02 2gh
机械能守恒定律
冲击时,冲击物在极短的时间间隔内速度发生很大的变化,其 加速度a很难测出,无法计算惯性力, 故无法使用动静法.在实用计 算中,一般采用能量法. 即在若干假设的基础上,根据能量守恒定律 对受冲击构件的应力与变形进行偏于安全的简化计算.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

下重要关系：
Kd
Pd Pst
d st
d st
d st
式中 Pd , d , d , d 分别表示动载荷，动应力，动应变和动位移； Pst , st , st , st 分别表示静载荷，静应力，静应变和静位移。
例题 图示20a槽钢，以等加速下降，若在0.2s的时间内速度由
1.8m/s降至0.6m/s，试求槽钢中最大弯曲正应力。已知L＝6m，
解：求沿圆环轴线的均匀分布惯性力集度 qD
qD
A
g
an
A
g
D 2
2
圆环横截面上的内力：
y
qD
qD
D 2
d
d
x
2FN d
0
qD
D 2
d sin
qD D
FN d
qD D 2
AD2 2
4g
o
FN d
FN d
圆环横截面上的应力：
D
FN d A
D2 2
4g
v2
g
式中 v D 是圆环轴线上各点的线速度。
根据动静法，列平衡方程：
X 0即
FNd (x)
Ax
Ax
g
aQ
Q g
a
0
2.等加速直线运动构件的应力计算
解得：
FNd (x)
( Ax
Q)(1
a) g
吊索中的动应力为：
d (x)
FNd A
Ax Q (1
A
a) g
当重物静止或作匀速直线运动时，吊索横截面上的静荷应力为：
st
代入上式，并引入记号 Kd
g
max j
M max j Wy
36.7MPa
dk d max j 59.1MPa
第十四章 动荷载/二、等加速运动构件的应力计算
3 圆环等角度转动时构件的应力与变形计算：
(1)圆环横截面上的应力
图示匀质等截面圆环,绕着通过环中心且
an
Do
t
垂直于圆环平面的轴以等角速度旋转, 已知横截面面积为A,材料的容重为γ,壁厚 为t,求圆环横截面上的应力。
转动惯量为 Ix 0.5KN MS2 。轴的直径 d 100mm
刹车时使轴在10秒内均匀减速停止。求轴内最大动应力。
解：（1）飞轮与轴的转动角速度为
o
2n 60
100 30
10 3
rad
/
s
（2）当飞轮与轴同时做均匀减速转动时，其角加速度为
1 o
0 10 3
rad / s2
t
10
第十四章 动荷载
二、等加速运动构件的应力计算
第十四章 动荷载/二、等加速运动构件的应力计算
1.惯性力的概念 惯性力 = 运动物体的质量G/g×加速度a
构件处于匀速静直止线状状态态a 0, 惯性力 0 作为静荷载处理.
第十四章 动荷载/二、等加速运动构件的应力计算
1.惯性力的概念
构件处于加速运动状态变等加加速速状状态态
例题 一吊车以匀加速度起吊ቤተ መጻሕፍቲ ባይዱ物Q,若吊索的横截面积为A，材料
比重为，上升加速度为a，试计算吊索中的应力。
解：将吊索在x处切开，取下面
Fd (x)
部分作为研究对象。
mm
Ax
作用在这部分物体上的外力有： 重物的重量：Q；
a
x
Ax a
g
x
x段的吊索重量：Ax，
惯性力为：Q
g
a，Agx
a
Q
Q
Qa g
吊索截面上的内力：FNd (x)
b＝1m。
q
F 运动方向
o
qL qb 2 qb2 2
qL qb 2 qb2
2
b
L
b a vt v0 6 m s2
＋
t
q 22.639.8 222 kN m
qd
qst
a g
qL2 qb2 g2
Wy 24.2106 m3
qst 22.63kg m
kd
1
a g
1.61
q
qst
qst
2
（2）圆环等角度转动 时构件的强度条件为：
D
v 2
g
[]
圆环横截面上的应力与A无关，而与线 速度由强度条件可得容许的最大线速度为
[ ]
g []
（3）圆环等角度转动时构件的变形计算
旋转圆环的变形计算
在惯性力集度的作用下，圆环将胀大。令变形后的直径为 D ， 则其直径变化 D D D ，径向应变为
静应力:构件在静荷载作用下产生的应力. 特点:1.与加速度无关
2.不随时时间的改变而改变. 动应力:构件由于动荷载引起的应力.
第十四章 动荷载/一、动荷载的概念与实例
起重机吊重物,若悬 挂在吊索上的重物W是静 止不动或以匀速直线运动 上升时,重物对吊索就是 静荷载,吊索横截面上的 应力就是静应力.
3
（其中负号表示 与 o 的方向相反，如上图。）
（3）按动静法，在飞轮上加上方向与 相反的
惯性力偶矩 M d
且
Md
Ix
0.5( )
3
0.5
3
KN
m
（4）设作用于轴上的摩擦力矩为 M，t 由平衡方程
M x 0 ，设：
r
D D
(D D
D)
t
t
E
所以
D D d v2D
E Eg
D D D D(1 v2 )
gE
由上式可见，圆环直径增大主要取决于其线速度。
例题 在AB轴的B端有一个质量很大的飞轮（如 下图）。与飞轮相比，轴的质量可忽略不计。轴的另 一端A装有刹车离合器。飞轮的转速为 n 100r / ，min
第十四章 动荷载/一、动荷载的概念与实例
但当物体以加速度上
升(如重物吊离地面的一
瞬间)时,重物对吊索就是
a
动荷载,此时吊索横截面
上的应力就是动应力.
07年11月14日中午11点左 右无锡某工地升降机从百 米高空直接坠地,升降机内 17人,6人死亡,11人重伤.
上海世博会场馆 建设中心的锤击打桩.
Ax Q
A 1
a
，称为动荷系数，则：
g
d stKd
3.动荷载作用下构件的强度条件
于是，动载荷作用下构件的强度条件为：
d max ( st )max Kd [ ]
式中得[]仍取材料在静载荷作用下的许用应力。
动荷系数 Kd的物理意义：是动载荷、动荷应力和动荷变形与
静载荷、静荷应力和静荷变形之比。因此根据胡克定律，有以
受冲击荷载作用时构件的应力 和变形计算
第十四章 动荷载/一、动荷载的概念与实例
静荷载:作用在构件上的荷载由零逐渐增加到最终 值,以后就保持不变或变动不显著的荷载.
动荷载:构件明显处在加速度状态或静止构件受到 处于运动状态的物体的作用时,构件受到的荷载为动荷 载.
第十四章 动荷载/一、动荷载的概念与实例
等加速运动状况—惯性力是个定值
变加速运动状况—惯性力是时间的函数 (是变荷载)
这里讨论等加速运动状态
2.等加速直线运动构件的应力计算
等加速直线运动：
a
FD
FD
a
W
W g
a
1
a g
W
D
W A
W Ag
a
1
a g
st
惯性力
W 静荷载
W a 动荷载
g
D kD st
k D
1
a g
动荷系数
2.等加速直线运动构件的应力计算