【学霸笔记】物理必修一2.3匀变速直线运动位移与时间的关系
- 格式:docx
- 大小:50.78 KB
- 文档页数:3


匀变速直线运动的位移与时间、速度的关系【知识点归纳】1、匀变速直线运动位移与时间的关系的公式表达:2021at t v s += s 为t 时间内的位移。
当a=0时,t v s 0= 当v 0=0时,221at s =当a<0时,2021at t v s -= 可见2021at t v s +=是匀变速直线运动位移公式的一般表示形式,只要知道运动物体的初速度v 0和加速度a ,就可以计算出任意一段时间内的位移,从而确定任意时刻物体所在的位置。
位移公式也可以用速度——时间图像求出面积得位移而推出。
2、匀变速直线运动的位移和速度的关系as v v t 2202=-这个关系式是匀变速直线运动规律的一个重要的推论。
关系式中不含时间t ,在一些不涉及到时间的问题中,应用这个关系是较方便的。
3、匀变速直线运动的两个推论1.匀变速直线运动的物体在连续相等的时间(T)内的位移之差为一恒量。
公式:S 2-S 1=S 3-S 2=S 4-S 3=…=S n -S n-1=△S=aT2 2.某段时间中间时刻的瞬时速度等于这段时间的平均速度,即: v v t =2【案例分析】例1.某物体作变速直线运动,关于此运动下列论述正确的是( )A .速度较小,其加速度一定较小B .运动的加速度减小,其速度变化一定减慢C .运动的加速度较小,其速度变化一定较小D .运动的速度减小,其位移一定减小例2.火车从车站由静止开出做匀加速直线运动,最初一分钟行驶540米,则它在最初l0秒行驶的距离是( )A .90米B .45米C .30米D .15米例3一物体由静止沿光滑斜面匀加速下滑距离为L 时,速度为V ,当它的速度是v /2时,它沿全面下滑的距离是A .L /2 B.2L/2 C .L /4 D .3L /4例4:一物体以初速度v 1做匀变速直线运动,经时间t 速度变为v 2求:(1)物体在时间t 内的位移. (2)(3)比较vt/2和v s/2例5:一辆沿平直路面行驶的汽车,速度为36km/h .刹车后获得加速度的大小是4m/s 2,求:(1)刹车后3s 末的速度;(2)从开始刹车至停止,滑行一半距离时的速度.例6、一个质点作初速为零的匀加速运动,试求它在1s ,2s ,3s ,…内的位移s 1,s 2,s 3,…之比和在第1s ,第2s ,第3s ,…内的位移S Ⅰ,S Ⅱ,S Ⅲ,…之比各为多少?【一试身手】1.下列说法正确的是A .加速度增大,速度一定增大B .速度变化量Δv 越大,加速度就越大C .物体有加速度,速度就增加D .物体速度很大,加速度可能为零2. 关于速度和加速度的关系A .物体的速度为零时,加速度一定为零B .物体的加速度为零时,速度一定为零C .物体的速度改变时,加速度不一定改变D .物体的加速度方向改变时,速度方向不一定改变3.如图所示,Ⅰ、Ⅱ两条直线分别描述P 、Q 两个物体的s —t 图象,下列说法正确的是A .两物体均做匀速直线运动B .M 点表示两物体在时间t 内有相同的位移C .t 时间内P 的位移较小D .0~t ,P 比Q 的速度大,t 以后P 比Q 的速度小 4.某质点做匀变速直线运动,加速度的大小为2m/s 2,则在任意1s 内A .质点的末速度一定是初速度的2倍B .质点的末速度一定比初速度大2m/sC .质点的初速度可能比末速度大2m/sD .质点的速度大小一定改变了2m/s 5.做匀变速直线运动的质点,它在通过某一段位移中点位置的速度为v ,通过这段位移所用时间的中间时刻的速度为u ,则该质点A .做匀加速运动时,v <uB .做匀减速运动时,v <uC .做匀加速运动时,v >uD .做匀减速运动时,v >u6.一个质点做方向不变的直线运动,加速度的方向始终与速度的方向相同,但加速度的大小逐渐减小为零,在此过程中( )A .速度逐渐减小,当加速度减小到零时,速度达到最小值B .速度逐渐增大,当加速度减小到零时,速度达到最大值C .位移逐渐增大,当加速度减小到零时,位移将不再增大D .位移逐渐减小,当加速度减小到零时,位移达到最小值7.关于匀变速直线运动,下列说法中正确的是A 、加速度越大,物体的速度一定越大B 、加速度越小,物体的位移一定越小C 、物体在运动过程中的加速度保持不变D 、匀减速直线运动中,位移随时间的增加而减小8.质点做直线运动,当时间t = t 0时,位移S > 0,速度v > 0,加速度a > 0,此后加速度a 逐渐减小,则它的 ( )A .速度的变化越来越慢B .速度逐渐减小C .位移继续增大D .位移、速度始终为正值t st o M Ⅰ Ⅱ9.甲、乙、丙和丁是以时间为横轴的匀变速直线运动的图象,下面说法正确的是( )A .图甲是加速度—时间图象B .图乙是加速度—时间图象C .图丙是位移—时间图象D .图丁是速度—时间图象10.滑块以某一初速度冲上斜面做匀减速直线运动,到达斜面顶端时的速度为零.已知滑块通过斜面中点时的速度为v ,则滑块在前一半路程中的平均速度大小为A 、212 vB 、(2+1)vC 、2vD 、21v 11.一匀变速运动物体的位移随时间变化的函数关系是S=4t+t 2(m), 则它运动的初速度、加速度及2s末的速度分别是( )A . 0、 4m/s 2 、4m/sB . 4m/s 、 2m/s 2 、8m/sC . 4m/s 、1m/s 2 、8m/sD . 4m/s 、 2m/s 2 、6m/s12.一个物体做初速度为零的匀加速运动,该物体通过前一半位移和通过后一半位移所用的时间之比是( )A .2∶1B .2∶ 1C .(2+1)∶1D .(2-1)∶1二、填空题1.汽车以2m/s 2的加速度由静止开始启动,则第5s 末汽车的速度是_______m/s ,第5s 内汽车的平均速度是________m/s, 第5s 内汽车的位移是___________m 。

高一物理期末必背知识点匀变速直线运动的位移与时间的关系
高一物理期末必背知识点匀变速直线运动的位移与时间的关系
目标:
1. 知道匀变速直线运动的基本规律。
2. 掌握位移公式及它的推导,会应用公式分析计算有关问题。
3. 掌握匀变速直线运动的.平均速度公式,会应用公式分析计算有关问题。
4. 灵活运用速度公式和位移公式进行有关运动学问题的计算。
学习重点:
1. 推导和理解匀变速直线运动的位移公式。
2. 匀变速直线运动速度公式和位移公式的运用。
学习难点: 对匀变速直线运动位移公式的物理意义的理解。
主要内容:
一、匀速直线运动的位移
二、匀变速直线运动的平均速度
某段匀变速直线运动的平均速度等于该段运动的初速度和末速度的平均值。
问题:
1.匀变速直线运动的平均速度跟其加速度有关吗?
2.匀变速直线运动物体的平均速度变化跟其运动时间有关吗?
【高一物理期末必背知识点匀变速直线运动的位移与时间的关系】。

匀变速直线运动的位移与时间的关系公式
匀变速直线运动的位移与时间的关系公式可以由运动学公式推导得到,具体分为两种情况:
1. 匀速直线运动的位移与时间的关系公式:
位移 = 速度 ×时间
其中,位移表示物体在运动过程中从起点到终点的距离,速度表示物体的运动速度,时间表示运动的时间长度。
2. 变速直线运动的位移与时间的关系公式:
位移 = 初速度 ×时间 + 0.5 ×加速度 ×时间²
其中,初速度表示运动开始时的速度,加速度表示运动过程中的加速度。
这个公式描述了的位移与时间的关系可以用来计算变速直线运动下物体在不同时间点的位置。
注意,这个公式的适用条件是运动过程中加速度是一个常量。
另外还有一种特殊情况,匀变速直线运动中,如果物体的位移与时间的关系符合二次函数的形式,可以使用二次函数公式来描述位移与时间的关系。
例如:位移 = a ×时间² + b ×时间 + c,其中a、b和c是常数。




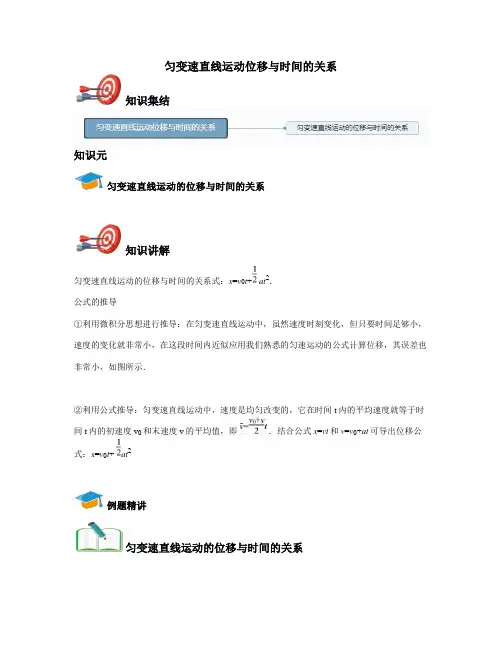
匀变速直线运动位移与时间的关系知识集结知识元匀变速直线运动的位移与时间的关系知识讲解匀变速直线运动的位移与时间的关系式:x=v0t+at2.公式的推导①利用微积分思想进行推导:在匀变速直线运动中,虽然速度时刻变化,但只要时间足够小,速度的变化就非常小,在这段时间内近似应用我们熟悉的匀速运动的公式计算位移,其误差也非常小,如图所示.②利用公式推导:匀变速直线运动中,速度是均匀改变的,它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值,即.结合公式x=vt和v=v0+at可导出位移公式:x=v0t+ at2例题精讲匀变速直线运动的位移与时间的关系例1.一个物体由静止开始做匀加速直线运动,第1s内的位移是1m,物体在第3s内的位移是()A.2m B.3m C.5m D.8m例2.为了测定某轿车在平直路上启动阶段的加速度(轿车启动时的运动可近似看成是匀加速直线运动),某人拍摄一张在同一底片上多次曝光的照片,如图所示,如果拍摄时每隔2s曝光一次,轿车车身总长为4.5m,那么这辆轿车的加速度为()A.1m/s2B.2.25m/s2C.3m/s2D.4.25m/s2例3.2015年9月2日,“抗战专列”在武汉地铁4号线亮相,引得乘车市民纷纷点赞.若该地铁列车先从甲站开始做初速度为零、加速度大小为a的匀加速直线运动,通过位移L后,立即做加速度大小也为a的匀减速直线运动,恰好到乙站停下.则列车从甲站到乙站所用时间为()A.B.2C.2D.4当堂练习单选题练习1.一个物体在水平直线上做匀加速直线运动,初速度为3m/s,经过4s它的位移为24m,则这个物体运动的加速度等于()A.1.5m/s2B.2m/s2C.4m/s2D.0.75m/s2练习2.小球以某一较大初速度冲上一足够长光滑斜面,加速度大小为5m/s2则小球在沿斜面上滑过程中最后一秒的位移是()A.2.0m B.2.5m C.3.0m D.3.5m练习3.“蛟龙号”是我国首台自主研制的作业型深海载人潜水器,它是目前世界上下潜能力最强的潜水器.假设某次海试活动中,“蛟龙号”完成海底任务后竖直上浮,从上浮速度为v时开始计时,此后“蛟龙号”匀减速上浮,经过时间t上浮到海面,速度恰好减为零,则“蛟龙号”在t0(t0<t)时刻距离海平面的深度为()A.B.C.D.练习4.一个物体由静止开始做匀加速直线运动,第1s内的位移是1m,物体在第3s内的位移是()A.2m B.3m C.5m D.8m练习5.为了测定某轿车在平直路上启动阶段的加速度(轿车启动时的运动可近似看成是匀加速直线运动),某人拍摄一张在同一底片上多次曝光的照片,如图所示,如果拍摄时每隔2s曝光一次,轿车车身总长为4.5m,那么这辆轿车的加速度为()A.1m/s2B.2.25m/s2C.3m/s2D.4.25m/s2练习6.2015年9月2日,“抗战专列”在武汉地铁4号线亮相,引得乘车市民纷纷点赞.若该地铁列车先从甲站开始做初速度为零、加速度大小为a的匀加速直线运动,通过位移L后,立即做加速度大小也为a的匀减速直线运动,恰好到乙站停下.则列车从甲站到乙站所用时间为A.B.2C.2D.4。


2 匀变速直线运动的研究2.3 匀变速直线运动位移与时间的关系一:位移与时间关系1、匀变速直线运动位移时间关系的推导在v-t图像中,图线与t轴围城的面积代表位移。
我们就据此来推导匀变速直线运动的位移与时间的关系。
如图所示,为初速度为vo的匀加速直线运动的v-t 图象:由图可知,梯形OAPQ的面积为s=0.5(OA + PQ)xOQ,即:s==0.5(vo+vt)t ①vt=vo+ at ②将②代入①可得:s==0.5(vo+vt)t所以,对于匀变速直线运动,位移与时间的关系为也可以这样理解:梯形OAPQ的面积可看成S1和S2之和。
其中,则二、对公式的理解(1)位移公式说明匀变速直线运动的位移与时间是二次函数关系,式中的vo是初速度,时间应是物体实际运动的时间。
(2)此公式反映的是位移和时间的关系,公式中的vo、a、s都是矢量, 使用公式应该先规定正方向,在取初速度vo方向为正方向的前提下,匀加.速直线运动a取正值,匀减速直线运动a取负值;计算的结果s>0,说明位移的方向与初速度的方向相同;s<0说明位移的方向与初速度的方向相反。
(3)对于初速度为零(v=0)的匀变速直线运动,位移公式简化为位移s与时间t的二次方成正比。
二匀变速直线运动连续相等时间位移特点1、必须是匀变速直线运动。
2、时间是相等的。
3、必须是连续等时间内的位移。
(1)物体做匀加速直线运动,设第一一个t时间内位移为x,第二个t 时间内位移为x2,求其加速度。
分析:,V中时=vo+at,两式消去vo得:,两式相减得: x2-x1=at2。
结论为:匀变速直线运动连续相等时间内的位移差为定值,即:△x=x2-x1=x3-x2=x4-x3=...=xN-xn-1= at2进一步分析:该结论是判定物体运动是否做匀变速的重要方法,即: 若匀加速直线运动,a>0,△x>0, xn↑;若匀减速直线运动,a<0,△x<0, xn↓。
物理匀变速直线运动的位移和时间的关系物理中的匀变速直线运动是指物体在相等时间内位移的增量是逐渐增加的运动。
在这种运动中,位移与时间之间存在着一定的关系。
我们来了解一下匀变速直线运动的基本概念。
匀变速直线运动是指物体在相等时间间隔内,其位移的增量是逐渐增加的运动。
这意味着物体在单位时间内的位移是不断增加的,即速度在变化。
而这种变化是有规律可循的。
在匀变速直线运动中,位移与时间之间的关系可以通过速度来描述。
速度是指物体在单位时间内位移的增量,可以用公式v = Δx/Δt来表示,其中v表示速度,Δx表示位移的增量,Δt表示时间的增量。
根据速度的定义,我们可以得出位移与时间的关系。
假设物体的初始位移为x0,初始时间为t0,位移的增量为Δx,时间的增量为Δt,那么根据速度的定义,我们可以得到以下关系:v = Δx/Δt将上述公式稍作变形,可以得到:Δx = v * Δt这个公式表明,位移的增量等于速度乘以时间的增量。
也就是说,位移的增量与时间的增量成正比,且比例系数为速度。
进一步地,我们可以将上述公式进行积分,得到位移与时间之间的具体关系。
假设物体的初始位移为x0,初始时间为t0,位移为x,时间为t,速度为v,则有:x - x0 = ∫(v dt)这个公式表示,位移与时间之间的关系可以通过速度的积分来描述。
通过对速度关于时间的积分,我们可以得到位移与时间之间的具体关系。
匀变速直线运动的位移与时间之间存在着一定的关系。
位移的增量等于速度乘以时间的增量,而位移与时间之间的具体关系可以通过速度的积分来描述。
这些关系可以帮助我们更好地理解和分析匀变速直线运动的特性和规律。
希望本文对您有所帮助,谢谢阅读!。
匀变速直线运动的位移与时间的关系【高中】一、匀变速直线运动的位移1.思维过程:可以把甲所表示的运动过程划分为很多的小段,如图乙、丙所示,用所有这些小段的位移之和,近似代表物体在整个过程中的位移。
从v-t 图上看,就是用更多的但是更窄的小矩形的面积之和代表物体的位移。
如果把整个运动过程划分得非常非常细,很多很多小矩形的面积之和就能非常准确地代表物体的位移了。
这时,“很多很多”小矩形顶端的“锯齿形”就看不出来了,这些小矩形合在一起成了一个梯形OABC 。
梯形OABC 的面积就代表做匀变速直线运动的物体从0(此时速度是v 0)到t (此时速度是v )这段时间间隔的位移。
如图丁所示。
2.位移在v -t 图像中的表示:做匀变速直线运动的物体的位移对应着v -t 图像中的图线和时间轴包围的面积。
如图所示,在0~t 时间内的位移大小等于梯形的面积。
3.位移公式2210at t v x +=4.对位移公式x =v 0t +12at 2的进一步理解 (1)因为v 0、a 、x 均为矢量,使用公式时应先规定正方向,一般以v 0的方向为正方向。
若a 与v 0同向,则a 取正值;若a 与v 0反向,则a 取负值;若位移计算结果为正值,说明这段时间内位移的方向为正;若位移计算结果为负值,说明这段时间内位移的方向为负。
(2)因为位移公式是关于t 的一元二次函数,故x -t 图像是一条抛物线(一部分)。
但它不表明质点运动的轨迹为曲线。
(3)对于初速度为零(v 0=0)的匀变速直线运动,位移公式为x =12vt =12at 2,即位移x 与时间t 的二次方成正比。
(4)x =v 0t +12at 2是矢量式,应用时x 、v 0、a 都要根据选定的正方向带上“+”“-”号。
【初中】一、匀速直线运动的路程做匀速直线运动的物体在时间t 内的路程s =vt 。
其v -t 图像是一条平行于时间轴的直线,如图所示。
路程在数值上等于v -t 图线与对应的时间轴所包围的矩形的面积。
高一物理必修一匀变速直线运动的位移与时间的关系在高一物理的课堂上,匀变速直线运动就像是一场刺激的旅程,咱们要在这个运动中寻找位移和时间的关系。
想象一下,骑着自行车在公园里飞驰,刚开始你可能慢慢发力,后来车速越来越快,那种感觉就像是飞一样,简直太爽了!这时候,位移和时间就成了你最好的朋友。
位移就像是你骑车到达目的地的里程碑,而时间则是你从出发到抵达的那个不知不觉的过程。
你看,慢慢的、快快的,时间在变化,位移也在变化,这两者就像是相辅相成的,缺一不可。
先说说匀变速运动。
这个名字听起来好像很严肃,但其实它就是在说:在一段时间里,速度是变化的,变化的方式是均匀的。
比如说,你在街上骑车,刚开始你慢慢加速,可能前面有个小伙伴在追,你不想被他超越,于是就拼命踩踏板,速度渐渐变快。
这个过程就是匀变速运动。
位移与时间的关系,就像你追赶朋友的比赛,时间越长,位移也越大!而且这段距离不是简单的直线,而是随着时间的推进,位移会越来越多,就像是滚雪球一样,越滚越大。
让我们来聊聊公式。
别紧张,这个公式可不难!位移s等于初速度u加上加速度a 乘以时间t的一半再乘以时间t的平方。
哎呀,听起来复杂,但其实一想就明白。
想象一下,初速度就是你起步的速度,加速度是你骑车时逐渐加速的感觉,时间就是你从出发到现在的那段时光。
将这些因素结合起来,就能知道你在这段时间里跑了多远。
咱们生活中的许多事情都可以用这个公式来解释,比如你去超市购物的时间,越买越多,最终的消费就跟你逛的时间成正比。
说到这里,大家可能会想:“那我怎么才能快点到达目的地呢?”嗯,这就得看你如何利用加速度了。
如果你能有效地加速,那你就能迅速拉开与朋友的距离,成为骑车小达人!这就像你在生活中努力追赶自己的目标一样,时不时加把劲,搞得自己越来越快。
不过,要注意哦,速度不是越快越好,有时候慢慢来也许会更稳妥,关键是找到那个平衡点。
在学习这个概念的时候,可以做个有趣的实验。
找个空旷的地方,拿上个计时器,跟朋友比比谁骑得快,看看自己在不同时间段内的位移变化。
第三节匀变速直线运动的位移与时间的关系
一、位移时间公式
1、推导:
①图像法:(由v-t图像求位移)---微元的思想
结论:做匀变速直线运动的物体的位移对应着v-t图象中的图线与对应的时间轴所包围的面积.
即:位移与时间关系式:x=v0t+
1
2at
2.
②解析法:(由平均速度求得)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
+
=
+
=
=
at
v
v
v
v
v
t v
x
t
t
2
得:x=v0t+
1
2at
2.
2、物理意义:在匀变速直线运动中位移随时间变化的规律。
3、注意:
①适用范围:匀变速直线运动。
②决定关系:位移的决定式,即匀变速直线运动中位移是由初速度、加速度、时间共同决定。
③比例关系:二次关系,也叫非线性关系。
④同一性:x、a、v0、vt具有同一性。
⑤合理性:已知位移反求时间,可能有两个值,要合理取舍。
二、速度--时间公式应用
1、使用方法:
①判断:运动性质(a为定值)。
②确定:研究对象和研究过程。
③设定:正方向(一般初速度的方向为正方向,无初速度则选择加速度为正方向)。
④公式应用:x=v0t+
1
2at
2;(此式子为矢量式,应将方向带入求解)
⑤结果:结果如何为矢量,大小方向都需要求解。
2、例子:
已知一个物体以向西的初速度4m/s做匀变速直线运动,其加速度大小为2m/s2,求1s末、2s末、4s末、8s末的速度和位移和路程,如果该物体是汽车,则结果又将如何?.
三、推论
1、逐差相等原理:在匀变速直线运动中,相邻相等的时间间隔位移之差是一个定值。
表达式:△x=aT 2.
推导:⎪⎪⎪⎩
⎪⎪⎪⎨⎧
+=+=+=2
12
0220
19213421221T a T v x T a T v x aT T v x ⎪⎪⎩⎪⎪⎨
⎧+=-+=-20232
012521321T a T v x x T a T v x x 2aT x =∆ 2、比例关系:初速度为零的匀加速直线运动中
①在前T ,前2T ,前3T 的位移之比1:4:9……n2
②在第T ,第2T ,第3T 的位移之比1:3:4……(2n-1) 3、逆向思维法:末速度为零的匀减速直线运动可以看做反向的初速度为零的匀加速直线运动。
(结论成立)
专题:图像问题(略)。