打印讲义7

【一轮复习】1-2.集合与简易逻辑1.1集合【知识要点归纳】1.概念：一般地，指定的某些对象的全体称为集合，记作：A ，B ，C ，D ，…集合中的每个对象叫做这个集合 的元素，记作：a ，b ，c ，d ，…，元素与集合的关系口答：请指出下列集合中的元素是什么？ （1）}12|{2++==x x y x A ； （2）}12|{2++==x x y y B ； （3）}12|),{(2++==x x y y x C ；（4）}12|{2++==x x x x D ；（5）},,12|),{(2Z y Z x x x y y x E ∈∈++==；2.分类：按照元素个数，分为 、 和4.运算5.常用数集：自然数集记作 ，正整数集记作 ，整数集记作 ，有理数集记作 ，实数集记作6.设集合A 中元素个数为n 个，则集合A 的子集个数为 【经典例题】例1：已知集合M=⎭⎬⎫⎩⎨⎧=+149|22y x x ，N=⎭⎬⎫⎩⎨⎧=+123|y x y ，则=N M （ ）A ．∅B ．)}0,2(),0,3{(C ．[]3,3-D ．{}2,3例2：已知集合A={x|x 2－3x －10≤0}，集合B={x|p ＋1≤x≤2p－1}．若B ÍA ，求实数p 的取值范围．例3：已知集合A={y|y 2-(a 2+a+1)y+a(a 2+1)>0},B={y|y 2-6y+8≤0}，若A ∩B ≠φ，则实数a 的取值范围为？．例4：有限集合P 中元素的个数记作card()P .已知card()10M =，A M ⊆，B M ⊆，A B =∅，且card()2A =，card()3B =.若集合X 满足X M ⊆，且A X ⊄，B X ⊄，则集合X 的个数是（ ） （A ）672（B ）640（C ）384（D ）3521.2 简易逻辑 【知识要点归纳】 一、 命题概念：用语言、符号或式子表达的，可以判断真假的陈述句叫做命题，其中判断为真的语句叫做 命题，判断为假的语句叫做 命题。

1.故重阴必阳，重阳必阴。

故曰：故曰:冬伤于寒，春必病温;春伤于风，夏生飧泄；夏伤于暑,秋必痎疟；秋伤于湿，冬生咳嗽。

2.阳气者，若天与日，失其所则折寿而不彰，故天运当以日光明。

是故阳因而上，卫外者也。

（因于寒，欲如运枢，起居如惊，神气乃浮。

因于暑，汗，烦则喘喝，静则多言,体若燔炭,汗出而散.因于湿，首如裹，湿热不攘，大筋緛短，小筋弛长,緛短为拘，弛长为屡。

因于气,为肿,四维相代，阳气乃竭.）3.阳气者，精则养神，柔则养筋。

4.凡阴阳之要，阳密乃固,两者不和，若春无秋，若冬无夏,因而和之，是谓圣度。

故阳强不能密，阴气乃绝；阴平阳秘，精神乃治；阴阳离决，精气乃绝。

5.肾藏精，精舍志，肾气虚则厥，实则胀，五藏不安。

6。

五脏：风掉眩，皆属于肝.诸寒收引，皆属于肾。

诸气膹郁，皆属于肺。

诸湿肿满，皆属于脾。

诸痛痒疮,皆属于心。

7.五火：诸热瞀瘛，皆属于火。

诸禁鼓栗,如丧神守，皆属于火.诸逆冲上，皆属于火。

诸躁狂越，皆属于火。

诸病胕肿，疼酸惊骇，皆属于火.8。

四热：诸胀腹大,皆属于热.诸病有声，鼓之如鼓，皆属于热。

诸转反戾,水液混浊，皆属于热。

诸呕吐酸，暴注下迫，皆属于热。

9.诸风掉眩，皆属于肝。

诸寒收引，皆属于肾。

诸气膹郁，皆属于肺.诸湿肿满，皆属于脾。

诸热瞀瘛,皆属于火。

诸痛痒疮，皆属于心.诸厥固泄，皆属于下.诸痿喘呕，皆属于上。

诸禁鼓栗，如丧神守，皆属于火。

诸痉项强,皆属于湿。

诸逆冲上，皆属于火。

诸胀腹大,皆属于热。

诸躁狂越，皆属于火。

诸暴强直，皆属于风。

诸病有声,鼓之如鼓，皆属于热。

诸病胕肿，疼酸惊骇，皆属于火。

诸转反戾，水液混浊,皆属于热。

诸病水液,澄澈清冷,皆属于寒.诸呕吐酸，暴注下迫，皆属于热。

10. 岐伯曰∶巨阳者,诸阳之属也,其脉连于风府，故为诸阳主气。

人之伤于寒也，则为病热,热虽甚不死；其两感于寒而病者，必不免于死。

11。

诊法常以平旦，阴气未动，阳气未散，饮食未进，经脉未盛，络脉调匀，气血未乱,故乃可诊有过之脉。

Office 2007 打印设置
在对演示文稿打印输入之前，首先应对其进行相应的设置。

单击Office按钮，执行【打印】|【打印】命令，即可弹出如图9-54所示的对话框。

图9-54 【打印】对话框
在【打印范围】栏中，用户可以选择要打印的幻灯片。

选择【全部】单选按钮，即可打印演示文稿中所有的幻灯片；选择【当前幻灯片】单选按钮，即可打印当前选择的幻灯片；选择【幻灯片】单选按钮，则可以在文本框中输入要打印的幻灯片编号或范围。

在【打印内容】对话框中，用户可以选择要打印的内容，例如，幻灯片、讲义、备注或者大纲等。

如果用户选择【讲义】选项，则可以在右侧指定每页要打印的幻灯片张数及排放顺序。

在【份数】栏中，可以指定要打印的份数；如果用户想打印黑白演示文稿，可以单击【颜色/灰度】下拉按钮，选择【纯黑白】选项。

另外，对话框下方各复选框的作用如表9-7所示：
表9-7 打印设置。

第一讲 随机事件与概率考试要求1. 了解样本空间的概念, 理解随机事件的概念, 掌握事件的关系与运算.2. 理解概率、条件概率的概念, 掌握概率的基本性质, 会计算古典型概率和几何型概率, 掌握概率的加法公式、减法公式、乘法公式、全概率公式, 以及贝叶斯公式.3. 理解事件独立性的概念, 掌握用事件独立性进行概率计算；理解独立重复试验的概率, 掌握计算有关事件概率的方法. 一、古典概型与几何概型1．试验，样本空间与事件.2．古典概型：设样本空间Ω为一个有限集，且每个样本点的出现具有等可能性，则 基本事件总数中有利事件数A A P =)(3．几何概型：设Ω为欧氏空间中的一个有界区域, 样本点的出现具有等可能性，则、体积）Ω的度量（长度、面积、体积）A的度量（长度、面积=)(A P【例1】 一个盒中有4个黄球, 5个白球, 现按下列三种方式从中任取3个球, 试求取出的球中有2个黄球, 1 个白球的概率. （1） 一次取3个；（2） 一次取1 个, 取后不放回； （3） 一次取1个, 取后放回.【例2 】从 （0，1） 中随机地取两个数，试求下列概率： （1） 两数之和小于1.2； （2） 两数之和小于1且其积小于163. 一、 事件的关系与概率的性质1. 事件之间的关系与运算律（与集合对应）, 其中特别重要的关系有： （1） A 与B 互斥（互不相容） ⇔ Φ=AB （2） A 与B 互逆（对立事件） ⇔ Φ=AB ,Ω=B A（3） A 与B 相互独立⇔ P （AB ）=P （A ）P （B ）.⇔ P （B|A ）=P （B ） （P （A ）>0）. ⇔(|)(|)1P B A P B A += （0<P （A ）<1）.⇔P （B|A ） =P （B|A ） （ 0 < P （A ） < 1 ）注: 若（0<P （B ）<1）,则,A B 独立⇔ P （A|B ）=P （A ） （P （B ）>0）⇔ 1)|()|(=+B A P B A P （0<P （B ）<1）. ⇔ P （A |B ）=P （A |B ） （0<P （B ）<1） ⇔ P （A |B ）=P （A |B ） （0<P （B ）<1）（4） A, B, C 两两独立 ⇔ P （AB ）=P （A ）P （B ）;P （BC ）=P （B ）P （C ）; P （AC ）=P （A ）P （C ）.（5） A, B, C 相互独立 ⇔ P （AB ）=P （A ）P （B ）;P （BC ）=P （B ）P （C ）; P （AC ）=P （A ）P （C ）;P （ABC ）=P （A ）P （B ）P （C ）.2. 重要公式 （1） )(1)(A P A P -=（2）)()()(AB P A P B A P -=-（3） )()()()(AB P B P A P B A P -+=)()()()()()()()(ABC P AC P BC P AB P C P B P A P C B A P +---++=（4） 若A 1, A 2,…,A n 两两互斥, 则∑===ni i ni iA P AP 11)()(.（5） 若A 21,A , …, A n 相互独立, 则 )(1)(11in i n i iA P A P ∏==-= )](1[11ini A P ∏=--=.∏===ni i n i i A P A P 11)()( .（6） 条件概率公式: )()()|(A P AB P A B P =（P （A ）>0）【例3】 已知（A ＋B ）（B A +）＋B A B A +++＝C, 且P （ C ）＝31, 试求P （B ）. 【例4】 设两两相互独立的三事件A, B, C 满足条件: ABC ＝Φ, P （A ）＝P （B ）＝P （C ）<21,且已知9()16P A B C =, 则P （A ）＝ .【例5】 设三个事件A 、B 、C 满足P （AB ）＝P （ABC ）, 且0<P （C ）<1, 则 【 】（A ）P （A B|C ）＝P （A|C ）+ P （B|C ）. （B ）P （A B|C ）＝P （AB ）.（C ）P （AB|C ）＝P （A|C ）+ P （B|C ）. （D ）P （AB|C ）＝P （AB ）.【例6】 设事件A, B, C 满足条件: P （AB ）＝P （AC ）＝P （BC ）18=, P （ABC ）＝116, 则事件A, B, C 中至多一个发生的概率为 .【例7】 设事件A, B 满足 P （B| A ）＝1则【 】（A ） A 为必然事件. （B ） P （B|A ）=0.（C ） A B ⊃. （D ） A B ⊂.【例8】 设A, B, C 为三个相互独立的事件, 且0<P （C ）<1, 则不独立的事件为 【 】 （A ）B A +与C . （B ） AC 与C（C ）B A -与C （D ） AB 与C【例9】 设A ，B 为任意两个事件，试证P （A ）P （B ）－P （AB ） ≤ P （A －B ） P （B －A ） ≤41. 三、乘法公式，全概率公式，Bayes 公式与二项概率公式 1． 乘法公式：).|()|()|()()().|()()|()()(1212131212121212121-===n n n A A A A P A A A P A A P A P A A A P A A P A P A A P A P A A P2． 全概率公式：11()(|)(),,,.i i i j i i i P B P B A P A A A i j A ∞∞====Φ≠=Ω∑ 3．Bayes 公式：11(|)()(|),,,.(|)()j j j i j i i iii P B A P A P A B A i j A P B A P A ∞∞====Φ≠=Ω∑　A 4．二项概率公式:()(1),0,1,2,,.k kn k n n P k C P P k n -=-=　,【例10】 10件产品中有4件次品, 6件正品, 现从中任取2件, 若已知其中有一件为次品,试求另一件也为次品的概率.【例11】设10件产品中有3件次品, 7件正品, 现每次从中任取一件, 取后不放回.试求下列事件的概率. （1） 第三次取得次品; （2） 第三次才取得次品;（3） 已知前两次没有取得次品, 第三次取得次品; （4） 不超过三次取到次品;【例12】 甲, 乙两人对同一目标进行射击,命中率分别为0.6和0.5, 试在下列两种情形下, 分别求事件“已知目标被命中,它是甲射中”的概率.（1）在甲, 乙两人中随机地挑选一人, 由他射击一次; （ 2）甲, 乙两人独立地各射击一次.【例13】设有来自三个地区的各10名、15名和25名考生的报名表,其中女生的报名表分别为3份,7份和5份. 随机地取一个地区的报名表,从中先后任意抽出两份. (1) 求先抽到的一份是女生表的概率p;(2)已知后抽到的一份是男生表,求先抽到的一份是女生表的概率q .第二讲 随机变量及其分布考试要求1. 理解随机变量及其概率分布的概念.理解分布函数（()()F x P X x =≤） 的概念及性质.会计算与随机变量有关的事件的概率.2. 理解离散型随机变量及其概率分布的概念，掌握0－1分布、二项分布、几何分布、超几何分布、泊松（Poisson ）分布及其应用.3. 了解泊松定理的结论和应用条件，会用泊松分布近似表示二项分布.4. 理解连续型随机变量及其概率密度的概念，掌握均匀分布、正态分布2(,)N μσ、指数分布及其应用，其中参数为(0)λλ>的指数分布的概率密度为,0,()0,0.x e x f x x λλ-⎧>=⎨≤⎩5. 会求随机变量函数的分布. 一、分布函数1．随机变量：定义在样本空间上，取值于实数的函数称为随机变量. 2．分布函数：∞+-∞=＜＜),≤ ()(x x X P x FF （x ）为分布函数 ⇔（1） 0≤F （x ） ≤1（2） F （x ）单调不减 （3） 右连续F （x+0）=F （x ） （4）1)(,0)(=+∞=-∞F F3．离散型随机变量与连续型随机变量（1） 离散型随机变量∑∞=====1i 10,≥,,,2,1,)(i i i i p p n i p x X P分布函数为阶梯跳跃函数.（2） 连续型随机变量⎰∞-=xtt f x F d )( )(f （x ）为概率密度 ⇔ （1） f （x ）≥0, （2） ⎰+∞∞- f （x ）1d =x⎰=≤≤=<<bax f b X a P b X a P )()()(4．几点注意【 例1 】 设随机变量X 的分布函数为0,1,57(),11,16161, 1.x F x x x x <-⎧⎪⎪=+-≤<⎨⎪≥⎪⎩则2(1)P X== .【 例2 】 设随机变量X 的密度函数为 f （x ）, 且 f （－x ） = f （x ）, 记()X F x 和()X F x -分别是X 和X -的分布函数, 则对任意实数x 有 【 】 （A ）()()X X F x F x -=. （B ）()()X X F x F x -=-.（C ）()1()X X F x F x -=-.（D ）()2()1X X F x F x -=-.【 例3 】 设 随机变量X 服从参数为0λ>的指数分布, 试求随机变量 Y= min { X, 2 } 的分布函数【 例4 】设某个系统由 6 个相同的元件经两两串联再并联而成, 且各元件工作状态相互独立 每个元件正常工作时间服从参数为 0λ>的指数分布, 试求系统正常工作的时间 T 的概率分布.【 例5】设随机变量X 的概率密度为⎩⎨⎧<-=.,0,1|||,|1)(其他x x x f 试求（1）X 的分布函数)(x F ; （2）概率)412(<<-X P .二、 常见的一维分布（1） 0-1分布：1,0,)1()(1 =-==-k p p k XP k k .（2） 二项分布n k p p C k X P p n B k n k k n ,,1,0,)1()(:),( =-==- .（3） Poisson 分布)(λP ： ,2,1,0,0＞,e !)(===-k k k XP k λλλ.（4） 均匀分布⎪⎩⎪⎨⎧-=.,＜＜1)(:),(其他０，，　b x a a b x f b a U（5） 正态分布N （μ，σ2）：0,,eπ21)(222)(+∞<<∞->=--μσσσμ x x f（6） 指数分布⎩⎨⎧=-. ,0 ＞0,,e )(:)(其他x x f E x λλλ ＞0λ.（7） 几何分布.2110,)1()(:)(1 ,,k ,＜p＜p p k XP p G k =-==- （8） 超几何分布H （N,M,n ）: },min{,,1,0,)(M n k C C C k X P nNkn M N k M ===--　. 【例6】某人向同一目标独立重复射击,每次射击命中目标的概率为p （0<p<1）, 则此人第4次射击恰好第2次命中目标的概率为【 】 （A ） 2)1(3p p -.（B ） 2)1(6p p -.（C ） 22)1(3p p-. （D ） 22)1(6p p-.【例7】 设X ～Ｎ （μ, σ2）, 则 P （ X ≤1＋μ） 【 】 （A ） 随μ的增大而增大 . （B ） 随μ的增大而减小. （C ） 随σ的增大而不变 . （D ） 随σ的增大而减小. 【例8】 设X ～Ｎ （μ, σ2）, ()F x 为其分布函数，0μ<，则对于任意实数a ，有 【 】（A ） ()() 1.F a F a -+> （B ） ()() 1.F a F a -+= （C ） ()() 1.F a F a -+< （D ） 1()().2F a F a μμ-++=【例9】 甲袋中有1个黑球，2个白球，乙袋中有3个白球，每次从两袋中各任取一球交换放入另一袋中，试求交换n 次后，黑球仍在甲袋中的概率.三、 随机变量函数的分布： 1. 离散的情形2. 连续的情形3. 一般的情形【例10】 设随机变量X 的概率密度为⎪⎪⎪⎩⎪⎪⎪⎨⎧<≤<<-=.,0,20,41,01,21)(其他x x x f X令),(,2y x F X Y=为二维随机变量（X, Y ）的分布函数.（Ⅰ） 求Y 的概率密度)(y f Y ;（Ⅱ） )4,21(-F . 第三讲 多维随机变量及其分布考试要求1. 理解多维随机变量的概念，理解多维随机变量的分布的概念和性质，理解二维离散型随机变量的概率分布、边缘分布和条件分布，理解二维连续型随机变量的概率密度、边缘密度和条件密度.会求与二维随机变量相关事件的概率.2. 理解随机变量的独立性及不相关的概念，掌握随机变量相互独立的条件.3. 掌握二维均匀分布，了解二维正态分布的概率密度，理解其中参数的概率意义 .4. 会求两个随机变量简单函数的分布，会求多个相互独立随机变量简单函数的分布. 一、 各种分布与随机变量的独立性 1. 各种分布（1）一般二维随机变量 F （x, y ）=P{ X ≤ x, Y ≤ y }, x ∈ （−∞, +∞）, y ∈ （−∞, +∞）的性质F （x, y ）为联合分布函数 ⇔ 1） 0 ≤F （x, y ）≤1 , ∀x ∈ （−∞, +∞）,, y ∈ （−∞, +∞）;2） F （−∞, y ）= F （x, −∞）=0, F （+∞,+∞）=1;3） F （x, y ）关于x, y 均为单调不减函数； 4） F （x, y ）关于x, y 均分别右连续.（2）二维离散型随机变量的联合概率分布、边缘分布、条件分布联合概率分布律 P{X = x i , Y = y j } = p i j , i, j =1, 2 ,⋅⋅⋅ , p i j ≥ 0,1=∑∑ijji p.边缘分布律 p i • = P{X = x i }=∑jji p, i =1, 2 ,⋅⋅⋅ ,p • j = P{ Y = y j }=∑iji p, j =1, 2 ,⋅⋅⋅ ,条件分布律 P{X = x i |Y = y j } =jj i p p •, P{ Y = y j | X = x i } =•i j i p p .二维连续型随机变量的联合概率密度、边缘密度和条件密度f （x, y ）为联合概率密度 ⇔ 1︒ f （x, y ）≥0,2︒1=⎰⎰∞+∞-∞+∞- ),(dxdy y x f .设（ X, Y ）~ f （x, y ）则分布函数: ⎰⎰∞-∞-=xydxdy y x f y x F ),(),(;边缘概率密度:⎰∞+∞-= ),()(dy y x f x f X , ⎰∞+∞-= ),()(dx y x f x f Y .条件概率密度:)(),()|(|y f y x f y x f Y Y X =, )(),()|(|x f y x f x y f X X Y =.⎰⎰=∈Ddxdy y x f D Y X P ),(}),{(.),(),(yx y x F y x f ∂∂∂=22. 随机变量的独立性和相关性X 和Y 相互独立 ⇔ F （x, y ）= F X （x ）F Y （y ）;⇔ p i j = p i • ⨯ p • j （离散型）⇔ f （x, y ）= f X （x ）f Y （y ） （连续型）【注】1︒ X 与Y 独立, f （x ）, g （x ）为连续函数 ⇒ f （X ）与g （Y ）也独立. 2︒ 若X 1, ⋅⋅⋅⋅, X m , Y 1, ⋅⋅⋅⋅, Y n 相互独立, f , g 分别为m 元与 n 元连续函数 ⇒ f （X 1, ⋅⋅⋅⋅, X m ）与g （Y 1, ⋅⋅⋅⋅, Y n ）也独立. 3︒ 常数与任何随机变量独立.3. 常见的二维分布（1）二维均匀分布 （X, Y ）~ U （D ）, D 为一平面区域. 联合概率密度为⎪⎩⎪⎨⎧∈=.,.),(,)(),(其他01D y x D S y x f （2）二维正态分布 （X, Y ）~ N （μ1 , μ2, σ12,σ22, ρ ）, −∞ <μ1, μ2 < +∞, σ1>0, σ2 > 0, | ρ | <1. 联合概率密度为221121ρσπσϕ-=),(y x ⎥⎥⎦⎤⎢⎢⎣⎡-+------22222121212122121σμσσμμρσμρ)())(()()(y y x x e性质:（ a ） X ~ N （μ1, σ12 ）, Y ~ N （μ2, σ22） （ b ） X 与Y 相互独立 ⇔ ρX Y =0 , 即 X 与Y 不相关.（ c ） C 1X+C 2Y ~ N （C 1 μ1+ C 2 μ2, C 12σ12+ C 22σ22+2C 1C 2 ρ σ1σ2 ）. （ d ） X 关于Y=y 的条件分布为正态分布: )](),([22122111ρσμσσρμ--+y N 【 例1 】 设A ，B 为事件，且P （A ）＝41, P （B|A ）＝21, P （A|B ）＝12令 X ＝⎩⎨⎧否则发生若,0,1A , Y ＝⎩⎨⎧否则发生若,0B ,1（1） 试求（X, Y ）的联合分布律； （2）计算Cov （ X, Y ）； （3） 计算 22(2,43)Cov XY +.【 例2 】设随机变量X 与Y 相互独立，下表列出了二维随机变量（X, Y ）联合分布律及关于X 和关于Y 的边缘分布律中的部分数值, 试将其余数值填入表中的空白处.【 例3 】设随机变量X 与Y 独立同分布, 且X 的概率分布为313221PX 记{}{}Y X V Y X U,m in ,,m ax ==.（I ）求（U, V ）的概率分布;（II ）求（U, V ）的协方差Cov （U, V ）.【详解】（I ）易知U, V 的可能取值均为: 1, 2. 且{}{}})1,m in ,1,(m ax )1,1(=====Y X Y X P V U P)1,1(===Y X P 94)1()1(====Y P X P , {}{}0})2,m in ,1,(m ax )2,1(======Y X Y X P V U P , {}{}})1,m in ,2,(m ax )1,2(=====Y X Y X P V U P)2,1()1,2(==+===Y X P Y X P)2()1()1()2(==+===Y P XP Y P X P 94=, {}{}})2,m in ,2,(m ax )2,2(=====Y X Y X P V U P)2()2()2,2(======Y P X P Y X P 91=, 故（U, V ）的概率分布为:（II ） 9122941209411)(⨯⨯+⨯⨯++⨯⨯=UV E 916=, 而 914952941)(=⨯+⨯=U E , 910912981)(=⨯+⨯=V E . 故 814910914916)()()(),(=⨯-=-=V E U E UV E V U Cov . 【 例4】 设随机变量X 在区间（0, 1）上服从均匀分布, 在)10(<<=x x X 的条件下,随机变量Y 在区间),0(x 上服从均匀分布, 求（Ⅰ）随机变量X 和Y 的联合概率密度;（Ⅱ）Y 的概率密度; （Ⅲ）概率}1{>+Y XP .二、 二维（或两个）随机变量函数的分布 1．分布的可加性（1）若X~B （m, p ）, Y~B （n, p ）, 且X 与Y 相互独立，则 X+Y ~ B （m+n, p ）. （2）若X~P （λ1）, Y~P （λ2）, 且X 与Y 相互独立，则 X+Y ~ P （λ1+λ2）.（3）若X~N （211,μσ）, Y~P （222,μσ）, 且X 与Y 相互独立，则 X+Y ~ N （221212,μμσσ++）.一般地，若X i ~N （2,i i μσ）, i =1, 2, …, n, 且X 1，X 2，…，X n 相互独立，则Y=C 1X 1+C 2X 2+…+C n X n +C 仍服从正态分布，且此正态分布为2211(,),n ni i i i i i N C C Cμσ==+∑∑ 其中C 1，…，C n 为不全为零的常数.2. 两个随机变量函数的分布. 【例5】 设X 与Y 相互独立, 且~(1),~(2),X P Y P 则{max(,)0}______;P X Y ≠={min(,)0}__________.P X Y ≠=【 例6】 设X 与Y 相互独立, 其密度函数分别为:1,01,()X x f x <<⎧=⎨⎩0,其他. ,0,()y Y e y f x -⎧>=⎨⎩0,其他.求Z ＝2X ＋Y 的概率密度.【 例7】设二维随机变量（X, Y ）的概率密度为2,01,01,(,)0,x y x y f x y --<<<<⎧=⎨⎩其它.（I ）求{}Y X P 2>；（II ）求Z ＝Ｘ+Ｙ的概率密度)(z f Z .【详解】（I ）{}Y X P 2>⎰⎰>=yx dxdy y x f 2),(⎰⎰--=12210)2(ydx y x dy 247=. （II ）方法一： 先求Z 的分布函数: ⎰⎰≤+=≤+=zy x Z dxdy y x f Z Y X P z F ),()()(当z<0时, 0)(=z F Z ; 当10<≤z 时, ⎰⎰=1),()(D Z dxdy y x f z F ⎰⎰---=yz zdx y x dy 00)2(3231z z -=；当21<≤z 时, ⎰⎰-=2),(1)(D Z dxdy y x f z F ⎰⎰-----=111)2(1yz z dx y x dy3)2(311z --=； 当2≥z时, 1)(=z F Z .故Z ＝Ｘ+Ｙ的概率密度)(z f Z =)(z F Z '⎪⎩⎪⎨⎧<≤-<<-=.,0,21,)2(,10,222其他z z z z z方法二：⎰∞+∞--=dx x z x f z f Z ),()(，⎩⎨⎧<-<<<---=-.,0,10,10),(2),(其他x z x x z x x z x f ⎩⎨⎧+<<<<-=.,0,1,10,2其他x z x x z 当z ≤0 或z ≥ 2时, 0)(=z f Z ;当01z <<时,⎰-=z Z dx z z f 0)2()()2(z z -=；当21<≤z 时, ⎰--=11)2()(z Z dx z z f 2)2(z -=；故Z ＝Ｘ+Ｙ的概率密度)(z f Z ⎪⎩⎪⎨⎧<≤-<<-=.,0,21,)2(,10,222其他z z z z z【例8】 设随机变量X 与Y 相互独立, X 有密度函数f （x ）, Y 的分布律为 ()i i P Y a p ==,　i =1,2. 试求Z ＝X ＋Y 的概率分布.第四讲 数字特征与极限定理考试要求1．理解随机变量数字特征（数学期望、方差、标准差、矩、协方差、相关系数）的概念, 会运用数字特征的基本性质, 并掌握常用分布的数字特征.2．会根据随机变量X 的概率分布求其函数)(X g 的数学期望)(X Eg ；会根据随机变量X 和Y 的联合概率分布求其函数),(Y X g 的数学期望),(Y X Eg .3．了解切比雪夫不等式.4．了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律（独立同分布随机变量的大数定律）5．了解棣莫弗—拉普拉斯定理（二项分布以正态分布为极限分布）和列维—林德伯格定理（独立同分布的中心极限定理）；（经济类还要求）会用相关定理近似计算有关随机事件的概率 一、 数学期望与方差（标准差） 1. 定义（计算公式）离散型{}i i p x X P ==, ∑=iii px X E )(连续型)(~x f X , xx xf X E d )()(⎰+∞∞-=方差：[]222)()())(()(X E X E X E X E X D -=-=标准差：)(X D ,2. 期望的性质：1° )())((,)(X E X E E C C E == 2° )()()(2121Y E C X E C Y C X C E +=+ 3° )()()(Y E X E XY E ，Y X =则独立与若4° [])()(≤)(222Y E X E XY E3. 方差的性质：1° 0))((,0))((,0)(===X D D X E D C D 2°)()()(Y D X D Y X D Y X +=±相互独立，则与3° )()(2121X D C C X C D =+ 4° 一般有 ),Cov(2)()()(Y X Y D X D Y XD ±+=±)()(2)()(Y D X D Y D X D ρ±+=5°2()()C D X E X <-, )(X E C ≠【例1】设试验成功的概率为43, 失败的概率为41, 独立重复试验直到成功两次为止. 试求试验次数的数学期望. 【例2】 n 片钥匙中只有一片能打开房门, 现从中任取一片去试开房门, 直到打开为止. 试在下列两种情况下分别求试开次数的数学期望与方差: （1）试开过的钥匙即被除去; （2）试开过的钥匙重新放回.【例3】 设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤≤=.,0,0,2cos 21)(其他πx x x f 对X 独立地重复观察4次, 用Y 表示观察值大于3π的次数, 求2Y 的数学期望.【例4】 设有20人在某11层楼的底层乘电梯上楼, 电梯在中途只下不上, 每个乘客在哪一层（2-11层）下是等可能的, 且乘客之间相互独立, 试求电梯须停次数的数学期望. 二、随机变量函数的期望（或方差） 1、一维的情形 )(X g Y =离散型：{}i i P Xx p == ， ∑=ii ipx g Y E )()(连续型：~()X f x x x f x g Y E d )()()(⎰+∞∞-=2、二维的情形 ),(Y X g Z =离散型{}iji i p y Y x X P Y X ===,~),(,∑∑=jij jiipy x g Z E ),()(连续型),(~),(y x f Y X , y x y x f y x g Z E d d ),(),()(⎰⎰+∞∞-+∞∞-=【例5】 设X 与Y 独立且均服从N （0，1），求Z ＝22Y X + 的数学期望与方差.【例6】设两个随机变量X 与Y 相互独立且均服从N （0，21）, 试求Z ＝｜X －Y ｜的数学期望与方差. 三 、协方差，相关系数与随机变量的矩 1、重要公式与概念：协方差 []))()((()Cov(Y E Y X E X E X,Y --=相关系数 )()()Cov(Y D X D X,Y XY =ρ)(k X E k 阶原点矩[]kX E X E k ))((- 阶中心矩2、性质：1°),(Cov ),(Cov X Y Y X =2° ),(Cov ),(Cov Y X ab bY aX = 3° ),(Cov ),(Cov ),(Cov 2121Y X Y X Y X X +=+4° |(,)|1X Y ρ≤5° 1)(1),(=+=⇔=b aX Y P Y X ρ )＞0(a 1)(1),(=+=⇔-=b aX Y P Y X ρ )＜0(a 3、下面5个条件互为充要条件：（1）0),(=Y X ρ（2）0)Cov(=X,Y （3）)()()(Y E X E XY E = （4）)()()(Y D X D Y X D +=+ （5）)()()(Y D X D Y X D +=- 【例7】设)2(,,,21>n X X X n 为独立同分布的随机变量, 且均服从)1,0(N , 记∑==ni iX n X 11,.,,2,1,n i X X Y i i =-= 求:（I ） i Y 的方差n iY D i ,,2,1),( =；（II ） 1Y 与n Y 的协方差),(1n Y Y Cov ; （III ） }.0{1≤+n Y Y P四、极限定理1. 切比雪夫不等式{}{}()()|()|,|()|<1-22D X D X P XE X P X E X εεεε-≥≤-≥或2. 大数定律3. Poisson 定理4. 中心极限定理列维—林德伯格定理: 设随机变量X 1，X 2，…，X n ，…相互独立同分布, 且2(),(),i i E X D X μσ== 1,2,,,i n =， 则对任意正数x ，有2-2lim d n t i x n X n P x t μ-∞→∞⎧⎫-⎪⎪⎪≤=⎬⎪⎪⎪⎩⎭∑⎰ 棣莫弗—拉普拉斯定理: 设~(,),nB n p η（即X 1，X 2，…，X n，…相互独立, 同服从0一1分布） 则有22lim d t x n P x t --∞→∞⎧⎫⎪≤=⎬⎪⎭⎰. 【例8】 银行为支付某日即将到期的债券须准备一笔现金，已知这批债券共发放了500张，每张须付本息1000元，设持券人（1人1券）到期到银行领取本息的概率为0.4.问银行于该日应准备多少现金才能以99.9%的把握满足客户的兑换.【分析】 若X 为该日到银行领取本息的总人数，则所需现金为1000X ，设银行该日应准备现金x 元.为使银行能以99.9%的把握满足客户的兑换，则 P （1000X ≤x ）≥0.999.【详解】 设X 为该日到银行领取本息的总人数，则X~B （500，0.4）所需支付现金为1000X ，为使银行能以99.9%的把握满足客户的兑换，设银行该日应准备现金x 元，则 P （1000 X ≤x ）≥0.999.由棣莫弗—拉普拉斯中心极限定理知：(1000)()1000x P X x P X ≤=≤5000.4x P ⎛⎫-⨯ ⎪=≤=≤0.999(3.1).ΦΦ≈≥=即3.1,≥得 x ≥ 233958.798.因此银行于该日应准备234000元现金才能以99.9%的把握满足客户的兑换.第五讲 数理统计考试要求1. 理解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念.其中样本方差定义为.)(11212X X n S i ni --=∑=2. 了解2χ分布、t 分布和F 分布的概念及性质，了解分位数的概念并会查表计算. 3. 了解正态总体的常用抽样分布.4. 理解经验分布函数的概念和性质, 会根据样本值求经验分布函数.5. 理解参数的点估计、估计量与估计值的概念.6. 掌握矩估计法（一阶、二阶矩）和最大似然的估计法.7. 了解估计量的无偏性、有效性（最小方差性）和一致性（相合性）的概念，并会验证估计量的无偏性.8. 理解区间估计的概念，会求单个正态总体的均值和方差的置信区间，会求两个正态总体的均值差和方差比的置信区间. 9. 理解显著性检验的基本思想，掌握假设检验的基本步骤，了解假设检验可能产生的 两类错误.10. 了解单个及两个正态总体的均值和方差的假设检验 一、样本与抽样分布1. 总体、个体与简单随机样本:2. 常用统计量:1° 样本均值 i ni X nX ∑==112° 样本方差 212)(11X X n S i ni --=∑=3° 样本标准差: S =4° 样本k 阶原点矩 11,1,2,n kk i i A X k n ===∑5° 样本k 阶中心矩 11(),1,2,n kk i i B X X k n ==-=∑3．分位数 4. 重要抽样分布（1）分布2χ （2） t 分布 （3） F 分布5. 正态总体的常用抽样分布:22,,,(,),n X X X N μσ1设为来自正态总体的样本11nii X X n ==∑,2211()1ni i S X X n ==--∑, 则 （1）2~,~(0,1).X N N n σμ⎛⎫ ⎪⎝⎭ （2）222221(1)1()~(1).ni i n S X X n χσσ=-=--∑（3）22211()~().ni i X n μχσ=-∑（4） ~(1).X t n - （5）X 与2S 相互独立, 且 μ=)(X E , 22)(σ=S E , nX D 2)(σ=.【例1】 设总体2~(,),XN μσ设12,,,n X X X 是来自总体X 的一个样本, 且22111,()nni nii i X X S XX n====-∑∑，求21()n E X S .【例2】 设总体2~(,),X N μσ 设12,,,nX X X 是取自总体X 的一个样本, 且221111,()1nni i i i X X S X X nn ====--∑∑，则 2()_________D S=.【例3】设随机变量~()(1),X t n n >, 则 21~________Y X =【例4】 设总体X 服从正态分布)2,0(2N , 而1521,,,X X X 是来自总体X 的简单随机样本, 求随机变量)(221521121021X X X X Y ++++= 的分布. 【例5】 设总体2~(,),X N μσ 设121,,,,n n X X X X +是来自总体X 的一个样本, 且*221111,()()nni ii i X X S XX nn====-∑∑，试求统计量的分布. 二、参数估计1. 矩估计2. 最大似然估计3. 区间估计4. 估计量的评选标准 【例6】设总体12~(,)XU θθ，n X X X ,,,21 为来自总体X 的样本，试求12,θθ的矩估计和最大似然估计.【例7】设总体X 的概率密度为⎪⎩⎪⎨⎧<≤-<<=.,0,21,1,10,),(其他x x x f θθθ其中θ是未知参数)10(<<θ, n X X X ,,2,1 为来自总体X 的简单随机样本, 记N 为样本值n x x x ,,2,1 中小于1的个数, 求：（1）θ的矩估计；（2） θ的最大似然估计.【例8】设总体X 的概率密度为36(),0,()0,xx x f x θθθ⎧-<<⎪=⎨⎪⎩其他. n X X X ,,,21 为来自X 的简单随机样本，（1） 求θ的矩估计量ˆθ； （2） 判断θ的无偏性; （3） 判断θ的一致性. 三、假设检验1. 假设检验的基本思想：对总体分布中的未知参数作出某种假设，根据样本在假设为真的前提下构造一个小概率事件，基于“小概率事件”在一次试验中几乎不可能发生而对假设作出拒绝或接受.2. 单个正态总体均值和方差的假设检验.3. 假设检验两类错误：第一类错误：原假设0H 为真，但拒绝了0H .第二类错误；原假设0H 为假，但接受到了0H .。

前言《大学语文》是高等教育自学考试的一门公共课，几乎所有参加自学考试的同学都要参加此门课的考试。

自考的课程，只要是考试大纲、教材没有变动，每次的考试出题的内容、难度是不会有变化的。

《大学语文》主要复习四部分的内容：一、认真研读教材中的课文本课程共52篇课文，议论文10篇，记叙文17篇，诗词18篇，小说7篇。

这里特别强调的是，考生一定要加强对教材所选取的课文内容的理解。

对课文内容的掌握，可以分成两个层次：浅层次的掌握就是要求考生记忆课文中的内容，在过去《大学语文》考试中，考核考生对课文的内容是否记忆的试题较多；深层次的掌握则要求考生在对课文记忆的基础上对课文所涉及的内容加以深刻理解，考核考生的分析问题、理解问题的能力。

对于古文，要能够读通、读懂，同时对重点字词（课文后面的注释）要一一掌握。

二、在熟练掌握每篇课文的基础上，根据考试大纲的要求，结合课文后面的提示，逐个掌握每一个知识点。

对【考试大纲】、【提示】的考核是每次考试的重中之重，所占分值较多。

三、要灵活掌握语文知识这是学习的难点，历年来考生丢分很多。

要求掌握的语文知识主要有：1、议论文的论点、论据、论证。

其中两种论据、三种论证方法是重点；2、10种修辞手法；3、记叙文的表现手法；4、描写人物的五种方法；5、诗词的直接抒情手法，间接抒情的六种手法；6、记叙的顺序。

参照教材50页、148页、217页、287页学习。

四、作文自考作文一般可以写成夹叙夹议夹抒情的文章。

在写作作文时，可以参看《纪念傅雷》一文的写法。

从试卷的组成来看，除去作文，考核课文知识的题目中，非常容易的题目大约占15分；较容易的题目大约占20分；较难的题大约占20分，难的题目大约占15分。

第一单元议论文部分《寡人之于国也》孟子《作家作品》孟子：（1）名轲，字子舆。

战国时人。

是孔子之后儒家学派的主要代表。

（2）主张施仁政，行王道。

倡导民贵君轻的民本思想。

（3）其散文善用“欲擒故纵，引君入彀”的论辩方法。

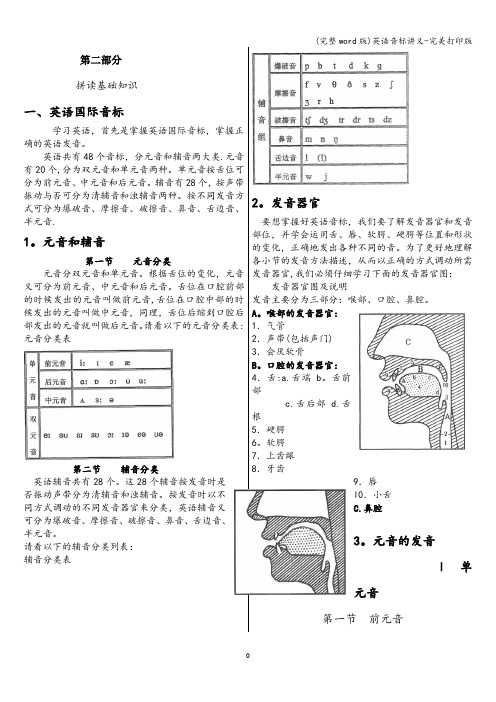
第二部分拼读基础知识一、英语国际音标学习英语，首先是掌握英语国际音标，掌握正确的英语发音。

英语共有48个音标，分元音和辅音两大类.元音有20个,分为双元音和单元音两种。

单元音按舌位可分为前元音、中元音和后元音。

辅音有28个，按声带振动与否可分为清辅音和浊辅音两种。

按不同发音方式可分为爆破音、摩擦音、破擦音、鼻音、舌边音、半元音.1。

元音和辅音第一节元音分类元音分双元音和单元音。

根据舌位的变化，元音又可分为前元音、中元音和后元音。

舌位在口腔前部的时候发出的元音叫做前元音,舌位在口腔中部的时候发出的元音叫做中元音，同理，舌位后缩到口腔后部发出的元音就叫做后元音。

请看以下的元音分类表:元音分类表第二节辅音分类英语辅音共有28个。

这28个辅音按发音时是否振动声带分为清辅音和浊辅音。

按发音时以不同方式调动的不同发音器官来分类，英语辅音又可分为爆破音、摩擦音、破擦音、鼻音、舌边音、半元音。

请看以下的辅音分类列表：辅音分类表2。

发音器官要想掌握好英语音标，我们要了解发音器官和发音部位，并学会运用舌、唇、软腭、硬腭等位置和形状的变化，正确地发出各种不同的音。

为了更好地理解各小节的发音方法描述，从而以正确的方式调动所需发音器官,我们必须仔细学习下面的发音器官图：发音器官图及说明发音主要分为三部分：喉部、口腔、鼻腔。

A。

喉部的发音器官：1．气管2．声带(包括声门)3．会厌软骨B。

口腔的发音器官：4．舌:a.舌端 b。

舌前部c.舌后部d.舌根5．硬腭6。

软腭7．上齿龈8．牙齿9．唇l0．小舌C.鼻腔3。

元音的发音Ⅰ单元音第一节前元音发音方法描述:发音时舌尖轻抵下齿,前舌部向上腭抬起,口形扁而平。

发音时间延续较长。

例词：l ea f树叶 ch ee se奶酪t ea茶 th ie f贼b ea ch海滩 w ee k星期t ea m队 m ea t肉sh ee p羊词组:Green Street格林街iced tea冰茶Chinese and Japanese food中国和日本菜发音方法描述：发音时舌尖抵下齿，舌前部向硬腭抬起,口形扁平，发音时间短促.例词：cl i p夹子 g y m体育馆 s i t坐 th i n薄的p i zza比萨饼 tax i出租车 un i t单元 v i s i t游览词组:play tennis打网球 pop music流行音乐 music festival音乐节发音方法描述：舌尖抵下齿，前舌部向硬腭抬起，口形扁平，气流从口腔泄出，声带振动。

课题七Adobe Illustrator图形优化存储输出和自动化作业目的要求：1．掌握用于Web各种图像格式的应用范围。

2．掌握GIF、JPEG、PNG、SWF、SVG格式输出选项的设定。

3．掌握“打印”对话框中的各个选项的设定。

4．掌握分色原理和透明拼合。

5．了解Adobe Illustrator CS2自动化作业。

教学重点：自动化作业、打印输出教学难点：打印设置授课时数:2 学时授课内容：引入：图形文档的存储和输出一、Adobe Illustrator CS2 文档存储和输出1．印刷图形格式在桌面出版领域，常用的图形格式有AI、EPS、PDF，以及CDR（CorelDRAW原生文件格式）、FH（FreeHand原生文件格式）。

在Illustrator虽然不能存储为CDR和FH格式，但可以打开CDR5、6、7、8、9、10版本和FH4、5、7、8、9版本的文件。

Illustrator中有5个关于存储的命令：存储、存储为、存储副本、存储为模版、存储为Web所用格式，以及“输出”命令。

（1）存储：以原文件名存储文件，将原文件替换掉。

Illustrator可以直接存储为AI、EPS、PDF和SVG格式。

◆AI格式Illustrator原生文件格式，可以同时保存矢量信息和位图信息。

Illustrator专用文件格式，可以保存的数据包括画笔、蒙版、效果、透明度、色样、混合、图表数据等。

“版本”“字体”：百分比——低于该百分比时嵌入字体的子集。

“创建PDF兼容文件”：存储一个PDF重新版本，让AI文件与其他Adobe软件兼容。

“包含链接文件”：将当前文档中链接的文件一起存储在AI文档中。

底部窗格中显示低版本不支持的功能。

“使用压缩”：压缩AI文档中的PDF数据。

“嵌入ICC配置文件”：创建颜色管理文件。

“透明选项”：当存储为AI9.0以下版本时，决定如何处理透明对象。

✧“保留路径”——取消透明，不透明度设为100%✧“保留外观和叠印”——保留不带透明属性对象的叠印设置，带透明属性对象的叠印将会被拼合。

第七章皮类中药【字体：大中小】【打印】一、概述皮类中药通常是指裸子植物或被子植物的茎干、枝和根的形成层以外部位入药的药材。

它由外向内包括周皮、皮层、初生和次生韧皮部等部分。

其中大多为木本植物茎干的皮，如黄柏、杜仲；少数为根皮，如牡丹皮、桑白皮；或为枝皮，如秦皮。

（一）性状鉴别皮类中药因植物来源、取皮部位、采集和加工干燥的方法不同，形成了外表形态上的特征变化，在鉴定时应仔细观察，正确运用术语。

现分述如下：1.形状：由粗大老树上剥的皮，大多粗大而厚，呈长条状或板片状；枝皮则呈细条状或卷筒状；根皮多数呈短片状或筒状。

一般描述术语有：平坦状或弯曲状。

由于弯曲的程度不同，又分槽状或半管状如企边桂、管状或筒状如牡丹皮、单卷状如肉桂、双卷筒状如厚朴、复卷筒状如锡兰桂皮、反曲状如石榴树皮等。

2.表面：外表面颜色多为灰黑色、灰褐色、棕褐色或棕黄色。

内表面颜色各不相同，一般较平滑或具粗细不同的纵向皱纹。

3.折断面：皮类中药横向折断面的特征和皮的各组织的组成和排列方式有密切关系，因此是皮类中药的重要鉴别特征，折断面的性状主要有平坦状（富有薄壁细胞而无石细胞群或纤维束）、颗粒状（富有石细胞群的皮）、纤维状（富含纤维）、层状（纤维束和薄壁组织成环带状间隔排列，如黄柏）等。

4.气味：气味和皮中所含成分有密切关系，各种皮的外形有时很相似，但其气味却完全不同。

如香加皮和地骨皮，前者有特殊香气，味苦而有刺激感，后者气味均较微弱。

肉桂和桂皮外形亦较相似，但肉桂味甜而微辛，桂皮则味辛辣而凉。

（二）显微鉴别组织构造：皮类中药构造可分为周皮、皮层、韧皮部三部分。

各部位在观察时应注意如下特征：1.周皮：包括木栓层、木栓形成层与栓内层三部分。

2.皮层：大多是薄壁细胞，其中常可见纤维、石细胞、各种分泌组织，如秦皮、黄柏皮层可见纤维、石细胞；肉桂、厚朴皮层可见油细胞；桑白皮可见乳汁管等。

常见的细胞内含物有草酸钙结晶，如桑白皮、黄柏含方晶；牡丹皮、苦楝皮含簇晶；肉桂含针晶。

WPS打印讲义1. 概述本文将介绍如何使用WPS进行讲义的打印，包括设置打印选项、调整页面布局和导出为PDF格式等操作。

通过本文的指导，您将能够高效地利用WPS进行讲义的打印工作。

2. 打印选项设置在进行讲义打印之前，首先需要设置一些打印选项，以确保打印效果符合预期。

2.1 页面设置在WPS中，可以通过以下步骤进行页面设置：1.打开WPS软件，选择需要打印的讲义文件。

2.点击菜单栏中的“文件”选项，然后选择“页面设置”。

3.在弹出的页面设置对话框中，可以设置纸张大小、页边距、页眉页脚等选项。

根据讲义的要求进行相应的设置。

2.2 打印机设置在进行讲义打印之前，还需要设置一些打印机选项，以确保打印效果符合要求。

1.点击菜单栏中的“文件”选项，然后选择“打印”。

2.在弹出的打印对话框中，选择合适的打印机。

3.点击“打印机属性”按钮，进入打印机属性设置界面。

4.在打印机属性设置界面中，可以设置打印质量、纸张类型、双面打印等选项。

根据讲义的要求进行相应的设置。

3. 页面布局调整在进行讲义打印之前，可能需要对页面布局进行调整，以确保打印效果符合要求。

3.1 页面缩放在WPS中，可以通过以下步骤进行页面缩放：1.打开讲义文件。

2.点击菜单栏中的“视图”选项，然后选择“页面缩放”。

3.在弹出的页面缩放对话框中，可以设置页面的缩放比例。

根据讲义的要求进行相应的设置。

3.2 页面分割在WPS中，可以通过以下步骤进行页面分割：1.打开讲义文件。

2.点击菜单栏中的“视图”选项，然后选择“页面分割”。

3.在弹出的页面分割对话框中，可以设置页面的分割方式和分割线样式。

根据讲义的要求进行相应的设置。

4. 导出为PDF格式在进行讲义打印之前，可以将讲义文件导出为PDF格式，以便在不同平台上进行打印。

4.1 导出为PDF在WPS中，可以通过以下步骤将讲义文件导出为PDF格式：1.打开讲义文件。

2.点击菜单栏中的“文件”选项，然后选择“另存为”。