江西省横峰中学2017-2018学年高二第16周周练数学试题

2017—2018学年度下学期高二年级期中考试数学(文）试卷考试时间:120分钟一、选择题：（本题包括12小题，共60分,每小题只有一个选项符合题意）1．若集合A=｛x| ｜x﹣1｜≤1｝，B=｛﹣2,﹣1,0,1,2｝,则集合A∩B=（）A．｛0,2｝ B．｛﹣2，2} C．{0,1，2} D．｛﹣2，﹣1,0}2．设复数z满足（1+i)z=2i，则｜z｜=（）A．B．C．D．23．命题“∃x＞0，使2x＞3x”的否定是（)A．∀x＞0,使2x≤3x B．∃x＞0，使2x≤3xC．∀x≤0，使2x≤3x D．∃x≤0,使2x≤3x4．为评估一种农作物的种植效果,选了n块地作试验田．这n块地的亩产量(单位:kg）分别是x1,x2,…，x n ，下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( ）A．x1，x2,…，x n的平均数B．x1,x2，…，x n的中位数C．x1,x2，…,x n的最大值D．x1，x2,…,x n的标准差5．设a∈R，则“a＞1”是“a2＞1”的（）A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分也非必要条件6．直线l经过椭圆的一个顶点和一个焦点,若椭圆中心到l的距离为其短轴长的,则该椭圆的离心率为（)A．B．C．D．7．在明朝程大位《算法统宗》中有这样的一首歌谣：“远看巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯？"这首古诗描述的这个宝塔（古称浮屠）,本题说它一共有7层，每层悬挂的红灯数是上一层的2倍，共有381盏灯，问塔顶有几盏灯？你算出的结果是（）A．6 B．5 C．4 D．38．如图,正方形ABCD内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是（）A．B．C．D．9．若某多面体的三视图（单位：cm）如图所示，则此多面体的体积是（）A． B．cm3C．cm3D．cm310．已知双曲线的实轴长为8,则该双曲线的渐近线的斜率为（）A．B．C．D．11．已知点F为抛物线y 2=﹣8x的焦点，O为原点,点P是抛物线准线上一动点，点A在抛物线上，且|AF｜=4，则｜PA｜+｜PO|的最小值为( ）A．6 B．C．D．4+212．已知函数f（x）=，设a∈R，若关于x的不等式f（x）≥｜+a｜在R上恒成立，则a的取值范围是（）A．［﹣2，2] B．C．D．二、填空题：(本题包括4小题，共20分）13．已知向量=（﹣2,3），=（3,m），且,则m= ．14．函数f（x)= x+e x+1 在x =﹣1处的切线方程为．15．若x,y满足约束条件,则z= x +y的最大值为．16．设函数f（x）=,则满足f（x)+f(x﹣）＞1的x的取值范围是．三、填空题：（本题包括6小题,共70分)17．（本小题12分）在△ABC中，内角A,B,C所对的边分别为a，b，c,已知asin2B=bsinA．(1）求B；（2）已知cosA=,求sinC的值．18．(本小题12分)已知等差数列{a n}的前n项和为S n，等比数列｛b n｝的前n项和为T n，a1=﹣1,b1=1，a2+b2=2．（1）若a3+b3=5，求｛b n｝的通项公式；（2）若T3=21，求S3．19．（本小题12分）已知椭圆的离心率为，又点在该椭圆上．（1）求椭圆E的方程;（2）若斜率为的直线l与椭圆E交于不同的两点B，C，求△ABC 的最大面积．20．（本小题12分）已知函数f（x）=（x+1）lnx﹣a（x﹣1)．（I）当a=4时，求曲线y=f（x)在（1，f(1)）处的切线方程；（II)若当x∈（1，+∞）时，f（x）＞0，求a的取值范围．21．(本小题11分）在直角坐标系xOy中，曲线C1的参数方程为（t为参数,a＞0）．在以坐标原点为极点,x轴正半轴为极轴的极坐标系中，曲线C2:ρ=4cosθ．(Ⅰ）说明C1是哪种曲线，并将C1的方程化为极坐标方程；(Ⅱ）直线C3的极坐标方程为θ=α0，其中α0满足tanα0=2，若曲线C1与C2的公共点都在C3上，求a．22．(本小题11分)已知函数f(x)=｜x﹣｜+｜x+｜,M为不等式f （x）＜2的解集．(Ⅰ）求M；(Ⅱ）证明：当a，b∈M时,｜a + b|＜｜1 + a b｜．横峰中学高二年级下学期期中考试一．选择题123456789101112C C AD A B D B A C C A 二．填空题13．2; 14．2x﹣y+2=0；15．8; 16．(，+∞）;三．解答题17。

2017-2018学年度高二年级上学期第一次月考数学(理)试卷考试时间：120分钟一．选择题（60分）1。

某市A，B，C三个区共有高中学生20 000人，其中A区高中学生7 000人，现采用分层抽样的方法从这三个区所有高中学生中抽取一个容量为600人的样本进行学习兴趣调查，则A区应抽取( ）A。

200人 B.205人 C.210人 D.215人2．设x，y满足x＋4y＝40,且x，y都是正数，则lg x＋lg y的最大值是( ）A．40 B．10 C．4 D．23．若正数x，y满足x＋3y＝5xy，则3x＋4y的最小值是( ）A.错误!B.错误!C．5 D．64.运行以下程序时，执行循环体的次数是( )i=1Doi=i+1i=i*iLoop While i<10输出iA。

2 B.8 C.10 D。

115。

执行如上图所示的算法框图，若输入的a值为1，则输出的k值为( ）A。

1 B。

2 C.3 D。

46.不等式组错误!表示的平面区域是( ）A．矩形B．三角形C．直角梯形D．等腰梯形7．不等式组错误!表示的平面区域的面积为错误!,则a＝（）A.错误!B．1 C．2 D．38.对某商店一个月内每天的顾客人数进行统计，得到样本的茎叶图(如图所示）.则该样本的中位数、众数、极差分别是（）) A.46 45 56 B.46 45 53C。

47 45 56 D。

45 47 539.某同学设计了如图所示的算法框图用以计算和式1×10+3×12+5×14+…+19×28的值，则在判断框中可以填写的表达式为( )A.i≥19B.i〉20 C。

i〉21 D.i<2110．设正实数x,y,z满足x2－3xy＋4y2－z＝0，则当xyz取得最大值时，错误!＋错误!－错误!的最大值为（)A．0 B．1 C。

错误!D．311。

已知一组正数x1，x2,x3,x4的方差为s2=×（+++—16），则数据x1+2，x2+2，x3+2,x4+2的平均数为( )A。

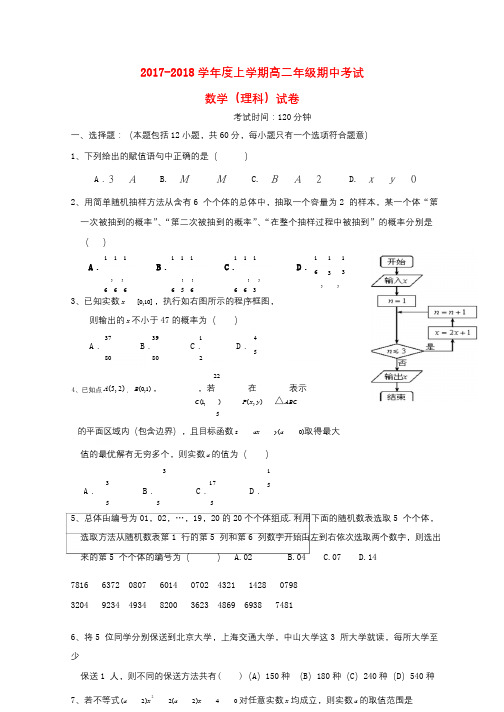
2017-2018学年度上学期高二年级期中考试数学（理科）试卷考试时间：120分钟一、选择题：（本题包括12小题，共60分，每小题只有一个选项符合题意）1、下列给出的赋值语句中正确的是（）A．3A B. MM C. B A 2 D. x y2、用简单随机抽样方法从含有6个个体的总体中，抽取一个容量为2的样本，某一个体“第一次被抽到的概率”、“第二次被抽到的概率”、“在整个抽样过程中被抽到”的概率分别是（）111111111A．B．C．D．,,,,,,6666566633、已知实数x [0,10]，执行如右图所示的程序框图，16,1313,则输出的x不小于47的概率为（）37391A．B．C．D．8080245224、已知点A(5,2)，B(0,1)，，若在表示C(1,)P(x,y)△ABC5的平面区域内（包含边界），且目标函数z ax y(a 0)取得最大值的最优解有无穷多个，则实数a的值为（）3317A．B．C．D．555155、总体由编号为01，02，…，19，20的20个个体组成.利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（） A.02 B.04 C.07 D.147816 6372 0807 6014 0702 4321 1428 07983204 9234 4934 8200 3623 4869 6938 74816、将5位同学分别保送到北京大学，上海交通大学，中山大学这3所大学就读，每所大学至少保送1人，则不同的保送方法共有( )（A）150种（B）180种（C）240种（D）540种7、若不等式(a 2)x22(a 2)x 40对任意实数x均成立，则实数a的取值范围是- 1 -（）A．(2,2]B．[2,2]C．(2,)D．(,2]8、若s(p)表示p所示平面图形的面积，如A{(x,y)|(x a)2(y b)2r2,r0}，1008B{(x,y)|2x3y50}s()，且(A B)s A，则以下式子一定成立的是（）20179、如图，从上往下读（不能跳读）构成句子“构建和谐社会，创美好未来”的不同读法种数是（）A．250B．240C．252D．30010、已知等式：x4a x3a x2a xa1234(x1)b(x1)b(x1)b(x1)b，定义映射4321234f:(a,a,a,a)(b,b,b,b)，则f(4,3,2,1)（）12341234A．(1,2,3,4)B．(0,3,4,0)C．(0,3,4,1)D．(1,0,2,2)11、已知三角形ABC三边长分别为a,b,c，均为整数，且满足b25,a b c，则符合条件的三角形有（）个，A,124、B,225、C,300、D,325。

横峰中学2017-2018学年度上学期 高二数学 第15周周练试卷（文科） 出卷人：程凤娟 时间：45分钟一、选择题（每题8分）1．已知i 是虚数单位，若()21a ia R i+∈-为纯虚数，则a =（ ）A. 1B. -1C. 0D. 1±2．在复平面内，复数z 的对应点为（1，-1），则()2z i z +⋅=（ ） A. 22i + B. 2 C. 0 D. 2i 3．命题“存在00,20x x R ∈≤”的否定是（ ） A. 不存在00,20x x R ∈> B. 存在00,20x x R ∈≥ C. 对任意的,20x x R ∈≤ D. 对任意的,20xx R ∈> 4．设,x y R ∈，则“0x >”是“1x >-”的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 5．下列说法中，正确的是（ ）A. 命题“若22am bm <，则a b <”的逆命题为真命题B. 命题“存在2000,0x R x x ∈->”的否定是“对任意的2,0x R x x ∈-≤”C. 命题“p 或q ”为真命题，则命题p 和命题q 均为真命题D.已知x R ∈，则“1x >”是“2x >”的充分不必要条件6.某运动队对,,,A B C D 四位运动员进行选拔，只选一人参加比赛，在选拔结果公布前，甲、乙、丙、丁四位教练对这四位运动员预测如下：甲说：“是C 或D 参加比赛”； 乙说：“是B 参加比赛”；丙说：“是,A D 都未参加比赛”；丁说：“是C 参加比赛”.若这四位教练中只有两位说的话是对的，则获得参赛的运动员是_________． A.A B.B C.C D.D二、填空题（每题8分）7．已知命题x e a x p ∈∈∃],1,0[:，命题,0,:2>++∈∀a x x R x q 若命题q p ∧是真命题，则实数a 的取值范围是__________．8．命题p ：任意两个等边三角形都是相似的．①它的否定是_________________________________________________________； ②否命题是_____________________________________________________________． 9．若命题0,2<-∈∃a t R t 是真命题，则实数a 的取值范围是_____．三、解答题10．（每题18分）7．已知命题：“}{ 11x x x ∀∈-≤≤，都有不等式20x x m --<成立”是真命题.（1）求实数m 的取值集合B ；（2）设不等式()()320x a x a ---<的解集为A ，若x A ∈是x B ∈的充分不必要条件，求实数a 的取值范围.参考答案D D D A B B若A 参赛，甲、乙、丙、丁四人话都错，不符；若C 参赛，甲、丙、丁三人话对，不符；若D 参赛，乙、丙、丁三人话错，不符合；若B 参赛，乙、丙话对，甲、丁话错，符合；综上，参赛运动员为B.7．【解析】因，故，即；又恒成立，则，故当是真命题时，，应填答案。

横峰中学2017-2018学年高二上学期数学第十周周练试卷一、选择、填空题（1-5题每题10分）1．已知一组数据54321,,,,x x x x x 的平均数是2，方差是31，那么另一组数据23,23,23,23,2354321-----x x x x x 的平均数，方差是（ ）A ．31,2 B ．1,2 C ．32,4 D ． 3,4 2．某高中数学老师从—张测试卷的12道选择题、4道填空题、6道解答题中任取3道题作分析，则在取到选择题时解答题也取到的概率为（ ）A ．11112620332210C C C C C ⋅⋅- B ．111121264126332210C C C C C C C ⋅⋅+⋅- C ．()11122112646126332210C C C C C C C C ⋅++⋅- D ．333221016332210C C C C C --- 3．若执行如图所示的程序框图，输出S 的值为（ ）A ．22log 3B ．2log 7C ．2D ．34．已知,x y 满足41y x x y x ≥⎧⎪+≤⎨⎪≥⎩，则22223y xy x x -+的取值范围为_____ _______． 5．甲、乙两位同学玩游戏，对于给定的实数1a ，按下列方法操作一次产生一个新的实数：由甲、乙同时各掷一枚均匀的硬币，如果出现两个正面朝上或两个反面朝上，则把1a 乘以2后再减去12；如果出现一个正面朝上，一个反面朝上，则把1a 除以2后再加上12，这样就可得到一个新的实数2a ，对实数2a 仍按上述方法进行一次操作，又得到一个新的实数3a ，当31a a >时，甲获胜，否则乙获胜，若甲胜的概率为34，则1a 的取值范围是 ． 二、解答题 6．（20分）已知函数y=的定义域为R ．（1）求a 的取值范围．（2）若函数的最小值为，解关于x 的不等式x 2﹣x ﹣a 2﹣a ＜0．7、（30分）为检验寒假学生自主学生的效果，年级部对某班50名学生各科的检测成绩进行了统计，下面是物理成绩的频率分布直方图，其中成绩分组区间是：[)[)[)[)[)[]40,50,50,60,60,70,70,80,80,90,90,100．（1）求图中的x 值（2）估计平均成绩和中位数；（3）从分数在[)70,80中选5人记为125,,,a a a ，从分数在[)40,50中选3人，记为123,,,8b b b 人组成一个学习小组现从这5人和3人中各选1人做为组长，求1a 被选中且1b 未被选中的概率．附加题（解答过程写反面）8、（20分）已知函数()f x x m =-，函数()()m m x f x x g 72-+⋅=． （1）若1=m ，求不等式()0≥x g 的解集；（2）若对任意(]4,1∞-∈x ,均存在[)23,x ∈+∞,使得()()21x g x f >成立，求实数m 的取值范围．参考答案DCD 4．[]2,6 5．(,12][24,)-∞+∞．6、（1）∵函数y=的定义域为R ，∴a=0时，满足题意； a ＞0时，△=4a 2﹣4a≤0，解得0＜a≤1；∴a 的取值范围是{a|0≤a≤1}；（2）∵函数y 的最小值为，∴≥， a ∈[0，1]；∴ax 2+2ax+1≥； 当a=0时，不满足条件；当1≥a＞0时，ax 2+2ax+1的最小值是=，∴a=； ∴不等式x 2﹣x ﹣a 2﹣a ＜0可化为x 2﹣x ﹣＜0，解得﹣＜x ＜；∴不等式的解集是{x|﹣＜x ＜}．7．解：（1）由(0.006*3+0.01+0.054+x)*10=1，得x=0.018(2)平均成绩为()0.064555950.1650.54750.188574⨯+++⨯+⨯+⨯=中位数为70+（0.28/0.54）=78.2（3）从这5个和3人中各随机选1人，所有结果有：()()()()()()()()()()()()()()()111213212223313233414243515253,,,,,,,,,,,,,,,,,,,,,,,,,,,,a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b 共15个．事件A 为“1a 被选中，1b 未被选中”包含的基本事件有：()()1212,b ,,a a b 共2 个． 所以1a 被选中， 1b 未被选中的概率215P = 考点：频率分布直方图和列举法古典概型公式等有关知识的综合运用．8．（1）依题意得160x x --≥当1x ≥时，260x x --≥，∴32x x ≥≤-或，∴3x ≥；当1x <时，260x x -+≤，无解所以原不等式的解集为[3,)+∞（2）因为2()||7g x x x m m m =-+-所以当m m m x x g m x 7432)(22-+⎪⎭⎫ ⎝⎛-=≥时； 当m m m x x g m x 7452)(22-+⎪⎭⎫ ⎝⎛--=<时 所以当m m m <<>200时，， 上单调减上单调增，在上单调增，在在],2[]2,(),[)(m m m m x g -∞+∞ 当020<<<m m m 时，， 则上单调增上单调减，在上单调增，在在],[]2,[),()(+∞-∞m m m m x g 当上单调增在时，R x g m )(0=，又因为),3[+∞∈x所以①当3≤m 时，),3[)(+∞在x g 上单调增，m m m g x g 739)3()(2min -+-==②当3>m 时，又因为)()0(m g g =，结合0>m 时)(x g 的单调性，故)()3(m g g > ，m m m g x g 7)()(2min -==综上，⎪⎩⎪⎨⎧>-≤+-==3,73,910)()(22min m m m m m m m h x g ,()||,x m x m f x x m m x x m-≥⎧=-=⎨-<⎩，又因为(,4]x ∈-∞， 所以①当4<m 时，0)()(min ==m f x f ；②当4≥m 时，4)4()(min -==m f x f 综上得：1°当3≤m 时，由m m m 73902-+->得91<<m ，故31≤<m2°当43<<m 时，由m m 702->得70<<m ，故43<<m3°当4≥m 时，由m m m 742->-得324324+<<-m ，故3244+<≤m综上所述：m 的取值范围是)324,1(+．。

横峰中学2017-2018学年度上学期期中考试高二数学试卷(文) 考试时间：120分钟一、选择题：（本题包括12小题，共60分，每小题只有一个选项符合题意）1．一个年级有12个班，每个班的同学从1至50排学号，为了交流学习经验，要求每班学号 为14的同学留下进行交流，这里运用的是 （ ）A ．分层抽样B ．抽签抽样C ．随机抽样D ．系统抽样 2．同时掷3枚硬币，至少有1枚正面向上的概率是 （ ） A． B． C ．D．3．如右图是计算12＋14＋16＋…＋120的值的一个程序框图，其中在判断框中应填入的条件是 ( )A ．i <10B ．i>10C ．i <20D ．i >204.一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A ，“第2次拿出的是白球”为事件B ，则()|P B A 是（ ） A ．58 B ．516 C ．47 D ．5145．实数x ，y 满足条件⎪⎩⎪⎨⎧->≤≤+-1101x y y x 则()222y x +-的最大值为 （ ） A ．5 B ．9 C ．10 D ．25 6．已知0,0a b >>，若不等式3103m a b a b--≤+恒成立，则m 的最大值为 （ ）A ． 3B ．4C ． 9D ． 167．函数f （x ）=x 2﹣x ﹣2，x ∈[﹣5，5]，在定义域内任取一点x 0，使f （x 0）≤0的概率是（ ）A．B． C．D．8．某商场为了了解毛衣的月销售量y （件）与月平均气温x （C ︒）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：由表中数据算出线性回归方程y bx a =+中的2b =-，气象部门预测下个月的平均气温为6C ︒，据此估计该商场下个月毛衣销售量约为（ ）A ．58件B ．40件C ．38件D ．46件9. 设,a b 是非零实数， 若a b > ，则一定有 （ ）A ．11a b < B ．2a ab > C.2211ab a b > D ．11a b a b->- 11．若函数f(x)＝2x＋12x －a是奇函数，则使f(x)>3成立的x 的取值范围为( )A ．(－∞，1)B ．(0，1)C ．(－1，0)D ．(1，＋∞) 12．如图圆C 内切于扇形AOB ，3AOB π∠=，若在扇形AOB 内任取一点，则该点在圆C 内的概率为（ ）A ．16 B ．13 C ．23 D ．3412．已知函数2,0()2,0x x f x x x x -≤⎧=⎨-+>⎩，若方程21()()04f x bf x ++=有六个相异实根，则实数b 的取值范围（ ） A ．（54-，﹣1） B ．（﹣2，﹣1） C ．（54-，0） D ．（﹣2，0） 二、填空题：（本题包括4小题，共20分）13．某高中计划从全校学生中按年级采用分层抽样方法抽取20名学生进行心理测试，其中高三有学生900人，已知高一与高二共抽取了14人，则全校学生的人数为________ 14.已知0x >，观察下列几个不等式：23414272562;3;4;5;x x x x x x x x+≥+≥+≥+≥；归纳猜想一般的不等式为__________．15. 已知不等式 ()()22454130m m x m x +---+>对一切实数x 都成立， 则实数m 的取值范围是 __________.16.已知)(x f 是定义在R 上的增函数，函数)1(-=x f y 的图象关于点（1，0）对称．若对任意的R y x ∈,，不等式0)8()216(22<-++-y y f x x f 恒成立，则当3>x 时，22y x +的取值范围是 .三、解答题：（本题包括6小题，17题10分，18—22题每小题12分，共70分） 17．（本小题10分）已知函数b ax x x f ++=2)(．(1)若对任意的实数x ，都有a x x f +≥2)(，求b 的取值范围； (2)当]1,1[-∈x 时，)(x f 的最大值为M ，求证：1+≥b M ；18.（本小题12分）为了了解某校学生喜欢吃辣是否与性别有关，随机对此校100人进行调查，得到如下的列表：已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为35．（1）请将上面的列表补充完整；（2）是否有99.9%以上的把握认为喜欢吃辣与性别有关？说明理由： 下面的临界值表供参考：（参考公式))()()(()(22d b c a d c b a bc ad n k ++++-=：，其中n a b c d =+++）19．（本小题12分）一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4． （1）从袋中随机抽取两个球，求取出的球的编号之积不大于4的概率；（2）先从袋中随机取一个球，该球的编号为m ，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n ，求|n ﹣m|<2的概率．20．（本小题12分）已知f(x)＝－3x 2＋a(6－a)x ＋6. (1)解关于a 的不等式f (1)>0；(2)若不等式f(x)> b 的解集为(－1,3)，求实数a ，b 的值．21．（本小题12分）由507名画师集体创作的999 幅油画组合而成了世界名画《蒙娜丽莎》，某部门从参加创作的507名画师中随机抽出100名画师，得到画师年龄的频率分布表如下表．（1）求a ，b 的值(即①②)；并补全频率分布直方图； （2）根据频率分布直方图估计这507名画师年龄的平均数；（3）在抽出的[20,25)岁的5名画师中有3名男画师,2名女画师.在这5名画师中任选两人去参加某绘画比赛，选出的恰好是一男一女的概率是多少？22. （本小题12分）已知0x >，0y >，24xy x y a =++（1）当6a =时，求xy 的最小值； （2）当0a =时，求212x y x y+++的最小值。

2017-2018学年度上学期高二年级第一次月考数学试卷（文）考试时间：120分钟一、选择题：（本题包括12小题，每小题5分，共60分，每小题只有一个选项符合题意） 1. 设集合2{|60}M x x x =+-< ，{|13}N x x =≤≤，则M N （ ） A ．[1,2) B ．[]1,2 C ．(]2,3 D ．[]2,32. 若直线),0(,(022+∞∈=-+b a by ax 平分圆224260x y x y +---=，则12a b+的最小值是（ ）A. B.3+ C.2 D.5 3. 下列各函数中，最小值为2的是 ( )A ．1y xx =+ B ．1sin sin y x x =+，(0,)2x π∈ C ．2y = D ．1y x =-4. 执行如图的程序框图，则输出的λ是（ ）A ．4-B ．2-C ．0D ．2-或05. 不等式3(1)(1)(2)0x x x --+>的解集是（ ） A ．{2}x x >-B.{21}x x x >-≠且C ．{12}x x x ><-或D ．{21}x x x -<<6. 某工厂的质检人员对生产的100件产品，采用随机数法抽取10件检查，对100件产品进行编号，下列编号正确的为( )①1,2,3，…，100； ②001,002，…，100； ③00,01,02，…，99； ④01,02,03，…，100. A ．②③④ B ．③④ C ．②③ D ．①②7. 已知变量x 和y 满足关系0.11y x =-+，变量y 与z 正相关.下列结论中正确的是（ ）A. x 与y 正相关，x 与z 负相关B. x 与y 正相关，x 与z 正相关C. x 与y 负相关，x 与z 负相关 D . x 与y 负相关，x 与z 正相关 8. 若平面区域30,230,230x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是（ ）9. 如图是一算法的程序框图，若此程序运行结果为S=720，则在判断框中应填入关于k 的判断条件是（ ）A ．k≥6？B ．k≥7？C ．k≥8？D ．k≥9？ 10. 甲、乙两名运动员在某项测试中的6次成绩的茎叶图如图所示，1x ，2x 分别表示甲、乙两名运动员这项测试成绩的平均数，1s ，2s 员这项测试成绩的标准差，则有（ ） A ．1x >2x ,1s <2s B ．1x =2x ,1s >2s C ．1x =2x ,1s =2s D ．1x =2x ,1s <2s11. 不等式2220x axy y -+≥对于任意]2,1[∈x 及]3,1[∈y 恒成立，则实数a 的取值范围是（ ）A ．a ≤22B ．a ≥22C ．a ≤311D ．a ≤2912. 已知实数a b c <<，设方程1110x a x b x c++=---的两个实根分别为()1212,x x x x <，则下列关系中恒成立的是（ ）A ．12x a b x c <<<<B ．12a x b x c<<<<C ．12a x x b c <<<< D.12a x b c x <<<<二、填空题：（本题包括4小题，每小题5分，共20分）13.总体编号为01，02，……19，20的20个个体组成利用下面的随机数表选取5个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为________.14. 不等式1111+>+xx 的解集是________. 15. 若y x ,满足约束条件⎪⎩⎪⎨⎧≥≤+≤-131y y x x y ，则2+=x y z 的最大值为________.16. 使关于x 的不等式k x x ≥-+-63有解的实数k 的取值范围是________. 三、解答题：（共70分）17. （本小题满分10分）下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量x (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.(1)求线性回归方程ˆˆˆybx a =+所表示的直线必经过的点. (2)请根据上表提供的数据,用最小二乘法求出y 关于x 的线性回归方程ˆˆˆy bx a =+，并预测生产1000吨甲产品的生产能耗多少吨标准煤？(参考:1221ˆˆˆ,ni ii nii x y nx ybay bx xnx ==-∙==--∑∑)18. （本小题满分12分）统计局就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图如图，每个分组包括左端点，不包括右端点，如第一组表示收入在 三、解答题：17. （本小题满分10分） 【答案】(1) 4.5X =, 3.5Y =,线性回归方程ˆˆˆybx a =+所表示的直线必经过的点(4.5,3.5) ……4分 (2)4166.5i ii X Y ==∑ 4222221345686ii X==+++=∑,又 4.5X = , 3.5Y =所以266.54 4.5 3.566.563ˆ0.7864 4.58681b-⨯⨯-===-⨯- ;ˆˆ 3.50.7 4.50.35aY bX =-=-⨯= 所求的回归方程为: 0.70.35y x =+ ……8分35.70035.07.01000,1000=+⨯==y x 吨,预测生产1000吨甲产品的生产能耗700.35吨 ……10分 18. （本小题满分12分）【答案】(1)月收入在[3 000,3 500)的频率为0.000 3×(3 500－3 000)＝0.15. ……2分 (2)0.000 2×(1 500－1 000)＝0.1， 0．000 4×(2 000－1 500)＝0.2， 0．000 5×(2 500－2 000)＝0.25， 0．1＋0.2＋0.25＝0.55>0.5， 所以，样本数据的中位数为2 000＋0.50.10.20.0005-+＝2 000＋400＝2 400(元)．……7分(3)居民月收入在[2 500,3 000)的频率为0.000 5×(3 000－2 500)＝0.25，所以10 000人中月收入在[2 500,3 000)的人数为0.25×10 000＝2 500(人)，再从10 000人用分层抽样方法抽出100人，则月收入在[2 500，3 000)的这段应抽取100×250010000＝25(人)． ……12分 19. （本小题满分12分）【答案】解： (1)因为x ＞0，所以x ＋4x≥4，所以y ＝2－⎝ ⎛⎭⎪⎫x ＋4x ≤2－4＝－2，t所以当且仅当x ＝4x(x ＞0)，即x ＝2时，y max ＝－2. ……4分 (2)因为x ＞2，所以x －2＞0，所以y ＝x ＋1x －2＝x －2＋1x －2＋2≥2（x －2）⎝ ⎛⎭⎪⎫1x －2＋2＝4.所以当且仅当x －2＝1x －2(x ＞2)，即x ＝3时，y min ＝4. ……8分(3)因为0＜x ＜12，所以1－2x ＞0，所以y ＝14×2x ·(1－2x)≤14⎝ ⎛⎭⎪⎫2x ＋1－2x 22＝116，所以当且仅当2x ＝1－2x ⎝⎛⎭⎪⎫0＜x ＜12，即x ＝14时，y max ＝116. ……12分20. （本小题满分12分）【答案】(1)由f(1)＞0，得－3＋a(6－a)＋b ＞0， 即a 2－6a ＋3－b ＜0.Δ＝(－6)2－4(3－b)＝24＋4b.①当Δ≤0，即b≤－6时，原不等式解集为∅. ……4分 ②当Δ＞0时，即b ＞－6时， 方程有两根 所以不等式解集为综上所述：b≤－6时，原不等式解集为∅； b ＞－6时，原不等式解集为……8分(2)由f(x)＞0，得－3x 2＋a(6－a)x ＋b ＞0， 即3x 2－a(6－a)x －b ＜0.因为它的解集为(－1,3)，所以－1与3是方程3x 2－a(6－a)x －b ＝0的两根，所以(6)133133a a b -⎧-+=⎪⎪⎨⎪-⨯=-⎪⎩解得:……12分21. （本小题满分12分） 【答案】（1）0x =;（2）4 解：（1）因为12,2a b ==，所以()22x xf x -=+， 方程()2f x =，即222x x -+=，亦即()222210x x -⨯+=所以()2210x -=，于是21x =，解得0x = ……6分（2）由条件知2222(2)22(22)2[()]2x x x x f x f x --=+=+-=-因为()()24f x m f x ⎡⎤+⎣⎦≤对于x R ∈恒成立而()()()()2444f x f x f x f x ⎡⎤+⎣⎦=+≥=，且()()20440f f ⎡⎤+⎣⎦= 所以4m ≤，故实数m 的最大值为4 ……12分 22. （本小题满分12分） 【答案】解：（1）因为14>，所以)(x f 在]4,161[上，单调递增，所以=A )]4(),161([f f ]1,2[-=，又由)(2)21(3R a x a x ∈>+可得：x a x 22)3(>+-即：x a x >--3，所以4ax -<，所以)4,(a B --∞=， 又A B B = 所以可得：B A ⊆，所以14>-a，所以4-<a 即实数a的取值范围为)4,(--∞. ……6分（2）因为015≥+-x x ,所以有015≤+-x x ,所以15x -<≤,所以]5,1(-=C , 对于集合C m x m x D ⊆-<≤+=}121|{有:①当121-≥+m m 时,即20≤<m 时∅=D ,满足C D ⊆. ②当121-<+m m 时,即2>m 时∅≠D ,所以有:⎩⎨⎧≤-->+51211m m 32≤<-⇒m ,又因为2>m ,所以32≤<⇒m 综上：由①②可得：实数m 的取值范围为]3,0(. ……12分。

16周文科练 2017.12.11使用 命题 汪一峰 1．数列{}n a 中，已知对任意正整数n ，有123.....21nn a a a a ++++=-，则22212......n a a a +++=（ ）A. ()221n - B.()1413n - C. ()1213n - D. 41n - 2．已知等差数列中，有，且该数列的前项和有最大值，则使得成立的的最大值为( ) A. 11 B. 19 C. 20 D. 213．下列命题：①函数f （x ）＝sin 2x 一cos 2x 的最小正周期是π；②在等比数列〔n a ｝中，若151,4a a ==，则a 3＝士2； ③设函数f （x ）＝()11x mm x +≠+，若21t f t -⎛⎫ ⎪⎝⎭有意义，则0t ≠ ④平面四边形ABCD 中， ()0,?0AB CD AB AD AC +=-=，则四边形ABCD 是 菱形． 其中所有的真命题是：( ) A. ①②④ B. ①④ C. ③④ D.4．已知各项均为正数的等比数列{}n a 的公比为2864,16,24q a a a a =-=，则q =__________. 5．已知等差数列{}n a ， {}n b 前n 项和分别为n S 和n T ，若2113n n S n T n -=+，则1591326812a a a ab b b b ++++++=__________．6．已知数列{}n a 的前n 项和n S 满足231n n S a =-. （1）求数列{}n a 的通项公式；（2）求数列21n n a ⎧⎫-⎨⎬⎩⎭的前n 项和n T .7．已知等差数列{}n a 前n 项和n S ，等比数列{}n b 前n 项和为n T ， 11a =， 11b =，224a b +=.（1）若337a b +=，求数列{}n b 的通项公式； （2）若1313T =，求5S8．已知25,a a ,是方程212270x x -+=的两根，数列{}n a 是公差为正的等差数列，数列{}n b 的前n 项和为n T ，且112n n T b =-.（n ∈N *） (Ⅰ)求数列{}n a ， {}n b 的通项公式； (Ⅱ)记n c =n a n b ，求数列{}n c 的前n 项和n s .参考答案【解析】∵123.....21n n a a a a ++++=- ∴()11231.....212n n a a a a n --++++=-≥∴12n n a -=（2n ≥）当11,1n a ==也适合12n n a -=，故()1*2n n a n N -=∈ 所以{}2na 是以1为首项，4为公比的等比数列，所以()22212141 (41143)n nn a a a -+++==--，故选B.【解析】为等差数列,有最大值，则，，又，说明，， ，则 ， ，，则为最小正值.选B.【解析】①函数()22sin cos cos2f x x x x =-=-，则函数的周期22T ππ==，故①正确；②在等比数列{}n a 中，若151,4a a ==，则23154a a a ==，则32a =±，又22130a a a => ，13,a a 同号， 32a =-不合题意，故②不正确；③设函数()()11x mf x m x +=≠+，则函数的定义域为{}|1x x ≠-，若21t f t -⎛⎫⎪⎝⎭有意义，则211{ 0t t t -≠-≠，即1{ 30t t ≠≠，则0t ≠且13t ≠，故③错误；④平面四边形ABCD 中， 0AB CD +=，则AB CD DC =-=，则四边形ABCD 为平行四边形，()0,0AB AD AC DB AC -⋅=∴⋅=，则四边形ABCD 的对角线垂直，则四边形ABCD 是菱形，故④正确，故选B. 4．2【解析】很明显数列的公比为正数，由题意可得： 2285516,4a a a a ==∴=，则： 564528244a a a a q q q q-=-=-=， 整理可得： 220q q --=， 结合0q >可得： 2q =.5．1516【解析】1591311377268121137744a a a a a a a a b b b b b b b b ++++===++++ 1131311313213111513316a a S b b T +⨯-====++，故答案为15166．（1）13n n a -=；（2）1133n n -+- 【解析】（1）当1n =时， 11231S a =-，得11a =，当2n ≥时， 11231n n S a --=-，将231n n S a =-与1231n n S a -=-左右相减得1233n n n a a a -=-，即13n n a a -=，又因为11a =，所以{}n a 是以1为首项，3为公比的等比数列，所以13n n a -=. （2）由（1）得121213n n n n a ---=，∴122135232113333n n n n n T ----=+++++，① 3252321333333n n n n n T ----=+++++，②，②-①得22223233nT =+++++2122133n n n ----= 1111213321313n n n ----+⨯-- 12263n n -+=-，∴1133n n n T -+=-. 7．(1) 12n n b -= (2) 当4q =-时， 7d =， 575S =；当3q =时， 0d =，试题解析：设等差数列{}n a 公差为d ，等比数列{}n b 公比为()0q q ≠有()14d q ++=，即3d q +=.（1）∵()2127d q ++=，结合3d q +=得2q =，∴12n n b -=.（2）∵23113T q q =++=，解得4q =-或3， 当4q =-时， 7d =，此时554517752S ⨯=⨯+⨯=； 当3q =时， 0d =，此时5155S a ==.8．（1）()*21n a n n N =-∈， ()*23n n b n N =∈（2）2223n n n S +=-试题解析：(1)由252512,27a a a a +=⋅=.且0d >得253,9a a ==，()5212,1,21*3n a a d a a n n N -===∴=-∈ 在112n n T b =-中,令1n =得123b = 当2n ≥时, 112n n T b =-， 11112n n T b --=-两式相减得11122n n n b b b -=-， ()1123n n b n b -=≥ ∴()1212*333n n nb n N -⎛⎫==∈ ⎪⎝⎭. (2) ()2422133n n nn c n -=-⋅= ∴231352123333n nn S -⎛⎫=++++⎪⎝⎭， 234113523212333333n n n S n n +--⎛⎫=+++++ ⎪⎝⎭， ∴234121111121223333333n n n n S +⎡⎤-⎛⎫=+++++- ⎪⎢⎥⎝⎭⎣⎦11112112193213313n n n -+⎡⎤⎛⎫⨯- ⎪⎢⎥-⎝⎭⎢⎥=+-⎢⎥-⎢⎥⎣⎦11111214442333333n n n n n ++-+⎛⎫=+--=- ⎪⎝⎭∴ 2223n nn S +=-。

横峰中学2017-2018学年度下学期第15周周练高二数学（文零）试卷1.若0a b >>，0c d <<，则一定有（ ）A ．a b d c >B ．a b d c <C ．a b c d >D ． a b c d< 2．设OA →＝(1，－2)，OB →＝(a ，－1)，OC →＝(－b,0)(a >0，b >0，O 为坐标原点)，若A ，B ，C 三点共线，则2a ＋1b的最小值是( ) A ．4 B. 92C ．8D ．9 3. 已知,x y 满足约束条件10230x y x y --≤⎧⎨--≥⎩，当目标函数(0,0)z ax by a b =+>>在该约束条件下取到最小值22a b +的最小值为（ ）4.若平面区域30,230,230x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是（ ）5．若实数a ，b 满足1a ＋2b ＝ab ，则ab 的最小值为( ) A. 2 B ．2 C ．2 2 D ．46．已知O 为坐标原点，A (1,2)，点P 的坐标(x ，y )满足约束条件⎩⎪⎨⎪⎧ x ＋|y |≤1，x ≥0，则z ＝OA →·OP→的最大值为( )A ．－2B ．－1C ．1D ．27．已知x ，y 满足⎩⎪⎨⎪⎧ x 2＋y 2≤1，x ＋y ≤1，y ≥0，则z ＝x －y 的取值范围是( )A ．[－2，1]B ．[－1,1]C ．[－2，2]D ．[－1，2]8.若b a ab b a +=+则）（,log 43log 24的最小值是( )A. 326+B.327+C.346+D.347+9.设x ，y 满足约束条件,1,x y a x y +≥⎧⎨-≤-⎩且z x ay =+的最小值为7，则a =（A ）-5 （B ）3 （C ）-5或3 （D ）5或-310.已知圆()()22:1C x a y b -+-=，设平面区域70,30,0x y x y y +-≤⎧⎪Ω=-+≥⎨⎪≥⎩，若圆心C ∈Ω,且圆C与x 轴相切，则22a b +的最大值为 （ ）.5.29.37.49A B C D 11.设实数x ，y 满足2102146x y x y x y +≤⎧⎪+≤⎨⎪+≥⎩，则xy 的最大值为( )(A )252 (B )492(C )12 (D )14 1．已知点(－3，－1)和点(4，－6)在直线3x －2y －a ＝0的两侧，则a 的取值范围为________. 2．已知0<x <1，则1x ＋11－x的最小值是________。

横峰中学 2017-2018 学年度放学期高二数学第八周练试卷（文科）一、选择题 ( 本大题共 5 小题，每题 5 分，共 50 分)1．以下事件是随机事件的是 ()①同种电荷，相互排挤；②明日是晴日；③自由着落的物体作匀速直线运动；④函数 y ＝ a x ( a ＞ 0 且 a ≠ 1) 在定义域上是减函数．A ．①③B．①④C．②④ D ．③④2．气象台预告“本市明日降雨概率是80%”, 以下理解正确的选项是 ( ) A ．本市明日将有 80%的地域降雨 B ．本市明日将有 80%的时间降雨 C ．明日出行不带雨具一定淋雨D．明日出行不带雨具淋雨的可能性很大 3 某程序框图如下图，该程序运转后输出的 k 的值是（ ）A ． 4B． 5C． 6 D． 7 4．从一批羽毛球中任取一个，假如其质量小于 4.8 g的概率是 0. 3 ，质量不小于 4.85 g 的概率是 0.32 ，那么质量在 [4.8, 4.85) 范围内的概率是 ()A ． 0.62B． 0.38 C ． 0.70 D ． 0.685．小敏翻开计算机时，忘掉了开机密码的前两位，只记得第一位 是 A,B,C,D,E 中的一个字母，第二位是 1,2,3, 中的一个数字，则小敏输入一次密码就可以成功开机的概率是( ) 3 题8B.1 1 D. 1A.C.15301586. 从某校高二年级的全部学生中，随机抽取20 人，测得他们的身高分别为： ( 单位： cm)162,148,154,165,168,172,175,162,171,170,150,151,152,160,163,175,164,179,149,172.依据样本频次散布预计整体散布的原理，在该校高二年级任抽一名同学身高在155.5 cm ～ 170.5 cm 之间的概率为 ________． ( 用分数表示 )7. 甲乙两人玩猜数字游戏， 先由甲心中任想一个数字记为 a ，再由乙猜甲方才想的数字，把乙猜的数字记为b ，且 a 、 b ∈ {0,1,2 ， ， 9} ．若 | － | ≤ 1，则称甲乙“心有灵犀” ．现随意a b找两人玩这个游戏，则二人“心有灵犀”的概率为________ ．8. 右侧的程序框图， 能判断随意输入的数 x 的奇偶性， 此中判断框内的条件是 _____．9.( 本小题满分 20 分 ) 某商场举行购物抽奖促销活动，规定每位顾客从装有编号为 0,1,2,3 四个同样小球的抽奖箱中， 每次拿出一球， 记下编号后放回，连续取两次，若拿出的两个小球号码相加之和等于6，则中一等奖，等于 5 中二等奖，等于 4 或 3 中三等奖．(1)求中三等奖的概率；(2)求中奖的概率．。