高中数学知识点题库 058直线与平面所成的角

直线与平面所成的角1、直线和平面所成的角，应分三种情况：（1）直线与平面斜交时，直线和平面所成的角是指此直线和它在平面上的射影所成的锐角；（2）直线和平面垂直时，直线和平面所成的角的大小为90°；（3）直线和平面平行或在平面内时，直线和平面所成的角的大小为0°．显然，斜线和平面所成角的范围是（0，）；直线和平面所成的角的范围为[0，]．2、一条直线和一个平面斜交，它们所成的角的度量问题（空间问题）是通过斜线在平面内的射影转化为两条相交直线的度量问题（平面问题）来解决的．具体的解题步骤与求异面直线所成的角类似，有如下的环节：（1）作﹣﹣作出斜线与射影所成的角；（2）证﹣﹣论证所作（或找到的）角就是要求的角；（3）算﹣﹣常用解三角形的方法（通常是解由垂线段、斜线段、斜线段的射影所组成的直角三角形）求出角．（4）答﹣﹣回答求解问题．在求直线和平面所成的角时，垂线段是其中最重要的元素，它可起到联系各线段的纽带的作用．在直线与平面所成的角的定义中体现等价转化和分类与整合的数学思想．3、斜线和平面所成角的最小性：斜线和平面所成的角是用两条相交直线所成的锐角来定义的，其中一条直线就是斜线本身，另一条直线是斜线在平面上的射影．在平面内经过斜足的直线有无数条，它们和斜线都组成相交的两条直线，为什么选中射影和斜线这两条相交直线，用它们所成的锐角来定义斜线和平面所成的角呢？原因是斜线和平面内经过斜足的直线所成的一切角中，它是最小的角．对于已知的斜线来说这个角是唯一确定的，它的大小反映了斜线关于平面的“倾斜程度”．根据线面所成的角的定义，有结论：斜线和平面所成的角，是这条斜线和这个平面内的直线所成的一切角中最小的角．用空间向量直线与平面所成角的求法：（1）传统求法：可通过已知条件，在斜线上取一点作该平面的垂线，找出该斜线在平面内的射影，通过解直角三角形求得．（2）向量求法：设直线l的方向向量为，平面的法向量为，直线与平面所成的角为θ，与的夹角为φ，则有sinθ＝|cos φ|＝．。

直线与平面所成角方法归纳和典例分析直线和平面所成的角是数学中的一个重要概念。

在几何学中，我们经常使用直线和平面的交点来确定它们所成的角度。

本文将从方法归纳和典例分析两个方面介绍直线与平面所成角。

一、方法归纳要理解直线与平面所成角的概念，我们首先需要了解直线和平面的基本概念。

直线：直线是一条无限延伸的线段。

它只有一个维度，即长度，不具备宽度和厚度。

平面：平面是一个无限的二维表面，有长度和宽度，但没有厚度。

在几何中，直线和平面可以相交或平行，这取决于它们的位置关系。

当直线与平面相交时，它们形成一个角。

这个角的大小可以通过以下方法归纳：1.直线与平面的交点处的两条线段构成的角叫做直线与平面所成的角。

这个角的大小可以用直线与平面交点的切线来表示。

2.直线与平面的交点处的两条线段构成的角叫做直线与平面所成的角。

这个角的大小可以通过测量直线和平面之间的夹角来确定。

二、典例分析为了更好地理解直线与平面所成角的概念，我们来看一些典型的例子。

1.垂直线与平面的角当一条直线与平面垂直相交时，直线与平面所成的角为90度。

例如，一根垂直立在平地上的杆与地面所成的角度就是90度。

2.平行线与平面的角当一条直线与平面平行时，直线与平面所成的角为0度。

例如，一条水平的直线与铺在地面上的平地相交，它与地面所成的角就是0度。

3.斜线与平面的角当一条直线与平面斜交时，直线与平面所成的角大于0度且小于90度。

具体角度的大小取决于直线和平面的相对位置。

例如，一个斜靠在地面上的直线与地面所成的角度就是小于90度的一个锐角。

总结：1.直线与平面交点处的两条线段构成的角叫做直线与平面所成的角。

这个角的大小可以用直线与平面交点的切线来表示。

2.直线与平面交点处的两条线段构成的角叫做直线与平面所成的角。

这个角的大小可以通过测量直线和平面之间的夹角来确定。

典型例子表明，直线与平面所成角的大小与直线和平面的位置关系紧密相关。

当直线与平面垂直相交时，所成角度为90度；当直线与平面平行相交时，所成角度为0度；当直线与平面斜交时，所成角为大于0度且小于90度的一个锐角。

直线与平面所成角的求法直线与平面所成角的求法直线与平面所成角是几何学中的一个重要概念，它是指一条直线与一个平面之间的夹角。

在实际应用中，我们经常需要求解直线与平面所成角的大小，因此掌握直线与平面所成角的求法是非常必要的。

求解直线与平面所成角的方法有多种，下面我们将介绍其中的两种常用方法。

方法一：余弦定理余弦定理是三角函数中的一个重要定理，它可以用来求解任意三角形的边长和角度。

对于直线与平面所成角的求解，我们可以利用余弦定理来求解。

假设直线L与平面P所成角为θ，直线L的方向向量为a，平面P的法向量为n，则有：cosθ = (a·n) / (|a|·|n|)其中，a·n表示向量a和向量n的点积，|a|和|n|分别表示向量a和向量n的模长。

通过上述公式，我们可以求解出直线与平面所成角的大小。

需要注意的是，余弦定理只适用于三维空间中的直线与平面所成角的求解，对于二维空间中的直线与平面所成角的求解，需要使用其他方法。

方法二：向量法向量法是求解直线与平面所成角的另一种常用方法。

假设直线L与平面P所成角为θ，直线L的方向向量为a，平面P的法向量为n，则有：sinθ = |a×n| / (|a|·|n|)其中，a×n表示向量a和向量n的叉积，|a|和|n|分别表示向量a和向量n的模长。

通过上述公式，我们同样可以求解出直线与平面所成角的大小。

需要注意的是，向量法同样只适用于三维空间中的直线与平面所成角的求解，对于二维空间中的直线与平面所成角的求解，需要使用其他方法。

总结直线与平面所成角的求解方法有多种，其中余弦定理和向量法是两种常用的方法。

在实际应用中，我们可以根据具体情况选择合适的方法来求解直线与平面所成角的大小。

掌握直线与平面所成角的求解方法，可以帮助我们更好地理解几何学中的相关概念，并在实际应用中得到更好的应用。

直线和平面所成的角与二面角知识要点1．直线与平面所成角的范围若θ表示直线与平面所成的角，则0°≤θ≤90°。

2．公式cosθ=cosθ1·cosθ2。

斜线AB与平面α所成的角为θ1，A为斜足，AC在α内，且与AB的射影成θ2角，∠BAC=θ, 则有cosθ=cosθ1·cosθ2。

3．公式。

如图所示，在二面角α-l-β中，A∈平面β，B∈平面α，AD⊥l于D，BC⊥l于C，AD=m,BC=n, CD=d, AB=l, 二面角α-l-β的平面角为φ，则有：。

4．公式S'=Scosθ。

如果平面多边形所在平面与平面所成角为，这个平面多边形及其在平面内的射影的面积分别为S、S'，那么S'=Scosθ。

5. 向量知识(1)；(2)(3)a·b=|a|·|b|cosθ (其中θ是a与b的夹角)(4)若a=(x1,y1,z1), b=(x2,y2,z2), 则：a·b=x1x2+y1y2+z1z2。

典型题目例1．如图，在棱长为a的正方体OABC-O'A'B'C'中，E、F分别是棱AB、BC上的动点，且AE=BF。

(1)求证：A'F⊥C'E；(2)当三棱锥B'-BEF的体积取得最大值时，求二面角B'-EF'B的大小。

（结果用反三角函数表示）。

(1)证明：如图所示，以O为原点建立空间直角坐标系，设AE=BF=x, 则A'(a,0,a), F(a-x,a,0), C'(0,a,a,), E(a,x,0)。

∵，∴ A'F⊥C'E。

(2)解：记BF=x, BE=y, 则x+y=a, 三棱锥B'-BEF的体积，当且仅当，时，取得最大值。

过B作BD⊥EF交EF于D，连B'D,B'D⊥EF,∴∠B'DB是二面角B'-EF-B的平面角。

空间中直线与平面所成角的范围一、引言空间中直线与平面所成角的研究是几何学中的重要内容，涉及到许多实际问题的求解。

本文将对空间中直线与平面所成角的范围进行详细探讨，以期提高大家对几何知识的理解和应用能力。

二、空间中直线与平面所成角的定义与性质1.定义空间中直线与平面所成角是指直线与平面内任意一条直线所成的最小角。

这个角度可以用直线与平面内直线之间的夹角来表示。

2.性质（1）直线与平面平行时，所成角为0°。

（2）直线与平面垂直时，所成角为90°。

（3）直线与平面斜交时，所成角的范围为0°～90°。

三、空间中直线与平面所成角的变化范围1.直线与平面平行时，所成角为0°。

2.直线与平面垂直时，所成角为90°。

3.直线与平面斜交时，所成角的范围为0°～90°。

四、应用与实例1.几何问题求解在几何问题中，了解空间中直线与平面所成角的范围有助于快速判断线面关系，进而解决问题。

例如，在解决立体图形的表面积和体积问题时，可以通过计算直线与平面所成角来确定几何体的形状。

2.工程实践中的应用在工程实践中，空间中直线与平面所成角的应用也十分广泛。

例如，建筑设计师在设计建筑物的空间结构时，需要了解直线与平面所成角的大小，以确保建筑物的稳定性。

此外，机械工程师在设计机械零件时，也需要考虑直线与平面所成角的影响，以保证零件的装配精度。

五、总结与拓展本文对空间中直线与平面所成角的范围进行了详细探讨，从定义、性质、变化范围等方面进行了分析。

通过对这一知识点的掌握，大家可以在几何问题求解和工程实践中发挥重要作用。

此外，对于空间几何中的其他知识点，如直线与直线、直线与曲线、曲线与曲线之间的角度问题，也可以采用类似的方法进行研究和探讨。

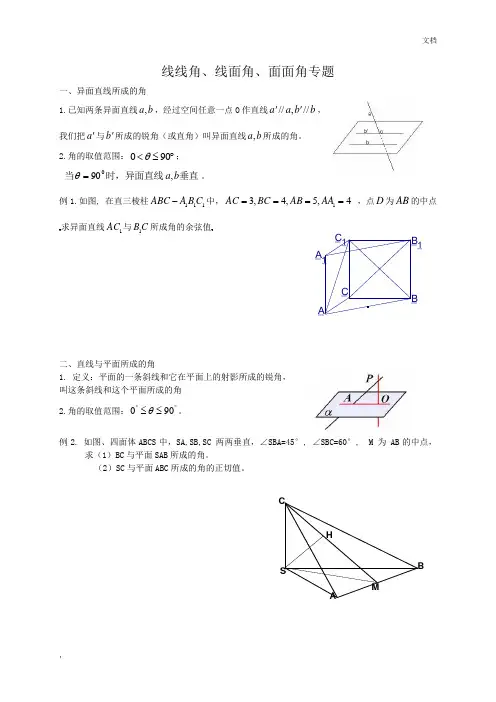
线线角、线面角、面面角专题一、异面直线所成的角1.已知两条异面直线,a b ，经过空间任意一点O 作直线//,//a a b b ''，我们把a '与b '所成的锐角（或直角）叫异面直线,a b 所成的角。

2.角的取值范围：090θ<≤︒；垂直时，异面直线当b a ,900=θ。

例1.如图, 在直三棱柱111ABC A B C -中，13,4,5,4AC BC AB AA ==== ，点D 为AB 的中点求异面直线1AC 与1B C 所成角的余弦值二、直线与平面所成的角1. 定义：平面的一条斜线和它在平面上的射影所成的锐角， 叫这条斜线和这个平面所成的角2.角的取值范围：︒︒≤≤900θ。

例2. 如图、四面体ABCS 中，SA,SB,SC 两两垂直，∠SBA=45°, ∠SBC=60°, M 为 AB 的中点，求（1）BC 与平面SAB 所成的角。

（2）SC 与平面ABC 所成的角的正切值。

BMH S CA _ C _1_1_ A _1A_ C一、 二面角：1. 从一条直线出发的两个半平面所组成的图形叫做二面角。

这条直线叫做二面角的棱，这两个半平面叫做二面角的面。

2. 二面角的取值范围：︒︒≤≤1800θ 两个平面垂直：直二面角。

3.作二面角的平面角的常用方法有六种：1.定义法 ：在棱上取一点O ，然后在两个平面内分别作过棱上O 点的垂线。

2.三垂线定理法：先找到一个平面的垂线，再过垂足作棱的垂线，连结两个垂足即得二面角的平面角。

3.向量法：分别作出两个半平面的法向量，由向量夹角公式求得。

二面角就是该夹角或其补角。

二面角一般都是在两个平面的相交线上，取恰当的点，经常是端点和中点。

例3.如图，E 为正方体ABCD －A 1B 1C 1D 1的棱CC 1的中点，求 (1)二面角111D C A D --所成的角的余弦值 (2)平面AB 1E 和底面C C BB 11所成锐角的正切值.A 1D 1B 1C 1 EDBCA巩固练习1.若直线a 不平行于平面α，则下列结论成立的是（ ）A.α内所有的直线都与a 异面；B.α内不存在与a 平行的直线；C.α内所有的直线都与a 相交；D.直线a 与平面α有公共点.2.空间四边形ABCD 中，若AB AD AC CB CD BD =====，则AD 与BC 所成角为（ ）A.030B.045C.060D.090 3．正方体ABCD-A 1B 1C 1D 1中，与对角线AC 1异面的棱有（ ）条A.3B.4C.6D.84.如图长方体中，AB=AD=23，CC 1=2，则二面角C 1—BD —C 的大小为（ ） A.300B.450C.600D.9005．如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ，点E 、F 分别是AB 、BD 的中点．求证：(1)直线EF ∥面ACD .(2)平面EFC ⊥平面BCD .6．如图，DC ⊥平面ABC ，EB ∥DC ，AC ＝BC ＝EB ＝2DC ＝2，∠ACB ＝120°，P ，Q 分别为AE ，AB 的中点．(1)证明：PQ ∥平面ACD ；(2)求AD 与平面ABE 所成角的正弦值．ABC D A 1B 1C 1D 17.如图，已知四棱锥S－ABCD的底面ABCD是正方形，SA⊥底面ABCD，设SA＝4，AB＝2，求点A到平面SBD的距离；。

专题18直线与平面所成的角空间直线与平面所成的角,在复杂空间图形中隐藏得比较深,不易发现或作出,再加上参数渗透其中,导致思维痛点产生.空间线面角计算问题是高考数学命题中的必选项,必须寻找排除卡壳点的有效途径.补形后找到重要位置关系以利于寻找到“垂足”或“射影”.平面化可以将复杂的线面位置关系转化为线线位置关系,使问题简单化.没有掌握此技术,或不熟悉此技术都将导致思维障碍,形成痛点.一、平面化挖掘隐藏的线面角问题1:如图1,在直三棱柱ABC−A1B1C1中,底面是等腰直角三角形,∠ACB=90∘.侧棱AA1=2,D,E分别是CC1,A1B的中点,点E在平面ABD上的射影是ΔABD的重心G,求A1B与平面ABD所成角的正弦值.【解析】卡壳点:找不到隐藏的“垂足”.应对策略:面对复杂的空间图形,要䓊于把其中重要的平面图形拿出来分析.问题解答:将这个几何体补上关于平面ABB1A1的对称图形,即直三棱柱ABF−A1B1F1,就得到正四棱柱AFBC−A1F1B1C1,如图2ΔABD的重心G与点E都在正四棱柱AFBC−A1F1B1C1的对角面CFF1C1内,如图3. 记AB的中点为O,由OD=3GO,EO2=GO⋅DO,得EO=√3GO.又DC=EO=1,所以DO=√3EO=√3,GO=√33,CO=BO=√2,GE=EO⋅DEDO=1×√2√3=√63,EB=C1E=DO=√3.所以sin∠EBG=EGEB =√63⋅1√3=√23,故A1B与平面ABD所成角的正弦值为√23,【反思】(1)将三棱柱补形得到四棱柱,把最主要的数量关系线段所在的平面拿出来,这样便于直观地再现线段间的数量关系,这一过程就像电视节目中的特写镜头,突出重点.（2）通过补形使线面垂线的“垂足”易找、易求，这是一个智慧点.二、巧妙寻找直线在平面上射影问题2:如图4,在平行四边形ABCD中,AB=2BC,∠ABC=2π3,E为线段AB的中点,将ΔADE沿直线DE翻折成ΔA1DE,使平面A1DE⟂平面BCD,F为线段A1C的中点.设M为线段DE的中点,求直线FM与平面A1DE所成角的余弦值.【解析】卡壳点:不会在复杂图形中寻找直线在平面上的射影.应对策略:在FM上找一点,从该点向平面A1DE引垂线,或找FM在平面A1DE上的射影.问题解答:解法1将点F投影到平面A1DE上,其射影为点N,可证点N在A1E上. 因为CE⟂DE,CE⟂A1M,所以CE⟂平面A1DE.又FN//CE,N为A1E的中点,所以∠FMN为直线FM与平面A1DE所成的角.设BC=1,所以MN=12,FN=√32,FM=1,cos∠FMN=12.解法2 将直线FM投影到平面A1DE上,其射影是MN,同解法1,∠FMN为直线FM 与平面A1DE所成的角.设BC=1,所以MN=12,FN=√32,FM=1,cos∠FMN=12.【反思】(1)求直线与平面所成角的关键是寻找平面的垂线、找斜线在平面内的射影,因此投影法就有了用武之地,要特别说明的是此题最容易出错的地方就是认为点F 在平面A 1DE 上的投影在A 1M 上.(2)由点、线、图形的投影来寻找空间图形问题的突破口,一是需要基本的空间想象能力;二是可以训练或提升学生的空间想象力;三是要能将寻找到辅助线或图形与给定的问题有机结合,突破几何量的计算关，而这又涉及平面几何的基本功.三、平面化寻找线面垂直关系问题3:如图5,在单位正方体ABCD −A 1B 1C 1D 1中,E,F 分别是BC,CD 的中点,平面A 1EF 交BB 1于点M ,交DD 1于点N .(I)画出几何体A 1MEFN −ABEFD 的直观图与三视图;(II)设AC 的中点为O ,在CC 1上存在一点G ,使CG ⃗⃗⃗⃗⃗ =λCC 1⃗⃗⃗⃗⃗⃗⃗ 且OG⟂平面A 1EF ,求λ;(III)求A 1C 与平面A 1EF 所成角的正弦值.【解析】卡壳点:一是画不出截面图;二是不会计算.应对策略:利用平面的性质切割正方体,要熟悉“三公理”“三推论”及其实际应用,会用一个平面切割正方体,找截面形状.问题解答:(I)几何体的直观图如图6,三视图如图7.(II)解法1由已知在CC 1上存在一点G ,使CG ⃗⃗⃗⃗⃗ =λCC 1⃗⃗⃗⃗⃗⃗⃗ 且OG⟂平面A 1EF ,如图8,取OC 的中点H ,CG 的中点I ,则ΔA 1HI 为直角三角形.在Rt ΔHCI 中,HI =√18+λ24.在Rt ΔA 1AH 中,A 1H =√344.在Rt ΔA 1C 1I 中,A 1I =√2+(1−λ2)2,于是在Rt ΔA 1HI 中,由A 1I 2=A 1H 2+HI 2得λ=0.75.解法2选择A 为坐标原点,AB,AD,AA 1所在直线为x 轴、y 轴、z 轴,则E (1,0.5,0),F (0.5,1,0),A 1(0,0,1),G (1,1,λ),O (0.5,0.5,0),从而OG ⃗⃗⃗⃗⃗ =(0.5,0.5,λ),A 1E ⃗⃗⃗⃗⃗⃗⃗ =(1,0.5,−1).由OG ⃗⃗⃗⃗⃗ ⟂A 1E ⃗⃗⃗⃗⃗⃗⃗ 得0.5+0.25−λ=0,解得λ=0.75.当λ=0.75时,OG ⃗⃗⃗⃗⃗ ⟂A 1F ⃗⃗⃗⃗⃗⃗⃗ ,所以OG⟂平面A 1EF .(III)解法1因为A 1C 与HI 均在平面A 1ACC 1上,设它们相交于点J ,则A 1J 在平面A 1EF 上射影为A 1H ,从而∠CA 1H 为直线A 1C 与平面A 1EF 所成的角.在ΔCA 1H 中,cos ∠CA 1H =3+3416−2162×√344×√3=100102,sin 2∠CA 1H =1−5051=151,sin ∠CA 1H =√5151 解法2由(II)知,平面A 1EF 的一个法向量是OG⃗⃗⃗⃗⃗ =(0.5,0.5,0.75),又A 1C ⃗⃗⃗⃗⃗⃗⃗ =(1,1,−1),所以A 1C 与平面A 1EF 所成角的正弦值为sin ∠CA 1H =OG ⃗⃗⃗⃗⃗⃗ ⋅A 1C⃗⃗⃗⃗⃗⃗⃗⃗ |OG ⃗⃗⃗⃗⃗⃗ ||A 1C ⃗⃗⃗⃗⃗⃗⃗⃗ |=√5151. 【反思】(1)正方体的截面将正方体分割成两个几何体,研究它们的直观图与三视图,这是检测空间想象能力的极好素材,看似简单的图形中蕴藏着学生极易犯错的种种情况,如不能准确画出直观图,三视图.（2）虽然是在简单的正方体中,但计算直线与平面所成的角时,射影难找.四、平面图形翻折中寻找线面角问题4:如图9,四边形ABCD 为正方形,E,F 分别为AD,BC 的中点,以DF 为折痕把ΔDFC 折起,使点C 到达点P 的位置,且PF⟂BF .(I)证明:平面PEF⟂平面ABFD ;(II)求DP 与平面ABFD 所成角的正弦值.【解析】卡壳点:空间模型比较泽楚,计算中出现错误导致失败.应对策略:平面图形翻折后,要看哪些线段位置关系变了,度量关系有哪些变化. 问题解答:(I)由已知可得BF⟂PF,BF⟂EF ,所以BF⟂平面PEF .又BF ⊂平面ABFD ,所以平面PEF⟂平面ABFD .(II)作PH⟂EF ,垂足为H .由(I)得PH⟂平面ABFD .以H 为坐标原点,HF ⃗⃗⃗⃗⃗ 的方向为y 轴正方向,|BF⃗⃗⃗⃗⃗ |为单位长度,建立如图10所示的空间直角坐标系H −xyz .由(I)可得,DE⟂PE ,又DP =2,DE =1,所以PE =√3. 又PF =1,EF =2,故PE⟂PF ,可得PH =√32,EH =32. 从而得H (0,0,0),P (0,0,√32),D (−1,−32,0),DP ⃗⃗⃗⃗⃗ =(1,32,√32),易知HP ⃗⃗⃗⃗⃗⃗ =(0,0,√32)为平面ABFD 的法向量.设DP 与平面ABFD 所成角为θ,则sinθ=|HP ⃗⃗⃗⃗⃗⃗ ⋅DP ⃗⃗⃗⃗⃗⃗ |HP ⃗⃗⃗⃗⃗⃗ ||DP ⃗⃗⃗⃗⃗⃗ ||=34√3=√34. 所以DP 与平面ABFD 所成角的正弦值为√34.【反思】(1)用传统的逻辑推理方法求DP 与平面ABFD 所成角的正弦值,只要求出PH 的值,设正方形氻长为2,则PF =1,EF =2,PE =√22−1=√3,PH =√32,PD =2,sinθ=sin ∠PDH =PH PD =√34. （2）第(I)问为寻找射影做了铺垫,只需要从点P 向棱EF 引垂线即可,给定的图形也非常直观,所以通过传统逻辑推理方法求直线与平面所成的角更容易些.（3）此题可以用硬纸折叠构造模型,增加空间直观,观察线面位置关系,为计算各线段长度奠定基础.五、选择最佳途径探求线面角问题5:如图11,棱雉P −ABCD 的底面是菱形,AB =2,∠DAB =π3,侧面PAB 垂直于底面ABCD ,且ΔPAB 是正三角形.PD⟂AB ,求直线PC 与平面PBD 所成角的正弦值.【解析】卡壳点:建立空间坐标系计算时失误多.应对策略:根据题设条件建立空间坐标系求解运算量较大,根据线面角概念,利用体积转化法运算量较小.问题解答:设点C 到平面PBD 的距离为ℎ,直线PC 与平面PBD 所成角为θ,则sinθ=ℎPC .已知侧面PAB 垂直于底面ABCD ,设O 为AB 中点,则PO⟂AB .所以PO⟂平面ABCD,PD =√PO 2+DO 2=√6.由PD⟂AB 得PD⟂CD,PC =√PD 2+CD 2=√10.由V C−PBD =V P−BCD ,得13S ΔPBD ℎ=13×√3×√3,故ℎ=2√155,因此sinθ=ℎPC =√65. 故直线PC 与平面PBD 所成角的正弦值为√65.【反思】(1)此题也可以建立空间坐标系,利用向量坐标法解决,立体几何解答题一般都有多种解法与思路,复习训练强化一题多解,有利于增加获胜的可能性.(2)上述求解中,体积转化法较易,运算量较少,而向量坐标法是比较麻烦的,涉及线性方程组求解,数字运算中,稍微出一点错,就会前功尽弃.(3)此题给出的直观图,必须运用逻辑推理来思考.六、提升线面所成角的运算力问题6:如图12,AC =2r 为圆的直径,B 为圆周上不与点A,C 重合的点,PA 垂直于圆所在的平面,∠PCA =45∘.(I)点B 在AC 上的投影为点D ,求证:BD⟂平面PAC ;(II)设PB 与平面PAC 所成的角为θ,求sinθ的最大值.【解析】卡壳点:不会寻找线面垂直条件;不会求复杂函数最值.应对策略:直线与平面垂直关系采取推理方式,训练空间图形中的逻辑推理能力.问题解答:(I)连接PD .解法1{PA⟂平面ABC,PA⊂平面PAC⇒{平面PAC⟂平面ABC,平面PAC∩平面ABC=AC,⇒BD⟂平面PAC.BD⟂AC解法2{PA⟂平面ABC,BD⊂平面ABC⇒{BD⟂AC,BD⟂PA,AC∩PA=A⇒BD⟂平面PAC.(II)由(I)知∠BPD为PB与平面PAC所成的角θ.设∠ACB=α,0<α<π2,则BD=2rcosαsinα.因为∠PCA=45∘,PB=√AB2+PA2=2r√1+sin2α,所以sinθ=BDPB =√1+sin2α出现根式,需化为整式,平方得sin2θ=sin2αcos2α1+sin2α(∗),函数名统一,即sin2θ=sin2α(1−sin2α)1+sin2α.换元结构简化:令sin2α=t,得sin2θ=t(1−t)1+t.令u=t(1−t)1+t,得u(1+t)=−t2+t.整理得t2+(u−1)t+u=0,由Δ=(u−1)2−4u⩾0,u2−6u+1⩾0,解得u⩽3−2√2,故sinθ⩽√2−1.【反思】引人一个角作为桥梁,建立线段间数量关系.求(∗)式最值的方法很多,且这是学生的一个运算障碍点.强化练习1.在长方体ABCD−A1B1C1D1中,已知二面角A1−BD−A的大小为π6,若空间有一条直线l与直线CC1所成的角为π4,则直线l与平面A1BD所成角的取值范围是A.[π12,7π12] B.[π12,π2] C.[π12,5π12] D.[0,π2].【解析】采用特殊化思想,考虑正方体情形,设棱长为1,线面所成角的范围是[0,π2],首先可以排除选项A;符合条件的直线不可能平行于平面A1BD,也不会垂直于平面A1BD,所以排除选项D,B,最后选择C.【反思】(1)若将此题作为解答题思考,如答图1,过点A作AO⊥BD,连接A1O,则∠AOA1为二面角A1−BD−A的平面角,所以∠AOA1=π6.把直线l平移到AM,则∠A1AM=∠MAO=π4.过点A作AP⊥A1O,则AP⊥平面A1BD,所以AM(即直线l)与平面A1BD所成的最大角为∠AMA1=∠MAO+∠MOA=π4+π6=5π12.假设∠A1AN=π4,AN与直线OP相交于点N,则AN(即直线l)与平面A1BD所成的最小角为∠ANP=∠PA1A−∠A1AN=π3−π4=π12,选择C.第1题答图1第1题答图2(2)若将此题设计为填空题,也需要按照上述思维进行求解.(3)为了清晰地挖掘直线与平面所成角的变化范围,将重要的平面拿出来分析是求解立体几何问题的一个重要手段,如答图2.2.如图,设E为长方形ABCD的边CD的中点,沿AE折叠,设AB=2,BC=1,折D叠后,BD1=√3.(I)证明:平面AD1E⟂平面ABCE;(II)求CD1与平面ABCE所成角的正弦值.,【解析】(I)如答图所示,取AE的中点G,连接D1G,BG,则AG=D1G=√22BG=√AG2+AB2−2AG⋅AB⋅cos⁡45∘=√10,2BD12=D1G2+BG2,所以BG⊥D1G.又D1G⊥AE,所以D1G⊥平面ABCE,且D1G⊂平面AD1E,所以平面AD1E⊥平面ABCE.第2题答图(II)由(I)知,D1G⊥平面ABCE,所以∠D1CG为CD1与平面ABCE所成的角,D1G=√22,CG=√CE2+GE2−2CE⋅GE⋅cos⁡135∘=√102,所以CD1=√3.故CD1与平面ABCE所成角的正弦值sin⁡∠D1CG=√66.【反思】折叠问题最重要的就是分析折叠前后线与线、线与面的位置关系变化情况.3.在长方体ABCD−A1B1C1D1中,已知二面角A1−BD−A的大小为π6.(I)若C1C,C1B1,C1D1的中点分别为R,S,T,求证:平面RST//平面A1BD;(II)若空间一直线l与直线CC1所成的角为π4,求直线l与平面A1BD所成角的取值范围.【解析】(I)已知C1C,C1B1,C1D1的中点分别为R,S,T,所以RS//A1D,RT//A1B,所以平面RST//平面A1BD.(II)如答图,过点A作AO⊥BD,连接A1O,由三垂线定理可得BD⊥A1O,则∠AOA1为二面角A1−BD−A的平面角,所以∠AOA1=π6.把直线l平移到AM,则∠A1AM=∠MAO=π4.过点A作AP⊥A1O,则AP⊥平面A1BD.第3题答图所以AM(即直线l)与平面A1BD所成的最大角为∠AMA1=∠MAO+∠MOA=π4+π6=5π12.假设∠A1AN=π4,AN与直线OP相交于点N,则AN(即直线l)与平面A1BD所成的最小角为∠ANP=∠PA1A−∠A1AN=π3−π4=π12.故直线l与平面A1BD所成角的取值范围是[π12,5π12].【反思】将直线l与平面A1BD所成角转化到平面A1AO内思考是一个智慧点.4.如图,四棱雉P−ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120∘,∠PBC=90∘.(I)求证:平面PAD⟂平面PAB;(II)求直线PC与平面ABCD所成角的正弦值.【解析】(I)证明:由题意得AD ⊥AB 且AD//BC .又BC ⊥PB ,则DA ⊥PB ,从而DA ⊥平面PAB .故平面PAD ⊥平面PAB .(II)以点A 为坐标原点,AB 所在的直线为y 轴建立空间直角坐标系,如答图所示,第4题答图则D(0,0,1),C(0,2,1),P (√32,−12,0), 可得CP⃗⃗⃗⃗⃗ =(√32,−52,−1). 平面ABCD 的单位法向量为m ⃗⃗ =(1,0,0). 设直线PC 与平面ABCD 所成所角为θ,则cos⁡(π2−θ)=m ⃗⃗ ⋅CP⃗⃗⃗⃗⃗ ∣m ⃗⃗⃗⃗⃗⃗ ||CP ⃗⃗⃗⃗⃗ ∣=√321×√34+254+1=√68. 于是sin⁡θ=√68,即直线PC 与平面ABCD 所成角的正弦值为√68. 【反思】由于空间图形中垂直关系明显,建立空间直角坐标系来求线面所成角是一个智慧点.5.如图,已知圆O 的直径AB 的长度为4,D 为线段AB 上一点,且AD =13DB,C 为圆O 上一点,且BC =√3AC .点P 在圆O 所在平面上的正投影为点D,PD =BD . (I )求证:CD⟂平面PAB ;(II)求PD 与平面PBC 所成的角的正弦值.【解析】(I)连接CO ,由3AD =DB 知,D 为AO 的中点. 又AB 为圆O 的直径,所以AC ⊥AB .由√3AC =BC 知∠CAB =60∘,所以△ACO 为等边三角形,从而CD ⊥AO . 因为点P 在圆O 所在平面上的正投影为点D ,所以PD ⊥平面ABC . 又CD ⊂平面ABC ,所以PD ⊥CD . 由PD ∩AO =D 得CD ⊥平面PAB .(II)解法1过点D 作DH ⊥平面PBC ,交平面PBC 于点H ,连接PH ,则∠DPH 即为所求的线面角.由(I)可知CD =√3,PD =DB =3,所以V P−BDC =13S △BDC ⋅PD =13⋅12DB ⋅DC ⋅PD =13×12×3×√3×3=3√32.又PB=√PD2+DB2=3√2,PC=√PD2+DC2=2√3,BC=√DB2+DC2= 2√3,所以△PBC为等腰三角形,则S△PBC=12×3√2×√12−92=3√152由V P−BDC=V D−PBC得DH=3√55,所以sin⁡∠DPH=DHPD =√55.解法2由(I)可知CD=√3,PD=DB=3.如答图所示,过点D作DE⊥CB,垂足为E,连接PE.再过点D作DF⊥PE,垂足为F.因为PD⊥平面ABC,又CB⊂平面ABC,所以PD⊥CB.第5题答图又PD∩DE=D,所以CB⊥平面PDE.又DF⊂平面PDE,所以CB⊥DE.又CB∩PE=E,所以DF⊥平面PBC. 故∠DPF为所求的线面角.在Rt△DEB中,DE=DB⋅sin⁡30∘=32,PE=√PD2+DE2=3√5 2sin⁡∠DPF=sin⁡∠DPE=DEPE =√55.【反思】解法1用体积法寻找线面角的正弦值,解法2找射影,然后求线面角的正弦值,两种思路都是常规思路,需要有良好的逻辑推理基本功.6.如图,在平面四边形PACB中,∠PAB为直角,ΔABC为等边三角形,现把ΔPAB沿着AB折起,使得ΔAPB与ΔABC垂直,且M为AB的中点.(I)求证:平面PAB⟂平面PCM;(II)若2PA=AB,求直线PB与平面PMC所成角的余弦值.【解析】(I)证明:因为平面APB⊥平面ABC且交线为AB,又∠PAB为直角,所以AP⊥平面ABC,故AP⊥CM.又△ABC为等边三角形,M为AB的中点,所以CM⊥AB.因为PA∩AB=A,所以CM⊥平面PAB.因为CM⊂△ABC,所以平面PAB⊥平面PCM.（II)假设PA=a,则AB=2a.解法1(等体积法)V P−MBC=V B−PMC,13PA⋅S△MBC=13ℎB⋅S△PMC,而△PMC为直角三角形,故面积为√62a2,故ℎB=√22a.所以直线PB与平面PMC所成角的正弦值sin⁡θ=ℎBPB =√1010所以余弦值cos⁡θ=3√1010. 解法2(向量坐标法)以M 点为坐标原点,以MB 为x 轴,以MC 为y 轴建立如答图所示的空间直角坐标系.第6题答图设PA =a ,则M(0,0,0),P(−a,0,a),B(a,0,0),C(0,√3a,0). 故MC ⃗⃗⃗⃗⃗⃗ =(0,√3a,0),MP ⃗⃗⃗⃗⃗⃗ =(−a,0,a),BP ⃗⃗⃗⃗⃗ =(−2a,0,a). 假设平面PMC 的法向量为n ⃗⃗ =(x,y,z),则y =0,x =z . 令x =1,则n⃗ =(1,0,1). 直线PB 与平面PMC 所成角的正弦值sin⁡θ=√1010,所以余弦值cos⁡θ=3√1010.【反思】解法1运用体积法显示简洁运算智慧;解法2建立空间直角坐标系,运用向量工具,需要数学运算能力支摚.7.如图.,在三棱锥P−ABC中,AB=BC=2√2,PA=PB=PC=AC=4,O为AC的中点.(I)证明:PO⟂平面ABC;(II)若点M在棱BC上,且二面角M−PA−C为30∘,求PC与平面PAM所成角的正弦值.【解析】(I)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=2√3.AC,所以△ABC为等腰直角三角形,且OB⊥AC,OB=连接OB,因为AB=BC=√221AC=2.2由OP2+OB2=PB2知PO⊥OB.由OP⊥OB,OP⊥AC知PO⊥平面ABC.⃗⃗⃗⃗⃗ 的方向为x轴正方向,建立空间直角坐标系O−(II)如答图所示,以O为坐标原点,OBxyz.⃗⃗⃗⃗⃗ =(0,2,2√3). 由已知得O(0,0,0),B(2,0,0),A(0,−2,0),C(0,2,0),P(0,0,2√3),则AP⃗⃗⃗⃗⃗ =(2,0,0).取平面PAC的法向量OB第7题答图设M(a,2−a,0)(0<a ⩽2),则AM ⃗⃗⃗⃗⃗⃗ =(a,4−a,0).设平面PAM 的法向量n ⃗⃗ =(x,y,z).由AP ⃗⃗⃗⃗⃗ ⋅n ⃗⃗ =0,AM ⃗⃗⃗⃗⃗⃗ ⋅n ⃗⃗ =0,得{2y +2√3z =0,ax +(4−a)y =0,可取n⃗ =(√3(a −4),√3a,−a), 所以cos⁡⟨OB⃗⃗⃗⃗⃗ ,n ⃗ ⟩=√3(a−4)2√3(a−4)2+3a 2+a 2.由已知得cos⁡⟨OB⃗⃗⃗⃗⃗ ,n ⃗ ⟩=√32, 所以√3|a−4|2√3(a−4)2+3a 2+a 2=√32. 解得a =−4(舍去),或a =43.所以n ⃗ =(−8√33,4√33,−43). 又PC ⃗⃗⃗⃗⃗ =(0,2,−2√3),所以cos⁡⟨PC ⃗⃗⃗⃗⃗ ,n ⃗ ⟩=√34.所以PC 与平面PAM 所成角的正弦值为√34.【反思】建立空间直角坐标系,运用向量工具求直线与平面所成的角,可避免在立体图形中寻找的苦恼.8.如图,正四面体ABCD 的棱CD 在平面α上,E 为棱BC 的中点.当正四面体ABCD绕CD 旋转时,求直线AE 与平面a 所成最大角的正弦值.【解析】建立空间直角坐标系,如答图1所示,设棱长为2,点A,B 在平面yOz 上的以O 为圆心√3为半径的圆上,故可设A(0,√3cos⁡φ,√3sin⁡φ),B(0,√3cos⁡θ,√3sin⁡θ),C(−1,0,0),E (−12,√32cos⁡θ,√32sin⁡θ).第8题答图1在△AOB 中,用余弦定理可得cos⁡(θ+φ)=13,于是AE⃗⃗⃗⃗⃗ =(−12,√36cos⁡θ+2√63sin⁡θ,√36sin⁡θ−2√63cos⁡θ).设直线AE 与平面α所成角为β,n ⃗⃗ =(0,0,1),则sin⁡β=|AE ⃗⃗⃗⃗⃗ ⋅n ⃗ ||AE⃗⃗⃗⃗⃗ ||n ⃗ |=|√36sin⁡θ−2√63cos⁡θ|√3=|16sin⁡θ−2√23cos⁡θ|⩽√336【反思】(1)审题的第一阶段,建立空间直角坐标系后,就想把向量AE ⃗⃗⃗⃗⃗ 的坐标用θ表示,并没有注意到点A,B 均在以O 为圆心,√3为半径的圆上,运算太繁,思维停滞不前.(2)审题的第二阶段,发现点A,B 均在以O 为圆心,√3为半径的圆上.设A(0,√3cos⁡φ,√3sin⁡φ),B(0,√3cos⁡θ,√3sin⁡θ)后,为消去φ大费周章,计算繁杂到算不下去.(3)计算sin⁡β=|AE ⃗⃗⃗⃗⃗⋅n ⃗ ||AE ⃗⃗⃗⃗⃗ ||n ⃗ |时,求|AE ⃗⃗⃗⃗⃗ | =|(−12,√36cos⁡θ+2√63sin⁡θ,√36sin⁡θ−2√63cos⁡θ)|=√14+(√36cos⁡θ−2√632+(√36sin⁡θ+2√63cos⁡θ)2太花时间,此时忽略了|AE⃗⃗⃗⃗⃗ ∣是一个定值. 启示:利用空间坐标系解决立体几何中的度量关系,离不开计算,但是计算也要时时关注几何条件,不能一味地“死”算!事实上,给定模型等价于正四面体不动,而平面α围绕CD 旋转,CD ⊥平面ABMCD ⊂平面α}⇒平面α⊥平面ABM ⇒平面α的法向量n ⃗ ⊂平面ABM ,故法向量n⃗ 围绕点A 旋转. 如答图2,作EH ⊥平面ABM ,连接AM .第8题答图2所有n⃗与AE⃗⃗⃗⃗⃗ 所成的角中,∠EAH最小,故余弦值取最大.设CM=1,则EH=12,AE=√3,AH=√112,故cos⁡∠EAH=√112√3=√336.。

直线与平面所成的角精选题29道一．选择题（共11小题）1．在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为（）A．8B．6C．8D．82．如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（）A．[，1]B．[，1]C．[，]D．[，1]3．已知正四棱柱ABCD﹣A1B1C1D1中，AA1＝2AB，则CD与平面BDC1所成角的正弦值等于（）A．B．C．D．4．如图，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝1，则BC1与平面BB1D1D所成角的正弦值为（）A．B．C．D．5．如图，在直三棱柱ABC﹣A1B1C1中，AB＝1，AC＝2，BC＝，D，E分别是AC1和BB1的中点，则直线DE与平面BB1C1C所成的角为（）A．B．C．D．6．正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，BC的中点，则PB与平面PEF所成角的正弦值为（）A．B．C．D．7．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为O），地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为（）A．20°B．40°C．50°D．90°8．已知正四棱柱ABCD﹣A1B1C1D1中，AB＝2，CC1＝2，E为CC1的中点，则直线AC1与平面BED的距离为（）A．2B．C．D．19．如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，底面是边长为2的正三角形，侧棱长为3，则BB1与平面AB1C1所成的角是（）A．B．C．D．10．正四面体ABCD，CD在平面α内，点E是线段AC的中点，在该四面体绕CD旋转的过程中，直线BE与平面α所成角不可能是（）A．0B．C．D．11．在正方体ABCD﹣A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F∥平面D1AE，则A1F与平面BCC1B1所成角的正切值t构成的集合是（）A．{t|}B．{t|≤t≤2}C．{t|2}D．{t|2}二．填空题（共16小题）12．已知圆锥的顶点为S，母线SA，SB所成角的余弦值为，SA与圆锥底面所成角为45°，若△SAB的面积为5，则该圆锥的侧面积为．13．已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°．若△SAB 的面积为8，则该圆锥的体积为．14．如图，二面角α﹣l﹣β的大小是60°，线段AB⊂α．B∈l，AB与l所成的角为30°．则AB与平面β所成的角的正弦值是．15．如图，平面ABCD⊥平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，且AF ＝＝a，G是EF的中点，则GB与平面AGC所成角的正弦值为．16．如图，已知正三棱柱ABC﹣A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD 与平面B1DC所成角的正弦值为．17．如图，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝1，则AC1与平面A1B1C1D1所成角的正弦值为．18．如图，在正四棱柱ABCD﹣A1B1C1D1中，底面边长为2，直线CC1与平面ACD1所成角的正弦值为，则正四棱柱的高为．19．如图，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝1，则BC1与平面BDD1B1所成角的正弦值为．20．已知四棱锥P﹣ABCD的底面ABCD是边长为2的正方形，，平面ABCD⊥平面P AD，M是PC的中点，O是AD的中点，则直线BM与平面PCO所成角的正弦值是．21．正方体ABCD﹣A1B1C1D1中，则C1A与平面ABCD所成角的正弦值为．22．如图：二面角α﹣l﹣β的大小是60°，线段AB⊂α，B∈l，AB与l所成角为45°，则AB与平面β所成角的正弦值是．23．如图，正三棱柱ABC﹣A1B1C1的底面边长为2，侧棱长为2，则AC1与面ABB1A1所成的角为．24．如图，在棱长为2的正方体中ABCD﹣A1B1C1D1，点M是AD的中点，动点P在底面ABCD内（包括边界），若B1P∥平面A1BM，则C1P与底面ABCD所成角的正切值的取值范围是．25．已知正六棱锥底面边长为a，体积为a3，则侧棱与底面所成的角为．26．已知A∈α，p∉α，＝（﹣，，），平面α的一个法向量＝（0，﹣，﹣），则直线P A与平面α所成的角为．27．如图，在长方体ABCD﹣A'B'C'D'中，点P，Q分别是棱BC，CD上的动点，BC＝4，CD＝3，CC'＝2，直线CC'与平面PQC'所成的角为30°，则△PQC'的面积的最小值是．三．解答题（共2小题）28．如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF．（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值．29．如图，四棱锥P﹣ABCD中，P A⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，P A＝BC ＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．（1）证明：MN∥平面P AB；（2）求直线AN与平面PMN所成角的正弦值．直线与平面所成的角精选题29道参考答案与试题解析一．选择题（共11小题）1．在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为（）A．8B．6C．8D．8【分析】画出图形，利用已知条件求出长方体的高，然后求解长方体的体积即可．【解答】解：长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，即∠AC1B＝30°，可得BC1＝＝2．可得BB1＝＝2．所以该长方体的体积为：2×＝8．故选：C．【点评】本题考查长方体的体积的求法，直线与平面所成角的求法，考查计算能力．2．如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（）A．[，1]B．[，1]C．[，]D．[，1]【分析】由题意可得：直线OP于平面A1BD所成的角α的取值范围是∪．再利用正方体的性质和直角三角形的边角关系即可得出．【解答】解：由题意可得：直线OP于平面A1BD所成的角α的取值范围是∪．不妨取AB＝2．在Rt△AOA1中，＝＝．sin∠C1OA1＝sin（π﹣2∠AOA1）＝sin2∠AOA1＝2sin∠AOA1cos∠AOA1＝，＝1．∴sinα的取值范围是．故选：B．【点评】本题考查了正方体的性质和直角三角形的边角关系、线面角的求法，考查了推理能力，属于中档题．3．已知正四棱柱ABCD﹣A1B1C1D1中，AA1＝2AB，则CD与平面BDC1所成角的正弦值等于（）A．B．C．D．【分析】设AB＝1，则AA1＝2，分别以的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，设＝（x，y，z）为平面BDC1的一个法向量，CD与平面BDC1所成角为θ，则sinθ＝||，在空间坐标系下求出向量坐标，代入计算即可．【解答】解：设AB＝1，则AA1＝2，分别以的方向为x轴、y轴、z轴的正方向建立空间直角坐标系，如下图所示：则D（0，0，2），C1（1，0，0），B（1，1，2），C（1，0，2），＝（1，1，0），＝（1，0，﹣2），＝（1，0，0），设＝（x，y，z）为平面BDC1的一个法向量，则，即，取＝（2，﹣2，1），设CD与平面BDC1所成角为θ，则sinθ＝||＝，故选：A．【点评】本题考查直线与平面所成的角，考查空间向量的运算及应用，准确理解线面角与直线方向向量、平面法向量夹角关系是解决问题的关键．4．如图，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝1，则BC1与平面BB1D1D所成角的正弦值为（）A．B．C．D．【分析】由题意，由于图形中已经出现了两两垂直的三条直线所以可以利用空间向量的方法求解直线与平面所成的夹角．【解答】解：以D点为坐标原点，以DA、DC、DD1所在的直线为x轴、y轴、z轴，建立空间直角坐标系（图略），则A（2，0，0），B（2，2，0），C（0，2，0），C1（0，2，1）∴＝（﹣2，0，1），＝（﹣2，2，0），且为平面BB1D1D的一个法向量．∴cos＜，＞＝＝．∴BC1与平面BB1D1D所成角的正弦值为故选：D．【点评】此题重点考查了利用空间向量，抓住直线与平面所成的角与该直线的方向向量与平面的法向量的夹角之间的关系这一利用向量方法解决了抽象的立体几何问题．5．如图，在直三棱柱ABC﹣A1B1C1中，AB＝1，AC＝2，BC＝，D，E分别是AC1和BB1的中点，则直线DE与平面BB1C1C所成的角为（）A．B．C．D．【分析】根据题意得ED∥BF，进而得到直线DE与平面BB1C1C所成的角等于直线BF 与平面BB1C1C所成的角．利用几何体的结构特征得到∠FBG＝．即可得到答案．【解答】解：取AC的中点为F，连接BF、DF．因为在直三棱柱ABC﹣A1B1C1中，CC1∥BB1，又因为DF是三角形ACC1的中位线，故DF＝CC1＝BB1＝BE，故四边形BEDF是平行四边形，所以ED∥BF．过点F作FG垂直于BC交BC与点G，由题意得∠FBG即为所求的角．因为AB＝1，AC＝2，BC＝，所以∠ABC＝，∠BCA＝，直角三角形斜边中线BF是斜边AC的一半，故BF＝AC＝CF，所以∠FBG＝∠BCA＝．故选：A．【点评】解决此类问题的关键是熟悉线面角的作法，即由线上的一点作平面的垂线再连接斜足与垂足则得到线面角．6．正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，BC的中点，则PB与平面PEF所成角的正弦值为（）A．B．C．D．【分析】以P为原点，P A为x轴，PB为y轴，PC为z轴，建立空间直角坐标系，利用向量法能求出PB与平面PEF所成角的正弦值．【解答】解：∵正三棱锥P﹣ABC的侧面都是直角三角形，E，F分别是AB，BC的中点，∴以P为原点，P A为x轴，PB为y轴，PC为z轴，建立空间直角坐标系，设P A＝PB＝PC＝2，则A（2，0，0），B（0，2，0），C（0，0，2），E（1，1，0），F（0，1，1），＝（0，2，0），＝（1，1，0），＝（0，1，1），设平面PEF的法向量＝（x，y，z），则，取x＝1，得＝（1，﹣1，1），设PB与平面PEF所成角为θ，则sinθ＝＝＝．∴PB与平面PEF所成角的正弦值为．故选：C．【点评】本题考查线面角的正弦值的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．7．日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为O），地球上一点A的纬度是指OA与地球赤道所在平面所成角，点A处的水平面是指过点A且与OA垂直的平面．在点A处放置一个日晷，若晷面与赤道所在平面平行，点A处的纬度为北纬40°，则晷针与点A处的水平面所成角为（）A．20°B．40°C．50°D．90°【分析】由纬度的定义和线面角的定义，结合直角三角形的性质，可得晷针与点A处的水平面所成角．【解答】解：可设A所在的纬线圈的圆心为O'，OO'垂直于纬线所在的圆面，由图可得∠OHA为晷针与点A处的水平面所成角，又∠OAO'为40°且OA⊥AH，在Rt△OHA中，O'A⊥OH，∴∠OHA＝∠OAO'＝40°，另解：画出截面图，如下图所示，其中CD是赤道所在平面的截线．l是点A处的水平面的截线，由题意可得OA⊥l，AB是晷针所在直线．m是晷面的截线，由题意晷面和赤道面平行，晷针与晷面垂直，根据平面平行的性质定理可得m∥CD，根据线面垂直的定义可得AB⊥m，由于∠AOC＝40°，m∥CD，所以∠OAG＝∠AOC＝40°，由于∠OAG+∠GAE＝∠BAE+∠GAE＝90°，所以∠BAE＝∠OAG＝40°，也即晷针与A处的水平面所成角为∠BAE＝40°，故选：B．【点评】本题是立体几何在生活中的运用，考查空间线面角的定义和求法，属于基础题．8．已知正四棱柱ABCD﹣A1B1C1D1中，AB＝2，CC1＝2，E为CC1的中点，则直线AC1与平面BED的距离为（）A．2B．C．D．1【分析】先利用线面平行的判定定理证明直线C1A∥平面BDE，再将线面距离转化为点面距离，最后利用等体积法求点面距离即可【解答】解：如图：连接AC，交BD于O，在三角形CC1A中，易证OE∥C1A，从而C1A∥平面BDE，∴直线AC1与平面BED的距离即为点A到平面BED的距离，设为h，在三棱锥E﹣ABD中，V E﹣ABD＝S△ABD×EC＝××2×2×＝在三棱锥A﹣BDE中，BD＝2，BE＝，DE＝，∴S△EBD＝×2×＝2∴V A﹣BDE＝×S△EBD×h＝×2×h＝∴h＝1故选：D．【点评】本题主要考查了线面平行的判定，线面距离与点面距离的转化，三棱锥的体积计算方法，等体积法求点面距离的技巧，属基础题9．如图，在三棱柱ABC﹣A1B1C1中，侧棱垂直于底面，底面是边长为2的正三角形，侧棱长为3，则BB1与平面AB1C1所成的角是（）A．B．C．D．【分析】以B为坐标原点，建立空间直角坐标系，利用与平面AB1C1所的一个法向量的夹角，求出则BB1与平面AB1C1所成的角．【解答】解：以B为坐标原点，以与BC垂直的直线为x轴，BC为y轴，建立空间直角坐标系，则A（，1，0），B1（0，0，3），C1（0，2，3），＝（﹣，﹣1，3），＝（0，2，0），＝（0，0，3）．设平面AB1C1所的一个法向量为＝（x，y，z）则即，取z＝1，则得＝（，0，1），∵cos＜，＞＝＝＝，∴BB1与平面AB1C1所成的角的正弦值为，∴BB1与平面AB1C1所成的角为故选：A．【点评】本题考查线面角的计算，利用了空间向量的方法．要注意相关点和向量坐标的准确性，及转化时角的相等或互余关系．10．正四面体ABCD，CD在平面α内，点E是线段AC的中点，在该四面体绕CD旋转的过程中，直线BE与平面α所成角不可能是（）A．0B．C．D．【分析】由正四面体ABCD，可得所有棱长都相等．①点E是线段AC的中点，BE⊥AC．在该四面体绕CD旋转的过程中，直线BE与平面α所成角不可能是．利用反证法可以证明．②在该四面体绕CD旋转的过程中，当BE∥α时，可得直线BE与平面α所成角为0．③如图所示的正四面体B﹣ABC．作BO⊥平面ACD，垂足为O．设直线BE与平面ACD所成的角为θ，可得cosθ＝．于是可得在该四面体绕CD旋转的过程中，可得直线BE与平面α所成角为，．【解答】解：由正四面体ABCD，可得所有棱长都相等．①∵点E是线段AC的中点，∴BE⊥AC．在该四面体绕CD旋转的过程中，直线BE与平面α所成角不可能是．反证法：若直线BE与平面α所成角是，则BE⊥平面α．则在某一过程必有BE⊥CD．事实上，在该四面体绕CD旋转的过程中，BE与CD是不可能垂直的，因此假设错位，于是直线BE与平面α所成角不可能是90°．②在该四面体绕CD旋转的过程中，当BE∥α时，可得直线BE与平面α所成角为0．③如图所示的正四面体B﹣ABC．作BO⊥平面ACD，垂足为O．则E，O，D三点在同一条直线上．设直线BE与平面ACD所成的角为θ，可得cosθ＝．∴θ＞．于是可得在该四面体绕CD旋转的过程中，可得直线BE与平面α所成角为，．综上可得：直线BE与平面α所成角不可能是．故选：D．【点评】本题考查了正四面体的性质、线面垂直性质定理、正三角形的性质、线面角，考查了数形结合方法、推理能力与计算能力，属于难题．11．在正方体ABCD﹣A1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F∥平面D1AE，则A1F与平面BCC1B1所成角的正切值t构成的集合是（）A．{t|}B．{t|≤t≤2}C．{t|2}D．{t|2}【分析】设平面AD1E与直线BC交于点G，连接AG、EG，则G为BC的中点．分别取B1B、B1C1的中点M、N，连接AM、MN、AN，可证出平面A1MN∥平面D1AE，从而得到A1F是平面A1MN内的直线．由此将点F在线段MN上运动并加以观察，即可得到A1F 与平面BCC1B1所成角取最大值、最小值的位置，由此不难得到A1F与平面BCC1B1所成角的正切取值范围．【解答】解：设平面AD1E与直线BC交于点G，连接AG、EG，则G为BC的中点分别取B1B、B1C1的中点M、N，连接AM、MN、AN，则∵A1M∥D1E，A1M⊄平面D1AE，D1E⊂平面D1AE，∴A1M∥平面D1AE．同理可得MN ∥平面D1AE，∵A1M、MN是平面A1MN内的相交直线∴平面A1MN∥平面D1AE，由此结合A1F∥平面D1AE，可得直线A1F⊂平面A1MN，即点F是线段MN上上的动点．设直线A1F与平面BCC1B1所成角为θ运动点F并加以观察，可得当F与M（或N）重合时，A1F与平面BCC1B1所成角等于∠A1MB1，此时所成角θ达到最小值，满足tanθ＝＝2；当F与MN中点重合时，A1F与平面BCC1B1所成角达到最大值，满足tanθ＝＝2∴A1F与平面BCC1B1所成角的正切取值范围为[2，2]故选：D．【点评】本题给出正方体中侧面BCC1B1内动点F满足A1F∥平面D1AE，求A1F与平面BCC1B1所成角的正切取值范围，着重考查了正方体的性质、直线与平面所成角、空间面面平行与线面平行的位置关系判定等知识，属于中档题．二．填空题（共16小题）12．已知圆锥的顶点为S，母线SA，SB所成角的余弦值为，SA与圆锥底面所成角为45°，若△SAB的面积为5，则该圆锥的侧面积为40π．【分析】利用已知条件求出圆锥的母线长，利用直线与平面所成角求解底面半径，然后求解圆锥的侧面积．【解答】解：圆锥的顶点为S，母线SA，SB所成角的余弦值为，可得sin∠ASB＝＝．△SAB的面积为5，可得sin∠ASB＝5，即×＝5，即SA＝4．SA与圆锥底面所成角为45°，可得圆锥的底面半径为：＝2．则该圆锥的侧面积：＝40π．故答案为：40π．【点评】本题考查圆锥的结构特征，母线与底面所成角，圆锥的截面面积的求法，考查空间想象能力以及计算能力．13．已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°．若△SAB 的面积为8，则该圆锥的体积为8π．【分析】利用已知条件求出母线长度，然后求解底面半径，以及圆锥的高．然后求解体积即可．【解答】解：圆锥的顶点为S，母线SA，SB互相垂直，△SAB的面积为8，可得：，解得SA＝4，SA与圆锥底面所成角为30°．可得圆锥的底面半径为：2，圆锥的高为：2，则该圆锥的体积为：V＝＝8π．故答案为：8π．【点评】本题考查圆锥的体积的求法，母线以及底面所成角的应用，考查转化思想以及计算能力．14．如图，二面角α﹣l﹣β的大小是60°，线段AB⊂α．B∈l，AB与l所成的角为30°．则AB与平面β所成的角的正弦值是．【分析】过点A作平面β的垂线，垂足为C，在β内过C作l的垂线．垂足为D，连接AD，从而∠ADC为二面角α﹣l﹣β的平面角，连接CB，则∠ABC为AB与平面β所成的角，在直角三角形ABC中求出此角即可．【解答】解：过点A作平面β的垂线，垂足为C，在β内过C作l的垂线．垂足为D连接AD，有三垂线定理可知AD⊥l，故∠ADC为二面角α﹣l﹣β的平面角，为60°又由已知，∠ABD＝30°连接CB，则∠ABC为AB与平面β所成的角设AD＝2，则AC＝，CD＝1AB＝＝4∴sin∠ABC＝；故答案为．【点评】本题主要考查了平面与平面之间的位置关系，以及直线与平面所成角，考查空间想象能力、运算能力和推理论证能力，属于基础题．15．如图，平面ABCD⊥平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，且AF＝＝a，G是EF的中点，则GB与平面AGC所成角的正弦值为．【分析】由面面垂直的性质证明CB⊥AG，用勾股定理证明AG⊥BG，得到AG⊥平面CBG，从而面AGC⊥面BGC，在平面BGC内作BH⊥GC，垂足为H，则BH⊥平面AGC，故∠BGH是GB与平面AGC所成的角，解Rt△CBG，可得GB与平面AGC所成角的正弦值．【解答】解：∵ABCD是正方形，∴CB⊥AB，∵面ABCD⊥面ABEF且交于AB，∴CB⊥面ABEF．∵AG，GB⊂面ABEF，∴CB⊥AG，CB⊥BG，又AD＝2a，AF＝a，ABEF是矩形，G是EF的中点，∴AG＝BG＝a，AB＝2a，∴AB2＝AG2+BG2，∴AG⊥BG，∵BG∩BC＝B，∴AG⊥平面CBG，而AG⊂面AGC，故平面AGC⊥平面BGC．在平面BGC内作BH⊥GC，垂足为H，则BH⊥平面AGC，∴∠BGH是GB与平面AGC 所成的角．在Rt△CBG中，BH＝＝，BG＝a，∴sin∠BGH＝＝．故答案为：．【点评】本题考查面面垂直的判定方法，以及求线面成的角的求法，考查学生的计算能力，属于中档题．16．如图，已知正三棱柱ABC﹣A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与平面B1DC所成角的正弦值为．【分析】如图，先证出B1D⊥平面AC1，过A点作AG⊥CD，证AG⊥平面B1DC，可知∠ADG即为直线AD与平面B1DC所成角，求其正弦即可．【解答】解：如图，连接B1D易证B1D⊥平面AC1，过A点作AG⊥CD，则由B1D⊥平面AC1，得AG⊥B1D由线面垂直的判定定理得AG⊥平面B1DC，于是∠ADG即为直线AD与平面B1DC所成角，由已知，不妨令棱长为2，则可得AD＝＝CD，由等面积法算得AG＝＝所以直线AD与面DCB1的正弦值为；故答案为．【点评】考查正棱柱的性质以及线面角的求法．考查空间想象能力以及点线面的位置关系17．如图，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝1，则AC1与平面A1B1C1D1所成角的正弦值为．【分析】由题意连接A1C1，则∠AC1A1为所求的角，在△AC1A1计算出此角的正弦值即可．【解答】解：连接A1C1，在长方体ABCD﹣A1B1C1D1中，∴A1A⊥平面A1B1C1D1，则∠AC1A1为AC1与平面A1B1C1D1所成角．在△AC1A1中，sin∠AC1A1＝＝＝．故答案为：．【点评】本题主要考查了求线面角的过程：作、证、求，用一个线面垂直关系，属于中档题．18．如图，在正四棱柱ABCD﹣A1B1C1D1中，底面边长为2，直线CC1与平面ACD1所成角的正弦值为，则正四棱柱的高为4．【分析】建立空间直角坐标系，设棱柱的高为a，求出平面ACD1的一个法向量，令，求出a的值即可．【解答】解：以D为坐标原点，DA，DC，DD1所在直线分别为x轴，y轴，z轴建立如图所示的空间直角坐标系，设DD1＝a，则A（2，0，0），C（0，2，0），D1（0，0，a），故，设平面ACD1的一个法向量为，则，可取，故，又直线CC1与平面ACD1所成角的正弦值为，∴，解得a＝4．故答案为：4．【点评】本题考查了空间向量在立体几何中的运用，考查计算能力，属于基础题．19．如图，在长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AA1＝1，则BC1与平面BDD1B1所成角的正弦值为．【分析】连接A1C1交B1D1于O，连接BO，则可得∠C1BO为BC1与平面BBD1B1所成角，利用正弦函数，即可求得结论．【解答】解：连接A1C1交B1D1于O，连接BO，则∵长方体ABCD﹣A1B1C1D1中，AB＝BC＝2∴C1O⊥平面BDD1B1∴∠C1BO为BC1与平面BDD1B1所成角∵C1O＝A1C1＝，BC1＝∴sin∠C1BO＝＝＝故答案为：【点评】本题考查线面角，解题的关键是正确作出线面角，属于中档题．20．已知四棱锥P﹣ABCD的底面ABCD是边长为2的正方形，，平面ABCD⊥平面P AD，M是PC的中点，O是AD的中点，则直线BM与平面PCO所成角的正弦值是．【分析】以O为原点，OA为x轴，过O作AB平行线为y轴，OP为z轴，建立空间直角坐标系，利用向量法能求出直线BM与平面PCO所成角的正弦值．【解答】解：以O为原点，OA为x轴，过O作AB平行线为y轴，OP为z轴，建立空间直角坐标系，B（1，2，0），P（0，0，2），C（﹣1，2，0），M（﹣，1，1），O（0，0，0），，，设平面PCO的法向量＝（x，y，z），，可得＝（2，1，0），设直线BM与平面PCO所成角为θ，则sinθ＝|os|＝||＝故答案为：【点评】本题考查线面角的正弦值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．21．正方体ABCD﹣A1B1C1D1中，则C1A与平面ABCD所成角的正弦值为．【分析】设正方体ABCD﹣A1B1C1D1的棱长为1，以D为原点，建立空间直角坐标系，利用向量法能求出C1A与平面ABCD所成角的正弦值．【解答】解：设正方体ABCD﹣A1B1C1D1的棱长为1，以D为原点，建立空间直角坐标系，A（1，0，0），C1（0，1，1），＝（﹣1，1，1），平面ABCD的法向量＝（0，0，1），设C1A与平面ABCD所成角为θ，则sinθ＝|cos＜＞|＝＝．∴C1A与平面ABCD所成角的正弦值为．故答案为：．【点评】本题考查直线与平面所成角的正弦值的求法，解题时要认真审题，注意向量法的合理运用．22．如图：二面角α﹣l﹣β的大小是60°，线段AB⊂α，B∈l，AB与l所成角为45°，则AB与平面β所成角的正弦值是．【分析】根据二面角和直线和平面所成角的定义，先作出对应的平面角，结合三角形的边角关系进行求解即可．【解答】解：过点A作平面β的垂线，垂足为C，在β内过C作l的垂线，垂足为D．连结AD，根据三垂线定理可得AD⊥l，因此，∠ADC为二面角α﹣l﹣β的平面角，∠ADC＝60°又∵AB与l所成角为45°，∴∠ABD＝45°连结BC，可得BC为AB在平面β内的射影，∴∠ABC为AB与平面β所成的角．设AD＝2x，则Rt△ACD中，AC＝AD sin60°＝，Rt△ABD中，AB＝，∴Rt△ABC中，sin∠ABC＝＝，故答案为：．【点评】本题主要考查线面垂直的定义与性质、二面角的平面角的定义和直线与平面所成角的定义及求法等知识．23．如图，正三棱柱ABC﹣A1B1C1的底面边长为2，侧棱长为2，则AC1与面ABB1A1所成的角为．【分析】取A1B1中点D，连结C1D，AD，推导出C1D⊥A1B1，C1D⊥AA1，从而AC1与面ABB1A1所成的角为∠DAC1，由此能求出AC1与面ABB1A1所成的角．【解答】解：取A1B1中点D，连结C1D，AD，∵正三棱柱ABC﹣A1B1C1的底面边长为2，侧棱长为2，∴C1D⊥A1B1，C1D⊥AA1，∵A1B1∩AA1＝A1，∴C1D⊥平面ABB1A1，∴AC1与面ABB1A1所成的角为∠DAC1，∵C1D＝＝，AD＝＝3，∴tan∠DAC1＝＝，∴∠DAC1＝．∴AC1与面ABB1A1所成的角为．故答案为：．【点评】本题考查线面角的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．24．如图，在棱长为2的正方体中ABCD﹣A1B1C1D1，点M是AD的中点，动点P在底面ABCD内（包括边界），若B1P∥平面A1BM，则C1P与底面ABCD所成角的正切值的取值范围是．【分析】取BC的中点N，连接DN、B1N、B1D，利用面面平行的判定定理可证得面B1DN ∥面A1BM，从而确定点P在线段DN上运动；连接CP、C1P，则∠C1PC为直线C1P与面ABCD所成的角，而tan∠C1PC＝＝，于是求出线段CP的取值范围即可得解．【解答】解：如图所示，取BC的中点N，连接DN、B1N、B1D，则B1N∥A1M，DN∥BM，∵B1N∩DN＝N，B1N、DN⊂面B1DN，A1M∩BM＝M，A1M、BM⊂面A1BM，∴面B1DN∥面A1BM，∵B1P∥平面A1BM，且点P在底面ABCD上，∴点P在线段DN上运动．连接CP、C1P，则∠C1PC为直线C1P与面ABCD所成的角，∴tan∠C1PC＝＝．在Rt△CDN中，当点P与点D重合时，CP最长为2；当CP⊥DN时，CP最短为，即CP∈[，2]，∴tan∠C1PC∈[1，]．故答案为：[1，]．【点评】本题考查空间中直线与平面的夹角问题、线面平行关系，熟练运用面面平行的判定定理与性质定理是解题的关键，考查学生的空间立体感、逻辑推理能力和运算能力，属于中档题．25．已知正六棱锥底面边长为a，体积为a3，则侧棱与底面所成的角为45°．【分析】由已知条件推导出棱锥的高h＝a，侧棱长为a，由此能求出侧棱与底面所成的角的大小．【解答】解：∵正六棱锥的底面边长为a，∴S底面积＝6×＝a2，∵体积为a 3，∴棱锥的高h＝a，∴侧棱长为a∴侧棱与底面所成的角为45°，故答案为：45°．【点评】本题考查侧棱与底面所成的角的大小的求法，是中档题，解题时要注意正六棱锥的结构特征的合理运用．26．已知A∈α，p∉α，＝（﹣，，），平面α的一个法向量＝（0，﹣，﹣），则直线P A与平面α所成的角为60°．【分析】设直线P A与平面α所成的角为θ．利用sinθ＝|cos＜，＞|，即可得出．【解答】解：设直线P A与平面α所成的角为θ．则sinθ＝|cos＜，＞|＝＝．∵θ∈[0°，90°]．∴θ＝60°．故答案为：60°．【点评】本题考查了利用向量的夹角公式求线面角、数量积运算及其模的计算公式，考查了推理能力与计算能力，属于中档题．27．如图，在长方体ABCD﹣A'B'C'D'中，点P，Q分别是棱BC，CD上的动点，BC＝4，CD＝3，CC'＝2，直线CC'与平面PQC'所成的角为30°，则△PQC'的面积的最小值是8．【分析】设直角三棱锥C﹣C′PQ的高为h，CQ＝x，CP＝y，根据直角三棱锥的性质可知，由直线CC’与平面C’PQ成的角为30°，得到xy≥8，再由V C﹣C′PQ＝V C′﹣CPQ，能求出△PQC'的面积的最小值．【解答】解：设直角三棱锥C﹣C′PQ的高为h，CQ＝x，CP＝y，根据直角三棱锥的性质可知：，∵直线CC’与平面C’PQ成的角为30°，∴h＝2＝，∴＝，，∴xy≥8，再由体积可知：V C﹣C′PQ＝V C′﹣CPQ，得，S△C′PQ＝xy，∴△PQC'的面积的最小值是8．故答案为：8．【点评】本题考查三角形面积的最小值的求法，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、函数与方程思想、数形结合思想，是中档题．三．解答题（共2小题）28．如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC 折起，使点C到达点P的位置，且PF⊥BF．（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值．【分析】（1）利用正方形的性质可得BF垂直于面PEF，然后利用平面与平面垂直的判断定理证明即可．（2）利用等体积法可求出点P到面ABCD的距离，进而求出线面角．【解答】（1）证明：由题意，点E、F分别是AD、BC的中点，则，，由于四边形ABCD为正方形，所以EF⊥BC．由于PF⊥BF，EF∩PF＝F，则BF⊥平面PEF．又因为BF⊂平面ABFD，所以：平面PEF⊥平面ABFD．（2）在平面PEF中，过P作PH⊥EF于点H，连接DH，由于EF为面ABCD和面PEF的交线，PH⊥EF，则PH⊥面ABFD，故PH⊥DH．在三棱锥P﹣DEF中，可以利用等体积法求PH，因为DE∥BF且PF⊥BF，所以PF⊥DE，又因为△PDF≌△CDF，所以∠FPD＝∠FCD＝90°，所以PF⊥PD，由于DE∩PD＝D，则PF⊥平面PDE，故V F﹣PDE＝，因为BF∥DA且BF⊥面PEF，所以DA⊥面PEF，所以DE⊥EP．设正方形边长为2a，则PD＝2a，DE＝a在△PDE中，，所以，故V F﹣PDE＝，又因为，所以PH＝＝，所以在△PHD中，sin∠PDH＝＝，即∠PDH为DP与平面ABFD所成角的正弦值为：．【点评】本题主要考查点、直线、平面的位置关系．直线与平面所成角的求法．几何法的应用，考查转化思想以及计算能力．29．如图，四棱锥P﹣ABCD中，P A⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，P A＝BC ＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．（1）证明：MN∥平面P AB；（2）求直线AN与平面PMN所成角的正弦值．【分析】（1）法一、取PB中点G，连接AG，NG，由三角形的中位线定理可得NG∥BC，且NG＝，再由已知得AM∥BC，且AM＝BC，得到NG∥AM，且NG＝AM，说明四边形AMNG为平行四边形，可得NM∥AG，由线面平行的判定得到MN∥平面P AB；法二、证明MN∥平面P AB，转化为证明平面NEM∥平面P AB，在△P AC中，过N作NE ⊥AC，垂足为E，连接ME，由已知P A⊥底面ABCD，可得P A∥NE，通过求解直角三角形得到ME∥AB，由面面平行的判定可得平面NEM∥平面P AB，则结论得证；（2）连接CM，证得CM⊥AD，进一步得到平面PNM⊥平面P AD，在平面P AD内，过A作AF⊥PM，交PM于F，连接NF，则∠ANF为直线AN与平面PMN所成角．然后求解直角三角形可得直线AN与平面PMN所成角的正弦值．【解答】（1）证明：法一、如图，取PB中点G，连接AG，NG，∵N为PC的中点，∴NG∥BC，且NG＝，又AM＝，BC＝4，且AD∥BC，∴AM∥BC，且AM＝BC，则NG∥AM，且NG＝AM，∴四边形AMNG为平行四边形，则NM∥AG，∵AG⊂平面P AB，NM⊄平面P AB，∴MN∥平面P AB；法二、。

直线与平面所成的角教学目标：理解线面角概念，熟练运用三垂线定理及其逆定理找出线面角。

教学过程：1．直线和平面所成的角（1）平面的斜线和它在平面内的射影所成的锐角，叫做这条直线和平面所成的角。

（2）平面的垂线和平面所成的角是直角。

（3）平面的平行线和平面所成的角是︒0角。

（4）平面内的直线和平面所成的角是︒0角。

2．直线与平面所成的角的范围是{}︒≤≤︒900|θθ3．最小角定理：平面的一条斜线与平面所成的角，是这条直线和平面内过斜足的直线所成的一切角中最小的角。

典型例题：例1 正方体ABCD —A 1B 1C 1D 1中，（1）分别指出对角线A 1C 与六个面所成的角；（2）E 、F 分别是直线AA 1、A 1D 1的中点，求直线EF 与平面ABCD 所成角的大小。

例2 正四面体ABCD 中，Q 是AD 的中点，求CQ 与平面DBC 所成的角的正弦值。

例3 AO 是平面OCB 的斜线，O 是斜足，AB ⊥平面OCB ，B 为垂足，⊂OD 平面OCB ，OD 与OB 不重合，α=∠AOB ，锐角β=∠BOD ，锐角γ=∠AOD ，求证：βαγcos cos cos ⋅=。

例4 线段AB 的两端点在平面α的同侧，斜线段AM 、BN 所在的直线分别与平面α成︒︒60,30角，且AM ⊥AB ，BN ⊥AB ，AM=6，BN=32，AB=6。

（1）求证：AB//α；（2）求MN 的长。

作业：1．从平面α外一点P 向平面α引垂线PO 和斜线PA 、PB ，垂足为O ，斜足为A 、B 。

若PA 、PB 与平面α所成的角的差为︒45，且在平面α上的射影长分别为2和12，试求P 到平面α的距离。

2．空间四边形ABCD 中，α⊂AB ，AB BC AD ⊥⊥,α，BC 与α成︒30角，AB=a,AD=BC=b 。

求直线CD 与α所成的角的正弦值。

3．直角三角形ABC 中，斜边AB 在平面α内，AC 、BC 与α所成的角分别为︒30、︒45，求斜边上的高CD 与α所成的角。