你知道黑洞数有哪些吗(修改版,对源代码进行了完善)

黑洞数黑洞数又称陷阱数,是类具有奇特转换特性的整数。

任何一个数字不全相同整数,经有限“重排求差”操作,总会得某一个或一些数,这些数即为黑洞数。

"重排求差"操作即把组成该数的数字重排后得到的最大数减去重排后得到的最小数。

举个例子，三位数的黑洞数为495简易推导过程：随便找个数，如297，三个位上的数从小到大和从大到小各排一次，为972和279，相减，得693 按上面做法再做一次，得到594，再做一次，得到495之后反复都得到495再如，四位数的黑洞数有6174但是，五位数及五位以上的数还没有找到对应的黑洞数神秘的6174－黑洞数随便造一个四位数，如a1=1628,先把组成部分1628的四个数字由大到小排列得到a2＝8621，再把1628的四个数字由小到大排列得a3＝1268，用大的减去小的a2-a1=8621-1268＝7353，把7353按上面的方法再作一遍，由大到小排列得7533，由小到大排列得3357，相减7533-3367＝4176把4176再重复一遍：7641-1467＝6174。

如果再往下作，奇迹就出现了！7641-1467＝6174，又回到6174。

这是偶然的吗？我们再随便举一个数1331，按上面的方法连续去做：3311-1133＝2178 8721-1278＝7443 7443-3447＝3996 9963-3699＝62646642-2466＝4176 7641-1467＝6174好啦！6174的“幽灵”又出现了，大家不妨试一试，对于任何一个数字不完全的四位数，最多运算7步，必然落入陷阱中。

这个黑洞数已经由印度数学家证明了。

在数学中由有很多有趣，有意义的规律等待我们去探索和研究，让我们在数学中得到更多的乐趣。

苏联的科普作家高基莫夫在他的著作《数学的敏感》一书中，提到了一个奇妙的四位数6174，并把它列作“没有揭开的秘密”。

不过，近年来，由于数学爱好者的努力，已经开始拨开迷雾。

黑洞数123探秘王凯成（陕西省小学教师培训中心 710600）设正整数A 中的偶数字个数为m(A 中没有偶数字时m=0)，奇数字个数为n(A 中没有奇数字时n=0)，A 是m+n 位数，把A 的偶数字个数m 、奇数字个数n 、总位数m+n 按照“偶奇总”顺序排列得到一个新的整数B(B 的首位可以为0)，我们把从A 得到B 的过程叫做A 的黑洞数变换f ，即f(A)=B 。

例如：A=36925037186，A 中的偶数字个数为m=5,奇数字个数为n=6，A 是m+n=11位数。

把A 的偶数字个数5、奇数字个数6、总位数11按照“偶奇总”顺序排列得到一个新的整数B=5611。

从A=36925037186得到B=5611的过程就是A=36925037186的一次黑洞数变换，即有：f(36925037186)=5611。

任意一个正整数A ，经过有限次黑洞数变换f 后，总能得到123。

例如：A=3546980001有6个偶数字、4个奇数字，6+4=10，那么f(3546980001)=6410； 6410有3个偶数字、1个奇数字，3+1=4，那么f(6410)=314；314有1个偶数字、2个奇数字，是3位数，所以f(314)=123（将123黑洞数变换f 后仍然是123，即f(123)=123）。

A 经过三次黑洞数变换f ，最终成为123。

再如：A=555555有0个偶数字6个奇数字，0+6=6，那么f(555555)=066(066是形式上的3位数，本文仍然称为3位数，以下类同)；066有3个偶数字0个奇数字，3+0=3，那么f(066)=303； 303有1个偶数字2个奇数字，1+2=3，所以f(303) =123。

命题1：设k 位数A= 12k a a a ⋅⋅⋅（i a 是数字），A 有m 个偶数字、n 个奇数字（m 、n 是自然数），m+n=k 。

则A 经过有限次黑洞数变换f 后，总能得到123。

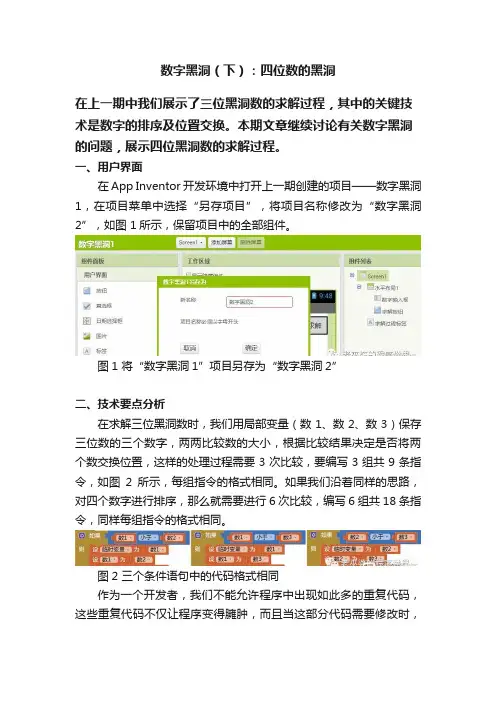
数字黑洞（下）：四位数的黑洞在上一期中我们展示了三位黑洞数的求解过程，其中的关键技术是数字的排序及位置交换。

本期文章继续讨论有关数字黑洞的问题，展示四位黑洞数的求解过程。

一、用户界面在App Inventor开发环境中打开上一期创建的项目——数字黑洞1，在项目菜单中选择“另存项目”，将项目名称修改为“数字黑洞2”，如图 1所示，保留项目中的全部组件。

图1 将“数字黑洞1”项目另存为“数字黑洞2”二、技术要点分析在求解三位黑洞数时，我们用局部变量（数1、数2、数3）保存三位数的三个数字，两两比较数的大小，根据比较结果决定是否将两个数交换位置，这样的处理过程需要3次比较，要编写3组共9条指令，如图2所示，每组指令的格式相同。

如果我们沿着同样的思路，对四个数字进行排序，那么就需要进行6次比较，编写6组共18条指令，同样每组指令的格式相同。

图2 三个条件语句中的代码格式相同作为一个开发者，我们不能允许程序中出现如此多的重复代码，这些重复代码不仅让程序变得臃肿，而且当这部分代码需要修改时，极易给程序带来错误，例如由于疏忽忘记了修改其中的部分代码。

解决这一问题的关键技术有两点——列表与循环。

将四位数的四个数字转换为列表，利用循环语句，对列表项进行两两比较，通过交换列表项的位置，来实现数字的排序。

这也是解决大量数字排序问题的通用方法，例如，对班级考试成绩进行排序。

三、编写程序将开发工具切换到编程视图，保留项目中的部分代码，将最大值、最小值过程删除，如图 3所示。

图3 保留项目中的部分代码1、定义过程——数字转列表、列表转数字为了利用列表和循环语句简化排序代码，首先需要将数字转化为列表，待排序完成后，再将列表转为数字，这样才能进行减法运算。

代码如图 4及图 5所示。

图4 定义过程——数字转列表图5 定义过程——列表转数字2、定义过程——极值在数学语言中，最大值、最小值统称为“极值”，这里定义一个有返回值的过程——极值，来取代最大值、最小值两个过程，代码如图 6所示。

黑洞数及其简单理论黑洞是宇宙中最神秘的天体之一，它的存在引发了科学家们长期的困惑与探索。

黑洞数是研究黑洞的一个重要指标，它们的数量和特征对于理解宇宙的结构和演化过程具有重要意义。

本文将介绍黑洞数的定义、计算方法以及对宇宙演化的影响。

1. 黑洞数的定义黑洞数指的是在给定的空间范围内存在的黑洞的数量。

它是对黑洞分布和密度进行统计的结果。

由于黑洞是无法直接观测到的，科学家们只能通过观测黑洞周围的物质运动以及引力效应来推测其存在。

通过统计这些观测结果，可以得出一个相对准确的黑洞数。

2. 黑洞数的计算方法黑洞数的计算方法通常涉及测量黑洞的质量和距离。

科学家们利用射电望远镜、X 射线望远镜等装置观测天空，探测到黑洞的辐射或者通过星系中恒星轨道的变化来推断黑洞的存在。

通过这些观测数据，可以计算出黑洞的质量以及距离。

3. 黑洞数的影响黑洞数的变化对宇宙的演化过程有着重要的影响。

首先，黑洞的形成和演化是宇宙星系形成和演化的重要因素之一。

恒星在演化的过程中，当它们燃尽燃料时会发生引力坍缩，形成黑洞。

这些黑洞会继续吸积周围的物质，增加质量并影响周围星系的演化。

其次，根据黑洞数目的统计，科学家们可以推测宇宙中的物质分布和结构。

黑洞的存在会对周围的星系、星团和宇宙大尺度结构产生引力影响，形成所谓的「大尺度结构形成引擎」。

通过观测和研究黑洞数分布的变化，可以揭示宇宙的演化历程和结构形成的规律。

此外，黑洞数还与宇宙背景辐射有关。

黑洞的辐射会对周围的物质进行加热，产生热辐射。

这些辐射主要是X 射线和γ 射线辐射，对研究宇宙背景辐射的特性和起源有着重要的意义。

4. 黑洞数的研究进展与未来展望随着观测和理论的发展，科学家们对黑洞数的研究取得了重要的进展。

天文学家利用射电望远镜、X 射线望远镜等高精度观测装置，逐渐建立了相对准确的黑洞数统计模型。

未来，随着技术的进步和观测装置的提升，科学家们将能够精确测量黑洞的质量和距离，并进一步完善黑洞数的统计。

你知道哪些神奇的数字？西西弗斯串在古希腊神话中，科林斯国王西西弗斯被罚将一块巨石推到一座山上，但是无论他怎么努力，这块巨石总是在到达山顶之前不可避免地滚下来，于是他只好重新再推，永无休止。

著名的西西弗斯串就是根据这个故事而得名的。

什么是西西弗斯串呢？也就是任取一个数，例如35962，数出这数中的偶数个数、奇数个数及所有数字的个数，就可得到2（2个偶数）、3（3个奇数）、5（总共五位数），用这3个数组成下一个数字串235。

对235重复上述程序，就会得到1、2、3，将数串123再重复进行，仍得123。

对这个程序和数的'宇宙'来说，123就是一个数字黑洞。

是否每一个数最后都能得到123呢？用一个大数试试看。

例如：88883337777444992222，在这个数中偶数、奇数及全部数字个数分别为11、9、20，将这3个数合起来得到11920，对11920这个数串重复这个程序得到235，再重复这个程序得到123，于是便进入'黑洞'了。

这就是数学黑洞'西西弗斯串'。

孔雀开屏数：（20＋25）的平方=2025类似的数还有两个：（30＋25）的平方=3025（98＋01）的平方=9801 与此相类似的还有：（2 4 0 1）的4次方=2401（5 1 2）的立方=512（8 1）的平方=81回归数英国大数学家哈代（G.H.Hardy,1877-1947）曾经发现过一种有趣的现象:153=1^3 5^3 3^3371=3^3 7^3 1^3370=3^3 7^3 0^3407=4^3 0^3 7^3他们都是三位数且等于各位数字的三次幂之和,这种巧合不能不令人感到惊讶.更为称奇的是,一位读者看过哈代的有趣发现后,竟然构造出其值等于各位数字四（五,六）次幂之和的四（五,六）位数:~ 1 / 9 ~1634=1^4 6^4 3^4 4^454748=5^5 4^5 7^5 4^5 8^5548834=5^6 4^6 8^6 8^6 3^6 4^6注:3位3次幂回归数又称位“水仙花数”像这种其值等于各位数字的 n 次幂之和的 n 位数,称为 n 位 n 次幂回归数.本文只讨论这种回归数,故简称为回归数,人们自然要问:对于什么样的自然数 n 有回归数?这样的 n 是有限个还是无穷多个?对于已经给定的 n ,如果有回归数,那么有多少个回归数?1986年美国的一位数学教师安东尼.迪拉那（Anthony Diluna）巧妙地证明了使 n 位数成为回归数的 n 只有有限个.设 An 是这样的回归数,即:An=a1a2a3...an=a1^n a2^n ... an^n （其中0<=a1,a2,...an<=9）从而10^n-1<=An<=n9^n 即n 必须满足n9^n>10^n-1 也就是（10/9）^n<10n （1）随着自然数 n 的不断增大,（10/9）^n 值的增加越来越快,很快就会使得（1）式不成立,因此,满足（1）的 n 不能无限增大,即 n 只能取有限多个.进一步的计算表明:（10/9）^60=556.4798...<10*60=600 （10/9）^61=618.3109...>10*61=610对于n>=61,便有（10/9）^n>10n由此可知,使（1）式成立的自然数 n<=60.故这种回归数最多是60位数.迪拉那说,他的学生们早在1975年借助于哥伦比亚大学的计算机得到下列回归数:一位回归数:1,2,3,4,5,6,7,8,9二位回归数:不存在三位回归数:153,370,371,407四位回归数:1634,8208,9474五位回归数:54748,92727,93084六位回归数:548834七位回归数:1741725,4210818,9800817。

重排求差中6、7位黑洞数的理论探索重排求差中六、七位黑洞数的理论探索邬金华前面已详细介绍了四位数和五位数的重排求差规律，所用方法大体相同，都是三个步骤：第一步，通过最大数减最小数的竖式得到基本关系式；第二步，按基本关系式揭示的差数特征写出所有可能的差数；第三步，对所有差数反复重排求差或逆推，得到差数的步进关系和黑洞数。

下面也按此三步进行。

已知五位数和四位数的差数具有承袭关系，即将四位数差数中间插进“9”就变成了五位数差数，同样，六位数和七位数也有相同的关系，即将六位数差数中间插进“9”也会成为七位数的差数，故这里只对六位数作详细介绍，对七位数只给出最终结果。

一、基本关系式仍用大写和小写字母ABCDEF和mnstpk分别表示最大数和差数。

按最大数中间2个或4个数字是否相同，可将六位数分为3种类型，其基本关系式各不相同。

类型1：中间2个数字不同，即有A≥B≥C > D≥E≥F（可以同时取等号），基本关系式和差数特征见下图：类型2：中间2个数字相同（但中间4个数字不同）即最大数具有ABCCEF的形式，各数字间的关系为A≥B≥C≥E≥F（不同时取等号，或可同时取不超过3个的等号），其基本关系式和差数特征见下图：类型3：中间4个数字相同，即最大数具有ABBBBF形式（A≥B ≥F，不同时取等号），其基本关系式和差数特征为：上述关系式表明，任何差数都是由某个数核（由并排的“9”构成）和若干个数偶所构成（类型1表面上没有数核，称0数核，有关问题将在后续文章中专门介绍），数偶中的两个数都对称地分布在数核的两侧，这是差数极为重要的构成特点，在以后的讨论中将会有很多用处。

二、六位差数对照4位数和六位数的差数发现，6位数类型2和类型3的差数与4位数的类型1和类型2的差数具有完全相同的数偶，而差数的多少也只与数偶有关，因此，与4位数相比，六位数差数个数就是在4位数差数个数（54个）基础上增加了这里类型1的差数个数，而这里类型1的差数个数为1+(1+2)+(1+2+3)+……+(1+2+3+……+9)=165故六位数差数共有165+54=219个，归并成等效差数数组后仍有115个，详细情况可参看后附的步进图。

黑洞数河北张家口市第十九中学贺峰一、一位黑洞数（0）黑洞数0:随意取4个数，如8，3，12，5写在圆周的四面。

用两个相邻数中的大数减小数，将得数写在第二圈圆周。

如此做下去，必会得到4个相同的数。

这个现象是意大利教授杜西在1930年发现的，所以叫作"杜西现象"。

其实把“杜西现象”再继续下去必会得到这个圆周的最外层是四个0。

因为得到的4个相同的数两两相减差为0，也就得到：任意地在圆周的四面写上4个数，用两个相邻数中的大数减小数（相同的也相减），将得数写在第二圈圆周。

如此做下去，必会得到4个0。

这就是黑洞0。

二、两位黑洞数（13）（2004重庆北碚区）自然数中有许多奇妙而有趣的现象，很多秘密等待着我们去探索！比如：对任意一个自然数，先将其各位数字求和，再将其和乘以3后加上1，多次重复这种操作运算，运算结果最终会得到一个固定不变的数R，它会掉入一个数字“陷井”，永远也别想逃出来，没有一个自然数能逃出它的“魔掌”。

那么最终掉入“陷井”的这个固定不变的数R＝__13_。

三、三位黑洞数（495、123）黑洞数123随便找一个数，然后分别数出这个数中的奇数个数和偶数个数以及这个数有多少位，并用数出来的个数组成一个新数，最后组成的数字总会归结到123。

举个例子，如：58967853，这里面有8、6、8共3个偶数，5、9、7、5、3共5个奇数，共8位数。

然后我们用新得到的几个数字重新组合，把原数中的偶数个数放在最左边，中间放原数的奇数个数，最右边表示原数的位数。

根据这个规则，上面的数就变成358了，然后按照这个规则继续变换下去，就会得到123。

再取任一个数，如：81872115378，其中偶数个数是4，奇数个数是7，是11位数，又组成一个新的数4711。

该数有1个偶数，3个奇数，是4位数，又组成新数134。

再重复以上程序，1个偶数，2个奇数，是3位数，便得到123黑洞。

反复重复以上程序，始终是123，就再也逃不出去，得不到新的数了。

A B C D - D C B A m n p kA B B D - D B B A m 9 9k 4位黑洞数的证明及相关问题剖析邬金华自原苏联人卡普耶卡提出4位数反复重排求差会得到黑洞数6174至今，这种看似简单的数字游戏隐含的数学道理已逐渐引起越来越多的人的兴趣，并很快被推演到更多位的情形。

网上有消息称，该问题已被“印度学者”和台湾中学生李光宇各自解决，大陆人王景之稍后也在网上公布了他的研究结论，但是，在可以搜索到的材料中却一直没有见到有关的严格的数学证明，而且，台湾李光宇和大陆王景之的结论也不完全一致。

为弥补这些缺憾，这里先介绍几种对经典4位黑洞数的证明方法和相关结论，随后再陆续公布对其它位数的研究结果。

一、操作过程中的差数在反复重排求差的演算过程中，除首次演算时的被减数是某个任意4位数（但4个数字不全相同）以外，以后操作的被减数都是上一次差数的重排，就是说，以后的操作都是在差数基础上进行的，而且黑洞数本身也是一个差数，只是较为特殊罢了。

为了揭示一般差数的特点，这里将重排求差时的最大数用大写字母ABCD的形式写出（最小数随之而定），差数用小写字母mnpk的形式写出。

按最大数中间二位数字是否相同，可将最大数和相应得到的差数分为两种类型。

类型1：最大数中间二位数字不同，即A≥B＞C≥D，称无核类型（0核类型），或普通类型。

将相减操作写成竖式，可以得到被减数、减数和差数各构成数字之间的基本关系式：m=A-D m+k=10n=B-C-1 n+p=8p=C-B+9 m>nk=D-A+10很明显，所有差数的共同特点是：首尾二数字之和必为10，中间二数字之和必为8，首位数大于二位数。

这样，能作为差数出现的数并不多，这里将它们从小到大全部罗列如下，共1+2+3+……+9=45个：10892085 21783087 3177 32674086 4176 4266 43565085 5175 5265 5355 54456084 6174 6264 6354 6444 65347083 7173 7263 7353 7443 7533 76238082 8172 8262 8352 8442 8532 8622 87129081 9171 9261 9351 9441 9531 9621 9711 9801类型2：最大数中间二位数字相同，即A≥B=C≥D（不能同时都取等号），称有核类型。