4.2 理想流体的运动微分方程讲解
- 格式:doc
- 大小:438.00 KB
- 文档页数:8

流体力学01-理想流体运动微分方程建立与应用18世纪,在机械工业的推动下,经典力学在微积分支撑下进入建立系统理论体系和广泛应用的时代。
这期间基于微积分连续可微函数概念和质点系力学理论的结合,构成了经典连续介质力学体系。
基于质点系概念的连续介质假设,是力学引进微积分建立理论体系的基础。
01故事的引子1738年瑞士科学家伯努利(Daniel Bernoulli, 1700-1782年,如图1所示),如将质点动能定理沿着同微元流管两截面建立,导出一元流机械能守恒方程,即著名的理想流体定常流动能量方程(后称为伯努利方程)。
图2 瑞士流体力学家欧拉图1 瑞士科学家伯努利1757年瑞士数学家欧拉,(Leonhard Euler, 1707-1783年,如图2所示)将这方程推广至可压缩流动。
对于理想不可压缩流体的定常流动,在质量力为重力作用下,沿同一条流线上的单位重量流体质点的总机械能守恒(单位重量流体质点的位置势能、压强势能和动能之和不变)。
其中,z为流体质点的位置;p为流体质点的压强;V为流体质点的速度;γ为流体容重;g为重力加速度;C为常数。
在不计质量力的条件下(空气的质量密度小,可以忽略重力的影响),此时沿同一条流线单位质量流体质点的压强势能和动能之和不变。
伯努利方程的发现,正确地回答了机翼上翼面吸力对升力的贡献。
后来的风洞试验表明:对于翼型而言,上翼面吸力的贡献约占翼型总升力的60%-70%。
1752年法国科学家达朗贝尔,(Jean le Rond d'Alembert, 1717-1783年,如图3所示在发表的“流体阻尼的一种新理论” 一文中,首次用流体力学的微分方程表示场,提出了任意三维物体理想流体定常绕流无阻力的达朗贝尔佯谬。
1753年欧拉提出了连续介质假设,1755年提出描述流体运动的空间点法(即欧拉方法),并基于连续介质假设和理想流体模型,利用牛顿第二定理建立了理想流体运动微分方程。








理想流体运动微分方程是一种描述理想流体运动的重要工具,它由许多参数组合而成,可以用来描述流体的位置、速度、压力和温度等物理量。
这种方程可以用于分析流体的运动,从而更好地理解流体的性质。
理想流体运动微分方程的主要参数包括动量方程、能量方程和物质守恒方程。
动量方程描述了流体的运动,即流体的加速度、动量和能量。
能量方程描述了流体的能量,即流体的温度、压力和功率。
物质守恒方程描述了物质的守恒,即流体中各种物质的变化。
理想流体运动微分方程在实际应用中非常重要,它可以用来分析流体的运动,从而对流体的性质有更深入的了解。
例如,它可以用来分析和计算流体的流量、速度、压力和温度等物理量。
它还可以用来研究和计算流体的热传导和热扩散等热力学性质。
此外,它还可以用于计算流体的流变性能,从而更好地了解流体的流变特性。
“让我们体会一下流体的美,让它们去探索它们的未知领域。
”——爱因斯坦理想流体运动微分方程在实际应用中可以用来分析和计算各种流体的运动特性,例如水、空气、液体和气体等。
例如,它可以用来计算气体的声速、空气的声压等。
它还可以用来研究和计算流体的粘性、密度、粘度等流变特性。
此外,它还可以用来研究流体的流动结构,比如涡旋结构、涡流结构等。
“每一个人都应该为自己的行为负责,而不是为自己的梦想负责。
”——马克思理想流体运动微分方程也可以用来研究和计算流体的结构性能,比如流体的抗压强度、稳定性和抗冲击性等。
它还可以用来研究流体的热物理性质,比如流体的温度场、压力场和温度分布等。
此外,它还可以用来研究流体的电磁特性,比如流体的电阻率、电导率和磁导率等。
“让我们一起探索未知的流体世界,让它们去发掘它们的奥秘!”——爱迪生理想流体运动微分方程对于科学家们来说是一种重要的研究工具,它可以帮助我们更好地理解流体的性质,从而更好地利用流体的物理量。
它可以用来分析流体的运动,从而更好地理解流体的动力学特性。
它还可以用来研究和计算流体的流变性能,从而更好地了解流体的流变特性。

4.2 理想流体的运动微分方程理想流体是指无粘性的且不可压缩流体,是一种假想的,不存在的流体。
实际流体有粘性,粘性流体。
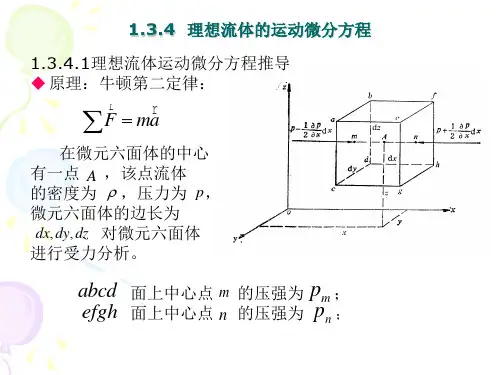
1. Enler 运动微分方程H G图 4-3 理想流体的作用力取微六面体如图4-3所示;中心点为),,(z y x M ,M 处的压强为),,,(t z y x p 。
作用在六面体的力有质量力z y x X d d d ρ,z y x Y d d d ρ,z y x Z d d d ρ;流体运动时的惯性力z y x d d d ρa ;由压强产生的表面力,在x向分别为z y x x p p d d )d 21(∂∂-和z y xx p p d d )2d (∂∂+-。
按牛顿第二定律不难列出x 向的力平衡方程如下:z y x a z y xx p p x x p p z y x X d d d d d )]2d ()2d [(d d d x ρρ=∂∂+-∂∂-+列出y 、z 向力平衡方程。
整理x 、y 、z 向力平衡方程(同除m z y x d d d d =ρ)如下⎪⎪⎪⎩⎪⎪⎪⎨⎧==∂∂-==∂∂-==∂∂-t u a z p Z t u a y p Y t u a x p X d d 1d d 1d d 1zzy y x x ρρρ (4.2-1a) 上式也可简记为tua x p X d d 1i i i i ==∂∂-ρ 3,2,1=i (4.2-1b) 式(4.2-1a)也可写成矢量形式tp d d 1ua G ==∇-ρ(4.2-1c) 式中 Z Y X k j i G ++=为单位质量的体积力。
式(4.2-1a)便是理想流体的运动微分方程,是Euler 1755年推导出来的,故又称Euler 运动微分方程。
4.3 理想的流体运动方程的积分-Bernoulli 方程Bernoulli 方程在工程流体力学基本理论中占有重要地位,其形式简单、意义明确,在工程中有着广泛应用。
理想流体的运动微分⽅程你刚刚更新第四节在流动的理想流体中,取出⼀个微元平⾏六⾯体的微团,它的各边长度分别为d、d和d,如图3-2所⽰。
由于是理想流体,没有黏性,运动时不产⽣内摩擦⼒,所以作⽤在流体微团上的外⼒只有质量⼒和压强。
该压强与静压强⼀样,垂直向内,作⽤在流体微团的表⾯上。
假设六⾯体形⼼的坐标为、、,压强为。
先分析⽅向的运动,在垂直于轴的左右两个平⾯中⼼点上的压强各等于,由于是微元⾯积,所以这些压强可以作为各表⾯上的平均压强。
设在六⾯体形⼼上的单位质量的质量⼒分量为、、和,则作⽤在微元平⾏六⾯体的流体微团上的质量⼒在轴⽅向的分量为⼜流体微团的加速度在轴上的投影为,则根据⽜顿第⼆定律得轴⽅向的运动微分⽅程将上式各项除以流体微团的流体质量,化简后得:]同理:这就是理想流体的运动微分⽅程。
对于静⽌的流体,,则由上式可以直接得出流体平衡微分⽅程,即欧拉平衡微分⽅程式。
因此欧拉平衡微分⽅程只是欧拉运动微分⽅程的⼀个特例。
如果把加速度写成展开式,可将欧拉运动微分⽅程写成如下形式你刚刚更新第五节理想流体微元流束的伯努利(Bernoulli)⽅程⼀.理想流体微元流束的伯努利⽅程理想流体的运动微分⽅程只有在少数特殊情况下才能求解。
在下列⼏个假定条件下:(1)不可压缩理想流体的定常流动;(2)沿同⼀微元流束(也就是沿流线)积分;(3)质量⼒只有重⼒。
即可求得理想流体微元流束的伯努利⽅程。
根据欧拉运动微分⽅程和流线微分⽅程可以推导出或上式称为理想流体微元流束的伯努利⽅程。
该⽅程的适⽤范围是:理想不可压缩均质流体在重⼒作⽤下作定常流动,并沿同⼀流线(或微元流束)。
若1、2为同⼀条流线(或微元流束)上的任意两点,则上式也可写成,在特殊情况下,绝对静⽌流体,可以得到静⼒学基本⽅程。
⼆.⽅程的物理意义和⼏何意义1.物理意义第⼀项z表⽰单位重量流体所具有的位势能;第⼆项表⽰单位重量流体的压强势能;第三项表⽰单位重量流体具有的动能位势能、压强势能和动能之和称为机械能。
4.2 理想流体的运动微分方程理想流体是指无粘性的且不可压缩流体,是一种假想的,不存在的流体。
实际流体有粘性,粘性流体。
1. Enler 运动微分方程H G图 4-3 理想流体的作用力取微六面体如图4-3所示;中心点为),,(z y x M ,M 处的压强为),,,(t z y x p 。
作用在六面体的力有质量力z y x X d d d ρ,z y x Y d d d ρ,z y x Z d d d ρ;流体运动时的惯性力z y x d d d ρa ;由压强产生的表面力,在x向分别为z y x x p p d d )d 21(∂∂-和z y xx p p d d )2d (∂∂+-。
按牛顿第二定律不难列出x 向的力平衡方程如下:z y x a z y xx p p x x p p z y x X d d d d d )]2d ()2d [(d d d x ρρ=∂∂+-∂∂-+列出y 、z 向力平衡方程。
整理x 、y 、z 向力平衡方程(同除m z y x d d d d =ρ)如下⎪⎪⎪⎩⎪⎪⎪⎨⎧==∂∂-==∂∂-==∂∂-t u a z p Z t u a y p Y t u a x p X d d 1d d 1d d 1zzy y x x ρρρ (4.2-1a) 上式也可简记为tua x p X d d 1i i i i ==∂∂-ρ 3,2,1=i (4.2-1b) 式(4.2-1a)也可写成矢量形式tp d d 1ua G ==∇-ρ(4.2-1c) 式中 Z Y X k j i G ++=为单位质量的体积力。
式(4.2-1a)便是理想流体的运动微分方程,是Euler 1755年推导出来的,故又称Euler 运动微分方程。
4.3 理想的流体运动方程的积分-Bernoulli 方程Bernoulli 方程在工程流体力学基本理论中占有重要地位,其形式简单、意义明确,在工程中有着广泛应用。
Bernoulli 方程是Euler 方程或葛罗米柯方程的积分形式。
一 运动微分方程在流线上的积分形式在流线上取质点,不论是否定常运动,经过时间t d ,质点沿流线的微位移z y x d d d d k j i s ++=;s d 的分量,d ,d ,d z y x 可表示为t u z t u y t u x d d ,d d ,d d z y x === (4.3-1)对式(4.2-1a )的三式依次乘z y x d ,d ,d ,相加则有)d d d (1d d d z z p y y p x x p z Z y Y x X ∂∂+∂∂+∂∂-++ρz tuy t u x t u d d d z y x ∂∂+∂∂+∂∂= t u tut u t u t u t u d d d z z y y x x ∂∂+∂∂+∂∂=z z y y x x d d d u u u u u u ++= (4.3-2)引入力势函数),,,(t z y x U ,则有t tUU z Z y Y x X d d d d d ∂∂-=++ (4.3-3) 注意到t tpz z p y y p x x p p d d d d d ∂∂+∂∂+∂∂+∂∂=(4.3-4) 另外由标量速度关系式 2z 2y2x 2u u u u ++=可求 z z y y x x 2z 2y 2x 2d d d )2(d )2(d u u u u u u u u u u ++=++= (4.3-4) 将以上三式代入式(4.3-2),则有)2(d d 1d 1d d 2u t t p p t t U U =∂∂+-∂∂-ρρ或者t t f t tpt U u p U d )(d )1()2(d d 1d 2=∂∂-∂∂=--ρρ (4.3-5) 积分上式则有)(2d 2t F u p U =--⎰ρ (4.3-6)式中 ⎰=t t f t F d )()(如果密度ρ不是压力的函数,则有)(22t F u p U =--ρ (4.3-7)对于定常流=)(t F const ,则有c u pU =--22ρ (4.3-8)如果质量力只有重力,即g Z o Y X -===,,则⎰+-=-=1d c gz z g U将上式代入式(4.3-8),则有022c u p gz -=---ρ (4.3-9)或者022c gu pz =++γ (4.3-10) 式(4.3-10)即是Bernoulli 方程的常见形式。
对于同流线上的任意两点1和2,则上式写成gu p z g u p z 2222222111++=++γγ (4.3-11)对于静止流体,o u =则有0c pz =+γ(4.3-12)γγ2211p z p z +=+(4.3-13)上两式即是流体静力学的基本方程。
二 其他形式的Bernoulli 方程 1实际流体微小流面的Bernoulli 方程图 4-4 实际流体微流束的Bernoulli 方程Bernoulli 方程是在无粘性流体质点沿流线运动或微流束运动条件下导出的。
实际流体有粘性,流体内部存在摩擦力。
为克服这种阻力,流体在运动中要消耗能量,使单位重量的液体沿流过的路程的能量不断减少。
参看图4-4,假定流体从断面1-1流向断面2-2,设断面(1-1)—(2-2)之间的单位重量的流体能量损失―水头损失(Water head loss )为f h ,则有f 2222211122h gu p z g u p z +++=++γγ (4.3-16)其中f h 为流体从断面(1-1)流向断面(2-2)水头损失,由于流体在流动过程中总能量是不断减少的,如果0f <h ,则表明流体的流动是从断面(2-2)流向断面(1-1)。
式(4.3-16)两边同乘重度γ,则有f 2222211122p u z p u z p ∆+++=++ργργ (4.3-17)其中f f h p γ=∆为)22()11(---之间的压力损失。
2 实际总流的Bernoulli 方程2图 4-5 总流的Bernoulli 方程总流由无数微束构成,而每一微束都包含一条或多线流线,称之微流管,这样总流就是含有若干条微流管的流管。
因而用一条真实的管道代替假想的抽象的流管,就得出实际总流的Bernoulli 方程。
参看图4-5,在总流中取微流束,根据已有结论则有f2222211122h g u p z g u p z +++=++γγ如果单位时间通过微流束断面(1-1)和(2-2)的流体重量为Q r d (N/s )。
以Q r d 乘上式两侧各项,然后对总流断面1A 和2A 作积分,则得出总流的能量(功率)关系式如下⎰⎰+++=++21d )2(d )2(22222111A f A Q h u p z Q u p z γγγγ (4.3-18) 现讨论上式中的各积分项:1) ⎰+1d )(1A Q pz γγ为单位时间内通过过流断面的A 的势能和(位置能和压力能之和),该积分不易求出。
但是可以取过流断面为一维缓变流:即0,0x z y ≠==u u u ,并且流向基本与x 轴相符和(图4-6)。
缓变流的流线接近于直线,流线的曲率和彼此的夹角很小,过流断面近于平面(图4-6)。
这种流动的直线和向心加速度都很小,故惯性力可以不计。
因而缓变流压力分布规律符合重力场流体静力学基本规律,即0c pz =+γ故有Q pz Q p z Q p z A A )(d )(d )(212211γγγγγγ+=+=+⎰⎰ (4.3-19)2) ⎰Q gu d 221γ为单位时间内流过过流断面的动能。
由于过流断面各点速度u 不同A u gA u gQ u gAA332)(2d 2d 2γγγ≠=⎰⎰,又很难简单求出,因此采用平均速度u 代替点速度u ,可用系数α加以修正,即取Au Au Au gA u gAA3333)(d )(2d 2⎰⎰==γγα则有 A u gA u gA33)(2d 2γαγ=⎰(4.3-20)3) ⎰AQ h d f γ为因阻力损失的能量。
因不了解f h 和u 的关系难以积分,为简化,假定f h 为常量,即Q h Q h Affd γγ=⎰ (4.3-21)将式(4.3-19)~(4.3-21)代入式(4.3-18)整理,则有f 22222211112)(2)(h gu p z gu p z +++=++αγαγ(4.3-22)在紊流中,一般10.1~05.1=α,因而在工程上可取1≈α。
3 Bernoulli 方程的物理意义参看式(4.3-10),其中z 称位置水头,表示流线上的点或微小流束的断面相对基准面的位置高度,对于单位重量的流体)1(N G =,z 表示流体的位置能。
γp—称压力水头,是压力的液柱高度表示,它表示单位重量液体的压力能。
因1=⋅=V G γ,故γ1=V ,液体的压力能为γppV =。
gu 22—称速度水头,为单位重量的液体的动能。
液体的动能221mu T =,则有)1(2221222====G g u g u G g mgu T 。
Bernoulli 方程表明,对于理想流体,其位置能、压力能和动能可以互相转换,但总和不变。
Bernoulli 方程为能量守恒方程在理想液体中的应用或表现形式。
式(4.3-22)为不可压缩粘性流体在重力场中作定常流时的总流Bernoulli 方程,是工程流体力学中很重要的方程。
在使用时必须注意:(1)对于水平管道,通常取轴线为重力零势位,即021==z z ;对于倾斜放置的管道,则取某过流断面的形心为重力零势位,这时有h z z ==21,0或0,21==z h z 。
对于不变管径u u u ==21;对于渐变管径,可利用连续方程2211u A u A =求出1u 与2u 的关系;21,p p 为两形心处的压力,它们的相互关系可根据静压基本方程导出。
(2) 对于无粘性流体,式(4.3-22)则变形为gu p z gu p z 2)(2)(2222221111αγαγ++=++(4.3-23)其中121==αα时,与理想流体微小流束的Bernouli 方程是十分相近的,唯一的差别是u 和u 的差别。
(3)在两过流断面有能量输入或输出的情况下式(4.3-22)可改写为f 22222211112)(2)(h gu p z E gu p z +++=±++αγαγ(4.3-24)其中E 为以高度形式表示的能量或功率,输入能量(泵和风机)时取“+”号,输出能量(水轮机)取“-”号。
(4) 21,p p 可为绝对压力,也可为相对压力,两者必须一致,在工程上取相对压力比较方便。