粘性流体运动微分方程(了解性学习)讲解

传递过程原理讲课提纲04粘性流体运动的微分方程及其应用2仅供学习与交流，如有侵权请联系网站删除 谢谢36§2—4 N —S 方程在柱坐标及球坐标中的表示 1. 柱坐标中的表示x= rcos αy= rsin αz= z在r 分量方向 zuu r u u r u r u u u r z r r r r ∂∂+-∂∂+∂∂+∂∂2αααθ = ()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫ ⎝⎛∂∂+∂∂-∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂+∂∂-2222222111z u u r u r ru r r r r p X r rr r ααυρα 在α分量方向zuu r u u u r u r u u u z r r ∂∂++∂∂+∂∂+∂∂αααααααθ = ()⎭⎬⎫⎩⎨⎧∂∂+∂∂+∂∂+⎥⎦⎤⎢⎣⎡∂∂∂∂+∂∂-2222222111z u r u r u r ru r r r p r X r αααααυαρ 在z 分量方向zuu u r u r u u u z z z z r z ∂∂+∂∂+∂∂+∂∂αθα = ]1)(1[122222z u u r r u r r r z p X zz z z ∂∂+∂∂+∂∂∂∂+∂∂-αυρ 2. 球坐标中的表示x= (rsin α)cos φ y= (rsin α)sin φ z= rcos α r 分量：yy图 19仅供学习与交流，如有侵权请联系网站删除 谢谢36ru u u r u u r u r u u u r r r r r 22sin φαφαφααθ+-∂∂⋅+∂∂+∂∂+∂∂ ]sin 1)(2sin 1sin sin 11[122222222φαααφαααααυρφαα∂∂++∂∂+-∂∂+⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂-u ctg u u u r u r u r r u r r r r p X r r rr r ＝α分量：rctg u r u u u r u u r u r u u u r r αφααθφααφαααα2sin -+∂∂⋅+∂∂+∂∂+∂∂]sin cos 2sin 2sin 1sin sin 11[11222222222222φααααφαααααυαρφααααα∂∂--∂∂+∂∂+⎪⎭⎫⎝⎛∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂-u r r u u r u r u r r u r r r p r X r ＝φ分量：r ctg u u r u u u r u u r u ru u u r r rθφααθφφφφφαφφ++∂∂⋅+∂∂+∂∂+∂∂sin ]sin cos 2sin sin 2sin 1sin sin 11[sin 112222222222222φαααφαφαααααυφαραφφφφφ∂∂+-∂∂+∂∂+⎪⎪⎭⎫⎝⎛∂∂∂∂+⎪⎪⎭⎫ ⎝⎛∂∂∂∂+∂∂-u r r u u r u r u r r u r r r p r X r ＝§3 流体运动方程的应用§3-1 平壁间的稳定层流设平板无限大，相互平行，作层流运动一维稳定流动，不可压缩于是 u y =u z=0 (1)x图 20仅供学习与交流，如有侵权请联系网站删除 谢谢36由连续性方程有0=∂∂xu x(2) 又对稳定流动0=∂∂θxu (3) 故N —S 方程简化为：)(12222zu y u X x px x ∂∂+∂∂+=∂∂υρ 对无限大平板可认为 0=∂∂z u x故022=∂∂zu x ， 又在x 方向 X = 0于是 222211dy u d dx dpy u x p x x υρυρ=⇒∂∂=∂∂ 边界条件(Boundary Condition) y=y 0, u x =0 初始条件(Initial condition) y=0,0=dydu x于是 ()22021y y dx dp u --=μ 及 ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛-=2max 1y y u u 式中： dxdpy u ⋅-=20max 21μ 又设平板的宽度为w ，则流体流过二平行平板间的体积流量为⎰⎰⎪⎭⎫ ⎝⎛-===Ay v y dx dp w udy w udA Q 0300322μ 另一方面，若设平板间的主体流速（即截面平均流速）A图 21仅供学习与交流，如有侵权请联系网站删除 谢谢36为u b 则有Q V =u b ·B ·(2y 0) 可得： 2031y dx dp u b ⎪⎭⎫ ⎝⎛-=μ 故32=x b u u 及 203y u dx dp b μ-= §3-2 圆形直管内的稳定层流 化工原理中已得出了相应的结论。

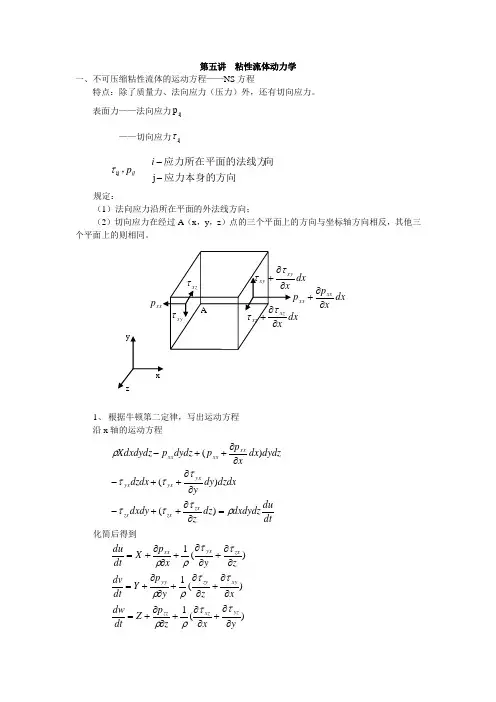
第五讲 粘性流体动力学一、不可压缩粘性流体的运动方程——NS 方程特点：除了质量力、法向应力（压力）外，还有切向应力。

表面力——法向应力ij p——切向应力ij τ应力本身的方向向应力所在平面的法线方，--j ij i p ij τ规定：（1）法向应力沿所在平面的外法线方向；（2）切向应力在经过A （x ，y ，z ）点的三个平面上的方向与坐标轴方向相反，其他三个平面上的则相同。

1、 根据牛顿第二定律，写出运动方程沿x 轴的运动方程 dt du dxdydz dz z dxdy dzdx dy y dzdx dydz dx x p p dydz p Xdxdydz zx zxzx yxyx yx xx xx xx ρττττττρ=∂∂++-∂∂++-∂∂++-)()()( 化简后得到 )(1)(1)(1yx z p Z dt dw xz y p Y dt dv zy x p X dt du yz xz zz xy zy yy zx yx xx ∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=ττρρττρρττρρdx x p xx xx ∂∂+九个应力和三个速度分量均为未知数，四个方程。

2、 切向应力之间的关系由达朗伯原理，对M 点力矩之和为0；质量力和惯性力对该轴的力矩是四阶小量，略去不计，得到02)(22)(2=∂∂+++∂∂+--dx dydz dx x dx dydz dy dxdz dy y dy dxdz xy xy xy yx yx yx ττττττ 再略去四阶小量，得到xzzx zx yz yxxy ττττττ===则九个应力中只有六个是独立变量。

3、 广义牛顿内摩擦定律速度梯度等于流体微团的角变形速率，则有y xz x yzz xy e xw z u e z v y w e y u x v μμτμμτμμτ2)(2)(2)(=∂∂+∂∂==∂∂+∂∂==∂∂+∂∂=4、 法向应力对于理想流体 p p p p zz yy xx -===对于粘性流体，有线变形，使法向应力有变化，产生附加的法向应力，关系式如下。

第三章 粘性流体运动的微分方程及其应用主要包括三个方程:即：微分质量衡算方程---连续性方程；微分动量衡算方程---奈维-斯托克斯（Navier-Stokes ）方程； 微分能量衡算方程---特定条件下的傅立叶第二导热定律。

§1 连续性方程§1—1 连续性方程的推导取如图10微元体，作质量衡算，有：(输入微元体的流体质量流量) =(输出微元体的流体质量流量)+ (微元体中累积的流体质量流量)① 分三个方向讨论:ρ=ρ(x, y , z,θ) u = u (x, y, z,θ)在x 方向输入的流体质量：abcd 面为： ρu x ·dydza 1b 1c 1d 1 面为： [ρu x +()xu x ∂∂ρdx]dy dz x 方向净输出为：[()x u x ∂∂ρdx]dy dz同理， y 方向净输出为：[()yu y ∂∂ρdy]dx dzz 方向净输出为：[()zu z∂∂ρdz]dy dx②微元体中累积的流体质量流量为：dxdydzd dxdydzdxdydz d ⋅∂∂=-⎪⎭⎫⎝⎛⋅∂∂+θρθρθθρρ于是 ：()()()=∂∂+∂∂+∂∂+∂∂θρρρρzu yu xu zyx(1)xz图 11或（表示法①）()0=∇+∂∂uρθρ▽－微分算符(哈密特算符),亦称散度§1－2 连续性方程的分析与简化由于流体流动时： ρ=ρ(x, y , z,θ)故 d ρ=dz z dy y dx x d ∂∂+∂∂+∂∂+⋅∂∂ρρρθθρ即 d ρ/d θ=θρθρθρθρd dz z d dy y d dx x ∂∂+∂∂+∂∂+∂∂=θρρρθρ∂∂+∂∂+∂∂+∂∂zy x u yu xu (2)式中d ρ/d θ称为随体导数,记作θρD D定义:)(zu yu xu D D zy x∂∂+∂∂+∂∂+∂∂=θθ(3)随体导数＝局部导数＋对流导数故上述连续性方程亦可写作（表示法②）：⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂-=z u y u x u D D zy x ρθρ即θρD D = -ρ▽()u(4)讨论 : ①对稳态流动( 运动参数不随时间但可随位置而变化 ),0=∂∂θρ故： ()0=∇uρ② 对不可压缩流体，不论流动是否稳定，因为ρ = 常数故 0=⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂z u y u x u z y x 常用此方程来判别流体的可压缩性③ 由于ρ·υ= 1故: 0=+θρυθυρD D D D 或11=+θρρθυυD D D D式中:θυυD D 1反映了微元流体流动时的体积随时间的变化率, 形变速率θρρD D 1反映了微元流体流动时的密度随时间的变化率比较式(4)可知（表示法③）：u zu yu xu D D z y x∇=∂∂+∂∂+∂∂=θυυ1增例: 某流体运动时其运动速度服从如下空间分布，试判别其压缩性。

连续性方程：单位时间内从x, y, z 方向流入体积元的质量流量为:dydx v dxdz v dydz v z y x ρρρ,, 单位时间内从x, y, z 方向流出体积元的质量流量为:dydx v dxdz v dydz v dz z dy y dx x +++ρρρ,, 有:dydx v v dxdz v v dydz v v dxdydz tdz z z dy y yx dx x x )()()(+++-+-+-=∂∂ρρρρρρρ其中: dx x v v v x x dxx ∂∂+=+ρρρ；dy yv v v y y dy y ∂∂+=+ρρρ；dz z v v v zz dz z ∂∂+=+ρρρ； 可得连续性方程:v div v zv y v x v t i z y x ρρρρρρ-=∙-∇=∂∂+∂∂+∂∂-=∂∂)()( 全微分形式推导：密度ρ是时间t 和空间x, y, z 的函数，即ρ= ρ(t, x, y , z )，则根据全微分定义可得：dz zdy y dx x dt t d ∂∂+∂∂+∂∂+∂∂=ρρρρρ 对t 求导可得：z v y v x v t dt dz z dt dy y dt dx x t dt d zy x ∂∂+∂∂+∂∂+∂∂=⋅∂∂+⋅∂∂+⋅∂∂+∂∂=ρρρρρρρρρ zv y v x v t t dt d zy x v ∂∂+∂∂+∂∂+∂∂=∇∙+∂∂=ρρρρρρρ…………全微分形式 ρρρρρ)(∇∙+∂∂=∇∙+∂∂=v v tt dt d , 由ρρρρ∇∙-∙∇-=∙-∇=∂∂v v v t )(可得：)( zvy v x v d i v dt d z y x v v v v v ∂∂+∂∂+∂∂-=-=∙∇-=∇∙+∇∙-∙∇-=ρρρρρρρ随体导数：dt d ；定义为：zv y v x v t t Dt D z y x v ∂∂+∂∂+∂∂+∂∂=∇∙+∂∂=)( 任一物理量随体导数形式为：zFv y F v x F v t F F t F Dt DF zy x v ∂∂+∂∂+∂∂+∂∂=∇∙+∂∂=运动方程：物理意义：∑=ii F dt d mv ；其中dt d dxdydz dt d V dt d m v v v ⋅=⋅=ρρzv y v x v t t dt d v v v v v v v v z y x ∂∂+∂∂+∂∂+∂∂=∇∙+∂∂=：x 方向：zvv y v v x v v t v dt dv x z x y x x x x ∂∂+∂∂+∂∂+∂∂= y 方向：zv v y v v x v v t v dt dv y z y y y x y y ∂∂+∂∂+∂∂+∂∂= z 方向：zv v y v v x v v t v dt dv z z z y z x z z ∂∂+∂∂+∂∂+∂∂= 质量力：zz g y y g xx g g dxdydz mg F g dxdydz mg F g dxdydz mg F z y x )()()(ρρρ======表面力：定义：SFS n δδσδlim)(→= 流出流体表面力的泰勒级数展开（x 向为例）：dxdydz zdxdy dxdz dy y dxdz dydz dx x dydz zx zx x dz z xyyx x dy y xxxx x dx x )()()()()()(∂∂+=∂∂+=∂∂+=+++σσσσσσσσσ净面力计算（x 向为例）：dxdydz z y x dxdydz z dxdy dxdy dxdydz y dxdz dxdz dxdydz x dydz dydz F zxyx xx xzzx x dz z xy yxx dy y xx xx x dx x )()()()(∂∂+∂∂+∂∂=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡∂∂=-∂∂=-∂∂=-=+++∑σσσσσσσσσσσσdxdydzz y x F dxdydz zy x F dxdydz z y x F zz yz xz z zyyy xy y zxyx xx x )()()(∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=∂∂+∂∂+∂∂=σσσσσσσσσ各轴向动量变化率： 各轴向∑F ：dt d dxdydz dt d m dt d dxdydz dt d m dtd dxdydz dt d m zz y y x x νρννρννρν=== dxdydz zy x dxdydz g F F F dxdydz z y x dxdydz g F F F dxdydz z y x dxdydz g F F F zz yz xz z z gz z zyyy xy y y gy y zx yx xx x x g xx )()()(∂∂+∂∂+∂∂+=+=∂∂+∂∂+∂∂+=+=∂∂+∂∂+∂∂+=+=∑∑∑σσσρσσσρσσσρ各轴线方向分量的运动方程：zy x g dt d zy x g dt d z y x g dt d zz yz xz z zzy yy xy y y zx yx xx x x ∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=∂∂+∂∂+∂∂+=σσσρνρσσσρνρσσσρνρ 运动方程的张量形式：ij i i j ji i i g DtDvx g Dt Dv σρρσρρ∙∇+=∂∂+=或 ij ij ij p τδσ+-=实用的粘性流体剪切流动的运动方程： ij i ip g DtDv τρρ∙∇+∇-= )(zy x i p g Dt Dv ziyi xi i i ∂∂+∂∂+∂∂+∂∂-=τττρρ运动方程在直角坐标系中各方向分量的全微分展开形式：x 方向：)()(zy x x p g z v v y v v x v v t v zx yx xx x x z x y x x x ∂∂+∂∂+∂∂+∂∂-=∂∂+∂∂+∂∂+∂∂τττρρy 方向：)()(z y x y p g z v v y v v x v v t v zyyy xy y y z y y y x y ∂∂+∂∂+∂∂+∂∂-=∂∂+∂∂+∂∂+∂∂τττρρ z 方向：)()(zy x z p g z v v y v v x v v t v zzyz xz z z z z y z x z ∂∂+∂∂+∂∂+∂∂-=∂∂+∂∂+∂∂+∂∂τττρρ 运动方程物理意义：表面粘性力压力重力体积动量局部动量)()(z y x i p g z v v y v v x v v t v ziyi xi i i z i y i x i ∂∂+∂∂+∂∂+∂∂-=∂∂+∂∂+∂∂+∂∂τττρρ能量方程：物理意义：总能量变化率＝单位体积流动能量E 1＋热能净流量E 2＋应力做功E 3＋重力做功E 4 总能量变化率：tE ∂∂)(ρ 单位体积流动能量E 1：)(1i E E ρν∙-∇=x 方向：dV x E dxdydz x E dxdydz x E dydz E dydz E x x x x x ∂∂-=∂∂-=∂∂+-)()())((ρνρνρννρνρ y 方向：dV yE dydxdz y E dydxdz y E dxdz E dxdz E y y y y y ∂∂-=∂∂-=∂∂+-)()())((ρνρνρννρνρz 方向：dV z E dzdxdy z E dzdxdy z E dxdy E dxdy E z z z z z ∂∂-=∂∂-=∂∂+-)()())((ρνρνρννρνρ热能净流量E 2：)(2i q E ∇-=设沿着x 轴，y 轴，z 轴方向在单位时间、单位面积流入的热流密度（即热通量）分别为q x ， q y ，q z ： x 方向：dV x qdydz dx x q q dydz q x x x x ∂∂-=∂∂+-)( y 方向：dV yqdxdz dy y q q dxdz q y y y y ∂∂-=∂∂+-)( z 方向：dV zqdxdy dz z q q dxdy q z z z z ∂∂-=∂∂+-)( 应力做功E 3： )(3i ij j i ijv x v E ∙∙∇=∂∂=σσ 推导原理：dv dF dtdsdF dt dE F ⋅=⋅= x 方向： dV xz xz y xy x xx )(νσνσνσ++∂∂y 方向：dV yz yz y yy x yx )(νσνσνσ++∂∂z 方向：dV zz zz y zy x zx )(νσνσνσ++∂∂ji ij j i jix x ∂∂=∂∂νσνσσ有，作为 对称张量 重力做功E 4：i i v g E ⋅=ρ4 能量方程张量形式：i i ij i i v g v q E tE ∙+∙∙∇+∇-∙-∇=∂∂i )()()(ρσρνρ 能量方程全微分形式推导（实用能量方程）：总能量E = 内能U + 动能K 单位体积能量变化率：dtdKdt dU dt dE ρρρ+= 1. 求解dtdE做随体导数展开：E tE dt dE v ∇∙+∂∂= 同乘以ρ得：E t Edt dE v ∇∙+∂∂=ρρρ有能量方程张量形式：v v v g q E tE t E t E ∙+∙∙∇+∇-∙-∇=∂∂+∂∂=∂∂ρσρρρρ)()()(有运动方程偏微分形式：)(v tρρ∙-∇=∂∂ )(v E tEρρ∙∇-=∂∂ 带入随体导数形式可得： E E g q E E tE t E dt dE v v v v v v ∇∙+∙∇∙+∙∙∇+∇-∙-∇=∇∙+∂∂-∂∂=+ρρρσρρρρρ)()()()(对第一项做∇运算展开：E E E vv v ∇∙+∙∇=∙∇ρρρ)()( 代入可得：v v g q dtdE∙+∙∙∇+-∇=ρσρ)( 2. 求解dt dU有：v v g q dtdK dt dU dt dE ∙+∙∙∇+-∇=+=ρσρρρ)(其中：dtdv v dt v d dt m mvd dt dK ⋅===222121，所以dt d dt dK v v ⋅=ρρ 代入可得：dtd g q dt dK dt dE dt dU v v v v ⋅-∙+∙∙∇+-∇=-=ρρσρρρ)( 有运动方程全微分形式：σρρ∙∇+=g dtd v ， 代入可得： )()()()(σσσρρσρ∙∇∙-∙∙∇+-∇=∙∇∙-∙-∙+∙∙∇+-∇=v v v v v v q g g q dtdU 有张量恒等式置换： v v v ∇=∙∇∙-∙∙∇:)()(σσσ(其中v ∇为并矢运算)，代入可得：i ij i v q dtdU∇+-∇=:σρ又ij ij ij p τδσ+-=，代入可得：i ij i i v v p q dtdU∇+∇--∇=:τρ3. 求解dtdT内能U 是温度T 和体积V 的函数，其全微分形式为：dV V U dT C dV V U dT T U dU T V T V )()()(∂∂+=∂∂+∂∂=，其中V V TU C )(∂∂=………定容比热容； 由热力学第二定律，将dU 写为熵变与体积关系：pdV TdS dW dQ dU -=-=将其在恒温下对体积求导可得： p V ST V U T T -∂∂=∂∂)()(由麦克斯韦热力学函数关系：T V V S T p )()(∂∂=∂∂，代入可得：p Tp T V U V T -∂∂=∂∂)()( 将其代入dU 全微分形式：dV p TpT dT C dU V V ])([-∂∂+= 写为dt dU形式：dtdV p T p T dt dT C dt dU V V ρρρ])([-∂∂+=其中，iv dt d dt d dt d dt dV v ∙∇=∙∇-⋅-=⋅-=⎪⎭⎫ ⎝⎛-⋅=⎪⎪⎭⎫⎝⎛=)(11112ρρρρρρρρρρ代入可得：i V V v p T pT dt dT C dt dU ∙∇-∂∂+=])([ρρ联立dtdU ρ两个表达式：i ij i i i V V v v p q v p T p T dt dT C ∇+∇--∇=∙∇-∂∂+:])([τρ至此，可求得以dtdT描述的能量方程全微分形式：i ij i i V v v Tp T q dt dT C ∇+∙∇∂∂--∇=:)()(τρρ，其中V T p T p )()(∂∂≡∂∂ρ能量方程全微分展开形式：∑+∂∂+∂∂+∂∂∂∂-∂∂+∂∂+∂∂-=∂∂+∂∂+∂∂+∂∂ij z y x V z y x z y x V A zv y v x v T p T z q y q x q z Tv y T v x T v t T C )()()()(或ρρ 其中:)()()()(yv z v x vz v x v y v z v y v x v A z y yz z x xz y x xy z zz y yy x xxij ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=∑ττττττ 注：i ij v ∇:τ的并矢运算和双点积)()()(::332211zvy v x v z v y v x v z v y v x v A A A z v z v z v y v y v y v x v x v xv v A z zz z zy z zx y yz y yy y yx x xz x xy x xx z y x z y x z y x zz zy zx yz yy yx xz xy xx i ij ij ∂∂∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=++=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∇=∑τττττττττττττττττττ 又ji ij ττ=，移项整理可得：)()()()(yv z v x vz v x v y v z v y v x v A z y yz z x xz y x xy z zz y yy x xxij ∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂+∂∂=∑ττττττ 傅立叶热传导方程推导：设流体不可压缩，且流体粘度很低，则可忽略膨胀功与摩擦生热作用；能量方程可简化为：i Vq dtdTC -∇=ρ 将导热通量i q 在x, y, z 三个方向展开：zTq y T q x T q z y x ∂∂-=∂∂-=∂∂-=λλλ, , 则单位时间通过流体微元的导热量为：T zT yT xT q ∇-=∂∂+∂∂+∂∂-=λλλλ)(代入简化能量方程，有：T C T q dt dT C Vi V∆=∇--∇=-∇=ρλλρ)(定义扩散系数（导温系数）a ：VC a ρλ=单位：s m /2 其中：λ为导热系数，单位：K m W ⋅/；ρ为密度； V C 为定容比热容，单位：K kg J ⋅/ 引入扩散系数a ，则写为傅立叶热传导方程：T a DtDT∆=。