三角形的认识PPT课件
- 格式:ppt
- 大小:2.05 MB
- 文档页数:15



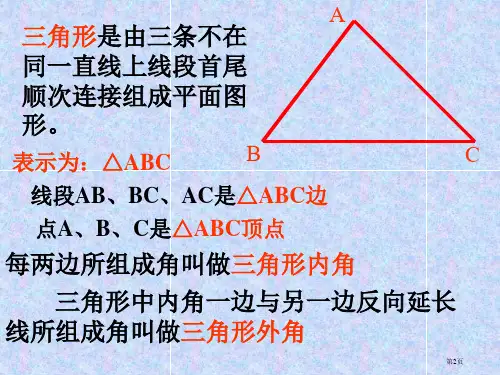
三角形定义及分类三角形的定义由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形。
三角形的分类按边可分为不等边三角形、等腰三角形;按角可分为锐角三角形、直角三角形、钝角三角形。
0102三角形的内角和等于180°。
通过测量或撕拼的方法验证三角形的内角和等于180°。
三角形内角和定理验证方法三角形内角和定理三角形外角性质三角形外角的定义三角形的一边与另一边的延长线组成的角,叫做三角形的外角。
三角形外角性质三角形的外角等于与它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角。
等腰、等边三角形特性等腰三角形特性有两边相等,且两底角相等;具有轴对称性,对称轴是底边的垂直平分线。
等边三角形特性三边相等,三个内角也相等,每个内角都是60°;具有轴对称性,有三条对称轴分别是三边的垂直平分线。
01勾股定理在直角三角形中,直角边的平方和等于斜边的平方。
02勾股定理的逆定理如果三角形的三边满足勾股定理,则这个三角形是直角三角形。
03应用举例通过勾股定理求解直角三角形中的未知边长或角度。
勾股定理及其逆定理正弦、余弦、正切在三角形中应用正弦、余弦、正切的定义及性质在直角三角形中,正弦值等于对边比斜边,余弦值等于邻边比斜边,正切值等于对边比邻边。
应用举例通过已知角度和一边长,利用正弦、余弦或正切求解三角形的其他边长或角度。
两个三角形如果对应角相等,则这两个三角形相似。
相似三角形的定义通过比较对应角或对应边是否成比例来判断两个三角形是否相似。
相似三角形的判定方法相似三角形的对应边成比例,对应角相等。
相似三角形的性质利用相似三角形的性质求解未知边长或角度,或者证明两个三角形相似。
应用举例全等三角形的定义两个三角形如果三边及三角分别相等,则这两个三角形全等。
全等三角形的性质全等三角形的对应边和对应角分别相等。
全等三角形的判定方法通过比较三边及三角是否分别相等来判断两个三角形是否全等,如SSS、SAS、ASA、AAS等判定方法。






小班数学《认识三角形》PPT课件目录CONTENCT •三角形基本概念•三角形图形识别•三角形边长与角度关系•三角形面积计算及应用•三角形变换与操作实践•总结回顾与拓展延伸01三角形基本概念三角形定义及性质三角形的定义由三条线段首尾顺次连接而成的图形。
三角形的基本性质三角形的任意两边之和大于第三边;三角形的三个内角之和等于180度。
三角形分类与特点按角分类锐角三角形(三个角都小于90度)、直角三角形(有一个角等于90度)、钝角三角形(有一个角大于90度)。
按边分类等边三角形(三边相等)、等腰三角形(有两边相等)、不属于以上两种的其他三角形。
生活中三角形应用举例建筑结构在建筑设计中,三角形结构常被用于增强稳定性,如桥梁的支撑结构、房屋的屋顶等。
交通工具部分交通工具的设计中融入了三角形元素,如自行车的车架、飞机的机翼等,以提供稳固的支撑和减少风阻。
物品设计许多日常用品也采用了三角形设计,如三脚架、三角形的桌子和椅子等,这些设计往往具有稳定性和美观性。
02三角形图形识别01 02 03 04 05等边三角形三边长度相等,三个内角均为60度。
等腰三角形有两边长度相等,两个内角相等。
直角三角形有一个内角为90度,其余两个内角之和为90度。
锐角三角形三个内角均小于90度。
钝角三角形有一个内角大于90度,其余两个内角为锐角。
常见三角形图形展示相似与全等三角形判断方法相似三角形判断方法如果两个三角形的对应角相等,则这两个三角形相似。
全等三角形判断方法如果两个三角形的三边及三个内角分别相等,则这两个三角形全等。
观察法拆分法标记法利用已知条件复杂图形中三角形识别技巧通过观察图形的形状和特征,寻找可能存在的三角形。
将复杂图形拆分成简单的图形,再寻找其中的三角形。
在图形上标记出可能的三角形,以便后续分析和计算。
如果已知某些线段或角度的信息,可以利用这些信息来辅助识别三角形。
03三角形边长与角度关系010203三角形两边之和大于第三边三角形两边之差小于第三边等腰三角形两腰相等,等边三角形三边相等三角形边长关系定理介绍角度和定理及其推论三角形内角和为180°等腰三角形底角相等,等边三角形三个角均为60°直角三角形中,两锐角互余,且其中一个锐角的度数为90°减去另一个锐角的度数1 2 3短直角边等于斜边的一半,长直角边等于短直角边的√3倍30°-60°-90°三角形两直角边相等,斜边等于直角边的√2倍45°-45°-90°三角形两直角边相等,斜边等于直角边的√2倍,且两个锐角均为45°等腰直角三角形特殊角度下三角形性质探讨04三角形面积计算及应用海伦公式介绍海伦公式表达式海伦公式应用举例海伦公式求解任意三角形面积假设三角形三边长度分别为a 、b 、c ,半周长p=(a+b+c)/2,则三角形面积S=√[p(p -a)(p-b)(p-c)]。