偏振的矩阵表示

常见偏振器件的jones矩阵常见偏振器件的Jones矩阵1. 引言偏振光是指在特定方向上振动的光波。

为了描述偏振光的性质和行为，人们使用了一种被称为Jones矩阵的工具。

Jones矩阵是一种描述偏振光传播过程中的线性光学器件的数学方法。

在本文中，我们将探讨几种常见的偏振器件，并分析它们的Jones矩阵。

2. 偏振器的基本概念偏振器是一种用于过滤、操作和分析偏振光的器件。

它们根据其内部结构和特性可以分为很多不同的类型。

在讨论Jones矩阵之前，让我们先了解一些常见的偏振器件和它们的特点。

2.1 偏振片偏振片是最基本的偏振器件之一。

它们由具有特殊光学性质的材料制成，可以将非偏振光转化为具有特定偏振方向的偏振光。

偏振片的Jones矩阵非常简单，它只有一个元素，即眯式参数（transmittance）。

2.2 波片波片也是一种常见的偏振器件，它们可以将一个偏振状态的光波转化为另一个偏振状态。

波片的Jones矩阵取决于其光学轴的方向和波片的类型。

最常见的波片类型是快轴在特定角度上旋转的正交波片和半波片。

2.3 偏振旋转器偏振旋转器是可以通过改变其内部光学路径或材料，改变输入偏振态的偏振角度的器件。

偏振旋转器的Jones矩阵是一个旋转角度相关的矩阵，并且可以由绕轴旋转操纵。

3. 常见偏振器件的Jones矩阵3.1 线性偏振器件线性偏振器件是最简单的偏振器件之一，它们只能产生特定方向上的线偏振光。

对于一个线性偏振器件，它的Jones矩阵可以表示为：```J = [cos^2θ sinθcosθ][sinθcosθ sin^2θ ]```其中，θ表示偏振方向与输入光方向之间的夹角。

3.2 偏振分束器偏振分束器是一种可以将输入光分成两个正交偏振态的器件。

它们的Jones矩阵可以表示为：```J = [ T R][ R T]```其中，T表示透过的光的振幅传输率，R表示反射灯（Reflectance）。

3.3 光电调制器光电调制器是利用外部控制电场的变化来改变光的偏振状态的器件。

偏振片的琼斯矩阵偏振片是一种具有选择性通过光波振动方向的光学元件，它是光学偏振的重要组成部分，在光学成像、通讯、光学检测等领域均有广泛的应用。

为了描述偏振片对光波的影响，需要采用琼斯矩阵（Jones matrix）的方法，该方法能够描述光在偏振片中的传播和传输规律。

偏振片的构造通常是由一些具有各向同性的晶体制成，晶体会将入射光线产生双折射，让其沿着不同的方向分离出两个波矢，进而使光线发生偏振现象。

在这种情况下，我们可以用一个二阶矩阵来描述偏振片对一个光线进行处理和分析。

下面我们将详细介绍如何利用琼斯矩阵描述偏振片。

琼斯矩阵是一个二阶复数矩阵。

在偏振片的情况下，琼斯矩阵可以用一个$2\times2$的矩阵表示：$$J=\begin{bmatrix}j_{11} & j_{12} \\j_{21} & j_{22}\end{bmatrix}$$其中，$j_{11}$和$j_{22}$分别是水平方向和垂直方向的偏振片透过率系数，$j_{12}$和$j_{21}$则是偏振轴方向与水平或垂直方向的交叉透过率系数。

可以将矩阵中的元素看作是偏振片对不同方向光线的透射率进行的线性变换。

一般情况下，矩阵元素都是复数。

因为如果考虑自然光通过偏振片，这些元素虽然不会改变光的总强度，但它们却可以改变光波的相位和振幅，从而改变光的偏振状态。

具体来说，当一个电磁波的电场矢量沿与偏振片偏振轴垂直的方向时，沿这个方向的透过率系数为$j_{11}$，而沿着偏振轴方向的透射率系数为$j_{22}$。

考虑当一个平面直线偏振波$E_1$通过偏振片时，它将变成一个另一个透过偏振片的射线$E_2$，琼斯矩阵可以用下面的表达式来描述：这个等式告诉我们，通过偏振片的射线$E_2$是由原始输入射线$E_1$通过琼斯矩阵所描述的线性变换得到的。

这个变换将原始阅读从横向变成了与偏振片偏振轴吻合的方向，因而在偏振片中透过的光就会被这个偏振轴给筛选，被选择出来的光成为透射光，不同于没有被筛选出来的偏振方向，这样偏振轴吻合的组分就有更高的透射率。

常用光学元器件琼斯矩阵
光学元器件是光学系统中不可或缺的组成部分，通常由多种光学元件组合而成，用于调制、分光、合成、偏振和转换光线等。

琼斯矩阵则是描述光学元器件对光线偏振状态影响的标准表达方式。

下面我们将介绍一些常用的光学元器件的琼斯矩阵。

1. 偏振片
偏振片是一种常用的光学元件，它可以使光线偏振态发生变化，并且具有很强的选择性，只允许一定方向的光通过。

偏振片的琼斯矩阵如下：
⎡cos^2θ sinθcosθ⎡
⎡sinθcosθ sin^2θ ⎡
其中，θ为偏振片的传输轴与x轴的夹角。

该矩阵表示了偏振片对于通过的光线偏振状态的影响。

2. 波片
波片可以转化光线的偏振状态，将偏振光线分解为正交的两个部分。

一般来说，波片有四种类型：1/4波片、1/2波片、3/4波片和全波片。

它们的琼斯矩阵分别如下：
1/4波片: ⎡1 0 ⎡
⎡0 -i ⎡
这些矩阵描述了波片对于通过的光线偏振状态的转换。

3. 反射器
反射器是一种将光线反射并改变其方向和偏振状态的元器件。

它的琼斯矩阵如下：
其中，θ为照射反射器的光线与反射器表面法线的夹角。

4. 可调偏振器
可调偏振器是一种可以控制光线偏振方向的元器件。

它的琼斯矩阵可以通过旋转矩阵来描述，旋转角度为α，旋转矩阵为：
5. 偏振束分束器
偏振束分束器可以将偏振光线按照它们的偏振状态分开。

其琼斯矩阵如下：
其中，θ为分束器的切割角。

米勒矩阵琼斯矩阵斯托克斯参数米勒矩阵、琼斯矩阵和斯托克斯参数均是电磁场的描述工具。

它们广泛应用于各种电磁波传播和光学问题的研究中。

本文将分别介绍这三种工具及其在电磁场中的应用。

一、米勒矩阵米勒矩阵是描述各向同性介质中电磁波偏振状态的工具。

在自然光（非偏振光）通过介质时，会发生振动方向的改变，这就是偏振现象。

米勒矩阵描述了光波经过各向同性介质后的偏振状态和光强变化情况。

米勒矩阵可以理解为一个4x4的矩阵，其元素表示光的电场分量与偏振状态的关系。

假设光在入射面的偏振状态描述为E=(Ex, Ey, Ez)T，则米勒矩阵M可以表示为：M = |E'x1| E'=(E'x, E'y, E'z)T为透射面的偏振状态描述。

|E'y2||E'z3||E' 4|米勒矩阵可以用来描述光线经过介质气体、液体或固体时的偏振状态的变化，从而有助于分析光的传播过程。

米勒矩阵在液晶显示器中也有广泛应用。

二、琼斯矩阵J = |J11 J12| J21和J22为复数，描述了光波通过器件后的偏振状态。

|J21 J22|琼斯矩阵可以用来描述偏振光在具有线性或圆偏振光学器件中传输后的偏振状态变化情况。

在应用领域上，琼斯矩阵被广泛用于在激光器件和传感器中来解决光传播的问题。

三、斯托克斯参数斯托克斯参数是描述偏振光波的4个参数，包括偏振度P、方向角度Phi、椭圆度E和振幅As，它们可以描述光波的偏振状态和强度。

偏振度P表示光波偏振的程度，其数值范围为0<P<1，当P=0时为非偏振光，P=1时为全偏振光；振幅As表示光波的强度，其数值可以是任意正实数。

斯托克斯参数可以用于描述偏振光波的状态和变化情况，被广泛用于天文学、大气物理学以及光学测量中。

总结以上三种描述电磁场的工具在光学和电磁学中都有广泛的应用。

米勒矩阵主要用于描述各向同性介质中电磁波偏振状态和光强变化情况；琼斯矩阵被广泛用于解决激光器件和传感器中光传播的问题；斯托克斯参数可以用于描述偏振光波的状态和变化情况，被广泛用于天文学、大气物理学以及光学测量中。

偏振光和偏振器件的矩阵表示和运算陈海云（浙江师范大学信息光学研究所 浙江 金华 321004）摘要 本文研究了偏振光的琼斯矢量和斯托克斯矢量表示方法和偏振器件的琼斯矩阵和密勒矩阵表示和运算方法。

关键词 偏振 琼斯矩阵 密勒矩阵 斯托克斯矢量Matrix Description and Calculus of PolarizedLight and Polarized ElementsCHEN Hai-yun(Institute of Information Optics,Zhejiang Normal University ,Jinhua,Zhejiang 321004)Abstract :This paper studies and analyses the description of the polarized light using the Jones Vector and Stokes Vector and furthermore the description and calculus of the polarized elements are also discussed in this paper.Key words : polarization, Jones matrix, Mueller matrix, Stokes vector 1. 引言偏振是光学中的一个重要概念，描述偏振光和偏振器件有多种方式，如指数函数法，邦加球法等，用琼斯矢量和斯托克斯矢量表示光的偏振态，用琼斯矩阵和密勒矩阵表示偏振器件是一种很好的也很有效的数学方法，在一些文献中也有所涉及，但均不全面，本文从研究光的偏振含义出发，结合高等光学学习中的具体问题，系统地介绍了偏振光和偏振器件的矩阵表示方法，以及琼斯矩阵和密勒矩阵两种矩阵表示方法的联系和区别，对学习和应用偏振光的矩阵表示和运算有一定的指导意义。

2. 偏振光平面光波的矢量场可以表示为[4]：(,)()exp[()]x y z E r t E i E j E k i t k r ω=++--⋅exp[()]E i t k r ω=--⋅ (,)exp[()]H r t H i t k r ω=--⋅结合麦克斯韦旋度方程，运用运算关系：()(),()()i ik tω∂→-∇⨯→⨯∂。

偏振光的矩阵陈泽（西华师范大学物电学院）摘要：偏振是物理光学中的一个重要部分。

近年来，科学实验研究中已经广泛应用了光的偏振特性。

而琼斯（Jones ）矩阵的提出和发展迄今已历半个多世纪之久，其形式的简明有目共睹。

本文将利用琼斯(Jones)矩阵来描述偏振。

引言：我们知道，波的振动方向和波的传播方向相同的波称为纵波；波的振动方向和波的传播方向相互垂直的波称为横波，在纵波的情况下，通过波的传播方向的所有平面内的运动情况都相同，其中没有一个平面显示出比其他任何平面特殊，这通常称为波的振动对传播方向具有对称性。

对横波来说，通过波的传播方向且包含振动矢量的那个平面显然和其他不包含振动矢量的任何平面有区别，这通常称为波的振动方向对传播方向没有对称性，波的振动方向对于传播方向的不对称性叫做偏振，它是横波区别于纵波的一个最明显的标志，只有横波才有偏振现象。

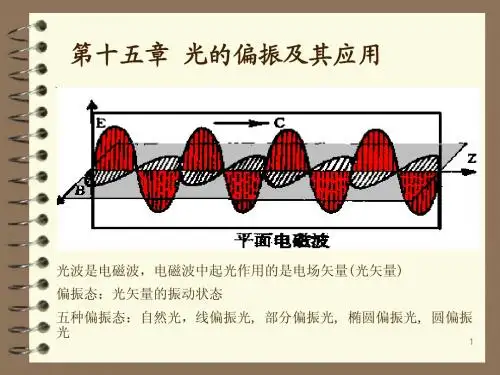
光波是电磁波，光波的传播方向就是电磁波的传播方向，光波中的电矢量E 和磁矢量H 都与传播速度ν垂直，因此光波是横波，它具有偏振性。

1、光波的偏振态平面电磁波是横波，电场和磁场彼此正交，因此当光沿Z 方向传输时，电场只有x 、y 方向的分量，平面波取如下形式：)cos(00δκ+-=E ut E E （1） 式中，写成分量形式为：⎪⎩⎪⎨⎧=+=+=0)cos()cos(21E oy ox E E Ey E Ex δτδτ （2）为了求得电场矢量的端点所描绘的曲线，把上式中参变量Z 消去可得：δδ2022sin cos 2)1(2)1(=-+oy y x oy x E E E E E E Eox （3）偏振情况一般分为两种，一种是电矢量E 的方向永远保护不变，即是线偏振；另一种是电矢量E 端点轨迹为一圆，即圆偏振。

这两种情况都是椭圆偏振的特例：由式（3），当)2,1,0(12 ±±==-=m m πδδδ时，椭圆就退化的一条直线。

x oy mE E Ex Ey 0)1((-= （4） 这时电矢量E 称为线偏振（亦称平面偏振）当Ex.Ey 两分量的振幅相等，且其相位差为2/π的奇数倍，即o oy ox E E E ==)5,3,1(2/12 ±±±==-=m m πδδδ，则试（3）椭圆退化为圆：222E E E y x =+ （6） 则称电矢量是圆偏振。

琼斯矩阵计算偏振状态全文共四篇示例，供读者参考第一篇示例：琼斯矩阵是描述电磁波传播过程中的偏振状态的重要工具，它可以用来计算光束经过各种光学元件后的偏振状态的变化。

在实际的光学系统中，通过琼斯矩阵来分析和设计偏振控制器和偏振分束器等设备，以实现对光束偏振状态的精确控制。

本文将详细介绍琼斯矩阵的基本概念和计算方法，以及其在光学系统中的应用。

1. 琼斯矩阵的基本概念琼斯矩阵是由英国物理学家罗伯特·琼斯在19世纪提出的一种描述光波偏振状态的数学方法。

在光学中，光波的偏振状态可以通过沿着任意方向的振动电场分量来描述。

一个完整的光波偏振状态可以用一个二维复数矢量来表示，即琼斯矢量。

而两个光学元件之间的偏振状态变化则可以用一个二阶矩阵来表示，即琼斯矩阵。

假设一个光束的偏振状态可以用一个复数列向量来表示：\[E = \begin{pmatrix} E_x \\ E_y \end{pmatrix}\]其中E_x和E_y分别表示光波在x和y方向的振幅。

而光学元件对光束的作用可以用一个2 \times 2的矩阵表示：\[M = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\]其中a,b,c,d为复数，且ad - bc = 1。

这个矩阵描述了光束经过该光学元件后的偏振状态的变化。

2. 琼斯矩阵计算方法通过矩阵乘法可以将连续光学元件的琼斯矩阵进行相乘，从而得到整个光学系统的琼斯矩阵。

如果一个光束经过一系列光学元件后，其偏振状态由E_{in}变为E_{out}，则系统的琼斯矩阵可以表示为：\[M_{sys} = M_nM_{n-1}...M_2M_1\]其中M_i表示第i个光学元件的琼斯矩阵。

3. 琼斯矩阵在光学系统中的应用在激光器系统中，通过控制偏振器和相位调制器的琼斯矩阵，可以实现对激光输出光束偏振态的调节，以满足不同应用场景的需求。

在光学通信系统中，通过设计和优化偏振控制器和偏振分束器的琼斯矩阵，可以有效地实现光信号的偏振调制和分析。

半波片和四分之一波片的琼斯矩阵
半波片和四分之一波片是常见的光学元件，它们可以将入射的自然光线偏振成特定方向的偏振光线。

这种偏振转换的过程可以用琼斯矩阵来描述。

半波片是一种光学元件，它可以将入射的线偏振光线转化为垂直方向的偏振光线，或将垂直方向的偏振光线转化为水平方向的偏振光线。

它的琼斯矩阵为：
J = 1/sqrt(2) *
[1 -i;
-i 1]
其中，i为虚数单位，sqrt(2)为常数。

四分之一波片是一种光学元件，它可以将入射的线偏振光线转化为45°方向的偏振光线，或将垂直方向的偏振光线转化为135°方向的偏振光线。

它的琼斯矩阵为：
J = 1/2 *
[1 -i;
-i -1]
需要注意的是，这里的i同样为虚数单位，1/2为常数。

这些琼斯矩阵是通过对偏振光线进行数学分析推导出来的。

在实际应用中，我们可以利用这些矩阵来计算光学系统中的光线传输和偏振转换。

- 1 -。