伯努利方程【课堂资料】

伯努利方程三种形式公式
第一种形式的伯努利方程公式是：
P₁ + 1/2ρv₁² + ρgh₁ = P₂ + 1/2ρv₂² + ρgh₂
其中P₁和P₂分别表示两个位置的压力，ρ表示流体的密度，v₁和v₂表示两个位置的流速，g为重力加速度，h₁和h₂表示两个位置的高度。

这个公式描述了流体在两个位置之间能量守恒的关系。

等式左边的第
一项表示压力能，第二项表示动能，第三项表示单位质量的重力势能。

等
式右边的三项表示相应位置的压力能、动能和重力势能。

这个公式适用于
流体在不完全关闭的管道、管道两端处于同一高度的情况。

第二种形式的伯努利方程公式是：
P + 1/2ρv² + ρgh = const
这是一个简化形式的伯努利方程，它将两个位置的参数合并成一个常数。

这个公式的物理意义是，当流体在流动过程中没有受到外界力的作用时，流体的总能量保持不变。

这个公式适用于理想的水平管道、无摩擦的
流动。

第三种形式的伯努利方程公式是：
P + 1/2ρv² = const
这是伯努利方程的最简形式，它忽略了重力势能的影响。

这个公式适
用于理想的非粘性流体在无重力情况下的流动，如气体等。

这三种形式的伯努利方程公式分别适用于不同的流体力学问题。

选择
适用的公式取决于具体的流动条件和需要分析的问题。

无论选择哪种形式，
伯努利方程都提供了一个重要的工具，可以帮助我们研究流体力学中的能量转换和守恒。

化工原理伯努利方程伯努利方程是流体力学中的一个重要方程，描述了流体在不同位置的速度、压力和高度之间的关系。

它是根据能量守恒定律得到的，并且适用于连续、稳定、摩擦小的流体流动。

伯努利方程的表达式为：P + 1/2ρv^2 + ρgh = constant其中，P代表流体的压力，ρ代表流体的密度，v代表流体的速度，g代表重力加速度，h代表流体在其中一点的高度。

在伯努利方程中，P + 1/2ρv^2项代表了流体的动能或者压力能，ρgh项代表了流体的势能。

考虑一个水流通过管道的情况。

假设水流在管道的其中一点1的速度为v1，压力为P1，高度为h1；在另一点2的速度为v2，压力为P2，高度为h2、根据伯努利方程，我们可以得到以下等式：P1 + 1/2ρv1^2 + ρgh1 = P2 + 1/2ρv2^2 + ρgh2可以看出，这个方程说明了当流体流动时，速度越大，压力越小；而当速度较小时，压力较大。

这是因为伯努利方程通过流体的动能和流体的势能之间的转换关系，描述了流体在流动过程中的能量变化。

伯努利方程在实际应用中有着广泛的应用。

例如，在气象学中，它用于解释风的形成和气候变化等现象。

在流体力学中，它用于计算液体的流速和压力分布等问题，如管道流动、喷嘴流动等。

伯努利方程也有一些限制和假设。

首先，它假设流体是理想流体，即没有黏性和湍流的影响。

其次，它假设流体是连续、稳定的，没有明显的扰动和压力波动。

此外，在应用伯努利方程时，需要注意选择起始点和终止点，并确保考虑到所有影响因素，如摩擦损失、管道的形状等。

总之，伯努利方程是流体力学中的一条重要定律，描述了流体在不同位置的速度、压力和高度之间的关系。

它在实际应用中具有广泛的用途和重要性，但也需要考虑到一些假设和限制。

关于伯努利方程的知识讲解把一个乒乓球放在倒置的漏斗中间(图8－29)，向漏斗口吹气，会把乒乓球吹跑吗？实际正好相反，乒乓球会贴在漏斗上不掉下来．平行地竖放两张纸，向它们中间吹气，会把两张纸吹开吗？实际正好相反，两张纸会贴近(图8－30)．怎样解释上述现象呢？现象中涉及空气的流动．你可能不会想到，解释上述现象，跟说明飞机能够上天，用的是同一个道理，这就是流动的流体中压强和流速的关系．通常把液体和气体统称流体。

这一节把功能关系应用到流动的流体中，推导压强和流速的关系．研究流体的流动，是一门复杂的学问．初步进行研究，需要作一些限定，采用简单的物理模型，这就是理想流体的定常流动．理想流体液体不容易被压缩，在不十分精确的研究中可以认为液体是不可压缩的．气体容易被压缩，但在研究流动的气体时，如果气体的密度没有发生显著的改变，也可以认为气体是不可压缩的．流体流动时，速度不同的各层流体之间有摩擦力，也就是说，流体具有粘滞性．不同的流体，粘滞性不同．油类的粘滞性较大，水、酒精的粘滞性较小，气体的粘滞性更小．研究粘滞性小的流体，在有些情况下可以认为流体没有粘滞性．不可压缩的、没有粘滞性的流体，称为理想流体．定常流动观察一段河床比较平缓的河水的流动，你可以看到河水平静地流着，过一会儿再看，河水还是那样平静地流着，各处的流速没有什么变化．河水不断地流走，可是这段河水的流动状态没有改变．河水的这种流动就是定常流动．流体质点经过空间各点的流速虽然可以不同，但如果空间每一点的流速不随时间而改变，这样的流动就叫做定常流动．自来水管中的水流，石油管道中石油的流动，都可以看作定常流动．流体的流动可以用流线形象地表示．在定常流动中，流线表示流体质点的运动轨迹．图8－31是液体流过圆柱体时流线的分布．AB处液体流过的横截面积大，CD处液体流过的横截面积小，液体在CD处流得急，流速大．AB处的流线疏，CD处的流线密．这样，从流线的分布可以知道流速的大小．流线疏的地方，流速小；流线密的地方，流速大．伯努利方程现在研究理想流体做定常流动时，流体中压强和流速的关系．图8－32表示一个细管，其中流体由左向右流动．在管的a1处和a2处用横截面截出一段流体，即a1处和a2处之间的流体，作为研究对象．a1处的横截面积为S1，流速为v1，高度为h1．a1处左边的流体对研究对象的压强为p1，方向垂直于S1向右．a2处的横截面积为S2，流速为v2，高度为h2．a2处右边的流体对研究对象的压强为p2，方向垂直于S2向左．经过很短的时间间隔Δt，这段流体的左端S1由a1移到b1，右端S2由a2移到b2．两端移动的距离分别为Δl1和Δl2．左端流入的流体体积为ΔV1=S1Δl1，右端流出的流体体积为ΔV2=S2Δl2，理想流体是不可压缩的，流入和流出的体积相等，ΔV1=ΔV2，记为ΔV．现在考虑左右两端的力对这段流体所做的功．作用在左端的力F1=p1S1，所做的功W1=F1Δl1=p1S1Δl1=p1ΔV．作用在右端的力F2=p2S2，所做的功W2=-F2Δl2=-p2S2Δl2=-p2ΔV．外力所做的总功W=W1＋W2=(p1-p2)ΔV．(1)外力做功使这段流体的机械能发生改变．初状态的机械能是a1到a2这段流体的机械能E1，末状态的机械能是b1到b2这段流体的机械能E2．由b1到a2这一段，经过时间Δt，虽然流体有所更换，但由于我们研究的是理想流体的定常流动，流体的密度ρ和各点的流速v没有改变，动能和重力势能都没有改变，所以这一段的机械能没有改变．这样，机械能的改变E2-E1就等于流出的那部分流体的机械能减去流入的那部分流体的机械能．力势能为mgh2=ρgh2ΔV．机械能的改变为右边对这段液体的的作用力向左，而这段液体的位移向右，所以功是负值。

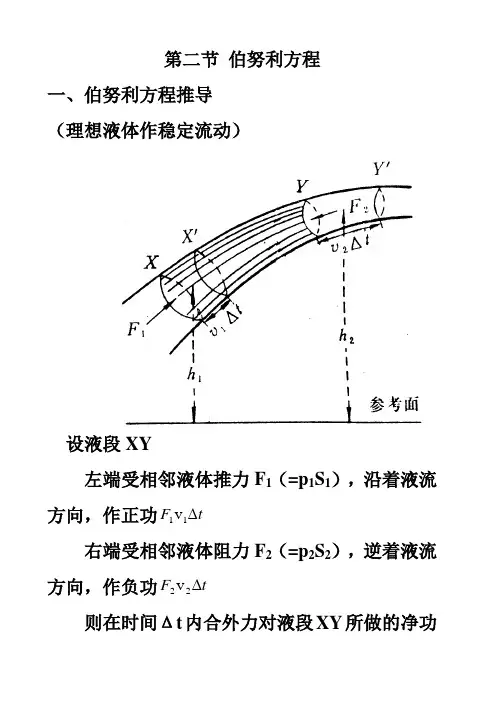
第二节 伯努利方程一、伯努利方程推导 （理想液体作稳定流动）设液段XY左端受相邻液体推力F 1（=p 1S 1），沿着液流方向，作正功t F ∆11v右端受相邻液体阻力F 2（=p 2S 2），逆着液流方向，作负功t F ∆22v则在时间Δt 内合外力对液段XY 所做的净功为t s p t s p W ∆-∆=222111v v按液流连续性原理 V t s t s =∆=∆2211v v 得 V p V p W 21-=若以m 表示XX ’液段或YY ’液段液体的质量 则在时间Δt 内 ，动能的改变量为2122v 21v 21m m E k -=∆势能的改变量为12mgh mgh E p -=∆ 根据功能原理，合外力对这段液体所作的总功等于系统机械能的改变)()v 21v 21(12212221mgh mgh m m V p V p -+-=-整理后，得22221211v 21v 21mgh m V p mgh m V p ++=++ =++mgh m pV v 21常量pV 项具有能量的性质，可以把它看成是体积V的液体处于压强p 时具有的能量，叫做压强能。

用体积V 除上式各项，22221211v 21v 21gh p gh p ρρρρ++=++=++gh p ρρ2v 21常量 p 和gh ρ被称为静压强，2v 21ρ 被称为动压强。

伯努利方程叙述：1．理想液体作稳定流动时，在流管中任一截面处，其动能、势能和压强能之和保持不变。

2．理想液体作稳定流动时，在流管中任一截面处，单位体积液体的动压强、静压强和压强（即该处的压强）之和保持不变。

二、伯努利方程的应用 1．压强和流速的关系若液体在水平管中运动，则 21h h =，其伯努利方程为2222112121v v ρ+=ρ+p p 或=ρ+221v p 常量结论：在水平的管子中流动的液体，流速小的地方压强较大，流速大的地方压强较小。

⑴流量计水平管伯努利方程2222112121v v ρ+=ρ+p p (1) 连续性方程 2211v v s s = (2) 压强差 gh p p ρ=-21(3)联立求解2221212v s s gh s -=体积流量222121112v Q s s ghs s s -== ⑵流速计（皮托管：测流体流速的装置）①原理比较图中c 、d 两处的压强可得d c c P P =+2v 21ρ 即gh p p c d c 2)(2v =-=ρ只要测出两管的液面高度差，便可得到p d与p c的差值，进而求得流速。

流体力学伯努利方程
伯努利方程是描述流体在不可压缩、不黏性、定常流动条件下的基本定律。

它揭示了流体在沿流线运动过程中的能量转换关系。

下面按照列表的形式对伯努利方程进行说明：
1. 方程含义
伯努利方程是流体力学中的一条重要方程，描述了流体在沿流线运动过程中压强、速度和位能之间的关系。

2. 方程表达式
伯努利方程的数学表达式为：
P + 1/2ρv^2 + ρgh = constant
其中，P是流体的压强，ρ是流体的密度，v是流体的流速，g是重力加速度，h是流体元素的高度。

3. 方程意义
伯努利方程可以从宏观上描述流体的能量守恒。

方程右侧的常数表示流体在不同位置的能量之和，包括压力能、动能和重力势能。

4. 各项参数的意义
- 压强：表示流体内部分子之间的相互作用力，与流体的密度和速度无关，随着深度增加而增加。

- 速度：表示单位时间内流体通过某一横截面的体积，与压强和密度的乘积成反比。

- 位能：表示流体元素相对于某一参考点的高度，与压强和速度无关，
随着高度增加而增加。

5. 应用范围
伯努利方程可应用于多个领域，如工程中的管道流动、航空航天中的
气体动力学、水力学中的水流运动等。

总结：
伯努利方程是流体力学的重要定律，可以揭示流体在运动过程中压强、速度和位能之间的转换关系。

它广泛应用于工程、航空航天、水力学
等领域，对于理解和分析流体运动具有重要意义。

伯努利方程知识点总结一、基本概念1. 流体流动在物理学和工程学中，流体流动是一个非常重要的研究领域。

流体包括气体和液体，其流动特性受到各种因素的影响，如流速、流量、压力、密度等。

2. 伯努利方程伯努利方程是描述流体流动的基本方程之一，它是根据能量守恒定律和流体动力学原理推导而来的。

伯努利方程可以用来描述流体在不同位置的流速、静压和动压之间的关系。

它的最基本形式可以表示为：P + 1/2 ρv^2 + ρgh = 常数其中，P代表流体的静压力，ρ代表流体的密度，v代表流体的流速，g代表重力加速度，h代表流体的高度。

这个方程表明了在流体流动的过程中，静压力、动压力和重力势能之间的相互转化关系。

3. 流线与流线管在描述流体流动的过程中，我们经常会使用流线和流线管这两个概念。

流线是指流体在流动过程中所呈现出的路径，它可以用来描述流体的流动轨迹和速度分布。

流线管是指将流线沿着其流动方向构成的管道，它是探索流体流动规律的有力工具。

二、公式推导现在我们来推导伯努利方程的基本形式。

我们假设在一个流线管内部的流体流动，忽略粘性和外部力的影响。

根据流体力学原理和能量守恒定律，我们可以得到以下推导过程：首先，我们考虑流体在不同位置的能量变化。

在流线管的两个不同位置1和2，流体分别具有静压力P1和P2，动压力1/2 ρv1^2和1/2 ρv2^2，重力势能ρgh1和ρgh2。

根据能量守恒定律，我们有：P1 + 1/2 ρv1^2 + ρgh1 = P2 + 1/2 ρv2^2 + ρgh2将上式简化，可得到伯努利方程的基本形式：P1 + 1/2 ρv1^2 + ρgh1 = P2 + 1/2 ρv2^2 + ρgh2这就是伯努利方程的基本公式，它描述了流体在不同位置的静压、动压和重力势能之间的关系。

三、应用领域伯努利方程在许多领域都具有广泛的应用价值，下面我们将对其应用领域进行简要介绍。

1. 空气动力学在航空航天领域，伯努利方程被广泛应用于描述飞机在不同飞行状态下的空气动力学性能。

伯努利方程相关知识点P + 1/2ρv² + ρgh = 常数其中，P表示流体的压强，ρ表示流体的密度，v表示流体的流速，g表示重力加速度，h表示流体的高度。

1.流速与压力的关系：伯努利方程表明，在流体流动的过程中，流体速度越大，压力就越小。

这是因为流体在流动过程中，速度增加时，其动能也随之增加，而根据能量守恒定律，当动能增加时，压力就会减小。

这个现象在日常生活中可以观察到，比如当我们用手指挡住水龙头出口时，水的流速会变小，但是压力会增加。

2.流速与高度的关系：伯努利方程表明，流体速度越大，流体的高度就越低。

这是因为当流体速度增加时，其动能增加，而能量守恒要求总能量保持不变，所以流体的势能就要减小，即流体的高度要降低。

3.流速与压强的关系：伯努利方程表明，流体速度越大，压强越小。

这可以通过对伯努利方程进行推导来证明。

假设在两个不同位置上，流体速度分别为v₁和v₂，流动过程中没有能量损失，即没有粘滞和摩擦损失，那么根据能量守恒定律，有：P₁ + 1/2ρv₁² + ρgh₁ = P₂ + 1/2ρv₂² + ρgh₂由于流动过程中没有液体的体积发生变化，所以ρgh是相等的。

令P₁ - P₂ = ΔP表示压强差，可以得到：1/2ρv₁²+P₁=1/2ρv₂²+P₂=1/2ρv₂²+(P₁-ΔP)由此可知，流体速度越大，压强就越小。

4.伯努利方程的应用：伯努利方程是流体力学中一个非常重要的方程，广泛应用于实际生活和工程领域。

例如，用于飞机、汽车和火箭等交通工具的空气动力学研究中，用于设计水泵和风扇等设备，还可以用来解释血液在血管中流动的现象，以及船只的漂泊和飞行器的升空等。

伯钕利方程公式伯努利方程是流体力学中的一个重要公式，在我们的物理学习中可是个厉害的角色呢！先来说说伯努利方程的表达式：p + 1/2ρv² + ρgh = 常量（p 为压强，ρ 为流体密度，v 为流体速度，g 为重力加速度，h 为高度）。

这看起来是不是有点复杂？别担心，咱们一点点来理解。

想象一下，你在公园里拿着一个喷水枪，水从水枪里喷出来的时候，速度挺快的。

这时候，靠近水枪出口的地方压强就比较小，而水的速度就比较大。

再想想家里的水龙头，如果把水龙头开得小一点，水流出来的速度就慢，这时候出水口附近的压强就相对大一些。

这其实就是伯努利方程在生活中的简单体现。

我还记得有一次，学校组织我们去参观一个工厂。

在那里，我们看到了一个巨大的通风管道系统。

工程师叔叔给我们讲解说，通风管道设计的时候就得用到伯努利方程。

管道里风速快的地方压强小，风速慢的地方压强大，这样才能保证空气能按照需要的方向和速度流动。

我当时就特别好奇，一直盯着那些管道看，心里想着这个神奇的方程是怎么让这一切都有条不紊地运作的。

回到课堂上，老师给我们做了一个实验。

在一个透明的水槽里，有两根粗细不同的管子，水从粗管流进细管的时候，水流的速度明显变快了。

老师就指着这个现象，跟我们说这就是伯努利方程在起作用。

因为细管里水流速度快了，压强就小了，所以水才能加速流过去。

伯努利方程在飞机飞行中也起着至关重要的作用。

飞机的机翼可不是平平的，上面是弧形，下面相对比较平。

当飞机飞行时，空气在机翼上方流动的速度比下方快，根据伯努利方程，机翼上方的压强就小，下方的压强大，这样就产生了一个向上的升力，飞机才能飞起来。

在医学领域，伯努利方程也有它的用武之地。

比如在血液流动的研究中，医生们可以通过这个方程来了解血液在血管中的压力和流速的关系，从而诊断和治疗一些心血管疾病。

总的来说，伯努利方程虽然看起来有点复杂，但它在我们的生活中无处不在，从日常的水流到高科技的飞机飞行，都离不开它的身影。

伯努利原理公式伯努利原理往往被表述为p+1/2ρv2+ρgh=C，这个式子被称为伯努利方程。

式中p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，C是一个常量。

它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。

伯努利方程是丹尼尔•伯努利在 1726 年研究理想液体作稳定流动时提出的。

静压是流体真实存在的压强值，动压也称为速压或速度头，其单位也是Pa。

动压起到调节静压在总压中所占比例的作用：动压越大，静压越小；动压越小，静压越大；动压为零时，即流速为零，静压最大且等于总压值。

因此，伯努利方程式的物理含义也可以说成是流体的压强能和动能之间可以相互转化，但流动的总机械能保持不变。

伯努利方程是流体力学的基本方程，它反映了理想液体作稳定流动时，压强、流速和高度三者之间的关系。

答案】一、一般条件下伯努利方程在各项的意义P +1/2ρv2 +ρgh = 常量该方程说明理想流体在流管中作稳定流动时,单位体积的动能1/2ρv2 、重力势能ρgh 、该点的压强P 之和为一个常量.其中1/2ρv2相与流速有关,常称为动压,ρgh 和P 相与流速无关,常称为静压.二、单位重量流体中伯努利方程各项的物理意义ρg =m/u g =mg/u表示单位体积的重力,以ρg 除各项得:p/ρg+v平方/2 g+ h = 常量该方程表示流场中一点上单位重量流体所具有的总机械能. 其中p/ρg表示流场中一点上单位重量流体所具有的压力潜能,也就是压力对单位体积重量流体所做的功,v平方/2 g 表示单位重量流体所具有的动能, h 就是流场中该点的高度.由于v平方/2 g+ p/ρg+ z = 常数,定理中每一项都具有长度的量纲. 所以p/ρg 表示所考察点的压力潜能的同时也可表示它能将流体压升到某一高度的能力.三、单位质量流体中伯努利方程p/ρ项的物理意义以ρ除各项得:p/ρ+1/2 v平方 + gh = 常量该方程中:p/ρ项表示流场中某一点上单位质量流体所具有的压力或弹性势能,从能量的角度讨论p/ρ项也可理解为单位质量流体相对于p = 0 状态所蕴涵的能量.综上所述：通过以上的分析推导可以看出伯努利方程是能量方程式,尽管分析问题所用的动力学原理不同,但导出方程的意义是完全相同的,说明在管内作稳定流动的理想液体具有压力能、势能和动能三种形式的能量,在适合限定条件的情况下,流场中的三种能量都可以相互转换,但其总和却保持不变,这三种能量统称为机械能. 由此可以得出:伯努利方程在本质上是机械能的转换与守恒.。

伯努利方程知识点伯努利方程是流体力学中最重要的方程之一。

它描述了沿流体流动方向的速度变化、压力变化以及液体高度的变化之间的关系。

伯努利方程在解决各种流体问题时都起着重要的作用，例如管道流动、飞行器设计和气象学等。

伯努利方程表示为：[ P + v^2 + gh = ]其中，P是流体的压力，ρ是流体的密度，v是流体的速度，g是重力加速度，h是流体的高度。

这个方程可以从动能定理、连续性方程和静力学平衡等基本原理推导出来。

接下来，我们将逐步解释伯努利方程的各个部分。

1.压力项（P）：压力是流体分子对容器壁或其他物体施加的力。

在伯努利方程中，压力项表示流体的动能转化为静能的过程中产生的压力变化。

2.动能项：动能项（(v^2)）表示流体的动能，其中ρ是流体的密度，v是流体的速度。

这一项表示流体速度的平方与流体密度的乘积，即动能密度。

当流体速度增加时，动能项也会增加。

3.重力项：重力项（(gh)）表示流体由于高度变化而产生的重力势能。

ρ是流体的密度，g是重力加速度，h是流体的高度。

当流体高度增加时，重力项也会增加。

4.常数项：伯努利方程右侧的常数项表示在流体流动过程中保持不变的量。

这个常数可以代表某个特定位置的流体状态，或者是在某个位置上的初始状态。

伯努利方程的应用非常广泛，下面我们将通过几个具体的例子来说明。

1.管道流动：伯努利方程可以用来分析管道内的液体或气体流动。

当液体或气体通过管道时，速度、压力和高度会发生变化。

通过应用伯努利方程，我们可以计算出流体在不同位置上的压力或速度。

2.飞行器设计：伯努利方程在飞行器的设计中起着重要作用。

例如，在飞机的机翼上方存在着较快的气流速度，而底部的气流速度较慢。

根据伯努利方程，较快的气流速度会导致较低的气压，而较慢的气流速度会导致较高的气压。

这种压差会产生升力，使飞机能够飞行。

3.气象学：伯努利方程也可以用来解释气象现象。

例如，当风穿过山谷或峡谷时，由于流速增加，气压会降低。

一例关于伯努利方程知识点的教学案例教学目标：1.理解伯努利方程的基本概念和公式2.掌握应用伯努利方程解决物理问题的方法3.培养学生的观察、分析和解决问题的能力教学重点和难点：1.理解伯努利方程的物理含义2.运用伯努利方程解决实际问题教学过程：一、导入（5分钟）1.向学生提出问题：为什么飞机在飞行时可以离开地面？学生提出自己的看法，引导学生思考空气的压强、速度和高度的关系。

2.提示学生回顾气体传递速度时学到的内容，引出本节课要学习的伯努利方程。

二、概念讲解（10分钟）1. 在黑板上展示伯努利方程的基本公式：P + 1/2ρv^2 + ρgh = 常数2.解释公式中各个变量的物理意义，如压强P，流体速度v，流体密度ρ，流体高度h等。

3.结合实际图示，讲解伯努利方程的物理含义，如流体速度变快时，压强会降低；流体高度增加时，压强也会降低。

三、应用练习（15分钟）1. 给学生分发纸张上面有一些问题，让学生利用伯努利方程进行计算。

如：一个水管里的水流速度为4 m/s，水管口内外的压强分别为2 atm和1 atm，则水管口内外的水平面差多高？2.学生进行小组讨论，解决问题并写出解题过程和答案。

四、实验演示（20分钟）1.在教室里进行伯努利定律的实验演示。

准备一个塑料瓶，向瓶子下方吹气，瓶口上方放置一张纸片。

学生观察纸片的情况，解释为什么纸片会被吸住。

2.进行进一步解释，使用伯努利方程解释纸片被吸住的现象。

五、案例分析（20分钟）1.展示一些有关伯努利方程应用的案例，如：血管狭窄引起血压升高的原因，火山喷发中岩浆喷出的原理等。

2.分析每个案例的实际情况，让学生运用伯努利方程解释它们，并讨论结果。

六、总结和拓展（10分钟）1.总结伯努利方程的基本概念和公式。

2.引导学生思考其他可能应用伯努利方程的实际问题，鼓励学生进行拓展学习。

教学辅助：1. PowerPoint幻灯片2.实验材料：塑料瓶、纸片等3.大屏幕或投影仪4.学生纸张教学评估：1.针对案例分析阶段，教师进行课堂点名，检查学生对伯努利方程的理解和应用能力。