机械振动阻尼自由振动共32页文档

第三十一页，共32页。
内容总结
第四课 单自由度系统： 阻尼自由振动。库仑阻尼与结构阻尼。库仑阻尼与结构阻尼。比如汽车上常用的液压筒式减振器，其内部的工 作缸被活塞分成上下两腔，并充满液体。当活塞与工作缸有相对运动时，强迫液体经过活塞上的阀在上下腔运 动，液体经脱阀时产生的阻力，使运动能量变为热能耗散掉。在理论分析中最常用的阻尼是气体和液体的粘性 阻尼，它是由于气体或液体在某些机械部件中运动，因而扩散到气体或液体中的热量等能量耗散的度量。例 题
(2.3-2)
第十一页，共32页。
粘性阻尼振动系统
s1,2
c 2m
c
c
2
k
2m 2m m
c
2
2m
k m
c 2m
c
i
2m
k c 2 m 2m
k
c
c
2
k
2m m
c
2
k
2m m
c 2 k 2m m
x m
第十二页，共32页。
粘性阻尼振动系统
考虑 x Aest Aeσ iω ( Aeσ )eiω ，如果 0 ，则物体的运动将不
fd jx
式中 为结构阻尼系数，它与刚度 k 成正比，
gk
式中 g 为结构阻尼损耗因子，或称结构阻尼比。结构阻尼系统运动
方程为
mx kx jx f
第三十页，共32页。
Homework
▪ Write the differential equation of motion for the system in the following figure and determine the natural frequency of damped oscillation and critical damping coefficient.

kx H sin(t ) m x
2 令 n k , h H 则 m m 2 x x h sin(t ) n
无阻尼受迫振动微分方程的标准形式 ，二阶常系数非齐次线性微分方程。
x x1 x2
x1 A sin( n t ) 为对应齐次方程的通解 x2 b sin(t ) 为特解 h h b 2 , x sin(t ) 2 2 2 2 n n h x A sin( t ) sin(t ) 全解为 n 2 2 n ：
——初相位，决定振体运动的起始位置。
T ——周期，每振动一次所经历的时间。
2 f —— 频率，每秒钟振动的次数， f = 1 / T，T 。 n n —— 固有频率，振体在2秒内振动的次数。
n 1 c fn 2 2 a
n反映振动系统的动力学特性，只与系统本身的固有参数有关。
则自由振动的微分方程的标准形式 ： 2
q q 0
其解为 也可以写成 有
q A sin(nt ) q C1 cos nt C2 sin nt
2 1 2 2
A C C
C1 tg C2
1
6
对于初始扰动引起的自由运动
=q 0 设 t = 0 时， q = q0 , q
单自由度系统无阻尼自由振动
一、自由振动的例子

J
k
实验确定转动惯量装置
5
二、单自由度系统无阻尼自由振动微分方程及其解 对于任何一个单自由度系统，以q 为广义坐标（从平衡位 置开始量取 ），则自由振动的运动微分方程必将是：
c a, c是与系统的物理参数有关的常数，令 a
2 n

线性阻尼的数学模型通常表示为： y''(t) + 2*zeta*omega*y'(t) +
omega^2*y(t) = 0，其中 y(t) 是振动 位移，zeta 是阻尼比，omega 是无阻
尼自然频率。
该模型描述了阻尼振动的基本特征，即 线性阻尼适用于描述大多数物理系统的
振幅随时间衰减的现象。
阻尼行为。
故障诊断与预测
通过监测机械设备的振动数据，结合振动公式，可以对设备故障进 行诊断和预测，及时发现潜在问题，提高设备维护效率。
在航空航天中的应用
1 2 3
飞行器稳定性分析
航空航天领域的飞行器在飞行过程中会受到各种 气动力的作用，振动公式的应用可以帮助分析飞 行器的稳定性。
结构强度与疲劳寿命评估
航空航天器的结构和零部件在长期使用过程中会 受到疲劳损伤，振动公式的应用可以评估结构的 强度和疲劳寿命。
受迫振动
当物体受到周期性外力作用时， 会产生受迫振动。受迫振动公式 的推导基于牛顿第二定律和周期
性外力模型。
多自由度系统的振动公式推导
多自由度系统
当一个物体有多个自由度时，其运动可以用多个振动公式 的组合来表示。多自由度系统的振动公式推导基于牛顿第 二定律和多自由度系统模型。
耦合振动
当多个自由度之间存在耦合作用时，其振动规律更为复杂 。耦合振动公式的推导需要考虑各自由度之间的相互作用 。
实验步骤与操作
步骤一
准备实验器材，包括振动平台、 阻尼器、测量仪器等。
步骤三
启动振动平台，记录物体在不同 阻尼条件下的振动情况。
步骤二
将待测物体放置在振动平台上， 调整阻尼器以模拟不同阻尼情况 。

0.8 (e nTd ) 20 0.16
ln5 20 nTd 20 n 2 n 1 2
由于 很小，ln5 40
ln5 W W ln5 1502 c 2 m k 2 2 40 g st 40 1980 0.122( Ns/cm)
nt
2 t n2 n
C2 e
2 t n2 n
)
代入初始条件 (t 0时 , x x0 , x x 0 )
C1
2 0 ( n n 2 n x ) x0
2 n
2
2 n
; C2
2 0 ( n n 2 n ) x0 x 2 2 n 2 n
可见阻尼使自由振动的周期增大，频率降低。当阻尼小时， 影响很小，如相对阻尼系数为5%时，为1.00125，为20%时， 影响为1.02，因此通常可忽略。
14
振幅的影响： 为价评阻尼对振幅衰减快慢的影响，引入减 幅系数η ，定义为相邻两个振幅的比值。
Ai Aewnti wnti td ewntd Ai 1 Ae
5
也可写成
x Ae nt sin(d t )
2 d n n2
—有阻尼自由振动的圆频率
x 0 , 则 设 t 0 时, x x0 , x
2 2 2 x n ( x nx ) 0 n 2 A x0 0 2 02 ; tg1 0 nx0 n n x
16
例4 如图所示，静载荷P去除后质量块越过平衡位置的最大 位移为10%，求相对阻尼系数。
17
x(t ) e
wnt
0 wn x0 x ( x0 cos wd t sin wd t ) wd
18

解：（1）由动量矩定理 ：（1
&& & & J Aθ = − akx − lcx = − a 2 kθ − l 2 cθ
系统的动力学方程： 系统的动力学方程：
l 2c & a 2 k && θ+ θ+ θ =0 JA JA
&& J oθ = ∑ M o
&& & J Aθ + l 2 cθ + a 2 kθ = 0
可以看出： 可以看出： t → ∞ 时，
x (t ) → 0
是指数衰减运动，非振动。 是指数衰减运动，非振动。
例题1 例题1
由弹簧k 阻尼器c及质量为m的匀质杆，组成的系统如图。 由弹簧k、阻尼器c及质量为m的匀质杆，组成的系统如图。 试求： 试求： 系统的动力学方程； 系统的动力学方程； 发生自由振动的条件； 发生自由振动的条件； 最大初始转角； 最大初始转角； 不产生振动的条件； 不产生振动的条件； 对数减缩率。 对数减缩率。 ξ << 1 ( )
2π
实际计算时，常用对数系数， 实际计算时，常用对数系数，
Λ = lnη = δTd = ξω 0Td
Td =
Λ=
即
ωd
=
ω0 1 − ξ 2
一般为： 一般为：
பைடு நூலகம்
1 A1 Λ = ln j A j +1
用途： 用途：此公式在振动实验中有重要应用 （利用实验测出对数减缩并换算出阻尼比） 利用实验测出对数减缩并换算出阻尼比） 当
& & Fd = −c d x 2 sgn x
c d 为阻力系数

y sy(t)机械振动分析------单自由度无阻尼系统的自由振动机械振动是物体(或物体的一部分)在平衡位置（物体静止时的位置）附近作的往复运动。

可分为自由振动、受迫振动。

又可分为无阻尼振动与阻尼振动。

常见的简谐运动有弹簧振子模型、单摆模型等。

振动在机械中的应用非常普遍,例如在振动筛分行业中基本原理系借电机轴上下端所安装的重锤（不平衡重锤），将电机的旋转运动转变为水平、垂直、倾斜的三次元运动，再把这个运动传达给筛面。

若改变上下部的重锤的相位角可改变原料的行进方向。

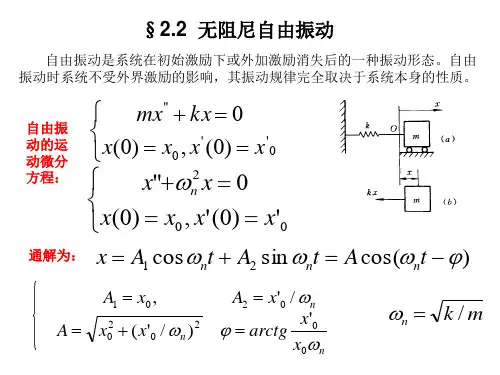
物体受到初干扰后，仅在系统的恢复力作用下在其平衡位置附近的振动称为无阻尼自由振动。

其中仅需用一个独立坐标就可确定振体位置的系统为单自由度系统。

单自由度系统的振动理论是振动理论的基础。

研究单自由度系统的振动有着非常普遍的实际意义，因为工程上有许多问题通过简化，用单自由度系统的振动理论就能得到满意的结果。

而同时对多自由度系统和连续系统的振动，在特殊坐标系中考察时，显示出与单自由度系统类似的性态。

因此，揭示单自由度振动系统的规律、特点，为进一步研究复杂振动系统奠定了基础。

影响振动作用的因素是振动频率、加速度和振幅。

现在我们就此方面展开对单自由度无阻尼振动的讨论。

主要包括两部分：单自由度无阻尼系统的自由振动和单自由度无阻尼系统的受迫振动。

一、单自由度无阻尼系统的自由振动如下图，设此梁上的集中质量为m ，其重量为W mg ，梁由于质量的重力引起的质量处的静力位移用s y 表示，与s y 相应的质量位置称为质量的静力平衡位置。

若此质量受到扰动离开了静力平衡位置，当扰动除去后，则体系将发生振动，这样的振动称为体系的自由振动。

由于振动的方向与梁轴垂直，故称为横向振动。

在此，只讨论微小振幅的振动，由振动引起的内力限于材料的弹性极限以内，用以表示质量运动的方程将为线性微分方程。

1、建立运动方程建立运动方程常用的基本原理是达朗伯原理（亦称惯性力法或动静法）。

利用能量守恒原理——求系统微分方程和固有频率的重要手段
例2.3 如图所示系统，绳索一端接一质量，另一端绕过一转动惯量为I的滑轮与 弹簧相接，弹簧的另一端固定。设绳索无伸长，绳索与滑轮之间无滑动。此时 系统可视为单自由度系统，求系统的固有频率。
解： 原点取在静平衡位置，弹簧的相对伸长为x ，滑轮 沿顺时针方向转过一个角度 x/r 系统的势能为
2
以 0.05 为例，算得 e
1
2
1.37
即物体每振动一次，振幅就减少27%。由此 可见 ，在欠阻尼情况下，周期的变化虽然微 小（ Td=1.00125T，周期 Td 仅增加0.125% ）， 但振幅的衰减却非常显著 ，它是按几何级数衰 减的。


例 图示系统的薄板质量为m, 系统在空气中(认为无阻尼)振动周期为T1 , 在粘性液体中振 动周期为T2 , 液体阻尼力可表示为f d 2 Au, 其中2 A为板的面积， 为粘性系数，为板 u 运动的速度。求证： 2 m 2 2 T2 T1 ATT2 1
d
sin d t )
d n
nTd 2
即
阻尼比较大的系统其自由振动衰减的较快。 如果两个系统的阻尼比相同，则具有较高固有 频率的系统其自由振动衰减较快。这也就是常 说的“高频成分衰减快”
具有临界阻尼的系统与过阻尼系统比较，它为最小阻
尼系统。质量m将以最短的时间回到静平衡位置，并不作
§2.2 无阻尼自由振动
自由振动是系统在初始激励下或外加激励消失后的一种振动形态。自由 振动时系统不受外界激励的影响，其振动规律完全取决于系统本身的性质。
自由振 动的运 动微分 方程：
x" x 0 x(0) x0 , x' (0) x'0 通解为： x A cos t A sin t A cos( t ) n 1 n 2 n

阻尼振动是否具有“周期性"和“等时性”简谐运动在不考虑摩擦和其他阻力等因素的影响时,振动过程中系统的机械能守恒，所以不管是单摆还是弹簧振子在振动过程中振幅始终保持不变，这种振动称为无阻尼振动。

然而，实际的振动总要受到阻力的影响，由于要克服阻力做功，振动系统的机械能不断减少。

同时振动系统与周围介质相互作用，振动向外传播形成波，随着波的传播,系统的机械能不断减少，因此振幅也逐渐减小.这种振幅逐渐减小的振动叫做阻尼振动,阻尼振动的图象如图1所示。

学生学完这节内容后，存在两方面疑问：一是阻尼振动是否具有“周期性"，二是阻尼振动是否具有“等时性”（振子连续两次通过平衡位置的时间间隔相同）。

这两个问题教材没有涉及，在图象中也不能反映出来,但是课后有些学生会提出，有些资料中也会出现相关的问题。

一、定性分析要想知道阻尼振动是否具有“周期性”，首先要知道什么是机械振动的周期。

人教版高二《物理》教材（必修加选修)中对周期的定义是这样的:物体完成一次全振动所需的时间，叫做振动的周期。

在周期的定义中存在全振动这个概念，全振动是指做机械振动的物体从某个点出发，等到下次回到该点时的运动状态和开始振动时的运动状态完全相同，且所用时间最短.所以能重复原来的运动状态（位移、速度、加速度等)的机械振动才是全振动，非等幅的阻尼振动不是全振动，所以它是没有周期的.关于阻尼振动是否具有“等时性”，有两种不同的说法。

第一种说法认为具有“等时性”,理由是阻尼振动的振幅虽然在不断减小，但可以看成是由很多个振幅不断减小的简谐运动的叠加，由于简谐运动具有等时性，它的周期与振幅无关，所以阻尼振动和简谐运动的相位是一致的，节奏也是相同的,所以具有“等时性”。

第二种说法认为不具有“等时性”，理由是物体做阻尼振动时，由于机械能的损失。

振子前后两次通过同一点时，后一次的速度肯定比前一次的小。

这样，从平衡位置到达最大位移处的平均速度总比返回时的平均速度大,所以回来就变慢了,对应的时间也就长了。

相位
t
xA co t s) (
1） t (x ,v )存在一一对应的关系;
物理意义：可据以描述物体在任一时刻的运动状态.
2）相位在 0~2π内变化，质点无相同的运动状态； 相差 2nπ(n为整数)质点运动状态全同.（周期性）
4 初相位 (t0)描述质点初始时刻的运动状态.
( 取 [ π π或][0 2 π) ]
1 振幅
A xmax
2 周期、频率
xAcots()
x xt图
A
o
Tt
T
A
2
A co (ts T [) ]
周期 T 2π
频率 1
弹簧振子周期
T 2π m k
单摆周期
T 2 l g
T 2π
角频率 2π2π
周期和频率仅与振动系 统 本身的物理性质有关
T
一是作为领导干部一定要树立正确的 权力观 和科学 的发展 观，权 力必须 为职工 群众谋 利益， 绝不能 为个人 或少数 人谋取 私利
F
o
m
x
x
Fk xma
令 2 k
m
a2x
xA co t s) (
积分常数，根据初始条件确定
d2x 2x 0 二阶常系数微分方程
dt2
2
一是作为领导干部一定要树立正确的 权力观 和科学 的发展 观，权 力必须 为职工 群众谋 利益， 绝不能 为个人 或少数 人谋取 私利
单摆
msginmt a
mlmdl2m••l
t t 时
o
A
t
xAcots()
以 o为 原点的 旋转
矢量A在 x
x 轴上的投影 点的运动为
简谐运动.

2.5
有阻尼系统的自由振动
阻力可能来自多方面。例如，两物体之间在 润滑表面或干燥表面上相对滑动时的阻力;物体 在磁场或流体中运动所遇到的阻力;以及由于材 料的粘弹性产生的内部阻力等等。在振动中,这 些阻力称为阻尼。
阻尼的分类：
1．干摩擦阻尼 2．结构阻尼 3．流体阻尼 4．粘性阻尼
F N
(2.5-1)
x e nt ( B1eid t B2 e id t )
x e nt A1 cosd t A2 sin d t
(2.5-17)

式中A1=B1+B2，A2=i(B1-B2),为待定系数。仍决定 于初始条件。 设在t=0时，有x=x0, x x0，则代入解式(2.517)及其导数，得
2
2
由解(2.5-18)可见，系统振动已不再是等幅 的简谐振动，而是振幅被限制在曲线 Ae t 之 内，随时间不断衰减。
n
图 2.5-2
当t， x0，振动最终将消失，所以小阻 尼的自由振动也称为衰减振动。
●阻尼对自由振动的影响有两个方面：
(1)使系统振动的周期略有增大，频率略有 降低，即
n
x0 n x0 , A x0 d
2
2
d x0 tg x0 n x0
将A与代入式(2.5-18)即得系统对于初始条件 x0 与 n t 的 x0 响应。 x Ae sin t
d
粘性阻尼系统自由振动响应
d
A2
经 A1与 A2代入式(2.5-17)即得系统对于初始条件x0 与x0 的响应。
通常，经过三角函数变换A1=Asin，A2=Acos，方 程的解(2.5-17)可以简化为

12/9/2021
123 第三十页，共三十一页。
解析 答案
内容(nèiróng)总结
4 阻尼振动 受迫振动。1.判断下列说法的正误.。√。一、简谐运动、阻尼振动和受迫振动。(2)从有没有系统外力 作用角度看弹簧振子的振动属于什么振动。(4)用不同的转速匀速转动手柄，弹簧振子的振动有何不同。①简谐运动是一
①利用：由共振的条件知，要利用共振，就应尽量使驱动力的频率与物体的固有
频率一致.如共振筛、荡秋千、共振转速计等.
12/9/2021
第二十页，共三十一页。
②防止：由共振曲线可知，在需要防止共振危害时，要尽量使驱动力的频 率和固有频率不相等，而且相差越多越好.如：部队过桥应便步走.
说明：共振是物体做受迫振动时的一种特殊(tèshū)现象.
12/9/2021
第二页，共三十一页。
内容(nèiróng)索引
自主预习
预习新知 夯实基础
重点(zhòngdiǎn)探究
启迪思维 探究重点
达标检测(jiǎn cè)
检测评价 达标过关
12/9/2021
第三页，共三十一页。
自主 预习 (zìzhǔ)
12/9/2021
第四页，共三十一页。
一、阻尼振动 自由振动
例1 (多选)一单摆做阻尼振动，则在振动过程中
A.振幅越来越小，频率也越来越小
√B.振幅越来越小，频率不变
C.在振动过程中，通过(tōngguò)某一位置时，机械能始终不变
√D.在振动过程中，机械能不守恒
解析 因单摆做阻尼振动(zhèndòng)，所以振幅越来越小，机械能越来越小，振动
(zhèndòng)频率不变，故选B、D.
12/9/2021

s22 n2 ir2
（4-60）
将式(4—60) sij 代入式(4-62)中，并利用以下数学关系式
eir1t cos r1t i sin r1t eir2t cosr2t i sin r2t
eir1t cosr1t i sin r1t （4-63）
eir2t cos r 2t i sin r 2 t
M
s2
22 11
R22 s11
K22
R21s11 K21
12
A112 A212
R12s12 K12 M11s122 R11s12 K11
M 22s122 R22s12 K22 R21s12 K21
21
A121 A221
R12s21 K12 M11s221 R11s21 K11
M
s2
A222
,
[进行第一次变量代换]
8
利用相角形式，方程的解可以写成：【幅角形式】
x1
C e (1) n1t 1
sin(r1t
1) C1(2)e n2t
s in( r 2 t
2 )
x2
C e (1) n1t 2
sin(r1t
1) C2(2)en2t
sin(r 2t
2 )
(4 65)
其中
C (1) 1
1)
C e (2) n2t 2
sin(r 2t
2
)
(4 65)
比较式(65)及无阻尼自由振动响应式(42)可以看出——
有粘性阻尼自由振动与无阻尼自由振动 其解在形式上相似，
但二者又有区别，如：
(1) 在有阻尼情况下，质体振幅随 e n1t 和 e n2t而减小，
直至最后完全消失；

tan1 x0 n x0 d x0
ppt课件
23
小阻尼的运动曲线
如图所示的为衰减振 5
动。在 cos(dt ) 1 4
的时候，物体的运动 3
2
曲线和曲线：
1
振幅
x Aent
相切， 0 -1
在切点的x值的绝对 -2
值 Aent
称为振幅。 -3 -4
ppt课件
10
方程求解
由于方程为齐次的，因此，方程的解具有 如下形式：
x est
将解的形式带入微分方程：

s
2

c m
s

k m

e
st

0
ppt课件
11
特征方程及其解
由于est 0 ，因此，要想方程成立；
必须： s2 c s k 0 称为微分方程 的特 征方程 m m
19
临界阻尼系统的运动特点
可见：临界阻尼下的系统的运动也不是振动；
但在相同的条件下，临界阻尼的系统的自由 运动最先停止；
因此，仪表都将系统的阻尼设置为临界阻尼。
ppt课件
20
作业3
有粘性阻尼的弹簧质量系统，无阻尼振动的
固有频率为n ，从平衡位置拉开 x0 后释放，
初速度为零。
（1）求 1.25 和 1 时的系统运动情况。
所以，当时 0.3 ，通常忽略阻尼对固 有频率和周期的影响。
ppt课件
28
阻尼对振幅的影响
阻尼对振幅的影响却非常大。设 x1 和 x2分别
是相邻两次的振幅，对应的时间分别为：t1 和 t2 ，则：t2 t1T d

•14
共振的应用和防止
利用共振时，应如何去做?
利用共振时，应使驱动力的频率接近 或等于物体的固有频率
防止共振时，应如何做?
在需要防止共振时，应使驱动力的频率远
离振动物体的固有频率，而且相差越大越好
•.
•15
1.在张紧的水平绳上挂7个单摆，先让D摆振动起来，其余
各摆也随之振动，已知A、D、G三摆的摆长相同，则下列
•.
•6
共振
•7
•.
实验表明：
受迫振动的频率与物体的固有频率无关，但 是如果驱动力的频率接近或等于物体的固有 频率时，振动物体的振幅将达到最大.
因此：受迫振动的振幅A跟 驱动力的频率f’和振动物
体的固有频率之间的关系 有关，它们之间的这种关 系可用图象来表示：这个 图象叫共振曲线（如右 图）.
便桥时，由于马蹄节奏整齐，桥梁发生共振而 断裂。
军队过桥便步走•. ，火车过桥慢行
•12
共振的应用
声音的“共鸣”，是声现象中的共振。
•.
•13
共振的防止
1、军队或火车过桥时要放慢速度或便步走 2、机器运转时为了防止共振要调节转速 3、在振动物体底座加防振垫 4、装修剧场、房屋时使用吸声材料等
•.
0.5
•.
•18
4、下列说法中正确的是（ABC） A、某物体做自由振动时，其振动频率与振幅无关 B、某物体做受迫振动时，其振动频率与固有频率无关 C、某物体发生共振时的频率就是其自由振动的频率 D、某物体发生共振时的振动就是无阻尼振动
5、A、B两个弹簧振子，A的固有频率为f，B的固有 频率为4f，若它们均在频率为3f的驱动力作用下做受
应用共振的有：BD；防止共振的有：AC

阻尼自由振动的特性取决于阻尼 系数c的值，当c越大时，振幅衰 减越快，频率降低越快，相位滞 后越大。
03
阻尼自由振动的实验研究
实验设备与实验方法
实验设备
阻尼自由振动实验装置、测量仪 器、计算机等。
实验方法
搭建阻尼自由振动实验装置，设 定初始条件，记录振动数据，分 析实验结果。
实验结果与分析
结果
注重实际应用
在研究过程中注重实际应用的需求，将研究成果转化 为实际产品和技术，推动社会的发展和进步。
谢谢您的聆听
THANKS
阻尼自由振动还可以用于机械设备的故障诊断，通过监测 和分析异常振动信号，及时发现潜在的故障和问题。
阻尼自由振动在航空航天工程中的应用
飞机设计
在飞机设计中，阻尼自由振动对 于控制机翼、机身等结构的振动 和噪声具有重要意义，可以提高 飞行的安全性和舒适性。
航天器设计
在航天器设计中，阻尼自由振动 有助于控制航天器的姿态和轨道 稳定性，提高航天器的可靠性和 精度。
阻尼自由振动是振动理论 中的一个重要概念，广泛 应用于工程、物理、生物 等多个领域。
阻尼自由振动的研究有助 于深入了解各种实际系统 中振动现象的本质和规律 。
阻尼自由振动的物理意义
01
阻尼自由振动揭示了系统能量耗散的机制，即振动过程中能量 不断转化为其他形式的能量，如热能、光能等。
02
阻尼自由振动对于理解非线性动力学行为、混沌现象等复杂系
新材料开发
阻尼自由振动的研究将推动新材料的发展， 特别是具有优异阻尼性能的材料，为新产品 的开发提供更多可能性。
对阻尼自由振动研究的建议与展望
加强基础研究
进一步深入阻尼自由振动的基础研究，探索其内在规 律和机理，为实际应用提供理论支持。

2018年9月20日 《振动力学》 12
原坐标的系统稳态响应：
q(t ) u(i ) ηi (t )
i 1
n
u(i ) ai 0 2 H ij ( j ) [aij cos( jt ij ) bij sin( jt ij )] i 1 i 2 j 1
并令：cPi 2 ii
则n 自由度系统运动方程变为：
i 2 ii η i i2ηi Ni (t ), i 1 ~ n η
这一方法有很大的实用价值 ，一般适用于振型比例阻尼 ζ i 不 大于0.2的弱阻尼系统。
若系统阻尼较大，不能用振型矩阵超出本课程范围。
其中， i u
(i )T
Cu (i )
2i (i )T N i (t ) u F (t ) (i 1,2, , n)
9
(i 1,2,, n)
下面对几种激励分别讨论 2018年9月20日
《振动力学》
1. 有阻尼系统对简谐激励的响应
假设激励为 F (t ) F sin t 0 将运动方程写成复数形式：
《振动力学》
i2
H i ( ) ei (t i ) , (i 1 ~ n)
1
10
正弦激励下正则坐标的稳态响应：
N 0i i (t i ) ηi (t ) Im 2 H i ( ) e i N 0i sin(t i ) i2 (1 i2 ) 2 (2 i i ) 2
有： uT Muη uT Cuη uT Kuη uT F (t )
即：
C pη Λη N (t ) η
其中：
C p uT Cu
模态阻尼矩阵

1 质量60kg 为40cm 圆筒，盛有质量密度为31100kg m 废料，圆筒被直径为30mm 的钢缆所吊起E=210000000000，当圆筒被吊起10m 时，测出系统固有频率为40Hz ，求圆筒中的废料的容量。

解： 这个系统可以看成如下的模型：一个物体连接在一个弹性杆的末端，所测得频率是纵向振动的频率，这个钢缆的等效刚度是()29272N 0.015m 8010N m =1.4810mAE k Lπ∞⎛⎫⨯ ⎪⎝⎭==⨯总质量为722N1.4810m ==234.3kg rad 402s n n k k m m ωωπ∞∞⨯=→=⎛⎫ ⎪⎝⎭周周因此，废料的质量为 234.3kg-60kg=174.3kg d m m m ω=⋅=它的容量为 33174.3k g =0.158m kg 1100mm V ωρ==2 质量为110kg 的机器固定在刚度为6210N m ⨯的弹性基础上，当机器的运作频率为150rad s 时，机器产生1500N 的谐振力，机器的稳态振幅测得为1.9m m ，则基础的阻尼比为多少？ 解 系统的固有频率为6N210rad m 134.8110kg sn k mω⨯=== 运动过程放大因子为()()22o rad 110kg 134.80.0019m s ==2.531500Nn m X M F ω⎛⎫ ⎪⎝⎭=当运动频率为150rad s 时，频率比为rad150s ==1.113rad 134.8snr ωω=为解阻尼比，方程()3.12可化为()22211-1-2rrMξ=因此，解得()()()22211=-1-13113=0.1422 1.113 2.53ξ⎡⎤⎣⎦3 运用两个自由度来模型化一个两端固定的梁的振动，该梁的长度为L ，E I 弹性模量为，横截面的惯性矩为。

假设广义坐标为梁上等间距点的位移，求该模型的柔度矩阵。

()22223z 1z 1z y z =1--1-1+226L EI L L L L L L ααααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎢⎥⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦解 在距梁上的左侧为的点上施加一个集中单位载荷。