高一数学二倍角的正

1吉林省吉林市高一数学 第三章第2节《二倍角的正弦、余弦、正切（2）》教案 新人教B 版必修4：（一）复习：1．二倍角的正弦、余弦、正切公式。

2．练习：①=π-ππ+π)125cos125)(sin125cos125(sin2365cos125cos125sin22=π-=π-π．②若tan 3θ=，求sin 2cos 2θθ-的值。

（解答：2222222sin cos sin cos 2tan tan 17sin 2cos 2sin cos 1tan 5θθθθθθθθθθθ+-+--===++）．（二）新课讲解：例1．利用三角公式化简：)10tan 31(50sin+．解：原式10cos )10sin 2310cos 21(250sin )10cos 10sin 31(50sin +⋅=+=10cos 40sin 50sin 210cos 10sin 30cos 10cos 30sin 50sin 2=+⋅=110cos 80sin 10cos 40sin 40cos 2===．例2．求证21sin 4cos 41sin 4cos 42tan 1tan θθθθθθ+-++=-．证明：原式等价于22tan 1sin 4cos 4(1sin 4cos 4)1tan θθθθθθ+-=++-， 即：1sin 4cos 4tan 2(1sin 4cos 4)θθθθθ+-=++ （*）而（*）式右边tan 2(1cos 4sin 4)θθθ=++ 2sin 2(2cos 2sin 2cos 2)cos 2θθθθθ=+222sin 2cos 22sin 2θθθ=+ sin 41cos 4θθ=+-=左边， 所以，（*）式成立，原式得证。

【变式练习】已知223sin 2sin 1,3sin 22sin 20αβαβ+=-=，求证：cos(2)0αβ+=． 例3．求函数)7cos(2)722cos(π+-π+=x x y 的值域。

第三章 三角恒等变换3.1两角和与差的正弦、余弦和正切公式3.1.1 两角差的余弦公式一、学习目标 1.知识与技能(1)掌握用向量的数量积推导出两角差的余弦公式的过程，进一步体会向量方法的作用. (2)能用两角差的余弦公式化简、求值.(重点) 2.过程与方法通过公式的推导，领会其中的数学基本思想，掌握研究数学的基本方法，从而提高数学素质.3.情感、态度与价值观通过公式的推导，了解它们的内在联系和知识的发展过程，体会一般与特殊的关系与转化，培养利用联系、变化的辩证唯物主义观点去分析问题的能力.二、教学重点难点重点：灵活运用两角差的余弦公式. 难点：用向量推导两角差的余弦公式. 三、专家建议通过对两角差的余弦公式的推理，变形应用的学习，以及两角差的余弦公式的正用、逆用和变用的学习，从而培养发现思维能力，变异思维能力，分析问题解决问题的能力，强化数学探究意识，掌握转化与化归的数学思想方法。

四、教学方法自学-训练-点拨-练习-总结 五、教学过程 ●课堂探究知识点 两角差的余弦公式 【问题导思】1.单位圆中(如图)，∠AOx ＝α，∠BOx ＝β，那么A ，B 的坐标是什么？OA →与OB →的夹角是多少？【提示】A (cos α，sin α)，B (cos β，sin β). OA →与OB →的夹角是α－β.2.你能用哪几种方法计算OA →·OB →的数量积？【提示】 ①OA →·OB →＝|OA →||OB →|cos(α－β)＝cos(α－β)，②OA →·OB →＝cos αcos β＋sin αsin β. 3.根据上面的计算可以得出什么结论？ 【提示】 cos(α－β)＝cos αcos β＋sin αsin β. 两角差的余弦公式●典例剖析类型1 运用公式求值例1.求下列各式的值：(1)cos(α－35°)cos(25°＋α)＋sin(α－35°)sin(25°＋α)； (2)cos 7°－sin 15°sin 8°cos 8°.【思路探究】 (1)将α－35°，25°＋α分别视为一个角，逆用公式可得解. (2)由7°＝15°－8°，可用两角差的余弦公式解决.【自主解答】 (1)原式＝cos[(α－35°)－(25°＋α)]＝cos(－60°)＝cos 60°＝12. (2)原式＝cos (15°－8°)－sin 15°sin 8°cos 8°＝cos 15°cos 8°＋sin 15°sin 8°－sin 15°sin 8°cos 8°＝cos 15°cos 8°cos 8°＝cos 15°＝cos(45°－30°)＝cos 45°cos 30°＋sin 45°sin 30°＝22×32＋22×12＝6＋24.【总结提升】1.两角差的余弦公式中，α，β可以是单个角，也可以是两个角的和或差，在运用公式时常将两角的和或差视为一个整体.2.在两角差的余弦公式求值应用中，一般思路是：(1)把非特殊角转化为特殊角的和或差，正用公式直接求值.(2)在转化过程中，充分利用诱导公式，构造两角和差的余弦公式的结构形式，然后逆用公式求值.【变式训练】求值：cos 75°cos 15°－sin 255°sin 15°.【解】cos 75°cos 15°－sin 255°sin 15°＝cos 75°cos 15°＋sin 75°sin 15°＝cos(75°－15°)＝cos 60°＝1 2.类型2 给值求值例2.设cos(α－β2)＝－19，sin(α2－β)＝23，且π2＜α＜π，0＜β＜π2，求cosα＋β2的值.【思路探究】由已知可求得α－β2，α2－β的正弦、余弦.只须将α＋β2用已知条件中的角α－β2，α2－β表示出来，注意α－β2和α2－β的范围.用两角和与差的三角函数公式展开即得结论. 【自主解答】∵π2＜α＜π，0＜β＜π2，∴π4＜α－β2＜π，－π4＜α2－β＜π2.又cos(α－β2)＝－19，sin(α2－β)＝23.∴sin(α－β2)＝1－cos2(α－β2)＝459，cos(α2－β)＝1－sin 2(α2－β)＝53.∴cos α＋β2＝cos[(α－β2)－(α2－β)] ＝cos(α－β2)cos(α2－β)＋sin(α－β2)sin(α2－β) ＝－19×53＋459×23＝7527.【总结提升】1.利用差角的余弦公式求值时，不能机械地从表面去套公式，而要变通地从本质上使用公式，即把所求的角分解成某两个角的差，并且这两个角的正、余弦函数值是已知的或可求的，再代入公式即可求解.2.在将所求角分解成某两角的和(差)时，应注意如下变换：α＝(α＋β)－β，α＝β－(β－α)，α＝(2α－β)－(α－β)， 2α＝[(β＋α)－(β－α)]等. 【变式训练】α，β为锐角，cos(α＋β)＝1213，cos(2α＋β)＝35，求cos α的值. 【解】∵α，β为锐角，∴0＜α＋β＜π. 又∵cos(α＋β)＝1213，∴0＜α＋β＜π2， ∴0＜2α＋β＜π.又∵cos(2α＋β)＝35，∴0＜2α＋β＜π2， ∴sin(α＋β)＝513，sin(2α＋β)＝45， ∴cos α＝cos[(2α＋β)－(α＋β)]＝cos(2α＋β)·cos(α＋β)＋sin(2α＋β)·sin(α＋β) ＝35×1213＋45×513＝5665. 类型3 给值求角例3.已知α，β均为锐角，cos α＝17，sin(α＋β)＝5314，求角β的值.【思路探究】 解决本题的关键是根据已知条件，分别求出α的正弦值与α＋β的余弦值.再由β＝(α＋β)－α求出cos α，从而可以根据β的范围求出β的值.【自主解答】 ∵0＜α＜π2，cos α＝17. ∴sin α＝1－cos 2α＝437.又∵0＜β＜π2，∴0＜α＋β＜π.∵sin(α＋β)＝5314＜sin α，∴cos(α＋β)＝－1－sin 2(α＋β)＝－1114.∴cos β＝cos[(α＋β)－α] ＝cos(α＋β)cos α＋sin(α＋β)sin α ＝(－1114)×17＋5314×437＝12. 又∵0＜β＜π2，∴β＝π3.【总结提升】解答给值求角问题的步骤： (1)求角的某一个三角函数值； (2)确定角所在的范围； (3)根据角的范围写出所求的角.特别注意：根据题意选择求角的正弦值、余弦值还是正切值，同时要注意缩小所求角的范围，最好把角的范围缩小在某一三角函数的单调区间内.【变式训练】已知sin α＝16，cos β＝13，且α，β均为锐角，求cos(α-β)的值.【解】∵sin α＝16，cos β＝13，且α，β均为锐角，∴cos α＝1－sin 2α＝1－⎝ ⎛⎭⎪⎫162＝356，sin β＝1－cos 2β＝1－⎝ ⎛⎭⎪⎫132＝223.∴cos(α-β)＝cos αcos β+sin αsin β＝356×13+16×223＝.●课堂小结对公式C (α－β)的理解：(1)公式中的α，β为任意角公式中的α，β不仅可以是任意具体的角，也可以是一个“团体”，比如cos(α＋β2－α－β2)中的“α＋β2”相当于角α，“α－β2”相当于角β，可用两角差的余弦公式展开.因此对公式的理解要注重结构形式，而不要局限于具体的角，完全可以把α，β视为一个“代号”，将公式记作cos(△－□)＝cos△cos□＋sin△sin□.(2)公式C(α－β)的结构特点①同名函数相乘：即两角余弦乘余弦，正弦乘正弦.②把所得的积相加.六、板书设计两角差的余弦公式七．当堂检测1.(2014·天水高一检测)cos 15°＝()A.6－22 B.6＋22C.6－24 D.6＋24【解析】cos 15°＝cos(45°－30°)＝cos 45°·cos 30°＋sin 45°sin 30°＝22×32＋22×12＝6＋24，故选D.【答案】 D2.(2014·乐清高一检测)化简sin(x＋y)sin(x－y)+cos(x＋y)cos(x－y)的结果为()A.sin 2xB.cos 2yC.－cos2yD.－sin 2x【解析】原式＝cos[(x＋y)-(x－y)]＝cos 2y，故选B.【答案】 B3.(2014·青岛高一检测)已知sin θ＝－513，且θ∈⎝ ⎛⎭⎪⎫π，32π，那么cos ⎝ ⎛⎭⎪⎫θ－π4＝________. 【解析】 ∵sin θ＝－513且θ∈⎝ ⎛⎭⎪⎫π，32π，∴cos θ＝－1213，∴cos ⎝ ⎛⎭⎪⎫θ－π4＝cos θcos π4＋sin θ·sin π4＝22×⎝ ⎛⎭⎪⎫－513－1213＝－17226.【答案】 －172264.已知α，β均为锐角，且sin α＝55，cos β＝1010，求α－β的值. 【解】 ∵cos β＝1010，sin α＝55，α，β为锐角， ∴sin β＝31010，cos α＝255. ∴cos(α－β)＝cos αcos β＋sin αsin β ＝255×1010＋55×31010＝22. 又∵sin α＜sin β，∴α＜β. ∴－π2＜α－β＜0.∴α－β＝－π4.。

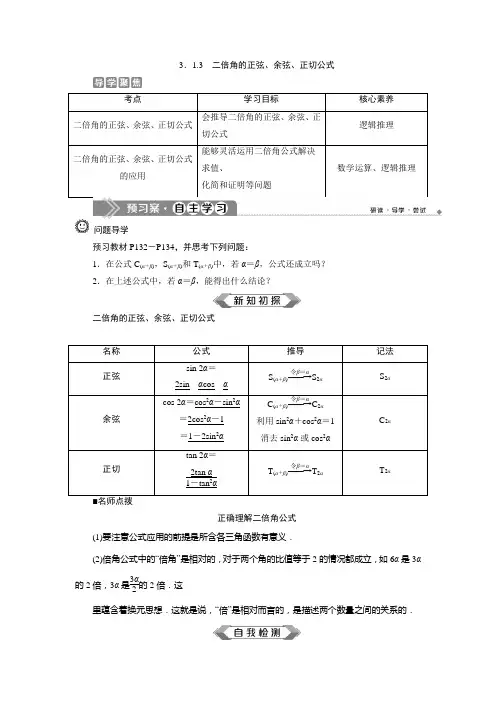
3．1.3二倍角的正弦、余弦、正切公式考点学习目标核心素养二倍角的正弦、余弦、正切公式会推导二倍角的正弦、余弦、正切公式逻辑推理二倍角的正弦、余弦、正切公式的应用能够灵活运用二倍角公式解决求值、化简和证明等问题数学运算、逻辑推理问题导学预习教材P132－P134，并思考下列问题：1．在公式C(α＋β)，S(α＋β)和T(α＋β)中，若α＝β，公式还成立吗？2．在上述公式中，若α＝β，能得出什么结论？二倍角的正弦、余弦、正切公式名称公式推导记法正弦sin 2α＝2sin__αcos__αS(α＋β)――→令β＝αS2αS2α余弦cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2αC(α＋β)――→令β＝αC2α利用sin2α＋cos2α＝1消去sin2α或cos2αC2α正切tan 2α＝2tan α1－tan2αT(α＋β)――→令β＝αT2αT2α正确理解二倍角公式(1)要注意公式应用的前提是所含各三角函数有意义．(2)倍角公式中的“倍角”是相对的，对于两个角的比值等于2的情况都成立，如6α是3α的2倍，3α是3α2的2倍．这里蕴含着换元思想．这就是说，“倍”是相对而言的，是描述两个数量之间的关系的．判断(正确的打“√”，错误的打“×”) (1)10α是5α的倍角，5α是5α2的倍角．( ) (2)二倍角的正弦、余弦、正切公式的适用范围是任意角．( ) (3)存在角α，使得sin 2α＝2sin α成立．( ) (4)对于任意角α，总有tan 2α＝2tan α1－tan 2α.( )答案：(1)√ (2)× (3)√ (4)×已知sin α＝35，cos α＝45，则sin 2α等于( )A.75 B.125 C.1225 D.2425答案：D计算1－2sin 222.5°的结果等于( ) A.12 B.22 C.33D.32 答案：B已知tan α＝43，则tan 2α＝________．答案：－247给角求值求下列各式的值． (1)sin π8cos π8；(2)cos 2π6－sin 2π6；(3)2tan 150°1－tan 2150°； (4)cos π5cos 2π5.【解】 (1)sin π8cos π8＝12×2sin π8cos π8＝12×sin π4＝12×22＝24.(2)cos2π6－sin2π6＝cos⎝⎛⎭⎫2×π6＝cosπ3＝12.(3)原式＝tan(2×150°)＝tan 300°＝tan(360°－60°)＝－tan 60°＝－ 3.(4)原式＝2sinπ5cosπ5cos2π52sinπ5＝sin2π5cos2π52sinπ5＝sin4π54sinπ5＝sinπ54sinπ5＝14.给角求值问题的两类解法(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．1．cos4π12－sin4π12等于()A．－12B．－32C.12 D.32解析：选D.原式＝⎝⎛⎭⎫cos2π12－sin2π12⎝⎛⎭⎫cos2π12＋sin2π12＝cos π6＝32.2．求下列各式的值．(1)tan 30°1－tan2 30°；(2)1sin 10°－3cos 10°.解：(1)tan 30°1－tan230°＝12×2tan 30°1－tan230°＝12tan 60°＝32.(2)原式＝cos 10°－3sin 10°sin 10°cos 10°＝2⎝⎛⎭⎫12cos 10°－32sin 10°sin 10°cos 10°＝4（sin 30°cos 10°－cos 30°sin 10°）2sin 10°cos 10°＝4sin （30°－10°）sin （2×10°）＝4sin 20°sin 20°＝4.给值求值已知cos ⎝⎛⎭⎫α＋π4＝35，π2≤α＜3π2，求cos(2α＋π4)的值． 【解】 因为π2≤α＜3π2，所以3π4≤α＋π4＜7π4.因为cos ⎝⎛⎭⎫α＋π4>0，所以3π2<α＋π4<7π4. 所以sin ⎝⎛⎭⎫α＋π4＝－1－cos 2⎝⎛⎭⎫α＋π4 ＝－1－⎝⎛⎭⎫352＝－45. 所以cos 2α＝sin ⎝⎛⎭⎫2α＋π2 ＝2sin ⎝⎛⎭⎫α＋π4cos ⎝⎛⎭⎫α＋π4 ＝2×⎝⎛⎭⎫－45×35＝－2425， sin 2α＝－cos ⎝⎛⎭⎫2α＋π2＝1－2cos 2⎝⎛⎭⎫α＋π4 ＝1－2×⎝⎛⎭⎫352＝725.所以cos ⎝⎛⎭⎫2α＋π4＝22cos 2α－22sin 2α ＝22×⎝⎛⎭⎫－2425－725＝－31250.三角函数求值问题的一般思路(1)一是对题设条件变形，将题设条件中的角、函数名向结论中的角、函数名靠拢；另一种是对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论．(2)注意几种公式的灵活应用，如： ①sin 2x ＝cos ⎝⎛⎭⎫π2－2x ＝cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ＝2cos 2⎝⎛⎭⎫π4－x －1＝1－2sin 2⎝⎛⎭⎫π4－x ； ②cos 2x ＝sin ⎝⎛⎭⎫π2－2x ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ＝2sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x .1．已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan 2x ＝( ) A.724 B ．－724 C.247D ．－247解析：选D.由cos x ＝45，x ∈⎝⎛⎭⎫－π2，0， 得sin x ＝－35，所以tan x ＝－34，所以tan 2x ＝2tan x1－tan 2x ＝2×⎝⎛⎭⎫－341－⎝⎛⎭⎫－342＝－247，故选D.2．若α∈⎝⎛⎭⎫π2，π，且3cos 2α＝sin ⎝⎛⎭⎫π4－α，则sin 2α的值为( )A.118 B ．－118 C.1718D ．－1718解析：选 D.cos 2α＝sin ⎝⎛⎭⎫π2－2α＝sin 2⎝⎛⎭⎫π4－α＝2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α，代入原式，得6sin ⎝⎛⎭⎫π4－α·cos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4－α.因为α∈⎝⎛⎭⎫π2，π，所以cos ⎝⎛⎭⎫π4－α＝16，所以sin 2α＝cos ⎝⎛⎭⎫π2－2α＝2cos 2⎝⎛⎭⎫π4－α－1＝－1718.化简与证明(1)化简2cos 2α－12tan ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α；(2)证明tan ⎝⎛⎭⎫π4＋α－tan ⎝⎛⎭⎫π4－α＝2tan 2α. 【解】 (1)原式＝cos 2α2tan ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π2－π4－α＝cos 2α2tan ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π4－α＝cos 2α2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α ＝cos 2αsin ⎝⎛⎭⎫2×π4－2α ＝cos 2αcos 2α＝1. (2)证明：法一：左边＝sin ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋α－sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4－α－sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4＋α－π4＋αcos ⎝⎛⎭⎫π4＋αsin ⎝⎛⎭⎫π4＋α＝sin 2α12sin ⎝⎛⎭⎫π2＋2α＝2sin 2αcos 2α＝2tan 2α＝右边．所以等式成立．法二：左边＝1＋tan α1－tan α－1－tan α1＋tan α＝4tan α1－tan 2α＝2tan 2α＝右边．故原式成立．三角函数式的化简与证明(1)化简的方法①弦切互化，异名化同名，异角化同角；②降幂或升幂；③一个重要结论：(sin θ±cos θ)2＝1±sin 2θ.(2)证明三角恒等式的方法①从复杂的一边入手，证明一边等于另一边；②比较法，左边－右边＝0，左边右边＝1；③分析法，从要证明的等式出发，一步步寻找等式成立的条件．1．若α为第三象限角，则1＋cos 2αcos α－1－cos 2αsin α＝________．解析：因为α为第三象限角，所以cos α＜0，sin α＜0， 所以1＋cos 2αcos α－1－cos 2αsin α＝2cos 2αcos α－2sin 2αsin α＝－2cos αcos α－－2sin αsin α＝0.答案：02．求证：4sin αcos α1＋cos 2α·cos 2αcos 2α－sin 2α＝tan 2α.证明：左边＝2sin 2α2cos 2α·cos 2αcos 2α＝tan 2α＝右边．1．已知sin α＝3cos α，那么tan 2α的值为( ) A ．2 B ．－2 C.34D ．－34解析：选D.因为sin α＝3cos α，所以tan α＝3， 所以tan 2α＝2tan α1－tan 2α＝2×31－32＝－34.2．已知sin θ2＋cos θ2＝233，那么sin θ＝________，cos 2θ＝________．解析：因为sin θ2＋cos θ2＝233，所以⎝⎛⎭⎫sin θ2＋cos θ22＝43， 即1＋2sin θ2cos θ2＝43，所以sin θ＝13，所以cos 2θ＝1－2sin 2θ＝1－2×⎝⎛⎭⎫132＝79. 答案：13 793．已知α∈⎝⎛⎭⎫π2，π，sin α＝55. (1)求sin 2α，cos 2α的值； (2)求cos ⎝⎛⎭⎫5π6－2α的值． 解：(1)因为α∈⎝⎛⎭⎫π2，π，sin α＝55， 所以cos α＝－1－sin 2α＝－255.sin 2α＝2sin αcos α＝2×55×⎝⎛⎭⎫－255＝－45， cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫552＝35. (2)由(1)知cos ⎝⎛⎭⎫5π6－2α＝cos 5π6cos 2α＋sin 5π6sin 2α ＝⎝⎛⎭⎫－32×35＋12×⎝⎛⎭⎫－45 ＝－4＋3310.[A 基础达标]1．已知sin ⎝⎛⎭⎫π4－x ＝35，则cos ⎝⎛⎭⎫π2－2x 的值为( )A.1925 B.1625 C.1425D.725解析：选D.因为sin ⎝ ⎛⎭⎪⎫π4－x ＝35，所以cos ⎝ ⎛⎭⎪⎫π2－2x ＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4－x＝1－2sin 2⎝ ⎛⎭⎪⎫π4－x ＝725.2．已知sin α＝55，则cos 4α－sin 4α的值为( ) A ．－35B ．－15C.15D.35解析：选D.cos 4α－sin 4α＝(cos 2α＋sin 2α)(cos 2α－sin 2α)＝cos 2α＝1－2sin 2α＝1－25＝35.3．设－3π<α<－5π2，化简1－cos （α－π）2的结果是( )A ．sin α2B ．cos α2C ．－cos α2D ．－sin α2解析：选C.因为－3π<α<－5π2，－3π2<α2<－5π4，所以1－cos （α－π）2＝1＋cos α2＝⎪⎪⎪⎪⎪⎪cos α2＝－cos α2.4．已知cos ⎝⎛⎭⎫α－π4＝－13，则sin(－3π＋2α)＝( )A.79 B ．－79C.35D ．－35解析：选A.易得cos ⎝ ⎛⎭⎪⎫2α－π2＝2cos 2⎝ ⎛⎭⎪⎫α－π4－1＝2×⎝⎛⎭⎫－132－1＝－79.又cos ⎝⎛⎭⎪⎫2α－π2＝cos ⎝ ⎛⎭⎪⎫π2－2α＝sin 2α，所以sin(－3π＋2α)＝sin(π＋2α)＝－sin 2α＝－⎝⎛⎭⎫－79＝79.故选A. 5．化简tan 14°1－tan 214°·cos 28°的结果为( )A.sin 28°2B ．sin 28°C ．2sin 28°D ．sin 14°cos 28°解析：选A.tan 14°1－tan 214°·cos 28°＝12×2tan 14°1－tan 214°·cos 28°＝12tan 28°·cos 28°＝sin 28°2，故选A.6．已知sin α－2cos α＝0，则tan 2α＝________． 解析：由sin α－2cos α＝0，得tan α＝sin αcos α＝2，tan 2α＝2tan α1－tan 2α＝2×21－22＝－43. 答案：－437．已知tan α＝－13，则sin 2α－cos 2α1＋cos 2α＝________．解析：sin 2α－cos 2α1＋cos 2α＝2sin αcos α－cos 2α1＋2cos 2α－1＝2sin αcos α－cos 2α2cos 2α＝tan α－12＝－56.答案：－568.1－2sin 20°cos 20°2cos 210°－1－cos 2160°－1＝________．解析：1－2sin 20°cos 20°2cos 210°－1－cos 2160°－1＝（cos 20°－sin 20°）2cos 20°－sin 20°＝cos 20°－sin 20°cos 20°－sin 20°＝1.答案：19．已知sin 2α＝513，π4<α<π2，求sin 4α，cos 4α的值．解：由π4<α<π2，得π2<2α<π. 因为sin 2α＝513，所以cos 2α＝－1－sin 22α＝－1－⎝⎛⎭⎫5132＝－1213. 于是sin 4α＝2sin 2αcos 2α＝2×513×⎝⎛⎭⎫－1213＝－120169； cos 4α＝1－2sin 22α＝1－2×⎝⎛⎭⎫5132＝119169. 10．已知π2<α<π，sin α＝45. (1)求tan 2α的值；(2)求cos ⎝⎛⎭⎫2α－π4的值． 解：(1)由题意得cos α＝－35， 所以tan α＝－43， 所以tan 2α＝2tan α1－tan 2α＝－831－169＝247. (2)因为sin α＝45，所以cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫452＝－725， sin 2α＝2sin α·cos α＝2×45×⎝⎛⎭⎫－35＝－2425. 所以cos ⎝⎛⎭⎪⎫2α－π4＝cos 2α·cos π4＋sin 2α·sin π4＝⎝⎛⎭⎫－725×22＋⎝⎛⎭⎫－2425×22＝－31250. [B 能力提升]11．已知tan x ＝2，则tan ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4等于( ) A.43B ．－43 C.34 D ．－34解析：选C.tan ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π4 ＝tan ⎝ ⎛⎭⎪⎫2x －π2＝sin ⎝ ⎛⎭⎪⎫2x －π2cos ⎝ ⎛⎭⎪⎫2x －π2＝－cos 2x sin 2x ＝－1tan 2x＝－1－tan 2x 2tan x ＝4－12×2＝34. 12．已知θ∈⎝⎛⎭⎫π2，π，1sin θ＋1cos θ＝22，则sin ⎝⎛⎭⎫2θ＋π3＝________． 解析：1sin θ＋1cos θ＝22⇒sin θ＋cos θsin θcos θ＝22 ⇒sin θ＋cos θ＝22sin θcos θ⇒1＋sin 2θ＝2sin 22θ，因为θ∈⎝ ⎛⎭⎪⎫π2，π，所以2θ∈(π，2π)， 所以sin 2θ＝－12，所以sin θ＋cos θ<0， 所以θ∈⎝ ⎛⎭⎪⎫3π4，π，所以2θ∈⎝ ⎛⎭⎪⎫3π2，2π， 所以cos 2θ＝32，所以sin ⎝⎛⎭⎪⎫2θ＋π3＝sin 2θ·cos π3＋sin π3cos 2θ＝12. 答案：1213．已知sin ⎝⎛⎭⎫π4－x ＝513，0<x <π4，求cos 2x cos ⎝⎛⎭⎫π4＋x 的值． 解：因为0<x <π4，所以0<π4－x <π4. 又因为sin ⎝ ⎛⎭⎪⎫π4－x ＝513， 所以cos ⎝ ⎛⎭⎪⎫π4－x ＝1213. 因为cos 2x ＝sin ⎝ ⎛⎭⎪⎫π2－2x ＝2sin ⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x ＝2sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π4＋x cos ⎝ ⎛⎭⎪⎫π4－x＝2cos ⎝ ⎛⎭⎪⎫π4＋x cos ⎝ ⎛⎭⎪⎫π4－x ， 所以cos 2x cos ⎝ ⎛⎭⎪⎫π4＋x ＝2cos ⎝ ⎛⎭⎪⎫π4－x ＝2413. 14．(选做题)已知sin x 2－2cos x 2＝0. (1)求tan x 的值；(2)求cos 2xcos ⎝⎛⎭⎫5π4＋x sin （π＋x ）的值．解：(1)由sin x 2－2cos x 2＝0， 知cos x 2≠0，所以tan x 2＝2， 所以tan x ＝2tan x 21－tan 2 x 2＝2×21－22＝－43. (2)由(1)知tan x ＝－43， 所以cos 2x cos ⎝ ⎛⎭⎪⎫5π4＋x sin （π＋x ） ＝cos 2x－cos ⎝ ⎛⎭⎪⎫π4＋x （－sin x ） ＝cos 2x －sin 2x ⎝⎛⎭⎫22cos x －22sin x sin x ＝（cos x －sin x ）（cos x ＋sin x ）22（cos x －sin x ）sin x ＝2×cos x ＋sin x sin x＝2×1＋tan x tan x ＝24.。

能 力 提 升一、选择题1．(2013·长沙模拟)若cos2αsin (α－π4)＝－22，则cos α＋sin α的值为( )A ．－72 B ．－12 C.12 D.72[答案] C[解析] cos2αsin (α－π4)＝cos 2α－sin 2α22(sin α－cos α) ＝(cos α＋sin α)(cos α－sin α)22(sin α－cos α)＝－2(cos α＋sin α)＝－22. ∴sin α＋cos α＝12.2．已知sin θ＝45，sin θcos θ<0，则sin2θ的值为( ) A ．－2425 B ．－1225 C ．－45 D.2425 [答案] A[解析] ∵sin θ＝45>0，sin θcos θ<0， ∴cos θ<0.∴cos θ＝－1－sin 2θ＝－35.∴sin2θ＝2sin θcos θ＝－2425.3．若x ＝π12，则cos 2x －sin 2x 的值等于( ) A.14 B.12 C.22 D.32[答案] D[解析] 当x ＝π12时，cos 2x －sin 2x ＝cos2x ＝cos(2×π12)＝cos π6＝32.4．(2013·济南模拟)已知cos2θ＝23，则sin 4θ＋cos 4θ的值为( ) A.1318 B.1118 C.79 D ．－1 [答案] B[解析] sin 4θ＋cos 4θ＝(sin 2θ＋cos 2θ)2－2sin 2θcos 2θ ＝1－12sin 22θ＝1－12(1－cos 22θ)＝1118.5．已知向量a ＝⎝ ⎛⎭⎪⎫cos θ，12的模为22，则cos2θ等于( ) A.2－32 B ．－14 C ．－12 D.12 [答案] C[解析] |a |＝cos 2θ＋14＝22，则cos 2θ＝14，所以cos2θ＝2cos 2θ－1＝－12.6．(2013·新课标Ⅱ文)已知sin2α＝23，则cos 2(α＋π4)＝( ) A.16 B.13 C.12 D.23[答案] A[解析] 本题考查半角公式及诱导公式．由倍角公式可得，cos 2(2＋π4)＝1＋cos (2α＋π2)2＝1－sin2α2＝1－232＝16，故选A.二、填空题7．在△ABC 中，cos A ＝513，则sin2A ＝________. [答案] 120169[解析] ∵0<A <π，∴sin A ＝1－cos 2A ＝1213.∴sin2A ＝2sin A cos A ＝120169.8．(2013山东师大附中模拟)若α∈(0，π2)，且sin 2α＋cos2α＝14，则tan α的值等于________．[答案]3[解析] 由sin 2α＋cos2α＝14得sin 2α＋1－2sin 2α＝1－sin 2α＝cos 2α＝14.∵α∈(0，π2)，∴cos α＝12，∴α＝π3，∴tan α＝tan π3＝ 3.9．2002年北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形接成的一个大正方形(如图)．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为θ，那么cos2θ的值等于________．[答案] 725[解析] 设直角三角形的两直角边长分别为a ，b ，则有4×⎝ ⎛⎭⎪⎫12ab ＋1＝25，∴ab ＝12.又a 2＋b 2＝25，即直角三角形的斜边c ＝5.解方程组⎩⎪⎨⎪⎧ab ＝12，a 2＋b 2＝25，得⎩⎪⎨⎪⎧a ＝3，b ＝4或⎩⎪⎨⎪⎧a ＝4，b ＝3，∴cos θ＝45.∴cos2θ＝2cos 2θ－1＝725. 三、解答题10．已知sin(π4－x )＝513，0<x <π4，求cos2xcos (π4＋x )的值． [解析] 原式＝sin (π2＋2x )cos (π4＋x )＝2sin (π4＋x )·cos (π4＋x )cos (π4＋x )＝2sin(π4＋x )．∵sin(π4－x )＝cos(π4＋x )＝513， 且0<x <π4， ∴π4＋x ∈(π4，π2)， ∴sin(π4＋x )＝1－cos 2(π4＋x )＝1213.∴原式＝2×1213＝2413.11．已知cos(x －π4)＝210，x ∈(π2，3π4)． (1)求sin x 的值． (2)求sin(2x ＋π3)的值． [解析] (1)因为x ∈(π2，3π4)， 所以x －π4∈(π4，π2)，于是sin(x －π4)＝1－cos 2(x －π4)＝7210，则sin x ＝sin[(x －π4)＋π4] ＝sin(x －π4)cos π4＋cos(x －π4)sin π4 ＝7210×22＋210×22＝45. (2)因为x ∈(π2，3π4)， 故cos x ＝－1－sin 2x ＝－1－(45)2＝－35，sin2x ＝2sin x cos x ＝－2425，cos2x ＝2cos 2x －1＝－725，所以sin(2x ＋π3)＝sin2x cos π3＋cos2x sin π3＝－24＋7350.12．设函数f (x )＝2cos x sin(x ＋π3)－3sin 2x ＋sin x cos x ，当x ∈[0，π2]时，求f (x )的最大值和最小值．[解析] f (x )＝2cos x (12sin x ＋32cos x )－3sin 2x ＋sin x cos x ＝2sin x cos x ＋3(cos 2x －sin 2x )＝sin2x ＋3cos2x ＝2sin(2x ＋π3)． ∵x ∈[0，π2]，∴2x ＋π3∈[π3，4π3]， ∴－32≤sin(2x ＋π3)≤1， 从而－3≤f (x )≤2π2]时，f(x)max＝2，f(x)min＝－ 3.故当x∈[0，。

3.1.3二倍角的正弦、余弦、正切公式知识④自主预习新知初探⍓知识点.二倍角公式【思考】（1）在公式C (α＋β)，S (α＋β)和T (α＋β)中，若α＝β，公式还成立吗？（2）在上述公式中，若α＝β，你能得到什么结论？【答案】（1）成立(2) cos2α＝cos 2α－sin 2α，sin2α＝2sin αcos α，tan2α＝2tan α1－tan 2α.自我测评⍓1．判断下列命题是否正确．(正确的打“√”，错误的打“×”)(1)二倍角的正弦、余弦、正切公式的适用范围是任意角．( )(2)存在角α，使得sin 2α＝sin α成立．( )(3)对任意角α，总有tan 2α＝2tan α1－tan 2α.( ) 【答案】(1)× (2)√ (3)×2．已知sin α＝35，cos α＝45，则sin 2α等于( ) A.75 B.125 C.1225 D.2425【答案】D3．设sin(π4＋θ)＝13，则sin 2θ＝( ) A ．－79 B ．－19 C.19 D.79【解析】 sin 2θ＝－cos(π2＋2θ)＝2sin 2(π4＋θ)－1＝2×(13)2－1＝－79. 【答案】A4．已知α为第三象限角，cos α＝－35，则tan 2α＝________. 【答案】－2475．函数f (x )＝2sin x (sin x ＋cos x )的单调增区间为____________．【解析】 f (x )＝2sin 2x ＋2sin x cos x＝2×1－cos 2x 2＋sin 2x ＝sin 2x －cos 2x ＋1 ＝2sin(2x －π4)＋1，由－π2＋2k π≤2x －π4≤π2＋2k π，k ∈Z ，得－π8＋k π≤x ≤3π8＋k π，k ∈Z . 所以所求区间为[－π8＋k π，3π8＋k π](k ∈Z )． 【答案】[－π8＋k π，3π8＋k π](k ∈Z )【反馈记录】哪里不会问哪里，课堂全过关！题型 多维探究题型1给角求值问题【例1】求下列各式的值：(1)sin π12cos π12；(2)1－2sin 2750°； (3)2tan 150°1－tan 2150°；(4)1sin 10°－3cos 10°； (5)cos 20°cos 40°cos 80°.【解】(1)原式＝2sin π12cos π122＝sin π62＝14. (2)原式＝cos(2×750°)＝cos 1 500°＝cos(4×360°＋60°)＝cos 60°＝12. (3)原式＝tan(2×150°)＝tan 300°＝tan(360°－60°)＝－tan 60°＝－ 3.(4)原式＝cos 10°－3sin 10°sin 10°cos 10°＝2⎝⎛⎭⎫12cos 10°－32sin 10°sin 10°cos 10°＝4（sin 30°cos 10°－cos 30°sin 10°）2sin 10°cos 10°＝4sin 20°sin 20°＝4. (5)原式＝2sin 20°·cos 20°·cos 40°·cos 80°2sin 20°＝2sin 40°·cos 40°·cos 80°4sin 20°＝2sin 80°·cos 80°8sin 20°＝sin 160°8sin 20°＝18. 【方法总结】化简求值的四个方向三角函数的化简有四个方向，即分别从“角”“函数名”“幂”“形”着手分析，消除差异．【变式训练1】化简：sin 50°(1＋3tan 10°)＝________.【解】sin 50°(1＋3tan 10°)＝sin 50°(1＋3·3sin10°cos 10°) ＝sin 50°×cos 10°＋3sin 10°cos 10° ＝sin 50°×2(12cos 10°＋32sin 10°)cos 10°＝2sin50°·cos 50°cos 10°＝sin 100°cos 10°＝cos 10°cos 10°＝1. 【答案】1题型2给值求值【例2】已知cos ⎝⎛⎭⎫α＋π4＝35，π2≤α<3π2，求cos ⎝⎛⎭⎫2α＋π4的值． 【解】∵π2≤α<3π2，∴3π4≤α＋π4<7π4. ∵cos ⎝⎛⎭⎫α＋π4>0，∴3π2<α＋π4<7π4. ∴sin ⎝⎛⎭⎫α＋π4＝－ 1－cos 2⎝⎛⎭⎫α＋π4＝－ 1－⎝⎛⎭⎫352＝－45. ∴cos 2α＝sin ⎝⎛⎭⎫2α＋π2＝2sin ⎝⎛⎭⎫α＋π4cos ⎝⎛⎭⎫α＋π4 ＝2×⎝⎛⎭⎫－45×35＝－2425， sin 2α＝－cos ⎝⎛⎭⎫2α＋π2＝1－2cos 2⎝⎛⎭⎫α＋π4＝1－2×⎝⎛⎭⎫352＝725. ∴cos ⎝⎛⎭⎫2α＋π4＝22cos 2α－22sin 2α ＝22×⎝⎛⎭⎫－2425－725＝－31250. 【方法总结】条件求值问题的解决方法给值求值问题，注意寻找已知式与未知式之间的联系，有两个观察方向：(1)有方向地将已知式或未知式化简，使关系明朗化；(2)寻找角之间的关系，看是否适合相关公式的使用，注意常见角的变换和角之间的二倍关系．【变式训练2】本例条件不变，求cos 2αsin ⎝⎛⎭⎫π4＋α的值． 【解】原式＝cos 2α－sin 2αsin π4cos α＋cos π4sin α＝2(cos α－sin α)＝2cos ⎝⎛⎭⎫α＋π4＝65. 题型3化简问题【例3】化简：2cos 4x －2cos 2x ＋122tan (π4－x )sin 2(π4－x ). 【解】原式＝－2sin 2x cos 2x ＋122sin (π4－x )cos 2(π4－x )cos (π4－x ) ＝12(1－sin 22x )2sin (π4－x )cos (π4－x )＝12cos 22x sin (π2－2x )＝12cos2x . 【方法总结】三角函数式的化简要遵循“三看”原则(1)一看“角”，这是最重要的一环，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式；(2)二看“函数名称”，看函数名称之间的差异，从而确定使用的公式，常见的有“切化弦”；(3)三看“结构特征”，分析结构特征，可以帮助我们找到变形的方向，如“遇到分式要通分”等．【变式训练3】 化简：(1tan α2－tan α2)·(1＋tan α·tan α2)． 【解】(1tan α2－tan α2)·(1＋tan α·tan α2)＝(cos α2sin α2－sin α2cos α2)·(1＋sin αcos α·sin α2cos α2) ＝cos 2α2－sin 2α2sin α2cos α2·cos αcos α2＋sin αsin α2cos αcos α2＝2cos αsin α·cos α2cos αcos α2＝2sin α. 3.1.3二倍角的正弦、余弦、正切公式总分：_____ 用时：_______A 组（学业基础）一．选择题1.2sin 2α1＋cos 2α·cos 2αcos 2α等于( ) A ．tan α B ．tan 2α C ．1D.12【解析】原式＝2sin 2α2cos 2α·cos 2αcos 2α＝sin 2αcos 2α＝tan 2α. 【答案】B2．已知cos 2α＝14，则sin 2α＝ ( ) A.12 B.34 C.58 D.38【解析】cos 2α＝1－2sin 2α＝14，解得sin 2α＝38. 【答案】D3．若tan θ＋1tan θ＝4，则sin 2θ＝( ) A.15 B.14 C.13 D.12【解析】法一：∵tan θ＋1tan θ＝1＋tan 2 θtan θ＝4， ∴4tan θ＝1＋tan 2 θ，∴sin 2θ＝2sin θcos θ＝2sin θcos θsin 2 θ＋cos 2 θ＝2tan θ1＋tan 2θ＝2tan θ4tan θ＝12. 法二：∵tan θ＋1tan θ＝sin θcos θ＋cos θsin θ＝1cos θsin θ＝2sin 2θ∴4＝2sin 2θ，故sin 2θ＝12. 【答案】D 4.1＋sin 100°－1－sin 100°＝( )A ．－2cos 50°B ．2cos 50°C ．－2sin 50°D ．2sin 50°【解析】原式＝sin 250°＋2sin 50°cos 50°＋cos 250°－sin 250°－2sin 50°cos 50°＋cos 250°＝sin 50°＋cos 50°－sin 50°＋cos 50°＝2cos 50°.【答案】B5．若sin ⎝⎛⎭⎫3π2－x ＝35，则cos 2x 的值为( )A ．－725 B.1425 C ．－1625 D.1925【解析】∵sin ⎝⎛⎭⎫3π2－x ＝－cos x ＝35， ∴cos x ＝－35. ∴cos 2x ＝2cos 2x －1＝2×925－1＝－725. 【答案】A6．已知向量a ＝(2，sin x )，b ＝(cos 2x,2cos x )，则函数f (x )＝a·b 的最小正周期是( ) A.π2 B ．π C ．2π D ．4π【解析】∵f (x )＝a·b ＝2cos 2x ＋2sin x cos x＝1＋cos 2x ＋sin 2x＝1＋2sin ⎝⎛⎭⎫2x ＋π4， ∴f (x )＝a·b 的最小正周期是π.【答案】B二．填空题7．化简1＋cos 2α＋2sin 2α＝________.【解析】原式＝2cos 2α＋2sin 2α＝2(sin 2α＋cos 2α)＝2.【答案】28．函数f (x )＝2cos 2x ＋sin 2x 的最小值是________．【解析】f (x )＝1＋cos 2x ＋sin 2x＝1＋2sin(2x ＋π4)， ∴f (x )的最小值为1－ 2.【答案】1－29．已知等腰三角形ABC 的腰长为底长的2倍，则顶角A 的正切值是________．【解析】取BC 的中点D ，令BD ＝1，则AB ＝4，则AD ＝15，在Rt △ABD 中，tan θ＝BD AD ＝115(令∠BAD ＝θ)， ∴tan ∠BAC ＝tan 2θ＝2tan θ1－tan 2θ＝2151－(115)2＝157. 【答案】15710．已知α∈⎝⎛⎭⎫0，π2，sin α＝35，计算1cos 2α＋tan 2α的值为________． 【解析】∵α∈⎝⎛⎭⎫0，π2，sin α＝35，∴cos α＝45. ∴1cos 2α＋tan 2α＝1＋sin 2αcos 2α＝sin 2α＋cos 2α＋2sin αcos α1－2sin 2α＝(sin α＋cos α)21－2sin 2α＝⎝⎛⎭⎫35＋4521－2×925＝7. 【答案】7三．解答题11．已知α为锐角，且tan(π4＋α)＝2. (1)求tan α的值；(2)求sin 2αcos α－sin αcos 2α的值． 【解】(1)tan(π4＋α)＝1＋tan α1－tan α， 所以1＋tan α1－tan α＝2,1＋tan α＝2－2tan α， 所以tan α＝13. (2)sin 2αcos α－sin αcos 2α＝2sin αcos 2α－sin αcos 2α＝sin α(2cos 2α－1)cos 2α＝sin αcos 2αcos 2α＝sin α. 因为tan α＝13，所以cos α＝3sin α， 又sin 2α＋cos 2α＝1，所以sin 2α＝110， 又α为锐角，所以sin α＝1010， 所以sin 2αcos α－sin αcos 2α＝1010. 12．已知0<x <π2，sin 2 x 2＋3sin x 2cos ⎝⎛⎭⎫π＋x 2＝－110，求tan ⎝⎛⎭⎫2x ＋π3的值． 【解】∵sin 2 x 2＋3sin x 2cos ⎝⎛⎭⎫π＋x 2 ＝1－cos x 2－3sin x 2cos x 2＝12－⎝⎛⎭⎫32sin x ＋12cos x ＝12－sin ⎝⎛⎭⎫x ＋π6， ∴由已知得12－sin ⎝⎛⎭⎫x ＋π6＝－110，∴sin ⎝⎛⎭⎫x ＋π6＝35. ∵0<x <π2，结合sin ⎝⎛⎭⎫x ＋π6＝35易知π6<x ＋π6<π2.∴cos ⎝⎛⎭⎫x ＋π6＝45，∴tan ⎝⎛⎭⎫x ＋π6＝34. ∴tan ⎝⎛⎭⎫2x ＋π3＝2tan ⎝⎛⎭⎫x ＋π61－tan 2⎝⎛⎭⎫x ＋π6＝2×341－916＝247. B 组（能力提升）13．若cos ⎝⎛⎭⎫π4－θcos ⎝⎛⎭⎫π4＋θ＝26⎝⎛⎭⎫0<θ<π2，则sin 2θ的值为( ) A.23 B.73 C.76 D.346【解析】 cos ⎝⎛⎭⎫π4－θcos ⎣⎡⎦⎤π2－⎝⎛⎭⎫π4－θ＝26， 即cos ⎝⎛⎭⎫π4－θsin ⎝⎛⎭⎫π4－θ＝26，即12sin ⎝⎛⎭⎫π2－2θ＝26， 所以cos 2θ＝23. 又因为0<θ<π2，所以0<2θ<π，所以sin 2θ＝73. 【答案】B14．设a ∈R ，f (x )＝cos x (a sin x －cos x )＋cos 2⎝⎛⎭⎫π2－x 满足f ⎝⎛⎭⎫－π3＝f (0)，当x ∈⎣⎡⎦⎤π4，11π24时，f (x )的值域为( )A ．[1，2]B ．[2， 3 ]C ．[3，2]D ．[2，2]【解析】f (x )＝a 2sin 2x －1＋cos 2x 2＋1－cos 2x 2＝a 2sin 2x －cos 2x ， 因为f ⎝⎛⎭⎫－π3＝f (0)，所以a ＝23，所以f (x )＝3sin 2x －cos 2x ＝2sin ⎝⎛⎭⎫2x －π6， x ∈⎣⎡⎦⎤π4，11π24时，2x －π6∈⎣⎡⎦⎤π3，3π4，f (x )∈[2，2]． 【答案】D15．等腰三角形一个底角的余弦值为23，那么这个三角形顶角的正弦值为________． 【解析】设A 是等腰△ABC 的顶角，则cos B ＝23， sin B ＝1－cos 2B ＝ 1－⎝⎛⎭⎫232＝53. 所以sin A ＝sin(180°－2B )＝sin 2B ＝2sin B cos B ＝2×53×23＝459.【答案】45916．已知cos 2α＝13，π<2α<2π，求1＋sin α－2cos 2 α23sin α＋cos α的值． 【解】原式＝sin α－cos α3sin α＋cos α， 又∵cos 2α＝13，∴2cos 2α－1＝13， ∴cos 2α＝23，3π2<2α<2π， ∴3π4<α<π，∴⎩⎨⎧cos α＝－63，sin α＝33，∴原式＝5＋427. 17．设函数f (x )＝53cos 2x ＋3sin 2x －4sin x cos x .(1)求f ⎝⎛⎭⎫5π12；(2)若f (α)＝53，α∈⎝⎛⎭⎫π2，π，求角α. 【解】f (x )＝53cos 2x ＋3sin 2x －4sin x cos x ＝53cos 2x ＋53sin 2x －2sin 2x －43sin 2x ＝53－2sin 2x －23(1－cos 2x )＝33－2sin 2x ＋23cos 2x＝33－4⎝⎛⎭⎫sin 2x ×12－cos 2x ×32 ＝33－4⎝⎛⎭⎫sin 2x cos π3－cos 2x sin π3 ＝33－4sin ⎝⎛⎭⎫2x －π3. (1)f ⎝⎛⎭⎫5π12＝33－4sin ⎝⎛⎭⎫5π6－π3＝33－4sin π2＝33－4. (2)由f (α)＝53，得sin ⎝⎛⎭⎫2α－π3＝－32， 由α∈⎝⎛⎭⎫π2，π，得2α－π3∈⎝⎛⎭⎫2π3，5π3， ∴2α－π3＝4π3，α＝5π6.。

页眉内容第三章三角恒等变换3.1.3 二倍角的正弦、余弦、正切公式一、学习目标1.知识与技能1.理解二倍角公式的推导过程，知道倍角公式与和角公式之间的内在联系.2.掌握二倍角的正弦、余弦、正切公式，并能运用这些公式进行简单的恒等变换.(重点、难点)2.过程与方法经历二倍角公式的探究过程，培养学生发现数学规律的思维方法，分析问题和解决问题的能力，体会化归与转化的思想方法.3.情感、态度与价值观通过对二倍角公式的探究学习，培养学生的探索精神和应用意识，体会数学的科学价值和应用价值，不断提高自身的文化修养.二、教学重点难点重点：以两角和的正弦、余弦和正切公式为基础，推导二倍角正弦、余弦和正切公式.难点：二倍角的理解及其灵活运用.三、专家建议通过对二倍角推理，变形应用的学习，要特别加强二倍角公式的正用、逆用和变用的学习，从而培养发现思维能力，变异思维能力，分析问题解决问题的能力，强化数学探究意识，掌握转化与化归的数学思想方法。

四、教学方法自学-训练-点拨-练习-总结五、教学过程●课堂探究探究点一二倍角的正弦、余弦、正切公式的推导问题1二倍角的正弦、余弦、正切公式就是用α的三角函数表示2α的三角函数的公式．根据前面学过的两角和与差的正弦、余弦、正切公式．你能推导出二倍角的正弦、余弦、正切公式吗？试一试？答sin 2α＝sin(α＋α)＝sin αcos α＋cos αsin α＝2sin αcos α；cos 2α＝cos(α＋α)＝cos αcos α－sin αsin α＝cos2α－sin2α；tan 2α＝tan(α＋α)＝2tan α1－tan2α.问题2根据同角三角函数的基本关系式sin2α＋cos2α＝1，你能否只用sin α或cos α表示cos 2α？答∵cos 2α＝cos2α－sin2α＝cos2α－(1－cos2α)＝2cos2α－1；或cos 2α＝cos2α－sin2α＝(1－sin2α)－sin2α＝1－2sin2α.探究点二余弦的二倍角公式的变形形式及应用二倍角的余弦公式cos 2α＝cos 2α－sin 2α＝2cos 2α－1＝1－2sin 2α变形较多，应用灵活．其中sin 2α＝1－cos 2α2，cos 2α＝1＋cos 2α2称作降幂公式，1－cos α2＝sin 2α2，1＋cos α2＝cos 2α2称作升幂公式．这些公式在统一角或函数名时非常有用．练习1：函数f (x )＝3sin x cos x ＋cos 2x －12的最小正周期是 ．解析 ∵f (x )＝32sin 2x ＋12(2cos 2x －1)＝32sin 2x ＋12cos 2x ＝sin ⎝⎛⎭⎫2x ＋π6， ∴T ＝2π2＝π.练习2：函数f (x )＝cos 2x ＋4sin x 的值域是 ． 解析 f (x )＝cos 2x ＋4sin x ＝1－2sin 2x ＋4sin x ＝－2sin 2x ＋4sin x ＋1＝－2(sin x －1)2＋3. 当sin x ＝1时，f (x )max ＝3； 当sin x ＝－1时，f (x )min ＝－5.●新知展示1．倍角公式(1)S 2α：sin 2α＝ ，sin α2cos α2＝ ；(2)C 2α：cos 2α＝ ＝ ＝ ； (3)T 2α：tan 2α＝ . 2．倍角公式常用变形(1)sin 2α2sin α＝ ，sin 2α2cos α＝ ； (2)(sin α±cos α)2＝ ；(3)sin 2α＝ ，cos 2α＝ ； (4)1－cos α＝ ,1＋cos α＝ . ●典例剖析类型一 利用二倍角公式给角求值例1 .求下列各式的值：(1)cos π5cos 2π5；(2)12－cos 2π8；(3)2tan 150°1－tan 2150°； (4)sin 10°sin 50°sin 70°. 【分析】 第(1)题可根据2π5是π5的2倍构造二倍角的公式求值；第(2)题需将所求式变形逆用二倍角公式化简求值；(3)逆用二倍角的正切公式求解；(4)利用互余关系把正弦变成余弦，逆用二倍角公式化简、求值.【解析】(1)原式＝2sin π5cos π5cos 2π52sin π5＝sin 2π5cos 2π52sin π5＝sin 4π54sin π5＝sin π54sin π5＝14. (2)原式＝1－2cos 2π82＝－2cos 2π8－12＝－12cos π4＝－24.(3)原式＝tan 300°＝tan(360°－60°) ＝－tan 60°＝－ 3.(4)原式＝cos 20°cos 40°cos 80°＝ 2sin 20°cos 20°cos 40°cos 80°2sin 20°＝18·sin 160°sin 20°＝18. 【小结】对于给角求值问题，一般有两类：(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式进行转化，一般可以化为特殊角.(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现连用二倍角的正弦公式的形式.【变式训练】求下列各式的值. (1)cos 72°cos 36°；(2)1sin 50°＋3cos 50° . 【解】 (1)cos 36°cos 72°＝2sin 36°cos 36°cos 72°2sin 36°＝2sin 72°cos 72°4sin 36°＝sin 144°4sin 36°＝14.(2)原式＝cos 50°＋3sin 50°sin 50°cos 50°＝2⎝ ⎛⎭⎪⎫12cos 50°＋32sin 50°12×2sin 50°cos 50°＝2sin 80°12sin 100°＝2sin 80°12sin 80°＝4.类型二 利用二倍角公式给值求值例2.已知sin(π4－x )＝513，0<x <π4，求cos 2xcos (π4＋x )的值.【分析】【解析】∵0<x <π4，∴π4－x ∈(0，π4). 又∵sin(π4－x )＝513，∴cos(π4－x )＝1213. 又cos 2x ＝sin(π2－2x )＝2sin(π4－x )cos(π4－x ) ＝2×513×1213＝120169，cos(π4＋x )＝sin[π2－(π4＋x )] ＝sin(π4－x )＝513，∴原式＝120169513＝2413.【小结】1.条件求值问题常有两种解题途径：(1)对题设条件变形，把条件中的角、函数名向结论中的角、函数名靠拢；(2)对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论.2.当遇到π4±x 这样的角时可利用互余角的关系和诱导公式，将条件与结论沟通.【变式训练】 (2014·扬州高一检测)已知sin ⎝ ⎛⎭⎪⎫π4＋α·sin ⎝ ⎛⎭⎪⎫π4－α＝16，且α∈(π2，π)，求sin 4α的值.【解】 ∵⎝ ⎛⎭⎪⎫π4＋α＋⎝ ⎛⎭⎪⎫π4－α＝π2，∴sin ⎝ ⎛⎭⎪⎫π4－α＝cos ⎝ ⎛⎭⎪⎫π4＋α.∵sin ⎝ ⎛⎭⎪⎫π4＋αsin ⎝ ⎛⎭⎪⎫π4－α＝16，∴2sin ⎝ ⎛⎭⎪⎫π4＋αcos ⎝ ⎛⎭⎪⎫π4＋α＝13，∴sin ⎝ ⎛⎭⎪⎫π2＋2α＝13.∴cos 2α＝13.又∵α∈⎝ ⎛⎭⎪⎫π2，π，∴2α∈(π，2π).∴sin 2α＝－1－cos 22α＝－223.∴sin 4α＝2sin 2αcos 2α＝－429. 类型三 二倍角公式的综合应用 (1)化简：1＋cos 2θ－sin 2θ1－cos 2θ－sin 2θ；(2)化简：1＋sin 10°－1－sin 10°； (3)化简：2cos 2α－12tan ⎝ ⎛⎭⎪⎫π4－α·sin 2⎝ ⎛⎭⎪⎫π4＋α.【分析】 (2)1±sin 10°＝(sin 5°±cos 5°)2. (3)处理好2α与π4－α与π4＋α的关系. 【解析】(1)法一 1＋cos 2θ－sin 2θ1－cos 2θ－sin 2θ＝2cos 2θ－2sin θcos θ2sin 2θ－2sin θcos θ＝2cos θ(cos θ－sin θ)2sin θ(sin θ－cos θ)＝－1tan θ， ∴原式＝－1tan θ.法二 1＋cos 2θ－sin 2θ1－cos 2θ－sin 2θ＝(1－sin 2θ)＋cos 2θ(1－sin 2θ)－cos 2θ＝(sin θ－cos θ)2＋(cos 2θ－sin 2θ)(sin θ－cos θ)2－(cos 2θ－sin 2θ) ＝(sin θ－cos θ)(sin θ－cos θ－cos θ－sin θ)(sin θ－cos θ)(sin θ－cos θ＋sin θ＋cos θ)＝－2cos θ2sin θ＝－1tan θ， ∴原式＝－1tan θ.(2)1＋sin 10°－1－sin 10°＝1＋2sin 5°cos 5°－1－2sin 5°cos 5° ＝(cos 5°＋sin 5°)2－(cos 5°－sin 5°)2＝(cos 5°＋sin 5°)－(cos 5°－sin 5°) ＝2sin 5°. ∴原式＝2sin 5°. (3)原式＝cos 2α2sin ⎝ ⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α·cos2⎝ ⎛⎭⎪⎫π4－α＝cos 2α2sin ⎝ ⎛⎭⎪⎫π4－αcos ⎝ ⎛⎭⎪⎫π4－α＝cos 2αsin ⎝ ⎛⎭⎪⎫π2－2α＝cos 2αcos 2α＝1.【小结】1.对于三角函数式的化简有下面的要求：(1)能求出值的应求出值.(2)使三角函数种数尽量少.(3)使三角函数式中的项数尽量少.(4)尽量使分母不含有三角函数.(5)尽量使被开方数不含三角函数.2.化简的方法：(1)弦切互化，异名化同名，异角化同角. (2)降幂或升幂.(3)一个重要结论：(sin θ±cos θ)2＝1±sin2θ. 【变式训练】 化简下列各式.(1)π4＜α＜π2，则1－sin 2α＝________； (2)化简：(sin α＋cos α－1)(sin α－cos α＋1)sin 2α.【解析】 (1)∵α∈⎝ ⎛⎭⎪⎫π4，π2，∴sin α＞cos α，∴1－sin 2α＝1－2sin αcos α＝sin 2α－2sin αcos α＋cos 2α ＝(sin α－cos α)2＝sin α－cos α.【答案】 (1)sin α－cos α(2)原式＝⎝ ⎛⎭⎪⎫2sin α2cos α2－2sin 2α2⎝ ⎛⎭⎪⎫2sin α2cos α2＋2sin 2α24sin α2cos α2cos α＝⎝ ⎛⎭⎪⎫cos α2－sin α2⎝ ⎛⎭⎪⎫cos α2＋sin α2sin α2cos α2cos α＝⎝ ⎛⎭⎪⎫cos 2α2－sin 2α2sin α2cos α2cos α＝cos αsinα2cos α2cos α＝tan α2 ●课堂小结1.对于“二倍角”应该有广义上的理解，如：8α是4α的二倍；6α是3α的二倍；4α是2α的二倍；3α是32α的二倍；α2是α4的二倍；α3是α6的二倍；α2n ＝2 ·α2n ＋1(n ∈N *).2.二倍角余弦公式的运用在二倍角公式中，二倍角的余弦公式最为灵活多样，应用广泛.二倍角余弦公式的常用形式：①1＋cos 2α＝2cos 2α，②cos 2α＝1＋cos 2α2，③1－cos 2α＝2sin 2α，④sin 2α＝1－cos 2α2.六、板书设计3.1.3 二倍角的正弦、余弦、正切公式七．当堂检测1.12sin π12cos π12的值等于( ) A.14 B.18 C.116 D.12 【解析】 原式＝14sin π6＝18. 【答案】 B2.下列各式中，值为32的是( ) A.2sin 15°－cos 15° B.cos 215°－sin 215° C.2sin 215°－1 D.cos 215°＋sin 215° 【解析】 A ：2sin 15°－cos 15°≠32， B ：cos 215°－sin 215°＝cos 30°＝32， C ：2sin 215°－1＝－cos 30°＝－32， D ：cos 215°＋sin 215°＝1.故选B. 【答案】 B3.(2014·广州高一模拟)若3sin α＋cos α＝0，则1cos 2α＋sin 2α的值为________.【解析】 由3sin α＋cos α＝0，得tan α＝－13， 则1cos 2α＋sin 2α＝sin 2α＋cos 2αcos 2α＋2sin αcos α ＝tan 2α＋11＋2tan α＝⎝ ⎛⎭⎪⎫－132＋11＋2×⎝ ⎛⎭⎪⎫－13＝103. 【答案】 1034.(2014·盐城高一检测)证明：1＋sin 2α2cos2α＋sin 2α＝12tan α＋12.【证明】左边＝sin2α＋cos2α＋2sin αcos α2cos2α＋2sin αcos α＝(sin α＋cos α)22cos α(sin α＋cos α)＝sin α＋cos α2cos α＝12tan α＋12＝右边.所以1＋sin 2α2cos2α＋sin 2α。

高一数学必修四3.1.3二倍角公式编写：张惠玲 校审：高一数学组3.1.3二倍角的正弦、余弦、正切公式学习目标：熟练掌握二倍角的正弦、余弦、正切公式，并能运用其解决一些实际问题。

学习重点：二倍角的正弦、余弦、正切公式学习难点：二倍角的正弦、余弦、正切公式的灵活应用知识链接：复习()()()S C T αβαβαβ±±±：()sin αβ+= ；()sin αβ-= ；()cos αβ+= ；()cos αβ-= ；()tan αβ+= ；()tan αβ-= 。

学习过程：1.利用上述公式推导sin 2,cos 2,tan 2ααα公式：sin 2α= ;cos 2α= = =tan 2α= .2. cos 2α的变形式：2sin α= ，2c o s α= ，2.公式应用：例1.已知5sin 2,,1342ππαα=<<求sin 4,cos 4,tan 4ααα的值。

姓名： 班级： 第23页例2.在三角形ABC 中，4cos ,tan 2,5A B ==求()tan 22A B +的值。

目标测试：A 组：课本135页练习1---5题B 组：1.已知00cos 270,3θθ=-<<求sin 2,cos 2,tan 2θθθ的值。

2.已知11tan ,tan ,73αβ==求()tan 2αβ+的值。

3.已知等腰三角形一个底角的正弦值为513，求这个三角形的顶角的正弦、余弦、正切值。

4.已知()()1c o s c o s s i n s i n ,3αββαββ+++=且3,2,2παπ⎛⎫∈ ⎪⎝⎭求cos 24πα⎛⎫+ ⎪⎝⎭的值。

高一数学必修四3.1.3二倍角公式编写：张惠玲 校审：高一数学组5.化简：()()21.cos sin ;αα+ ()442.cos sin ;θθ-()3.sin cos cos2;x x x ()114.1tan 1tan θθ--+6.已知函数()22sin cos 2cos y x x x =++，求⑴它的减区间；⑵最大值，最小值。

高一数学必修一二倍角知识点二倍角是数学中常见且重要的概念，准确掌握二倍角的知识对于高一学生来说至关重要。

本文将为大家介绍高一数学必修一中与二倍角相关的几个重要知识点。

一、二倍角的定义：在三角函数中，二倍角指的是将角的度数翻倍，即原角的两倍角度。

记作2θ。

二、常见的二倍角公式：1. 正弦函数的二倍角公式：sin2θ = 2sinθcosθ2. 余弦函数的二倍角公式：cos2θ = cos²θ - sin²θ3. 正切函数的二倍角公式：tan2θ = 2tanθ / (1 - tan²θ)三、利用二倍角公式解题的方法：1. 利用二倍角公式化简函数表达式：有时候，在解题过程中，我们会遇到一些复杂的函数表达式，利用二倍角公式可以将其化简为简化的形式，便于求解。

2. 利用二倍角公式证明恒等式：我们可以通过利用二倍角公式，将一个表达式转化为另一个表达式，从而证明恒等式的成立。

3. 利用二倍角公式求解方程：通过利用二倍角公式将方程中的角度关系转化为已知的角度关系，从而简化方程求解的过程。

四、二倍角知识在几何中的应用：1. 二倍角与角平分线关系：在平面几何中，如果一条直线将一个角分成两个相等的角，那么这条直线叫做该角的角平分线。

当我们遇到需要计算角平分线上某个点的坐标时，可以利用二倍角的知识进行求解。

2. 二倍角与三角函数图像关系：通过对二倍角公式的应用，可以推导出正弦函数、余弦函数和正切函数的图像与原函数图像之间的关系。

这对于理解和绘制三角函数图像是非常有帮助的。

五、二倍角知识在三角函数的求值中的应用：在具体的计算中，利用二倍角公式可以简化计算过程，使得计算更加高效。

例如，计算三角函数值时，如果角度较大，直接计算可能会比较困难，而利用二倍角公式可以将问题转化为计算已知角度下的三角函数值，从而简化计算。

六、总结：二倍角是高一数学中的一个重要概念，通过准确掌握二倍角的定义、常见公式和应用技巧，可以帮助同学们在解题过程中更加灵活和高效地运用二倍角知识，提高数学解题的能力。