高一数学三角函数二倍公式

高一数学必修一所有公式归纳高一数学必修一所有公式归纳是如下：1、锐角三角函数公式：sinα=∠α的对边/斜边。

2、三倍角公式：sin3α=4sinα·sin(π/3+α)sin(π/3-α)。

3、辅助角公式：Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)。

4、降幂公式：sin^2(α)=(1-cos(2α))/2=versin(2α)/2。

5、推导公式：tanα+cotα=2/sin2α。

数学必修一数学公式如下：1、2sinAcosB=sin(A+B)+sin(A-B)。

2、tan(A+B)=(tanA+tanB)/(1-tanAtanB)。

3、cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a。

4、tan(A-B)=(tanA-tanB)/(1+tanAtanB)。

5、-ctgA+ctgBsin(A+B)/sinAsinB。

数学必修一公式归纳：一、指数与指数幂的运算1、根式的概念：一般地，如果，那么叫做的次方根(nthroot)，其中>1，且∈*.当是奇数时，正数的次方根是一个正数，负数的次方根是一个负数.此时，的次方根用符号表示.式子叫做根式(radical)，这里叫做根指数(radicalexponent)，叫做被开方数(radicand).当是偶数时，正数的次方根有两个，这两个数互为相反数.此时，正数的正的次方根用符号表示，负的次方根用符号-表示.正的次方根与负的次方根可以合并成±(>0).由此可得：负数没有偶次方根;0的任何次方根都是0，记作。

注意：当是奇数时，当是偶数时。

2、分数指数幂。

正数的分数指数幂的意义，规定：0的正分数指数幂等于0，0的负分数指数幂没有意义指出：规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂.3、实数指数幂的运算性质。

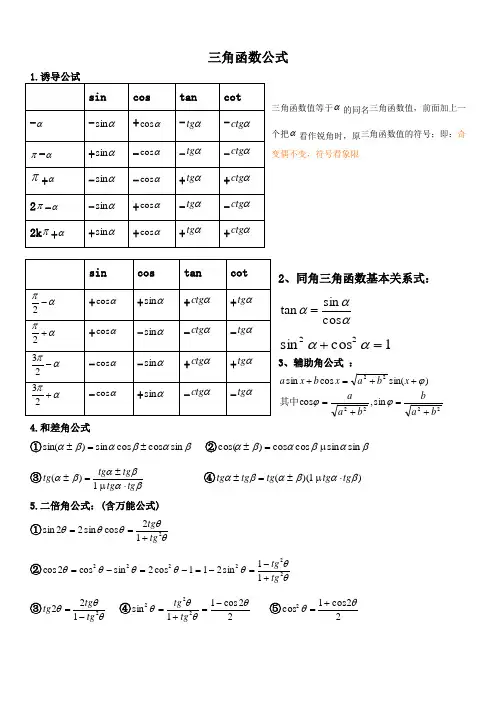
二倍角的三角函数【考点梳理】考点：二倍角的正弦、余弦、正切公式【题型归纳】题型一：二倍角的正弦公式1．（2022·黑龙江·佳木斯一中高一期末）已知角α的顶点在坐标原点，始边在x 轴非负半轴上，且角α的终边上一点()2,1P ，则sin 2α=（ ） A ．45-B ．25C 25D ．452．（2022·河北沧州·高一开学考试）已知3sin24α=，且42ππα<<，则cos 4πα⎛⎫+ ⎪⎝⎭的值为（ ）A ．14-B ．14C ．2D ．33．（2022·广东光明·高一期末）角α的终边经过点()3,4-，则cos cos 2424απαπ⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭的值为（ ）A ．25- B ．25 C ．310- D ．310题型二：二倍角的余弦公式4．（2022·福建龙岩·高一期末）已知1sin 63πα⎛⎫-= ⎪⎝⎭，则2cos 23πα⎛⎫+= ⎪⎝⎭（ ） A ．79B ．79-C ．29D ．29-5．（2022·湖北省武昌实验中学高一期末）若π2cos 63a ⎛⎫+= ⎪⎝⎭，则πsin 26a ⎛⎫-= ⎪⎝⎭（ ）A ．19- B ．459C ．19 D 4596．（2022·全国·高一）设α为锐角，若4cos()65πα+=，则sin(2)12πα+的值为（ ）A 172B 172C 312D 192题型三：二倍角的正切公式7．（2021·江苏省外国语学校高一期中）ABC 中，3tan 4A =，5cos B =，则()tan 22A B +=（ ） A ．112-B ．87-C ．44117D ．-118．（2021·北京丰台·高一期中）下列各数sin 25cos 27cos 25sin 27a =+，2sin 27cos 27b =，22cos 221c =-，22tan 22.51tan 22.5d =-中，最大的是（ ）A ．aB ．bC ．cD ．d9．（2021·山西·应县一中高一期末）若3tan 4x =，则tan tan 2424x x ππ⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭（ ） A ．2-B ．2C ．32D ．32-题型四：二倍角公式的综合应用10．（2021·江苏·高一课时练习）已知0,2πα⎛⎫∈ ⎪⎝⎭，()0,βπ∈，310cos β=，且tan(2)3αβ+=.（1）求tan2α的值；（2）求αβ+的值.11．（2021·江苏·启东中学高一）计算求值： （1）()sin 5013︒︒（2）sin15cos5sin 20cos15cos5cos 20︒︒-︒︒︒-︒12．（2021·江西·横峰中学高一期中（理））已知函数2()sin(2)2333f x x x π=+-（1）求函数()f x 的单调区间；（2）当,44x ππ⎡⎤∈-⎢⎥⎣⎦时，不等式(1)()212()2m f x m m f x +++≥+恒成立，求实数m 的取值范围.【双基达标】一、单选题13．（2022·河南许昌·高一期末）若1cos 23θ=-，则221tan 1tan θθ-=+（ ） A ．13- B ．13 C ．12- D ．1214．（2022·贵州威宁·高一期末）已知1sin 34πα⎛⎫+= ⎪⎝⎭，则cos 23πα⎛⎫-= ⎪⎝⎭（ ）A ．29 B ．78 C ．78- D ．29-15．（2022·山西孝义·高一开学考试）下列各式中，值为12的是（ ） A ．22cos sin 1212-ππB ．2tan22.51tan 22.5- C ．sin15cos15 D π1cos32+16．（2022·江苏省天一中学高一期末）设sin35sin72sin55sin18a =︒︒-︒︒，cos3214sin172cos188b ︒-=︒︒，221tan 361tan 36c -︒=+︒，则a ，b ，c 的大小关系为（ ） A ．a b c >>B ．a c b >>C ．c a b >>D ．c b a >>17．（2022·福建泉州·高一期末）将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，这样的分割被称为黄金分割，黄金分割蕴藏着丰富的数学知识和美学价值，被广泛运用于艺术创作、工艺设计等领51-，该值恰好等于2sin18︒，则cos36︒=（ ） A 52B 51-C 51+ D 51-18．（2022·河南·信阳高中高一期末（理））已知tan 24x π⎛⎫+= ⎪⎝⎭，则tan tan 2x x 的值为（ ）A ．49B ．23C ．59D ．9519．（2021·河南·高一阶段练习）已知函数()()4cos sin 63f x x x x ππ⎛⎫⎛⎫=+-∈ ⎪ ⎪⎝⎭⎝⎭R ，则（ ）A ．()f x 的最小正周期为2πB ．()f x 可以改写成()2sin 26f x x π⎛⎫=- ⎪⎝⎭C ．()f x 在区间,3ππ⎛⎫⎪⎝⎭上单调递减D ．()f x 的图象关于直线3x π=对称【高分突破】一：单选题20．（2022·新疆·乌鲁木齐市第四中学高一期末）已知角α的终边与单位圆交于点63(,)33P -，则sin()cos(2)2παπα-+-=（ ）A ．33-B ．613+ C ．33D ．613- 21．（2021·福建·厦门一中高一阶段练习）黄金三角形是一个顶角为36°的等腰三角形，其底边与腰长之比是黄金分割比.例如，国旗上的正五角星就是由5个黄金三角形和一个正五边形组成.如图所示：在黄金三角形ABC 中，512BC AC -=，根据这个信息，可求得cos144︒的值为（ ）A 15- B ．51-C ．51+D ．35+22．（2021·全国·高一课前预习）计算：24tan123tan312ππ=-（ ）A 23B ．23C 23D ．2323．（2022·湖南·长郡中学高一期末）若tan 2θ=-，则()sin 1sin 2sin cos θθθθ+=+（ ） A ．65- B ．25- C ．25D ．5624．（2021·福建省龙岩第一中学高一阶段练习）哥特式建筑是1140年左右产生于法国的欧洲建筑风格，它的特点是尖塔高耸、尖形拱门、大窗户及绘有故事的花窗玻璃，如图所示的几何图形，在哥特式建筑的尖形拱门与大窗户中较为常见，它是由线段AB 和两个圆弧AC ，弧BC 围成，其中一个圆弧的圆心为A ，另一个圆弧的圆心为B ，圆O 与线段AB 及两个圆弧均相切，则tan ∠AOB 的值是（ ）A ．247-B ．724-C ．43-D ．34-25．（2021·全国·高一课时练习）若53,42ππα⎛⎫∈ ⎪⎝⎭1cos 21cos 222αα+-=（ ） A ．cos sin αα- B ．cos sin αα-- C ．cos sin αα+D ．cos sin αα-+26．（2021·全国·高一专题练习）已知441sin cos ,0,32a παα⎛⎫-=∈ ⎪⎝⎭.则os 4(c 2)a π+=（ ）A ．426+B ．426C 42-+D 42--27．（2021·全国·高一专题练习）若,2παπ⎛⎫∈ ⎪⎝⎭202122sin 04παα⎛⎫+-=⎪⎝⎭，则tan2α=（ ） A 37B 7C ．37D ．7二、多选题28．（2022·重庆九龙坡·高一期末）若()1cos ,0,23ααπ=∈，则下列结论正确的是（ ） A ．7cos 9α=B ．42sin α=C ．1cos 223απ⎛⎫-=- ⎪⎝⎭D ．22cos 22πα⎛⎫+= ⎪⎝⎭29．（2022·广东光明·高一期末）下列各式的值为1的是（ ）A ．tan20tan25tan20tan251+-B ．13661log 27log 88-⎛⎫+- ⎪⎝⎭ C ．sin72cos18cos108sin18-D ．22cos 2251⋅-30．（2022·安徽巢湖·高一期末）下列计算结果正确的是（ ） A ．()62cos 15--︒=B ．1sin15sin 30sin 758︒︒︒=C ．()()()()1cos 35cos 25sin 35sin 252αααα-︒︒++-︒︒+=-D ．2tan 22.51tan 45tan 22.52︒=︒-︒31．（2022·湖南张家界·高一期末）若下列各式左右两边均有意义，则其中恒成立的有（ ） A ．cos 1sin 1sin cos x xx x+=-B ．cos()sin 2παα+=C ．2(sin 2cos 2)1sin 4ααα-=-D ．21cos 2tan 1cos 2θθθ-=+32．（2022·山西大同·高一期末）下列计算或化简结果正确的是（ ） A ．2tan cos 2sin ααα=B ．若1sin cos 2αα⋅=，则cos tan 2sin ααα+= C ．若1tan 2α=，则2sin 1cos sin ααα=- D ．若α21cos 21cos 2αα=+-33．（2021·江苏如东·高一期中）下列各式中，值为12的是（ ）A ．2tan 22.51tan 22.5-B ．22tan15cos 15C 22331212ππD ．1316sin 5016cos50+三、填空题34．（2022·河北沧州·高一期末）已知π02x <<，且2πcos cos 224x x ⎛⎫-= ⎪⎝⎭，则tan 2x =______. 35．（2022·安徽·六安一中高一期末）已知2sin 33x π⎛⎫+= ⎪⎝⎭，则cos 23x π⎛⎫-= ⎪⎝⎭_________．36．（2022·北京通州·高一期末）化简22cos(2)2tan (cos 21)θθθ--=+_____．37．（2021·全国·2212sin 20cos 202cos 101cos 1601-=---________．四、解答题38．（2022·天津市第九十五中学益中学校高一期末）已知(,)2παπ∈.(1)1sin 3α=，求tan α和cos2α的值； (2)若5cos()3πα-=cos α的值.39．（2022·湖南·高一课时练习）利用二倍角公式求下列各式的值： (1)sin15cos15︒︒；(2)22cos 751︒-；(3)21sin 15-︒；(4)22tan 751tan 75︒-︒．40．（2022·贵州威宁·高一期末）已知π04α<<，2cos 1sin 2()tan()22πc s πo 2f ααααα⎛⎫+- ⎪⎝⎭=+⋅+． (1)化简()f α；(2)若1()5f α=-，求tan2α的值．41．（2022·湖南·高一课时练习）已知α为锐角且tan 34πα⎛⎫+= ⎪⎝⎭.(1)求tan α的值；(2)求2)cos sin 4cos 2παααα+-的值． 42．（2022·湖南·高一课时练习）化简： (1)()2sin cos αα+； (2)22tan151tan 15︒-︒；(3)()cos4013︒︒；(4)44sin cos αα-；(5)111tan 1tan αα-+-；(6)23sin 702cos 10-︒-︒【答案详解】1．D 【详解】由题意，角α的顶点在坐标原点，始边在x 轴非负半轴上，且角α的终边上一点()2,1P ， 所以sin α==cos α== 所以4sin 22sin cos 25ααα===．故选：D ． 2．C 【解析】 【分析】根据α的范围可知cos sin 0αα-<，结合两角和的余弦公式、二倍角的正弦公式和同角三角函数的基本关系化简计算cos 4πα⎛⎫+ ⎪⎝⎭即可. 【详解】 因为42ππα<<，所以sin cos αα>，即cos sin 0αα-<，又3sin24α=，则)cos cos sin 4πααα⎛⎫+=-= ⎪⎝⎭4===-， 故选：C. 3．C 【解析】 【分析】根据三角函数的定义求出cos α，利用诱导公式和二倍角的正弦公式将原式化简计算即可. 【详解】 由题意可得3cos 5α=-，所以1cos cos cos sin sin 2424242422απαπαπαππα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-=++=+ ⎪ ⎪ ⎪ ⎪ ⎪1133cos 22510α⎛⎫==⨯-=- ⎪⎝⎭. 故选：C 4．B 【解析】 【分析】 根据2cos 23πα⎛⎫+= ⎪⎝⎭cos 26παπ⎡⎤⎛⎫-+ ⎪⎢⎥⎝⎭⎣⎦，结合诱导公式和余弦的倍角公式，代值计算即可. 【详解】 因为2cos 23πα⎛⎫+= ⎪⎝⎭2cos 2cos 22sin 1666πππαπαα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫-+=--=-- ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦， 又1sin 63πα⎛⎫-= ⎪⎝⎭，故2cos 23πα⎛⎫+= ⎪⎝⎭2172139⎛⎫⨯-=- ⎪⎝⎭. 故选：B. 5．A 【解析】 【分析】根据给定条件利用诱导公式及二倍角的余弦公式计算作答. 【详解】因π2cos()63a +=，则22π21sin(2)sin[(2)]cos 2()2cos ()12()16236639ππππαααα-=-+=+=+-=⨯-=-. 故选：A 6．A 【解析】 【分析】根据α为锐角，4cos()65πα+=，得到sin()6πα+，再利用二倍角公式得到sin(2)3πα+，cos(2)3πα+，然后再由sin(2)sin[(2)]1234πππαα+=+-求解.【详解】解：α为锐角，4cos()65πα+=，3sin()65πα∴+=，24sin(2)2sin()cos()36625πππααα∴+=++=，27cos(2)2cos ()13625ππαα+=+-=．故sin(2)sin[(2)]1234πππαα+=+-， sin(2)cos cos(2)sin 3434ππππαα=+-+，2472525=- 故选：A ． 7．C 【解析】 【分析】由已知求得tan B ，再由两角和的正切求()tan A B +，再由二倍角的正切求解． 【详解】在ABC 中，∵cos B =，∴sin B ==，则sin sin 2cos B B B==，又3tan 4A =，∴()32tan tan 114tan 31tan tan 2124A B A B A B +++===---⨯， ∴()()()21122tan 442tan 21211tan 11714A B A B A B ⎛⎫⨯- ⎪+⎝⎭+===-+-． 故选：C 8．D 【解析】 【分析】由两角和正弦公式，二倍角公式一、诱导公式等化简函数值，然后由三角函数性质判断． 【详解】观察发现tan 451d =︒=，而sin(2527)sin521a =︒+︒=︒<，sin541b =︒<，cos441c =︒<， 故选：D ． 9．C 【解析】利用正切函数的两角和与差的恒等变换，结合二倍角公式求得结果. 【详解】因为2tan 1tan 14tan3222tan tan 2tan 242421tan 1tan 1tan 222x x x x x x x x xππ+-⎛⎫⎛⎫++-=+=== ⎪ ⎪⎝⎭⎝⎭-+-. 故选：C ．10．（1）43.（2）4π【解析】（1）由已知根据同角三角函数的基本关系可求得tan β,根据tan 2tan[(2)]ααββ=+-代入即可求得求得结果. （2）由(1)利用二倍角公式22tan 4tan 21tan 3ααα==-,可求得tan α,进而可得tan tan tan()1tan tan αβαβαβ++=-的值,根据角的范围,即可确定结果. 【详解】（1）∵(0,)βπ∈，且cos β=∴sin β===sin 1tan cos 3βββ== 又∵tan(2)3αβ+=∴13tan(2)tan 43tan 2tan[(2)]11tan(2)tan 3133αββααββαββ-+-=+-===+++⨯ （2）22tan 4tan 21tan 3ααα==-∴22tan 3tan 20αα+-=∴1tan 2α=或tan 2α∵0,2πα⎛⎫∈ ⎪⎝⎭∴1tan 2α=又∵1tan 3β=∴11tan tan 23tan()1111tan tan 123αβαβαβ+++===--⨯ ∵1tan 3β=，且(0,)βπ∈∴0,2πβ⎛⎫∈ ⎪⎝⎭又∵0,2πα⎛⎫∈ ⎪⎝⎭∴(0,)αβπ+∈∴4παβ+=【点睛】本题考查同角三角函数的基本关系,二倍角公式,两角和与差的三角函数,考查已知三角函数值求角,属于基础题. 11．（1）1；（2）2-【解析】 【分析】（1）先通过切化弦进行化简整理，利用两角和的正弦公式的逆应用，再结合二倍角公式和诱导公式化简即得结果； （2）先拆分20155︒=︒+︒，结合两角和的正弦公式和余弦公式化简整理成cos15sin15-︒︒，再拆分154530︒=︒-︒，结合两角差的正弦公式和余弦公式化简即得结果. 【详解】 解：（1）()sin 501︒︒sin 501cos 40⎛=︒⋅= ⎝⎭()2sin 3010cos 40cos10︒+︒=︒⨯︒2sin 40cos 40sin80cos101cos10cos10cos10︒︒︒︒====︒︒︒；（2）()()sin15cos5sin 155sin15cos5sin 20cos15cos5cos 20cos15cos5cos 155︒︒-︒+︒︒︒-︒=︒︒-︒︒︒-︒+︒()()cos 4530sin15cos5sin15cos5cos15sin 5cos15sin 5cos15cos5cos15cos5sin15sin 5sin15sin 5sin 4530︒-︒︒︒-︒︒-︒︒-︒︒===-︒︒-︒︒+︒︒︒︒︒-︒cos 45cos30sin 45sin 30sin 45cos30cos 45sin 30︒︒+︒︒=-︒︒-︒︒1==)2122=-=-12．（1）增区间为5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，减区间为511,()1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦；（2）3,5⎡⎫+∞⎪⎢⎣⎭. 【解析】（1）结合三角恒等变化化简得()sin(2)3f x x π=-，根据三角函数性质求出其单调区间；（2）根据（1）求出当,44x ππ⎡⎤∈-⎢⎥⎣⎦时11()2f x -≤≤，进而()20f x +>，原不等式等价于()()1210m f x m -+-≥，看成关于()f x 的一次函数，其端点函数值大于等于0，得12102(1)210m m m m -⎧+-≥⎪⎨⎪--+-≥⎩，化简即可.【详解】解：（1）1()(sin 2)1)2f x x x x =++1sin 222x x =sin(2)3x π=-令222()232k x k k Z πππππ-≤-≤+∈，得5()1212k x k k Z ππππ-≤≤+∈ 令3222()232k x k k Z πππππ+≤-≤+∈， 得511()1212k x k k Z ππππ+≤≤+∈ 故函数()f x 的增区间为5,()1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦，减区间为511,()1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦； （2）当,44x ππ⎡⎤∈-⎢⎥⎣⎦时，52636πππ-≤-≤x ， 可得11()2f x -≤≤，由()20f x +>， 不等式(1)()212()2m f x m m f x +++≥+可化为()()()24121mf x m m f x m +≥+++，有()()1210m f x m -+-≥. 令()1,1,2t f x t ⎡⎤∈-⎢⎥⎣⎦=，则()1(0)21m t g t m -+-=≥ 若不等式(1)()212()2m f x m m f x +++≥+恒成立，则1()02(1)0g g ⎧≥⎪⎨⎪-≥⎩等价于12102(1)210m m m m -⎧+-≥⎪⎨⎪--+-≥⎩，解得：35m ≥故实数m 的取值范围为3,5⎡⎫+∞⎪⎢⎣⎭.【点睛】求三角函数单调区间的2种方法:（1）代换法:就是将比较复杂的三角函数处理后的整体当作一个角u (或t )，利用基本三角函数的单调性来求所要求的三角函数的单调区间；（2）图象法:函数的单调性表现在图象上是从左到右，图象上升趋势的区间为单调递增区间，图象下降趋势的区间为单调递减区间，画出三角函数的图象，结合图象易求它的单调区间. 13．A 【解析】 【分析】根据题意将条件变形为2222cos sin cos sin θθθθ-+，然后弦化切即可求得答案.【详解】由题意，222222cos sin 1tan 1cos 2cos sin 1tan 3θθθθθθθ--===-++. 故选：A. 14．C 【解析】 【分析】利用二倍角余弦公式求2cos 23πα⎛⎫+⎪⎝⎭，再由22233ππααπ⎛⎫-=+- ⎪⎝⎭结合诱导公式求目标函数的值. 【详解】 由2217cos 2cos 212sin 12333168πππααα⎛⎫⎛⎫⎛⎫+=+=-+=-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，又22233ππααπ⎛⎫-=+- ⎪⎝⎭， 所以227cos 2cos 2cos 23338πππααπα⎡⎤⎛⎫⎛⎫⎛⎫-=+-=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 故选：C ． 15．B 【详解】 选项A，22ππππcos sin cos 2cos 1212126⎛⎫-=⨯== ⎪⎝⎭，A 错误； 选项B ，22tan22.512tan22.511tan451tan 22.521tan 22.522=⋅==--，B 正确；选项C，11sin15cos15sin3024==，C 错误；选项D =D 错误. 故选: B 16．C 【解析】 【分析】利用三角变换化简,,a b c ，再根据正弦函数的单调性可得正确的选项. 【详解】sin35cos18cos35sin18sin17a =︒︒-︒︒=︒，2cos3212sin 16sin164sin172cos1884sin8cos8b ︒-︒===︒︒︒︒︒，22221tan 36cos 36sin 36cos 72sin181tan 36c -︒==︒-︒=︒=︒+︒，因为016171890︒<︒<︒<︒<︒，故sin16sin17sin18︒<︒<︒. 故c a b >>， 故选：C. 17．C 【解析】 【分析】根据余弦二倍角公式即可计算求值. 【详解】 ∵2sin18︒，∴sin18︒∴22cos3612sin 1812⎛=-=-⨯=⎝⎭. 故选：C. 18．A 【解析】 【分析】根据题意求得1tan 3x =，再结合正切的倍角公式，求得tan 2x 的值，即可求解.【详解】由tan 24x π⎛⎫+= ⎪⎝⎭，可得tan 121tan x x +=-，解得1tan 3x =， 又由22122tan 33tan 21tan 4113x x x ⨯===-⎛⎫- ⎪⎝⎭，所以1tan 433tan 294x x ==. 故选：A. 19．D 【解析】 【分析】由诱导公式、二倍角公式化简函数为一个角的一个三角函数形式，然后由余弦函数的性质判断各选项． 【详解】()4cos sin 4cos sin 6363f x x x x x ππππ⎛⎫⎛⎫⎛⎫⎛⎫=+-=-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭24cos cos 4cos cos 4cos 623666x x x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+--=-++=-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭222cos 112cos 2263x x ππ⎛⎫⎛⎫⎛⎫=-+-+=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．对于选项A ，最小正周期22T ππ==，即选项A 不正确． 对于选项B ，易知()f x 0≤，而选项B 中函数值可能大于0，函数不一致； 对于选项C ，令()2,23x πππ+∈，则5,36x ππ⎛⎫∈ ⎪⎝⎭，56x π=时，函数取得最大值，即选项C 不正确； 对于选项D ，由22cos 20333f πππ⎛⎫⎛⎫=-+-= ⎪⎪⎝⎭⎝⎭为最大值，故选项D 正确， 故选：D ． 20．D 【解析】 【分析】先利用诱导公式对要求解的式子进行化简，然后结合已知条件，求解出cos α的值，继而求解出cos2α，带入化简后的式子即可完成求解. 【详解】由已知sin()cos(2)2παπα-+-=cos cos2αα-，因为角α的终边与单位圆交于点63(,)33P -，所以22663cos 363()()33α==+-，21cos 22cos 13=-=αα 所以cos cos2αα-6161333-=-=， 故选：D. 21．C 【解析】 【分析】由已知求得72ACB ∠=︒，可得cos72︒的值，再由二倍角的余弦及三角函数的诱导公式求解cos144︒． 【详解】由图可知72ACB ∠=︒，且12cos 72BCAC ︒==所以2cos1442cos 721︒=︒-=故选：C. 22．D 【解析】 【分析】根据正切的二倍角公式即可化简求解. 【详解】原式22tan22212tan 33631tan 12πππ=-⋅=-=-=-故选：D. 23．C 【解析】 【分析】将式子先利用二倍角公式和平方关系配方化简，然后增添分母(221sin cos θθ=+)，进行齐次化处理，化为正切的表达式，代入tan 2θ=-即可得到结果． 【详解】解：因为tan 2θ=-，所以将式子进行齐次化处理得： ()()()22sin sin cos 2sin cos sin 1sin 2sin sin cos sin cos sin cos θθθθθθθθθθθθθθ+++==+++()2222sin sin cos tan tan 422sin cos 1tan 145θθθθθθθθ++-====+++．故选：C ． 24．A 【解析】 【分析】根据题意，结合勾股定理，以及正切的二倍角公式，即可求解. 【详解】如图所示，过点O 作⊥OD AB ，交AB 于点D ，设AB a ，圆O 的半径为r ，由题意知OD r =，OA a r =-，2a AD =， 因为222OA OD AD =+，得()2222a a r r ⎛⎫-=+ ⎪⎝⎭，解得38a r =， 因此42tan 3aAD AOD OA r ∠===， 故2422tan 243tan tan 2161tan 719AOD AOB AOD AOD ⨯∠∠=∠===--∠-. 故选：A. 25．D 【解析】 【分析】1cos 21cos 222αα+-α的范围确定cos α和sin α的符号即可求解. 【详解】由二倍角公式可知，221cos 2cos αα+=，21cos 22sin αα-=， 1cos 21cos 2|cos ||sin |22αααα+--， 又因为53,42ππα⎛⎫∈ ⎪⎝⎭，所以cos 0α<，sin 0α<， 1cos 21cos 2cos sin 22αααα+--+. 故选：D. 26．D 【解析】 【分析】根据441sin cos 3αα-=，利用平方关系和二倍角的余弦公式得到1cos23α=-，然后由()cos 2cos2sin24)a a a π+=-求解. 【详解】因为441sin cos 3αα-=，所以1cos23α=-，因为0,2πα⎛⎫∈ ⎪⎝⎭，所以sin20,sin2a α>=所以()cos 2cos2sin24)a a a π+=-，13==⎝⎭-故选：D. 27．A 【解析】 【分析】利用三角恒等变换化简已知条件，求得1cos sin 2αα+=，由此求得sin 2,cos 2αα，进而求得tan2α. 【详解】202152sin 2sin 44ππαααα⎛⎫⎛⎫+-=+- ⎪ ⎪⎝⎭⎝⎭)22cos sin sin )αααα=--1sin )cos sin 02αααα⎛⎫=-+-= ⎪⎝⎭，∵,2παπ⎛⎫∈ ⎪⎝⎭，∴cos sin 0αα-<，∴1cos sin 02αα+=>，∴3,24ππα⎛⎫∈ ⎪⎝⎭，32,2παπ⎛⎫∈ ⎪⎝⎭，且11sin 24α+=，∴3sin 24α=-，cos 2α=，∴tan 2α=故选：A 28．BD 【解析】 【分析】根据同角的三角函数关系式、诱导公式，结合二倍角公式进行逐一判断即可. 【详解】由()0,0,22απαπ⎛⎫∈⇒∈ ⎪⎝⎭，所以sin 2α===A ：因为1cos 23α=，所以217cos 2cos 121299αα=-=⨯-=-，本选项结论不正确；B ：因为1cos23α=，sin 2α=，所以1sin 2sin cos 2223ααα==⨯= C ：因为1cos 2cos 223ααπ⎛⎫-== ⎪⎝⎭，所以本选项结论不正确；D ：因为cos sin 222παα⎛⎫+=-= ⎪⎝⎭故选：BD 29．BC 【解析】 【分析】根据两角和的正切公式、诱导公式、两角和的正弦公式、二倍角的余弦公式，结合指数和对数的运算性质逐一判断即可. 【详解】()tan20tan25tan20tan25tan 2025tan451,A tan20tan2511tan20tan25++=-=-+=-=---错误；()1366666661log 27log 83log 33log 223log 3log 223log 621,B 8-⎛⎫+-=+-=+-=-= ⎪⎝⎭对；()sin72cos18cos108sin18sin72cos18cos72sin18sin 7218sin901,C -=+=+==对；222cos 22.51cos452-==，D 错误. 故选：BC. 30．BD 【解析】 【分析】根据三角函数恒等变换公式逐个分析计算即可 【详解】对于A ，()cos 15cos15cos(4530)cos 45cos30sin 45sin 30-︒=︒=︒-︒=︒︒+︒︒=，所以A 错误， 对于B ，111sin15sin 30sin 75sin15sin 30cos15sin15cos15sin 30248︒︒︒=︒︒︒=︒︒=︒=，所以B 正确，对于C ， ()()()()cos 35cos 25sin 35sin 25αααα-︒︒++-︒︒+ ()()cos 3525αα=-︒-︒+⎡⎤⎣⎦()1cos 60cos 602=-︒=︒= 所以C 错误，对于D ，22tan 22.512tan 22.511tan 45tan 45tan 22.521tan 22.522︒︒=⨯=︒=︒-︒-︒，所以D 正确， 故选：BD31．ACD【解析】【分析】根据三角函数恒等变换公式逐个选项加以判断.【详解】2cos cos (1sin )cos (1sin )1sin ==1sin (1sin )(1sin )cos cos x x x x x x x x x x x+++=--+，A 对， cos()sin 2παα+=-，B 错， 222(sin 2cos 2)cos n =si 22si 2cos 21si n 2n 4ααααααα--=-+，C 对， 2221cos 2112sin =tan 1cos 212cos 1θθθθθ--+=++-，D 对， 故选：ACD.32．ABD【解析】【分析】直接通过“切化弦”的思想即可判断AB ；通过对分式齐次式化简可判断C ；通过二倍角余弦公式化简可判断D.【详解】对于A ，sin 2cos 2tan cos cos 2sin sin ααααααα⨯==，故A 正确； 对于B ，因为1sin cos 2αα⋅=， 所以22cos sin cos sin cos tan 2sin cos sin sin cos ααααααααααα++=+==，故B 正确； 对于C ，因为1tan 2α=， 所以2sin 2tan 121cos sin 1tan 12ααααα===---，故C 错误； 对于D ，因为α为第一象限角，所以sin 0,cos 0αα>>，=D 正确； 故选：ABD.33．ABC【解析】【分析】利用三角恒等变换求出各选项中代数的值，由此可得出合适的选项.【详解】对于A 选项，22tan 22.512tan 22.511tan 451tan 22.521tan 22.522=⨯==--； 对于B 选项，222sin1512tan15cos 15cos 152sin15cos15sin 30cos152=⋅===；对于C 221121262πππ===； 对于D 选项，()()2sin 5030133sin 50cos50sin8016sin 5016cos5016sin 50cos508sin1004sin 18080+++===- sin 8014sin 804==. 故选：ABC.34【解析】【分析】化简已知条件，求得1cos sin 2x x -=，通过两边平方的方法求得sin 2x ，进而求得cos 2,tan 2x x . 【详解】πcos 24x x ⎛⎫-= ⎪⎝⎭， 221(cos sin )cos sin (cos sin )(cos sin )2x x x x x x x x +=-=+-①， π02x <<，sin cos 0x x ∴+≠， 化简得①1cos sin 02x x -=>，则π04x <<，π022x <<由21(cos sin )4x x -=，得3sin 24x =，cos 2x ==sin 2tan 2cos 2x x x ∴==35．19- 【解析】【分析】 先利用诱导公式求出cos 6x π⎛⎫- ⎪⎝⎭，再利用余弦的二倍角公式求解即可 【详解】 由2sin 33x π⎛⎫+= ⎪⎝⎭，得2cos 233x ππ⎡⎤⎛⎫-+= ⎪⎢⎥⎝⎭⎣⎦， 2cos 63x π⎛⎫-= ⎪⎝⎭， 所以3c s 26o x π⎛⎫-= ⎪⎝⎭， 所以cos 2cos 236x x ππ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭ 22cos 16x π⎛⎫=-- ⎪⎝⎭ 2212139⎛⎫=⨯-=- ⎪⎝⎭， 故答案为：19- 36．-2【解析】【分析】利用余弦的二倍角公式和正切的商数关系可得答案.【详解】()()()22222222222212sin 22cos 224sin 2sin 2sin tan cos 21tan 2cos tan 2cos cos cos θθθθθθθθθθθθθ-----===-=-+⨯⨯⨯. 故答案为：2-.37．1【解析】【分析】利用二倍角的余弦公式、同角三角函数的基本关系以及诱导公式化简可得结果.【详解】()()2cos 20sin 202sin 20cos20cos 20sin160cos 20sin 18020101cos 1601--==------cos 20sin 20c 1os 20sin 20-==-. 故答案为：1.38．(1)79(2) 【解析】【分析】（1）根据同角三角函数基本关系式，以及二倍角公式，即可求解；（2）根据角的变换33ππαα⎛⎫=-+ ⎪⎝⎭，再结合两角和的余弦公式，即可求解. (1)1sin 3α=，,2παπ⎛⎫∈ ⎪⎝⎭， cos α=sin tan cosααα== 2cos21279sin αα=-=；(2),2παπ⎛⎫∈ ⎪⎝⎭，2,363πππα⎛⎫∴-∈ ⎪⎝⎭， cos()3πα-=，sin 3πα⎛⎫∴-== ⎪⎝⎭，cos coscos cos sin sin 333333ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫=-+=--- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦12⎛=⨯= ⎝⎭39．(1)14(2) (4)【解析】【分析】（1）利用二倍角的正弦公式直接求得；（2）利用二倍角的余弦公式直接求得；（3）利用二倍角的余弦公式直接求得；（4）利用二倍角的正切公式直接求得. (1)()111sin15cos152sin15cos15sin 30224︒︒=︒︒=︒=.(2)22cos 751cos150︒-=︒=(3)()2211111sin 152cos 151cos302222-︒=︒-+=︒+=(4)22tan 75tan150tan 301tan 75︒=︒=-︒=-︒40．(1)()sin cos f ααα=- (2)247【解析】【分析】（1）结合诱导公式、同角三角函数的基本关系式、二倍角公式化简()f α.（2）利用已知条件求得sin ,cos αα，由此求得tan α，进而求得tan2α.(1)()f α=sin |sin cos |sin |cos |cos αααααα⋅-=-⋅， ∵π04α<<，sin cos 0αα-<，cos 0α>， ∴sin (cos sin )()sin cos sin cos cos f ααααααααα⋅-=-=-⋅． (2)∵π04α<<，∴cos sin 0αα>>， 由221sin cos 5sin cos 1αααα⎧-=-⎪⎨⎪+=⎩，可得3sin 54cos 5αα⎧=⎪⎪⎨⎪=⎪⎩， ∴sin 3tan cos 4ααα==， ∴2322tan 244tan 291tan 7116ααα⨯===--． 41．(1)12【解析】【分析】（1）利用两角和的正切公式展开得到方程，解得即可；（2）利用两角和的正弦公式及二倍角公式化简原式为sin cos αα+，再根据1tan 2α=及同角三角函数的基本关系求出sin α、cos α，即可得解；(1) 解：因为tan 34πα⎛⎫+= ⎪⎝⎭，所以tantan 4tan 341tan tan 4παπαπα+⎛⎫+== ⎪⎝⎭-，即1tan 31tan αα+=-，解得1tan 2α= (2)解：)cos sin 4cos 2παααα+-sin 2cos cos 2sin cos sin 44cos 2ππααααα=⎫+-⎪⎝⎭ ()sin 2cos 2cos sin cos 2ααααα+-= 22sin cos cos 2cos sin cos 2αααααα+-= ()2sin 2cos 1cos 2cos cos 2ααααα-+=()sin cos cos 2cos 2αααα+=sin cos αα=+因为α为锐角且1tan 2α=， 所以cos 2sin αα=.由22sin cos 1αα+=，得21sin 5α=，所以sin α，cos α=，可得sin cos αα+==42．(1)1sin 2α+；(3)1；(4)cos2α；(5)tan2α-；(6)2.【解析】【分析】（1）根据同角的三角函数关系式，结合正弦二倍角公式进行求解即可；（2）逆用正切二倍角公式，结合特殊角的正切值进行求解即可；（3）运用切化弦法，结合辅助角公式、二倍角公式、诱导公式进行求解即可；（4）运用平方差公式，结合同角的三角函数关系式、余弦的二倍角公式进行求解即可； （5）运用切化弦法，结合正弦和余弦的二倍角公式进行求解即可；（6）根据诱导公式，结合余弦二倍角公式进行求解即可.(1)()222sin cos sin cos 2sin cos 1sin 2ααααααα+=++=+ (2)22tan15tan(215)tan 301tan 15︒=⨯︒=︒=-︒； (3)()cos 401cos 40(1cos 402sin 40cos 40cos10sin 80cos10cos10cos101;︒︒=︒+=︒=︒⋅︒︒=︒︒=︒= (4)442222sin cos (sin cos )(sin cos )cos 2ααααααα-=+-=-； (5)111tan 1tan 11sin sin 11cos cos cos cos cos sin cos sin cos (cos sin )cos (cos sin )(cos sin )(cos sin )sin 2cos 2tan 2;ααααααααααααααααααααααααα-+-=-+-=-+---+=+--==- (6)2222223sin 703cos 203(2cos 101)2(2cos 10)22cos 102cos 102cos 102cos 10-︒-︒-︒--︒====-︒-︒-︒-︒.。

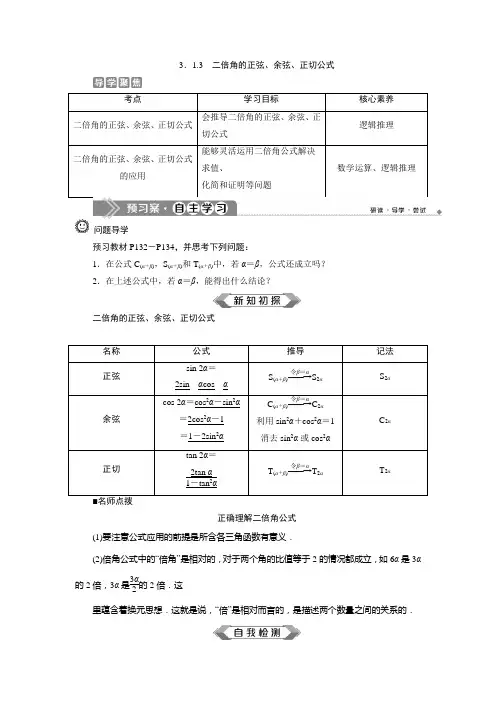
3．1.3二倍角的正弦、余弦、正切公式考点学习目标核心素养二倍角的正弦、余弦、正切公式会推导二倍角的正弦、余弦、正切公式逻辑推理二倍角的正弦、余弦、正切公式的应用能够灵活运用二倍角公式解决求值、化简和证明等问题数学运算、逻辑推理问题导学预习教材P132－P134，并思考下列问题：1．在公式C(α＋β)，S(α＋β)和T(α＋β)中，若α＝β，公式还成立吗？2．在上述公式中，若α＝β，能得出什么结论？二倍角的正弦、余弦、正切公式名称公式推导记法正弦sin 2α＝2sin__αcos__αS(α＋β)――→令β＝αS2αS2α余弦cos 2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2αC(α＋β)――→令β＝αC2α利用sin2α＋cos2α＝1消去sin2α或cos2αC2α正切tan 2α＝2tan α1－tan2αT(α＋β)――→令β＝αT2αT2α正确理解二倍角公式(1)要注意公式应用的前提是所含各三角函数有意义．(2)倍角公式中的“倍角”是相对的，对于两个角的比值等于2的情况都成立，如6α是3α的2倍，3α是3α2的2倍．这里蕴含着换元思想．这就是说，“倍”是相对而言的，是描述两个数量之间的关系的．判断(正确的打“√”，错误的打“×”) (1)10α是5α的倍角，5α是5α2的倍角．( ) (2)二倍角的正弦、余弦、正切公式的适用范围是任意角．( ) (3)存在角α，使得sin 2α＝2sin α成立．( ) (4)对于任意角α，总有tan 2α＝2tan α1－tan 2α.( )答案：(1)√ (2)× (3)√ (4)×已知sin α＝35，cos α＝45，则sin 2α等于( )A.75 B.125 C.1225 D.2425答案：D计算1－2sin 222.5°的结果等于( ) A.12 B.22 C.33D.32 答案：B已知tan α＝43，则tan 2α＝________．答案：－247给角求值求下列各式的值． (1)sin π8cos π8；(2)cos 2π6－sin 2π6；(3)2tan 150°1－tan 2150°； (4)cos π5cos 2π5.【解】 (1)sin π8cos π8＝12×2sin π8cos π8＝12×sin π4＝12×22＝24.(2)cos2π6－sin2π6＝cos⎝⎛⎭⎫2×π6＝cosπ3＝12.(3)原式＝tan(2×150°)＝tan 300°＝tan(360°－60°)＝－tan 60°＝－ 3.(4)原式＝2sinπ5cosπ5cos2π52sinπ5＝sin2π5cos2π52sinπ5＝sin4π54sinπ5＝sinπ54sinπ5＝14.给角求值问题的两类解法(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．1．cos4π12－sin4π12等于()A．－12B．－32C.12 D.32解析：选D.原式＝⎝⎛⎭⎫cos2π12－sin2π12⎝⎛⎭⎫cos2π12＋sin2π12＝cos π6＝32.2．求下列各式的值．(1)tan 30°1－tan2 30°；(2)1sin 10°－3cos 10°.解：(1)tan 30°1－tan230°＝12×2tan 30°1－tan230°＝12tan 60°＝32.(2)原式＝cos 10°－3sin 10°sin 10°cos 10°＝2⎝⎛⎭⎫12cos 10°－32sin 10°sin 10°cos 10°＝4（sin 30°cos 10°－cos 30°sin 10°）2sin 10°cos 10°＝4sin （30°－10°）sin （2×10°）＝4sin 20°sin 20°＝4.给值求值已知cos ⎝⎛⎭⎫α＋π4＝35，π2≤α＜3π2，求cos(2α＋π4)的值． 【解】 因为π2≤α＜3π2，所以3π4≤α＋π4＜7π4.因为cos ⎝⎛⎭⎫α＋π4>0，所以3π2<α＋π4<7π4. 所以sin ⎝⎛⎭⎫α＋π4＝－1－cos 2⎝⎛⎭⎫α＋π4 ＝－1－⎝⎛⎭⎫352＝－45. 所以cos 2α＝sin ⎝⎛⎭⎫2α＋π2 ＝2sin ⎝⎛⎭⎫α＋π4cos ⎝⎛⎭⎫α＋π4 ＝2×⎝⎛⎭⎫－45×35＝－2425， sin 2α＝－cos ⎝⎛⎭⎫2α＋π2＝1－2cos 2⎝⎛⎭⎫α＋π4 ＝1－2×⎝⎛⎭⎫352＝725.所以cos ⎝⎛⎭⎫2α＋π4＝22cos 2α－22sin 2α ＝22×⎝⎛⎭⎫－2425－725＝－31250.三角函数求值问题的一般思路(1)一是对题设条件变形，将题设条件中的角、函数名向结论中的角、函数名靠拢；另一种是对结论变形，将结论中的角、函数名向题设条件中的角、函数名靠拢，以便将题设条件代入结论．(2)注意几种公式的灵活应用，如： ①sin 2x ＝cos ⎝⎛⎭⎫π2－2x ＝cos ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ＝2cos 2⎝⎛⎭⎫π4－x －1＝1－2sin 2⎝⎛⎭⎫π4－x ； ②cos 2x ＝sin ⎝⎛⎭⎫π2－2x ＝sin ⎣⎡⎦⎤2⎝⎛⎭⎫π4－x ＝2sin ⎝⎛⎭⎫π4－x cos ⎝⎛⎭⎫π4－x .1．已知x ∈⎝⎛⎭⎫－π2，0，cos x ＝45，则tan 2x ＝( ) A.724 B ．－724 C.247D ．－247解析：选D.由cos x ＝45，x ∈⎝⎛⎭⎫－π2，0， 得sin x ＝－35，所以tan x ＝－34，所以tan 2x ＝2tan x1－tan 2x ＝2×⎝⎛⎭⎫－341－⎝⎛⎭⎫－342＝－247，故选D.2．若α∈⎝⎛⎭⎫π2，π，且3cos 2α＝sin ⎝⎛⎭⎫π4－α，则sin 2α的值为( )A.118 B ．－118 C.1718D ．－1718解析：选 D.cos 2α＝sin ⎝⎛⎭⎫π2－2α＝sin 2⎝⎛⎭⎫π4－α＝2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α，代入原式，得6sin ⎝⎛⎭⎫π4－α·cos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4－α.因为α∈⎝⎛⎭⎫π2，π，所以cos ⎝⎛⎭⎫π4－α＝16，所以sin 2α＝cos ⎝⎛⎭⎫π2－2α＝2cos 2⎝⎛⎭⎫π4－α－1＝－1718.化简与证明(1)化简2cos 2α－12tan ⎝⎛⎭⎫π4－αsin 2⎝⎛⎭⎫π4＋α；(2)证明tan ⎝⎛⎭⎫π4＋α－tan ⎝⎛⎭⎫π4－α＝2tan 2α. 【解】 (1)原式＝cos 2α2tan ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π2－π4－α＝cos 2α2tan ⎝⎛⎭⎫π4－αcos 2⎝⎛⎭⎫π4－α＝cos 2α2sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α ＝cos 2αsin ⎝⎛⎭⎫2×π4－2α ＝cos 2αcos 2α＝1. (2)证明：法一：左边＝sin ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋α－sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4－α－sin ⎝⎛⎭⎫π4－αcos ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4＋αcos ⎝⎛⎭⎫π4－α＝sin ⎝⎛⎭⎫π4＋α－π4＋αcos ⎝⎛⎭⎫π4＋αsin ⎝⎛⎭⎫π4＋α＝sin 2α12sin ⎝⎛⎭⎫π2＋2α＝2sin 2αcos 2α＝2tan 2α＝右边．所以等式成立．法二：左边＝1＋tan α1－tan α－1－tan α1＋tan α＝4tan α1－tan 2α＝2tan 2α＝右边．故原式成立．三角函数式的化简与证明(1)化简的方法①弦切互化，异名化同名，异角化同角；②降幂或升幂；③一个重要结论：(sin θ±cos θ)2＝1±sin 2θ.(2)证明三角恒等式的方法①从复杂的一边入手，证明一边等于另一边；②比较法，左边－右边＝0，左边右边＝1；③分析法，从要证明的等式出发，一步步寻找等式成立的条件．1．若α为第三象限角，则1＋cos 2αcos α－1－cos 2αsin α＝________．解析：因为α为第三象限角，所以cos α＜0，sin α＜0， 所以1＋cos 2αcos α－1－cos 2αsin α＝2cos 2αcos α－2sin 2αsin α＝－2cos αcos α－－2sin αsin α＝0.答案：02．求证：4sin αcos α1＋cos 2α·cos 2αcos 2α－sin 2α＝tan 2α.证明：左边＝2sin 2α2cos 2α·cos 2αcos 2α＝tan 2α＝右边．1．已知sin α＝3cos α，那么tan 2α的值为( ) A ．2 B ．－2 C.34D ．－34解析：选D.因为sin α＝3cos α，所以tan α＝3， 所以tan 2α＝2tan α1－tan 2α＝2×31－32＝－34.2．已知sin θ2＋cos θ2＝233，那么sin θ＝________，cos 2θ＝________．解析：因为sin θ2＋cos θ2＝233，所以⎝⎛⎭⎫sin θ2＋cos θ22＝43， 即1＋2sin θ2cos θ2＝43，所以sin θ＝13，所以cos 2θ＝1－2sin 2θ＝1－2×⎝⎛⎭⎫132＝79. 答案：13 793．已知α∈⎝⎛⎭⎫π2，π，sin α＝55. (1)求sin 2α，cos 2α的值； (2)求cos ⎝⎛⎭⎫5π6－2α的值． 解：(1)因为α∈⎝⎛⎭⎫π2，π，sin α＝55， 所以cos α＝－1－sin 2α＝－255.sin 2α＝2sin αcos α＝2×55×⎝⎛⎭⎫－255＝－45， cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫552＝35. (2)由(1)知cos ⎝⎛⎭⎫5π6－2α＝cos 5π6cos 2α＋sin 5π6sin 2α ＝⎝⎛⎭⎫－32×35＋12×⎝⎛⎭⎫－45 ＝－4＋3310.[A 基础达标]1．已知sin ⎝⎛⎭⎫π4－x ＝35，则cos ⎝⎛⎭⎫π2－2x 的值为( )A.1925 B.1625 C.1425D.725解析：选D.因为sin ⎝ ⎛⎭⎪⎫π4－x ＝35，所以cos ⎝ ⎛⎭⎪⎫π2－2x ＝cos ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4－x＝1－2sin 2⎝ ⎛⎭⎪⎫π4－x ＝725.2．已知sin α＝55，则cos 4α－sin 4α的值为( ) A ．－35B ．－15C.15D.35解析：选D.cos 4α－sin 4α＝(cos 2α＋sin 2α)(cos 2α－sin 2α)＝cos 2α＝1－2sin 2α＝1－25＝35.3．设－3π<α<－5π2，化简1－cos （α－π）2的结果是( )A ．sin α2B ．cos α2C ．－cos α2D ．－sin α2解析：选C.因为－3π<α<－5π2，－3π2<α2<－5π4，所以1－cos （α－π）2＝1＋cos α2＝⎪⎪⎪⎪⎪⎪cos α2＝－cos α2.4．已知cos ⎝⎛⎭⎫α－π4＝－13，则sin(－3π＋2α)＝( )A.79 B ．－79C.35D ．－35解析：选A.易得cos ⎝ ⎛⎭⎪⎫2α－π2＝2cos 2⎝ ⎛⎭⎪⎫α－π4－1＝2×⎝⎛⎭⎫－132－1＝－79.又cos ⎝⎛⎭⎪⎫2α－π2＝cos ⎝ ⎛⎭⎪⎫π2－2α＝sin 2α，所以sin(－3π＋2α)＝sin(π＋2α)＝－sin 2α＝－⎝⎛⎭⎫－79＝79.故选A. 5．化简tan 14°1－tan 214°·cos 28°的结果为( )A.sin 28°2B ．sin 28°C ．2sin 28°D ．sin 14°cos 28°解析：选A.tan 14°1－tan 214°·cos 28°＝12×2tan 14°1－tan 214°·cos 28°＝12tan 28°·cos 28°＝sin 28°2，故选A.6．已知sin α－2cos α＝0，则tan 2α＝________． 解析：由sin α－2cos α＝0，得tan α＝sin αcos α＝2，tan 2α＝2tan α1－tan 2α＝2×21－22＝－43. 答案：－437．已知tan α＝－13，则sin 2α－cos 2α1＋cos 2α＝________．解析：sin 2α－cos 2α1＋cos 2α＝2sin αcos α－cos 2α1＋2cos 2α－1＝2sin αcos α－cos 2α2cos 2α＝tan α－12＝－56.答案：－568.1－2sin 20°cos 20°2cos 210°－1－cos 2160°－1＝________．解析：1－2sin 20°cos 20°2cos 210°－1－cos 2160°－1＝（cos 20°－sin 20°）2cos 20°－sin 20°＝cos 20°－sin 20°cos 20°－sin 20°＝1.答案：19．已知sin 2α＝513，π4<α<π2，求sin 4α，cos 4α的值．解：由π4<α<π2，得π2<2α<π. 因为sin 2α＝513，所以cos 2α＝－1－sin 22α＝－1－⎝⎛⎭⎫5132＝－1213. 于是sin 4α＝2sin 2αcos 2α＝2×513×⎝⎛⎭⎫－1213＝－120169； cos 4α＝1－2sin 22α＝1－2×⎝⎛⎭⎫5132＝119169. 10．已知π2<α<π，sin α＝45. (1)求tan 2α的值；(2)求cos ⎝⎛⎭⎫2α－π4的值． 解：(1)由题意得cos α＝－35， 所以tan α＝－43， 所以tan 2α＝2tan α1－tan 2α＝－831－169＝247. (2)因为sin α＝45，所以cos 2α＝1－2sin 2α＝1－2×⎝⎛⎭⎫452＝－725， sin 2α＝2sin α·cos α＝2×45×⎝⎛⎭⎫－35＝－2425. 所以cos ⎝⎛⎭⎪⎫2α－π4＝cos 2α·cos π4＋sin 2α·sin π4＝⎝⎛⎭⎫－725×22＋⎝⎛⎭⎫－2425×22＝－31250. [B 能力提升]11．已知tan x ＝2，则tan ⎣⎡⎦⎤2⎝⎛⎭⎫x －π4等于( ) A.43B ．－43 C.34 D ．－34解析：选C.tan ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π4 ＝tan ⎝ ⎛⎭⎪⎫2x －π2＝sin ⎝ ⎛⎭⎪⎫2x －π2cos ⎝ ⎛⎭⎪⎫2x －π2＝－cos 2x sin 2x ＝－1tan 2x＝－1－tan 2x 2tan x ＝4－12×2＝34. 12．已知θ∈⎝⎛⎭⎫π2，π，1sin θ＋1cos θ＝22，则sin ⎝⎛⎭⎫2θ＋π3＝________． 解析：1sin θ＋1cos θ＝22⇒sin θ＋cos θsin θcos θ＝22 ⇒sin θ＋cos θ＝22sin θcos θ⇒1＋sin 2θ＝2sin 22θ，因为θ∈⎝ ⎛⎭⎪⎫π2，π，所以2θ∈(π，2π)， 所以sin 2θ＝－12，所以sin θ＋cos θ<0， 所以θ∈⎝ ⎛⎭⎪⎫3π4，π，所以2θ∈⎝ ⎛⎭⎪⎫3π2，2π， 所以cos 2θ＝32，所以sin ⎝⎛⎭⎪⎫2θ＋π3＝sin 2θ·cos π3＋sin π3cos 2θ＝12. 答案：1213．已知sin ⎝⎛⎭⎫π4－x ＝513，0<x <π4，求cos 2x cos ⎝⎛⎭⎫π4＋x 的值． 解：因为0<x <π4，所以0<π4－x <π4. 又因为sin ⎝ ⎛⎭⎪⎫π4－x ＝513， 所以cos ⎝ ⎛⎭⎪⎫π4－x ＝1213. 因为cos 2x ＝sin ⎝ ⎛⎭⎪⎫π2－2x ＝2sin ⎝ ⎛⎭⎪⎫π4－x cos ⎝ ⎛⎭⎪⎫π4－x ＝2sin ⎣⎢⎡⎦⎥⎤π2－⎝ ⎛⎭⎪⎫π4＋x cos ⎝ ⎛⎭⎪⎫π4－x＝2cos ⎝ ⎛⎭⎪⎫π4＋x cos ⎝ ⎛⎭⎪⎫π4－x ， 所以cos 2x cos ⎝ ⎛⎭⎪⎫π4＋x ＝2cos ⎝ ⎛⎭⎪⎫π4－x ＝2413. 14．(选做题)已知sin x 2－2cos x 2＝0. (1)求tan x 的值；(2)求cos 2xcos ⎝⎛⎭⎫5π4＋x sin （π＋x ）的值．解：(1)由sin x 2－2cos x 2＝0， 知cos x 2≠0，所以tan x 2＝2， 所以tan x ＝2tan x 21－tan 2 x 2＝2×21－22＝－43. (2)由(1)知tan x ＝－43， 所以cos 2x cos ⎝ ⎛⎭⎪⎫5π4＋x sin （π＋x ） ＝cos 2x－cos ⎝ ⎛⎭⎪⎫π4＋x （－sin x ） ＝cos 2x －sin 2x ⎝⎛⎭⎫22cos x －22sin x sin x ＝（cos x －sin x ）（cos x ＋sin x ）22（cos x －sin x ）sin x ＝2×cos x ＋sin x sin x＝2×1＋tan x tan x ＝24.。

高一（上） 两角和与差及二倍角公式入门测，每题5分，总分：60分 姓名 得分 一、公式背诵：1.两角和与差的正弦、余弦和正切公式 sin(α±β)＝ 。

cos(α∓β)＝ 。

tan(α±β)＝ 。

2.二倍角的正弦、余弦、正切公式 sin 2α＝ 。

cos 2α＝ ==。

tan 2α＝ 。

3.有关公式的逆用、变形等 (1)tan α±tan β＝ 。

(2)cos 2α＝，sin 2α＝。

(3)1＋sin 2α＝()2，1－sin 2α＝()2，sin α±cos α＝4.函数f (α)＝a sin α＋b cos α(a ，b 为常数)，可以化为f (α)＝⎝ ⎛⎭⎪⎫其中tan φ＝b a 或f (α)＝a 2＋b 2·cos(α－φ)⎝ ⎛⎭⎪⎫其中tan φ＝a b 。

二、判断正误(在括号内打“√”或“³”)5、两角和与差的正弦、余弦公式中的角α，β是任意的.()6、存在实数α，β，使等式sin(α＋β)＝sin α＋sin β成立. ()7、公式tan(α＋β)＝tan α＋tan β1－tan αtan β可以变形为tan α＋tan β＝tan(α＋β)(1－tan αtan β)，且对任意角α，β都成立. () 8、存在实数α，使tan 2α＝2tan α. ()9、(2015·全国Ⅰ卷)sin 20°cos 10°－cos 160°sin 10°＝( )A.－32 B.32C.－12D.1210、(2016·东北三省三校联考)已知sin α＋cos α＝13，则sin 2⎝ ⎛⎭⎪⎫π4－α＝( )A.118B.1718C.89D.2911、(2015·江苏卷)已知tan α＝－2，tan(α＋β)＝17，则tan β的值为________. 12、(2014²课标全国Ⅱ卷)函数f(x)＝sin(x ＋2φ)－2sin φcos(x ＋φ)的最大值为________.考点一 三角函数式的化简、求值【例1】 (1)化简：（1＋sin α＋cos α）·⎝⎛⎭⎪⎫cos α2－sin α22＋2cos α(0＜α＜π)＝________。