当前位置：文档之家 › !第六章弯曲应力

!第六章弯曲应力

  • 格式：doc
  • 大小：1.04 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

材料力学06(第六章 弯曲应力)分析

材料力学06(第六章 弯曲应力)分析

F / 4 2 103 mm 134 mm
30 MPa 5493104 mm4
F 24.6 kN
因此梁的强度由截面B上的最大拉应力控制
[F] 19.2 kN
§6-3 梁横截面上的切应力•梁的切应力强度条件
Ⅰ、梁横截面上的切应力
分离体的平衡
横截面上切应力 分布规律的假设
横截面上弯曲切 应力的计算公式
二.工字形截面梁 1、腹板上的切应力
h
d
y
d
O
y b
O
' A*
y dA
FS
S
* z
Izd
S
* z
bd
2
h
d
d 2
h 2
d
2
y2
腹板与翼缘交界处
max
min
FS Izd
bd

h d
max O
中性轴处
max
FS
S
* z,m
ax
Izd
y
min
FS
bd
h
d
d
h
d
2
I z d 2
160 MPa 148 MPa
2
Ⅲ 梁的正应力强度条件
max 材料的许用弯曲正应力
中性轴为横截面对称轴的等直梁
M max
Wz
拉、压强度不相等的铸铁等脆性材料制成的梁
为充分发挥材料的强度，最合理的设计为
t,max
M max yt,max Iz
[
t]
c,max
M max yc,max Iz
Myc,max Iz
典型截面的惯性矩与抗弯截面系数 ( d D)
b

第六章__弯曲应力及剪力流的知识点

第六章__弯曲应力及剪力流的知识点
Page 4
第六章 弯曲应力
上一讲回顾（12）
•梁变形与受力假设：平面假设，单向受力假设。 y My s •正应力公式： s E E Iz M Iz s max •最大正应力： Wz Wz y S z ydA, S y zdA •静矩：
A A
•惯性矩与惯性积 ：

50
a
F l
a
a = ? [ F ] 最大.
Page
27
第六章 弯曲应力
配重降低最大弯矩作用分析
M
Pa Pa F P
F a
P
l
a
a
l
a
M
Fl/4 +
M
Fl/4-Pa Pa
+
Pa
Page 28
第六章 弯曲应力
弯拉（压）组合分析
A F
l 2
q
B
C
l 2
F
C
FN M max
sN

sM
y
sN sM

20 kN 20 kN
C
D
解：计算截面形心 与惯性矩
A
B
1m
3m
1m
yC 139mm I z 40.3 106 mm 4
M 图:

10kN m

20kN m
200
为校核梁的强度，需计算 B截面a点的拉应力与b点 压应力，C截面b点拉应力
a
30
y1
z
170
yC
b 30
Page 19
3. 弯矩计算 或
EI z
bd 2s max M s max W 1.14kNM 6

第6章 弯曲应力

第6章 弯曲应力

称为抗弯截面系数
只有一根对称轴的横截面形状: yt，max yc，max O y
O y
z
t,max
My t ,max Iz
c,max
Myc,max Iz
z
简单截面的弯曲截面系数 b h ⑴ 矩形截面
z
bh3 Iz 12 b3h Iy 12
⑵ 圆形截面
y d
Iz bh2 Wz h/2 6 Iy b2h Wy 源自/2 63()
Ⅱ .纯弯曲理论的推广 对于细长梁（ l/h > 5 ），纯弯曲时的正应力计算 公式用于横力弯曲情况，其结果仍足够精确。 F
l
M ( x) y Iz
Fl
4
max
M ( x) Wz
解：
由弯曲曲率公式 可得：
M EIz
M EI z
1
代入弯曲正应力公式：
M EIZ Ed 533.3MPa WZ WZ 2
3.正应力的正负号与弯矩 及点的坐标 y的正负号有关。实际计算中，可根 据截面上弯矩的方向，直接判断中性 轴的哪一侧产生拉应力，哪一侧产生 压应力，而不必计及M和y的正负。
三、最大弯曲正应力 有两根对称轴的横截面形状: b h
z
y y
z
max
M M Mymax I z Wz Iz y max

基本假设2:
梁内各纵向纤维无挤压 假设，纵向纤维间无正应 力。

中性层与中性轴
纵向对称面 中性层 Z 中性轴
中性层 根据变形的连续性 可知，梁弯曲时从其凹 入一侧的纵向线缩短区 到其凸出一侧的纵向线 伸长区，中间必有一层 纵向无长度改变的过渡 层，称为中性层 。 中性轴: 中性层与横截面的交 线就是中性轴。

第六章 弯曲应力

第六章 弯曲应力

近似公式:
Q
hb
47
腹板切应力的近似公式
因为: (1)腹板切应力近似为均匀分布;
(2)腹板负担了绝大部分剪力。
近似公式:
Q
hb
翼缘的切应力
特点
(1) 除了有平行于剪力Q的切应力 分量外，还有与剪力Q垂直的 切应力分量；
(2) 切应力数值与腹板的切应力相比较小。 48
箱形薄壁梁
假设 : t //
My
Iz
总结
假设 平面假设，单向受力假设
综合考虑三方面
( y) y
结论
( y) E ( y)
dA0 ydA M
A
A
中性轴位置：中性轴过截面形心
❖ 中性层曲率：1 M （Iz －惯性矩）
EI z （EIz －截面弯曲刚度）
正应力公式： ( y) My
Iz
max
M Wz
（Wz －抗弯截面系数）
y2)
8
24
则，距中性层 y处的切应力公式为:
Q
[
B
(H
2
h2 )
b
h2 (
y 2 )]
Izb 8
24
切应力分布如图。
45
距中性层 y处的切应力公式为:
Q [ B (H 2 h2) b (h2 y2)]
Izb 8
24
切应力分布如图。
最大切应力发生在中性轴处
max
Q[ Izb
BH 2 8
由切应力互等定理，得
QS
* z
Izb
计算Sz*
可用公式
S
* z
A1
y1
S
* z
b( h 2
y) [y

材料力学课件第六章弯曲应力

材料力学课件第六章弯曲应力
第6章 弯曲应力
※ 梁的纯弯曲 ※ 纯弯曲时的正应力 ※ 横力弯曲时的正应力 ※ 弯曲切应力 ※ 提高弯曲强度的措施
第三章 扭 转
§6.1 梁的纯弯曲
横截面上同时存在弯矩和剪力
横力弯曲
横截面上只有弯矩并无剪力
纯弯曲
f1(M ) f2 (Q)
第三章 扭 转
aP P a
A
B
C
D
QP
x
P

a
2

h
2 4
2
b
a y
第三章 扭 转
附录 2. 惯性矩和惯性半径
一、惯性矩
z
定义：图形面积对某轴的二次矩
IzAy2dA , IyA z2dA
y
dA
z
工程中常把惯性矩表示为平面图形的
面积与某一长度平方的乘积, 即
O
y
Iz Az2i, IyAy2i
或
iy
Iy , A
iz
E E y
3. 静力学关系
M z
N A dA 0
(1 )
M yA zdA 0 (2 ) M zAy dA M (3 )
y z y
x
dA
E E y
第三章 扭 转
NxAdAAEρydA0
Sz 0
ydA 0
A
中性轴过形心
1、组合图形对某一轴的静矩等于组成它的各部分图形对同一 轴静矩的代数和，即：
n
n
Sz Aiyi , Sy Aizi
i1
i1
其中：Ai， yi， zi 分别代表第 i 个图形的面积和形心坐标， n为分割成的简单图形的个数。

Gg06-弯曲应力

Gg06-弯曲应力

max 1 故 max 2
L
P
分析和讨论
横截面上应力是如何分布的？ 两梁固结 两梁间光滑接触
为什么两梁间无摩擦时， 横截面上的弯矩由两梁均分？
如果梁由 n 层叠合而成，情况又怎样？
例
欲把直径为 d 的圆木锯成承受竖直方向荷载的矩形截面
梁，若要使梁具有最大的强度，矩形的高 h 和宽 b 应成什么 比例？
2. 最大正应力计算 （中性轴是对称轴的情况 ）
max
M max ymax [ ] Iz
Mmax：在梁的所有横截面中，选择弯矩为最大值的截面 ymax： 在弯矩最大的横截面上，选择离中性轴最远的点
M x
max
M max ymax M max M max [ ] Iz I z ymax Wz
W 1 0 b h 6
2b h
2
2
h 2 b
力学家与材料力学史
Galileo（1564-1642）
Galileo 在 1638 年出版的 Two New Sciences 一书中首次 对梁的弯曲进行了研究。
Hale Waihona Puke 力学家与材料力学史在其后的一百多年中，
经 Mariotte, J. Bernoulli 等
3M max b 44.7 mm 2[ ]
故取 b = 45 mm
动脑又动笔
撑杆跳过程中某时刻跳杆最小
曲率半径为 7.5m，增强玻璃钢跳
杆直径为 40 mm，E = 120 GPa， 求此时杆中的最大正应力。 120 240 320 480 (MPa)
M 由弯曲曲率公式 EI
跳杆中最大正应力
矩形横截面上的弯曲切应力是 如何分布的？

第6章 弯曲应力

第6章 弯曲应力

∗ FQ Sz
(
)
6.3 弯曲切应力
工字形截面梁
FQ B 2 2 b h2 2 τ= H − h + − y Iz b 8 2 4
(
)
h 分别代入： 以y = 0和y = ± 分别代入： 2
τ max
FQ BH 2 b Bh 2 = − (1 − ) Iz b 8 B 8
τmin =
∗ FQmax Sz
dI z
40×103 ×85140.97 = = 31.6MPa 7 6.5×1.66×10
3 工字钢梁最大弯曲剪应力的近似计算。 工字钢梁最大弯曲剪应力的近似计算。 腹板上平均剪应力为： 腹板上平均剪应力为：
40×103 τ= = = 38.8MPa A (180 − 2×10.7)×6.5 1 FQ
τmax =
∗ F max Sz max Q
dIz
=
∗ d ⋅ I z / Sz max
F max Q
40×103 = = 40.0MPa 6.5×15.4×10
2 求腹板上最小剪应力 最小剪应力位于腹板与翼缘交界处。 最小剪应力位于腹板与翼缘交界处。
6.3 弯曲切应力
∗ Sz = (10.7×94)×(180 / 2 −10.7 / 2) = 85140.97mm3
A
6.2 弯曲正应力
纯梁弯曲
因 FQ =0 所以 τ = 0，σ ≠ 0 ，
纵线 横线
m b a m M a m
n b a n
一、变形特点 纵线： 纵线： 变为同心圆弧线； 变为同心圆弧线； 凹侧缩短，凸侧伸长。 凹侧缩短，凸侧伸长。 横线： 横线： 仍为直线，且垂直于纵线； 仍为直线，且垂直于纵线； 不同横截面相对转过一个角度。 不同横截面相对转过一个角度。

工程力学教学 第6章 弯曲应力

工程力学教学 第6章 弯曲应力

17
max
M Iz
ymax
令
Wz
Iz , ymax
上式可改写为
max
M Wz
Wz 称为抗弯截面模量，单位：m3。
上述分析是在平面假设下建立的，对于横力弯曲，由于
横截面上还有剪力，变形后截面会发生翘曲，平面假设不再
成立。当截面尺寸与梁的跨度相比很小时，翘曲很小，可按
平面假设分析吗?
整理课件
18
横力弯曲
整理课件
19
6-2
横力弯曲正应力公式
弯曲正应力
M (x) y
IZ
弹性力学精确分析表明， 当跨度 l 与横截面高度 h 之 比 l / h > 5 （细长梁）时， 纯弯曲正应力公式对于横力 弯曲近似成立。
横力弯曲最大正应力
max
Mmaxymax IZ
整理课件
M max
max
Wz
20
弯曲正应力公式适用范围 •纯弯曲或细长梁的横力弯曲
4 2
2 F
3 F
A
s max
A
s max
A
矩形截面 圆形截面 环形截面
根据强度条件可进行下述工程计算：
⑴强度校核；
⑵设计截面尺寸；
⑶确定容许荷载。
整理课件
38
利用强度条件进行工程计算时，需首先确定梁的危险截面。
⑴梁的最大正应力发生在弯矩最大、截面离中性轴最远
点处；变截面梁要综合考虑 M与IZ;脆性材料抗拉和抗压性能
一、矩形截面切应力
基本假设： ⑴截面上各点切应力与剪力同向；
12
M
M+dM
⑵距中性轴等距离各点的切应力相 等。
Fs m n Fs

材料力学第6章弯曲应力

材料力学第6章弯曲应力

图6.5
页 退出
材料力学
出版社 理工分社
例6.1如图6.6所示，矩形截面悬臂梁受集中力和集中力偶作用。试求Ⅰ—Ⅰ 截面和固定端Ⅱ—Ⅱ截面上A，B，C，D ４点处的正应力。
图6.6
页 退出
材料力学
出版社 理工分社
解矩形截面对中性轴的惯性矩为 对于Ⅰ—Ⅰ截面，弯矩MⅠ=20 kN·m，根据式(6.2)，各点正应力分别为
页 退出
材料力学
出版社 理工分社
(1)变形几何关系 弯曲变形前和变形后的梁段分别表示于图6.4(a)和(b)。以梁横截面的对称 轴为y轴且向下为正(见图6.4(c))。以中性轴为z轴，但中性轴的位置尚待确 定。在中性轴尚未确定之前，x轴只能暂时认为是通过原点的横截面的法 线。根据弯曲平面假设，变形前相距为dx的两个横截面，变形后各自绕中性 轴相对旋转了一个角度dθ ，且仍然保持为平面。这就使得距中性层为y的纵 向纤维bb的长度变为
式中积分
是横截面对y轴和z轴的惯性积。由于y轴是横截面的对
称轴，必然有Iyz=0(见附录)。所以式(g)是自然满足的。 将式(b)代入式(e)，得
式中积分∫Ay2dA=Iz是横截面对z轴(中性轴)的惯性矩。于是式(h)改写为 式中 ——梁轴线变形后的曲率。
页 退出
材料力学
出版社 理工分社
式(6.1)表明，EIz越大，则曲率 越小，故EIz称为梁的抗弯刚度。从式 (6.1)和式(b)中消去 ，得
而对于变截面梁，虽然是等截面梁但中性轴不是横截面对称轴的梁，在计算 最大弯曲正应力时不能只注意弯矩数值最大的截面，应综合考虑My/Iz的值 (参看例6.5和例6.8)。
页 退出
材料力学
出版社 理工分社
引用记号

课件：第六章 弯曲应力

课件：第六章 弯曲应力

A y0dA 0
同理:
Iz Iz0 a2 A I y I y0 b2 A
Page
Cy0z0－形心直角坐标系 Oyz－任意直角坐标系
二者平行
16
思考：下列计算是否正确？ 其中C是截面形心。
IZ2 IZ1 Aa2
•C
解：不正确。
z1
a
因为 Z1 不是形心轴
z2
Page
17
典型截面的惯性矩与抗弯截面系数 ( d D)
( y) 1 dF
b dx
l F dA
My
Iz
M Iz
y * dA
ydA Sz ( )
MSz ( )
Iz
Sz()－面积 对中性轴 z 的静矩
l
( y) Sz ( ) dM
bIz dx
( y) FSSz ( )
I zb Page
1
2
M
M dM
y
FS
FS
y* mn
1
2
x
dx
d
l 2 0
0.002
3
x l
4(
x l
)2
dx
l l 2
0.002 1
x l
dx
0.002
3l 2
( x )2 l
l
4l 3
(
x l
)3
2 0
0.002 x
x2 l
2l
l
2 103 m 3
2
Page
29
作业
6-1 6-3 6-8 A-8
Page
30
§6-3 对称弯曲切应力
解：1. 问题分析
已知=(D+d)/2, E, 截面尺寸，可应

材料力学第六章弯曲应力

材料力学第六章弯曲应力

但相应的最大弯矩值变为
Fl ql2
M max
4
8
375 kN m 13 kN m 388 kN m
而危险截面上的最大正应力变为
max
388103 N m 2342106 m3
165.7106
Pa
165.7
MPa
显然，梁的自重引起的最大正应力仅为
165.7 160 MPa 5.7 MPa
<2>. 相邻横向线mm和nn，在梁弯曲后仍为直线，只是
相对旋转了一个角度，且与弧线aa和bb保持正交。
根据表面变形情况，并设想梁的侧面上的横向线mm和 nn是梁的横截面与侧表面的交线，可作出如下推论(假设)：
平面假设 梁在纯弯曲时，其原来的横截面仍保持为平面， 只是绕垂直于弯曲平面(纵向平面)的某一轴转动，转动后 的横截面与梁弯曲后的轴线保持正交。
力的值max为
max
M ym a x Iz
M
Iz ymax
M Wz
式中，Wz为截面的几何性质，称为弯曲截面系数（对Z轴）
(section modulus in bending)，其单位为m3。
b
h d
o
z
o
z
y
y
中性轴 z 不是横截面的对称轴时(参见图c)，其横截面 上最大拉应力值和最大压应力值为
A
r
(b)
M z
y d A E
A
r
y2 d A EI z M
A
r
(c)
由于式(a)，(b)中的
E
r
不可能等于零，因而该两式要求：
1. 横截面对于中性轴 z 的静矩等于零，A y d A 0 ；显

材料力学第6章弯曲应力

材料力学第6章弯曲应力

页 退出
材料力学
出版社 理工分社
图6.3 依据上述分析，弯曲变形可描述为横截面绕各自中性轴的轻微转动。由于梁 上的载荷都作用于梁的纵向对称面内，所以梁的整体变形应对称于纵向对称 面，这就要求中性轴与纵向对称面垂直。
页 退出
材料力学
出版社 理工分社
6.2.2纯弯曲正应力 纯弯曲时横截面上只有正应力，全部正应力的合力应该等于该横截面上的弯 矩。由于纯弯曲时梁横截面上正应力的分布规律未知，因此，不能直接由弯 矩M来确定正应力σ 。和推导圆轴扭转剪应力计算公式相似，需要从研究构 件的变形入手，综合考虑变形几何关系、物理关系以及静力平衡关系，才能 得到纯弯曲时的正应力。
其中，A点处为最大压应力，D点处为最大拉应力，B点处为拉应力。
页 退出
材料力学
对于Ⅱ—Ⅱ截面，弯矩MⅡ=20-15×3=-25 kN·m，所以
出版社 理工分社
其中，A点处为最大拉应力，D点处为最大压应力，B点处为压应力。
页 退出
材料力学
出版社 理工分社
例6.2如图6.7(a)所示简支梁，由56a号工字钢制成，其截面简 化后的尺寸如图6.7(b)所示。已知集中力F=150 kN。试求梁危 险截面上的最大正应力和同一截面上翼缘与腹板交界处a 点( 见图6.7(b))的正应力。
页 退出
材料力学
出版社 理工分社
6.3弯曲剪应力 横力弯曲的梁横截面上既有弯矩又有剪力，因此，横截面 上既有正应力又有剪应力。弯曲剪应力分布较复杂，截面 形状不同，分布规律也不相同。下面讨论几种常用的对称 截面梁横截面上的弯曲剪应力。
页 退出
材料力学
出版社 理工分社
6.3.1矩形截面梁 如图6.8(a)所示矩形截面梁的任意截面上，剪力Q皆与截面的对称轴y重合( 见图6.8(a))。关于横截面上剪应力的分布规律，作以下两个假设：①横截 面上各点的剪应力的方向都平行于剪力Q；②剪应力沿截面宽度均匀分布。 在截面高度h大于宽度b的情况下，以上述假设为基础得到的解，与精确解相 比有足够的准确度。按照这两个假设，在距中性轴为y的横线pq上，各点的 剪应力 都相等，且都平行于Q。再由剪应力互等定理可知，在沿pq切出的 平行于中性层的pr平面上，也必然有与相等 的 ′，而且 ′沿截面宽 度也是均匀分布的(见图6.8(d))。

第六章 - 弯曲应力

第六章 - 弯曲应力

查表 N0 12.6工字钢
WZ=77.5cm3
kN
15
28.1
13.16
kNm
3.75
例题
F 25kN
铸铁梁受荷载情况如图示。已知截面对形心轴
的惯性矩Iz=403×10－7m4，铸铁抗拉强度［σ ＋］ =50MPa，抗压强度［σ －］=125MPa。试按正应力强
度条件校核梁的强度。
200
q 12kN m
最大截面上的最大拉应力和最大压应力。
y
F
150
A
L 2
B
L 2
M max

FL 4
16kNm
y max

200 50 96.4 153.6mm
y max
96.4mm
50
96.4
z
200
C
50
max

My
max
IZ
24.09MPa
max

My max IZ
对梁的某一截面： 对全梁（等截面）：
max
Mymax Iz
M
WZ
max
M max ymax Iz
M max Wz
max

M max Wz


例题
长为L的矩形截面悬臂梁，在自由端作用一集中力
F，已知b＝120mm，h＝180mm、L＝2m，F＝1.6kN， 试求B截面上a、b、c各点的正应力。

1 M Z (b)

EIZ
由(a)(b)式得
Mzy
Iz
y
M
m
Mz
n
中性轴

第六章 弯曲应力材料力学安徽理工大学

第六章 弯曲应力材料力学安徽理工大学
方程：z y R
2 2 2
I z y 2 dA ( R 2 z 2 )dA
A A
y
dA 2 R 2 Z 2 dy
I z ( R 2 z 2 )2 R 2 y 2 dy
R R
dy y
0 Z

d
4
64
(然而： I p

A
dA ( y z )dA
A A A
设中性轴为z
y
z
dA
N x dA 0
A
E
A
y

dA 0
E
ydA 0
A
ydA S
A
z
0
中性轴Z必过截面形心
横截面对Z轴的静矩
M y z dA 0 z E
y
zydA I yz 0
A
A
A

dA
对于短跨、截面高的梁 P 须计算弯曲剪应力
h
x
q( x)
dx
b
M ( x)
M ( x) d M ( x)
z
My Iz
y
在hb的情况下 假设：1) 的方向都与Q平行 2) 沿宽度均布。

y

N II
NI
M My dA N I dA Iz * Iz * A A
D
B
P 2
P 2
B
主梁AB A
La M 2 La 2
M max AB
P (l a ) 4
P
附梁CD
C a M
M max CD Pa 4
D
解：

第六章 弯曲应力(习题解答)

第六章 弯曲应力(习题解答)

6-3、图示矩形截面梁受集中力作用，试计算1-1横截面上a 、b 、c 、d 四点的正应力。

解：（1）外力分析，判变形。

荷载在纵向对称面内，与轴线垂直，梁发生平面弯曲。

中性轴z 轴过形心C 与载荷垂直，沿水平方向。

（2）内力分析，弯矩图如图（b ）所示，1-1横截面的弯矩为：1115230(M -=-⨯=-⋅kN m)（3）应力分析，梁上边有弯矩图，上侧纤维受拉。

1-1横截面上的a 点处于拉伸区，正应力为正；c 点处于中性层上，正应力为零；b 、d 两点处于压缩区，正应力为负。

3111111max2301011.1110.1800.36a a zzzM M M y y I I W σ---⨯=⋅=⋅===⨯⨯Pa MPa 。

11.11b a σσ=-=-MPa0c σ= 31133010(0.1500.050)7.4110.1800.312d d zM y I σ-⨯=-⋅=-⨯-=-⨯⨯Pa MPa37M kN V 图(kN)(a)(c)(b)(c)(e)(d)2+q l /8MkN ·m)(f)(b)180q题6-3图 题6-5图6-5、两根矩形截面简支木梁受均布荷载q 作用，如图所示。

梁的横截面有两种情况，一是如图(b)所示是整体，另一种情况如图(c)所示是由两根方木叠合而成（二方木间不加任何联系且不考虑摩擦）。

若已知第一种情况整体时梁的最大正应力为10MPa ，试计算第二种情况时梁中的最大正应力，并分别画出危险截面上正应力沿高度的分布规律图示。

解：（1）外力分析，判变形。

荷载在纵向对称面内，与轴线垂直，梁发生平面弯曲。

第一种情况中性层为过轴线的水平纵向面，中性轴z 轴过整体形心C 与载荷垂直，沿水平方向。

而第二种情况，两根木梁以各自的水平纵向面为中性层发生弯曲，两根中性轴为与荷载垂直的水平形心主轴。

如图所示。

（2）内力分析，判危险面：弯矩图如图（b ）所示，跨中截面为危险面。

第六章 弯曲应力(土木)

第六章 弯曲应力(土木)

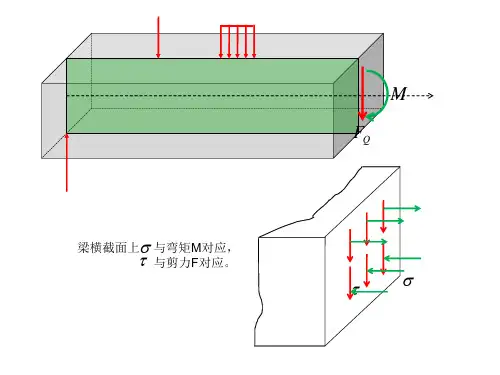
六章弯曲应力内容提要6-1 概述§6-2 弯曲正应力§6-3 弯曲剪应力§6-4 梁的强度计算§6-5 提高梁弯曲强度的主要措施§6-6 截面的弯心概念§6-7 组合梁重点、中性层、中性轴的概念；2、梁的横截面上正应力、剪应力公式及对应的强度条件；3.提高梁弯曲强度的措施难点1、危险截面的确定2、弯曲剪应力的求解6-1 概述轴向拉压：0τ,AN σ==圆轴扭转：ρI T τ,0σP==梁的弯曲：当梁上有横向外力作用时，一般情况下，梁的横截面上既又弯矩M ，又有剪力V 。

mm VM只有与正应力有关的法向内力元素dN = σdA 才能合成弯矩只有与剪应力有关的切向内力元素dV = τdA 才能合成剪力所以，在梁的横截面上一般既有正应力，又有剪应力m mVmmMτσ§6-2 弯曲正应力若梁在某段内各横截面上的弯矩为常量，剪力为零，则该段梁的弯曲就称为纯弯曲。

P P a aC D+-PP+PaCD 段就是纯弯曲。

1、实验观察与分析在矩形截面梁的侧面画上一些水平的纵线（aa、bb等）和一些横向线（mm、nn 等）观察到：纵线：相互平行的水平直线→相互平行的曲线，且上部被压短，下部被拉长；横向线：仍保持直线，仍与纵线垂直，但相互不再平行，相对转动了一个角度。

、实验观察与分析（1）横截面变形后仍为一平面（平截面假设），且仍与梁的轴线正交；（2）梁可看成是由一层层的纵向纤维组成的，由平面假设，同一层纤维的伸长（或缩短）相同；（3）纵向纤维间无挤压，上部纤维缩短，下部纤维伸长，由变形的连续性，必有一层纤维即不伸长，也不缩短，称之为中性层；中性层与横截面的交线称为中性轴。

、实验观察与分析中性层——即不伸长，也不缩短的一层纵向纤维中性层中性轴横截面中性轴——中性层与横截面的交线弯曲变形的特征——横截面绕中性轴转动了一个角度2、公式推导在推导纯弯曲梁横截面上正应力的计算公式时，要综合考虑几何，物理和静力学三方面。

材力第六章 弯曲应力

材力第六章 弯曲应力

3、切应力的分布：
Fs S z I zb
Fs
z
h y 2 h b h S z yc A ( 2 y ) b( y ) ( y2 ) 2 2 2 4
h y
max
y b
τ
3Fs 4y (1 2 ) 2bh h
2
3 Fs max 2 A
Mmax 6Mmax 6 4050 2 6.25MPa 7 MPa max 2 Wz bh 0.12 0.18
1 . 5 * 5400 Fs max 0. 375 MPa 0.9 MPa 1 . 5 max 0 . 12 * 0 . 18 A
几何方面
物理方面
静力方面
（一）、几何方面 1、实验：
纯弯曲梁横截面上的正应力公式
a c
b
d
2、变形规律： ⑴、横向线：仍为直线， 只是相对转动了一个角 度且仍与纵向线正交。
a
c
b
M a
d c
M
⑵、纵向线：由直线变 为曲线，且靠近上部的 纤维缩短，靠近下部的 b d 纤维伸长。 3、假设： （1）、平面假设：梁变形前的横截面变形后仍为平面，且仍垂 直于变形后的轴线，只是各横截面绕某轴转动了一个角度。
4 88106 46.2MPa 4 76310
Iz M C y2 2.5 88106 ct 28.2MPa 4 t max 28.2 t Iz 76310 M C y1 c max 46.2 c Cc Bc Iz
当
D12
4

[ D 2 (0.8D) 2 ]
4

材料力学第六章弯曲应力

材料力学第六章弯曲应力
3l/8 H
CD
Bx
l/4 l/4
x

1 ql
8
1 ql2 32
x
D
知正应力、正应变最 大值发生在H截面。
应用下述关系求应力与内力
应力～变形 关系：
E y
max

E
ymax

内力～变形或内力～应力关系：
1 M
EI z
或
M maxW
Page 15
第六章 弯曲应力
2. 应力计算
max

E
ymax

D d 0.701m
22
ymax
d
2
1.0 103 m
Page 5
第六章 弯曲应力
二、 组合变形
杆件的一般变形通常可分解为拉压、 扭转与弯曲变形的两种或三种基本 变形的组合。
三、 梁横截面上的弯曲应力 弯曲正应力 M 弯曲切应力 FS
四、 对称弯曲 梁具有对称截面，且在 纵向对称面承受横向外 力（或外力的合力）时 的受力与变形形式。
对称截面
Page 7
第六章 弯曲应力
§6-2 弯曲正应力
一、实验观测与假设（动画） 1. 外部变形观测
•纵向线：成圆弧线,上方纵向线 缩短，下方伸长
•横向线：保持直线，与横线正交 •顶与底部纵、横线变形比：符合 单向受力泊松效应
2. 内部变形假设
•平面假设：变形后横截面保持平面，仍与纵线正交 •单向受力假设
A
S y
zdA
A
分别称为对坐标轴x和y的静矩 或一次矩。
静矩的量纲： L3
o
y
z
z
dA
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

!第六章弯曲应力弯曲应力从7题之后差一个题号！！6-1 求图示各梁在m－m截面上A点的正应力和危险截面上最大正应力。

题6-1图解：（a ）mKN M mm ⋅=-5.2mKN M ⋅=75.3max48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A37.20108.490104105.2823=⨯⨯⨯⨯=--σ （压）MPa2.38108.4901051075.3823max=⨯⨯⨯⨯=--σ（b ）mKN M mm ⋅=-60mKN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯==MPaA 73.611058321061060823=⨯⨯⨯⨯=--σ （压）MPa 2.104105832109105.67823max=⨯⨯⨯⨯=--σ（c ）m KN M mm ⋅=-1 mKN M ⋅=1max48106.25m J x-⨯=36108.7m W x-⨯=cmy A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ （压）MPa 2.128106.2510183max=⨯⨯=-σ6-2 图示为直径D ＝6 cm 的圆轴，其外伸段为空心，内径d ＝4cm ，求轴内最大正应力。

解：)1(32431απ-=D Wx⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa88.521002.17109.0631=⨯⨯=-σMPa 26.551021.2110172.1631=⨯⨯=-σMPa26.55max=σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。

试求梁内最大拉应力与最大压应力。

已知I z =10170cm 4，h 1=9.65cm ，h 2=15.35cm 。

解：A 截面： Mpa 95.371065.9101017010402831max =⨯⨯⨯⨯=--σ （拉） Mpa 37.501035.15101017010402831min -=⨯⨯⨯⨯-=--σ（压）E 截面 Mpa 19.301035.15101017010202832max =⨯⨯⨯⨯=--σ （拉） Mpa 98.181065.9101017010202832min -=⨯⨯⨯⨯-=--σ（压）6-4 一根直径为d 的钢丝绕于直径为D 的圆轴上。

（1） 求钢丝由于弯曲而产生的最大弯曲正应力（设钢丝处于弹性状态）（2） 若 d ＝lmm ，材料的屈服极限sσ=700MPa ，弹性模量E =210GPa ，求不使钢丝产生残余变形的轴径D 。

解：EJM =ρ1Dd E EJM 324πρ==D dE d M W M ⋅===3max32πσcmm dE D s303.01070010110210639==⨯⨯⨯⨯=⋅≥-σ6-5 矩形悬臂梁如图示．已知l = 4 m ，32=h b ，q =10kN/m ，许用应力[σ]=10Mpa 。

试确定此梁横截面尺寸。

解：m KN ql M⋅=⨯⨯==80410212122max963266322h h h h W =⨯==910101080263h M W W M =⨯⨯==⇒=σσcm m h 6.41416.0==cmb 7.27=6-6 20a 工字钢梁的支承和受力情况如图所示。

若[σ]＝160MPa ，试求许用载荷P 。

解：3237cm W =P 32 m KN PM ⋅=32max[][]P W M 32102371016066=⨯⨯⨯=⋅=-σ （M 图）P 32[]KN P 880.5623716023=⨯⨯=6-7 压板的尺寸和载荷情况如图所示。

材料为 45钢，sσ＝380 MPa ，取安全系数5.1=n 。

试校核压板强度。

解：2331568)121230122030(101mm W =⨯-⨯⨯=m N M ⋅=⨯⨯⨯=-3601020101833[]σσ<=⨯==-MPa W M 6.22910156836096-7 由两个槽钢组成的梁受力如图示。

已知材料的许用应力[σ]＝150 MPa ，试选择槽钢号码。

解：mKN M⋅=60max[]33363m ax400104.010*******cm m M W x =⨯=⨯⨯==-σ查表：（22a ， 332006.217cm cm W x>=）mKN ⋅60m20KN（M 图）6-8割刀在切割工件时，受到P＝1kN的切销力的作用。

割刀尺寸如图所示。

试求割刀内最大弯曲应力。

解：mN p M ⋅=⨯⨯=-I81083mN p M ⋅=⨯⨯=-∏30103033242.706135.2mm W =⨯=I321506154mm W =⨯=∏()MPa W M 114104.7089m ax =⨯==-I I I σ ()MPa W M 20010150309m ax =⨯==-∏∏∏σ6-9 图示圆木，直径为D ，需要从中切取一矩形截面梁。

试问（1）如要使所切矩形截面的抗弯强度最高，h 、b 分别为何值？（2）如要使所切矩形截面的抗弯刚度最高，h 、b 又分别为何值？解：6)(6222b D b bh W -==0=dbdW∴06322=-b D∴322D b =2222323DD D h =-=∴从强度讲：D b 57735.0=∴ D h 8165.0=12)(123222b D b bh J -==0=dbdJ)2()(23)(21222322=-⨯-⨯⨯+-b b D b b D∴从刚度讲 D b 50.0=D h 866.0=6－10 T 字形截面的铸铁梁受纯弯曲如图示，欲使其最大压应力为最大拉应力的3倍，巳知h = 12cm ，t =3cm ，试确定其翼板宽度b 之值。

解：3maxmax＝下上拉压y y =σσ下上＝y y 3 12=h y y ＝＋下上cm y 3412＝＝下5.4)39()233)(3(=⨯⨯--⨯=b Scmb 275.135.439=⨯⨯⨯=611 图示简支梁，由No.18工字钢制成，在外载荷作用下，测得横截面A 处梁底面的纵向正应变4100.3-⨯=ε，试计算梁的最大弯曲正应力σmax 。

已知钢的弹性模量E =200GPa, a =1m 。

解：MPaE A60100.31020049=⨯⨯⨯==-εσ28/34/3max max ===A A M M σσMPaA 1206022max=⨯==σσ243qa283qa241qa（M图）612 试计算图示矩形截面简支梁的1-1面上a 点和b 点的正应力和剪应力。

解：1－1截面 KN Q 6364.3=mKN M ⋅=6364.3433375.210912155.712cm bh J =⨯==283105.310375.2109106364.3--⨯⨯⨯⨯==y J M a σMPa03.6=82310375.2109105.7106364.3--⨯⨯⨯⨯=b σMPa93.12=2863105.710375.2109105.5)5.74(106364.3---⨯⨯⨯⨯⨯⨯⨯⨯==Jb QS a τMPa 379.0=6-13 计算在均布载荷 q ＝10 kN ／m 作用下，圆截面简支梁的最大正应力和最大剪应力，并指出它们发生在何处。

解：232max110108181⨯⨯⨯==ql Mm N ⋅⨯=31025.1 1101021213max⨯⨯⨯==ql Q N3105⨯=633m ax 105321025.1-⨯⨯⨯==πσWMMPa86.101= 在跨中点上、下边缘 34105410534423max⨯⨯⨯⨯=⨯=-πτA QMPa46.25= 在梁端，中性轴上6-14 试计算6-12题工字钢简支梁在图示载荷下梁内的最大剪应力。

解：MPa Wqa 60832=qa 413185cm W =mKN q /6.29123810185106066=⨯⨯⨯⨯⨯=-qa 43KN qa Q 2.2216.294343max =⨯⨯==（Q 图） MPa Jt QS 12.22105.6104.15102.22323max=⨯⨯⨯⨯==--τ6-15 矩形截面木梁所受载荷如图示，材料的许用应力[σ]=10Mpa 。

试选择该梁的截面尺寸，设1:2:=b hKN 19 m KN ⋅141KN 8 KN 9KN 1m KN ⋅8KN 21 （Q 图） （ M 图） 解：KNR A19=KNR B 29=126132h bh W ==[]σσ≤⨯==12101433m axhW Mcm m h 6.25256.01010121014363==⨯⨯⨯=cmb 8.12=[]ττ<=⨯⨯⨯⨯==-MPa A Q 961.0106.258.1210215.15.143max6-16 试为图示外伸梁选择一工字形截面，材料的许用应力[σ]= 160MPa ，[τ]＝80Mpa 。

解：[]3612510160100020cm MW =⨯⨯==σ取16I ， 3141cm W = )(8.13:cm S J =[]ττ<=⨯⨯⨯==-MPa Jt QS 181.01068.13101533故 取No16工字钢)(x QKN15)(x MmKN ⋅20KN 5 m KN ⋅10KN 10 （Q 图） （M 图）6-17 图示起重机安装在两根工字形钢梁上，试求起重机在移动时的最危险位置及所采用工字型钢的号码。

已知 l ＝10 m ，a ＝4 m ，d =2 m 。

起重机的重量 W ＝50 kN ，起重机的吊重P =10 kN ，钢梁材料的许用应力［σ］=160 MPa ，[τ]= 100Mpa 。

解：轻压：KN 10 ，KN 50[]x x x R 658)8(10)10(50101-=-+-=xx Rx x M ⋅-==)658()(0=dxdM 01258=-x m x 833.4=m KN M ⋅=⨯⨯-=17.140833.4)833.4658(max[]63m ax101601017.140⨯⨯==σM W33387610876.0cm m =⨯=- 取 两个 aI 28 33438215.508cm Wcm Wz=>=KN10 KN 50d m 106-18 等腰梯形截面梁，其截面高度为h 。

用应变仪测得其上边的纵向线应变611042-⨯-=ε，下边的纵向线应变621014-⨯=ε。

试求此截面形心的位置。

解：11M εσ⋅=⋅E J y b＝上 22M εσ⋅=⋅E J y b＝下314422121==y y ＝εε hy y =+21 ∴h y y =+223∴h y 412=h y 431=6-19 简支梁承受均布载荷q ，截面为矩形hb ⨯，材料弹性模量E ，试求梁最底层纤维的总伸长。