简单数阵图PPT课件
- 格式:ppt
- 大小:2.14 MB
- 文档页数:8

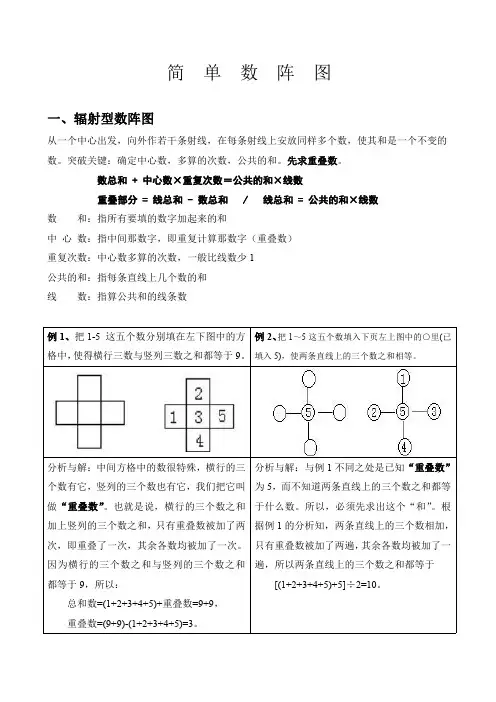
简单数阵图一、辐射型数阵图从一个中心出发,向外作若干条射线,在每条射线上安放同样多个数,使其和是一个不变的数。
突破关键:确定中心数,多算的次数,公共的和。
先求重叠数。
数总和+中心数×重复次数=公共的和×线数重叠部分=线总和-数总和/线总和=公共的和×线数数和:指所有要填的数字加起来的和中心数:指中间那数字,即重复计算那数字(重叠数)重复次数:中心数多算的次数,一般比线数少1公共的和:指每条直线上几个数的和线数:指算公共和的线条数例1、把1-5这五个数分别填在左下图中的方格中,使得横行三数与竖列三数之和都等于9。
例2、把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等。
分析与解:中间方格中的数很特殊,横行的三个数有它,竖列的三个数也有它,我们把它叫做“重叠数”。
也就是说,横行的三个数之和加上竖列的三个数之和,只有重叠数被加了两次,即重叠了一次,其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9,所以:总和数=(1+2+3+4+5)+重叠数=9+9,重叠数=(9+9)-(1+2+3+4+5)=3。
分析与解:与例1不同之处是已知“重叠数”为5,而不知道两条直线上的三个数之和都等于什么数。
所以,必须先求出这个“和”。
根据例1的分析知,两条直线上的三个数相加,只有重叠数被加了两遍,其余各数均被加了一遍,所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。
例3、把1~5这五个数填入右图中的○里,使每条直线上的三个数之和相等例4、将1~7这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都等于10。
分析与解:例1是知道每条直线上的三数之和,不知道重叠数;例2是知道重叠数,不知道两条直线上的三个数之和;本例是这两样什么都不知道。
但由例1、例2的分析知道,(1+2+3+4+5)+重叠数=每条直线三数之和×2,每条直线上三数之和=(15+重叠数)÷2。



第29讲、数阵图----初级版数阵是比较常见的填数问题,是一种老少都为之着迷的数学游戏。
无论数阵怎么变化,也都有规律可循,解题的关键就是求出重叠数。
只要你细心观察、分析,相信你一定能够解决更复杂的数阵问题。
一、数阵图的分类:1、数阵图分辐射型数阵图2、封闭型数阵图3、复合型数阵图。
二、解题方法1、去头、去尾、去中间。
2、求已知数总和,3、求数阵图中的总和,也就是图和-数和=“公用数”的总和。
1、1、将1、2、3、4、5填入下图的方格中,使横行、竖列的和都是10。
2、将1、3、5、7、9、11填入下图的圈内,使得对两个正方形,各自顶点上的数的和都等于22。
知识导引金典例题3、将1~7这七个数填入下图的圈内,使每一个正方形的四个数的和相等。
4、将1~9这九个数填在下图的圈中,使得横行的5个数,和是24.竖列的5个数,和也是24。
5、将1~8填入图中的圈内,使每条线上3个数的和都是12。
6、将3—9这七个数分别填入右图中的○里(其中9已填好),使每条直线上的三个数之和都相等。
9基础入门1、将1到9这九个数填入下图,使得从中心出发的每条线段上的三个数的和相等。
2、将1—7这7个自然数填入下图的7个○内,使得每条边上的3个数之和都等于10。
4623、将1—6这6个自然数分别填入右图的6个○内,使每条边上的3个数之和都等于10。
4、将2—9这8个数分别填入下图的○里,使每条边上的3个数之和等于18。
5、 右图中三个圆圈两两相交形成七个部分,分别填上自然数1~7,在一些部分中,自然数2、4、6三个数已经填好,请填上其余各数,使每个圆圈中四个数的和都是14.6、请将1、2、3、4、5、6、7、8、9九个数分别填入下图的九个小圆圈里,使每个三角形上三个数的和都等于15。
10658714102030每列、每条对角线上各数和都等于27。
2、在有图中的空格内填入适当的数,使每行、每列、每条对角线上各数的和都等于33。
3、在空格中填入不同的数,使每一横行、竖行、斜行三个数的和等于75。



第17讲数阵图(二)例1在右图的九个方格中填入不大于12且互不相同的九个自然数(其中已填好一个数),使得任一行、任一列及两条对角线上的三个数之和都等于21。
解:由上一讲例4知中间方格中的数为7。
再设右下角的数为x,然后根据任一行、任一列及每条对角线上的三个数之和都等于21,如下图所示填上各数(含x)。
因为九个数都不大于12,由16-x≤12知4≤x,由x+2≤12知x≤10,即4≤x≤10。
考虑到5,7,9已填好,所以x只能取4,6,8或10。
经验证,当x=6或8时,九个数中均有两个数相同,不合题意;当x=4或10时可得两个解(见下图)。
这两个解实际上一样,只是方向不同而已。
例2将九个数填入右图的空格中,使得每行、每列、每条对角线上的三个数之和都相等,则一定有证明:设中心数为d。
由上讲例4知每行、每列、每条对角线上的三个数之和都等于3d。
由此计算出第一行中间的数为2d——b,右下角的数为2d-c(见下图)。
根据第一行和第三列都可以求出上图中★处的数由此得到3d-c-(2d-b)=3d-a-(2d-c),3d-c-2d+b=3d-a-2d+c,d——c+b=d——a+c,2c=a+b,a+bc=2。
值得注意的是,这个结论对于a和b并没有什么限制,可以是自然数,也可以是分数、小数;可以相同,也可以不同。
例3在下页右上图的空格中填入七个自然数,使得每一行、每一列及每一条对角线上的三个数之和都等于90。
解:由上一讲例4知,中心数为90÷3=30;由本讲例2知,右上角的数为(23+57)÷2=40(见左下图)。
其它数依次可填(见右下图)。
例4在右图的每个空格中填入个自然数,使得每一行、每一列及每条对角线上的三个数之和都相等。
解:由例2知,右下角的数为(8+10)÷2=9;由上一讲例4知,中心数为(5+9)÷2=7(见左下图),且每行、每列、每条对角线上的三数之和都等于7×3=21。
