垂直平分线定义性质与判定

线垂直平分线的判定线垂直平分线是几何学中的一个重要概念，用于描述一个线段被等分成两等分的直线，且这条直线与线段垂直。

在本文中，我们将深入探讨线垂直平分线的定义、性质和判定方法。

我们将从简单的概念入手，逐渐深入探讨该主题的更复杂和有趣的方面。

1. 线垂直平分线的定义线垂直平分线是指一个直线将线段等分，且与线段垂直。

具体而言，对于一个线段AB，如果存在一条直线CD，使得CD将AB分为两等分，并且CD与AB垂直，则CD就是线段AB的垂直平分线。

线垂直平分线的存在可以帮助我们确定线段的中点，并且可以在几何证明中起到重要的作用。

2. 线垂直平分线的性质线垂直平分线具有一些重要的性质，这些性质使得它成为几何学中的一个重要工具：- 线垂直平分线平分线段：线垂直平分线将线段分成两个相等的部分，因此线段的两个端点到线垂直平分线的距离相等。

- 线垂直平分线垂直于线段：线垂直平分线与线段垂直，这意味着线垂直平分线所形成的两个角是直角。

- 线垂直平分线唯一性：对于给定的线段，存在唯一一条垂直平分线。

这是由线垂直平分线的定义所决定的。

如果有两条直线同时满足平分线和垂直线的条件，那么这两条直线将重合。

3. 线垂直平分线的判定方法线垂直平分线的判定方法有多种，我们将介绍两种常见的方法：- 利用垂直线段的性质：如果两条线段长度相等且垂直相交，那么它们的中垂线就是垂直平分线。

- 利用角的平分线的性质：如果两条边相等的角的平分线也相等，则该平分线是垂直平分线。

4. 个人观点和理解线垂直平分线作为几何学中的一个重要概念，对于解决几何问题和证明定理起到至关重要的作用。

它不仅可以帮助我们确定线段的中点，还可以与其他几何概念相结合，拓展我们的几何思维能力。

在解决实际问题时，线垂直平分线的概念也具有一定的应用价值，例如在建筑、地理测量等领域中，它可以帮助我们确保某些结构或地理位置的垂直平均。

深入理解线垂直平分线的概念对于我们的学习和应用都是十分重要的。

垂直平分线的性质与判定教案一、教学目标知识与技能：1. 理解垂直平分线的定义。

2. 掌握垂直平分线的性质与判定方法。

3. 能够运用垂直平分线的性质与判定解决实际问题。

过程与方法：1. 通过观察和操作，培养学生直观思维能力。

2. 利用几何画板或实物模型，引导学生探索垂直平分线的性质与判定。

情感态度价值观：1. 培养学生的团队合作精神，鼓励学生在探究过程中互相交流、合作。

2. 激发学生对数学的兴趣，培养学生的创新意识。

二、教学重点与难点重点：1. 垂直平分线的定义。

2. 垂直平分线的性质与判定方法。

难点：1. 垂直平分线的性质与判定在实际问题中的应用。

三、教学准备教师准备：1. 几何画板或实物模型。

2. 教学PPT或黑板。

3. 练习题。

学生准备：1. 笔记本。

2. 尺子、圆规、橡皮擦等学习工具。

四、教学过程1. 导入：利用一个实际问题引入垂直平分线的概念，例如：“在平面直角坐标系中，如何找到一点，使得该点到两点距离相等？”2. 探究垂直平分线的性质：学生分组讨论，每组尝试找出一条线段的垂直平分线，并观察其性质。

教师引导学生总结出垂直平分线的性质。

3. 验证垂直平分线的性质：利用几何画板或实物模型，教师引导学生验证垂直平分线的性质。

4. 学习垂直平分线的判定方法：教师引导学生从特殊情况入手，探索垂直平分线的判定方法。

学生分组讨论，总结出判定方法。

5. 应用垂直平分线的性质与判定：教师设计一些练习题，让学生运用所学知识解决问题。

五、课后作业1. 完成练习题。

教学反思：教师在课后对自己的教学进行反思，分析教学过程中的优点与不足，针对不足之处提出改进措施，以提高教学效果。

关注学生的学习情况，了解学生在垂直平分线性质与判定方面的掌握程度，为后续教学提供参考。

六、教学拓展1. 引导学生思考：垂直平分线在实际生活中的应用，例如电线杆的竖直放置、地图上的距离测量等。

2. 介绍垂直平分线的几何意义，如线段的中垂线、角平分线等。

线段的垂直平分线的性质
性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的
距离相等；三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点
的距离相等等。

1、垂直平分线垂直且平分其所在线段。

2、垂直平分线上任意一点，到线段两端点的距离相等。

3、三角形三条边的垂直平分线相交于一点，该点叫外心，并且这一点到三个顶点的
距离相等。

4、垂直平分线的判定：必须同时满足（1）直线过线段中点；（2）直线⊥线段。

若图形（这个图形可以是直线的、折线的、曲线的）关于某条直线对称，这条轴就称
为对称轴。

以五角星为例，它有五条对称轴。

垂直平分线是存在某条线段时才会有这个概念。

它的定义是经过某一条线段的中点，
并且垂直于这条线段的直线，叫做这条线段的垂直平分线（中垂线）。

它有一定的局限性。

轴对称图形的对称轴是对称图形中任意两个对应点连线段的垂直平分线。

感谢您的阅读，祝您生活愉快。

三角形的角平分线与垂直平分线角平分线与垂直平分线是三角形中重要的几何概念。

它们可以帮助我们研究三角形的性质和推导出一些有用的结论。

本文将详细介绍角平分线与垂直平分线的定义、性质和应用。

一、角平分线角平分线定义为从一个角的顶点出发，将这个角分成两个相等的角的线段。

以三角形ABC为例，假设角A的角平分线为AD，则角BAD 与角DAC是相等的。

这一定义可以推广到任意三角形中的任意角。

角平分线具有以下性质：1. 一个角的两条平分线相交于该角的顶点，并将该角平分成两个相等的角。

2. 三角形的内角平分线三条相交于一点，称为内心。

这个点到三角形三边的距离相等，可以证明是三角形内接圆的圆心。

3. 三角形的外角平分线三条相交于一点，称为外心。

这个点到三角形的顶点的距离相等，可以证明是三角形外接圆的圆心。

4. 三角形的角平分线分割对边成比例，即根据角平分线定理可得：AB/BC=AD/DC。

角平分线的应用广泛，特别是在证明三角形的性质和推导结论时非常有用。

例如，可以利用角平分线证明角的等分性质、三角形的相似性质、垂心定理等。

二、垂直平分线垂直平分线定义为从一个线段的中点出发，与该线段垂直且将该线段平分为两段相等的线段。

以三角形ABC为例，假设AB的垂直平分线为DE，则AD=BD=BE=CE=CD。

这一定义可以推广到任意线段。

垂直平分线具有以下性质：1. 一个三角形的三条垂直平分线交于一点，称为垂心。

这个点到三角形三顶点的距离相等，可以证明是三角形外接圆的圆心。

2. 一个角的垂直平分线经过角的顶点，并将该角平分成两个相等的角。

3. 垂直平分线等分线段，即对于一个线段AB，若点D是其垂直平分线的交点，则AD=DB。

垂直平分线也有许多应用，特别是在几何证明中常常能发挥关键作用。

例如，可以利用垂直平分线证明角的等分性质、直角三角形的性质、垂心定理等。

总结：角平分线与垂直平分线是三角形中重要的概念，它们有着许多有用的性质和应用。

垂直平分线的性质与判定教案第一章：垂直平分线的定义与性质1.1 垂直平分线的定义介绍线段垂直平分线的概念，即垂直平分线是线段所在的直线，且垂直平分线上的每一点到线段的两个端点的距离相等。

1.2 垂直平分线的性质性质1：线段的垂直平分线垂直于线段所在的直线。

性质2：线段的垂直平分线上的每一点到线段的两个端点的距离相等。

性质3：线段的垂直平分线段将线段平分成两个相等的部分。

第二章：垂直平分线的判定2.1 线段垂直平分线的判定条件判定1：如果一条直线垂直于线段所在的直线，并且通过线段的中点，这条直线是线段的垂直平分线。

判定2：如果一条直线上的每一点到线段的两个端点的距离相等，这条直线是线段的垂直平分线。

2.2 垂直平分线的判定方法方法1：使用直角三角形的性质，通过构造直角三角形来判断直线是否为垂直平分线。

方法2：使用尺规作图，通过作图来判断直线是否为垂直平分线。

第三章：垂直平分线与线段的关系3.1 垂直平分线与线段的交点介绍垂直平分线与线段的交点，即垂直平分线与线段相交的点，这个点到线段的两个端点的距离相等。

3.2 垂直平分线与线段的垂直关系介绍垂直平分线与线段的垂直关系，即垂直平分线与线段所在的直线垂直。

3.3 垂直平分线与线段的中点介绍垂直平分线与线段的中点的关系，即垂直平分线通过线段的中点，并且将线段平分成两个相等的部分。

第四章：垂直平分线的应用4.1 垂直平分线在几何作图中的应用介绍垂直平分线在几何作图中的应用，例如利用垂直平分线来作图求解几何问题。

4.2 垂直平分线在证明中的应用介绍垂直平分线在几何证明中的应用，例如利用垂直平分线的性质和判定来证明几何定理。

4.3 垂直平分线在实际问题中的应用介绍垂直平分线在实际问题中的应用，例如利用垂直平分线来解决生活中的问题。

第五章：总结与拓展5.1 垂直平分线的性质与判定的总结对垂直平分线的性质和判定进行总结，加深学生对垂直平分线的理解。

5.2 垂直平分线的拓展与应用介绍垂直平分线的拓展与应用，例如垂直平分线在平面几何中的重要作用，以及与垂直平分线相关的其他几何概念。

垂直平分线的性质与判定教案第一章：垂直平分线的定义与性质1.1 导入：引入线段的垂直平分线的概念，让学生直观地了解垂直平分线的作用和意义。

1.2 教学内容：1.2.1 垂直平分线的定义：介绍线段的垂直平分线的定义，即垂直平分线是线段上一点到线段两端点的距离相等的直线。

1.2.2 垂直平分线的性质：引导学生探究垂直平分线的性质，如垂直平分线上的任意一点到线段两端点的距离相等，垂直平分线与线段垂直相交等。

1.3 教学活动：1.3.1 实例分析：让学生观察和分析一些实例，加深对垂直平分线概念的理解。

1.3.2 小组讨论：让学生分组讨论垂直平分线的性质，并找出相关的证据和证明方法。

1.4 作业布置：布置一些有关垂直平分线性质的练习题，巩固所学知识。

第二章：垂直平分线的判定2.1 教学内容：2.1.1 垂直平分线的判定方法：介绍垂直平分线的判定方法，即如果一条直线垂直平分一条线段，则该直线满足一定的条件。

2.1.2 判定条件的应用：引导学生理解和掌握判定条件，并能够运用到实际问题中。

2.2 教学活动：2.2.1 实例分析：让学生观察和分析一些实例，加深对垂直平分线判定方法的理解。

2.2.2 小组讨论：让学生分组讨论垂直平分线的判定条件的应用，并找出相关的证据和证明方法。

2.3 作业布置：布置一些有关垂直平分线判定的练习题，巩固所学知识。

第三章：垂直平分线的性质与判定综合应用3.1 教学内容：3.1.1 综合应用：引导学生将垂直平分线的性质与判定方法综合运用到实际问题中，解决一些与垂直平分线相关的问题。

3.1.2 问题解决：让学生尝试解决一些与垂直平分线相关的问题，如寻找线段的垂直平分线、判断直线是否为线段的垂直平分线等。

3.2 教学活动：3.2.1 实例分析：让学生观察和分析一些实例，理解综合应用的意义和方法。

3.2.2 小组讨论：让学生分组讨论如何综合运用垂直平分线的性质与判定方法解决实际问题，并找出相关的证据和证明方法。

垂直平分线知识点
垂直平分线是经过某一条线段的中点，并且垂直于这条线段的直线。

以下是垂直平分线的一些知识点：
1.性质：垂直平分线上的任意一点到这条线段两个端点的距离相等，即线段垂直平分线上的点到线段两个端点的距离相等。

2.判定：如果直线过线段中点，并且垂直于这条线段，那么这条直线就是这条线段的垂直平分线。

3.三角形中的垂直平分线：三角形三条边的垂直平分线相交于一点，这一点叫做三角形的外心，并且这一点到三角形三个顶点的距离相等。

4.与对称轴的关系：如果一个图形关于某一直线对称，那么这个直线就是对应点连线的垂直平分线。

总之，垂直平分线是数学中的一个重要概念，它具有一些独特的性质和判定方法，并且在三角形等图形问题中有着广泛的应用。

知识点一：（线段垂直平分线的性质及其判定定理）垂直平分线的性质：垂直平分线上的点到线段两个端点的距离相等；垂直平分线的判定：到一条线段两个端点距离相等的点，在这条线段的垂直平分线上；三角形三边的垂直平分线定理：三角形三边的垂直平分线交于一点，并且这一点到三个顶点的距离相等。

我们把该交点称为三角形的外心，特别地：锐角三角形的外心位置在__________，直角三角形的外心位置在___________，钝角三角形的外心位置在___________。

知识点二：（线段垂直平分线的性质及其判定定理的应用）<1> 等腰三角形ABC中，AB=AC，的垂直平分线交，线段ABA︒=∠20AB于点D，交AC于点E，连接BE，则等于CBE∠______。

<2> 如图所示，。

于点交的垂直平分线中，在DACMNABACABABC,=∆若，︒=∠40A则=∠B D C_______。

<3> 已知A,B两个村庄的位置如图所示，现要在公路l边上修建一个人粮食收购站，使其到A,B两村庄的距离相等，试确定粮食收购站的位置。

<4> 已知:线段ha,（如图所示）。

求作：hADaBCACABABC===∆高且使,,,。

（不写作法，保留作图痕迹）<5>在BCDEABACBABCR交的垂直平分线，中，︒=∠∆90t的延长线于点F,若的长是，则，EFDEBFD130=︒=∠_____。

<6>有一张直角三角形的纸片，两直角边AC=6cm，BC=8cm,现将的长为则重合，折痕为与点折叠，使点BEDEABABC,∆_______。

<7> 平行四边形ABCD中，AB=3，BC=5，AC的垂直平分线交AD于点E, 则的周长是C D E∆_____。

<8> 已知：把),1重合与点所示方式摆放（点按如图和ECDEFRtABCRt∆∆点B,C(E),F在同一条直线上，cmBCcmACDEFEDFACB6,84590==︒=∠︒=∠=∠，，，cmEF9=。

题型分类： 无星代表普通高中 ★重点高中 ★ ★三大名校1、垂直平分线的定义如图1，直线l ⊥AB 于点D ，且AD ＝BD ，则 . 1) 直线l 叫做线段AB 的_______________。

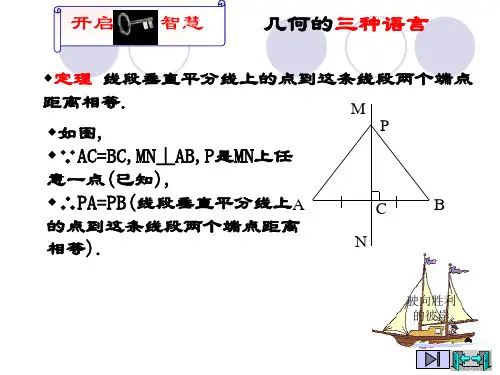
2) 求证PA ＝PB 。

总结：直平分线是垂直于一条线段并且平分这条线段的直线。

线段垂直平分线上的点到这一条线段两个端点距离相等。

即： ∵点P 在线段AB 的垂直平分线l 上，∴________＝___________2、线段垂直平分线的判定如图，已知线段BC 外两点A D ，且AB =AC ，BD =CD ， 则直线AD 与线段BC 的关系是_________.总结：线段垂直平分线逆定理：到一条线段两端点距离相等的点，在这条线段的垂直平分线上。

表述如下∵________＝___________，∴点P 在线段AB 的垂直平分线l 上。

第五讲 证明（二）垂直平分线角平分线ABlD图1P◆二、角平分线的性质与判定1、如图3，∵ 射线OC 是∠AOB 的平分线，∴ ∠AOC＝∠______1______2=∠。

2、角平分线的性质 如图，已知∠AOB 。

（1）求作∠AOB 的平分线OC 。

（2）在射线OC 上任取一点P ，过点P 分别作PD ⊥OA ，PE ⊥OB ，垂足为D 、E 。

求证：PD=PE即：角平分线上的点到角两边的距离相等。

3、角平分线的判定如图，DP ⊥AO ，EP ⊥BO ，垂足为D 、E ，且DP=EP求证：点P 在∠AOB 的角平分线上。

证明：总结：角的内部到角的两边的距离相等的点在角的平分线上。

OA BC图3图例1：如右图，P 是∠AOB 的平分线OM 上任意一点，PE ⊥CA 于E ，PF ⊥OB 于F ，连结EF .求证：OP 垂直平分EF .例2：如图12，CE⊥AB 于点E ，BD⊥AC 于点D ，BD 、CE 交于点O ，且OB ＝OC 。

求证：AO 平分∠BAC .★变式练习2：如图,在△ABC 中，∠C ＝90 ，AD 是∠BAC 的平分线，DE ⊥AB 于E ，F 在AC 上，BD ＝DF 。

垂直平分线的性质与判定教案第一章：垂直平分线的定义与性质1.1 引入：通过实际问题，引导学生思考线段垂直平分线的概念。

1.2 垂直平分线的定义：介绍线段的垂直平分线的定义，即垂直于线段并且将线段平分的直线。

1.3 性质1：线段的垂直平分线垂直于线段。

1.4 性质2：线段的垂直平分线将线段平分，即线段的两个端点到垂直平分线的距离相等。

第二章：垂直平分线的判定2.1 引入：通过实际问题，引导学生思考如何判定一条直线是线段的垂直平分线。

2.2 判定1：若一条直线垂直于一条线段，并且将线段平分，则该直线是线段的垂直平分线。

2.3 判定2：若一条直线与一条线段相交，并且交点将线段平分，则该直线是线段的垂直平分线。

第三章：垂直平分线的应用3.1 引入：通过实际问题，引导学生思考垂直平分线在几何中的应用。

3.2 应用1：利用垂直平分线证明线段相等。

3.3 应用2：利用垂直平分线证明直角三角形。

3.4 应用3：利用垂直平分线解决线段比例问题。

第四章：垂直平分线的作图4.1 引入：通过实际问题，引导学生思考如何作一条线段的垂直平分线。

4.2 作图方法1：利用直尺和圆规作图。

4.3 作图方法2：利用直尺和圆规作图的变体。

4.4 作图方法3：利用尺规作图的其他方法。

第五章：垂直平分线的综合应用5.1 引入：通过实际问题，引导学生思考垂直平分线在不同情境下的应用。

5.2 综合应用1：在几何题目中综合运用垂直平分线的性质与判定。

5.3 综合应用2：解决实际问题中涉及垂直平分线的问题。

5.4 拓展思考：探讨垂直平分线在其他数学领域中的应用。

第六章：线段垂直平分线与圆的关系6.1 引入：通过实际问题，引导学生思考线段垂直平分线与圆的关系。

6.2 性质3：线段的垂直平分线上的任意一点到线段两端点的距离相等。

6.3 判定3：若一条直线上的任意一点到线段两端点的距离相等，则该直线是线段的垂直平分线。

6.4 应用4：利用线段垂直平分线性质解决与圆相关的问题。