一阶线性微分方程的概念与解的结构

一阶非齐次线性微分方程解的结构
结构方程是描述系统的物理性质的最基本的数学表达式，它是系统的命令和动态解释的基础。

一阶非齐次线性微分方程(FLDE)是微分方程在研究系统动态性质时最常用的工具。

一
阶非齐次线性微分方程的特点是它的形式简单，只包含一阶阶导及一元函数，可以用来描
述动态系统的行为特征，但也可以用来描述更复杂的系统结构。

一阶非齐次线性微分方程的一般形式：
$$No\quad x n+1= A x n +B$$
其中，$x_n$是描述状态的变量，$A$是系统状态及输入之间的关系的系数矩阵，$B$是系
统的输入矩阵。

借助此方程，可以分析出对系统状态$x_n$有效控制的方法。

状态$x_n$可以通过输入信号$B$控制，当$B$设置为一个特定的值时，状态$x_n$可以驱动系统实现所需的结果。

在控制理论中，一阶非齐次线性微分方程可以用来解决调节问题，特别是用来设计控制器，从而控制系统的输出。

对系统控制有很大的作用，特别是通过控制控制任务，实现自动控
制的需要。

另外，一阶非齐次线性微分方程可以用来处理系统的不稳定性动态，例如系统的振荡运动，以及系统的偏差问题，从而使系统达到稳定的状态，从而提高系统的精度和准确性，确保
系统的正常运行。

总之，一阶非齐次线性微分方程在系统结构分析、动态控制和稳定性问题处理方面都有重
要用途。

它不仅有可解释性，而且能够处理复杂的系统动态，提高系统的稳定性，为系统
控制提供有效的解决方案。

一阶线性非齐次微分方程一、线性方程方程dy dxP x y Q x+=()()1叫做一阶线性微分方程(因为它对于未知函数及其导数均为一次的)。

如果Q x()≡0，则方程称为齐次的；如果Q x()不恒等于零，则方程称为非齐次的。

a)首先，我们讨论1式所对应的齐次方程dy dxP x y+=()02的通解问题。

分离变量得dyyP x dx =-()两边积分得ln()ln y P x dx c=-+⎰或y c e P x dx=⋅-⎰()其次，我们使用所谓的常数变易法来求非齐次线性方程1的通解。

将1的通解中的常数c换成的未知函数u x()，即作变换y u e P x dx=⋅-⎰()两边乘以得P x y uP x e P x dx ()()()⋅=-⎰两边求导得dydxu e uP x eP x dx P x dx ='--⎰-⎰()()()代入方程1得'=-⎰u e Q x P x dx ()() ， '=⎰u Q x e P x dx ()()u c Q x e dxP x dx =+⎰⎰()()于是得到非齐次线性方程1的通解[]y e c Q x e dxP x dx P x dx =⋅+-⎰⎰⎰()()()将它写成两项之和y c e e Q x e dx P x dx P x dx P x dx =⋅+⋅--⎰⎰⎰⎰()()()()不难发现：第一项是对应的齐次线性方程2的通解； 第二项是非齐次线性方程1的一个特解。

由此得到一阶线性非齐次方程的通解之结构。

【例1】求方程dy dxyxx-+=+21132()的通解。

解：]23)1([1212dxexcey dxxdxx⎰⎰++⋅⎰=+-+--]23)1([22)1(ln)1(ln dxexce xx+-+⎰⋅++⋅==+⋅++-⎰()[()]x c x dx11212=+⋅++()[()]x c x121212由此例的求解可知，若能确定一个方程为一阶线性非齐次方程，求解它只需套用公式。

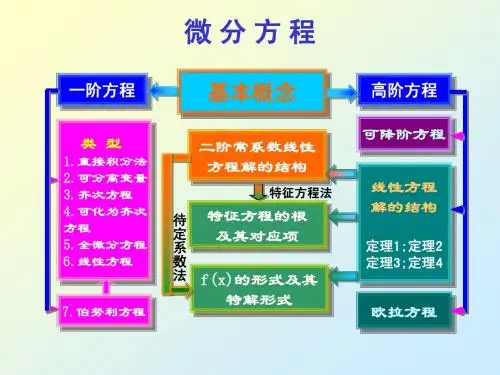
第六章常微分方程第1节基本概念1.常微分方程含未知函数的导数的方程。

2.阶未知函数有几阶导，就是几阶的微分方程。

3.解通解：含有任意常数的个数与阶数相同。

特解：通解中的任意常数确定。

初始条件：y(=，=，…，=4.线性方程y和y的各阶导数都是以一次式出现的。

第2节一阶微分方程1.可分离变量的微分方程：转化：=f(x)g(x)=两边同时积分2.齐次微分方程：如果=f()，那么设=u，则y=x u(x)那么=u(x)+x带入原方程得：u+x=f(u)= （可分离变量）3.一阶线性微分方程通式：+P(x)y=Q(x)，若Q(x)，则称之为一阶线性齐次微分方程。

一阶线性齐次微分方程通解：y=C一阶线性非齐次微分方程通解：y=(第3节高阶微分方程1.可降阶的高阶微分方程a)逐次积分解决。

b)令u(x)=,则=。

代入原式。

c)令=p(y),则=。

代入原式。

2.线性微分方程解的结构通式（二阶为例）：++Q(x)y=f(x) 若f(x)=0则为齐次。

（1）若y(x)为齐次的解，则ky(x)仍然是它的解。

（2）若,是齐次的解，则仍然是它的解。

（3）接（2）若,线性无关，则是它的通解。

（4）若Y是齐次的通解，是非齐次的特解，则y=Y+是非齐次的通解。

3.二阶常系数线性微分方程通式：++Qy=f(x)齐次：++Qy=0特征方程：a)>0，有两个不等实根、。

则Y=+是齐次方程的通解。

b)=0，有两个相等实根。

则Y=+=是齐次方程的通解。

c)<0，有两个不等虚根。

则Y=是齐次方程的通解。

非齐次：对应的齐次通解，加上本身特解。

只有两种f(x)能找到特解：a)f(x)==是特征方程的k重根。

Qn是和Pn相同形式多项式。

b)f(x)=[Cos+sin]=[Cos+sin]m=max{n,l}是特征方程的k重根。

更多资料信息联系QQ：3324785561。

高等数学各章知识结构高等数学是一门广泛涉及多个领域的学科，包括微积分、线性代数、概率论等。

下面将介绍高等数学各章的知识结构。

一、数列与数学归纳法（150字）数列与数学归纳法是高等数学的起点，包括等差数列、等比数列、递推数列等概念。

这一章主要讨论数列的性质、极限与收敛性等问题，并引入数学归纳法进行证明。

二、函数与极限（200字）函数与极限是高等数学的核心概念，也是微积分的基础。

这一章主要包括函数的定义、性质、基本函数、复合函数等内容，引入了极限的概念和计算方法。

三、导数与微分（250字）导数与微分是微积分的重要内容，也是应用最广泛的部分。

这一章主要讨论导数的定义、求导法则、高阶导数等内容，以及微分的定义与应用。

四、不定积分（200字）不定积分是微积分的另一个重要内容，研究的是函数的原函数。

这一章主要介绍不定积分的定义、基本积分法、换元积分法、分部积分法等内容。

五、定积分（200字）定积分是微积分的重要应用之一，主要研究函数在区间上的积分。

这一章主要包括定积分的定义、性质、基本公式、几何应用等内容。

六、微分方程（250字）微分方程是高等数学的又一重要内容，研究的是包含导数的方程。

这一章主要介绍了一阶线性微分方程、高阶线性微分方程、常微分方程的基本概念、解法和应用。

七、无穷级数（200字）无穷级数是数列的延伸，研究的是无穷多个数的求和。

这一章主要介绍级数的概念、收敛性、常用级数以及级数收敛的判定方法等内容。

八、多元函数与偏导数（250字）多元函数与偏导数是高等数学的另一个重要部分，研究的是多个变量间的关系。

这一章主要包括多元函数的概念、偏导数的定义与计算、全微分等内容。

九、多重积分（200字）多重积分是对多元函数求积分的扩展，研究的是多维空间中的积分。

这一章主要介绍二重积分、三重积分的定义、计算方法以及应用。

十、曲线与曲面积分（200字）曲线与曲面积分是高等数学的应用之一，主要研究曲线和曲面上的积分。

线性微分方程解的性质一、线性微分方程的解的结构1.1二阶齐次线性方程y ′ ′ + P ( x ) y ′ + Q ( x ) y = 0 (1)y''+P(x)y'+Q(x)y=0 \tag{1} y′′+P(x)y′+Q(x)y=0(1)定理1：如果函数 y 1 ( x ) y_1(x) y1(x)与 y 2 ( x ) y_2(x)y2(x)是方程（1）的两个解，那么y = C 1 y 1 ( x ) + C 2 y 2 ( x ) (2) y=C_1y_1(x)+C_2y_2(x) \tag{2} y=C1y1(x)+C2y2(x)(2)也是方程（1）的解，其中 C 1 , C 2 C_1,C_2 C1,C2是任意常数。

解（2）从形式上看含有C1C_1C1和C2C_2C2两个任意常数，但它不一定是方程（1）的通解。

那么在什么情况下（2）式才是方程（1）的通解呢？要解决这个问题，还得引入新概念，即函数组的线性相关与线性无关。

设 y 1 ( x ) , y 2 ( x ) , ⋅⋅⋅ , y n ( x )y_1(x),y_2(x),···,y_n(x) y1(x),y2(x),⋅⋅⋅,yn(x)为定义在区间 I I I上的n个函数，如果存在n个不全为零的常数 k 1 , k 2 , ⋅⋅⋅ , k n k_1,k_2,···,k_n k1,k2,⋅⋅⋅,kn，使得当x ∈ I x\in I x∈I时有恒等式k 1 y 1 + k 2 y 2 + ⋅⋅⋅ + k n y n = 0k_1y_1+k_2y_2+···+k_ny_n=0 k1y1+k2y2+⋅⋅⋅+knyn=0成立，那么称这n个函数在区间I上线性相关；否则线性无关。

应用上述概念可知，对于两个函数的情形，它们线性相关与否，只要看它们的比是否为常数；如果比为常数，那么它们就线性相关；否则就线性无关。

一阶微分方程构造辅助函数原理1. 引言1.1 概述在数学和科学领域中，微分方程是一个重要的研究对象。

一阶微分方程是其中最基础且常见的类型之一。

解一阶微分方程可以帮助我们理解自然现象、预测未来发展趋势以及解决各种实际问题。

辅助函数作为求解一阶微分方程的有效工具，在解题过程中起着至关重要的作用。

本文将深入探讨辅助函数原理，并介绍构造辅助函数的方法和技巧。

1.2 文章结构本文共包括五个部分。

首先，在引言部分我们将概述文章的主题和目标。

其次，我们会介绍一阶微分方程的基础知识，包括定义与形式、常见类型与解法以及初值问题与辅助函数的重要性。

接着，我们将详细阐述辅助函数原理及其构造方法，包括辅助函数的概念与作用、构造辅助函数的步骤和方法以及常用的辅助函数构造技巧。

然后，通过示例和应用案例分析，我们将展示辅助函数在求解一阶微分方程中的实际应用，包括小型一阶微分方程求解示例的详解、实际问题中辅助函数应用案例的分析以及辅助函数在数学模型建立中的实践应用。

最后，我们会总结本文的研究成果，并对未来研究方向进行展望。

1.3 目的本文旨在深入探讨一阶微分方程构造辅助函数原理，并介绍相关的构造方法和技巧。

通过对辅助函数在一阶微分方程求解过程中的作用和重要性进行分析，使读者能够更好地理解和运用辅助函数。

同时，通过具体示例和应用案例的分析，帮助读者将理论知识与实际问题相结合，提高问题求解能力。

最终，希望本文能为相关领域研究者提供有益的参考和启示，并促进一阶微分方程及其应用领域的发展与创新。

2. 一阶微分方程基础知识：2.1 定义与形式一阶微分方程是指未知函数的导数与自变量之间只包含一阶导数的关系式。

通常表示为dy/dx=f(x)的形式，其中y表示未知函数，x表示自变量，f(x)表示已知函数。

2.2 常见类型与解法一阶微分方程可以根据其类型进行分类和求解。

常见的类型包括可分离变量型、齐次型、线性型等。

可分离变量型：当一阶微分方程可以被写为dy/dx=g(x)h(y)时，我们可以将其转化为两个变量可分离的形式，并通过两边同时积分来求解。

常微分方程一、可分离变量方程一阶可分离变量方程：()()dy f x dx g y =，可分离变量，方程通解为： ()()G y f x C =+二、一阶线性微分方程一阶线性微分方程：()()y p x y Q x '+=，通解如下： 当()0Q x =时，上式称为线性齐次方程，通解为In y C =-或()p x dxy Ce -⎰= 当()0Q x ≠时，上式称为线性非齐次方程，通解为()()[()]p x dx p x dxy e Q x e dx C -⎰⎰=+⎰三、可降阶微分方程1、()()n y f x =对此类微分方程，多次直接积分即可求得通解。

2、(,)y f x y '''=——不显含y 的二阶微分方程，令y p '=，则y p '''=，代入得(,)p f x p '=，该一阶微分方程可求解，从而求得()y f x =。

3、(,)y f y y '''=——不显含x 的二阶微分方程，令y p '=，则dpy pdy''=，代入得(,)dppf y p dy=，该一阶微分方程可求解，再经分离变量可求得()y f x =。

四、二阶常系数线性微分方程1、二阶常系数齐次线性微分方程0y py qy '''++=，其中p 、q 为常数它的特征方程为20r pr q ++=，其中r 为特征根。

根据r 的情况，二阶常系数齐次微分方程的通解如下：(1)1r 、2r 为两个不等实根时，方程的通解为1212r x r x y C e C e =+；(2)1r 、2r 为两个相等实根时(12r r r ==)，方程的通解为12()rx y C C x e =+； (3)1r 、2r 为一对共轭复根i αβ±时，方程的通解为12(cos sin )x y e C x C x αββ=+； 2、二阶常系数齐次线性微分方程 设*()y y x =是非齐次线方程()y py qy f x '''++=，其中p 、q 为常数的一个特解，()y y x =是对应的齐次方程0y py qy '''++=的通解，则该二阶线性非齐次微分方程的通解为*()()y y x y x =+。