数列章末归纳整合1
- 格式:ppt
- 大小:1.67 MB
- 文档页数:33


一项的 等于同一个常数,这 个数列就叫做等等差数列前n 项和1).等差数列前n 项和公式① ② 2). 等差数列前n 项和的最大(小)值利用n a :当0,01<>d a ,前 n 项和有最 值,可由0≥n a ,且01≤+n a ,求得n 的值;当0,01><d a ,前 n 项和有最 值,可由0≤n a ,且01≥+n a ,求得n 的值。
n S :由n da n d S 2(212n -+=,利用(小)值时n 的值。
等比数列的前 n 项和①②二、探究互动1. 等差数列{a n }中,a 1=23,公差da 6>0,a 7<0. 1)求公差d 的值;(2)求通项a n例 2. 根据下面各个数列{}n a 的首项和递推关系,求其通项公式 ⑴==+11,1n a a )(2*N n n a n ∈+ ⑵==+11,1n a a 1+n n )(*N n a n ∈ ⑶==+11,1n a a 121+n a )(*N n ∈例3. 例3.已知1a , a 2, 3a , …, n a , …构成一等差数列,其前n 项和为n S =n 2, 设n b =n na 3, 记{n b }的前n 项和为n T , (1) 求数列{n a }的通项公式 (2) 证明:n T <1.三.巩固提升1. 下列说法正确的是 ( ) A. 数列1,3,5,7可表示为{}7,5,3,1 B. B.数列1,0,2,1--与数列1,0,1,2--是相同的数列C.数列⎭⎬⎫⎩⎨⎧+n n 1的第k 项是k 11+D. 数列可以看做是一个定义域为正整数集*N 的函数2.设等差数列{}n a 的前n 项的和n S ,若3789936,S a a a ==++6,S 则等于 A.、63 B 、 43 C 、36 D 、27 3.数列{}n a 的前n 项的和29n S n n =-,第K 项满足58k a <<,则K 等于A.、9 B 、 8 C 、7 D 、64.若{a n }是等差数列,510,a a 是方程x 2-3x-5=0的两根,则69a a + = .5. {}n a 设为公比q>1的等比数列,若2004a 和2005a 是方程24830x x -+=的两根,则20072006a a += 6. 设n S 是等差数列{}n a 的前n 项和,若9535=a a ,则59S S等于 。

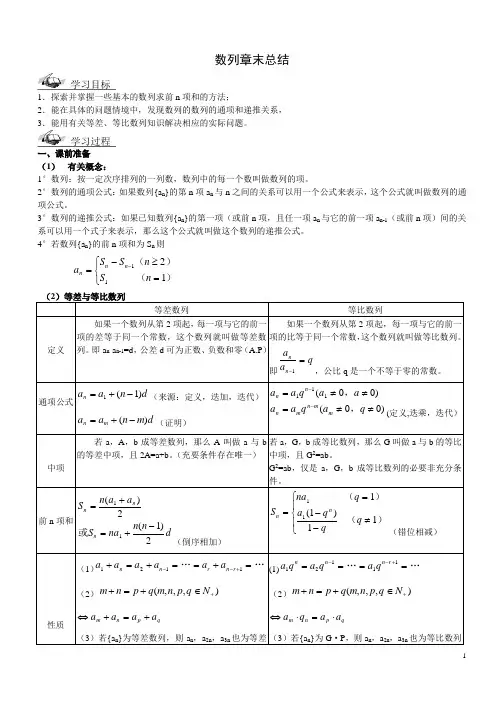
数列章末总结1.探索并掌握一些基本的数列求前n项和的方法;2.能在具体的问题情境中,发现数列的数列的通项和递推关系,一、课前准备(1)有关概念:1°数列:按一定次序排列的一列数,数列中的每一个数叫做数列的项。
2°数列的通项公式:如果数列{a n}的第n项a n与n之间的关系可以用一个公式来表示,这个公式就叫做数列的通项公式。
3°数列的递推公式:如果已知数列{a n}的第一项(或前n项,且任一项a n与它的前一项a n-1(或前n项)间的关系可以用一个式子来表示,那么这个公式就叫做这个数列的递推公式。
4°若数列{a n}的前n项和为S n则aS S nS nnn n=-≥=⎧⎨⎩-1121()()※数列通项公式的求法数列的通项公式是数列的核心内容之一。
它如同函数中的解析式一样,对研究数列的性质起着重要的作用。
围绕数列的通项公式,不仅可以判断数列的类型,研究数列的项的变化规律与趋势,而且还便于研究数列的前n 项和,因此求数列的通项公式往往是解决数列问题的突破口,在解题时,根据题目所给条件的不同,可以采用不同的方法求数列的通项公式,常见方法如下: 1.叠加法(累加法)对于形如a n+1-a n =f(n)型的,用叠加法例1:已知数列{a n }中,a 1=1,且a n+1-a n =3n-n ,求数列{a n }的通项公式。
变式:已知数列{}n a 满足211=a ,nn a a n n ++=+211,求n a 。
2.叠乘法(累乘法)对于形如1()n na f n a +=)型的,用叠加法 例2:已知数列{}n a 满足321=a ,n n a n na 11+=+,求n a 。
变式:已知31=a ,n n a n n a 23131+-=+ )1(≥n ,求n a 。
3.构造法其他的,已知数列递推公式求an ,用构造法(构造等差或等比数列) 例3:数列{}n a 中11=a ,)2(1211≥+=-n a a n n ,求该数列的通项公式n a 。

数列章节知识点归纳总结数列是数学中常见的一种数学对象,可以用于描述一系列按照规律排列的数字。
在数学中,数列的研究与应用非常广泛,涉及到各个领域。
本文将对数列的基本概念、分类、性质以及常见的数列类型进行归纳总结。
一、数列的基本概念数列是由一系列有序的数字组成的集合。
其中,每一个数字被称为数列的项,用a₁、a₂、a₃等表示。
数列可以有无穷多个项,也可以有有限个项。
对于一个数列,我们可以通过以下方式来表示:1. 列表法:数列的项按照顺序列出,用逗号隔开。
例如:1, 2, 3, 4, 5, ...2. 通项公式法:数列的每一项都可以用一个公式来表示。
例如:an = 2n,表示数列的第n项是2n。
二、数列的分类根据数列的规律和性质,数列可以分为以下几类:1. 等差数列(Arithmetic Progression, AP):在等差数列中,每一项与它的前一项之差都相等。
其中,公差(common difference)表示了相邻两项之间的差值。
通项公式为an = a₁ + (n - 1)d,其中a₁为首项,d 为公差。
2. 等比数列(Geometric Progression, GP):在等比数列中,每一项与它的前一项之比都相等。
其中,公比(common ratio)表示了相邻两项之间的比值。
通项公式为an = a₁ * r^(n-1),其中a₁为首项,r为公比。
3. 斐波那契数列(Fibonacci Sequence):斐波那契数列是一个特殊的数列,其每一项都是前两项之和。
通常情况下,将前两项定义为1,即F₁ = F₂ = 1。
后续项可以通过递推关系式Fn = Fn-1 + Fn-2计算得出。
4. 调和数列(Harmonic Progression):在调和数列中,每一项的倒数与一常数之差都相等。
通项公式为an = 1/(a₁ + (n - 1)d),其中a₁为首项,d为公差。
三、数列的性质除了上述分类,数列还具有一些重要的性质。




数列知识点总结大纲
一、数列的概念和性质
1.1 数列的定义
1.2 数列的项、通项公式和前n项和
1.3 数列的分类:等差数列、等比数列、等差数列
1.4 数列的性质:有界性、单调性、周期性
二、等差数列
2.1 等差数列的概念和性质
2.2 等差数列的通项公式和前n项和公式
2.3 等差数列的应用:等差数列的中项、倒数第n项等问题
三、等比数列
3.1 等比数列的概念和性质
3.2 等比数列的通项公式和前n项和公式
3.3 等比数列的应用:等比数列的中项、倒数第n项等问题
四、递推数列
4.1 递推数列的概念和性质
4.2 递推数列的通项公式和前n项和公式
4.3 递推数列的应用:如何构造递推数列、递推数列的性质
五、综合应用
5.1 几何问题与数列:等差数列、等比数列在几何图形中的应用5.2 累加与数列:数列的和与级数的求和
5.3 数列的特殊问题:收敛性、散度性、收敛上界、收敛下界等问题
六、挑战问题
6.1 数列的特殊性质:如何判断一个数列的性质
6.2 数列的极限问题:数列的极限性质与收敛性定理
6.3 数列的推广问题:数列在数学、物理、工程等领域中的应用
七、拓展应用
7.1 数列与函数:数列与函数的关系
7.2 数列与级数:级数求和与展开
7.3 数列与微积分:数列在微积分中的应用
以上是对数列知识点的一个大致总结,通过学习这些知识点,我们可以深入了解数列的概念、性质与应用,从而更好地应用数列知识解决实际问题。
希望这份总结对你有所帮助,谢谢!。

数列全章知识点总结一、数列的概念数列是按照一定规律排列的一组数的有序排列。
数列中排在第一位的数叫做第一个数,排在第二位的数叫做第二个数,以此类推。
根据数列的性质不同,可以将数列分为有限数列和无限数列。
有限数列是由有限个数构成的数列,而无限数列是由无限个数构成的数列。
根据数列中每个数的性质不同,数列可以分为等差数列、等比数列、递增数列、递减数列等。
二、等差数列等差数列是指数列中任意两个相邻的数之差都相等的数列。
设数列为{a1, a2, a3, ..., an},若满足ai+1 - ai = d,其中d为常数,则称数列为等差数列,其中d为公共差。
数列中每个数与其前一个数的差都相等,这类数列有着相对简单的性质。
等差数列的通项公式为an = a1 + (n-1)d,其中a1为首项,d为公差,an为第n项。
求等差数列的前n项和的公式为Sn = (a1 + an) * n / 2 = n * (a1 + an) / 2。
在等差数列中,首项、末项和项数的关系为an = a1 + (n-1)d。
对于等差数列,我们可以通过已知项数和首项、末项、公差等信息来求解等差数列的相关问题。
三、等比数列等比数列是指数列中任意两个相邻的数之比都相等的数列。
设数列为{a1, a2, a3, ..., an},若满足ai+1 / ai = q,其中q为常数,则称数列为等比数列,其中q为公比。
等比数列在实际应用中也有着重要的作用。
等比数列的通项公式为an = a1 * q^(n-1),其中a1为首项,q为公比,an为第n项。
求等比数列的前n项和的公式为Sn = a1 * (q^n - 1) / (q - 1),当|q| < 1时,Sn = a1 / (1 - q)。
对于等比数列,我们可以通过已知项数和首项、末项、公比等信息来求解等比数列的相关问题。
四、数列的求和公式在数列求和的过程中,常用的方法是利用通项公式或者递推公式来求解。

数列章节知识点归纳总结一、数列的定义数列是将自然数按照一定的方式排列而成的数的序列。
一般来说,数列可以用函数的形式表示,即数列中的每个数都可以用一个函数来描述。
例如,我们可以使用函数 f(n) = 2n + 1 来表示一个数列,其中 n 为自然数,这个数列的前几项为 3,5,7,9,11……数列有许多不同的分类方法,其中最常见的是将数列分为等差数列和等比数列。
等差数列是指数列中相邻两项的差值都相等,而等比数列是指数列中相邻两项的比值都相等。
这两种数列在数学中有许多重要的应用。
二、常见数列及其性质1.等差数列等差数列是数列中相邻两项的差值都相等的数列。
其通项公式为 a_n = a_1 + (n-1)d,其中a_n 为数列的第 n 项,a_1 为数列的第一项,d 为公差。
等差数列的性质有:(1)求和公式:等差数列的前 n 项和可表示为 S_n = (a_1 + a_n) * n / 2;(2)通项公式的推广:若已知数列的第 m 项和第 n 项,可通过通项公式求出数列的第 k 项。
2.等比数列等比数列是数列中相邻两项的比值都相等的数列。
其通项公式为 a_n = a_1 * q^(n-1),其中a_n 为数列的第 n 项,a_1 为数列的第一项,q 为公比。
等比数列的性质有:(1)求和公式:等比数列的前 n 项和可表示为 S_n = a_1 * (1 - q^n) / (1 - q);(2)通项公式的推广:若已知数列的第 m 项和第 n 项,可通过通项公式求出数列的第 k 项。
3.特殊数列在数学中还存在许多特殊的数列,如斐波那契数列、调和数列、算术-几何平均数列等。
这些数列在数学理论研究和实际应用中都具有重要的地位,它们有着独特的性质和规律。
三、数列的求和公式求和公式是数列研究中的重要内容之一,它有助于我们快速计算数列的部分和或者总和。
对于等差数列和等比数列,其求和公式已在前文进行了介绍。
除此之外,数列在数学中还涉及到其他类型的求和公式,如算术-几何平均数列的求和公式、斐波那契数列的求和公式等。
一.知识系统整合1.知识网络2.知识梳理二. 规律方法收藏(1)在求等差数列和等比数列的通项公式时,分别用到了累加法和累乘法;(2)在求等差数列和等比数列的前n项和时,分别用到了倒序相加和错位相减.(3)等差数列和等比数列各自都涉及5个量,已知其中任意三个求其余两个,用到了方程思想.(4)在研究等差数列和等比数列单调性,等差数列前n项和最值问题时,都用到了函数思想.(5)等差数列和等比数列在很多地方是相似的,发现和记忆相关结论时用到了类比.三.学科思想培优一、数学抽象数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养.主要表现为:获得数学概念和规则,提出数学命题和模型,形成数学方法和思想,认识数学结构与体系.在本章中,主要表现在构造新数列,及数列的函数性质中.【典例1】(2021·河南高三月考(理))“春雨惊春清谷天,夏满芒夏署相连,秋处露秋寒霜降,冬霜雪冬小大寒”,这首二十四节气歌,记录了中国古代劳动人民在田间耕作长期经验的积累和智慧.“二十四节气”已经被列入联合国教科文组织人类非物质文化遗产代表作名录.我国古代天文学和数学著作《周牌算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度)二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则晷长为七尺五寸时,对应的节气为( )A .春分、秋分B .雨水、处暑C .立春、立秋D .立冬、立夏【答案】A【解析】设从夏至开始到冬至,各节气的晷长分别为1a ,2a ,3a ,…,13a , 则夏至时晷长为115a =(寸),冬至时晷长为13135a =(寸), 因为每个节气晷长损益相同,则{}n a 为等差数列,设公差为d , 所以131121512135a a d d =+=+=, 解得10d =,所以()15110105n a n n =+-⨯=+, 由75n a =,得7n =,即晷长七尺五寸对应的节气为从夏至开始的第七个节气,即秋分; 设从冬至开始到夏至,每个节气的晷长为n b ,则()()135********n b n n =+-⋅-=-+, 由75n b =,得7n =,即晷长七尺五寸对应的节气是从冬至开始的第七个节气,即春分. 所以晷长为七尺五寸时,对应的节气为春分和秋分.故选:A.【典例2】(2021·河南驻马店市·高三期末(文))1975年,考古工作者在湖南省云梦县睡虎地秦墓出土了大量记载秦法律令的竹简,其中包括徭律一条.徭律是秦代关于徭役的法律,其中规定:服徭戍迟到处以申斥和赀罚.失期三日到五日,谇;六日到旬,赀一盾;过旬,赀一甲.意思是:迟到2天以内算正常,不处罚;迟到3~5天,口头批评;迟到6~10日,罚一面盾牌;迟到10天以上,罚一副甲胄.若有一队服徭役的农民从甲地出发前往乙地,甲、乙两地相距900里,第一天行60里,以后每天都比前一天少行2里,要求18天内到达,则该队服徭役的农民最可能受到的惩罚是( ). A .无惩罚 B .谇C .赀一盾D .赀一甲【答案】C【解析】由题意知,每日行走的路程成等差数列,记为{}n a , 因为首项为60,公差为2-,所以2=-+n a n 62. 设从甲地到乙地用k 天,则602629002-+⨯=k k ,即2619000-+=k k ,解得25k =或36k =(舍), 即从甲地出发前往乙地所用的时间为25天, 因为要求18天到达,所以迟到了7天,又因为迟到6~10日,罚一面盾牌,故应赀一盾.故选:C.【典例3】(2021·宁夏吴忠市·高三一模(文))已知数列{}n a满足1a =*1,n n n +∈N .(1)求数列{}n a 的通项公式; (2)设*n nb n =∈N ,数列{}n b 的前n 项和n S ,求证:1n S <.【答案】(1))*n a n =∈N;(2)证明见解析.【解析】(11n n +=,得1n n a a += ∴32121nn a aa a a a ⋅=-12n n⋅=-,∴1a =∴)*na n =∈N .(2)由(1)得n n b a ===,∴12111111112231n n S b b b n n=+++=-+-++-=-+ 当*n ∈N 时,0>,∴1n S <,即证. 二、数学运算数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养,主要表现为:理解运算对象,掌握运算法则,探究运算思路,求得运算结果.在本章中,主要表现在求等差、等比数列的特定项,公差(公比),前n 项和,项数的运算中.【典例4】(2021·河南郑州市·高二期末(文))在等比数列{}n a 中,有31598a a a =,数列{}n b 是等差数列,且99b a =,则711b b +等于( ) A .4 B .8C .16D .24【答案】C【解析】∴{}n a 是等比数列,∴2931598a a a a ==,90a ≠,所以98a =,即998b a ==,∴{}n b 是等差数列,所以7119216b b b +==. 故选:C .【典例5】(2021·湖北荆州市·荆州中学高二期末)设等比数列{}n a 的前n 项和为n S ,若10512S S =,则155S S =( ) A .12B .13C .23D .34【答案】D【解析】{}n a 是等比数列,51051510,,S S S S S ∴--也称等比数列,10512S S =,设5102,S k S k ==, 则105S S k -=-,15102k S S ∴-=,则1532k S =, 15533224kS S k ∴==.故选:D. 【典例6】(2021·安徽六安市·高三一模(文))设等差数列{}n a 的前n 项和为n S ,公差0d >且2217a a =,则n S 取得最小值时,n 的值为( )A .3B .4C .3或4D .4或5【答案】C【解析】由2217a a =,可得()()17170a a a a +-=,因为0d >,所以170a a -≠,所以17 0a a +=,所以44200a a =⇒=.因为0d >,所以{}n a 是递增数列,所以1234560a a a a a a <<<=<<<,显然前3项和或前4项和最小.故选:C【典例7】(2021·河南许昌市·高二期末(理))在数列{}n a 中,11a =,22a =,对n *∀∈N ,215322n n n a a a ++=-,则2021a =( ) A .20183212⎛⎫- ⎪⎝⎭B .20193212⎛⎫- ⎪⎝⎭C .20203212⎛⎫- ⎪⎝⎭D .20213212⎛⎫- ⎪⎝⎭【答案】C 【解析】由215322n n n a a a ++=-得2113()2n n n n a a a a +++-=-∴数列1{}n n a a +-是以211a a -=为首项,32为公比的等比数列, 1*13()()2n n n a a n N -+∴-=∈∴当2n ≥时,11232211()()()()n n n n n a a a a a a a a a a ---=-+-++-+-+23101133331222231213123212n n n n ----⎛⎫⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫- ⎪⎝⎭=+-⎛⎫=- ⎪⎝⎭经检验,1n =时成立.132()12n n a -∴=-.2020202132()12a ∴=-,故选:C.【典例8】(2021·广西河池市·高二期末(理))已知数列{}n a 的前n 项和为n S ,112a =,对任意的*n ∈N 都有1(2)n n na n a +=+,则2021S =( )A .20192020B .20202021C .20212022D .10101011【答案】C【解析】数列{}n a 满足112a =,对任意的*n ∈N 都有1(2)n n na n a +=+, 则有1(1)(1)(2)n n n n a n n a ++=++,可得数列{}(1)n n n a +为常数列, 有1(1)2n n n a a +=,得(1)1n n n a +=,得1(1)n a n n =+,又由111(1)1n a n n n n ==-++,所以20211111112021112232021202220222022S =-+-+⋅⋅⋅-=-=.故选:C 【典例9】【多选】(2020·广东揭阳市·揭阳三中高二期中)已知数列{}n a 的前n 项和为2n 33S n n =-,则下列说法正确的是( ) A .342n a n =- B .16S 为n S 的最小值C .1216272a a a +++= D .1230450a a a +++=【答案】AC【解析】1133132a S ==-=,()()()2213333113422n n n a S S n n n n n n -=-=---+-=-≥,对于1n =也成立,所以342n a n =-,故A 正确;当17n <时,0n a >,当n=17时n a 0=,当17n >时,n a 0<,n S ∴只有最大值,没有最小值,故B 错误;因为当17n <时,0n a >,∴21216163316161716272a a a S +++==⨯-=⨯=,故C 正确; 121617193300()a a a S a a a +++=+----2163022272(333030S S =-=⨯-⨯-)54490454=-=,故D 错误.故选:AC.三、逻辑推理逻辑推理是指从一些事实和命题出发,依据规则推出其他命题的素养,主要表现为:掌握推理基本形式和规则,发现问题和提出问题,探索和表述论证过程,理解命题体系,有逻辑地表达与交流.本章主要表现求数列的通项公式,在等差,等比数列判定、数列求和及数列开放题运用等方面. 【典例10】【多选】(2020·湖北高二期中)已知数列{}n a 的前n 项和n S 满足()2141n n S S n ++=+,下列说法正确的是( )A .若首项11a =,则数列{}n a 的奇数项成等差数列B .若首项11a =,则数列{}n a 的偶数项成等差数列C .若首项11a =,则15477S =D .若首项1a a =,若对任意*n ∈N ,1n n a a +<恒成立,则a 的取值范围是()3,5【答案】BCD【解析】由()2141n n S S n ++=+∴得()2124n n S n S n-+=≥∴,∴-∴可得()()12241421484n n a a n n n n +-=+==+++()2n ≥∴, 所以()()14213n n n a a n -+-≥=∴,∴-∴可得()1183n n a a n +-=-≥,因此数列{}n a 从第三项开始,奇数项成等差,偶数项也成等差;若11a =,即111S a ==,则()212411S S +=+,即21216a a +=,所以214a =; 由()322421S S +=+得32362a S +=,则36a =; 由()432431S S +=+得43264a S +=,则422a =; 所以3158a a -=≠,428a a -=,因此数列{}n a 的奇数项不成等差数列,偶数项成等差数列,即A 错,B 正确; 此时()()151********......S a a a a a a a =++++++++()()327717711787847722a a ⨯-⨯-⎡⎤⎡⎤=++⨯++⨯=⎢⎥⎢⎥⎣⎦⎣⎦,即C 正确;因为37215,,,...,n a a a a +成公差为8的等差数列,2482,,,...,n a a a a 也成公差为8的等差数列; 为使对任意*n ∈N ,1n n a a +<恒成立, 只需1234a a a a <<<,若1a a =,由()21241116S S +=+=,则2162a a =-;由()32242136S S +=+=,可得2336242a S a =-=+;由()43243164S S +=+=得34642242a S a =-=-所以42242162a a a a <+<-<-,解得35a <<,即D 正确.故选:BCD. 【典例11】(2021·辽宁大连市·高三期末)在①2*31,4(n S n kn n N k =-+∈为常数),①*1(,n n a a d n N d +=+∈为常数),①*1,,(0n n a qa q n N q +=>∈为常数)这三个条件中任选一个,补充到下面问题中,若问题中的数列存在,求数列()1*1n n n a N a +⎧⎫⎨⎭∈⎬⎩的前10项和;若问题中的数列不存在,说明理由.问题:是否存在数列{}*()∈n a n N ,其前n 项和为n S ,且131,4,a a ==___________?注:如果选择多个条件分别解答,按第一个解答计分. 【答案】答案见解析【解析】如果选择①,由11332,,a S a S S =⎧⎨=-⎩即31142743324k k k ⎧=-+⎪⎪⎨⎪=--+⎪⎩ 解得3414k k ⎧=⎪⎪⎨⎪=-⎪⎩该方程组无解, 所以该数列不存在.如果选择*1,(n n a a d n N d +=+∈②为常数),即数列{}n a 为等差数列,由131,4==a a ,可得公差31322a a d -==, 所以3122n a n =- 所以12231011122310111112111111538a a a a a a a a a a a a ⎛⎫++⋅⋅⋅+=-+-+⋅⋅⋅+-= ⎪⎝⎭ 如果选择*1(0,,n n a qa q n N q +=>∈③为常数),即数列{}n a 为等比数列,由131,4==a a,可得公比2q ==,所以11114(2)1n n n n n a a a a +-÷=≥, 所以数列11n n a a +⎧⎫⎨⎬⎩⎭是首项为12,公比为14的等比数列,所以其前10项和为1021134⎛-⎫ ⎪⎝⎭. 【典例12】(2021·江苏徐州市·徐州一中高三期末)设数列{}n a ,{}n b 是公比不相等的两个等比数列,数列{}n c 满足*,n n n c a b n =+∈N .(1)若2,3nnn n a b ==,是否存在常数k ,使得数列{}1n n c kc +-为等比数列?若存在,求k 的值;若不存在,说明理由;(2)证明:{}n c 不是等比数列.【答案】(1)存在,2k =或3k =;(2)证明见解析.【解析】(1)由题意知,若数列{}1n n c kc +-为等比数列,则有()()()21211n n n n n n c kc c kc c kc +++--=-⋅-,其中2n ≥且*n ∈N ,将23n n n c =+代入上式,得 ()()()211221111232323232323n n n n n n n n n n n n k k k ++++++--⎡⎤⎡⎤⎡⎤+-+=+-+⋅+-+⎣⎦⎣⎦⎣⎦, 即21111(2)2(3)3(2)2(3)3(2)2(3)3n n n n n n k k k k k k ++--⎡⎤⎡⎤⎡⎤-+-=-+-⋅-+-⎣⎦⎣⎦⎣⎦, 整理得1(2)(3)2306n n k k --⋅⋅=,解得2k =或3k =.(2)设数列{}n a ,{}n b 的公比分别为,,p q p q ≠且,0p q ≠,11,0a b ≠,则1111n n n c a p b q --=+,为证{}n c 不是等比数列,只需证2213c c c ≠⋅,事实上()22222221111112c a p b q a p a b pq b q =+=++, ()()()222222221311111111c c a b a p b q a p a b p q b q ⋅=+⋅+=+++,由于p q ≠,故222p q pq +>,又11,0a b ≠,从而2213c c c ≠⋅,所以{}n c 不是等比数列.【典例13】(2021·云南昆明市·高二期末(文))已知{}n a 是等差数列,{}n b 是递增的等比数列且前n 和为n S ,112822,10a b a a ==+=,___________.在①2345,,4b b b 成 等差数列,①12n n S λ+=+(λ为常数)这两个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件分别解答,按第一个解答计分).(1)求数列{}n a 和{}n b 的通项公式;(2)求数列{}n n a b +的前n 项和n T .【答案】条件选择见解析;(1)n a n =,2n n b =;(2)212222n n n n T +=-++. 【解析】选∴解:(1)设等差数列{}n a 的公差为d ,1281122,10,2810,1,1a a a a d a d =+=∴+=∴==,1(1)1n a n n ∴=+-⨯=. 由题意知132452,24b b b b ⎛⎫=⋅=+ ⎪⎝⎭,得324522b b b =+, 设等比数列{}n b 的公比为2222,522q b q b b q ⋅=+,即22520q q -+=, 解得2q ,或12q =,由数列{}n b 为递增等比数列可知12q =不合题意, 所以{}n b 是一个以2为首项,2为公比的等比数列.1222n n n b -∴=⨯=(2)由(1)知2n n n a b n +=+,()()()()1231222322n n T n ∴=++++++⋯++,()123(123)2222n n T n ∴=+++⋯+++++⋯+,()212(1)212n n n n T -+∴=+- 212222n n n n T +∴=-++. 选∴解:(1)设等差数列{}n a 的公差为d ,1281122,10,2810,1,1a a a a d a d =+=∴+=∴==,1(1)1n a n n ∴=+-⨯=.令1n =,则111112,42,2S b S λλλ+=+∴==+=∴=-,122n n S +∴=-当2n ≥时,()()1122222n n n n n n b S S +-=-=---=当1n =时,12b =也满足上式.2n n b =(2)由(1)知2n n n a b n +=+,()()()()1231222322n n T n ∴=++++++⋯++,()123(123)2222n n T n ∴=+++⋯+++++⋯+,()212(1)212n n n n T -+∴=+-,212222n n n n T +∴=-++ 四、数学建模数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学方法构建模型解决问题的素养,主要表现在:发现和提出问题,建立和求解模型,检验和完善模型,分析和解决问题,在本章主要表现在数列的的实际应用问题中.【典例14】(2021·河南信阳市·高二期末(理))“十二平均律”是通用的音律体系,明代朱载堉最早用数学方法计算出半音比例,为这个理论的发展做出了重要贡献.十二平均律将一个纯八度音程分成十二份,依次得到十三个单音,从第二个单音起,每一个单音的频率与它的前一个单音的频率的比都等于.若第一个单音的频率为f ,则第六个单音的频率为( )A.B. CD【答案】B【解析】由题意知,十三个单音的频率构成等比数列{}n a,公比为 ∴第六个单音的频率561a a q =⋅=.故选:B.【典例15】(2021·河南高二期末(文))疫苗是解决“新冠病毒”的关键,为了早日生产“新冠病毒”疫苗,某研究所计划建设n 个实验室,从第1到第n 实验室的建设费用依次构成等差数列,已知第7实验室比第2实验室的建设费用高15万元,第3实验室和第6实验室的建设费用共为61万元,现在总共有建设费用438万元.则该研究所最多可以建设的实验室个数是( )A .10个B .11个C .12个D .13个【答案】C【解析】设第n 实验室的建设费用为n a 万元,其中1,2,3n =, 由题意可得723615152761a a d a a a d -==⎧⎨+=+=⎩,解得1203a d =⎧⎨=⎩,则()23133720222n n n S n n n -=+=+, 令438n S ≤,即23378760n n +-≤且n N +∈,解得12n ≤.所以最多可以建设12个实验室.故选:C.【典例16】(2021·上海普陀区·曹杨二中高二期末)某公司自2020年起,每年投入的设备升级资金为500万元,预计自2020年起(2020年为第1年),因为设备升级,第n 年可新增的盈利()()5801,5100010.6,6n n n n a n -⎧-≤⎪=⎨-≥⎪⎩(单位:万元),求: (1)第几年起,当年新增盈利超过当年设备升级资金;(2)第几年起,累计新增盈利总额超过累计设备升级资金总额.【答案】(1)第7年;(2)第12年.【解析】(1)当5n ≤时,80(1)500na n =->,解得7.25n >,即8n ≥,不成立, 当6n ≥时,51000(10.6)500n n a -=->,即50.60.5n -<,50.6n -随着n 的增大而减小, 当6n =时,650.60.60.5-=<不成立,当7n =时,750.60.360.5-=<成立,故第7年起,当年新增盈利超过当年设备升级资金;(2)当5n =时,累计新增盈利总额5123450801602403208005005S a a a a a =++++=++++=<⨯,可得所求n 超过5,当6n ≥时,55600(10.6)1000(5)50010.6n n S S n n --=+-->-, 整理得530.611.4n n -+⨯>,由于530.6n -⨯随着n 的增大而减小又当11n =时,1151130.611.4-+⨯<,故不成立,当12n =时,1251230.611.4-+⨯>,故成立,故从第12年起,累计新增盈利总额超过累计设备升级资金总额.。
数列章末总结-----通项公式的求数列的通项公式是数列的核心知识之一,是数列的一种给出形式,其本质是函数的解析式。
有通项公式不仅可以判断数列的类型,研究数列的变化规律和趋势,而且有利于进一步研究数列的前n 项和等特征。
现将求数列的通项公式的常见类型及方法总结如下:1.观察法:横向观察各项之间的关系结构,纵向观察各项与项数n 的内在联系,从而归纳出数列的通项公式例1:写出下列数列的通项公式:(1)21-,43,87-,1615,3231-。
(2)3,33,333,3333,33333,。
(3)1,31,61,101,151。
(4)411,923,635,2547。
2.公式法:等差数列和等比数列是两种常见和非常重要的数列,所以公式法就是先分析该数列是否是等差数列和等比数列,或者通过变型整理转化为等差数列或者等比数列,确定好数列通项需要的量然后运用公式写出通项公式。
例2:(1)已知数列{}n a 为无穷数列,若),2(,2*11N n n a a a n n n ∈≥=++-,且,8,462==a a 求通项n a(2)已知等比数列2,a ,a+4。
写出通项n a 的表达式。
3.利用n a 与n S 的关系:前n 项和关系式有两种形式:一种是n S 与n 的关系式,记为()n f S n =,它可以由公式()⎪⎩⎪⎨⎧∈≥-==-,,,),,2.(..........1........................*11N n n S S n S a n n n 直接求出通项公式n a ,但要注意n=1与2≥n 两种情况能否统一;另一种是n S 与n a 的关系式,先转化为递推关系再求它的通项公式n a 。
例3:(1)已知数列{}n a 的前n 项和为n S ,且22n n S n -=,n n b a 5log =其中0>n b ,求数列{}n b 的前n 项和。
(2)已知数列{}n a 的前n 项和为n S ,且35-=n n S a ,求数列{}n a 通项公式。