必修一第3章末归纳整合

高中物理必修一第三章知识点总结物理必修一第三章知识点知识点一――力的概念（1）力是物体之间的相互作用。

力不能脱离物体而存在。

“物体”同时指施力物体和受力物体。

（2）力的作用效果：使物体发生形变或使物体的运动状态发生变化。

（3）力的三要素：大小、方向、作用点。

力的三要素决定了力的作用效果。

（4）力是矢量，既有大小，又有方向。

力的单位：N （5）力的分类：按力的性质分：可分为重力、弹力、摩擦力等。

按力的效果分：可分为压力、支持力、动力、阻力等。

知识点二――重力（1）重力不是万有引力，重力是由于万有引力产生的。

（2）重力的大小G=mg，在同一地点，物体的重力与质量成正比。

（3）重力的方向竖直向下或与水平面垂直。

但不能说重力的方向一定指向地心。

（4）物体的重心位置与物体的形状以及质量分布有关。

重心可以在物体上，也可以不在物体上。

知识点三――弹力（1）产生条件：直接接触、弹性形变（2）确定弹力的方向在硬接触中（除绳子和弹簧外），一定先找接触面，弹力的方向一定与接触面是垂直的。

（3）绳子、弹簧的弹力的方向一定沿绳子或弹簧。

轻杆所受力的方向不一定沿杆。

（4）胡克定律F＝kx，指的是在弹性限度内，弹簧的弹力与形变量成正比。

（5）同一根张紧的轻绳上拉力处处相等。

知识点四――摩擦力（1）产生条件：a：相互接触且发生弹性形变b：有相对运动或相对运动趋势c:接触面粗糙（2）求摩擦力一定要首先清楚是静摩擦力还是滑动摩擦力。

滑动摩擦力的大小才可以用F FN求解，FN指正压力，不一定等于物体的重力；μ是动摩擦因数，与相互接触的两个物体的材料有关，还跟粗糙程度有关。

（3）摩擦力的方向可以和运动方向相同也可以相反，但一定与相对运动或相对运动趋势的方向相反。

（4）摩擦力的方向一定与接触面平行，一定与弹力的方向垂直。

（5）摩擦力可以作为动力，也可以作为阻力。

知识点五――力的合成（1）力的合成满足平行四边形定则，不是代数加减。

（2）两个力合力的范围F1 F2 F F1 F2，在这之间的所有的力都有可能，这是由这两个力的夹角大小来确定的。

章末复习一、求函数的定义域1．求函数定义域的常用依据是分母不为0，偶次根式中被开方数大于或等于0等等；由几个式子构成的函数，则定义域是各部分定义域的交集．2．掌握基本的集合交并补运算，解简单的不等式，提升逻辑推理和数学抽象素养． 例1 (1)函数y ＝2x ＋1＋3－4x 的定义域为( )A.⎝ ⎛⎭⎪⎫－12，34 B.⎣⎢⎡⎦⎥⎤－12，34C.⎝ ⎛⎦⎥⎤－∞，12D.⎝ ⎛⎭⎪⎫－12，0∪(0，＋∞) 答案 B解析 由⎩⎪⎨⎪⎧2x ＋1≥0，3－4x ≥0，解得－12≤x ≤34，所以函数y ＝2x ＋1＋3－4x 的定义域为⎣⎢⎡⎦⎥⎤－12，34.(2)若函数y ＝f (x )的定义域是[－2,4]，则函数g (x )＝f (－x )的定义域是( ) A ．[－4,4] B ．[－4,2] C ．[－4，－2] D ．[2,4]答案 B解析 －2≤－x ≤4，得－4≤x ≤2. 所以函数g (x )＝f (－x )的定义域是[－4,2]． 反思感悟 求函数定义域的类型与方法(1)已给出函数解析式：函数的定义域是使解析式有意义的自变量的取值集合． (2)实际问题：求函数的定义域既要考虑解析式有意义，还应考虑使实际问题有意义． (3)复合函数问题：①若f (x )的定义域为[a ，b ]，f (g (x ))的定义域应由a ≤g (x )≤b 解出； ②若f (g (x ))的定义域为[a ，b ]，则f (x )的定义域为g (x )在[a ，b ]上的值域． 注意：①f (x )中的x 与f (g (x ))中的g (x )地位相同；②定义域所指永远是x 的范围． 跟踪训练1 函数f (x )＝2x21－x＋(2x －1)0的定义域为( )A.⎝⎛⎭⎪⎫－∞，12 B.⎝ ⎛⎭⎪⎫12，1 C.⎝ ⎛⎭⎪⎫－12，12D.⎝⎛⎭⎪⎫－∞，12∪⎝ ⎛⎭⎪⎫12，1 答案 D解析 由题意得⎩⎪⎨⎪⎧1－x>0，2x －1≠0，解得x <1且x ≠12.二、分段函数1．分段函数主要考查求值、画图、解不等式等，利用分段函数的图象能解决单调性、值域问题，画图时各部分图象合在一起才组成整个函数的图象，解不等式时要分类讨论，各部分取并集． 2．掌握基本函数求值运算，会画简单函数的图象，提升数学运算和直观想象素养．例2 已知函数f (x )＝⎩⎪⎨⎪⎧12x ，0<x<1，34－x4，1≤x<2，54－12x ，2≤x<52.(1)求f (x )的定义域，值域； (2)求f (f (1))； (3)解不等式f (x ＋1)>14.考点 分段函数题点 分段函数的综合应用 解 (1)f (x )的定义域为(0,1)∪[1,2)∪⎣⎢⎡⎭⎪⎫2，52＝⎝ ⎛⎭⎪⎫0，52. 易知f (x )在(0,1)上为增函数，∴0<f (x )<12，f (x )在⎣⎢⎡⎭⎪⎫1，52上为减函数，∴0<f (x )≤12， ∴值域为⎝ ⎛⎦⎥⎤0，12.(2)f (1)＝34－14＝12.f (f (1))＝f ⎝ ⎛⎭⎪⎫12＝12×12＝14.(3)f (x ＋1)>14等价于①⎩⎪⎨⎪⎧0<x ＋1<1，12(x ＋1)>14，或②⎩⎪⎨⎪⎧1≤x ＋1<2，34－14(x ＋1)>14，或③⎩⎪⎨⎪⎧2≤x ＋1<52，54－12(x ＋1)>14.解①得－12<x <0，解②得0≤x <1， 解③得x ∈∅.∴f (x ＋1)>14的解集为⎝ ⎛⎭⎪⎫－12，0∪[)0，1＝⎝ ⎛⎭⎪⎫－12，1. 反思感悟 分段函数也是对应关系f 的一种，在此对应f 上，仍整体上构成一个函数，故分段函数的定义域、值域分别只有一个集合，但在具体对应层面不论是由x 求y ，还是由y 求x ，都要按分段标准对号入座分别求解． 跟踪训练2设f (x )是定义在R 上的函数，且满足f (x ＋2)＝f (x )，当x ∈[－1,1)时，f (x )＝⎩⎪⎨⎪⎧－4x2＋2，－1≤x<0，x ，0≤x<1，则f ⎝ ⎛⎭⎪⎫32＝________.答案 1解析 因为f (x ＋2)＝f (x )，所以f ⎝ ⎛⎭⎪⎫32＝f ⎝ ⎛⎭⎪⎫2－12＝f ⎝ ⎛⎭⎪⎫－12 ＝－4×⎝ ⎛⎭⎪⎫－122＋2＝1. 三、函数性质的综合应用1．函数的性质主要有定义域、值域、单调性和奇偶性，利用函数的单调性和奇偶性求值、比较大小、解不等式是重点考查内容，解不等式时经常结合图象，要注意勿漏定义域的影响．2．掌握单调性和奇偶性的判断和证明，会简单的综合运用，提升数学抽象、逻辑推理和直观想象素养． 例3已知函数f (x )是定义在区间[－1,1]上的奇函数，且f (1)＝1，若对于任意的m ，n ∈[－1,1]，m ＋n ≠0，有f (m )＋f (n )m ＋n >0.(1)判断函数的单调性(不要求证明)；(2)解不等式f ⎝ ⎛⎭⎪⎫x ＋12<f (1－x )； (3)若f (x )≤－2at ＋2对于任意的x ∈[－1,1]，a ∈[－1,1]恒成立，求实数t 的取值范围． 考点 函数的单调性、奇偶性、最值的综合应用 题点 奇偶性、单调性及最值的综合问题 解 (1)函数f (x )在区间[－1,1]上是增函数． (2)由(1)知函数f (x )在区间[－1,1]上是增函数，由f ⎝ ⎛⎭⎪⎫x ＋12<f (1－x )， 得⎩⎪⎨⎪⎧－1≤x ＋12≤1，－1≤1－x ≤1，x ＋12<1－x ，解得0≤x <14.所以不等式f ⎝ ⎛⎭⎪⎫x ＋12<f (1－x )的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪0≤x<14. (3)因为函数f (x )在区间[－1,1]上是增函数，且f (1)＝1，要使得对于任意的x ∈[－1,1]，a ∈[－1,1]都有f (x )≤－2at ＋2恒成立， 只需对任意的a ∈[－1,1]，－2at ＋2≥1恒成立．令y ＝－2at ＋1，当t ≠0时y 可以看作a 的一次函数，且在a ∈[－1,1]时，y ≥0恒成立．因此只需⎩⎪⎨⎪⎧－2t ＋1≥0，2t ＋1≥0，解得－12≤t ≤12，且t ≠0.当t ＝0时，y ＝1，满足y ≥0恒成立．所以实数t 的取值范围为⎣⎢⎡⎦⎥⎤－12，12.反思感悟 (1)解决有关函数性质的综合应用问题的通法就是根据函数的奇偶性解答或作出图象辅助解答，先证明函数的单调性，再由单调性求最值．(2)研究抽象函数的性质时要紧扣其定义，同时注意根据解题需要给x 灵活赋值． 跟踪训练3 已知函数f (x )＝mx2＋23x ＋n 是奇函数，且f (2)＝53. (1)求实数m 和n 的值；(2)求函数f (x )在区间[－2，－1]上的最值． 解 (1)∵f (x )是奇函数，∴f (－x )＝－f (x )， ∴mx2＋2－3x ＋n ＝－mx2＋23x ＋n ＝mx2＋2－3x －n.比较得n ＝－n ，n ＝0. 又f (2)＝53，∴4m ＋26＝53，解得m ＝2. ∴实数m 和n 的值分别是2和0. (2)由(1)知f (x )＝2x2＋23x ＝2x 3＋23x .任取x 1，x 2∈[－2，－1]，且x 1<x 2， 则f (x 1)－f (x 2)＝23(x 1－x 2)⎝ ⎛⎭⎪⎫1－1x1x2 ＝23(x 1－x 2)·x1x2－1x1x2. ∵－2≤x 1<x 2≤－1，∴x 1－x 2<0，x 1x 2>1，x 1x 2－1>0， ∴f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)． ∴函数f (x )在[－2，－1]上为增函数． ∴f (x )max ＝f (－1)＝－43，f (x )min ＝f (－2)＝－53.四、函数图象的画法及应用1．利用函数的图象可以直观观察求函数值域、最值、单调性、奇偶性等，重点是一次函数、二次函数、反比例函数及幂函数图象．2．掌握简单的基本函数图象，提升直观想象和数据分析素养． 例4 已知函数f (x )＝|－x 2＋2x ＋3|. (1)画出函数图象并写出函数的单调区间；(2)求集合M ＝{m |使方程f (x )＝m 有四个不相等的实根}．解 (1)当－x 2＋2x ＋3≥0时，得－1≤x ≤3，函数y ＝－x 2＋2x ＋3＝－(x －1)2＋4， 当－x 2＋2x ＋3<0时，得x <－1或x >3，函数y ＝x 2－2x －3＝(x －1)2－4，即y ＝⎩⎪⎨⎪⎧－(x －1)2＋4，－1≤x ≤3，(x －1)2－4，x <－1或x >3的图象如图所示，单调递增区间为[－1,1]和[3，＋∞)，单调递减区间为(－∞，－1)和(1,3)．(2)由题意可知，函数y ＝f (x )与y ＝m 的图象有四个不同的交点，则0＜m ＜4. 故集合M ＝{m |0<m <4}．反思感悟 画函数图象的主要方法有描点法和先研究函数性质再根据性质画图，一旦有了函数图象，可以使问题变得直观，但仍要结合代数运算才能获得精确结果． 跟踪训练4已知函数f (x )＝⎩⎪⎨⎪⎧－x ，x ≤0，－x2＋2x ，x>0，方程f 2(x )－bf (x )＝0，b ∈(0,1)，则方程的根的个数是( ) A ．2 B ．3 C ．4 D ．5 答案 D解析 因为f 2(x )－bf (x )＝0， 所以f (x )＝0或f (x )＝b ，作函数f (x )＝⎩⎪⎨⎪⎧－x ，x ≤0，－x2＋2x ，x>0的图象如图，结合图象可知，f (x )＝0有2个不同的根，f (x )＝b (0<b <1)有3个不同的根，且5个根都不相同，故方程的根的个数是5.1．设f (x )＝⎩⎨⎧x ，0<x<1，2(x －1)，x ≥1，若f (a )＝f (a ＋1)，则f ⎝ ⎛⎭⎪⎫1a 等于( ) A ．2 B ．4 C ．6 D ．8 答案 C解析 由x ≥1时，函数f (x )为一次函数，得0<a <1， 由f (a )＝f (a ＋1)得a ＝2(a ＋1－1)，解得a ＝14，则f ⎝ ⎛⎭⎪⎫1a ＝f (4)＝2(4－1)＝6. 2．函数f (x )是定义在R 上的奇函数，且它是减函数，若实数a ，b 满足f (a )＋f (b )>0，则a 与b 的关系是( ) A ．a ＋b >0 B ．a ＋b <0 C ．a ＋b ＝0 D ．不确定答案 B解析 因为f (x )是奇函数， 所以－f (b )＝f (－b )． 因为f (a )＋f (b )>0， 所以f (a )>－f (b )＝f (－b )． 因为f (x )在R 上是减函数， 所以a <－b ，即a ＋b <0.3．若f (x )是偶函数，其定义域为(－∞，＋∞)，且在[0，＋∞)上是减函数，设f⎝ ⎛⎭⎪⎫－32＝m ，f⎝⎛⎭⎪⎫a2＋2a ＋52＝n ，则m ，n 的大小关系是________． 考点 单调性与奇偶性的综合应用题点 综合利用函数的单调性、奇偶性比较大小 答案 m ≥n解析 因为a 2＋2a ＋52＝(a ＋1)2＋32≥32，又f (x )在[0，＋∞)上是减函数，所以f ⎝ ⎛⎭⎪⎫a2＋2a ＋52≤f ⎝ ⎛⎭⎪⎫32＝f ⎝ ⎛⎭⎪⎫－32. 4．奇函数f (x )是定义域为(－1,1)上的减函数，且f (2a －1)＋f (a －1)>0，则a 的取值范围是________．答案 ⎝ ⎛⎭⎪⎫0，23解析 f (x )为奇函数，f (2a －1)>－f (a －1)， ∴f (2a －1)>f (1－a )， ∴⎩⎪⎨⎪⎧－1<1－a<1，－1<2a －1<1，1－a>2a －1，解得0<a <23.5．设f (x )为定义在R 上的偶函数，当0≤x ≤2时，y ＝x ，当x >2时，y ＝f (x )的图象是顶点为P (3,4)且过点A (2,2)的抛物线的一部分．(1)在图中的直角坐标系中画出函数f (x )的图象； (2)求函数f (x )在(－∞，－2)上的解析式； (3)写出函数的单调区间及值域． 解 (1)函数的图象如图所示：(2)当x ≥2时，设f (x )＝a (x －3)2＋4，代入点(2,2)， 所以a (2－3)2＋4＝2，解得a ＝－2， 故f (x )＝－2(x －3)2＋4，设x ∈(－∞，－2)，则－x ∈(2，＋∞)， 所以f (－x )＝－2(－x －3)2＋4＝－2(x ＋3)2＋4， 又因为f (x )为偶函数，所以f (－x )＝f (x )， 所以f (x )＝－2(x ＋3)2＋4，x ∈(－∞，－2)． (3)由图象观察可知f (x )的值域为{y |y ≤4}，单调增区间为(－∞，－3]和[0,3]，单调减区间为[－3,0]和[3，＋∞)．。

⾼中⽣物必修⼀第三章知识点归纳 学好⾼中⽣物，要学会总结归纳，对于章节性内容要善于总结复习，形成⾃⼰的知识系统。

下⾯就让店铺给⼤家分享⼀些⾼中⽣物必修⼀第三章知识点归纳吧，希望能对你有帮助! ⾼中⽣物必修⼀第三章知识点归纳篇⼀ 1、⽣命系统的结构层次依次为：细胞→组织→器官→系统→个体→种群→群落→⽣态系统 细胞是⽣物体结构和功能的基本单位;地球上最基本的⽣命系统是细胞 2、光学显微镜的操作步骤：对光→低倍物镜观察→移动视野中央(偏哪移哪)→ ⾼倍物镜观察：①只能调节细准焦螺旋;②调节⼤光圈、凹⾯镜 3、原核细胞与真核细胞根本区别为：有⽆核膜为界限的细胞核 ①原核细胞：⽆核膜，⽆染⾊体，如⼤肠杆菌等细菌、蓝藻 ②真核细胞：有核膜，有染⾊体，如酵母菌，各种动物 注：病毒⽆细胞结构，但有DNA或RNA 4、蓝藻是原核⽣物，⾃养⽣物 5、真核细胞与原核细胞统⼀性体现在⼆者均有细胞膜和细胞质 6、细胞学说建⽴者是施莱登和施旺，细胞学说建⽴揭⽰了细胞的统⼀性和⽣物体结构的统⼀性。

细胞学说建⽴过程，是⼀个在科学探究中开拓、继承、修正和发展的过程，充满耐⼈寻味的曲折 7、组成细胞(⽣物界)和⽆机⾃然界的化学元素种类⼤体相同，含量不同 8、组成细胞的元素 ①⼤量⽆素：C、H、O、N、P、S、K、Ca、Mg ②微量⽆素：Fe、Mn、B、Zn、Mo、Cu ③主要元素：C、H、O、N、P、S ④基本元素：C ⑤细胞⼲重中，含量最多元素为C，鲜重中含最最多元素为O 9、⽣物(如沙漠中仙⼈掌)鲜重中，含量最多化合物为⽔，⼲重中含量最多的化合物为蛋⽩质。

10、(1)还原糖(葡萄糖、果糖、麦芽糖)可与斐林试剂反应⽣成砖红⾊沉淀;脂肪可苏丹III染成橘黄⾊(或被苏丹IV染成红⾊);淀粉(多糖)遇碘变蓝⾊;蛋⽩质与双缩脲试剂产⽣紫⾊反应。

(2)还原糖鉴定材料不能选⽤⽢蔗 (3)斐林试剂必须现配现⽤(与双缩脲试剂不同，双缩脲试剂先加A液，再加B液) 11、蛋⽩质的基本组成单位是氨基酸，氨基酸结构通式为NH2—C—COOH，各种氨基酸的区H别在于R基的不同。

物理·必修1(人教版)章末总结弹力和摩擦力的分析1．弹力和摩擦力的对比.2.弹力或摩擦力的有无及方向的判断方法． (1)假设法．(2)结合物体运动状态判断． (3)效果法．3．认识摩擦力的“四个不一定”．(1)受静摩擦力的物体不一定静止，受滑动摩擦力的物体不一定运动． (2)静摩擦力不一定比滑动摩擦力小．(3)摩擦力不一定与运动方向相反，还可以与运动方向相同，甚至可以与运动方向成一定夹角． (4)摩擦力不一定是阻力，还可以是动力．把一重力为G 的物体用一水平推力F ＝kt(k 为常量，t 为时间)压在竖直的足够高的平整的墙上，如图所示．从t ＝0开始物体所受的摩擦力F f 随时间t 的变化关系是图中的( )解析：因物体在水平方向上受力平衡，故墙壁对物体的支持力F N 始终等于水平推力F 的大小，即F N ＝F ＝kt.墙壁对物体的摩擦力F f ＝μkt ＜G 时，物体加速下滑，摩擦力随时间t 成正比例增加；F f ＞G 后，物体减速下滑，但滑动摩擦力仍会随时间t 成正比例增加，且一直增大到物体停止滑行为止；物体速度减小到0时，物体受到的滑动摩擦力突变成静摩擦力，由二力平衡的条件得静摩擦力的大小F f ＝G.综上可知，B 正确．答案：B►跟踪训练1．(双选)某缓冲装置可抽象成如右图所示的简单模型．图中k 1、k 2为原长相等，劲度系数不同的轻质弹簧．下列表述正确的是()A ．缓冲效果与弹簧的劲度系数无关B ．垫片向右移动时，两弹簧产生的弹力大小相等C ．垫片向右移动时，两弹簧的长度保持相等D ．垫片向右移动时，两弹簧的长度不同 答案:BD将一个力分解为两个相互垂直的分力的方法称为正交分解法． 例如将力F 沿x 和y 两个方向分解，如右图所示，则F x ＝Fcos θ F y ＝Fsin θ力的正交分解的优点在于：其一，借助数学中的直角坐标系对力进行描述；其二，几何图形关系简单，是直角三角形，计算简便，因此很多问题中，常把一个力分解为互相垂直的两个力．特别是物体受多个力作用，求多个力的合力时，把物体受的各力都分解到相互垂直的两个方向上去，然后分别求每个方向上的分力的代数和，这样就把复杂的矢量运算转化为简单的代数运算，再求两个互成90°角的力的合力就简便得多．正交分解法多个力合成的正交分解法的步骤如下：第一步：建立坐标系，以共点力的作用点为坐标原点，直角坐标x轴和y轴的选择应使尽量多的力在坐标轴上．第二步：正交分解各力，即将每一个不在坐标轴上的力分解到x和y坐标轴上，并求出各分力的大小，如右上图所示．第三步：分别求x轴和y轴上各力的分力的合力，即F x＝F1x＋F2x＋…F y＝F1y＋F2y＋…第四步：求F x与F y的合力即为共点力合力．合力大小：F＝F2x＋F2y，合力的方向由F与x轴间夹角α确定，即α＝arctan F yF x .在运用正交分解法求解时，应注意的几个问题：(1)正交分解法在求三个以上的力的合力时较为方便．两个力合成时，一般直接进行力的合成，不采用正交分解法．(2)正交分解法的基本思路是：把矢量运算转化为代数运算，把解斜三角形转化为解直角三角形，正交分解法是在分力与合力等效的原则下进行的．(3)坐标系的选取要合理．正交分解时坐标系的选取具有任意性，但为了运算简单，一般要使坐标轴上有尽可能多的力，也就是说需要向两坐标轴上投影分解的力少一些．这样一来，计算也就方便一些，可以使问题简单化．一个物体受到三个力作用，如右图所示，已知一个力是80 N，指向东偏北30°的方向，一个力是40 N，指向西偏北45°方向，一个力20 N指向正南，求三个力的合力大小．解析：本题为三个共点力的合成问题，为了准确计算合力的大小，采用正交分解法．取向东方向为x 轴正方向，向北方向为y 轴正方向，建立平面直角坐标系，如下图所示，将F 1、F 2正交分解可知：F 1x ＝F 1·cos 30°，F 1y ＝F 1·sin 30°. F 2x ＝－F 2·cos 45°，F 2y ＝F 2·sin 45°， F 3x ＝0，F 3y ＝－F 3.x 方向的合力为：F x ＝F 1x ＋F 2x ＝F 1·cos 30°－F 2·cos 45°＝(80×32－40×22) N ＝41 N ； y 方向的合力为：F y ＝F 1y ＋F 2y ＋F 3y ＝F 1·sin 30°＋F 2·sin 45°－F 3＝(80×12＋40×22－20) N ＝48.28 N.最后三个力的合力为： F ＝F 2x ＋F 2y ＝412＋2N ＝63.3 N.答案：63.3 N►跟踪训练1．如下图所示，重力为500 N 的人通过跨过定滑轮的轻绳牵引重200 N 的物体，当绳与水平面成60°角时，物体静止．不计滑轮与绳的摩擦，求地面对人的支持力和摩擦力．答案:100(5－3)N 100 N2．如右图所示，物体受到F 1＝20 N ，F 2＝10 N ，F 3＝10 N 三个共点力的作用，其中F 1与F 2的夹角为30°，F 1和F 3的夹角为150°，求这三个共点力的合力．答案:合力大小为10 5 N ，与F 1的夹角正切值为12.1．抽象思维法．从大量生活事例中抽象出“力是物体间的相互作用”，再把这种抽象具体形象化——用有向线段进行描述，通过这种方法，把对力的运算转化为几何问题来处理．2．等效替代思想．等效替代是物理学中研究实际问题时常用的方法．重心的概念、力的合成与分解都是等效替代思想在本章的具体应用，合力与分力可以相互替代而不改变其作用效果．3．数学转化思想．(1)数形转化思想：数形转化是把物理问题转化为几何问题，利用几何图形的性质来研究物理问题的一种解题思想．例如，用图解法分析力分解的多种可能性和用相似三角形法求解力等．(2)函数转化思想：运用数学中的函数知识将物理问题转化为函数问题，然后结合函数所表达的物理意义进行分析，从而达到解决物理问题的目的．这种转化就叫函数转化．如图所示，人向右运动的过程中，物体A 缓慢地上升．若人对地面的压力为F 1、人受到的摩擦力为F 2、人拉绳的力为F 3，则()A ．F 1、F 2、F 3均增大B ．F 1、F 2增大，F 3不变C ．F 1、F 2、F 3均减小D ．F 1增大，F 2减小，F 3不变解析：设人和物体A 质量分别为m 、m A .物体A 缓慢上升，即物体A 在任何位置都可以认为是处于静止状态，故绳的物理思想方法的应用张力为m A g，人拉绳的力F3与绳的张力大小相等，故人拉绳的力F3＝m A g不变．对人进行受力分析，并建立直角坐标系如图所示，人始终处于静止状态，可得F2－F3′cos θ＝0，F1′＋F3′sin θ＝mg，由力的相互性知F1′＝F1，F3′＝F3，解得F1＝mg－m A gsin θ，F2＝m A gcos θ，显然，F1、F2是关于自变量θ的函数，当自变量θ减小时，函数F1、F2增大，故B正确．答案：B。

高中数学必修一第三章知识点总结第三章：函数的应用一、方程的根与函数的零点1、函数零点的定义：对于函数y=f(x) (x∈D)，使得f(x)=0成立的实数x被称为函数y=f(x) (x∈D)的零点。

2、函数零点的意义：函数y=f(x)的零点是方程f(x)=0的实数根，即函数y=f(x)的图像与x轴相交的横坐标。

即：方程f(x)=0有实数根⇔函数y=f(x)的图像与x轴有交点⇔函数y=f(x)有零点。

3、函数零点的求法：1）代数法：求解方程f(x)=0的实数根；2）几何法：对于不能用求根公式的方程，可以将它与函数y=f(x)的图像联系起来，并利用函数的性质找出零点。

4、基本初等函数的零点：①正比例函数y=kx (k≠0)只有一个零点；②反比例函数y=k/x (k≠0)没有零点；③一次函数y=kx+b (k≠0)只有一个零点；④二次函数y=ax²+bx+c (a≠0)。

1）△>0，方程ax²+bx+c=0有两个不等实根，二次函数的图像与x轴有两个交点，二次函数有两个零点。

2）△=0，方程ax²+bx+c=0有两个相等实根，二次函数的图像与x轴有一个交点，二次函数有一个二重零点或二阶零点。

3）△<0，方程ax²+bx+c=0无实根，二次函数的图像与x轴无交点，二次函数无零点。

⑤指数函数y=a^x (a>0，且a≠1)没有零点。

⑥对数函数y=logₐx (a>0，且a≠1)仅有一个零点1.⑦幂函数y=x^n，当n>0时，仅有一个零点，当n≤0时，没有零点。

5、非基本初等函数的零点：对于较为复杂的函数f(x)，可以先将其转化为αx²+y₁y₂，再将其拆分成两个我们常见的函数y₁,y₂（基本初等函数），这两个函数图像的交点个数就是函数f(x)的零点个数。

6、判断区间是否含有零点：只需满足f(a)f(b)<0.7、确定零点在某区间的个数的唯一条件是：①函数f(x)在区间上连续，且f(a)f(b)<0；②函数f(x)在区间(a,b)上单调。

高一化学必修一第三章知识点总结归纳高一化学必修一(一)金属的化学性质一金属的通性1.金属的存在(1)金属元素的存在绝大多数金属以化合态的形式存在于自然界中，如Al、Fe等，极少数化学性质不活泼的金属以游离态的形式存在于自然界中，如Au。

在地壳中的含量较多的为O、Si、Al、Fe、Ca。

2.金属单质的物理通性①状态：常温下，大部分为固体，唯一呈液态的是汞。

②色泽：除Cu、Au外，大多数金属为银白色，有金属光泽。

③三性：良好的导电性、导热性、延展性。

3.单质的化学性质(1)与非金属的反应常温下，镁在空气中跟氧气反应，生成一层致密的氧化物薄膜，能够阻止内部金属继续被氧化。

镁在空气中燃烧，产生耀眼的白光，生成白色固体，反应的化学方程式为：2Mg+O2点燃=====2MgO。

镁还可以和氮气点燃，反应方程式为：3Mg+N2点燃=====Mg3N2。

(2)与酸的反应Fe与稀H2SO4反应的离子方程式：Fe+2H+===Fe2++H2↑。

(3)与盐溶液的反应Cu与AgNO3溶液反应的离子方程式：Cu+2Ag+===Cu2++2Ag。

归纳金属的通性(1)金属化学性质特点(2)金属还原性的强弱取决于其失去电子的难易程度，而不是失去电子个数的多少。

【活学活用】1.判断下列说法是否正确，正确的划“√”，错误的划“×”(1)金属具有良好的导热、导电性()(2)金属单质在氧化还原反应中总是作还原剂()(3)钠原子在氧化还原反应中失去1个电子，而铝原子失去3个电子，所以铝比钠活泼()(4)金属在加热条件下均易与O2反应()答案(1)√(2)√(3)×(4)×解析(3)错误，金属的活泼性与原子失去电子个数无关，与失电子能力有关，钠比铝易失电子，钠比铝活泼;(4)错误，Au、Pt等金属不与O2反应。

二钠与氧气的反应按表中要求完成实验，并将观察到的实验现象及其原因解释填入表中。

[归纳总结]钠与氧气的反应(1)钠的性质及其保存钠是一种硬度小、熔点低的银白色的金属，具有金属光泽。

第三章第一节细胞膜——系统的边界一、细胞膜的成分1.制备生物膜：①取材：细胞原因：没有和众多的、没有。

②原理：细胞放到中，细胞吸水，细胞内容物流出，可得到细胞膜。

③再经过和方法，可获得较纯净的细胞膜。

④结果：消失，体积，细胞，内容物流出，获得细胞膜。

注意：①红细胞用生理盐水，作用②注意该盖玻片的方法，防止出现③用吸水纸吸引时，注意不要把细胞吸走。

④滴蒸馏水操作在杂物台上进行，载物台应保持水平。

否则易使蒸馏水流走。

⑤实验中，持续观察细胞的变化与引流前观察到的细胞形态形成对照。

2.细胞结构①细胞膜的主要成分：和，还有少量的注意：不同种类的细胞，细胞膜的成分含量不完全相同；不同生理状态下细胞膜的成分和功能不同。

②细胞膜成分的特点：组成细胞膜的脂质中，含量最丰富，功能越复杂的细胞膜，的种类和数量越多。

二、细胞膜的功能1.将细胞与外界环境分隔开2.控制物质进出细胞3.进行细胞间的信息交流①图A通过信号分子完成交流②图B两细胞间交流，例如③图C相邻两个细胞之间形成，携带信息的物质通过进入另一个细胞，例如高等植物细胞之间形成三、细胞壁1.主要成分①植物：和②真菌：③细菌：2.主要功能：对植物细胞有和的作用。

3.特性：细胞膜对细胞内外的物质具有性，而细胞壁具有性。

明辨正误1.细胞膜难以杜绝所有对细胞有害物质的进出，说明其控制作用进出的能力是有限的。

（）2.植物细胞之间的胞间连丝具有物质运输的作用。

（）3.细胞间的信息交流都依靠于信息分子和受体的识别。

（）4.植物细胞与细菌细胞都有细胞壁，细胞壁的主要成分均为纤维素和果胶。

（）5.细胞膜的主要成分是蛋白质，磷脂和多糖。

（）6.细胞膜中不含胆固醇。

（）7.细胞膜中的糖主要是纤维素。

（）3.哺乳动物成熟的红细胞中没有除细胞膜之外的其他膜结构。

（）第三章第二节细胞器——系统内的分工合作一、细胞器之间的分工4.双层膜的细胞器项目线粒体叶绿体（）（）亚显微结构（）（）（）（）（）（）增大膜面积方式功能分布酶的种类和分布与有氧呼吸有关的酶分布于与光合作用有关的酶分布于和中和中相同点①都具有层膜；②都含有少量的和；③都与能量转换有关；5.单层膜的细胞器细胞器名称结构功能分布①参与细胞内蛋白质内质网的和；②以及的合成。

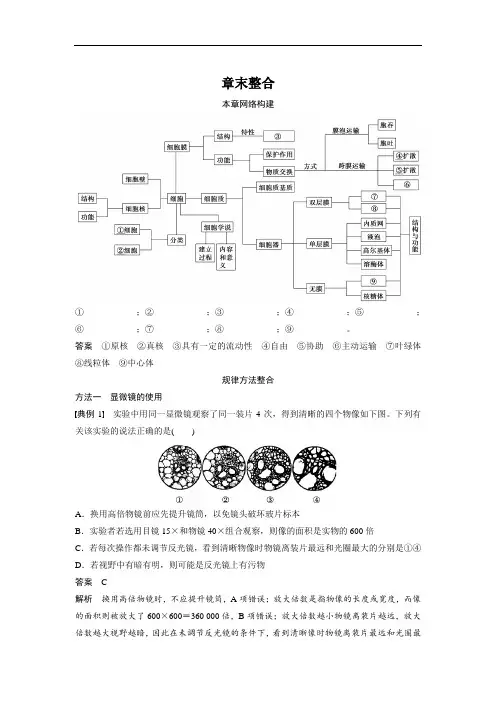
章末整合本章网络构建①____________；②____________；③____________；④____________；⑤____________；⑥____________；⑦____________；⑧____________；⑨____________。

答案①原核②真核③具有一定的流动性④自由⑤协助⑥主动运输⑦叶绿体⑧线粒体⑨中心体规律方法整合方法一显微镜的使用典例1实验中用同一显微镜观察了同一装片4次，得到清晰的四个物像如下图。

下列有关该实验的说法正确的是()A．换用高倍物镜前应先提升镜筒，以免镜头破坏玻片标本B．实验者若选用目镜15×和物镜40×组合观察，则像的面积是实物的600倍C．若每次操作都未调节反光镜，看到清晰物像时物镜离装片最远和光圈最大的分别是①④D．若视野中有暗有明，则可能是反光镜上有污物答案 C解析换用高倍物镜时，不应提升镜筒，A项错误；放大倍数是指物像的长度或宽度，而像的面积则被放大了600×600＝360 000倍，B项错误；放大倍数越小物镜离装片越远，放大倍数越大视野越暗，因此在未调节反光镜的条件下，看到清晰像时物镜离装片最远和光圈最大的分别是①④，C项正确；视野中有暗有明，最可能是反光镜的调节角度不对，D项错误。

方法链接1．显微镜的放大倍数(1)放大倍数是指物像的大小对物体大小的比例。

(2)放大倍数＝目镜放大倍数×物镜放大倍数，这里的放大倍数指的是长度或宽度，而不是面积和体积。

2．物像移动与装片移动的关系显微镜下所成的像与实物相比是倒置的，所以物像移动的方向与载玻片移动的方向是相反的。

3．放大倍数的变化与视野范围内细胞数量变化的关系(1)一行细胞数量的变化，可根据放大倍数与视野范围成反比的规律计算。

(2)圆形视野范围内细胞数量的变化，可根据看到的实物范围与放大倍数的平方成反比的规律计算。

4．低倍镜换高倍镜的程序将要观察的物像移至视野中央→转动转换器换高倍物镜→调节视野明亮(大光圈、凹面镜)→调节细准焦螺旋使图像清晰。