广东省高中数学---立体几何复习资料(文)

lαβm广东高考数学真题汇编：立体几何1、（2011•广东文数）正五棱柱中，不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线，那么一个正五棱柱对角线的条数共有（ ） A 、20 B 、15 C 、12 D 、101解答：解：由题意正五棱柱对角线一定为上底面的一个顶点和下底面的一个顶点的连线，因为不同在任何侧面内，故从一个顶点出发的对角线有2条．正五棱柱对角线的条数共有2×5=10条．故选D2、（2011•广东文数）如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为 （ ） A 、 B 、4 C 、 D 、23、（2011•广东理数）如某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则几何体的体积为（ ） A 、6 B 、9 C 、12 D 、185. （2009广东文科）给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行； ④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中，为真命题的是A ．①和②B ．②和③C ．③和④D ．②和④6．（2008广东文数）将正三棱柱截去三个角（如图1所示，AB C ，，分别是GHI △三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ ）7．（2007广东文数）若l mn ，，是互不相同的空间直线，αβ，是不重合的平面，则下列命题中为真命题的是（ ）Ａ．若l n αβαβ⊂⊂，，∥，则l n ∥Ｂ．若l αβα⊥⊂，，则l β⊥Ｃ．若l nm n ⊥⊥，，则l m ∥ Ｄ．若l l αβ⊥，∥，则αβ⊥ 8、（2006广东）给出以下四个命题①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行;②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面;EF DIA H GB C EF DA B C侧视 图1图2B EA ．B EB ．B EC ．B ED ．③如果两条直线都平行于一个平面,那么这两条直线互相平行;④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直. 其中真命题的个数是A.4B.3C.2D.19. (2005广东)给出下列关于互不相同的直线m 、l 、n 和平面α、β，的四个命题： ①若A l m =⊂αα ,，点m A ∉，则l 与m 不共面；②若m 、l 是异面直线, αα//,//m l , 且m n l n ⊥⊥,，则α⊥n ； ③若βα//,//m l , βα//，则m l //；④若=⊂⊂m l m l ,,αα点A ，ββ//,//m l ，则βα//． 其中为假命题的是A ．①B ．②C ．③D ．④11、（2006广东）若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为13．（2008广东文数）如图5所示，四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形，其中BD 是圆的直径，60ABD ∠=，45BDC ∠=，PD 垂直底面ABCD，PD =，E F ，分别是PB CD ，上的点，且PE DFEB FC =，过点E 作BC 的平行线交PC 于G ． （1）求BD 与平面ABP 所成角θ的正弦值； （2）证明：EFG △是直角三角形； （3）当12PE EB =时，求EFG △的面积．13．解：（1）在Rt BAD ∆中，60ABD ∠=，,AB R AD ∴==而PD 垂直底面ABCD ，PA ===PB ===,在PAB ∆中，222PA AB PB +=,即PAB ∆为以PAB ∠为直角的直角三角形。

广州市第一中学高三数学第二轮复习专题——立体几何专题复习1、如图，已知面ABC ⊥面BCD ，AB ⊥BC ，BC ⊥CD ，且AB=BC=CD ，设AD 与面AB C 所成角为α，AB与面ACD 所成角为β，则α与β的大小关系为 （A ）α＜β （B ）α=β （C ）α＞β （D ）无法确定2、下列各图是正方体或正四面体，P ，Q ，R ，S 分别是所在棱的中点，这四个点中不共面．．．的一个图是 PP PPQ Q QQRRR R SSS SPPPPQQQQ RRRRSS S SPPPPQQQQ R RRR SSS S PPPPQQQQRRRR SSS S（A ） （B ） （C ） （D ）3、在棱长为a 的正方体ABCD －A 1B 1C 1D 1中，P ，Q 是对角线A 1C 上的点，且PQ =2a，则三棱锥P －BDQ 的体积为（A ）3363a （B ）3183a （C ）3243a （D ）无法确定 4、已知球的内接三棱锥的三条侧棱两两垂直，长度分别为3cm ，2cm 和3cm ，则此球的体积为（A ）33312cm π （B ）33316cm π （C ）3316cm π （D ）3332cm π5、如图，在一根长11cm ，外圆周长6cm 的圆柱形柱体外表面，用一根细铁丝缠绕，组成10个螺旋，如果铁丝的两端恰好落在圆柱的同一条母线上，则铁丝长度的最小值为（A ） 61cm （B ）157cm （C ）1021cm （D ）1037cm6、设a 、b 是两条不同的直线，α、β是两个不同的平面，则下列四个命题：① 若b a ⊥，α⊥a ，α⊄b ，则α//b ；②若α//a , βα⊥，则β⊥a ； ③若β⊥a ，βα⊥，则α//a 或α⊂a ；④若b a ⊥，α⊥a ，β⊥b ，则βα⊥ 其中正确命题的个数为 ( )A ．0B ．1C ．2D ．37、正三棱锥ABC S —的侧棱长和底面边长相等，如果E 、F 分别为SC ，AB 的中点，那么异面直线EF 与SA 所成角为 （ ） A ．090 B ．060 C ．045 D ．030 8．右图是正方体的平面展开图，在这个正方体中： ①BM 与DE 平行； ②CN 与BE 是异面直线； ③CN 与BM 成60°角④DM 与BN 垂直以上四个命题中，正确的是 （ ） A ．①②③ B ．②④ C ．②③④D ．③④9．将棱长为1的正方体木块切削成一个体积最大的球，则该球的体积为（ ）A ．π23B ．π32 C ．6π D ．34π 10．正方体ABCD －A 1B 1C 1D 1中，E 是BC 的中点，则A 1C 与DE 所成的角的余弦为（ ）A ．1515B ． 1510 C ． 630 D ． 1010 11．有3个命题（1）底面是正三角形，其余各个面都是等腰三角形的棱锥是三棱锥； （2）各个侧面都是等腰三角形的四棱锥是正四棱锥；（3）底面是正三角形，相邻两侧面所成的二面角都相等的三棱锥是正三棱锥。

立体几何知识点归纳(复习资料)高考总复习主干知识三：立体几何主干知识三：立体几何知识点归纳一．直线和平面的三种位置关系：1. 线面平行l方法一：用线线平行实现。

l//m??m????l//? l????方法二：用面面平行实现。

α符号表示：αlAβl2. 线面相交?//????l//? l???方法三：用平面法向量实现。

符号表示：若n为平面?的一个法向量，n?l且lαnl3. 线在面内ααl??,则l//?。

符号表示：3. 面面平行：方法一：用线线平行实现。

二．平行关系： 1. 线线平行：方法一：用线面平行实现。

l?l//l’??l????l//m ????m?? l//???m//m’????//?l,m??且相交?αl’,m’??且相交?? 方法二：用线面平行实现。

βl’m’ml?ml//?方法二：用面面平行实现。

lβγαm?//???????l??l//m ????m??? ?m//???/ /??l,m??且相交?? 方法三：用向量方法：两个平面的法向量共线三．垂直关系： 1. 线面垂直：方法一：用线线垂直实现。

βml α方法三：用线面垂直实现。

若l??,m??，则l//m。

方法四：用向量方法：若向量l和向量m共线且l、m不重合，则l//m。

2. 线面平行： 1 / 8 l?AC?l?AB??lAC?AB?A??l?? ?CAC,AB? ???αAB方法二：用面面垂直实现。

????βl????m???l?? l?m,l???m?α方法三：用向量方法：直线与平面的法向量共线 2. 面面垂直：方法一：用线面垂直实现。

l???βll???????? α方法二：计算所成二面角为直角。

方法三：用向量方法：两平面的法向量垂直 3. 线线垂直：方法一：用线面垂直实现。

ll???m?????l?m mα 方法二：三垂线定理及其逆定理。

PO???Pl?OA???l?PA l????αAlO方法三：用向量方法：若向量l和向量m 的数量积为0，则l?m。

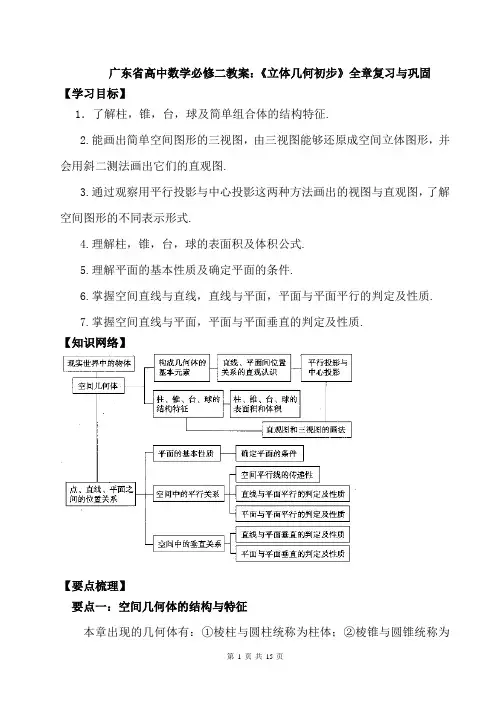
广东省高中数学必修二教案：《立体几何初步》全章复习与巩固【学习目标】1．了解柱，锥，台，球及简单组合体的结构特征.2.能画出简单空间图形的三视图，由三视图能够还原成空间立体图形，并会用斜二测法画出它们的直观图.3.通过观察用平行投影与中心投影这两种方法画出的视图与直观图，了解空间图形的不同表示形式.4.理解柱，锥，台，球的表面积及体积公式.5.理解平面的基本性质及确定平面的条件.6.掌握空间直线与直线，直线与平面，平面与平面平行的判定及性质.7.掌握空间直线与平面，平面与平面垂直的判定及性质.【知识网络】【要点梳理】要点一：空间几何体的结构与特征本章出现的几何体有：①棱柱与圆柱统称为柱体；②棱锥与圆锥统称为锥体；③棱台与圆台统称为台体；④球体．柱体常以直三棱柱、正三棱柱、正四棱柱、正六棱柱、圆柱等为载体，锥体一般以正三棱锥、正四棱锥、正六棱锥、圆锥等为载体，计算高、斜高、边心距、底面半径、侧面积和体积等．在研究正棱锥和圆锥、正棱台和圆台时要充分利用其中的直角三角形：高线，边心距，斜高组成的直角三角形；高线，侧棱(母线)，外接圆半径(底面半径)组成的直角三角形．空间几何体的三视图：主视图：它能反映物体的高度和长度；左视图：它能反映物体的高度和宽度；俯视图：它能反映物体的长度和宽度．先会读懂三视图，并还原为直观图，再研究其性质和进行计算．侧面展开图问题是经常出现的一个问题．平面图形的翻折与空间图形的展开问题，要对照翻折(或展开)前后两个图形，分清哪些元素的位置(或数量)关系改变了，哪些没有改变，哪些元素是同一个元素．与几何体的侧面积和体积有关的计算问题，基本概念和公式要熟练，计算要准确，重视方程的思想和割补法、等积转换法的运用，等积转换可使体积计算变得简单化．要点二：平面基本性质刻画平面的公理(或基本性质)是立体几何公理体系的基石，是研究空间图形问题、进行逻辑推理的基础．公理1：如果一条直线上的两点在一个平面内，那么这条直线上的所有点都在这个平面内．作用：是判定直线是否在平面内的依据．公理2：经过不在同一条直线上的三点，有且只有一个平面．作用：提供确定平面最基本的依据．公理3：如果不重合的两个平面有一个公共点，那么它们有且只有一条过这个点的公共直线．作用：是判定两个平面交线位置的依据．公理4：平行于同一条直线的两条直线互相平行．作用：是判定空间直线之间平行的依据．要点三：空间的平行与垂直关系理解和熟练应用空间中线面平行、垂直的有关性质与判定定理，是解决有关计算和证明的金钥匙．归纳出以下判定定理：(1)空间中的平行关系如果不在一个平面内的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行．如果一个平面内有两条相交直线平行于另一个平面，那么这两个平面平行．如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和两平面的交线平行．如果两个平行平面同时与第三个平面相交，那么它们的交线平行．如果两条直线垂直于同一个平面，那么这两条直线平行．(2)空间中的垂直关系如果一条直线与平面内的两条相交直线垂直，则这条直线与这个平面垂直．如果一个平面过另一个平面的一条垂线，则两个平面互相垂直．如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面．解决空间问题的重要思想方法：等价转化——化空间问题为平面问题．空间平行、垂直关系证明的基本思想方法——转化与联系，如图所示．【典型例题】类型一：空间几何体的三视图例1．某几何体的三视图如图1所示,它的体积为 （ ）A ．12πB ．45πC ．57πD ．81π【答案】C【解析】该几何体下部分是半径为3,高为5的圆柱,体积为23545V ππ=⨯⨯=,上部分是半径为3,高为4的圆锥,体积为2134123V ππ=⨯⨯⨯=,所以体积为57π.【总结升华】根据三视图判断空间几何体的形状，进而求几何体的表（侧/底）面积或体积，是高考必考内容，处理的关键是准确判断空间几何体的形状，一般规律是这样的：如果三视图均为三角形，则该几何体必为三棱锥；如果三视图中有两个三角形和一个多边形，则该几何体为N 棱锥（N 值由另外一个视图的边数确定）；如果三视图中有两个为矩形和一个多边形，则该几何体为N 棱柱（N 值由另外一个视图的边数确定）；如果三视图中有两个为梯形和一个多边形，则该几何体为N 棱柱（N 值由另外一个视图的边数确定）；如果三视图中有两个三角形和一个圆，则几何体为圆锥．如果三视图中有两个矩形和一个圆，则几何体为圆柱．如果三视图中有两个梯形和一个圆，则几何体为圆台． 举一反三：【变式1】某几何体的三视图如图所示,该几何体的表面积是_____.【答案】92【解析】由三视图可知,原几何体是一个底面是直角梯形,高为4的直四棱柱,其底面积为(25)42282+⨯=,侧面积为(4255)464+++⨯=,故表面积为92. 例2．如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正视图和侧视图在下面画出（单位：cm ）.（1）在正视图下面，按照画三视图的要求画出该多面体的俯视图； （2）按照给出的尺寸，求该多面体的体积； （3）在所给直观图中连结'BC ，证明：'BC ∥面EFG .【思路点拨】（1）按照三视图的要求直接在正视图下面，画出该多面体的俯视图；（2）按照给出的尺寸，利用转化思想V=V 长方体-V 正三棱锥，求该多面体的体积； （3）在长方体ABCD-A′B′C′D′中，连接AD′，在所给直观图中连接BC′，证明EG ∥BC′，即可证明BC′∥面EFG ． 【解析】 （1）如图（2）所求多面体体积V V V =-长方体正三棱锥1144622232⎛⎫=⨯⨯-⨯⨯⨯⨯ ⎪⎝⎭（俯视图）（正视图）（侧视图）正视图2284(cm )3=． （3）证明：在长方体ABCD A B C D ''''-中， 连结AD '，则AD BC ''∥． 因为E G ，分别为AA '，A D ''中点， 所以AD EG '∥，从而EG BC '∥．又BC '⊄平面EFG ， 所以BC '∥面EFG ．【总结升华】长方体的有关知识、体积计算及三视图的相关知识，对三视图的相关知识掌握不到位，求不出有关数据．三视图是新教材中的新内容，故应该是新高考的热点之一，要予以足够的重视． 类型二：几何体的表面积和体积例3．一个几何体的三视图如图所示，该几何体的表面积为 ()A ．280B ．292C ．360D ．372 【答案】 C【解析】该几何体由两个长方体组合而成，其表面积等于下面长方体的全面积加上面长方体的侧面积S ＝2×(10×8+10×2+8×2)+2×(6×8+8×2)AC DE FGA 'B 'C 'D '＝360．【总结升华】把三视图转化为直观图是解决问题的关键．又根据三视图很容易知道是两个长方体的组合体，画出直观图，得出各条棱的长度．把几何体的表面积转化为下面长方体的全面积加上面长方体的侧面积． 举一反三：【变式1】某三棱锥的三视图如图所示,该三棱锥的表面积是（ ）A ．28+B ．30+ C ．56+D ．60+【答案】B【解析】从所给的三视图可以得到该几何体为三棱锥,本题所求表面积为三棱锥四个面的面积之和.利用垂直关系和三角形面积公式,可得:10,10,10,S S S S ====后右左底因此该几何体表面积30S =+,故选B. 例4．设三棱柱的侧棱垂直于底面，所有棱长都为a ，顶点都在一个球面上，则该球的表面积为 ( )A ．2a πB ．273a π C ．2113a π D ．25a π 【答案】 B【解析】设三棱柱底面所在圆的半径为r ，球的半径为R ，易知2323r a a =⨯=，所以球的半径R 满足：2222173212R a a ⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭，所以22743S R a ππ==球．【总结升华】 这是一个球内接三棱柱，球心是三棱柱两底中心连线的中点，这是本题的关键之处． 举一反三：【变式1】如图,在长方体1111ABCD A B C D -中,3cm AB AD ==,12cm AA =,则四棱锥11A BB D D -的体积为 cm3.【答案】6.【解析】∵长方体底面ABCD 是正方形,∴△ABD 中BD BD 边上的高是cm(它也是11A BB D D -中11BB D D 上的高). ∴四棱锥11A BB D D -的体积为123⨯.类型三：直线、平面的平行与垂直例5.如图所示，直三棱柱ABC —A 1B 1C 1中，B 1C 1=A 1C 1，AC 1⊥A 1B ，M 、N 分别是A 1B 1、AB 的中点.（1）求证：C 1M ⊥平面A 1ABB 1； （2）求证：A 1B ⊥AM ；（3）求证：平面AMC 1∥平面NB 1C ； （1）【证明】方法一 由直棱柱性质可得AA 1⊥平面A 1B 1C 1，又∵C1M⊂平面A1B1C1，∴AA1⊥MC1.又∵C1A1=C1B1，M为A1B1中点，∴C1M⊥A1B1.又A1B1∩A1A=A1，∴C1M⊥平面AA1B1B.方法二由直棱柱性质得：平面AA1B1B⊥平面A1B1C1，交线为A1B1，又∵C1A1=C1B1，M为A1B1的中点，∴C1M⊥A1B1于M.由面面垂直的性质定理可得C1M⊥平面AA1B1B.（2）【证明】由（1）知C1M⊥平面A1ABB1，∴C1A在侧面AA1B1B上的射影为MA.∵AC1⊥A1B，MC1⊥A1B，MC1∩AC1=C1，∴A1B⊥平面AMC1，又AM⊂平面AMC1，∴A1B⊥AM.（3）【证明】方法一由棱柱性质知四边形AA1B1B是矩形，M、N分别是A1B1、AB的中点，∴AN//B1M.∴四边形AMB1N是平行四边形.∴AM∥B1N.连接MN，在矩形AA1B1B中有A1B1 //AB.∴MB1 //BN，∴四边形BB1MN是平行四边形.∴BB1 MN.又由BB1//CC1，知MN//CC1.∴四边形MNCC1是平行四边形.∴C1M//CN.又C1M∩AM=M，CN∩NB1=N，∴平面AMC1∥平面NB1C.方法二由（1）知C1M⊥平面AA1B1B，A1B⊂平面AA1B1B，∴C1M⊥A1B.又∵A1B⊥AC1，而AC1∩C1M=C1，∴A1B⊥平面AMC1.同理可证，A1B⊥平面B1NC.∴平面AMC1∥平面B1NC.【总结升华】证明线面之间的垂直关系，要注意在各个阶段以某一直线为主线进行推理，以使推理过程清晰、明朗.例6．如图所示，在五棱锥P-ABCDE，PA⊥平面ABCDE，AB∥CD，AC∥ED，AE∥BC，∠ABC＝45°，AB＝BC＝2AE＝4，三角形PAB是等腰三角形．(1)求证：平面PCD⊥平面PAC；(2)求直线PB与平面PCD所成角的大小；(3)求四棱锥P-ACDE的体积．【解析】(1)证明：因为∠ABC＝45°，AB＝BC＝4，所以在△ABC中，由余弦定理得：AC2＝22424cos458°，解得AC=+-⨯=以AB2+AC2＝8+8＝16＝BC2，所以AB⊥AC．又PA⊥平面ABCDE，所以PA ⊥AB．又PA∩AC＝A，所以AB⊥平面PAC．又AB∥CD，所以CD⊥平面PAC．又因为CDC平面PCD，所以平面PCD⊥平面PAC．(2)由(1)知平面PCD⊥平面PAC，所以在平面PAC内，过点A作AH⊥PC于H，则AH⊥平面PCD．又AB∥CD，AB⊄平面PCD，所以AB∥平面PCD，所以点A到平面PCD的距离等于点B到平面PCD的距离．过点B作BO⊥平面PCD于点O，连接PO，则∠BPO为所求角，且AH＝BO，又容易，即∠BPO＝30°，所以直线PB与平面PCD 求得AH＝2，所以sin∠BPO＝12所成角的大小为30°．(3)由(1)知CD ⊥平面PAC ，所以CD ⊥AC ．又AC ∥ED ，所以四边形ACDE 是直角梯形．又容易求得DE ＝，所以四边形ACDE 的面积为1)32⨯+=，所以四棱锥P -AC -DE 的体积为133⨯=． 【总结升华】本题考查了空间几何体的线面与面面垂直、线面角的求解以及几何体的体积，考查了同学们的空间想象能力．举一反三：【变式1】如图，在四棱锥P-ABCD 中，平面PAD ⊥平面ABCD ，AB//DC ，ΔPAD是等边三角形，已知BD=2AD=8，（1）设M 是PC 上的一点，证明：平面MBD ⊥平面PAD ；（2）求四棱锥P-ABCD 的体积.【证明】（1）在ΔABD 中，因为AD=4，BD=8，所以222AD BD AB +=，所以AD BD ⊥.又因为面PAD ⊥面ABCD ，面PAD ∩面ABCD=AD ，BD ⊂面ABCD所以BD ⊥面PAD.又BD ⊂面BDM ，所以面MBD ⊥面PAD.（2）过P 作PO ⊥AD ，∵面PAD ⊥面ABCD ，∴PO ⊥面ABCD ，即PO 为四棱锥P-ABCD 的高.又ΔPAD 是边长为4的等边三角形，∴PO=在底面四边形ABCD 中，AB//DC ，AB=2DC ，∴四边形ABCD 为梯形.在Rt ADB ∆中，斜边AB5=，此即为梯形的高.∴S 四边形ABCD =2425=，∴1243P ABCD V -=⨯⨯=类型四：折叠问题例7．在平面四边形ABCD 中，已知AB ＝BC ＝CD ，∠ABC ＝90°，∠BCD ＝135°，沿AC 将四边形折成直二面角B -C -D ．求证：平面ABC ⊥平面BCD ．证明：如下图，其中图(1)是平面四边形，图(2)是折后的立体图形．∵ 平面ABC ⊥平面ACD ，交线为AC ，又AB ＝BC ，∠ABC ＝90°，∠BCD ＝135°(在图(1)中)，∴ ∠ACD ＝90°，CD ⊥AC ．PP ∴ C D A B C C D B C D⊥⎫⇒⎬⎭平面平面Þ平面ABC ⊥平面BCD ． 举一反三：【变式1】如图1，在边长为3的正三角形ABC 中，E ，F ，P 分别为AB ，AC ，BC 上的点，且满足1AE FC CP ===.将△AEF 沿EF 折起到△1A EF 的位置，使平面1A EF ⊥平面EFB ，连结1A B ，1A P .（如图2） （Ⅰ）若Q 为1A B 中点，求证：PQ ∥平面1A EF ； （Ⅱ）求证：1A E ⊥EP .图1 图2【解析】证明：（Ⅰ）取1A E 中点M ，连结,QM MF ．在△1A BE 中，,Q M 分别为11,A B A E 的中点， 所以QM ∥BE ，且12QM BE =．因为12CF CP FA PB ==， 所以PF ∥BE ,且12PF BE =， 所以QM ∥PF ，且QM PF =．所以四边形PQMF 为平行四边形．所以PQ ∥FM ． 又因为FM ⊂平面1A EF ，且PQ ⊄平面1A EF ，所以PQ ∥平面1A EF ．（Ⅱ） 取BE 中点D ，连结DF .因为1AE CF ==，1DE =，所以2AF AD ==，而60A ∠=，即△ADF 是正三角形. 又因为1AE ED ==, 所以EF AD ⊥. 所以在图2中有1A E EF ⊥. 因为平面1A EF ⊥平面EFB ，平面1A EF 平面EFB EF =， 所以1A E ⊥平面BEF . 又EP ⊂平面BEF ，所以1A E ⊥EP .。

广东高二数学必修三知识点一、立体几何在数学的学习中，立体几何是一个重要的知识点。

它包含了立体图形的性质、平面与直线与立体图形的关系等内容。

1. 立体图形的表示在立体几何中，我们需要了解不同立体图形的表示方法。

常见的立体图形有正方体、长方体、棱锥、棱台等。

这些图形都有各自的特点和性质，需要我们通过图示和文字描述来表示。

2. 立体图形的性质每个立体图形都有其独特的性质。

比如正方体具有六个相等的面和八个顶点，长方体的六个面都是矩形等。

我们需要通过观察和推理，深入了解各种立体图形的性质。

3. 平面与立体图形的关系平面和立体图形之间有着密切的联系。

在立体几何中，我们经常需要通过平面截割、投影等方法来研究立体图形的性质。

这些方法不仅帮助我们理解立体图形，还可以应用到实际问题中。

二、三角函数与解三角形1. 三角函数的定义与性质三角函数是数学中一个重要的概念。

它们包括正弦函数、余弦函数、正切函数等。

我们需要通过定义和图像来了解它们的基本性质，如周期性、奇偶性等。

2. 解三角形的方法解三角形是三角函数的重要应用之一。

在解三角形时，我们可以利用正弦定理、余弦定理等方法来求解未知角度和边长。

这些方法可以帮助我们解决各种实际问题。

三、数列与级数在高中数学中，数列与级数是必修的内容之一。

了解和掌握数列与级数的性质和求解方法对于学习数学和解决实际问题都具有重要的意义。

1. 数列的概念与性质数列是由一系列按照一定规律排列的数所组成的。

我们可以通过数列的通项公式、首项、公差等来描述它的性质。

掌握数列的性质有助于我们进行数列的运算和推理。

2. 级数的定义与性质级数是由一系列数的和组成的数列。

级数的性质与数列类似，但需要注意级数的收敛性和发散性。

我们需要通过数列的极限、部分和等来研究级数。

3. 数列与级数的求解在数学中，我们经常需要求解数列的和或级数的部分和。

通过逐项求和、通项求和、求极限等方法，我们可以计算出数列与级数的结果。

四、函数与导数函数与导数是数学中一个重要的概念和工具。

XX广东高考数学立体几何知识点立体几何是高考数学考试中重要的知识点，也是高考考试中的高频考点之一。

下面为大家的广东高考数学立体几何知识点，希望大家喜欢。

一、平面通常用一个平行四边形来表示.平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示，也可用表示平行四边形的两个相对顶点字母表示，如平面AC.在立体几何中，大写字母A，B，C，…表示点，小写字母，a,b,c,…l,m,n,…表示直线，且把直线和平面看成点的集合，因而能借用集合论中的符号表示它们之间的关系，例如：a) A∈l—点A在直线l上;Aα—点A不在平面α内;b) lα—直线l在平面α内;c) aα—直线a不在平面α内;d) l∩m=A—直线l与直线m相交于A点;e) α∩l=A—平面α与直线l交于A点;f) α∩β=l—平面α与平面β相交于直线l.二、平面的根本性质公理1如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内.公理2如果两个平面有一个公共点，那么它们有且只有一条通过这个点的公共直线.公理3经过不在同一直线上的三个点，有且只有一个平面.根据上面的公理，可得以下推论.推论1经过一条直线和这条直线外一点，有且只有一个平面.推论2经过两条相交直线，有且只有一个平面.推论3经过两条平行直线，有且只有一个平面.公理4平行于同一条直线的两条直线互相平行是不等式一般地，用纯粹的大于号“>”、小于号“<”连接的不等式称为严格不等式，用不小于号(大于或等于号)“≥”、不大于号(小于或等于号)“≤”连接的不等式称为非严格不等式，或称广义不等式。

总的来说，用不等号(<,>,≥,≤,≠)连接的式子叫做不等式。

通常不等式中的数是实数，字母也代表实数，不等式的一般形式为F(x，y，……，z)≤G(x，y，……，z )(其中不等号也可以为<，≤,≥，> 中某一个)，两边的解析式的公共定义域称为不等式的定义域，不等式既可以表达一个命题，也可以表示一个问题。

可编辑修改精选全文完整版高考数学立体几何知识点总结(1)棱柱：定义：有两个面互相平行，别的各面都是四边形，且每相邻两个四边形的大众边都互相平行，由这些面所围成的几多体。

分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。

表示：用各极点字母，如五棱柱或用对角线的端点字母，如五棱柱几多特性：两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。

(2)棱锥定义：有一个面是多边形，别的各面都是有一个大众极点的三角形，由这些面所围成的几多体分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示：用各极点字母，如五棱锥几多特性：侧面、对角面都是三角形;平行于底面的截面与底面相似，其相似比即是极点到截面隔断与高的比的平方。

(3)棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示：用各极点字母，如五棱台几多特性：①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的极点(4)圆柱：定义：以矩形的一边所在的直线为轴旋转，别的三边旋转所成的曲面所围成的几多体几多特性：①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。

(5)圆锥：定义：以直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几多体几多特性：①底面是一个圆;②母线交于圆锥的极点;③侧面展开图是一个扇形。

(6)圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分几多特性：①上下底面是两个圆;②侧面母线交于原圆锥的极点;③侧面展开图是一个弓形。

(7)球体：定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几多体几多特性：①球的截面是圆;②球面上恣意一点到球心的隔断即是半径。

专题二：立体几何题型与方法（文科）一、考点回顾1．平面（1）平面的基本性质：掌握三个公理及推论，会说明共点、共线、共面问题。

（2）证明点共线的问题，一般转化为证明这些点是某两个平面的公共点（依据：由点在线上，线在面 ，推出点在面）， 这样，可根据公理2证明这些点都在这两个平面的公共直线上。

（3）证明共点问题，一般是先证明两条直线交于一点，再证明这点在第三条直线上，而这一点是两个平面的公共点，这第三条直线是这两个平面的交线。

（4）证共面问题一般用落入法或重合法。

（5）经过不在同一条直线上的三点确定一个面. 2. 空间直线.（1）空间直线位置分三种：相交、平行、异面. 相交直线—共面有反且有一个公共点；平行直线—共面没有公共点；异面直线—不同在任一平面。

（2）异面直线判定定理：过平面外一点与平面一点的直线和平面不经过该点的直线是异面直线.（不在任何一个平面的两条直线）（3）平行公理：平行于同一条直线的两条直线互相平行.（4）等角定理：如果一个角的两边和另一个角的两边分别平行并且方向相同，那么这两个角相等推论：如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成锐角（或直角）相等.（5）两异面直线的距离：公垂线的长度.空间两条直线垂直的情况：相交（共面）垂直和异面垂直.21,l l 是异面直线，则过21,l l 外一点P ，过点P 且与21,l l 都平行平面有一个或没有，但与21,l l 距离相等的点在同一平面. （l 1或l 2在这个做出的平面不能叫l 1与l 2平行的平面）3. 直线与平面平行、直线与平面垂直.（1）空间直线与平面位置分三种：相交、平行、在平面.（2）直线与平面平行判定定理：如果平面外一条直线和这个平面一条直线平行，那么这条直线和这个平面平行.（“线线平行，线面平行”）（3）直线和平面平行性质定理：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行.（“线面平行，线线平行”）（4）直线与平面垂直是指直线与平面任何一条直线垂直，过一点有且只有一条直线和一个平面垂直，过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α，a ⊥AO ，得a ⊥PO （三垂线定理）， 得不出α⊥PO . 因为a ⊥PO ，但PO 不垂直OA . ● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一：如果一条直线和一个平面的两条相交直线都垂直，那么这两条直线垂直于这个平面.（“线线垂直，线面垂直”）直线与平面垂直的判定定理二：如果平行线中一条直线垂直于一个平面，那么另一条也垂直于这个平面.推论：如果两条直线同垂直于一个平面，那么这两条直线平行.（5）a.垂线段和斜线段长定理：从平面外一点．．向这个平面所引的垂线段和斜线段中，①射影相等的两条斜线段相等，射影较长的斜线段较长；②相等的斜线段的射影相等，较长的斜线段射影较长；③垂线段比任何一条斜线段短.[注]：垂线在平面的射影为一个点. [一条直线在平面的射影是一条直线.（×）] b.射影定理推论：如果一个角所在平面外一点到角的两边的距离相等，那么这点在平面的射影在这个角的平分线上。

专题复习 立体几何总复习【知识要点】1. 空间几何体三视图与直观图① 由空间几何体画三视图 ② 由三视图还原实物图 ③ 斜二测画法及面积计算 2. 空间几何体的表面积与体积① 锥、柱、台、球体表面积、体积计算 ② 割补法、等体积法计算几何体的体积 ③ 画空间几何体的展开图及面积计算 3. 点、线、面之间的位置关系① 四个公理公理1： 如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

符号表示：ααα⊂⇒∈∈∈∈l B A l B l A ,,,。

公理2： 过不在一条直线上的三点，有且只有一个平面。

公理3： 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

符号表示：l P l P P ∈=⋂⇒∈∈,,βαβα。

公理4： 平行于同一条直线的两条直线互相平行。

符号表示：313221////,//l l l l l l ⇒ ② 直线之间的位置关系：（1）平行：在同一平面内，且没有交点。

（2）相交：在同一平面内，有且只有一个交点。

（3）异面：不同在任何一个平面内，没有公共点定理： 空间中如果有两个角的两条边分别对应平行，那么这两个角相等或互补。

③ 直线与平面之间的位置关系（1）直线在平面内----有无数个公共点（2）直线与平面相交--有且只有一个公共点 （3）直线与平面平行----没有公共点注：直线与平面相交或平行的情况统称为直线在平面外 ④ 平面与平面之间的位置关系（1）两个平面平行---没有公共点（2）两个平面相交---有一条公共直线 4. 直线、平面平行的判定与性质① 直线与平面平行（1)判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

符号表示：ααα////,,a b a b a ⇒⊂⊄.（2）性质定理：一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行 符号表示：l a l a a //,,//⇒=⋂⊂βαβα.② 平面与平面平行（1）判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

〔内部资料，请勿外传〕2010年广东高考热点题型聚焦（三）《立体几何》市教研室广东课标高考三年来风格特点“坚持对立体几何内容的考查重在空间想象能力，理科试题兼顾几何和向量方法”，“理科试题兼顾几何和向量方法”这句话实质上是淡化向量方法在立几中的工具作用，突出了第一句话中重在空间想象能力的考查.文理科要求差别较大.仅从对立体几何内容的考查重在空间想象能力，不追求图形的新颖、不迎合命题时尚考虑，可通过图形丰富的线段达到考查空间想象能力的要求. 文科参考题目：三棱柱ABC C B A -111中，侧棱1AA ⊥底面ABC .CB AC ⊥，D 为AB 中点，1=CB ，3=AC，1A A =（I ）求证：//1BC 平面CD A 1； （II ）求三棱锥11C A DC -的体积.（Ⅰ）证明：连接1AC ，设E C A AC =11 ，连接DE∵ABC C B A -111是三棱柱，侧棱1AA ⊥底面ABC .且31==AA AC ∴C C AA 11是正方形，E 是1AC 中点， 又D 为AB 中点 ∴ED ∥1BC 又⊂ED 平面CD A 1，⊄1BC 平面CD A 1∴//1BC 平面CD A 1（II ）在平面ABC 中过点D 作AC 的垂线，交AC 于H .由于底面ABC ⊥面11ACC A ，且AC 为两平面交线，∴DH ⊥面11ACC A .△ABC中，2AB ==，所以30BAC ∠=o，且1AD =.在△ADC 中，1sin 302HD AD ==o由于132AC C S =V ，所以111113133224D AC C AC C V DH S -=⋅⋅=⋅⋅=V ∴由等积法可得11114C A DCD AC C V V --==.本题几何构图常规，但线段丰富，能较好地考查考生的空间想象能力.在设问中，既考查线面平行，同时在体积的求解过程中涉及面面垂直、线面垂直等定理以及体积求解中的勾股定理1C1B1AABC1C1B1AABDCHE和等积法等知识.理科参考题目：已知正六棱柱111111ABCDEF A B C D E F-的所有棱长均为2，G为AF的中点.(Ⅰ)求证：1FG∥平面11BB E E；(Ⅱ)求证：平面1F AE⊥平面11DEE D；(Ⅲ)求异面直线EG与1F A所成角的余弦值.证明：(Ⅰ)因为AF∥BE，AF⊄平面11BB E E，所以AF∥平面11BB E E，同理可证，1AA∥平面11BB E E，所以，平面11AA F F∥平面11BB E E又1F G⊂平面11AA F F，所以1FG∥平面11BB E E(Ⅱ)因为底面ABCDEF是正六边形，所以AE⊥ED，又1E E⊥底面ABCDEF，所以1E E⊥AE，因为1E E ED E=，所以AE⊥平面11DD E E，又AE⊂平面1F AE，所以平面1F AE⊥平面11DEE D(Ⅲ)由于底面ABCDEF是正六边形，所以EF⊥BF.如图，建立如图所示的空间直角坐标系.则11(0,2,0),,0),(0,0,2),1,0)2E GF A--.则5,0)2EG=-uu u r，11,2)F A=--uuu r，从而两异面直线EG与1F A所成角的余弦值为11cos7EG F AEG F Aθ===uu u r uuu rguu u r uuu r.本题几何构图常规，但线段丰富，能较好地考查考生的空间想象能力.在设问中，既考查空间中的平行关系（线面、面面），同时考查空间中的垂直关系（线面、面面）.对于空间角的考查几何与向量方法均可使用，有助于全面而深刻地训练空间中元素的关系.从延续风格，迎合命题时尚考虑文科继续关注通过三视图体现对考生空间想象能力的考查的题型.xyzPABCDED ABC俯视图理科关注通过平面图形的翻折考查考生空间想象能力的题型.文科参考题目：1．已知一几何体的三视图如图（甲）示，（三视图中已经给出各投影面顶点的标记）（1）在已给出的一个面上（图乙），画出该几何体的直观图；（2）设点F 、H 、G 分别为AC , AD ,DE 的中点， 求证：FG//平面ABE ；（3）求该几何体的全面积． 解：（1）该几何体的直观图如图示：------------------------4分 （2）证明：由图（甲）知四边形CBED 为正方形∵F 、H 、G 分别为AC,AD ,DE 的中点∴FH//CD, HG//AE----------------------------------------5分 ∵CD//BE ∴FH//BE∵BE ⊂面ABE ，FH ⊄面ABE∴//FH 面ABE ----------------------------7分 同理可得//HG 面ABE 又∵FH HG H = ∴平面FHG//平面ABE---------------------------8分 又∵FG ⊂面FHG∴FG//平面ABE-------------------------------------9分 （3）由图甲知AC ⊥CD ，AC ⊥BC, BC ⊥CD∴CD ⊥平面ACB, ∴CD ⊥AB同理可得ED ⊥AD---------------------------------------10分∵2ACB ACD S S ∆∆==，122ABE ADE S S ∆∆==⨯⨯=，4CBEDS =------12分∴该几何体的全面积:ACB ACD ABE ADE CBEDS S S S S S∆∆∆∆=++++＝2＋2＋＝4(2.------14分 2．右图为一简单组合体，其底面ABCD 为 正方形，PD ⊥平面ABCD ，//EC PD ，且 2PD AD EC ===2 .（1）答题卡指定的方框内已给出了该几何 体的俯视图，请在方框内画出该几何体的正(主) 视图和侧(左)视图；（2）求四棱锥B －CEPD 的体积； （3）求证：//BE 平面PDA ．（图乙）DEBC(俯视图BHF DGEB CADEBCA正视图侧视图俯视图解：（1）该组合体的主视图和侧视图如右图示：-----3分 (2)∵PD ⊥平面ABCD ，PD ⊂平面PDCE ∴平面PDCE ⊥平面ABCD∵BC CD ⊥ ∴BC ⊥平面PDCE ----------5分 ∵11()32322S PD EC DC =+⋅=⨯⨯=梯形PDCE --6分 ∴四棱锥B －CEPD 的体积1132233B CEPD PDCE V S BC -=⋅=⨯⨯=梯形.----8分(3) 证明：∵//EC PD ，PD ⊂平面PDA ， EC ⊄平面PDA∴EC//平面PDA ,------------------------------------10分 同理可得BC//平面PDA ----------------------------11分∵EC ⊂平面EBC,BC ⊂平面EBC 且EC BC C =∴平面BEC //平面PDA -----------------------------13分又∵BE ⊂平面EBC ∴BE//平面PDA------------------------------------------14分 理科参考题目： 1．如图（甲），在直角梯形ABED 中，AB//DE ，AB ⊥BE ，AB ⊥CD,且BC=CD,AB=2,F 、H 、G 分别为AC ,AD ,DE 的中点，现将△ACD 沿CD 折起，使平面ACD ⊥平面CBED,如图（乙）． （1）求证：平面FHG//平面ABE ； （2）记,BC x =()V x 表示三棱锥B －ACE 的体积，求()V x 的最大值；（3）当()V x 取得最大值时，求二面角D －AB －C 的余弦值．解：（1）证明：由图（甲）结合已知条件知四边形CBED 如图（乙）∵F 、H 、G 分别为AC , AD,DE 的中点 ∴FH//CD, HG//AE-----------------------------------------------------------1分 ∵CD//BE ∴FH//BE∵BE ⊂面ABE ，FH ⊄面ABE∴//FH 面ABE -------------------------------------3分 同理可得//HG 面ABE又∵FH HG H = ∴平面FHG//平面ABE-----------------4分 （2）∵平面ACD ⊥平面CBED 且AC ⊥CD∴AC ⊥平面CBED----------------------------------------------------5分∴()V x ＝A BCE V -＝13BCE S AC ∆⋅ ∵BC x = ∴2AC x =-（02x <<）∴()V x ＝22111(2)(2)326x x x x ⨯-=-＝1(42)12x x x ⋅⋅---------------7分 解法1：∵34264(42)()327x x x x x x ++-⋅⋅-≤=(甲)HFD GEBCA(乙)∴()V x16416122781≤⨯=,当且仅当42x x=-即43x=时取“＝”∴()V x的最大值为1681-------------------------------------------9分[解法2：∵21'()(43)6V x x x=-，令'()0V x=得0x=（不合舍去）或43x=当43x>时'()0V x<，当43x<<时'()0V x>∴当43x=时()V x有最大值，max4()()3V x V==1681]（3）解法1：以点C为坐标原点，CB为x轴建立空间直角坐标系如右图示：由（2）知当()V x取得最大值时43x=，即BC=43这时AC=23,∴B4(,0,0)3,4(0,,0)3D,2(0,0,)3A-----10分∴平面ACB的法向量4(0,,0)3CD =设平面ABD的法向量为(,,)m a b c=∵42(,0,)33AB=-,44(,,0)33BD=--------------11分由m AB⊥,m BD⊥得4433a b-+=，4233a c-=令1c=得11(,,1)22m =----------------------------------------12分设二面角D－AB－C为θ，则2cos||||4m CDm CDθ⋅===⋅---------14分[解法2：由（2）知当()V x取得最大值时43x=，即BC=43这时AC=23，从而AB==过点C作CM⊥AB于M，连结MD∵,CD AC CD BC⊥⊥AC BC C=∴CD⊥面ABC∵CM⊂面ABC∴CM CD⊥∴AB⊥面MCD∵MD⊂面MCD∴AB MD⊥∴CMD∠是二面角D－AB－C的平面角yMACB EGHFEDC BA侧视图俯视图ABCDEF由AB CM AC BC⋅=⋅得AC BCCMAB⋅=24⨯=∴MD==在Rt△MCD中cosMCCMDMD∠===][解法3：设二面角D－AB－C为θ,∵,CD AC CD BC⊥⊥且AC BC C=∴CD⊥面ABC∴△ABC为△ABD在面ABC上的投影∵ACB∆≌ACD∆∴AB AD=,又∵O为BD的中点∴AO BD⊥∵AO∴12ABDS BD AO∆=⋅＝12339⨯=∵12ABCS AC BC∆=⋅=49, ∴cos ABCDABSSθ∆∆=4=2．已知几何体A—BCED的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．（1）求此几何体的体积V的大小;（2）求异面直线DE与AB所成角的余弦值；（3）试探究在DE上是否存在点Q，使得AQ⊥BQ并说明理由.解：（1）由该几何体的三视图知AC⊥面BCED,且EC=BC=AC=4 ，BD=1，∴1(41)4102BCEDS=⨯+⨯=梯形∴1140104333BCEDV S AC=⋅⋅=⨯⨯=梯形．即该几何体的体积V为16．----------------------------------3分ACB EGDFHoxOQABCD E（2）解法1:过点B 作BF//ED 交EC 于F ，连结AF ，则∠FBA 或其补角即为异面直线DE 与AB 所成的角．-------5分在△BAF 中，∵AB=BF=AF=5==．∴222cos 2BF AB AF ABF BF AB +-∠==⋅ 即异面直线DE 与AB--------------------------------------------7分 解法2：以C 为原点，以CA ，CB ，CE 所在直线为x,y,z 则A （4，0，0），B （0，4，0），D （0，4，1），E （0，0，4）∴(0,4,3),(4,4,0)DE AB =-=-，∴cos ,DE AB <>= ∴异面直线DE 与AB所成的角的余弦值为5． （3）解法1:在DE 上存在点Q ，使得AQ ⊥BQ.-----------------------------------------------------8分取BC 中点O ，过点O 作OQ ⊥DE 于点Q ，则点Q 满足题设.------------------------------10分 连结EO 、OD ，在Rt △ECO 和Rt △OBD 中 ∵2EC OBCO OD== ∴Rt ECO ∆∽Rt OBD ∆ ∴EOC OBD ∠= ∵90EOC CEO ∠+∠= ∴90EOC DOB ∠+∠= ∴90EOB ∠=．-----------------11分∵OE ==OD ==∴2OE OD OQ ED ⋅=== ∴以O 为圆心、以BC 为直径的圆与DE 相切．切点为Q ∴BQ CQ ⊥∵AC ⊥面BCED ,BQ ⊂面CEDB ∴BQ AC ⊥ ∴BQ ⊥面ACQ ---------13分 ∵AQ ⊂面ACQ∴BQ AQ ⊥．------------------------------------------------------------------------------------------14分 解法2: 以C 为原点，以CA ，CB ，CE 所在直线为x,y,z 轴建立空间直角坐标系．D C 1B 1A 1CBA OB 2DC 1B 1A 1CBA设满足题设的点Q 存在,其坐标为（0，m ，n ），则(4,,),(0,4,)AQ m n BQ m n =-=-(0,,4)EQ m n =-，(0,4,1)QD m n =--∵AQ ⊥BQ ∴2(4)0m m n -+= ----------------------------① ∵点Q 在ED 上，∴存在R λ∈(0)λ>使得EQ QD λ= ∴(0,,4)(0,4,1)m n m n λ-=--44,11m n λλλλ+⇒==++-----------② ②代入①得222416()81601(1)λλλλλλ+=⇒-+=++，解得4λ= ∴满足题设的点Q 存在，其坐标为168(0,,)55． 3．如图，已知三棱柱ABC －A 1B 1C 1的所有棱长都相等，且侧棱垂直于底面，由 B 沿棱柱侧面经过棱C C 1到点A 1的最短路线长为设这条最短路线与CC 1的交 点为D ．（1）求三棱柱ABC －A 1B 1C 1的体积；（2）在平面A 1BD 内是否存在过点D 的直线与平面ABC 平行？证明你的判断； （3）证明：平面A 1BD ⊥平面A 1ABB 1．解：(1)如图，将侧面BB 1C 1C 绕棱CC 1旋转120°使其与侧面AA 1C 1C 在同一平面上，点B 运动到点B 2的位置，连接A 1B 2，则A 1B 2就是由点B 沿棱柱侧面经过棱CC 1到点A 1的最短路线。

第六章：立体几何考点基本功训练考点一：认识直棱柱，正棱柱；棱锥，正四面体；圆柱，圆锥；球体★已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是24π ★正方体的内切球与其外接球的体积之比为（ C ）(A)1∶3 (B)1∶3 (C)1∶33 (D)1∶9★★★（2010辽宁文数）已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，BC =O 的表面积等于（A ）4π （B ）3π （C ）2π （D ）π解析：选A.由已知，球O 的直径为22R SC ==，∴表面积为244.R ππ=考点二：斜二侧画法的原理，上述几何体的三视图★有一个几何体的三视图及其尺寸如下（单位cm ），则该几何体的表面积为224cm π★★已知几何体的三视图（如右图），则该几何体的体积为 （ C ）A ．34B ．4C ．324 D ．334★★如图是一个正三棱柱的三视图，若三棱柱的 体积是38，则=a 32★已知三棱锥的俯视图与侧视图如右，俯视图是边长为2的正三角形，侧视图是有一直角边为2的直角三角形，则该三棱锥的正视图可能为( C )考点三：熟记常用的侧面积和体积公式侧面积： 圆柱：cl S =侧l r ⋅=π2 圆锥：cl S 21=侧l r ⋅=π 棱柱：ch S =直棱柱侧面积 棱锥：'21ch S =正棱锥侧面积球： 24R S π=球体积： 柱体：Sh V= 锥体：Sh V 31=球：334R V π= 考点四：懂得运用几何体中的重要三角形和矩形运算POA RT POB RT ∆∆和 ACO RT ∆★★正四棱锥底面边长为4，侧棱长为3，则其体积为316.★★ 已知OA 为球O 的半径，过OA 的中点M 且垂直于OA 的平面截球面得到圆M ，若圆M 的面积为3π，则球O 的表面积等于π16.★★ 用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为328π考点五：在计算过程中常用到的性质和技巧 (1) 面积比是相似比的平方，体积比是相似比的立方★在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间内，若两个正四面体的棱长的比为1：2，则它们的体积比为 1：8 . (2) 圆锥底面周长和侧面展开图的扇形弧长的关系★★若圆锥的母线长为2cm ，底面圆的周长为π2cm ，则圆锥的体积为π333cm .O P B AAOC图12图(3) 三角形中常用等面积变换求高，三棱锥中常用到等体积变换求高★★★图1，一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块，容器内盛有a 升水时，水面恰好经过正四棱锥的顶点P 。