2017-2018学年广东省湛江九年级下月考数学试卷(3月份)含解析
- 格式:pdf
- 大小:362.25 KB
- 文档页数:8
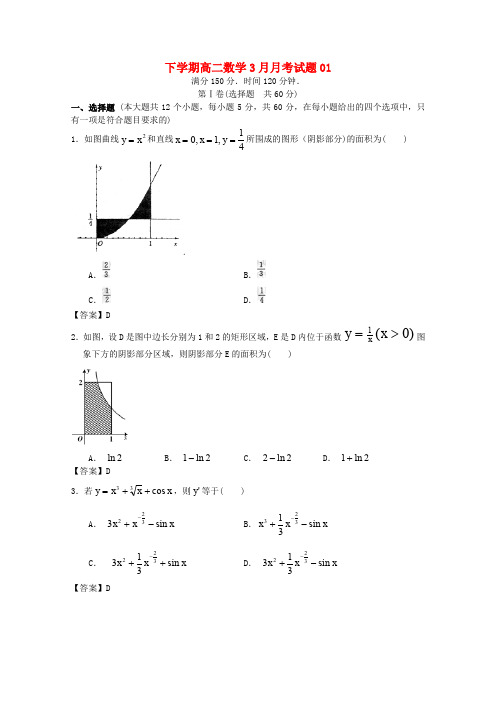
下学期高二数学3月月考试题01满分150分.时间120分钟. 第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图曲线2x y =和直线)的面积为( )A .B .C .D .【答案】D2.如图,设D 是图中边长分别为1和2的矩形区域,E 是D 象下方的阴影部分区域,则阴影部分E 的面积为( )A . 2lnB . 2ln 1-C . 2ln 2-D . 2ln 1+【答案】D3,则'y 等于( )A .BC .D .【答案】D4.一物体在力,2,4320,0)(⎩⎨⎧>+≤≤=x x x x F (单位:N)的作用下沿与力F 相同的方向,从x =0处运动到x =4(单位:m)处,则力F(x)作的功为( ) A .44 B .46 C .48 D .50【答案】B5.若0sin a xdx π=⎰,则二项式x 项的系数是( ) A .210 B .210-C .240D .240-【答案】C6( )A .223y e x e =-BC .2227y e x e =-D .222y e x e =- 【答案】B7.若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则的值为( ) A . '0()f xB . '02()f xC . '02()f x -D . 0【答案】B8.已知()ln f x x =,则()f e '的值为( )A .1B .-1C .eD 【答案】D9( )A . 1B . 2C .D . 3【答案】A10.某物体的运动方程为t t s +=23 ,那么,此物体在1=t 时的瞬时速度为( ) A . 4 ; B . 5 ;C . 6 ;D . 7【答案】D11图象上任意点处切线的斜率为k ,则k 的最小值是( )A . 1-B . 0C . 1D 【答案】A12( )A B C .0D 【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.定积分12n x e dx ⎰的值为 .【答案】114.已知函数()f x 在R 上满足22()(1)321f x f x x x +-=-+,则曲线()y f x =在点(1,(1))f 处的切线方程是 . 【答案】210x y --=15.一物体沿直线以()23(v t t t =-的单位:秒,v 的单位:米/秒)的速度做变速直线运动,则该物体从时刻t=0到5秒运动的路程s 为 米。

广东省湛江市数学中考模拟试卷(3月)姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)(2017·莒县模拟) 的倒数是()A . ﹣3B .C . 3D .2. (2分)(2016·福田模拟) 下列计算正确的是()A . (a2)3=a5B . a2•a=a3C . a6÷a3=a2D . (ab)2=ab23. (2分)(2017·深圳模拟) 据统计2017年5月深圳文博会期间,总参观人数达到了6 660 000人次,将6 660 000用科学记数法表示应为A . 666×104B . 6.66×105C . 6.66×106D . 6.66×1074. (2分) (2018九下·市中区模拟) 如果一组数据2,4,x,3,5的众数是4,那么该组数据的平均数是().A . 5.2B . 4.6C . 4D . 3.65. (2分)(2018·南充) 直线y=2x向下平移2个单位长度得到的直线是()A . y=2(x+2)B . y=2(x﹣2)C . y=2x﹣2D . y=2x+26. (2分)(2016高二下·连云港期中) 下列推理正确的是()A . 因为a∥d,b∥c,所以c∥dB . 因为a∥c,b∥d,所以c∥dC . 因为a∥b,a∥c,所以b∥cD . 因为a∥b,d∥c,所以a∥c7. (2分) (2017八下·抚宁期末) 已知一次函数y=(m -1)x + m的图象分别交x轴负半轴、y轴负半轴于点A、B,则m的取值范围是()A . m>1B . m<1C . m < 0D . m > 08. (2分)已知下列函数:①y=2﹣3x;②y=﹣(x>0);③y=x﹣2;④y=2x2﹣1(x>1),其中y随x的增大而增大的函数有()A . 1个B . 2个C . 3个D . 4个9. (2分) (2019九上·龙湾期中) 如图,抛物线的对称轴是直线,则下列结论正确的是A .B .C .D .10. (2分)如图,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1 = 0.5m,最下面一级踏板的长度A7B7 = 0.8m.则第五级踏板A5B5的长度为()A . 0.6mB . 0.65mC . 0.7mD . 0.75m二、填空题 (共8题;共8分)11. (1分)-8的立方根与4的算术平方根的和是________12. (1分)将(3﹣m)÷(m+2)写成分式为________,当m=2时,该分式的值为________;当m=________时,该分式的值为0.13. (1分)(2017·磴口模拟) 分解因式:﹣2x2+2=________.14. (1分)(2017·重庆模拟) 已知α,β为方程x2+4x+2=0的二实根,则α3+14β+50=________.15. (1分)已知a,b,c是△ABC的三边长,若方程(a-c)x2+2bx+a+c=0有两个相等的实数根,则△ABC 是 ________ 三角形.16. (1分)(2017·绥化) 在等腰△ABC中,AD⊥BC交直线BC于点D,若AD= BC,则△ABC的顶角的度数为________.17. (1分) (2011八下·新昌竞赛) 如图,在Rt△ABC中,∠ACB=90°,,CM是斜边AB的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A=________.18. (1分) (2017九上·泰州开学考) 如图,正方形ABCD的对角线交于点O,以AD为边向外作R t△ADE,∠AED=90°,连接OE,DE=6,OE=8 ,则另一直角边AE的长为________.三、解答题 (共7题;共62分)19. (10分)(2018·金华模拟) 计算:2-1-+4cos30°+(-1)201820. (5分)已知|x﹣2|+(y+1)2=0.(1)求x、y的值;(2)求﹣x3+y4的值.21. (5分)(2017·广陵模拟) 如图,甲、乙用4张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上,每人抽一张,甲先抽,乙后抽,抽出的牌不放回.甲、乙约定:只有甲抽到的牌面数字比乙大时甲胜;否则乙胜.请你用树状图或列表法说明甲、乙获胜的机会是否相同.22. (10分) (2018九上·孝感月考) 如图,是将抛物线平移后得到的抛物线,其对称轴为,与x轴的一个交点为A ,另一交点为B,与y轴交点为C.(1)求抛物线的函数表达式;(2)若点为抛物线上一点,且BC⊥NC,求点N的坐标;(3)点P是抛物线上一点,点Q是一次函数的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.23. (2分) (2018七上·银海期末) A、B两地相距216千米,甲、乙分别在A、B两地,若甲骑车的速度为15千米/时,乙骑车的速度为12千米/时。

南城实验中学初三年级第三次月考数学试题说明:1.本卷共有六个大题,24个小题,全卷满分120分;2.本卷分为试题卷和答题卷,答案要求写在答题卷上,否则不得分.一、选择题(本大题共6个小题,每小题3分,共18分,每小题只有一个正确选项)1.﹣2的相反数是( )A .2B .﹣2C .D .﹣2.下列运算正确的是( )A.3=B .632a a a ÷=C .235a a a +=D .()23639a a =3.如图放置的几何体的左视图是( )A .B .C .D .4.给出一种运算:对于函数n y x =,规定y ′1n nx -=.例如:若函数4y x =,则有y ′34x =.已知函数3y x =,则方程y ′12=的解是( )A .124,4x x ==-B .122,2x x ==-C .120x x == D.12x x ==-5.如图,在Rt △AOB 中,两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,将△AOB 绕点B 逆时针旋转90°后得到△A′O′B .若反比例函数的图象恰好经过斜边A′B的中点C ,S △ABO =4,tan ∠BAO=2,则k 的值为( )A .3B .4C .6D .86.如图,抛物线y=ax 2+bx+c (a ≠0)的对称轴为x=﹣1,与x 轴的一个交点在(﹣3,0)(第3题图)(第6题图)(第5题图)和(﹣2,0)之间,其部分图象如图所示,则下列结论:(1)b 2﹣4ac >0; (2)2a=b ;(3)点(﹣,y 1)、(﹣,y 2)、(,y 3)是该抛物线上的点,则y 1<y 2<y 3;(4)3b+2c <0; (5)t (at+b )≤a ﹣b (t 为任意实数).其中正确结论的个数是( )A .2B .3C .4D .5二、填空题(本大题共6个小题,每小题3分,共18分)7.分解因式:316a a -= .8.设m 、n 是一元二次方程2270x x +-=的两个根,则22m n += .9.如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠1=2∠2,则∠1= °.10.如图1,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A ,B ,AB=40cm ,脸盆的最低点C 到AB 的距离为10cm ,则该脸盆的半径为 cm .11.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O 1、O 2、O 3,…组成一条平滑的虚线,点P 从原点O 出发,沿这条曲线向右运动,速度为每秒个单位长度,则第2017秒时,点P 的坐标是 .(第9题图)(第10题图)(第11题图) (第12题图)12、如图,矩形ABCD 中,AB =6,BC =8,点E 是BC 边上一点,连接AE ,把∠B 沿AE 折叠,使点B 落在点B ′处,当△CEB ′为直角三角形时,BE 的长为 .三、(本大题共5个小题,每小题6分,共30分)13.(1)()202017112cos602-⎛⎫-+∙︒--+ ⎪⎝⎭(2)解方程:233011x x x +-=--14.如图,E 是平行四边形ABCD 的边CD 的中点,延长AE 交BC 的延长线于点F .(1)求证:△ADE ≌△FCE .(2)若∠BAF=90°,BC=5,EF=3,求CD 的长.15.关于x 的两个不等式①312x a +<与②130x -> (1)若两个不等式的解集相同,求a 的值;(2)若不等式①的解都是②的解,求a 的取值范围.16.“校园安全”受到全社会的广泛关注,抚州市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:(1)接受问卷调查的学生共有 人,扇形统计图中“基本了解”部分所对应扇形的圆心角为 ;(2)请补全条形统计图;(3)若该中学共有学生1500人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数.17.如图,线段AB 是⊙O 的直径, AD ⊥CD 于点D ,BC ⊥CD 于点C ,BC 交⊙O 于点M,请仅用无刻度的直尺按下列要求作图.(1)在图1中,当线段CD 与⊙O 相切时,请在CD 上确定一点E ,连接BE ,使BE 平分∠ABC ;(2)在图2中,当线段CD 与⊙O 相离时,请过点O 作OF ⊥CD ,垂足为F .四、(本大题共3个小题,每小题8分,共24分)18.如图,P 1、P 2是反比例函数y=(k >0)在第一象限图象上的两点,点A 1的坐标为(6,0).若△P 1OA 1与△P 2A 1A 2均为等腰直角三角形,其中点P 1、P 2为直角顶点.(1)求反比例函数的解析式.(2)①求P 2的坐标.②根据图象直接写出在第一象限内当x 满足什么条件时,经过点P 1、P 2的一次函数的函数值大于反比例函数y=的函数值.19.某课桌生产厂家研究发现,倾斜为12°—24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,M MAB可绕点A旋转,在点C处安装一根长度一定且C处固定,可旋转的支撑臂CD,AC=40cm.(1)如图2中,当CD⊥AB于D时,测得∠BAC=24°,求此时支撑臂CD的长.(2)在图3中,当CD不垂直AB时,测得∠BAC=12°,求此时AD的长(结果保留根号).【参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20】20. 田忌赛马的故事为我们熟知.小亮与小齐学习概率初步知识后设计了如下游戏:小亮手中有方块10、8、6三张扑克牌,小齐手中有方块9、7、5三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.(1)若每人随机取手中的一张牌进行比赛,求小齐本“局”获胜的概率;(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小亮的三张牌出牌顺序为先出6,再出8,最后出10时,小齐随机出牌应对,求小齐本次比赛获胜的概率.五、(本大题共2个小题,每小题9分,共18分)21. 如图1,AB为半圆O的直径,D为BA的延长线上一点,点C是半圆O上的一点,且∠ACD=∠B.(1)求证:DC是⊙O的切线;(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;①求tan∠CFE的值;②若AC=3,BC=4,求CE的长.22.如图1,在Rt△ABC中,∠B=90°,BC=2AB=4,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现①当α=0°时,=;②当α=180°时,=.(2)拓展探究试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△EDC旋转至A,D,E三点共线时,直接写出线段BD的长.六、(本大题共1个小题,共12分)23.如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.(1)求点M坐标.(2)当点E落在抛物线l1或l2上时,求m的值.(3)求△PEQ与正方形ODCB的重叠部分图形面积S与m之间的函数关系式.(4)直接写出△PEQ的一边被抛物线l1或l2平分时m的值.数学参考答案及评分标准一、选择题(每小题3分,共18分)1、A2、D3、C4、B5、C6、C二、填空题(每小题3分,共18分)7、a(a+4)(a﹣4).8、18.9、80 .10、25.11、(2017.12、6或3.三、(本大题共5个小题,每小题6分,共30分)13、(1)解:原式=﹣1+2×﹣4+1=﹣1+1﹣4+1=﹣3.(3分)(2)解:方程的两边同乘(x﹣1)(x+1),得3x+3﹣x﹣3=0,解得x=0.(2分)经检验x=0是原方程的解∴原方程的解为:x=0.(3分)14、(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠D=∠ECF,∵E是▱ABCD的边CD的中点,∴DE=CE,在△ADE和△FCE中,∠AED=∠FEC,∴△ADE≌△FCE(ASA);(3分)(2)解:∵ADE≌△FCE,∴AE=EF=3,∵AB∥CD,∴∠AED=∠BAF=90°,在▱ABCD中,AD=BC=5,∴DE===4,∴CD=2DE=8.(6分)15、解:(1)由①得:x <,由②得:x <, 由两个不等式的解集相同,得到=,解得:a=1; (3分)(2)由不等式①的解都是②的解,得到≤,解得:a ≥1. (6分)16、3、(1)60,90°; (2分)(2)60﹣15﹣30﹣10=5; (4分)补全条形统计图得:(3)根据题意得:1500×=500(人),则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为500人。

2018年广东省湛江市初中毕业水平考试数学试题参考答案及评分标准一、选择题:本大题共12小题,每小题3分,共36分.1.A 2.C 3.C 4.A 5.D 6.C 7.B8.B9.D10.A11.D12.C二、填空题:本大题共6小题,每小题4分,共24分.13.1014.2()a a b - 15.6π 16.∠DCE =∠A 或∠ECB =∠B 或∠A +∠ACE =180︒ 17.0.71 18.(6,5)三、解答题:本大题共5小题,每小题7分,共35分. 19.解:原式=112-+(4分) = 2(7分)20.解:设这个队胜了x 场,依题意得:3(145)19x x +--=(4分) 解得:5x =(6分) 答:这个队胜了5场.(7分)21.解:由题意可得:(4分)从表中可以看出,依次从甲乙两盒子中各取一张卡片,可能出现的结果有6个,它们出现的可能性相等,其中能拼成“奥运”两字的结果有1个.(5分) 所以能拼成“奥运”两字的概率为16.(7分)22.解:在Rt △ADE 中,tan ∠ADE =DEAE(2分)∵DE =10,∠ADE =40︒∴AE =DE tan ∠ADE =10tan 40︒≈100.84⨯=8.4(4分) ∴AB =AE +EB =AE +DC =8.4 1.59.9+=(6分) 答:旗杆AB 的高为9.9米. (7分) 23.解:∆ABC ≌∆DCB(2分)证明:∵在等腰梯形ABCD 中,AD ∥BC ,AB =DC ∴∠ABC =∠DCB(4分)在∆ABC 与∆DCB 中AB DCABC DCB BC CB =⎧⎪∠=∠⎨⎪=⎩∴∆ABC ≌∆DCB(7分)(注:答案不唯一)四、解答题:本大题共3小题,每小题10分,共30分. 24.解:(1)总体是某校2000名学生参加环保知识竞赛的成绩.(2分) (2)15150.256912151860==++++(5分) 答:竞赛成绩在79.5~89.5这一小组的频率为0.25. (6分) (3)9200030069121518⨯=++++(9分)答:估计全校约有300人获得奖励.(10分)25.证明:(1)∵AB 为⊙O 的直径,CD 是弦,且AB ⊥CD 于E ,∴CE =ED , CB DB = (2分) ∴∠BCD =∠BAC(3分)∵OA =OC ∴∠OAC =∠OCA ∴∠ACO =∠BCD(5分)(2)设⊙O 的半径为R cm ,则OE =OB -EB =R -8CE =21CD =21⨯24=12(6分)在Rt ∆CEO 中,由勾股定理可得OC 2=OE 2+CE 2即R 2= (R -8)2+122(8分)解得 R =13 ∴2R =2⨯13=26 答:⊙O 的直径为26cm .(10分)26. 解:(1)第20天的总用水量为1000米3(3分)(2)当x ≥20时,设y kx b =+∵函数图象经过点(20,1000),(30,4000)∴⎩⎨⎧+=+=bk bk 304000201000 (5分)59.549.5 79.5 89.5 69.5 人数99.5成绩解得⎩⎨⎧-==5000300b k∴y 与x 之间的函数关系式为:y =300x -5000(7分)(3)当y =7000时有7000=300x -5000 解得x =40答:种植时间为40天时,总用水量达到7000米3. (10分)五、解答题:本大题共2小题,其中第27题12分,28题13分,共25分. 27.解:(1)56(3分) (2)1+n n(6分)(3)1111......133557(21)(21)n n ++++⨯⨯⨯-+=)7151(21)5131(21)311(21-+-+-+ ┄ +)121121(21+--n n =)1211(21+-n =12+n n(9分)由 12+n n =3517解得17=n(11分)经检验17=n 是方程的根, ∴17=n(12分)28.解:(1)令0y =,得210x -=解得1x =± 令0x =,得1y =-∴ A (1,0)- B (1,0) C (0,1)- (2分)(2)∵OA =OB =OC =1∴∠BAC =∠ACO =∠BCO =45 ∵A P ∥CB ,∴∠P AB =45过点P 作PE ⊥x 轴于E ,则∆APE 为等腰直角三角形令OE =a ,则PE =1a + ∴P (,1)a a +∵点P 在抛物线21y x =-上 ∴211a a +=- 解得12a =,21a =-(不合题意,舍去)∴PE =3(4分)∴四边形ACBP 的面积S =12AB •OC +12AB •PE =112123422⨯⨯+⨯⨯= (6分)(3)假设存在.∵∠P AB =∠BAC =45 ∴P A ⊥AC∵MG ⊥x 轴于点G , ∴∠MGA =∠P AC =90 在Rt △AOC 中,OA =OC =1 ∴AC在Rt △P AE 中,AE =PE =3 ∴AP= (7分)设M 点的横坐标为m ,则M 2(,1)m m - ①点M 在y 轴左侧时,则1m <-.ⅰ)当∆AMG ∽∆PCA 时,有AG PA =MGCA∵AG =1m --,MG =21m -2= 解得11m =-(舍去) 223m =(舍去) ⅱ)当∆MAG ∽∆PCA 时,有AG CA =MGPA即2=解得:1m =-(舍去) 22m =-∴M (2,3)-(10分)②点M 在y 轴右侧时,则1m >ⅰ)当∆AMG ∽∆PCA 时,有AG PA =MGCA∵AG =1m +,MG =21m -∴2=解得11m =-(舍去) 243m =∴M 47(,)39ⅱ)当∆MAG ∽∆PCA 时,有AG CA =MGPA即2=解得:11m =-(舍去) 24m = ∴M (4,15)∴存在点M ,使以A 、M 、G 三点为顶点的三角形与∆PCA 相似. M 点的坐标为(2,3)-,47(,)39,(4,15)(13分)说明:以上各题如有其他解(证)法,请酌情给分.。

九年级下3月月考数学试卷有答案一、选择题(共12小题,每小题3分,共36分.) 1.2017的相反数是( ) A .-20171 B .-2017 C .20171D .2014 2. 2016年全国国民生产总值约为74 000 000 000 000元,比上年增长6.7%,将74 000 000 000 000元用科学计数法表示为( )元 A .0.74×1014B .7.4×1013C .74×1012D .7.40×10123. 下列运算正确的是( )A .532532a a a =+B .236a a a =÷C .623)(a a =- D .222)(y x y x +=+ 4. 下列所给图形中,既是中心对称图形又是轴对称图形的是( )5. 一个不透明的布袋里装有7个只有颜色不同的球,其中3个红球,4个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是( )A .B .C .D .6. 如图,a ∥b ,等边△ABC 的顶点B 在直线b 上,∠1=20°,则∠2的度数为( ) A .60° B .45° C .40° D .30°7. 某商品的标价为200元,8折销售仍赚40元,则商品进价 为( )元.A .140B .120C .160D .100 8.下列命题中错误..的是( ) A .等腰三角形的两个底角相等 B .对角线互相垂直的四边形是菱形 C .矩形的对角线相等 D .圆的切线垂直于经过切点的半径 9. 设a 是方程x 2-3x+1=0的一个实数根,则120162++a a a的值为( )A .502B .503C .504D .50510. 若直线y =kx +b 的大致图象如图所示,则不等式kx +b ≤3的解集是( ) A. x >0 B. x <2 C. x ≥0 D.x ≤211. 如图,四边形ABCD 为矩形,AB=6,BC=8,连接AC,分别以A 、C 为圆心,以大于AC 21长为半径画弧,两弧相交于点P 、Q,连接PQ 分别交AD 、BC 于点E 、F,则EF 的长为( )A . C . D . ba 第6题图A.415 B. 215C. 8D. 10 12. 如图,正方形ABCD 中,点E 、F 分别是BC 、CD 上的动点(不与点B ,C ,D 重合),且∠EAF=45°,AE 、AF 与对角线BD 分别相交于点G 、H,连接EH 、EF,则下列结论:① △ABH ∽△GAH; ② △ABG ∽△HEG; ③ AE=2AH; ④ EH ⊥AF; ⑤ EF=BE+DF 其中正确的有( )A. 2B. 3C. 4D. 5 4a= .14. 如图,正△ABC 的边长为2,以AB 为直径作⊙O,交AC 于点D, 交BC 于点E,连接DE ,则图中阴影部分的面积为 ;15. 如图,第1个图案由1颗“★”组成,第2个图案由2颗“★”组成,第3个图案由3颗“★”组成,第4个图案由5颗“★”组成,第5个图案由8颗“★”组成,……,则第6个图案由 颗“★”组成.16.如图,在直角坐标系中,矩形OABC 的顶点A 在x 轴上,顶点C 在y 轴上,B (4,3),连接OB ,将△OAB 沿直线OB 翻折,得△ODB,OD 与BC 相交于点E,若双曲线)0(>=x xky 经过点E,则k= ;17. (5分) 计算:()︒--+---60cos 22017|2|201π 18. (6分)解方程:24212xx x -=-- 19. (7分)为保证中小学生每天锻炼一小时,某校开展了形式多样的体育活动项目,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的频率统计表和频数分布直方图.请你根据图表信息完成下列各题: (1)填空: a= ;m= ;n= ;D EO CA B第14题图 第16题图(2)请将条形统计图补充完整;(3)该校共有学生1500人,估计参加乒乓球项目的学生有 人;20. (8分) 如图,将矩形ABCD 沿对角线BD 折叠,使点C 落在点E 处,BE 与AD 交于点F .⑴求证:ΔABF≌ΔEDF ;⑵将折叠的图形恢复原状,点F 与BC 边上的点G 正好重合,连接DG ,若AB=6,BC=8,.求DG 的长.21. (8分)某商场销售A ,B 元,40元. 商场销售5台A 型号和1台B 型号计算器,可获利润76元;销售6台A 型号和3台B 型号计算器,可获利润120元.(1)求商场销售A ,B 两种型号计算器的销售价格分别是多少元?(2)商场准备用不多于2500元的资金购进A ,B 两种型号计算器共70台,问最少需要购进A 型号的计算器多少台?22. (9分)如图,△AOB 中,A (-8,0),B (0,332),AC 平分∠OAB ,交y 轴于点C ,点P 是x 轴上一点,⊙P 经过点A 、C ,与x 轴于点D ,过点C 作CE ⊥AB ,垂足为E ,EC 的延长线交x 轴于点F , (1)⊙P 的半径为 ; (2)求证:EF 为⊙P 的切线;(3)若点H 是 上一动点,连接OH 、FH ,当点P 在 上运动时,试探究FHOH是否为定值?若为定值,求其值;若不是定值,请说明理由.G 第20题图23. (9分)如图(1),抛物线y=ax 2+bx+c 与x 轴交于A (x 1,0)、B (x 2,0)两点(x 1<0<x 2),与y 轴交于点C(0,-3),若抛物线的对称轴为直线x=1,且tan ∠OAC=3. (1)求抛物线的函数解析式;(2 若点D 是抛物线BC 段上的动点,且点D 到直线BC 距离为2,求点D 的坐标 (3)如图(2),若直线y=mx+n 经过点A,交y 轴于点E(0, -34),点P 是直线AE 下方抛物线上一点,过点P 作x 轴的垂线交直线AE 于点M,点N 在线段AM 延长线上,且PM=PN,是否存在点P ,使△PMN 的周长有最大值?若存在,求出点P 的坐标及△PMN 的周长的最大值;若不存在,请说明理由.初三数学月考试题(答案)一、选择题13、___a(a+2)(a-2)___14、___6π___15、___13___16、___218___计算题17解:原式=11221-+-…………4分=23-…………5分18解:2)4()2(2-=--+x x x …………3分 解得3-=x …………5分 经检验,3-=x 是原方程的解。

湛江市数学中考三模试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)天义地区某天的最高气温是8°C,最低气温是-2°C,则该地这一天的温差是().A . 10°CB . -6°CC . 6°CD . -10°C2. (2分)(2017·青海) 在下列各数中,比﹣1小的数是()A . 1B . ﹣1C . ﹣2D . 03. (2分)(2018·泸州) 下列计算,结果等于a4的是()A . a+3aB . a5-aC . (a2)2D . a8÷a24. (2分)(2019·银川模拟) 若n边形的内角和是720°,则n的值是()A . 5B . 6C . 7D . 85. (2分)(2018·福建) 如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于()A . 15°B . 30°C . 45°D . 60°6. (2分)(2017·陕西模拟) 下面四个几何体中,主视图与俯视图不同的共有()A . 1个B . 2个C . 3个D . 4个7. (2分) (2019·银川模拟) 如图,已知DE∥BC,CD和BE相交于点O,S△DOE∶S△COB=9∶16,则DE∶BC 为()A . 2∶3B . 3∶4C . 9∶16D . 1∶28. (2分)(2019·银川模拟) 王师傅驾车到某地办事,汽车出发前油箱中有50升油.王师傅的车每小时耗油12升,行驶3小时后,他在一高速公路服务站先停车加油26升,再吃饭、休息,此过程共耗时1小时,然后他继续行驶,下列图象大致反映油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系的是()A .B .C .D .二、填空题 (共8题;共8分)9. (1分) (2017七下·敦煌期中) 计算:(﹣3abc)(﹣a2c3)2(﹣5a2b)=________.10. (1分)(2019·银川模拟) 若点A(﹣2,n)在x轴上,则点B(n﹣1,n+1)关于原点对称的点的坐标为________.11. (1分)(2019·银川模拟) 在一次信息技术考试中,某兴趣小组9名同学的成绩(单位:分)分别是:7,10,9,8,10,7,9,9,8,则这组数据的中位数是________.12. (1分)(2019·银川模拟) 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=,抛物线与x轴的交点为A、B,则A、B两点的距离是________.13. (1分)(2019·银川模拟) 若关于x的一元二次方程x(x+2)=m总有两个不相等的实数根,则m的取值范围是________.14. (1分)(2018·宁夏) 不透明的布袋里有1个黄球、4个红球、5个白球,它们除颜色外其他都相同,那么从布袋中任意摸出一球恰好为红球的概率是________.15. (1分)(2019·银川模拟) 如图所示,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列各图:则第n个图形中需要用黑色瓷砖________块.(用含n的代数式表示)16. (1分)(2019·银川模拟) 矩形ABCD与CEFG如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=________.三、解答题 (共10题;共80分)17. (5分) (2019七上·黄埔期末) 计算:(1)(﹣10)+(+3)+(﹣5)﹣(﹣7);(2)(﹣2)2÷4+(﹣3);(3)(﹣2)3×(﹣)﹣|﹣2|18. (5分) (2019六下·广饶期中) 解答(1)(2)(3)(﹣2ab)(3a2﹣2ab﹣b2)(4)(2ab2)2-4ab3(ab-1)19. (10分)(2019·银川模拟) 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1 ,平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;(2)若将△A1B1C1绕某一点旋转可以得到△A2B2C2 ,请直接写出旋转中心的坐标.20. (10分)(2019·银川模拟) 某学校开展以素质提升为主题的研学活动,推出了以下四个项目供学生选择:A.模拟驾驶;B.军事竞技;C.家乡导游;D.植物识别.学校规定:每个学生都必须报名且只能选择其中一个项目.八年级(3)班班主任刘老师对全班学生选择的项目情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:(1)求八年级(3)班学生总人数,并将条形统计图补充完整;(2)刘老师发现报名参加“植物识别”的学生中恰好有两名男生,现准备从这些学生中任意挑选两名担任活动记录员,请用列表或画树状图的方法,求恰好选中1名男生和1名女生担任活动记录员的概率.21. (10分)(2019·银川模拟) 如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DE⊥BC于点F,连接EF,求证:(1)△ADE≌△CDF;(2)若∠A=60°,AD=4,求△EDF的周长.22. (10分)(2019·银川模拟) 在元旦期间,某商场计划购进甲、乙两种商品.(1)已知甲、乙两种商品的进价分别为30元,70元,该商场购进甲、乙两种商品共50件需要2300元,则该商场购进甲、乙两种商品各多少件?(2)该商场共投入9500元资金购进这两种商品若干件,这两种商品的进价和售价如表所示:售价(元/件)50100若全部销售完后可获利5000元(利润=(售价﹣进价)×销量),则该商场购进甲、乙两种商品各多少件?23. (2分)如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.24. (10分)(2019·银川模拟) 如图,直角三角形ABC,点A的坐标为(0,2),点B的坐标为(0,﹣2),BC的长为3,反比例函数y=的图象经过点C.(1)求反比例函数与直线AC的解析式;(2)点P是反比例函数图象上的点,若使△OAP的面积恰好等于△ABC的面积,求P点的坐标.25. (16分)(2019·银川模拟) 问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?问题探究:不妨假设能搭成m种不同的等腰三角形,为探究m与n之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.探究一:①用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?此时,显然能搭成一种等腰三角形.所以,当n=3时,m=1②用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形,所以,当n=4时,m=0③用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形,所以,当n=5时,m=1④用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形?若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形,所以,当n=6时,m=1综上所述,可得表①n3456m1011探究二:(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(仿照上述探究方法,写出解答过程,并把结果填在表②中)(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?(只需把结果填在表②中)n78910m你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,…(3)解决问题:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(设n分别等于4k﹣1、4k、4k+1、4k+2,其中k是整数,把结果填在表③中)n4k﹣14k4k+14k+2m(4)问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了________根木棒.(只填结果)26. (2分)(2017·黄冈) 已知:如图所示,在平面直角坐标系xoy中,四边形OABC是矩形,OA=4,OC=3,动点P从点C出发,沿射线CB方向以每秒2个单位长度的速度运动;同时,动点Q从点O出发,沿x轴正半轴方向以每秒1个单位长度的速度运动.设点P、点Q的运动时间为t(s).(1)当t=1s时,求经过点O,P,A三点的抛物线的解析式;(2)当t=2s时,求tan∠QPA的值;(3)当线段PQ与线段AB相交于点M,且BM=2AM时,求t(s)的值;(4)连接CQ,当点P,Q在运动过程中,记△CQP与矩形OABC重叠部分的面积为S,求S与t的函数关系式.参考答案一、单选题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共8题;共8分)9-1、10-1、11-1、12-1、13-1、14-1、15-1、16-1、三、解答题 (共10题;共80分)17-1、17-2、17-3、18-1、18-2、18-3、18-4、19-1、19-2、20-1、20-2、21-1、21-2、22-1、22-2、23-1、23-2、24-1、24-2、25-1、25-2、25-3、25-4、26-1、26-2、26-3、。
广东初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.的倒数是()A.B.C.D.2.下列几何体的主视图是三角形的是()A.B.C.D.3.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.方差C.平均数D.中位数4.在一个不透明的盒子中装2个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是,则黄球的个数为()A.2B.3C.4D.65.计算的结果是()A.B.C.D.6.如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为()A.10°B.15°C.20°D.25°7.一次函数()的图象大致是()A.B.C.D.8.已知关于的一元二次方程有两个相等的实数根,则的值是()A.4B.C.1D.9.如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形ABCD的周长为28,则OH的长等于()A.3.5 B.4 C.7 D.1410.小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支中性笔和2盒笔芯,用了56元;小丽买了2支中性笔和3盒笔芯,仅用了28元.设每支中性笔x元和每盒笔芯y元,根据题意所列方程组正确的是()A.B.C.D.二、填空题1.据报载,2014年我国发展固定宽带接入新用户25000000户,其中25000000用科学记数法表示为_________ .2.分解因式: _________ .3.如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为_________ .4.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 °.5.一个正多边形的内角和是其外角和的2倍,则这个正多边形的边数是_________ .三、计算题计算:四、解答题1.先化简,再求值:,其中.2.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:OE=OF.(2)当∠DOE等于度时,四边形BFDE为菱形.(直接填写答案即可)3.从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.(1)求普通列车的行驶路程;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.4.如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求二次函数的解析式;(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.5.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.6.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.(1)求线段CD的长;:(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQS=9:100?若存在,求出t的值;若不存在,则说明理由.△ABC(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.广东初三初中数学月考试卷答案及解析一、选择题1.的倒数是()A.B.C.D.【答案】B.【解析】的倒数是﹣2.故选B.【考点】倒数.2.下列几何体的主视图是三角形的是()A.B.C.D.【答案】B.【解析】四种图形的主视图依次是矩形,三角形,圆,正方形.故选B.【考点】简单几何体的三视图.3.在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.方差C.平均数D.中位数【答案】D.【解析】由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.故选D.【考点】统计量的选择.4.在一个不透明的盒子中装2个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是,则黄球的个数为()A.2B.3C.4D.6【答案】C.【解析】设黄球的个数为x个,根据题意得:=,解得:x=24,经检验:x=24是原分式方程的解;∴黄球的个数为24.故选C.【考点】概率公式.5.计算的结果是()A.B.C.D.【答案】C.【解析】=.故选C.【考点】幂的乘方与积的乘方.6.如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为()A.10°B.15°C.20°D.25°【答案】D.【解析】如图,∵∠1=65°,∴∠3=90°﹣∠1=90°﹣65°=25°,∵直尺的两边互相平行,∴∠2=∠3=25°.故选D.【考点】平行线的性质.7.一次函数()的图象大致是()A.B.C.D.【答案】A.【解析】当时,,图象经过一三四象限,A.,,故A符合题意;B.,故B不符合题意;C.,故C不符合题意;D.,,故D不符合题意;故选A.【考点】一次函数的图象.8.已知关于的一元二次方程有两个相等的实数根,则的值是()A.4B.C.1D.【答案】D.【解析】∵一元二次方程有两个相等的实数根,∴△=,即,解得,;故选D.【考点】根的判别式.9.如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形ABCD的周长为28,则OH的长等于()A.3.5 B.4 C.7 D.14【答案】A.【解析】∵菱形ABCD的周长为28,∴AB=28÷4=7,OB=OD,∵H为AD边中点,∴OH是△ABD的中位线,∴OH=AB=×7=3.5.故选A.【考点】1.菱形的性质;2.直角三角形斜边上的中线;3.三角形中位线定理.10.小锦和小丽购买了价格分别相同的中性笔和笔芯.小锦买了20支中性笔和2盒笔芯,用了56元;小丽买了2支中性笔和3盒笔芯,仅用了28元.设每支中性笔x元和每盒笔芯y元,根据题意所列方程组正确的是()A.B.C.D.【答案】B.【解析】设每支中性笔x元和每盒笔芯y元,由题意得,.故选B.【考点】由实际问题抽象出二元一次方程组.二、填空题1.据报载,2014年我国发展固定宽带接入新用户25000000户,其中25000000用科学记数法表示为_________ .【答案】.【解析】将25000000用科学记数法表示为户.故答案为:.【考点】科学记数法—表示较大的数.2.分解因式: _________ .【答案】.【解析】==.故答案为:.【考点】1.提公因式法与公式法的综合运用;2.因式分解.3.如图,等边△ABC中,点D、E分别为边AB、AC的中点,则∠DEC的度数为_________ .【答案】120°.【解析】由等边△ABC得∠C=60°,由三角形中位线的性质得DE∥BC,∴∠DEC=180°﹣∠C=180°﹣60°=120°,故答案为:120°.【考点】1.三角形中位线定理;2.平行线的性质;3.等边三角形的性质.4.如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=110°.连接AC,则∠A的度数是 °.【答案】35.【解析】连接OC,∵BD,CD分别是过⊙O上点B,C的切线,∴OC⊥CD,OB⊥BD,∴∠OCD=∠OBD=90°,∵∠BDC=110°,∴∠BOC=360°﹣∠OCD﹣∠BDC﹣∠OBD=70°,∴∠A=∠BOC=35°.故答案为:35.【考点】1.切线的性质;2.圆周角定理.5.一个正多边形的内角和是其外角和的2倍,则这个正多边形的边数是_________ .【答案】6.【解析】设这个正多边的外角为x°,由题意得:x+2x=180,解得:x=60,360°÷60°=6.故答案为:6.【考点】多边形内角与外角.三、计算题计算:【答案】1.【解析】原式==1.【考点】1.实数的运算;2.零指数幂;3.负整数指数幂;4.特殊角的三角函数值.四、解答题1.先化简,再求值:,其中.【答案】,0.【解析】解题关键是化简,再代入求值.试题解析:原式==,当时,原式=.【考点】整式的混合运算—化简求值.2.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:OE=OF.(2)当∠DOE等于度时,四边形BFDE为菱形.(直接填写答案即可)【答案】(1)证明见试题解析;(2)90.【解析】(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF,从而的得到结论;(2)首先证明四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.试题解析:(1)∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD和△FOB中,∵∠EDO=∠OBF,DO=BO,∠EOD=∠FOB,∴△DOE≌△BOF(ASA),∴OE=OF;(2)当∠DOE=90°时,四边形BFDE为菱形,理由:∵OE=OF,OB=OD,∴四边形EBFD是平行四边形,∵∠EOD=90°,∴EF⊥BD,∴四边形BFDE为菱形.【考点】1.平行四边形的性质;2.全等三角形的判定与性质;3.菱形的判定.3.从广州某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.(1)求普通列车的行驶路程;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.【答案】(1)520;(2)300.【解析】(1)根据高铁的行驶路程是400千米和普通列车的行驶路程是高铁的行驶路程的1.3倍,两数相乘即可得出答案;(2)设普通列车平均速度是x千米/时,根据高铁所需时间比乘坐普通列车所需时间缩短3小时,列出分式方程,然后求解即可;试题解析:(1)根据题意得:400×1.3=520(千米),答:普通列车的行驶路程是520千米;(2)设普通列车平均速度是x千米/时,则高铁平均速度是2.5x千米/时,根据题意得:,解得:x=120,经检验x=120是原方程的解,则高铁的平均速度是120×2.5=300(千米/时).答:高铁的平均速度是300千米/时.【考点】1.分式方程的应用;2.行程问题.4.如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.(1)求二次函数的解析式;(2)根据图象直接写出使一次函数值大于二次函数值的x的取值范围;(3)若直线与y轴的交点为E,连结AD、AE,求△ADE的面积.【答案】(1);(2)或;(3)4.【解析】(1)设二次函数的解析式为(,a、b、c常数),把点A、B、C的坐标分别代入函数解析式,列出关于系数a、b、c的方程组,通过解方程组求得它们的值即可;(2)根据图象直接写出答案;(3)先求出点D的坐标,再求出直线BD的解析式,从而求得点E的坐标,根据即可.试题解析:(1)设二次函数的解析式为(,a、b、c常数),根据题意得:,解得:,所以二次函数的解析式为;(2)如图,一次函数值大于二次函数值的x的取值范围是或.(3)∵对称轴:,∴D(﹣2,3),设直线BD:代入B(1,0)、D(﹣2,3),解得,∴直线BD:,当x=0时,y=1,∴E(0,1),∴OE=1,又∵AB=4,∴=.【考点】1.抛物线与x轴的交点;2.待定系数法求二次函数解析式;3.二次函数与不等式(组).5.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.(1)求证:AC平分∠DAB;(2)求证:PC=PF;(3)若tan∠ABC=,AB=14,求线段PC的长.【答案】(1)证明见试题解析;(2)证明见试题解析;(3)24.【解析】(1)先证OC∥AD,得到∠ACO=∠DAC.由OC=OA,得到∠ACO=∠CAO,故有∠DAC=∠CAO,即AC平分∠DAB;(2)由AD⊥PD,得到∠DAC+∠ACD=90°,又AB为⊙O的直径,得到∠ACB=90°,故∠PCB+∠ACD=90°,从而有∠DAC=∠PCB,又∠DAC=∠CAO,得到∠CAO=∠PCB,由CE平分∠ACB,得到∠ACF=∠BCF,故有∠CAO+∠ACF=∠PCB+∠BCF,从而∠PFC=∠PCF,故PC=PF;(3)易证∠△PAC∽△PCB,得到.又tan∠ABC=,得到,故.设,,则,由勾股定理有,得到,求出k的值.从而求出PC的长.试题解析:(1)∵PD切⊙O于点C,∴OC⊥PD.又AD⊥PD,∴OC∥AD.∴∠ACO=∠DAC.又OC=OA,∴∠ACO=∠CAO,∴∠DAC=∠CAO,即AC平分∠DAB.(2)∵AD⊥PD,∴∠DAC+∠ACD=90°,又AB为⊙O的直径,∴∠ACB=90°,∴∠PCB+∠ACD=90°,∴∠DAC=∠PCB,又∠DAC=∠CAO,∴∠CAO=∠PCB,∵CE平分∠ACB,∴∠ACF=∠BCF,∴∠CAO+∠ACF=∠PCB+∠BCF,∴∠PFC=∠PCF,∴PC=PF;(3)∵∠PAC=∠PCB,∠P=∠P,∴△PAC∽△PCB,∴.又tan∠ABC=,∴,∴.设,,则在Rt△POC中,,∵AB=14,∴,∵,∴,∴k=6(k=0不合题意,舍去).∴.【考点】圆的综合题.6.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.(1)求线段CD 的长;(2)设△CPQ 的面积为S ,求S 与t 之间的函数关系式,并确定在运动过程中是否存在某一时刻t ,使得S △CPQ :S △ABC =9:100?若存在,求出t 的值;若不存在,则说明理由.(3)是否存在某一时刻t ,使得△CPQ 为等腰三角形?若存在,求出所有满足条件的t 的值;若不存在,则说明理由.【答案】(1)4.8;(2),或;(3)t 为2.4或或.【解析】(1)利用勾股定理可求出AB 长,再用等积法就可求出线段CD 的长;(2)过点P 作PH ⊥AC ,垂足为H ,通过三角形相似即可用t 的代数式表示PH ,从而可以求出S 与t 之间的函数关系式;利用S △CPQ :S △ABC =9:100建立t 的方程,解方程即可解决问题;(3)可分三种情况进行讨论:由CQ=CP 可建立关于t 的方程,从而求出t ;由PQ=PC 或QC=QP 不能直接得到关于t 的方程,可借助于等腰三角形的三线合一及三角形相似,即可建立关于t 的方程,从而求出t . 试题解析:(1)如图1,∵∠ACB=90°,AC=8,BC=6,∴AB=10.∵CD ⊥AB ,∴S △ABC =BC•AC=AB•CD ,∴CD===4.8,∴线段CD 的长为4.8;(2)①过点P 作PH ⊥AC ,垂足为H ,如图2所示,由题可知DP=t ,CQ=t ,则CP=4.8﹣t ,∵∠ACB=∠CDB=90°,∴∠HCP=90°﹣∠DCB=∠B ,∵PH ⊥AC ,∴∠CHP=90°,∴∠CHP=∠ACB ,∴△CHP ∽△BCA ,∴,∴,∴PH=,∴S △CPQ =CQ•PH==;②存在某一时刻t ,使得S △CPQ :S △ABC =9:100.∵S △ABC =×6×8=24,且S △CPQ :S △ABC =9:100,∴():24=9:100,整理得:,即(5t ﹣9)(t ﹣3)=0,解得:或,∵0≤t≤4.8,∴当秒或秒时,S △CPQ :S △ABC =9:100;(3)①若CQ=CP ,如图1,则t=4.8﹣t ,解得:t=2.4; ②若PQ=PC ,如图2所示,∵PQ=PC ,PH ⊥QC ,∴QH=CH=QC=,∵△CHP ∽△BCA ,∴,∴,解得:t=;③若QC=QP ,过点Q 作QE ⊥CP ,垂足为E ,如图3所示,同理可得:t=.综上所述:当t 为2.4秒或秒或秒时,△CPQ 为等腰三角形.【考点】1.相似形综合题;2.一元二次方程的应用;3.等腰三角形的性质;4.勾股定理;5.相似三角形的判定与性质.。
广东省湛江市九年级下学期数学中考模拟试卷(3月)姓名:________ 班级:________ 成绩:________一、选择题(本题有12小题,每小题4分,共48分) (共12题;共48分)1. (4分)(2018·天桥模拟) 7的相反数是()A . 7B . -7C .D .2. (4分)(2013·钦州) 下列运算正确的是()A . 5﹣1=B . x2•x3=x6C . (a+b)2=a2+b2D .3. (4分) (2019七上·焦作期末) 经专家估算,整个南海属我国传统海疆线的油气资源约合15000亿美元,开采前景甚至要超过英国的北海油田,用科学记数法表示15000亿美元是()美元.A . 1.5×104B . 1.5×105C . 1.5×1012D . 1.5×10134. (4分)(2020·武侯模拟) 如图放置的几何体,它的俯视图是()A .B .C .D .5. (4分)(2016·文昌模拟) 不等式组的解集是()〉A . x>1B . 1<x<3C . x>﹣1D . x<36. (4分)(2019·阿城模拟) 下列图形中,既是轴对称图形,又是中心对称图形的是()A .B .C .D .7. (4分) (2020七下·江汉月考) 沿某一方向行驶的汽车经过两次拐弯后与开始行驶的方向正好相反,若汽车第一次是右拐40°,则第二次应该是()A . 左拐40°B . 左拐50°C . 左拐140°D . 右拐140°8. (4分)下列数据3,2,3,4,5,2,2的中位数是()A . 5B . 4C . 3D . 29. (4分)(2017·临沂模拟) 如图,已知圆锥侧面展开图的扇形面积为65πcm2 ,扇形的弧长为10πcm,则圆锥母线长是()A . 5cmB . 10cmC . 12cmD . 13cm10. (4分) (2019九下·建湖期中) 如图,在正方形ABCD中,G为CD的中点,连结AG并延长,交BC边的延长线于点E,对角线BD交AG于点F,已知AE=12,则线段FG的长是()A . 2B . 4C . 5D . 611. (4分)二次函数 y=x2-2x-3 的图象如图所示.当y<0时,自变量x的取值范围是()A . -1<x<3B . x<-1C . x>3D . x<-1或 x>312. (4分) (2020七下·大化期末) 如图,的度数比的度数的两倍少,设和的度数分别为,那么下面可以求出这两个角的度数的方程组是()A .B .C .D .二、填空题(本题有6小题,每小题4分,共24分) (共6题;共24分)13. (4分)(2017·云南) 使有意义的x的取值范围为________.14. (4分)(2019·浙江模拟) 分解因式4x2-(y-2)2=________.15. (4分)(2018·龙东) 掷一枚质地均匀的骰子,向上一面的点数为5的概率是________.16. (4分)(2017·湖州模拟) 一个小球由地面沿着坡度1:2的坡面向上前进了10米,此时小球距离地面的高度为________米.17. (4分)(2017·黔东南模拟) 如图,点P是⊙O外一点,过点P作⊙O的切线PA,切点为A,连接PO,延长PO交⊙O于点B,若∠P=30°,PA=3 ,则弧AB的长为________.18. (4分)如图,在平面直角坐标系中,直线y=﹣x+2与反比例函数y=的图象有唯一公点,若直线y=﹣x+b与反比例函数y=的图象没有公共点,则b的取值范围是________ .三、解答题(本题有8小题,共78分,各小题都必须写出解答过程) (共8题;共78分)19. (6分)(2017·临沂) 计算:|1﹣|+2cos45°﹣ +()﹣1 .20. (8分)(2019·抚顺模拟) 在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣5,1),B(﹣1,5),C(﹣2,2),将△ABC绕原点顺时针旋转90°得△A1B1C1 ,△A1B1C1与△A2B2C2关于x轴对称.(1)画出△A1B1C1和△A2B2C2;(2)sin∠CAB=________;(3)△ABC与△A2B2C2组成的图形是否是轴对称图形?若是轴对称图形,请直接写出对称轴所在的直线解析式.21. (9分)(2020·锦州模拟) 《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.我市某中学举办了网上诗词大赛,大赛的成绩分为四个等级:优秀、良好、及格、不及格(分别用A,B,C,D表示).为了了解该校学生对诗词的掌握程度,赛后随机抽取了部分学生的成绩进行整理,并将结果绘制了如下两幅不完整的统计图.(1)本次抽取的学生共有________人,扇形统计图中不及格学生所占的圆心角的度数为________.(2)请根据计算补全条形统计图;(3)若某校有1200名学生,请你根据调查结果估计该校学生诗词大赛成绩为“优秀”和“良好”两个等级共有多少人?22. (9.0分)(2017·深圳模拟) 如图1,边长为2的正方形ABCD中,E是BA延长线上一点,且AE=AB,点P从点D出发,以每秒1个单位长度沿D→C→B向终点B运动,直线EP交AD于点F,过点F作直线FG⊥DE于点G,交AB于点R.(1)求证:AF=AR;(2)设点P运动的时间为t,①求当t为何值时,四边形PRBC是矩形?②如图2,连接PB.请直接写出使△PRB是等腰三角形时t的值.23. (10分)厚坝镇某生态示范村种植基地计划用90亩~120亩的土地种植一批葡萄,原计划总产量要达到36万斤.(1)列出原计划种植亩数y(亩)与平均每亩产量x(万斤)之间的函数关系式,并写出自变量x的取值范围;(2)为了满足市场需求,现决定改良葡萄品种.改良后平均每亩产量是原计划的1.5倍,总产量比原计划增加了9万斤,种值亩数减少了20亩,原计划和改良后的平均每亩产量各是多少万斤?24. (10.0分)(2019·玉田模拟) 如图1,我们把一个半圆和抛物线的一部分围成的封闭图形成为“果圆”,已知A , B , C , D分别为“果圆”与坐标轴的交点,直线y= x﹣3与“果圆”中的抛物线y= x2+bx+c 交于BC两点.(1)求“果圆”中的抛物线的解析式,并直接写出“果圆”被y轴截得的线段BD的长;(2)如图2,E为直线BC下方“果圆”上一点,连接AE、AB、BE ,设AE与BC交于F ,△BEF的面积记为S△BEF ,△ABF的面积记为S△ABF ,求的最小值.(3)“果圆”上是否存在点P ,使∠APC=∠CAB ,如果存在,直接写出点P坐标,如果不存在,请说明理由.25. (12分)(2018·嘉定模拟) 已知在平面直角坐标系(如图)中,已知抛物线点经过、 .(1)求该抛物线的表达式;(2)设该抛物线的对称轴与轴的交点为,第四象限内的点在该抛物线的对称轴上,如果以点、、所组成的三角形与△ 相似,求点的坐标;(3)设点在该抛物线的对称轴上,它的纵坐标是,联结、,求 .26. (14.0分) (2020九下·常州月考) 如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.(1)分别以点(1,0),(1,1),(3,2)为圆心,1为半径作圆,得到⊙ ,⊙ 和⊙ ,其中是的角内圆的是________;(2)如果以点(,2)为圆心,以1为半径的⊙ 为的角内圆,且与一次函数图像有公共点,求的取值范围;(3)点在第一象限内,如果存在一个半径为1且过点(2,)的圆为的角内相切圆,直接写出的取值范围.参考答案一、选择题(本题有12小题,每小题4分,共48分) (共12题;共48分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题(本题有6小题,每小题4分,共24分) (共6题;共24分)13-1、14-1、15-1、16-1、17-1、18-1、三、解答题(本题有8小题,共78分,各小题都必须写出解答过程) (共8题;共78分)19-1、20-1、20-2、20-3、21-1、21-2、21-3、22-1、23-1、23-2、24-3、25-1、25-2、25-3、26-1、26-2、26-3、。
广东初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、解答题1.(10分)已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.2.如图,△ABC中,AB=AC,∠A=40°.(1)作边AB的垂直平分线MN(保留作图痕迹,不写作法);(2)在已作的图中,若MN交AC于点D,连结BD,求∠DBC的度数。
3.计算:4.某校学生会就全校1000名同学周末期间平均每天做家务活的时间,随机抽取部分同学进行调查,并绘制成条形统计图.(1)求样本容量,并估计全校同学在周末期间平均每夭做家务活的时间在40分钟以上(含40分钟)的人数;(2)校学生会拟在表现突出的A、B、C、D四名同学中,随机抽取两名同学向全校汇报.请用树状图或列表法表示出所有可能的结果,并求恰好抽到A、B两名同学的概率.二、选择题如图,已知等边三角形ABC的边长为2,E、F、G分别是边AB、BC、CA的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y与x的函数图象大致是()A. B.C. D.三、填空题1.如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC= °.2.如图,在□ABCD中,E、F分别是AB、DC边上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD ="16" cm2,S=25cm2,则图中阴影部分的面积为 cm2.△BQC3.因式分解:ab2﹣9a=____________.4.一个几何体的三视图如图所示,则该几何体的侧面展开图的面积为_________四、单选题1.下列事件是必然事件的是A.任意购买一张电影票,座位号是奇数B.打开电视,正在播出“奔跑吧,兄弟”C.13名同学中至少有两名同学出生的月份相同D.抛掷一枚硬币,反面朝上2.已知二次函数y= ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是A.抛物线开口向下B.抛物线的对称轴是y轴C.当x<2时,y随x的增大而减小D.抛物线与y轴交于负半轴3.如图,等腰直角△ABC中,∠ACB=90°,点E为△ABC内一点,且∠BEC=90°,将△BEC绕C点顺时针旋转90°,使BC与AC重合,得到△AFC,连接EF交AC于点M,已知BC=10,CF=6,则AM:MC的值为A.4:3B.3:4C.5:3D.3:54.若二次根式有意义,则a的取值范围为___________5.﹣5的相反数是()A.5B.C.﹣5D.6.下列图形中,既是轴对称图形又是中心对称图形的有()A.4个B.3个C.2个D.1个7.一组数据:3,2,1,2,2的众数,中位数,方差分别是()A.2,1,0.4B.2,2,0.4C.3,1,2D.2,1,0.28.下列运算中,正确的是()A.2a2+3a2=a4B.5a2﹣2a2=3C.a3×2a2=2a6D.3a6÷a2=3a49.将不等式组的解集在数轴上表示,下列表示中正确的是()A.B.C.D.10.给定一列按规律排列的数:则这列数的第6个数是()A.B.C.D.11.如图,小亮将一个直角三角板和一把直尺叠放在一起,如果∠α=43°,那么∠β是__度.五、判断题1.先化简,再求值()÷.其中x是﹣2、﹣1、0、2中的一个.2.如图,B为双曲线(x>0)上一点,直线AB平行于y轴交直线y=x于点A,交x轴于点D,与直线y=x交于点C,若OB2﹣AB2=4(1)求k的值;(2)点B的横坐标为4时,求△ABC的面积;(3)双曲线上是否存在点B,使△ABC∽△AOD?若存在,求出点B的坐标;若不存在,请说明理由.3.在△ABC中,∠A=90°,AB=8cm,AC=6cm,点M,点N同时从点A出发,点M沿边AB以4cm/s的速度向点B运动,点N从点A出发,沿边AC以3cm/s的速度向点C运动,(点M不与A,B重合,点N不与A,C重合),设运动时间为x s.(1)求证:△AMN∽△ABC;(2)当x为何值时,以MN为直径的⊙O与直线BC相切?(3)把△AMN沿直线MN折叠得到△MNP,若△MNP与梯形BCNM重叠部分的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?广东初三初中数学月考试卷答案及解析一、解答题1.(10分)已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.【答案】(1);(2)①OQ⊥AC,理由见试题解析;②.【解析】(1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度;(2)如图②,连接BC.由三角形中位线得到BC∥OQ.利用圆周角定理得到BC⊥AC,故OQ⊥AC;(3)利用割线定理来求PQ的长度.试题解析:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ===,即PQ=;(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ 的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC;(3)如图②,PC•PQ=PB•PA,即=2×6,解得PQ=.【考点】1.圆的综合题;2.探究型;3.综合题.2.如图,△ABC中,AB=AC,∠A=40°.(1)作边AB的垂直平分线MN(保留作图痕迹,不写作法);(2)在已作的图中,若MN交AC于点D,连结BD,求∠DBC的度数。
2016-2017学年广东省湛江二十七中九年级(下)月考数学试卷(3月份)一、选择题(本大题10小题,每小题3分,共30分)1.(3分)2的倒数是()A.B.﹣C.±D.22.(3分)在平面直角坐标系中,点M(﹣2,1)在()A.第一象限B.第二象限C.第三象限D.第四象限3.(3分)边长为3cm的菱形的周长是()A.6cm B.9cm C.12cm D.15cm4.(3分)二次函数y=2(x+2)2﹣4的最小值是()A.2B.﹣2C.4D.﹣45.(3分)一组数据7、4、5、5、4、4,这组数据的众数是()A.4B.5C.6D.76.(3分)已知△ABC∽△A′B′C′,且面积之比为1:9,则△ABC和△A′B′C′的对应边AB和A′B′的比为()A.3:1B.1:3C.1:9D.1:277.(3分)当x取何值时,根式有意义()A.x<3B.x≤3C.x>3D.x≥38.(3分)不等式5x﹣1≤2x+5的解集在数轴上表示正确的是()A.B.C.D.9.(3分)如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100°D.130°10.(3分)已知k1<0<k2,则函数y=﹣k2x﹣1和y=的图象大致是()A.B.C.D.二、填空题(本大题6小题,每小题4分,共24分)11.(4分)已知∠A=43°,则∠A的补角等于度.12.(4分)在比例尺1:3 000 000的地图上,量得甲地到乙地的距离是20cm,这两地的实际距离是km.13.(4分)若x,y为实数,且满足|x﹣2|+=0,则()2014的值是.14.(4分)已知圆锥的底面半径是3cm,母线长是5cm,则圆锥的侧面积为cm2.(结果保留π)15.(4分)如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠B′AB等于.16.(4分)用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:则第10个图案中有白色地面砖块.三、解答题(一)(本大题3小题,每小题6分,共18分)17.(6分)计算:()﹣1﹣|﹣2|+﹣(﹣1)2015.18.(6分)化简:(a2+3a)÷.19.(6分)已知等腰△ABC的顶角∠A=36°(如图).(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加墨);(2)通过计算说明△ABD和△BDC都是等腰三角形.四、解答题(二)(本大题3小题,每小题7分,共21分)20.(7分)为了推动课堂教学改革,打造“贵生课堂”,我县某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:(1)本次调查的八年级部分学生共有名;请补全条形统计图;(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?21.(7分)小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.(1)两种型号的地砖各采购了多少块?(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?22.(7分)现有形状、大小、颜色完全一样的三张卡片,上面分别标有数字“1”、“2”、“3”,第一次从这三张卡片中随机抽取一张,记下数字后放回;第二次在从这三张卡片中随机抽取一张并记下数字.请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽取的数字大于第一次抽取的数字的概率.五.解答题(本大题共3小题,每小题9分,共27分)23.(9分)如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.24.(9分)如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O 交AE于点F,连接CF,DE.(1)求证:△ABE≌DCE;(2)若点F是AE的中点,求证:DE=BC;(3)判断直线CF与⊙O的位置关系,并说明理由.25.(9分)如图,在四边形OABC中,OA∥BC,∠AOC=90°,OA=OC=4,BC=3.点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动,当其中一个动点达到终点时,另一个动点也随之停止运动,过点N作NP⊥OA于点P,连接AC交NP于点Q,连接MQ,设动点的运动时间为t秒.(1)当t为何值时,M和P两点重合?(2)求△AQM面积S的最大值,并求出此时t的值;(3)是否存在某一时刻t,使得△AQM为直角三角形?若存在,求出相应的t值;若不存在,请说明理由.2016-2017学年广东省湛江二十七中九年级(下)月考数学试卷(3月份)参考答案与试题解析一、选择题(本大题10小题,每小题3分,共30分)1.(3分)2的倒数是()A.B.﹣C.±D.2【解答】解:2的倒数是,故选:A.2.(3分)在平面直角坐标系中,点M(﹣2,1)在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:点M(﹣2,1)在第二象限.故选:B.3.(3分)边长为3cm的菱形的周长是()A.6cm B.9cm C.12cm D.15cm【解答】解:∵菱形的各边长相等,∴边长为3cm的菱形的周长是:3×4=12(cm).故选:C.4.(3分)二次函数y=2(x+2)2﹣4的最小值是()A.2B.﹣2C.4D.﹣4【解答】解:二次函数y=2(x+2)2﹣4中当x=﹣2时,取得最小值﹣4,故选:D.5.(3分)一组数据7、4、5、5、4、4,这组数据的众数是()A.4B.5C.6D.7【解答】解:因为这组数据中出现次数最多的数是4,所以4是这组数据的众数;故选:A.6.(3分)已知△ABC∽△A′B′C′,且面积之比为1:9,则△ABC和△A′B′C′的对应边AB和A′B′的比为()A.3:1B.1:3C.1:9D.1:27【解答】解:∵△ABC∽△A′B′C′,且面积之比为1:9,∴它们的相似比为1:3∴△ABC和△A′B′C′的对应边AB和A′B′的比为1:3,故选:B.7.(3分)当x取何值时,根式有意义()A.x<3B.x≤3C.x>3D.x≥3【解答】解:由题意得,3﹣x≥0,解得x≤3.故选:B.8.(3分)不等式5x﹣1≤2x+5的解集在数轴上表示正确的是()A.B.C.D.【解答】解:不等式移项合并得:3x≤6,解得:x≤2,表示在数轴上,如图所示:,故选:D.9.(3分)如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,则∠BCD的度数为()A.50°B.80°C.100°D.130°【解答】解:∵∠BOD=100°,∴∠BAD=100°÷2=50°,∴∠BCD=180°﹣∠BAD=180°﹣50°=130°故选:D.10.(3分)已知k1<0<k2,则函数y=﹣k2x﹣1和y=的图象大致是()A.B.C.D.【解答】解:∵k2>0,∴﹣k2<0,则直线y=﹣k2x﹣1过第二、三、四象限,∵k1<0,∴双曲线y=过第二、四象限,故选:C.二、填空题(本大题6小题,每小题4分,共24分)11.(4分)已知∠A=43°,则∠A的补角等于137度.【解答】解:∵∠A=43°,∴它的补角=180°﹣43°=137°.故答案为:137.12.(4分)在比例尺1:3 000 000的地图上,量得甲地到乙地的距离是20cm,这两地的实际距离是600km.【解答】解:设两地的实际距离是xcm,1:3 000 000=20:x,解得x=60 000 00060 000 000cm=600km.故这两地的实际距离是600km.故答案为:600.13.(4分)若x,y为实数,且满足|x﹣2|+=0,则()2014的值是1.【解答】解:由题意得,x﹣2=0,2+y=0,解得x=2,y=﹣2,所以()2014=()2014=1.故答案为:1.14.(4分)已知圆锥的底面半径是3cm,母线长是5cm,则圆锥的侧面积为15πcm2.(结果保留π)【解答】解:底面圆的半径为3cm,则底面周长=6πc,侧面面积=×6π×5=15πcm2.15.(4分)如图,在△ABC中,∠CAB=65°,在同一平面内,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,则∠B′AB等于50°.【解答】解:∵△ABC绕点A逆时针旋转到△AB′C′的位置,∴AC=AC′,∠C′AC=∠B′AB,∵C′C∥AB,∴∠C′CA=∠CAB=65°,∵AC=AC′,∴∠AC′C=∠C′CA=65°,∴∠C′AC=180°﹣2×65°=50°,∴∠B′AB=50°.故答案为:50°.16.(4分)用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:则第10个图案中有白色地面砖42块.【解答】解:∵第一个图案有白色地面砖2+4块,第二个有2+4+4块,第三个有2+4+4+4块,∴第10个图案中有白色地面砖有2+4×10=42块.故答案为:42.三、解答题(一)(本大题3小题,每小题6分,共18分)17.(6分)计算:()﹣1﹣|﹣2|+﹣(﹣1)2015.【解答】解:()﹣1﹣|﹣2|+﹣(﹣1)2015=3﹣2+4﹣(﹣1)=618.(6分)化简:(a2+3a)÷.【解答】解:原式=a(a+3)÷=a(a+3)×=a.19.(6分)已知等腰△ABC的顶角∠A=36°(如图).(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加墨);(2)通过计算说明△ABD和△BDC都是等腰三角形.【解答】解:(1)如图所示:BD即为所求;(2)∵∠A=36°,∴∠ABC=∠C=(180°﹣36°)÷2=72°,∵BD平分∠ABC,∴∠ABD=∠DBC=72°÷2=36°,∴∠CDB=180°﹣36°﹣72°=72°,∵∠A=∠ABD=36°,∠C=∠CDB=72°,∴AD=DB,BD=BC,∴△ABD和△BDC都是等腰三角形.四、解答题(二)(本大题3小题,每小题7分,共21分)20.(7分)为了推动课堂教学改革,打造“贵生课堂”,我县某中学对该校八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图,请根据图中提供的信息,回答下列问题:(1)本次调查的八年级部分学生共有54名;请补全条形统计图;(2)若该校八年级学生共有540人,请你估计该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)?【解答】解:(1)本次调查的八年级部分学生共有18÷=54(人),“非常喜欢”的人数为:54﹣18﹣6=30(人),补全条形统计图如图:(2)×540=480(人),答:估计该校八年级有480名学生支持“分组合作学习”方式.故答案为:(1)54.21.(7分)小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.(1)两种型号的地砖各采购了多少块?(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块?【解答】解:(1)设彩色地砖采购x块,单色地砖采购y块,由题意,得,解得:.答:彩色地砖采购40块,单色地砖采购60块;(2)设购进彩色地砖a块,则单色地砖购进(60﹣a)块,由题意,得80a+40(60﹣a)≤3200,解得:a≤20.故彩色地砖最多能采购20块.22.(7分)现有形状、大小、颜色完全一样的三张卡片,上面分别标有数字“1”、“2”、“3”,第一次从这三张卡片中随机抽取一张,记下数字后放回;第二次在从这三张卡片中随机抽取一张并记下数字.请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽取的数字大于第一次抽取的数字的概率.【解答】解:画树状图得:∵共有9种等可能的结果,第二次抽取的数字大于第一次抽取的数字的有3种情况,∴第二次抽取的数字大于第一次抽取的数字的概率为:=.五.解答题(本大题共3小题,每小题9分,共27分)23.(9分)如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.(1)求二次函数的解析式;(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.【解答】解:(1)∵二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点,∴,∴a=,b=﹣,c=﹣1,∴二次函数的解析式为y=x2﹣x﹣1;(2)当y=0时,得x2﹣x﹣1=0;解得x1=2,x2=﹣1,∴点D坐标为(﹣1,0);(3)图象如图,当一次函数的值大于二次函数的值时,x的取值范围是﹣1<x<4.24.(9分)如图,四边形ABCD为矩形,E为BC边中点,连接AE,以AD为直径的⊙O 交AE于点F,连接CF,DE.(1)求证:△ABE≌DCE;(2)若点F是AE的中点,求证:DE=BC;(3)判断直线CF与⊙O的位置关系,并说明理由.【解答】解:(1)证明:∵四边形ABCD为矩形,∴AB=DC,∠B=∠DCE=90°,∵E为BC边中点,∴AB=CE,在△ABE与△DCE中,,∴△ABE≌△DCE(SAS);(2)连接DE,∵AD是直径,∴∠AFD=90°,∵点F为AE的中点,∴DF为AE的垂直平分线,∴DE=AD,∵△ABE≌△DCE∴AE=DE,∴AE=DE=AD,∵四边形ABCD为矩形,∴AD=BC,∴DE=BC;(3)CF与⊙O相切,理由如下:连接OF、OC,∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∠ADC=90°,∵E为BC边中点,AO=DO,∴AO=AD,EC=BC,∴AO=EC,AO∥EC,∴四边形OAEC是平行四边形,∴AE∥OC,∴∠DOC=∠OAF,∠FOC=∠OF A,∵OA=OF,∴∠OAF=∠OF A,∴∠DOC=∠FOC,∵在△ODC和△OFC中,∴△ODC≌△OFC(SAS),∴∠OFC=∠ODC=90°,∴OF⊥CF,∴CF与⊙O相切.25.(9分)如图,在四边形OABC中,OA∥BC,∠AOC=90°,OA=OC=4,BC=3.点M从O出发以每秒2个单位长度的速度向A运动;点N从B同时出发,以每秒1个单位长度的速度向C运动,当其中一个动点达到终点时,另一个动点也随之停止运动,过点N作NP⊥OA于点P,连接AC交NP于点Q,连接MQ,设动点的运动时间为t秒.(1)当t为何值时,M和P两点重合?(2)求△AQM面积S的最大值,并求出此时t的值;(3)是否存在某一时刻t,使得△AQM为直角三角形?若存在,求出相应的t值;若不存在,请说明理由.【解答】解:(1)∵OA=OC=4,∠AOC=90°,∴∠OAC=45°,∵OA∥BC,∴∠BCA=∠OAC=45°,∵NP⊥OA,∴CN=NQ,PQ=AP,当运动t秒时,则有BN=t,OM=2t,且BC=3,∴CN=NQ=BC﹣BN=3﹣t,AP=PQ=PN﹣NQ=4﹣(3﹣t)=t+1,AM=OA﹣OM=4﹣2t,当M和P重合时,则有AM=PQ,即t+1=4﹣2t,解得t=1,∴当t的值为1秒时,M和P两点重合;(2)当运动时间为t秒时,由(1)可知PQ=t+1,AM=4﹣2t,∴S=AM•PQ=(t+1)(4﹣2t)=﹣(t﹣)2+,∵OA=4,∴M点的运动时间最大为2秒,∴0≤t≤2,∴当t=时,S max=,综上可知S=﹣(t﹣)2+(0≤t≤2),当t=时S有最大值;(3)∵∠OAC=45°∴当△AQM为直角三角形只能有QM⊥OA和MQ⊥AQ两种情况,①当QM⊥OA时,则M、P重合,由(1)可得到t=1,此时NQ=3﹣t=2;②当MQ⊥AQ时,则有MP=PQ,由(1)可知AM=4﹣2t,AP=t+1,∴PM=AM﹣AP=(4﹣2t)﹣(t+1)=3﹣3t,又PQ=t+1,∴3﹣3t=t+1,解得t=,此时NQ=3﹣t=;综上当t的值为1秒或秒时,△AQM为直角三角形,NQ的长分别为2或.。