2020届安徽省蚌埠市高三下学期第四次教学质量检查数学(文)试题(解析版)
- 格式:doc
- 大小:1.81 MB
- 文档页数:20

绝密★启用前安徽省蚌埠市普通高中2020届高三毕业班下学期第四次教学质量检查(四模)英语试题(解析版)本试卷分第Ⅰ卷﹙选择题)和第Ⅱ卷﹙非选择题)。
第Ⅰ卷1至8页,第Ⅱ卷9至10页。
满分150分。
考试时间120分钟。
考试结束,将答题卷交回。
注意事项:1.答题前,考生务必用0.5毫米的黑色墨水签字笔将自己的姓名、学校、班级、准考证号及座位号填写在答题卡上规定的位置。
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在本试卷上,否则无效。
第Ⅰ卷第一部分听力(共两节,满分30分)做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到客观题答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.15.C.£9.18.答案是B。
1. How much should the man pay?A.$15.B.$24.C.$30.2. What relation is the man to the woman?A. Her employer.B. Her doctor.C. Her teacher.3. What are the speakers discussing?A. The way to find websites.B. The advantage of the Internet.C. The common use of computers.4. What is the problem?A. The woman doesn't like the food.B. The man has a wrong order.C. The order arrives late.5. How does the man feel about the movie?A. Interested.B. Excited.C. Unsatisfied.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
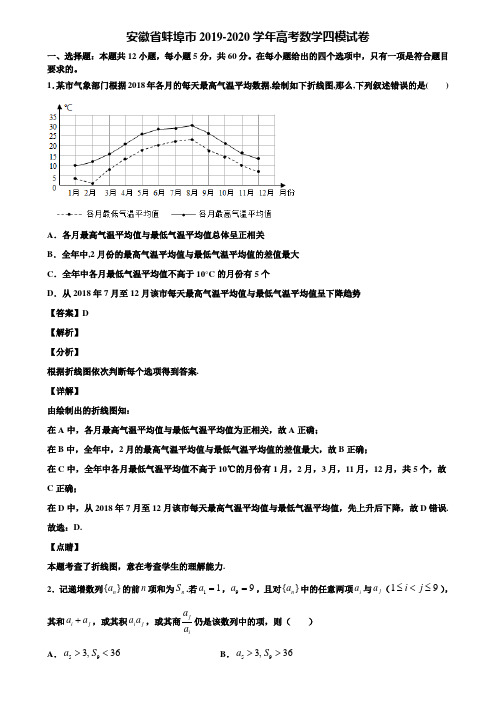
安徽省蚌埠市2019-2020学年高考数学四模试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.某市气象部门根据2018年各月的每天最高气温平均数据,绘制如下折线图,那么,下列叙述错误的是()A .各月最高气温平均值与最低气温平均值总体呈正相关B .全年中,2月份的最高气温平均值与最低气温平均值的差值最大C .全年中各月最低气温平均值不高于10°C 的月份有5个D .从2018年7月至12月该市每天最高气温平均值与最低气温平均值呈下降趋势 【答案】D 【解析】 【分析】根据折线图依次判断每个选项得到答案. 【详解】由绘制出的折线图知:在A 中,各月最高气温平均值与最低气温平均值为正相关,故A 正确;在B 中,全年中,2月的最高气温平均值与最低气温平均值的差值最大,故B 正确;在C 中,全年中各月最低气温平均值不高于10℃的月份有1月,2月,3月,11月,12月,共5个,故C 正确;在D 中,从2018年7月至12月该市每天最高气温平均值与最低气温平均值,先上升后下降,故D 错误. 故选:D. 【点睛】本题考查了折线图,意在考查学生的理解能力.2.记递增数列{}n a 的前n 项和为n S .若11a =,99a =,且对{}n a 中的任意两项i a 与j a (19i j ≤<≤),其和i j a a +,或其积i j a a ,或其商j ia a 仍是该数列中的项,则( )A .593,36a S ><B .593,36a S >>C .693,36a S >>D .693,36a S ><【答案】D 【解析】 【分析】 由题意可得955a a a =,从而得到53a =,再由53a =就可以得出其它各项的值,进而判断出9S的范围. 【详解】解:i j a a +Q ,或其积i j a a ,或其商j ia a 仍是该数列中的项,29a a ∴+或者29a a 或者92a a 是该数列中的项, 又Q 数列{}n a 是递增数列, 1239a a a a ∴<<<⋯<,299a a a ∴+>,299a a a >,只有92a a 是该数列中的项, 同理可以得到93a a ,94a a ,..,98a a 也是该数列中的项,且有99919872a a a a a a a a <<<⋯<<,∴955a a a =,53a ∴=或53a =-(舍),63a ∴>, 根据11a =,53a =,99a =,同理易得1423a =,1233a =,3443a =,5463a =,3273a =,7483a =,94912914133613S a a a -∴=++⋯+=<-,故选:D . 【点睛】本题考查数列的新定义的理解和运用,以及运算能力和推理能力,属于中档题.3.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )A .32B .323C .16D .163【答案】D 【解析】 【分析】根据三视图判断出几何体是由一个三棱锥和一个三棱柱构成,利用锥体和柱体的体积公式计算出体积并相加求得几何体的体积. 【详解】由三视图可知该几何体的直观图是由一个三棱锥和三棱柱构成,该多面体体积为1122223⨯⨯⨯+11622223⨯⨯⨯⨯=.故选D. 【点睛】本小题主要考查三视图还原为原图,考查柱体和锥体的体积公式,属于基础题. 4.已知i 是虚数单位,若z211i i=+-,则||z =( ) A .2 B .2C .10D .10【答案】C 【解析】 【分析】根据复数模的性质计算即可. 【详解】 因为z211i i=+-, 所以(1)(21)z i i =-+,|||1||21|2510z i i =-⋅+=⨯=,故选:C 【点睛】本题主要考查了复数模的定义及复数模的性质,属于容易题. 5.函数()2ln xf x x x=-的图象大致为( ) A . B .C .D .【答案】A 【解析】 【分析】根据函数()f x 的奇偶性和单调性,排除错误选项,从而得出正确选项. 【详解】因为()()f x f x -=,所以()f x 是偶函数,排除C 和D.当0x >时,()2ln x x f x x =-,()332ln 1'x x f x x=+-, 令()'0f x <,得01x <<,即()f x 在()0,1上递减;令()'0f x >,得1x >,即()f x 在()1,+∞上递增.所以()f x 在1x =处取得极小值,排除B. 故选:A 【点睛】本小题主要考查函数图像的识别,考查利用导数研究函数的单调区间和极值,属于中档题.6.若函数()x f x e =的图象上两点M ,N 关于直线y x =的对称点在()2g x ax =-的图象上,则a 的取值范围是( )A .,2e ⎛⎫-∞ ⎪⎝⎭B .(,)e -∞C .0,2e ⎛⎫⎪⎝⎭D .(0,)e【答案】D 【解析】 【分析】由题可知,可转化为曲线()2g x ax =-与ln y x =有两个公共点,可转化为方程2ln ax x -=有两解,构造函数2ln ()xh x x+=,利用导数研究函数单调性,分析即得解 【详解】函数()xf x e =的图象上两点M ,N 关于直线y x =的对称点在ln y x =上,即曲线()2g x ax =-与ln y x =有两个公共点, 即方程2ln ax x -=有两解,即2ln xa x+=有两解, 令2ln ()xh x x +=,则21ln ()xh x x --'=,则当10x e<<时,()0h x '>;当1x e >时,()0h x '<,故1x e =时()h x 取得极大值1h e e ⎛⎫= ⎪⎝⎭,也即为最大值, 当0x →时,()h x →-∞;当x →+∞时,()0h x →, 所以0a e <<满足条件. 故选:D 【点睛】本题考查了利用导数研究函数的零点,考查了学生综合分析,转化划归,数形结合,数学运算的能力,属于较难题.7.某工厂只生产口罩、抽纸和棉签,如图是该工厂2017年至2019年各产量的百分比堆积图(例如:2017年该工厂口罩、抽纸、棉签产量分别占40%、27%、33%),根据该图,以下结论一定正确的是( )A .2019年该工厂的棉签产量最少B .这三年中每年抽纸的产量相差不明显C .三年累计下来产量最多的是口罩D .口罩的产量逐年增加 【答案】C 【解析】 【分析】根据该厂每年产量未知可判断A 、B 、D 选项的正误,根据每年口罩在该厂的产量中所占的比重最大可判断C 选项的正误.综合可得出结论. 【详解】由于该工厂2017年至2019年的产量未知,所以,从2017年至2019年棉签产量、抽纸产量以及口罩产量的变化无法比较,故A 、B 、D 选项错误;由堆积图可知,从2017年至2019年,该工厂生产的口罩占该工厂的总产量的比重是最大的,则三年累计下来产量最多的是口罩,C 选项正确. 故选:C. 【点睛】本题考查堆积图的应用,考查数据处理能力,属于基础题.8.已知双曲线2222:1(0,0)x y C a b a b-=>>的一个焦点为F ,点,A B 是C 的一条渐近线上关于原点对称的两点,以AB 为直径的圆过F 且交C 的左支于,M N 两点,若|MN|=2,ABF ∆的面积为8,则C 的渐近线方程为( ) A.y = B.y x = C .2y x =± D .12y x =±【答案】B 【解析】 【分析】由双曲线的对称性可得'ABF AFF S S ∆∆=即8bc =,又222b MN c==,从而可得C 的渐近线方程.【详解】设双曲线的另一个焦点为'F ,由双曲线的对称性,四边形'AFBF 是矩形,所以'ABF AFF S S ∆∆=,即8bc =,由22222221x y c x y ab ⎧+=⎪⎨-=⎪⎩,得:2b yc =±,所以222b MN c ==,所以2b c =,所以2b =,4c =,所以a =C的渐近线方程为y x =. 故选B 【点睛】本题考查双曲线的简单几何性质,考查直线与圆的位置关系,考查数形结合思想与计算能力,属于中档题. 9.设全集U=R ,集合2{|340}A x x x =-->,则U A =ð( ) A .{x|-1 <x<4} B .{x|-4<x<1}C .{x|-1≤x≤4}D .{x|-4≤x≤1}【答案】C 【解析】 【分析】解一元二次不等式求得集合A ,由此求得U A ð 【详解】由()()234410x x x x --=-+>,解得1x <-或4x >.因为{|1A x x =<-或4}x >,所以U {|14}x x A =-≤≤ð. 故选:C 【点睛】本小题主要考查一元二次不等式的解法,考查集合补集的概念和运算,属于基础题. 10.二项式22)nx+的展开式中只有第六项的二项式系数最大,则展开式中的常数项是( ) A .180 B .90C .45D .360【答案】A 【解析】试题分析:因为22)nx+的展开式中只有第六项的二项式系数最大,所以10n =,551021101022•?()2r r rr r rr T C C x x--+==,令5502r -=,则2r =,23104180T C ==.考点:1.二项式定理;2.组合数的计算.11.已知y ax b =+与函数()2ln 5f x x =+和2()4g x x =+都相切,则不等式组3020x ay x by -+≥⎧⎨+-≥⎩所确定的平面区域在2222220x y x y ++--=内的面积为( ) A .2π B .3πC .6πD .12π【答案】B 【解析】 【分析】根据直线y ax b =+与()f x 和()g x 都相切,求得,a b 的值,由此画出不等式组所表示的平面区域以及圆2222220x y x y ++--=,由此求得正确选项.【详解】()()''2,2f x g x x x==.设直线y ax b =+与()f x 相切于点()00,2ln 5A x x +,斜率为02x ,所以切线方程为()()00022ln 5y x x x x -+=-,化简得0022ln 3y x x x =++①.令()'022g x x x ==,解得01x x =,200114g x x ⎛⎫=+ ⎪⎝⎭,所以切线方程为20001214y x x x x ⎛⎫⎛⎫-+=- ⎪ ⎪⎝⎭⎝⎭,化简得200214y x x x =-+②.由①②对比系数得02012ln 34x x +=-+,化简得02012ln10x x +-=③.构造函数()()212ln 10h x x x x=+->,()()()'3321122x x h x x x x+-=-=,所以()h x 在()0,1上递减,在()1,+∞上递增,所以()h x 在1x =处取得极小值也即是最小值,而()10h =,所以()0h x =有唯一解.也即方程③有唯一解01x =.所以切线方程为23y x =+.即2,3a b ==.不等式组3020x ay x by -+≥⎧⎨+-≥⎩即230320x y x y -+≥⎧⎨+-≥⎩,画出其对应的区域如下图所示.圆2222220x y x y ++--=可化为()()221124x y ++-=,圆心为()1,1A -.而方程组230320x y x y -+=⎧⎨+-=⎩的解也是11x y =-⎧⎨=⎩.画出图像如下图所示,不等式组230320x y x y -+≥⎧⎨+-≥⎩所确定的平面区域在2222220x y x y ++--=内的部分如下图阴影部分所示.直线230x y -+=的斜率为12,直线320x y +-=的斜率为13-.所以()tan tan BAC AED ADE ∠=∠+∠1123111123+==-⨯,所以4BAC π∠=,而圆A 的半径为2426=,所以阴影部分的面积是()2126324ππ⨯⨯=.故选:B【点睛】本小题主要考查根据公共切线求参数,考查不等式组表示区域的画法,考查圆的方程,考查两条直线夹角的计算,考查扇形面积公式,考查数形结合的数学思想方法,考查分析思考与解决问题的能力,属于难题.12.已知向量)3,1a =r ,)3,1b =-r ,则a r 与b r的夹角为( )A .6πB .3π C .23π D .56π【解析】 【分析】由已知向量的坐标,利用平面向量的夹角公式,直接可求出结果. 【详解】解:由题意得,设a r与b r的夹角为θ,311cos 222a b a bθ⋅-∴===⨯r rr r ,由于向量夹角范围为:0θπ≤≤, ∴π3θ=. 故选:B. 【点睛】本题考查利用平面向量的数量积求两向量的夹角,注意向量夹角的范围. 二、填空题:本题共4小题,每小题5分,共20分。


蚌埠市2020届高考模拟考试语文注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,只需将答题卡交回。
一.现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)阅读下面的文字,完成1-3题。
利用传统街区发展经济,早已经成为我国许多城市趋之若鹜的举措,大家热衷于把这些街区“打造”成一个地方的“名片”,以增加城市的影响力,招徕商家和顾客(特别是游客)。
充分利用好历史资源,让文化遗产活起来,本无可厚非。
但是在对传统街区新意迭出的“打造”中,也产生了形形色色的问题,甚至导致传统街区面目全非、名存实亡的悲剧,令人痛心。
究其原因,主要在于没有弄清传统街区本身的性质,以及该如何保护和利用。
所以,传统街区要慎言“打造”。
传统街区的价值就在于其“传统”,在于其所承载的历史文化。
几乎稍有名气的传统街区,其形成的过程都比较漫长,少则数十年,多则数百年,比如西安的西羊市,元朝时即已出现。
传统街区产生于人民群众的长期创造和积累,其住宅区、崇祀区、商业区、公共活动区等的构成,都体现着人民的生活理想与生存智慧,体现着社会的伦理道德关系,也体现着鲜明的地城特色,街区的灵魂即维系于此。
传统街区蕴含着丰富的历史信息、人文信息,是物质文化遗产与非物质文化遗产的和谐统一体。
以此观之,传统街区最值得关注的地方绝不仅仅在于那些年代不一、外形各异的房屋建筑,更在于这些建筑所承载的生存方式、风土人情。
因此,保护和利用传统街区,必须明白它自身的社会意义,明白它是否存在问题、我们需要做什么。
把原住民大量迁走,对街区进行彻底的改造和招商,是饮鸩止渴的短期行为。
因为,若没有对街区历史和现实的尊重,街区的文化特色将逐渐失去,其内涵必然会受到重创,所谓的招商引资能否产生长久效益十分令人怀疑。

高三下学期理数第四次教学质量检查试卷一、单项选择题1.集合,,那么〔〕A. B. C. D.2.设,其中,,那么〔〕A. B. 1 C. D.3.假设,那么以下不等式一定成立的是〔〕A. B. C. D.4.记为等差数列的前项和.假设,,那么数列的公差为〔〕A. -1B. -2C. 1D. 25.实数,满足约束条件,那么的最大值为〔〕A. B. -5 C. -25 D. 256.在中,,那么〔〕A. B. C. D.7.直线:,直线:,那么“ 〞是“ 〞的〔〕A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8.设抛物线的焦点为F,直线:,P为抛物线上一点,,M为垂足,如果直线MF的斜率为,那么等于〔〕A. B. C. D.9.假设随机变量,那么以下说法错误的选项是〔〕A. B. C. D.10.根底学科对于一个国家科技开展至关重要,是提高核心竞争力,保持战略领先的关键.其中数学学科尤为重要.某双一流大学为提高数学系学生的数学素养,特开设了“九章算术〞,“古今数学思想〞,“数学原理〞,“世界数学通史〞,“算术研究〞五门选修课程,要求数学系每位同学每学年至多项选择四门,大一到大三三学年必须将五门选修课程选完,那么每位同学的不同选修方式种数为〔〕A. 90B. 300C. 330D. 24011.函数有唯一零点,那么〔〕A. 0B.C. 1D. 212.函数在区间内有且仅有一个极大值点,那么的最大值为〔〕A. B. C. D.二、填空题13.曲线在处切线的斜率为,那么________.14.的展开式中的系数为________.15.双曲线:的左焦点为,右顶点为,虚轴上顶点为.假设双曲线的离心率是,那么________.16.有四个半径为1的小球,球、球、球放置在水平桌面上,第四个小球放在这三个小球的上方,且四个小球两两外切.在四个小球之间有一个小球O,与这四个小球均外切.那么球心O到水平桌面的距离为________.三、解答题17.在中,角,,所对的边分别为,,,其外接圆半径为,.〔1〕求角;〔2〕假设边的长是该边上高的倍,求.18.如图,四棱锥的底面是边长为2的菱形,底面.〔1〕求证:平面平面;〔2〕假设,求直线与平面所成角的正弦值.19.排球队的6名队员进行传球训练,每位队员把球传给其他5人的概率相等,由甲开始传球〔1〕求前3次传球中,乙恰有1次接到球的概率;〔2〕设第次传球后球在乙手中的概率为,求.20.函数,.〔1〕讨论函数的单调性;〔2〕设,在区间上的最大值为,求的最小值.21.椭圆的离心率为,过点.〔1〕求椭圆的标准方程;〔2〕设点、分别是椭圆的左顶点和上顶点,、为椭圆上异于、的两点,满足,求证:面积为定值.22.在直角坐标系中,直线的参数方程为〔为参数〕.以坐标原点为极点,轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.〔1〕求曲线与直线的直角坐标方程;〔2〕假设直线与直线和曲线分别交于点,〔均异于原点〕,假设,求实数的值.23. ,,为正数,且满足.证明:〔1〕;〔2〕.答案解析局部一、单项选择题1.【解析】【解答】由 ,所以,因,对于A : ,A 不正确;对于B :,B 符合题意;对于C : ,C 不正确;对于D :N ⫋M , D 不正确.故答案为:B【分析】化简集合N ,再对各选项进行相应的集合运算并判断得解。

蚌埠市2024届高三年级第四次教学质量检查考试数学(答案在最后)本试卷满分150分,考试时间120分钟注意事项:1.答卷前,务必将自己的姓名和座位号填写在答题卡和试卷上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,务必擦净后再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.若()()123a b m ==,,,,且a b ⊥,则实数m =()A.6B.6- C.3D.3-【答案】B 【解析】【分析】由向量垂直的坐标表示直接求解.【详解】若a b ⊥ ,则0a b ⋅=即1230m ⨯+⨯=,解得6m =-.故选:B2.已知双曲线2222:1(0,0)x y C a b a b-=>>,直线2y x =-是双曲线C 的一条渐近线,则该双曲线的离心率为()A.4 B.3C.2D.【答案】D 【解析】【分析】由题意可知:双曲线C 的焦点在x 轴上,且2ba =,结合离心率的定义分析求解.【详解】因为双曲线C 的焦点在x 轴上,由题意可知:2ba=,所以该双曲线的离心率为c e a ===故选:D.3.为维护市场秩序,保护消费者权益,在“五一”假期来临之际,我市物价部门对某商品在5家商场的售价x(元)及其一天的销售量y (件)进行调查,得到五对数据()(),12345i i x y i =,,,,,经过分析、计算,得108x y ==,,y 关于x 的经验回归方程为 3y x a=-+,则相应于点()910,的残差为()A.1-B.1C.3- D.3【答案】A 【解析】【分析】将样本点中心(),x y ,并代入回归方程,求ˆa,并代入9x =后,即可求解残差.【详解】因为回归直线过样本点中心()x y 即()10,8,代入 3y x a =-+,可得8310ˆa =-⨯+,解得ˆ38a=,当9x =时,39ˆ3811y =-⨯+=,所以残差为10111-=-.故选:A4.已知各项均为正数的等比数列{}n a 中,若59a =,则3436log log a a +=()A.2 B.3 C.4D.9【答案】C 【解析】【分析】利用对数运算性质结合等比中项求解即可.【详解】由题意得()3436346log log log a a a a +=,由等比中项性质得246581a a a ==,故()34363463log log log log 814a a a a +===.故选:C5.32(1)(2)x y -+的展开式中,满足4m n +=的m n x y 项的系数之和为()A.3- B.1- C.1D.3【答案】C 【解析】【分析】分别展开32,(1)(2)x y -+,结合题意分析可知22m n =⎧⎨=⎩或31m n ⎧⎨⎩==,进而运算求解即可.【详解】因为3223233(1,441)(2)x y x x x y y =-+-=+++-,若4m n+=,且03,02,,m n m n ≤≤≤≤∈N ,则22m n =⎧⎨=⎩或31m n ⎧⎨⎩==,所以m n x y 项的系数之和为31141-⨯+⨯=.故选:C.6.“函数()tan y x ϕ=-的图象关于π,04⎛⎫⎪⎝⎭对称”是“ππ4k ϕ=-+,Z k ∈”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】利用正切函数的性质结合集合间的基本关系判定充分、必要条件即可.【详解】当函数()tan y x ϕ=-的图象关于π,04⎛⎫⎪⎝⎭对称时,有ππ42k ϕ-=,Z k ∈,得()1ππππ4242k k ϕ-+=-=-+,Z k ∈,易知ππ4k ϕϕ⎧⎫=-+⎨⎬⎩⎭ππ42k ϕϕ⎧⎫=-+⎨⎬⎩⎭,Z k ∈所以“函数tan()y x ϕ=-的图象关于π,04⎛⎫⎪⎝⎭对称”是“ππ4k ϕ=-+,Z k ∈”的必要不充分条件.故选:B .7.如图所示,圆台的上、下底面半径分别为4cm 和6cm ,1AA ,1BB 为圆台的两条母线,截面11ABB A 与下底面所成的夹角大小为60︒,且1O 劣弧 11A B 的弧长为8πcm 3,则三棱台111ABO A B O -的体积为()A.319cm 3B.3C.319cmD.3【答案】C 【解析】【分析】分别取11A B ,AB 的中点E ,F ,则易知截面11ABB A 与下底面所成的夹角为60EFO ∠=︒,E 作EH FO ⊥于点H ,则1//EH O O ,且1EH O O =,再根据弧度数公式及解三角形可求出圆台的高,最后根据台体的体积公式,即可求解.【详解】如图,分别取11A B ,AB 的中点E ,F,则111O E A B ⊥,OF AB ⊥且1//O E OF ,又1O O ⊥平面ABO ,AB ⊂平面ABO ,所以1O O AB ⊥,1OF O O O = ,1,OF O O ⊂平面1FEO O ,所以AB ⊥平面1FEO O ,又EF ⊂平面1FEO O ,所以EF AB ⊥,∴截面11ABB A 与下底面所成的夹角为60EFO ∠=︒,过E 作EH FO ⊥于点H ,则1//EH O O ,且1EH O O =,又1O 劣弧 11A B 的弧长为8πcm 3,弧所在圆的半径为4,1118π2π343A OB ∴∠==,则111π6O A B ∠=,∴12π4sin 6EO ==,同理可得3OF =,321FH ∴=-=,又60EFO ∠=︒,1tan 60O O EH FH ∴==︒=又三角形111AO B的面积为134422⨯⨯⨯=,同理可得三角形AOB的面积为16622⨯⨯⨯=,∴三棱台111ABO A B O -的体积为(()3119cm 3⨯+=.故选:C .8.已知00m n >>,,则下列选项中,能使2m n +取得最小值18的为()A.32mn = B.8m n mn+= C.2868m n += D.224162m n +=【答案】B 【解析】【分析】本题根据基本不等式求最值可判断出A 、B 两项的正误;利用二次函数的性质可判断出C 项的正误;通过举反例可判断D 项的正误.【详解】对选项A :由0,0m n >>可知,216m n +≥=,当且仅当2m n =等号成立,最小值不是18,故选项A 不正确;对选项B :若8,m n mn +=,两边除以mn 得,811m n+=,则81162(2)()1010218n m m n m n m n m n+=++=++≥+,当且仅当164n mm n==时,即12,3m n ==时等号成立,故2m n +的最小值是18,故选项B 正确;对选项C :由2868m n +=,得211782n m =-+,故22117122()17824m n m m m m +=+-+=-++,由二次函数的性质,可知:当2m =时,2m n +的最大值为18,故选项C 不正确;对选项D :224162m n +=,则当6m n ==时,21218m n +=+,故2m n +不能取得最小值18,故选项D 不正确.故选:B二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项是符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知复数2i z a =+(a 为实数),若z =,则a 的值可能为()A.3-B.1- C.1D.3【答案】BC 【解析】【分析】根据题意结合复数的模长公式运算求解即可.【详解】由题意可知:z ==1a =±,结合选项可知:BC 正确;AD 错误.故选:BC.10.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,且阴影部分的面积为4π,则()A.函数()f x 的最小正周期为πB.点3π,08⎛⎫⎪⎝⎭为曲线()y f x =的一个对称中心C.直线2π3x =为曲线()y f x =的一条对称轴D.函数()f x 在区间3π,π4⎡⎤⎢⎥⎣⎦上单调递增【答案】ACD 【解析】【分析】根据题意结合五点法求函数解析式,即可判断A ;代入检验结合最值与对称轴、零点与对称中心之间的关系判断BC ;对于D :以π26x +为整体,结合正弦函数单调性分析判断.【详解】由题意可知:函数()f x 的最大值为2,即2A =,因为()02sin 1f ϕ==,即1sin 2ϕ=,且ππ22ϕ-<<,可得π6ϕ=,设()f x 的最小正周期为T ,则44πT =,即πT =,故A 正确;且0ω>,可得2π2Tω==,所以()π2sin 26f x x ⎛⎫=+⎪⎝⎭,对于选项B :因为3π3ππππ2sin 2sin π2sin 08461212f ⎛⎫⎛⎫⎛⎫=+=-=≠⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,所以点3π,08⎛⎫⎪⎝⎭不为曲线()y f x =的一个对称中心,故B 错误;对于选项C :因为2π4ππ3π2sin 2sin 23362f ⎛⎫⎛⎫=+==- ⎪ ⎪⎝⎭⎝⎭为最小值,所以直线2π3x =为曲线()y f x =的一条对称轴,故C 正确;对于选项D :因为3π,π4x ⎡⎤∈⎢⎥⎣⎦,则π5π13π2,636x ⎡⎤+∈⎢⎥⎣⎦,且sin y x =在5π13π,36⎡⎤⎢⎥⎣⎦内单调递增,所以函数()f x 在区间3π,π4⎡⎤⎢⎥⎣⎦上单调递增,故D 正确;故选:ACD.11.抛物线有如下光学性质:从焦点发出的光线,经抛物线上的一点反射后,反射光线平行于抛物线的对称轴.已知抛物线2:4E x y =的焦点为F ,准线为,,l A B 为抛物线E 上两个动点,且,,F A B 三点不共线,抛物线E 在,A B 两点处的切线分别为1212,,,,l l l l T A B ⋂=在l 上的射影点分别为11,A B ,则()A.点F 关于1l 的对称点在l 上B.点T 在l 上C.点T 为11FA B 的外心D.FT AB⊥【答案】AC 【解析】【分析】根据抛物线的光学性质及定义知11,A AT TAF B BT FBT ∠=∠∠=∠,从而1A F 的垂直平分线为1l ,1B F 的垂直平分线为2l ,即可判断选项AC,再利用,,F A B 三点共线时,得到点T 在l 上和FT AB ⊥判断CD.【详解】如图:由抛物线定义知,1AA AF =,1BB BF =,根据抛物线的光学性质知:从F 发出的光线经抛物线的反射光线AD 、BC 与y 轴平行,又抛物线E 在,A B 两点处的切线分别为12,l l ,结合平行线性质及对顶角相等得11,A AT TAF B BT FBT ∠=∠∠=∠,即1A F 的垂直平分线为1l ,1B F 的垂直平分线为2l ,所以11,AT TF TF TB ==,1BB BF =,所以点T 为11FA B 的外心,故选项C 正确;点F 关于1l 的对称点1A 在l 上,故选项A 正确;假设F A B ,,三点共线,设()11,A x y ,()22,B x y ,直线AB 方程为1y kx =+,因为24x y =,即214y x =,所以12y x '=,所以1112l k x =,2212l k x =,所以12,l l 的方程分别为()1112x y y x x -=-,()2222xy y x x -=-,即112x y x y =-,222x y x y =-,联立()()11122222x y y x x x y y x x ⎧-=-⎪⎪⎨⎪-=-⎪⎩,所以121222x x x y y ⎛⎫-=- ⎪⎝⎭,所以121222y y x k x x ⎛⎫-== ⎪-⎝⎭,则()1211112111211211112121222y y x x y x y x y x y x y x yy y y x x x x x x ----+=⋅-=-=---()()2112122121121212111x kx x kx x y x y x x x x x x x x +-+--====----,所以()2,1T k -,说明,,F A B 三点共线时,T 点才落在:1l x =-,因为,,F A B 三点不共线,所以点T 不在l 上,所以选项B 错误;当F A B ,,三点共线时,()2,1T k -,当0k =时,直线AB 方程为1y =,直线FT 方程为0x =,此时FT AB ⊥,当0k ≠时,11120FT k k k--==--,此时FT AB ⊥,故只有,,F A B 三点共线时,才有FT AB ⊥,因为,,F A B 三点不共线,所以FT 与AB 不垂直,故选项D 错误.故选:AC【点睛】结论点睛:抛物线的切线相关结论:抛物线C :()220x py p =>的焦点为F ,直线l 过焦点F 与抛物线相交于A ,B 两点,过A ,B 分别作抛物线C 的切线,两切线交于点G ,则点G 在抛物线的准线上,且GF ⊥AB.三、填空题:本题共3小题,每小题5分,共15分.12.已知集合{}1,3,21A m =--,集合{}23,B m =,若B A ⊆,则实数m =____.【答案】1【解析】【分析】根据子集的定义求解.【详解】因为B A ⊆,所以221m m =-,即()210m -=,所以1m =.当1m =时,{}1,3,1A =-,{}3,1B =,满足B A ⊆,故1m =.故答案为:1.13.今年3月5日,李强总理在政府工作报告中强调“大力推进现代化产业体系建设,加快发展新质生产力”.新质生产力代表一种生产力的跃迁,它是科技创新在其中发挥主导作用的生产力,具有高效能、高效率、高质量的特征,为了让同学们对新质生产力有更多的了解,某中学利用周五下午课外活动时间同时开设了四场公益讲座,主题分别是“新能源与新材料的广泛应用”、“AI +医疗的发展趋势”、“低空经济的前景展望”、“从人工智能、工业互联网到大数据”.已知甲、乙、丙、丁四人从中一共选择两场去学习,则甲、乙两人不参加同一个讲座的选择共有_________种(用数字作答).【答案】48【解析】【分析】先排甲、乙两人,再排丙、丁,根据题意结合分步乘法计算原理分析求解.【详解】由题意可知:先排甲、乙两人,则有4312⨯=种;再排丙、丁,每人均有2个选择,则有224⨯=种;所以共有12448⨯=.故答案为:48.14.已知函数()()1e 0220212242xx x f x x f x x -⎧<⎪⎪=-≤≤⎨⎪⎪-<≤⎩,,,,方程()f x m =有五个不等实根()12345i x i =,,,,,则实数m 的取值范围是______;令()51iii t x f x ==∑,则t 的最小值为______.【答案】①.10,2⎛⎫ ⎪⎝⎭②.91e -【解析】【分析】先化简函数()f x 解析式,然后做出函数()f x 的图象,数形结合即可求得m 的范围,设12345x x x x x <<<<,根据函数的对称性可得23452,6x x x x +=+=,从而可得()()15118e x i i i t x f x x ===+∑,令()()8e ,ln2x g x x x =+<-,利用导数求解()g x 的最小值即可求解.【详解】当24x <≤时,022x <-≤,所以()3222x f x --=-,所以()()1131e 0e 022022202112242242xx x x x x x f x x x x f x x ----⎧⎧<<⎪⎪⎪⎪=-≤≤=-≤≤⎨⎨⎪⎪-<≤⎪⎪⎩-<≤⎩,,,,,,,作出函数的图形,如图所示:又因为()132f =,方程()f x m =有五个不等实根,由图象可知102m <<,因为当02x ≤≤时,()122x f x -=-,故()()1222xf x f x --=-=,所以此时函数()f x 关于1x =对称,同理可得函数()f x 关于3x =对称,设12345x x x x x <<<<,当0x <时,令1e 2x=,解得ln 2x =-,所以12345ln 201234x x x x x <-<<<<<<<<<,且23452,6x x x x +=+=,所以()51iii t x f x ==∑()()()1123451188e x x x x x x m x m x =++++=+=+,令()()8e ,ln2xg x x x =+<-,则()()9e xg x x +'=,所以当()9x ∞∈--,时,()0g x '<,()g x 单调递减,当()9ln 2x ∈--,时,()0g x '>,()g x 单调递增,所以()()99min19e e g x g -=-=-=-,即()51i i i t x f x ==∑的最小值为91e -.故答案为:10,2⎛⎫ ⎪⎝⎭,91e -【点睛】方法点睛:已知方程根的个数,求参数的取值范围的常用方法:(1)直接法:直接根据题设条件列出关于参数的不等式,求解即可得出参数范围;(2)分离参数法:先将参数分离,转化成求函数的值域问题进行求解;(3)数形结合法:对解析式适当变形,构造两个函数,在同一平面直角坐标系中,画出两个函数的图象,其交点的个数就是方程根的个数,然后数形结合求解.常见类型有两种:一种是转化为直线与函数的图象的交点个数问题;另一种是转化为两个函数的图象的交点个数问题.四、解答题:本题共5小题,共77分.解答应写出说明文字、演算式、证明步骤.15.已知,,a b c 分别为ABC 内角,,A B C 的对边,())sin a B B b c =-.(1)求角A ;(2)若ABC 6,求a .【答案】(1)π3A =(2)2a =【解析】【分析】(1)根据正弦定理和三角恒等变换可得πsin 32A ⎛⎫+= ⎪⎝⎭,结合角A 的范围分析求解;(2)利用面积公式可得4bc =,再根据余弦定理运算求解.【小问1详解】因为sin cos a B B =-,由正弦定理可得sin sin cos A B A B B C -=-,又因为()sin sinsin cos cos sin C =A B A B A B +=+,可得sin sin sin A B A B B +=,且()0,πB ∈,则sin 0B ≠,可得sin A A =,整理得π3sin 32A ⎛⎫+= ⎪⎝⎭,又因为()0,πA ∈,则ππ4π,333A ⎛⎫+∈ ⎪⎝⎭,所以π2π33A +=,即π3A =.【小问2详解】因为13sin 24ABC S bc A === ,则4bc =,由余弦定理可得222222cos ()3(6)12a b c bc A b c bc a =+-=+-=--,解得2a =.16.某中学对学生钻研奥数课程的情况进行调查,将每周独立钻研奥数课程超过6小时的学生称为“奥数迷”,否则称为“非奥数迷”,从调查结果中随机抽取100人进行分析,得到数据如表所示:奥数迷非奥数迷总计男243660女122840总计3664100(1)判断是否有99%的把握认为是否为“奥数迷”与性别有关?(2)现从抽取的“奥数迷”中,按性别采用分层抽样的方法抽取3人参加奥数闯关比赛,已知其中男、女学生独立闯关成功的概率分别为34、23,在恰有两人闯关成功的条件下,求有女生闯关成功的概率.参考数据与公式:()2P K k ≥0.100.050.0100.001k2.7063.8416.63510.828()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.【答案】(1)没有99%的把握认为是否为“奥数迷”与性别有关(2)47【解析】【分析】(1)提出假设0H :“奥数迷”与性别无关,计算2K ,从而可判断假设是否成立得结论;(2)根据条件概率公式求解即可.【小问1详解】提出假设0H :“奥数迷”与性别无关.则()()()()()()2221002428123625 1.046040366424n ad bc K a b c d a c b d -⨯-⨯===≈++++⨯⨯⨯因为()26.6350.01P K ≥=,而1.04 6.635<,故没有99%的把握认为是否为“奥数迷”与性别有关.【小问2详解】根据分层抽样,抽取的男生人数为2人,女生人数为1人,记“恰有两人闯关成功”为事件A ,“有女生闯关成功”为事件B ,则()2123233271C 14344316P A ⎛⎫⎛⎫⎛⎫=-+-⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()123321C 14434P AB ⎛⎫=-⨯⨯=⎪⎝⎭由条件概率的公式得()()()1447716P AB P B A P A ===∣,故在恰有两人闯关成功的条件下,有女生闯关成功的概率为47.17.如图,平行六面体1111ABCD A B C D -中,侧面11AABB 为矩形,底面ABCD 是边长为2的菱形,且60ABC P ∠=︒,为线段11A B 上一点,满足112A PA PBB PC ∠=∠=,.(1)求证:平面PAB ⊥平面ABCD ;(2)若PA PB =,求二面角A PC D --的正弦值.【答案】(1)证明见解析(2)7【解析】【分析】(1)取AB 的中点O ,利用给定条件结合勾股定理逆定理证得CO OP ⊥,再利用线面、面面垂直的判定推理即得.(2)以O 为坐标原点,建立空间直角坐标系,求出二面角的两个半平面的法向量坐标,再利用面面角的向量求法求解即得.【小问1详解】取AB 的中点O ,连接,CO PO ,由ABCD 是边长为2的菱形,得2AB BC ==,又60ABC ∠=︒,则ABC 为等边三角形,即有,CO AB CO ⊥=由11A PA PBB ∠=∠,则111190BPB APA BPB PBB ∠+∠=∠+∠=︒,即PA PB ⊥,112OP AB ==,由22222212OP OC PC +=+==,得CO OP ⊥,而,,AB OP O AB OP =⊂ 平面PAB ,因此CO ⊥平面PAB ,又OC ⊂平面ABCD ,所以平面PAB ⊥平面ABCD .【小问2详解】由PA PB =,得PO AB ⊥,又平面PAB ⊥平面ABCD ,平面PAB ⋂平面,ABCD AB PO =⊂平面PAB ,于是PO ⊥平面ABCD ,直线,,OC OB OP 两两垂直,以O 为坐标原点,直线,,OC OB OP 分别为,,x y z 轴,建立空间直角坐标系O xyz -,则()()()()))0,0,0,0,1,0,0,0,1,0,1,0,,2,0O A P B CD--,)()()1,0,1,1,0,2,0PC AP DC =-==,设平面APC 的一个法向量为()1,,n x y z = ,平面DPC 的一个法向量为()2,,n a b c =,由1100n AP y z n PC z ⎧⋅=+=⎪⎨⋅=-=⎪⎩,令1x =,得(11,n = ,由22200n DC b n PC c ⎧⋅==⎪⎨⋅=-=⎪⎩ ,令1a =,得2n = ,因此12121227cos ,7||||n n n n n n ⋅〈〉===,所以二面角A PC D --721=.18.如图所示,平面直角坐标系xOy 中,O 为坐标原点,四边形KLMN 为矩形,()0,1A ,()()0,12,0B C -,分别为KN LM MN ,,的中点,E F ,两点满足:()1OE tOC CF t OA ==-,,其中t 为非零实数.直线AF 与BE 交于点R .已知椭圆2222Γ:1(0)x y a b a b+=>>过A B C ,,三点.(1)求椭圆Γ的标准方程及其焦距;(2)判断点R 与椭圆Γ的位置关系,并证明你的结论;(3)设()()1122,,P x y Q x y ,为椭圆Γ上两点,满足////OP BE OQ AF ,,判断22OP OQ +是否为定值,如果是,求出该定值;如果不是,说明理由.【答案】(1)椭圆Γ的方程为2214x y +=,焦距(2)点R 在椭圆Γ上,证明见解析(3)22OP OQ +为定值5【解析】【分析】(1)由题意可得2,1a b ==,可得椭圆的标准方程和焦距;(2)求得,E F 的坐标,以及直线BE 和直线AF的斜率之积,设()00,R x y ,可得R 的轨迹方程,可得结论;(3)设直线OP 和OQ 的斜率分别为12,k k ,联立直线方程与椭圆方程,求得22124x x +=,可得结论.【小问1详解】由题意2,1a b ==,所以椭圆Γ的方程为2214xy +=,且2413=-=c,焦距2c =【小问2详解】R 在椭圆Γ上,证明如下:由题意()()2,0,2,1E t F t -,则()1111224BE AF t k k t --⋅=⋅=-,设()00,R x y ,则00001114BE AF y y k k x x +-⋅=⋅=-,即220014x y +=,所以点R 在椭圆Γ上.【小问3详解】由题意直线,OP OQ 的斜率都存在,且不为0.设直线,OP OQ 的斜率分别为12,k k ,由(1)知:1214BE AF k k k k ⋅=⋅=-,1:OP y x k =,①22Γ:14x y +=,②联立①②得:2121441x k =+,同理,2222441x k =+所以22122222221211221212124411111411414144x x k k k k k k k k k k k k +=+=+=+-=++--++所以2222221122OP OQ x y x y +=+++()22222212121231125444x x x x x x ⎛⎫⎛⎫=+-++-=++= ⎪ ⎪⎝⎭⎝⎭即22OP OQ +为定值5.【点睛】关键点点睛:本题考查椭圆的方程和应用,以及直线和椭圆的位置关系,关键在于通过斜率找到12,x x 的关系,再将所求转化为用12,x x 表示,即可求解.19.已知函数()()()ln 1,axf x xg x x a =+=+,其中1a ≥.(1)若1a =,证明:0x >时,()()21xf xg x <+;(2)若函数()()()F x f x g x =-在其定义域内单调递增,求实数a 的值;(3)已知数列{}n a的通项公式为n n a =341e n n a a +>>.【答案】(1)证明见解析(2)2a =(3)证明见解析【解析】【分析】(1)构建()()()()2ln 1(0)21x x G x x x x +=+->+,利用导数判断其单调性,结合单调性分析证明;(2)求导可得()()()2221()x x a aF x x x a =+'-++,分12a ≤<、2a =和2a >三种情况,结合导数分析单调性即可;(3)根据(1)(2)分析可得()1111ln 11241n n n n ⎛⎫⎛⎫<++<+ ⎪ ⎪+⎝⎭⎝⎭,进而可得()1411e 1n n n naa -++<<,根据题意结合裂项相消法分析证明.【小问1详解】由题意可知:()()21xf xg x <+等价于()()()2ln 121x x x x ++<+,其中0x >.构建()()()()2ln 1(0)21x x G x x x x +=+->+,则()2222122012(1)2(1)x x x G x x x x '++=-=-<+++,可知()G x 在()0,∞+上单调递减,则0x >时,()()00G x G <=,所以0x >时,()()()221x x f x x +<+.【小问2详解】由题意可知:()()ln 1,1axF x x x x a=+->-+,则()()()2222211()1()x x a a a F x x x a x x a -+=-=++++'①若12a ≤<,则2120a a -≤-<,由()0F x '<可得220a a x -<<,可知()F x 在()22,0a a -上单调递减,不合题意;②若2a =,则()()2201(2)x F x x x =≥++',可知()F x ()0,∞+上为增函数,符合题意;③若2a >,则220a a ->,由()0F x '<可得202x a a <<-,可知()F x 在()20,2a a -上单调递减,不合题意;综上所述:2a =.【小问3详解】由(2)知:()()2ln 12xF x x x =+-+在()0,∞+上单调递增,所以0x >时,()()()2ln 1002x F x x F x =+->=+,即()11ln 112x x ⎛⎫++> ⎪⎝⎭,由(1)知:0x >时,()()()2ln 121x x x x ++<+,则()()()2211(2)ln 1124141x x x x x x +⎛⎫++<=+ ⎪++⎝⎭,所以0x >时,()()2111ln 11241x x x x ⎛⎫<++<+ ⎪+⎝⎭,令1x n =得:()1111ln 11241n n n n ⎛⎫⎛⎫<++<+ ⎪ ⎪+⎝⎭⎝⎭,即()1112411e 1en n n n +++⎛⎫<+< ⎪⎝⎭,因为1112e11n n n na a n ++++==⎛⎫+ ⎪⎝⎭,所以()1411e1n n n na a -++<<,由11n n a a +<知:1n n a a +<,又因为()1411e n n n na a -++>,所以1111111113114(1)414(1)141411113e eeeee nnk k nnk k k k k k k n n k k k a a a a ==⎛⎫----⎪+++⎝⎭⋅++++==∑∑=⋅>===>∏∏,所以341e n n a a +>>.【点睛】方法点睛:利用导数证明不等式的基本步骤(1)作差或变形;(2)构造新的函数()h x ;(3)利用导数研究()h x 的单调性或最值;(4)根据单调性及最值,得到所证不等式.特别地:当作差或变形构造的新函数不能利用导数求解时,一般转化为分别求左、右两端两个函数的最值问题.。
蚌埠市2022届高三年级第四次教学质量检查考试数 学(文史类)本试卷满分150分,考试时间120分钟注意事项:1 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2 回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
第1题图1 若全集U和集合A,B的关系如图所示,则图中阴影部分表示的集合为A 瓓U(A∪B) B A∩(瓓UB)C 瓓U(A∩B) D (瓓UA)∩B2 已知i为虚数单位,复数z=-i,则下列复数与z互为共轭复数的是A z3B izC z+iD z-i3 “a=-2”是“直线ax+3y-1=0与直线6x+4y-3=0垂直”的A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分又不必要条件4 已知点P是△ABC的重心,则下列结论正确的是A (sin2A)PA→+(sin2B)PB→+(sin2C)PC→=0B (sinA)PA→+(sinB)PB→+(sinC)PC→=0 第5题图C (tanA)PA→+(tanB)PB→+(tanC)PC→=0D PA→+PB→+PC→=05 某几何体的三视图如图(每个小网格是边长为1的正方形),则该几何体的表面积为A 87π4+12 B 18π+12C 12π D 9π6 已知点O是原点,点F是双曲线C:x2a2-y2b2=1(a>0,b>0)的右焦点,过双曲线C的右顶点且垂直于x轴的直线与双曲线C的一条渐近线相交于点A,若|FA|=|FO|,则双曲线C的渐近线为槡A 3x±y=0B x槡±3y=0C 2x±y=0D x±2y=07 设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点不在一条直线上的概率为A15B25C12D458 已知a=log310,b=lg27,c槡=3,则a,b,c的大小关系为A a<b<cB a<c<bC c<b<aD b<c<a9 已知数列{an}满足a1=2,an+1=1+an1-an,则a2022=A 2B -3C -12D13 第10题图10 从空中某个角度俯视北京冬奥会主体育场“鸟巢”顶棚所得的局部示意图如图,在平面直角坐标系中,下列直线系方程(其中θ为参数,θ∈R)能形成这种效果的是A x+ysinθ-2=0 B xcosθ+y-2sinθ=0C xcosθ+ysinθ-2=0 D xcosθ+y-2=011 若幂函数f(x)=xα(α∈R)满足(α+1)f(x)=f(ex),则下列关于函数f(x)的判断正确的是A f(x)是周期函数 B f(x)是单调函数C f(x)关于点(0,1)对称 D f(x)关于原点对称12 阻尼器是一种以提供运动的阻力,耗减运动能量,从而达到减振效果的专业工程装置 如图,是被称为“镇楼神器”的我国第一高楼上海中心大厦的阻尼器 由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其离开平衡位置的位移S(cm)与时间t(s)的函数关系式为S(t)=3sin(ωt+φ)(ω>0),若该阻尼器模型在摆动过程中连续三次位移为S0(-3<S0<3)的时间分别为t1,t2,t3,且t1+t2=2,t2+t3=4,则下列为S(t)的单调区间的是第12题图A [k,k+1](k∈N)B k+12,k+[]32(k∈N)C [k,k+2](k∈N)D k+32,k+[]52(k∈N)二、填空题:本题共4小题,每小题5分,共20分。
安徽省蚌埠市2019-2020学年高考第四次质量检测数学试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知52i 12ia =+-(a ∈R ),i 为虚数单位,则a =( ) A .3B .3C .1D .5 【答案】C【解析】【分析】利用复数代数形式的乘法运算化简得答案.【详解】由52i 12ia =+-,得12i 2i a +=+,解得1a =. 故选:C.【点睛】 本题考查复数代数形式的乘法运算,是基础题.2.若函数f(x)=a |2x -4|(a>0,a≠1)满足f(1)=19,则f(x)的单调递减区间是( ) A .(-∞,2]B .[2,+∞)C .[-2,+∞)D .(-∞,-2] 【答案】B【解析】由f(1)=得a 2=,∴a=或a=-(舍),即f(x)=(.由于y=|2x-4|在(-∞,2]上单调递减,在[2,+∞)上单调递增,所以f(x)在(-∞,2]上单调递增,在[2,+∞)上单调递减,故选B.3.若不等式32ln(1)20a x x x +-+>在区间(0,)+∞内的解集中有且仅有三个整数,则实数a 的取值范围是( )A .932,2ln 2ln 5⎡⎤⎢⎥⎣⎦B .932,2ln 2ln 5⎛⎫ ⎪⎝⎭C .932,2ln 2ln 5⎛⎤ ⎥⎝⎦D .9,2ln 2⎛⎫+∞⎪⎝⎭【分析】由题可知,设函数()ln(1)f x a x =+,32()2g x x x =-,根据导数求出()g x 的极值点,得出单调性,根据32ln(1)20a x x x +-+>在区间(0,)+∞内的解集中有且仅有三个整数,转化为()()f x g x >在区间(0,)+∞内的解集中有且仅有三个整数,结合图象,可求出实数a 的取值范围.【详解】设函数()ln(1)f x a x =+,32()2g x x x =-,因为2()34g x x x '=-,所以()0g x '=, 0x ∴=或43x =, 因为403x << 时,()0g x '<, 43x >或0x <时,()0g x '>,(0)(2)0g g ==,其图象如下:当0a …时,()()f x g x >至多一个整数根;当0a >时,()()f x g x >在(0,)+∞内的解集中仅有三个整数,只需(3)(3)(4)(4)f g f g >⎧⎨⎩…, 3232ln 4323ln 5424a a ⎧>-⨯∴⎨-⨯⎩…, 所以9322ln 2ln 5a <…. 故选:C.【点睛】4.给出50个数 1,2,4,7,11,L ,其规律是:第1个数是1,第2个数比第1个数大 1,第3个数比第2个数大2,第4个数比第3个数大3,以此类推,要计算这50个数的和.现已给出了该问题算法的程序框图如图,请在图中判断框中的①处和执行框中的②处填上合适的语句,使之能完成该题算法功能( )A .i 50≤;p p i =+B .i 50<;p p i =+C .i 50≤;p p 1=+D .i 50<;p p 1=+【答案】A【解析】【分析】 要计算这50个数的和,这就需要循环50次,这样可以确定判断语句①,根据累加最的变化规律可以确定语句②.【详解】因为计算这50个数的和,循环变量i 的初值为1,所以步长应该为1,故判断语句①应为1i i =+,第1个数是1,第2个数比第1个数大 1,第3个数比第2个数大2,第4个数比第3个数大3,这样可以确定语句②为p p i =+,故本题选A.【点睛】本题考查了补充循环结构,正确读懂题意是解本题的关键.5.已知函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩,则方程[]()3f f x =的实数根的个数是( ) A .6B .3C .4D .5【答案】D【解析】【分析】 画出函数21,0()x x f x +≤⎧=⎨ ,将方程[]()3f f x =看作()(),3t f x f t ==交点个数,运用图象判断根【详解】 画出函数21,0()ln ,0x x f x x x +≤⎧=⎨>⎩令()(),3t f x f t =∴=有两解()()120,1,1,+t t ∈∈∞ ,则()()12,t f x f x t ==分别有3个,2个解,故方程[]()3f f x =的实数根的个数是3+2=5个故选:D【点睛】本题综合考查了函数的图象的运用,分类思想的运用,数学结合的思想判断方程的根,难度较大,属于中档题.6.在长方体1111ABCD A B C D -中,1123AB AD AA ==,,1DD 与平面1ABC 所成角的余弦值为( )A 3B .3C 15D 10【答案】C【解析】【分析】在长方体中11//AB C D , 得1DD 与平面1ABC 交于1D ,过D 做1DO AD ⊥于O ,可证DO ⊥平面11ABC D ,可得1DD A ∠为所求解的角,解1Rt ADD ∆,即可求出结论.【详解】在长方体中11//AB C D ,平面1ABC 即为平面11ABC D ,过D 做DO AD ⊥于O ,AB ⊥Q 平面AA D D ,DO ∴⊥平面11ABC D ,1DD A ∴∠为1DD 与平面1ABC 所成角, 在1111,3,2,5Rt ADD DD AA AD AD ∆===∴=, 111315cos 55DD DD A AD ∴∠===, ∴直线1DD 与平面1ABC 所成角的余弦值为155. 故选:C.【点睛】本题考查直线与平面所成的角,定义法求空间角要体现“做”“证”“算”,三步骤缺一不可,属于基础题. 7.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l 丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )A .10000立方尺B .11000立方尺C .12000立方尺D .13000立方尺【答案】A【解析】由题意,将楔体分割为三棱柱与两个四棱锥的组合体,作出几何体的直观图如图所示:则三棱柱的 四棱锥的体积 由三视图可知两个四棱锥大小相等,立方丈立方尺.故选A . 【点睛】本题考查三视图及几何体体积的计算,其中正确还原几何体,利用方格数据分割与计算是解题的关键.8.已知双曲线()2222:10,0x y C a b a b-=>>的一条渐近线经过圆22:240E x y x y ++-=的圆心,则双曲线C 的离心率为( )A 5B .5C 2D .2【答案】B【解析】【分析】求出圆心,代入渐近线方程,找到a b 、的关系,即可求解.【详解】解:()1,2E -,()2222:10,0x y C a b a b-=>>一条渐近线b y x a =- ()21b a=-⨯-,2a b = ()222222+b ,2,5c a c a a e ==+=故选:B【点睛】利用a b 、的关系求双曲线的离心率,是基础题.9.已知ABC ∆中内角,,A B C 所对应的边依次为,,a b c ,若2=1,7,3a b c C π+==,则ABC ∆的面积为( )A .332B 3C .33D .23由余弦定理可得227a b ab +-=,结合2=1a b +可得a ,b ,再利用面积公式计算即可.【详解】由余弦定理,得2272cos a b ab C =+-=22a b ab +-,由22721a b ab a b ⎧=+-⎨=+⎩,解得23a b =⎧⎨=⎩, 所以,11333sin 2322ABC S ab C ∆==⨯⨯⨯=. 故选:A.【点睛】 本题考查利用余弦定理解三角形,考查学生的基本计算能力,是一道容易题.10.函数cos ()cos x x f x x x+=-在[2,2]ππ-的图象大致为 A . B .C .D .【答案】A【解析】【分析】【详解】因为(0)1f =,所以排除C 、D .当x 从负方向趋近于0时,0cos cos x x x x <+<-,可得0()1<<f x .故选A .11.设i 是虚数单位,则()()2332i i +-=( )A .125i +B .66i -C .5iD .13利用复数的乘法运算可求得结果.【详解】由复数的乘法法则得()()22332656125i i i i i +-=+-=+. 故选:A.【点睛】本题考查复数的乘法运算,考查计算能力,属于基础题.12.函数tan 42y x ππ⎛⎫=- ⎪⎝⎭ 的部分图象如图所示,则 ()OA OB AB +⋅=u u u r u u u r u u u r ( )A .6B .5C .4D .3【答案】A【解析】【分析】 根据正切函数的图象求出A 、B 两点的坐标,再求出向量的坐标,根据向量数量积的坐标运算求出结果. 【详解】由图象得,令tan 42y x ππ⎛⎫=- ⎪⎝⎭=0,即42x ππ-=kπ,k Z ∈ k=0时解得x=2,令tan 42y x ππ⎛⎫=- ⎪⎝⎭=1,即424x πππ-=,解得x=3, ∴A(2,0),B(3,1),∴()()()2,0,3,1,1,1OA OB AB ===u u u r u u u r u u u r ,∴()()()5,11,1516OA OB AB +⋅=⋅=+=u u u r u u u r u u u r . 故选:A.【点睛】本题考查正切函数的图象,平面向量数量积的运算,属于综合题,但是难度不大,解题关键是利用图象与13.在()()6411 x y ++的展开式中,23x y 的系数为________.【答案】60【解析】【分析】根据二项展开式定理,求出6(1)x +含2x 的系数和4(1)y +含3y 的系数,相乘即可. 【详解】()()6411 x y ++的展开式中, 所求项为:2233232364654602C x C y x y x y ⨯=⨯=, 23x y 的系数为60.故答案为:60.【点睛】本题考查二项展开式定理的应用,属于基础题.14.已知等差数列{}n a 的前n 项和为S n ,若366,8S S ==-,则9S =____.【答案】42-【解析】【分析】由3S ,63S S -,96S S -成等差数列,代入366,8S S ==-可得9S 的值.【详解】解:由等差数列的性质可得:3S ,63S S -,96S S -成等差数列,可得:633962()S S S S S -=+-,代入366,8S S ==-,可得:942S =-,故答案为:42-.【点睛】本题主要考查等差数列前n 项和的性质,相对不难.15.已知数列{}n a 满足:点(),n n a 在直线210x y -+=上,若使1a 、4a 、m a 构成等比数列,则m =______【答案】13【解析】【分析】【详解】(),n n a Q 在210x y -+=上,21n a n ∴=+,14,,m a a a Q 成等比数列,241m a a a ∴=,即()81321m =+,解得:13m =.故答案为:13.【点睛】本题考查根据三项成等比数列求解参数值的问题,涉及到等比中项的应用,属于基础题.16.已知函数()()22,2,{2,2,x x f x x x -≤=-> 函数()()2g x b f x =-- ,其中b R ∈,若函数()()y f x g x =- 恰有4个零点,则的取值范围是__________.【答案】7,24⎛⎫ ⎪⎝⎭【解析】 ∵()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩, ∴()222,02{,0x x f x x x ---=<… ,∵函数y=f(x)−g(x)恰好有四个零点,∴方程f(x)−g(x)=0有四个解,即f(x)+f(2−x)−b=0有四个解,即函数y=f(x)+f(2−x)与y=b 的图象有四个交点,()()222,02{2,0258,2x x x y f x f x x x x x ++<=+-=-+>剟 , 作函数y=f(x)+f(2−x)与y=b 的图象如下,115572222224f f f f ⎛⎫⎛⎫⎛⎫⎛⎫+-=+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ , 结合图象可知,74<b<2, 故答案为7,24⎛⎫ ⎪⎝⎭. 点睛: (1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值,当出现f(f(a))的形式时,应从内到外依次求值.(2)当给出函数值求自变量的值时,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验,看所求的自变量的值是否满足相应段自变量的取值范围.三、解答题:共70分。
安徽省蚌埠市2019-2020学年高考数学第四次调研试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知直线,m n 和平面α,若m α⊥,则“m n ⊥”是“//n α”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .不充分不必要【答案】B 【解析】 【分析】由线面关系可知m n ⊥,不能确定n 与平面α的关系,若//n α一定可得m n ⊥,即可求出答案. 【详解】,m m n α⊥⊥Q ,不能确定αn ⊂还是αn ⊄,//m n n α∴⊥¿,当//n α时,存在a α⊂,//,n a , 由,m m a α⊥⇒⊥ 又//,n a 可得m n ⊥,所以“m n ⊥”是“//n α”的必要不充分条件, 故选:B 【点睛】本题主要考查了必要不充分条件,线面垂直,线线垂直的判定,属于中档题. 2.已知直线22+=mx ny ()0,0m n >>过圆()()22125x y -+-=的圆心,则11m n+的最小值为( ) A .1 B .2 C .3 D .4【答案】D 【解析】 【分析】圆心坐标为(1,2),代入直线方程,再由乘1法和基本不等式,展开计算即可得到所求最小值. 【详解】圆22(1)(2)5x y -+-=的圆心为(1,2),由题意可得222m n +=,即1m n +=,m ,0n >, 则1111()()24n m m n m n m n m n +=++=++…,当且仅当n mm n =且1m n +=即12m n ==时取等号, 故选:D .本题考查最值的求法,注意运用乘1法和基本不等式,注意满足的条件:一正二定三等,同时考查直线与圆的关系,考查运算能力,属于基础题.3.已知EF 为圆()()22111x y -++=的一条直径,点(),M x y 的坐标满足不等式组10,230,1.x y x y y -+≤⎧⎪++≥⎨⎪≤⎩则ME MF ⋅u u u r u u u r的取值范围为( )A .9,132⎡⎤⎢⎥⎣⎦B .[]4,13C .[]4,12D .7,122⎡⎤⎢⎥⎣⎦【答案】D 【解析】 【分析】首先将ME MF ⋅u u u r u u u r转化为21MT -u u u r ,只需求出MT 的取值范围即可,而MT 表示可行域内的点与圆心(1,1)T -距离,数形结合即可得到答案.【详解】作出可行域如图所示设圆心为(1,1)T -,则()()ME MF MT TE MT TF ⋅=+⋅+=u u u r u u u u r u u u r u u r u u u r u u u r22()()MT TE MT TE MT TE +⋅-=-u u u r u u r u u u r u u r u u u r u u r 21MT =-u u u r ,过T 作直线10x y -+=的垂线,垂足为B ,显然MB MT MA ≤≤,又易得(2,1)A -, 所以22[1(2)](11)13MA =--+--=22321(1)TB ==+- 故ME MF ⋅u u u r u u u r 271[,12]2MT =-∈u u u r .【点睛】本题考查与线性规划相关的取值范围问题,涉及到向量的线性运算、数量积、点到直线的距离等知识,考查学生转化与划归的思想,是一道中档题.4.如图,点E 是正方体ABCD-A 1B 1C 1D 1的棱DD 1的中点,点F ,M 分别在线段AC ,BD 1(不包含端点)上运动,则( )A .在点F 的运动过程中,存在EF//BC 1B .在点M 的运动过程中,不存在B 1M ⊥AEC .四面体EMAC 的体积为定值D .四面体FA 1C 1B 的体积不为定值 【答案】C 【解析】 【分析】采用逐一验证法,根据线线、线面之间的关系以及四面体的体积公式,可得结果. 【详解】 A 错误由EF ⊂平面AEC ,1BC //1AD 而1AD 与平面AEC 相交,故可知1BC 与平面AEC 相交,所以不存在EF//BC 1 B 错误,如图,作11B M BD ⊥由11,,AC BD AC BB BD BB B ⊥⊥⋂=又1,BD BB ⊂平面11BB D D ,所以AC ⊥平面11BB D D 又1B M ⊂平面11BB D D ,所以1B M AC ⊥ 由OE //1BD ,所以1B M OE ⊥AC OE O =I ,,AC OE ⊂平面AEC所以1B M ⊥平面AEC ,又AE ⊂平面AEC 所以1B M AE ⊥,所以存在 C 正确四面体EMAC 的体积为13M AEC AEC V S h -∆=⋅⋅ 其中h 为点M 到平面AEC 的距离,由OE //1BD ,OE ⊂平面AEC ,1BD ⊄平面AEC 所以1BD //平面AEC ,则点M 到平面AEC 的距离即点B 到平面AEC 的距离, 所以h 为定值,故四面体EMAC 的体积为定值D 错误由AC //11A C ,11A C ⊂平面11A C B ,AC ⊄平面11A C B 所以AC //平面11A C B ,则点F 到平面11A C B 的距离1h 即为点A 到平面11A C B 的距离, 所以1h 为定值所以四面体FA 1C 1B 的体积1111113F A C B A C B V S h -∆=⋅⋅为定值 故选:C 【点睛】本题考查线面、线线之间的关系,考验分析能力以及逻辑推理能力,熟练线面垂直与平行的判定定理以及性质定理,中档题.5.已知集合{}{13,},|2xA x x x ZB x Z A =|-≤∈=∈∈,则集合B =( ) A .{}1,0,1- B .{}0,1C .{}1,2D .{}0,1,2【答案】D 【解析】 【分析】弄清集合B 的含义,它的元素x 来自于集合A ,且2x 也是集合A 的元素. 【详解】因|1|3x -≤,所以24x -≤≤,故{}2,1,0,1,2,3,4A =--,又x ∈Z ,2x A ∈ ,则0,1,2x =, 故集合B ={}0,1,2. 故选:D. 【点睛】本题考查集合的定义,涉及到解绝对值不等式,是一道基础题.6.已知P 为圆C :22(5)36x y -+=上任意一点,(5,0)A -,若线段PA 的垂直平分线交直线PC 于点Q ,则Q 点的轨迹方程为( )A .221916x y +=B .221916x y -=C .221916x y -=(0x <)D .221916x y -=(0x >)【答案】B 【解析】 【分析】如图所示:连接QA ,根据垂直平分线知QA QP =,610QC QA -=<,故轨迹为双曲线,计算得到答案. 【详解】如图所示:连接QA ,根据垂直平分线知QA QP =,故610QC QA QC QP PC -=-==<,故轨迹为双曲线,26a =,3a =,5c =,故4b =,故轨迹方程为221916x y -=.故选:B .【点睛】本题考查了轨迹方程,确定轨迹方程为双曲线是解题的关键. 7.设()f x x =()00O ,,()01A ,,()()n A n f n ,,*n N ∈,设n n AOA θ∠=对一切*n N ∈都有不等式22223122222sin sin sin sin 123n nθθθθ+++⋅⋅⋅⋅⋅⋅+ 222t t <--成立,则正整数t 的最小值为( ) A .3 B .4C .5D .6【答案】A 【解析】 【分析】先求得222sin 111n 1n n n n n θ==-++,再求得左边的范围,只需2221t t --≥,利用单调性解得t 的范围. 【详解】由题意知sin 2n n n θ=+,∴222sin 111n 1n n n n n θ==-++, ∴22223122222sin sin sin sin 111111111112322334n 1n 1n n n θθθθ+++⋅⋅⋅⋅⋅⋅+=-+-+-+⋯+-=-++,随n 的增大而增大,∴11112n 1≤-<+, ∴2221t t --≥,即2210t t --≥,又f(t)=221t t --在t 1≥上单增,f(2)= -1<0,f(3)=2>0, ∴正整数t 的最小值为3. 【点睛】本题考查了数列的通项及求和问题,考查了数列的单调性及不等式的解法,考查了转化思想,属于中档题.8.,,a b αβαβ//////,则a 与b 位置关系是 ( ) A .平行 B .异面C .相交D .平行或异面或相交【答案】D 【解析】结合图(1),(2),(3)所示的情况,可得a 与b 的关系分别是平行、异面或相交.选D .9.函数()()()22214f x xxx =--的图象可能是( )A .B .C .D .【答案】A 【解析】 【分析】先判断函数()y f x =的奇偶性,以及该函数在区间()0,1上的函数值符号,结合排除法可得出正确选项. 【详解】函数()y f x =的定义域为R ,()()()()()()()2222221414f x x x x xxx f x ⎡⎤⎡⎤-=-⋅--⋅--=--=⎣⎦⎣⎦,该函数为偶函数,排除B 、D 选项; 当01x <<时,()()()222140f x x xx =-->,排除C 选项.故选:A. 【点睛】本题考查根据函数的解析式辨别函数的图象,一般分析函数的定义域、奇偶性、单调性、零点以及函数值符号,结合排除法得出结果,考查分析问题和解决问题的能力,属于中等题.10.设全集U =R ,集合{}02A x x =<≤,{}1B x x =<,则集合A B =U ( ) A .()2,+∞B .[)2,+∞C .(],2-∞D .(],1-∞【答案】C 【解析】∵集合{}02A x x =<≤,{}1B x x =<, ∴A B ⋃= (],2-∞点睛:本题是道易错题,看清所问问题求并集而不是交集. 11.已知函数()cos sin 2f x x x =,下列结论不正确的是( ) A .()y f x =的图像关于点(),0π中心对称 B .()y f x =既是奇函数,又是周期函数C .()y f x =的图像关于直线2x π=对称D .()y f x =【答案】D 【解析】 【分析】通过三角函数的对称性以及周期性,函数的最值判断选项的正误即可得到结果. 【详解】解::(2)cos(2)sin 2(2)cos sin 2()A f x x x x x f x πππ-=--=-=-,正确; :()cos()sin 2()cos sin 2()B f x x x x x f x -=--=-=-,为奇函数,周期函数,正确; :()cos()sin 2()cos sin 2()C f x x x x x f x πππ-=--==,正确;D : 232sin cos 2sin 2sin y x x x x ==-,令sin t x =,[]1,1t ∈-则()322g t t t =-,()226g t t '=-,[1t ∈-,1],则t <<时()0g t '>,1t -<<1t >>()0g t '<,即()g t 在⎛ ⎝⎭上单调递增,在1,⎛- ⎝⎭和⎫⎪⎪⎝⎭上单调递减;且39g ⎛= ⎝⎭,()10g -=,max y g ∴==<⎝⎭,故D 错误. 故选:D . 【点睛】本题考查三角函数周期性和对称性的判断,利用导数判断函数最值,属于中档题.12.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015 年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为70%.2015年开始,全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的( ) A .2728倍 B .4735倍 C .4835倍 D .75倍 【答案】B 【解析】 【分析】设贫困户总数为a ,利用表中数据可得脱贫率000000002409521090P =⨯⨯+⨯⨯,进而可求解. 【详解】设贫困户总数为a ,脱贫率0000000000240952109094a aP a⨯⨯+⨯⨯==,所以000094477035=. 故2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的4735倍. 故选:B 【点睛】本题考查了概率与统计,考查了学生的数据处理能力,属于基础题. 二、填空题:本题共4小题,每小题5分,共20分。
一、单选题1. 已知圆台上底面的半径为1,下底面的半径为2,高为,则该圆台的侧面积为( )A.B.C.D.2. 函数的大致图象是( )A.B.C.D.3. 已知幂函数是定义在区间上的奇函数,则( )A .8B .4C .2D .14. ( )A.B.C.D.5. 函数的部分图象如图所示,将函数图象上所有点的横坐标变为原来的(纵坐标不变),再向左平移个单位得到的图象,则下列说法的是()A .函数的最小正周期为B .函数在上单调递增C .函数的一个极值点为D .函数的一个零点为不正确6. 已知圆台的上、下底面直径分别为和,高为,则圆台的侧面展开图(扇环)的圆心角为( )A .B.C.D.7. 已知,,,则( )A.B.C.D.8. 唐朝的狩猎景象浮雕银杯如图1所示,其浮雕临摹了国画、漆绘和墓室壁画,体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体(假设内壁表面光滑,忽略杯壁厚度),如图2所示.已知球的半径为R ,酒杯的容积,则其内壁表面积为( )安徽省蚌埠市2022届高三下学期第四次教学质量检查文科数学试题(1)安徽省蚌埠市2022届高三下学期第四次教学质量检查文科数学试题(1)二、多选题三、填空题四、解答题A.B.C.D.9. 正多面体也称帕拉图立体,被喻为最有规律的立体结构,其所有面都只由一种正多边形构成(各面都是全等的正多边形,且每个顶点所接的面数都一样,各相邻面所成的二面角都相等).某中学在劳动技术课上,要求学生将一个近似正八面体的玉石切制成如图所示的棱长为2的正八面体P -ABCD -Q (其中E 、F 、H 分别为PA ,PB ,BC 的中点),则()A .AP 与CQ 为异面直线B .平面PAB ⊥平面PCDC .经过E 、F 、H 的平面截此正八面体所得的截面为正六边形D .此正八面体外接球的表面积为8π10.已知点为抛物线:上一点,为的焦点,,是上两个动点,则( )A .若的中点的横坐标为4,的最大值为8B .若直线经过点时,的最小值为4C .若,则直线的斜率为或D .直线,的倾斜角互补,与的另一个交点为A ,则直线的斜率为11.已知点为椭圆()的左焦点,过原点的直线交椭圆于,两点,点是椭圆上异于,的一点,直线,分别为,,椭圆的离心率为,若,,则( )A.B.C.D.12. 下列命题为真命题的是( )A.函数在定义域内是单调增函数B .函数的表达式可以改写为C .是最小正周期为的偶函数D .若一扇形弧长为,圆心角为,则该扇形的面积为13.抛物线的准线与轴相交于点P ,过点P作斜率的直线交抛物线于两点,F 为抛物线的焦点,若,则直线AB 的斜率k =_______.14. 已知,若恒成立,则实数的最大值为.15.若,其中是虚数单位,则_____________.16. 在中,角,,的对边分别为,,,已知,,,为三个相邻的自然数,且.(1)证明:;(2)若,,求的值.17. 设.(1)当时,求证:;(2)证明:对一切正整数n,都有.18. 如图,在三棱锥中,平面,,点、、分别是、、的中点.(1)求证:平面;(2)求证:平面平面.19. 在中,满足,M是中点.(1)若,求向量与向量的夹角的余弦值;(2)若O是线段上任意一点,且,求的最小值.20. 已知抛物线的焦点为为上异于原点的任意一点,过作直线的垂线,垂足为为轴上点.且四边形为平行四边形.直线与抛物线的另一个交点分别为(1)求抛物线的方程;(2)求三角形面积的最小值.21. 如图,已知椭圆C:+=1(a>b>0)的离心率为,左、右焦点分别为F1,F2,A为椭圆C上一点,AF1与y轴相交于点B,|AB|=|F2B|,|OB|=.(1)求椭圆C的标准方程;(2)设椭圆C的左、右顶点分别为A1,A2,过A1,A2分别作x轴的垂线l1,l2,椭圆C的一条切线l:y=kx+m(k≠0)与l1,l2分别交于M,N两点,求证:∠MF1N=∠MF2N.。