第十四章 量子力学基础

量子力学基础
量子力学是描述微观粒子行为的物理学理论。

它基于几个重要的基
本概念：
1. 粒子的波粒二象性：根据量子力学，微观粒子（如电子、光子等）既具有波动特性也具有粒子特性。

这意味着粒子的运动和行为可以通
过波动的方式来描述。

2. 不确定性原理：由于波粒二象性，确定粒子的位置和动量同时存
在的精确值是不可能的。

不确定性原理表明，我们无法同时准确测量
粒子的位置和动量，只能得到它们的概率分布。

3. 波函数：波函数是描述量子系统状态的数学函数。

它包含了粒子
的所有可能位置和动量的信息。

根据波函数，可以得出粒子的概率分布。

4. 算符和观测量：在量子力学中，物理量（如位置、动量、能量等）被表示为算符，而不是直接的数值。

物理系统的状态和性质可以通过
算符的作用来描述和测量。

5. 薛定谔方程：薛定谔方程是量子力学的基本方程，描述了量子系
统的时间演化。

它通过波函数的时间导数和能量算符之间的关系来表示。

量子力学的基础原理提供了一种独特而全面的方式来理解微观世界
的行为。

它已经在许多领域获得了成功应用，如原子物理、核物理、
量子化学和量子计算等。

量子力学的基础知识
量子力学是物理学中一种重要的理论，是对微观世界运动规律的
研究。

它不仅推动了物理学的发展，而且深刻影响了化学、生物学和
其他学科的发展。

量子力学以爱因斯坦的能量等离子体模型为基础，
以普朗克的统计力学和波动力学为补充，建立了一个用来描述微型物
体（尤其是粒子）的完整理论。

量子力学的核心思想是对微观世界物体运动规律的研究和解释，
即“量子”这个词。

量子是用来描述它们的最小基本单位，其大小只
有原子的尺寸。

量子力学认为，量子不仅能描述物体的性质，而且也
能描述它们的运动。

量子力学的基本原理有四个：第一，物体的运动
是概率性的；第二，波函数能完整地描述物体的性质；第三，能量的
变化是离散的；第四，波粒二象性原理。

量子力学看似简单，但它提供了许多有用的工具，帮助人们更好
地理解微观世界。

例如，它可以用来解释和解释自然界中复杂的现象，比如电磁现象、原子特性、原子结构、以及化学反应。

此外，它有助
于揭开古老的谜题，如结晶结构的形成，量子调控效应的作用，原子
核的物理性质，以及费米子的发现。

量子力学提供了一套全新的手段来探索物质的结构，特性和行为。

它不仅改变了物理学，而且也深刻影响了其他学科，比如化学、生物学、工程学和信息科学。

今天，量子力学已经发展成为一门独立的学科，它可以用来描述和研究微观世界中令人惊讶的现象，并有助于发
展各种新技术，有助于深入了解物质的结构和行为。

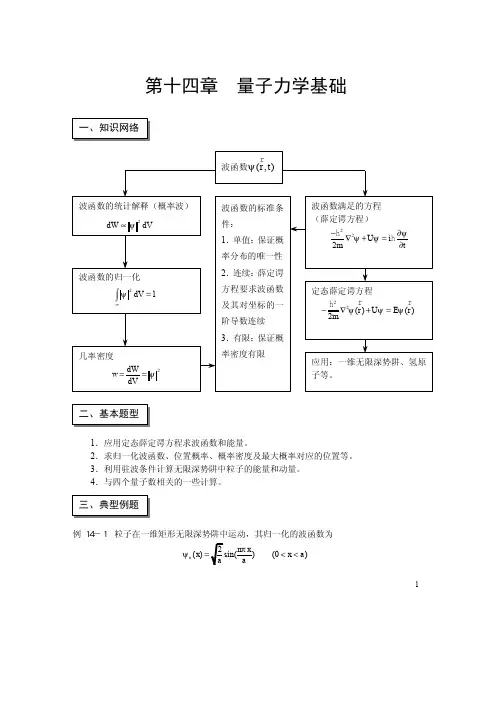
1第十四章 量子力学基础1．应用定态薛定谔方程求波函数和能量。

2．求归一化波函数、位置概率、概率密度及最大概率对应的位置等。

3．利用驻波条件计算无限深势阱中粒子的能量和动量。

4．与四个量子数相关的一些计算。

例１４－１ 粒子在一维矩形无限深势阱中运动，其归一化的波函数为()sin()(0)n n xx x a aπψ<<2若粒子处在n=1和n =2的状态，求发现粒子几率最大的位置各是多少？ ［解］ 在一维无限深方势阱中，粒子处在()n x ψ状态，在x 处发现粒子的概率密度为将w 对x 求导得 *2222()()()sin ()22sin cos22sin n n n x w x x x a adw n n x n xdx a aa n n x aa πψψπππππ==== （1）当n=1时，22sin0,x x k a aπππ==（k =0，1，2，），概率极值位置在2kax =处，选择k 值使x 满足0x a <<，则1,2ak x ==为极值处。

又 22223322424|cos()|cos 0a a x x d w x a dx a a ππππ====<所以， 2ax =处概率有极大值。

（2）当n =2时，44sin 0,x xk a aπππ==（k =0，1，2，3，）4kax =（k =0，1，2，3，）选择k 使x 满足0x a <<，则k =1，2，3，即3,,424a a ax =处概率有极值又 2223164cos()d w xadx a ππ=对2a x =，上式大于零，其他3,44a x a =上式小于零。

所以在3,44a ax =处概率有极大值。

例１４－２ 质量为m 的微观粒子在宽度为a 的刚性盒子里作一维运动（沿宽度方向），那么此粒子的动量、能量如何？ ［解］ 粒子封闭在一个宽度为a 的盒子里作一维运动，则与粒子对应的德布罗意波穿不出盒子的壁，因此在x =0和x =a 这两点永远是波节，即描述粒子运动的波函数()x ψ在这两点为零：(0)()0a ψψ==。

大学物理理论：量子力学基础1. 介绍量子力学是现代物理学的重要分支，它描述了微观粒子的行为和性质。

本文将介绍一些关于量子力学的基本概念和原理。

2. 原子结构和波粒二象性2.1 光电效应光电效应实验证明了光具有粒子性。

解释光电效应需要引入光量子（光子）概念，并讨论能量、动量和波长之间的关系。

2.2 德布罗意假设德布罗意假设认为微观粒子也具有波动性。

通过计算微观粒子的德布罗意波长，可以得出与经典物理不同的结果。

3. 波函数和不确定性原理3.1 波函数及其统计解释波函数描述了一个系统的状态，并包含了关于该状态各个可观测量的信息。

通过波函数，可以计算出一系列平均值，用来描述系统的特征。

3.2 不确定性原理不确定性原理指出，在某些情况下，无法同时准确地确定一个粒子的位置和动量。

这涉及到测量的本质和粒子与波的性质之间的关系。

4. 玻尔模型和量子力学4.1 玻尔模型玻尔模型是描述氢原子中电子运动的经典物理学模型。

它通过量子化角动量来解释氢原子光谱，并提供了首个对原子结构和能级分布的定性解释。

4.2 泡利不相容原理泡利不相容原理说明电子在同一能级上必须具有不同的状态。

这为填充多电子原子如何达到稳态提供了解释。

5. 薛定谔方程及其解析方法5.1 薛定谔方程薛定谔方程是量子力学中最基本的方程。

它描述了波函数随时间演化的规律，以及如何通过波函数求得可观测量的平均值。

5.2 解析方法介绍几种求解薛定谔方程的解析方法，如分离变量法、变换法等，并通过示例问题演示其使用过程和计算结果。

6. 哈密顿算符与算符方法6.1 哈密顿算符哈密顿算符是用于描述系统总能量的数量。

介绍哈密顿算符的概念和性质，并讨论如何通过其本征值和本征函数求解问题。

6.2 算符方法算符是量子力学中描述可观测量的数学工具，介绍常见的一些算符，如位置算符、动量算符等，并讨论它们之间的对易关系。

结论量子力学作为现代物理学的基石，为我们理解微观世界提供了全新的视角。

量子力学基础
1 量子力学
量子力学是20世纪初在物理学中提出的理论，它是研究微观物理
现象的科学理论。

它可以描述元子、原子和分子的一般特性，还可以
用于解释多种物质的晶体结构及其他物理性质。

它的基本概念是微观世界中的物理量不再遵循经典物理学。

量子
力学认为，物质的基本特性不再是经典物理学中的连续性和可压缩性，而是量子概念体现的离散性和不可分割性。

2 基本原理
量子力学的基本原理是基本物质粒子是和弦性，也就是物质具有
波和粒子双重性，不同物质之间及物质量之间都有联系，这种联系实
际上在量子力学中被形象描述为薛定谔方程。

此外，量子力学还涉及光子、原子、电子和晶体之间的相互作用，以及晶体结构的形成。

例如，量子理论可以用来解释晶体中的空间结构，特性的微观原因，以及晶体的光学性质，磁性，热力学性质等。

3 应用
量子力学存在了很长时间，但是真正开始发挥作用一直到20世纪
初才开始，因为它为研究微观物理现象提供了一种新的和不同的视角，甚至可以被用来解释一些在经典物理学无法解释的现象。

现在，量子力学的基本理论已经被广泛应用于化学、物理学、凝聚态物理学、核物理学和天体物理学。

量子力学的基本原理也被用于一些新的和先进的技术，比如超导电子学、量子计算机等。

量子力学基础量子力学是一门研究微观世界的物理学科，其研究对象是原子，分子以及更小的粒子。

相比经典力学而言，量子力学更加深奥、多变，虽然被数学化的描述形式非常精致，但仍然存在着一些难以理解的问题。

1. 粒子的波粒二象性：偏振实验回归到物理学的起点，我们会想到牛顿第一定律、摩擦力等经典概念，这些概念结合起来就可以很好地解释力学现象，却无法解释一些现象如光学实验中的偏振现象，也就是说，光具有波动性质，这丝毫不起眼的光子却颠覆了科学家们对物质的认识。

波粒二象性既是一种直观表现，又是一种对量子粒子行为的描述。

最著名的实验就是二十世纪初由英国科学家Thomas Young首次提出的杨氏双缝干涉实验，这个实验在光学和其他领域都被广泛用于解释量子力学基础概念，它不仅欧洲牛津大学的量子力学教材中出现，而且出现在了《生活大爆炸》等大众文化中。

这项实验能够说明光实际上是由一系列能够相互干扰的波构成的，而同样可以得出这一结论的实验不仅仅局限于光学，例如，Young实验也在微观粒子的电子双缝干涉实验中被重复实现，这一实验表明了量子粒子行为上的奇异性质。

2. 物理量的不确定性：海森堡测不准原理在粒子的量子状态下，物理特征指标可以发生变化，并且量子比经典物理学更复杂得多。

海森堡测不准原理是量子力学中的一个基本概念，它断言在某些物理实验中，同时测量粒子的两个或更多个性质（例如，位置和动量）是不可能获得一个完全准确的结果的。

例如，我们试图通过测量粒子的位置来确定其精确的动量，我们需要测量粒子位置的变化，这样粒子就不能在特定时间的某个位置上。

这种粒子位置和动量之间的不确定性，是一种基本的量子现象，可以在许多实验中观察到。

3. 量子纠缠：特别的量子机制量子纠缠也是量子力学基础领域的一个重要现象，可以帮助我们更好地理解量子领域中的基本概念。

粒子的量子状态能够纠缠，这意味着，当两个或更多粒子在某种特定的方式下存在时，它们的抽象量子状态将是相互依存的。

量子力学基础量子力学是现代物理学的基石之一，它描述了微观世界中粒子的行为和性质。

本文将介绍量子力学的基础知识，包括波粒二象性、波函数、测量和不确定性原理等内容。

一、波粒二象性量子力学的核心观念之一是波粒二象性，即物质既可以表现出粒子的离散性质，又可以表现出波的波动性质。

这一观念由德布罗意提出，他认为任何物体都具有波函数。

二、波函数与波动方程波函数是量子力学中描述微观粒子状态的数学函数。

它可以用来计算粒子的位置、动量和能量等物理量。

根据薛定谔方程，波函数满足定态和非定态的波动方程。

三、量子力学中的测量在量子力学中，测量是指对粒子某个物理量进行观测并得到相应的结果。

与经典物理学不同的是，量子物理学中的测量结果是随机的，只能得到概率分布。

四、不确定性原理不确定性原理是量子力学中的重要概念，由海森堡提出。

不确定性原理指出，在给定的时刻，不能同时准确测量一个粒子的位置和动量。

精确测量其中一个物理量，将会导致对另一个物理量的测量结果存在不确定性。

五、量子力学中的算符在量子力学中，算符是用来描述物理量的操作。

比如，位置算符、动量算符和能量算符等。

根据算符的性质，可以求得粒子的期望值和本征态等信息。

六、量子纠缠和超导量子纠缠是量子力学中的一个重要现象，它描述了两个或多个粒子之间的紧密联系。

超导是一种物质在低温条件下具有零电阻和完全抗磁的特性。

七、量子力学的应用量子力学在许多领域都有广泛的应用，尤其是在量子计算、量子通信和量子传感器等前沿科技领域。

量子力学的发展为人类带来了许多革命性的技术和突破。

八、总结量子力学作为现代物理学的重要理论基础，对我们理解微观世界具有重要意义。

本文介绍了量子力学的基础知识，包括波粒二象性、波函数、测量和不确定性原理等内容。

希望读者通过阅读本文，对量子力学有更深入的了解，并能进一步探索其在科学和技术中的应用前景。

量子力学基础量子力学是物理学中一门非常重要的学科，它研究的是微观世界中的粒子和它们的行为。

通过量子力学可以解释和预测原子、分子和更小尺度的粒子的性质和现象。

本文将简要介绍量子力学的基础概念和原理，帮助读者初步了解这一领域。

1. 微观粒子的双重性量子力学的一个基本原理是微观粒子具有双重性。

这意味着微观粒子既可以表现出波动性，也可以表现出粒子性。

这个原理最早可以通过Young双缝实验来解释。

实验中，光通过两个小缝后，形成了干涉图样，这表明光具有波动性。

然而，如果将光的强度逐渐降低，最终只有一个光子通过，它却在屏幕上留下了一点，这表明光具有粒子性。

这种波粒二象性对于微观粒子是普遍存在的。

2. 波函数和概率解释在量子力学中，一种描述微观粒子的方式是使用波函数。

波函数可以提供有关粒子位置、动量和能量等方面的信息。

然而，波函数本身不是物理量，而是只包含了所有可能的观测结果的信息。

通过波函数的模的平方，我们可以得到在特定条件下测量特定性质的概率分布。

3. 不确定性原理量子力学的不确定性原理表明，某些性质无法同时被精确测量。

最著名的不确定性原理是海森堡不确定性原理，它指出对于一对共轭变量（如位置和动量，能量和时间等），无法同时精确测量两者。

测量其中一个属性的精确度越高，另一个属性的测量结果就越不确定。

4. 薛定谔方程薛定谔方程是量子力学的核心方程，它描述了量子体系的演化和态函数的变化。

薛定谔方程是一个偏微分方程，其中包含了哈密顿算符和波函数的时间和空间导数。

通过求解薛定谔方程，我们可以得到粒子的能级和波函数的时间演化。

5. 量子态和量子测量在量子力学中，粒子的量子态可以用量子力学的符号形式表示，如波函数、态矢量、密度矩阵等。

量子测量是将粒子从一个态转变为另一个态的过程。

在测量过程中，粒子会塌缩到某个特定的态上，并得到对应的观测结果。

这种塌缩是随机的，由波函数的概率分布决定。

6. 力学量和算符在量子力学中，物理量（如位置、动量、角动量等）由算符来表示。

物理十四章知识点物理是一门让人类对世界更深入了解的科学，而自古至今，人们对于物理的探索一直没有停止过。

近代物理则是自19世纪中后期所出现的科学分支。

这门学科的研究，带来了磁场、电场、光、热、声、运动等多领域的发展和进步，不仅为人类生产和生活带来了帮助，而且让人们对于宇宙更深入的探索也产生了重大的震撼。

而本文，将围绕物理的十四章内容，带领读者一步步了解物理学的奥秘。

第一章：物理学的基本观念在这一章，我们将了解物理学的定义以及物理学家的研究思路。

物理学所研究的是自然界现象，这些现象可以被测量和描述，物理学家追求的是通过理论推理的方法，发现规律性的现象。

我们还将介绍物理学所面临的难题以及物理学在人类历史上的地位。

第二章：运动的描述在这一章，我们将介绍运动的基本概念及其描述方式。

运动包括匀速直线运动和非匀速直线运动等。

可以通过坐标和速度来描述物体的运动状态。

除此之外，我们还将了解伽利略变换和洛伦兹变换的原理以及它们分别适用的条件。

第三章：牛顿运动定律在这一章，我们将介绍牛顿运动定律，这是高中物理学习中必须掌握的基本概念。

这一定律描述了物体的受力情况及其运动状态的关系。

我们还将学习到重力、弹性力、摩擦力等常见力的作用方式。

第四章：功、能、能量守恒定律在这一章，我们将学习到功、能、能量守恒定律。

功表示力做功的大小及其方向，能表示物体的运动状态，而能量守恒定律描述了能量在物理系统中的转化和守恒。

这一章也将介绍机械能的概念及其转化关系。

第五章：动量、冲量在这一章，我们将介绍动量和冲量。

动量是描述物体运动状态的一种物理量，而冲量描述了物体所受到的合外力的作用。

我们还将将学到策动原理的思想及其应用。

第六章：角动量在这一章，我们将学习到角动量的概念及其转化关系。

旋转点、旋转轴等都是与角动量相关的概念，在应用当中需要熟练掌握。

第七章：振动、波动在这一章，我们将学习到振动和波动两种基本的物理过程。

振动表示物体围绕平衡位置做周期性的运动，而波动是机械波和电磁波等物理现象的集合。

量子力学基础概述量子力学，作为现代物理学的基石之一，探索了微观世界中的奇妙现象和规律。

本文将为您简要介绍量子力学的基础知识，帮助您对这一领域有更清晰的认识。

什么是量子力学？量子力学是描述微观世界的物理理论，它的提出在20世纪初掀起了物理学的革命。

传统的经典物理学可以很好地描述宏观世界的行为，但在微观尺度下，经典物理学无法解释一些观测到的现象。

量子力学通过引入量子概念，提供了对微观世界中粒子行为的新解释。

量子力学的基本原理波粒二象性量子力学中最核心的概念之一就是波粒二象性。

根据量子力学的观点，粒子既可以表现出粒子的特性，也可以表现出波的特性。

这意味着它们既有确定的位置，又有确定的动量和波长。

不确定性原理不确定性原理是量子力学的另一个重要原理。

它表明，在某些情况下，无法同时准确测量一个粒子的位置和动量。

这种不确定性关系表明，粒子的位置和动量存在一种固有的局限性。

波函数和量子态在量子力学中，波函数是描述系统状态的数学函数。

通过波函数，我们可以得知粒子的位置和动量等信息。

量子态则是波函数的统计解释，它描述了一个物理系统的状态。

量子力学的应用量子力学已经取得了许多重要的应用，以下是其中的几个方面：原子物理量子力学提供了对原子结构和原子能级的解释。

它解释了为什么不同的元素有不同的特性，以及为什么只有特定的光子能被原子吸收或发射。

量子计算与量子通信量子力学在计算机科学和通信领域有着重大的应用潜力。

量子计算利用了量子叠加和量子纠缠等量子效应，可以执行某些问题的快速计算。

量子通信则利用了量子纠缠的特性，实现了更加安全和高效的数据传输。

量子光学量子光学研究的是光与物质之间的相互作用，并探索光的粒子性和波动性。

它对发展新型光学器件和技术具有重要意义，如激光、光纤通信和光存储等。

量子力学作为现代物理学的重要支柱，为我们解释了微观世界的奇妙现象。

通过波粒二象性、不确定性原理和波函数等概念，我们可以更好地理解微观粒子的行为。

大学物理量子力学的基础量子力学是一门研究微观世界的物理学科，它是对自然界最基本的物质粒子行为进行描述的理论。

在大学物理学课程中，量子力学作为重要的一部分，对于学生来说是一门具有挑战性的学科。

本文将介绍大学物理中量子力学的基础知识，包括量子力学的起源、基本理论、波粒二象性等内容。

一、量子力学的起源量子力学最早起源于20世纪初的实验观察，其中包括普朗克黑体辐射定律和爱因斯坦光电效应等重要实验结果。

这些实验现象无法被经典物理学所解释，迫使科学家们提出一种新的理论来描述微观尺度的物理现象。

1918年，德国物理学家玻恩提出了量子假设，为后来的量子力学奠定了基础。

二、量子力学的基本理论量子力学的基本理论由薛定谔方程和量子力学算符理论构成。

薛定谔方程是描述量子系统演化的基本方程，它描述了系统波函数随时间的演化规律。

而量子力学算符则用来描述物理量的测量和运算，它们对应于物理量的观测值和运动方程。

三、波粒二象性波粒二象性是量子力学的核心概念之一。

根据量子力学的理论，微观粒子在不同的实验条件下既可以呈现出波动性质，又可以表现出粒子性质。

具体而言，光的行为表现为波动性，在双缝实验中呈现出干涉和衍射现象；而电子、中子等微观粒子也可以表现出波动性质，例如在杨氏实验中呈现出干涉条纹。

四、量子力学中的基本概念为了更好地理解量子力学，我们需要掌握其基本概念。

首先是波函数，它描述了量子系统的状态，并且可以用来计算物理量的平均值。

其次是量子态，量子系统所处的状态可以用量子态来描述，量子力学中的态叠加原理也是量子力学与经典物理学的一个重要差异。

最后是测量，量子力学中的测量与经典物理学有很大的不同，测量结果会塌缩波函数，并且存在不确定性原理。

五、量子力学在实际应用中的意义量子力学不仅是基础物理学的重要学科，还被广泛应用于许多领域。

在材料科学中，量子力学的理论模型可以用来解释材料的电子结构和性质。

在计算机科学中，量子计算的概念正在成为未来计算机技术的重要方向。

量子力学基础知识量子力学是描述微观物体行为的理论，其基本概念和原理在20世纪初由物理学家们提出，并在随后的发展中得到了广泛的应用。

本文将介绍一些量子力学的基础知识，包括波粒二象性、不确定性原理、波函数与叠加原理等。

一、波粒二象性波粒二象性是指微观物体既可以表现为粒子，也可以表现为波动。

在经典物理学中，物体被认为是粒子，其运动轨迹可以用精确的数学公式表示。

然而，当物体的尺寸减小到微观尺度时，量子力学揭示了一种全新的特性。

以光子为例，光子是光的基本单位，既可以看作是粒子也可以看作是波动。

在光的干涉和衍射实验中，光呈现出波动性质，表现为波的干涉和衍射现象。

而在光电效应和康普顿散射实验中，光呈现出粒子性质，发生光电效应或散射，与电子产生相互作用。

二、不确定性原理不确定性原理是量子力学中的基本原理之一，由海森堡提出。

该原理指出，在某些物理量的测量中，位置和动量、能量和时间等物理量的精确测量是不可能的。

以位置和动量为例，不确定性原理表明，越精确地测量粒子的位置，对其动量的测量就越不准确，反之亦然。

这是由于测量过程本身对粒子的状态产生了不可避免的干扰，以致无法同时准确测量两个共轭变量。

三、波函数与叠加原理波函数是描述量子力学系统的主要工具，它包含了对系统的所有可能状态的信息。

波函数的平方表示了在某一状态下测得某个特定物理量的概率。

波函数的演化由薛定谔方程描述。

叠加原理是指两个或两个以上波函数可以相互叠加形成新的波函数。

在量子力学中，粒子同时处于多个状态的叠加是合理的。

例如，双缝干涉实验中，一个粒子可以通过两个缝同时传播，形成干涉图样。

四、量子纠缠量子纠缠是量子力学中一个重要的现象，表明两个或两个以上粒子之间存在着神秘的联系。

当纠缠的量子系统中的一个粒子状态发生改变时，与其纠缠在一起的其他粒子的状态也会瞬间发生改变，无论它们之间有多远的距离。

量子纠缠有广泛的应用，如量子通信、量子密钥分发和量子计算等。

通过利用量子纠缠，可以实现更安全的通信和更高效的计算。

（完整）量子力学14编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）量子力学14）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）量子力学14的全部内容。

§3-6 力学量的平均值按照前面的假设，量子力学中表示力学量的算符为厄米算符,它们的本征函数组成正交归一完备函数系。

比如,力学量算符Fˆ的本征值方程为 )()(ˆx x F nn n ψλψ= 则{}()n x ψ构成正交归一完备本征函数系。

如果量子体系处于状态)(x ψ，则可把它向{}()n x ψ作展开，即∑=ψnn n x c x )()(ψ展开系数⎰ψ=dx x x c n n )()(*ψ如果)(x ψ已归一化，则∑∑∑⎰⎰===ψψ=nn mnmn n m mnn m n m c c c dx c c dx x x 2****)()(1δψψ可以看出，2n c 具有概率的意义，它表示在)(x ψ态下测得ˆF的本征值为n λ的概率。

特别地，如果)(x ψ是算符F ˆ的某一个本征函数()n x ψ,则上式中除21nc =外,其余系数皆为0，此时测量F 时得到的值必为n λ。

因此，力学量F 在)(x ψ态下的平均值为∑=nn n c F 2λ因为∑∑∑⎰∑⎰⎰====ψψnnn mnmn n nm mnn n m n m mnn m n m c c c dxc c dx F c c dx x F x 2******ˆ)(ˆ)(λδλψλψψψ所以,平均值公式又可写成⎰ψψ=dx x Fx F )(ˆ)(* 在三维空间时,平均值公式*ˆ()()F r Fr d τ=ψψ⎰ 例如，在(,)r t ψ态下，坐标的平均值为*(,)(,)r r r t r r t d τ∞-∞==ψψ⎰这一点容易理解，因为2(,)r t d τψ表示t 时刻在r d r r+→内找到粒子的概率,因此2*(,)(,)(,)r r t rd r t r r t d ψτψψτ∞∞-∞-∞==⎰⎰再如，在(,)r t ψ态下，动量的平均值为*ˆ(,)(,)p r t pr t d τ=ψψ⎰ 这一点也可以从动量算符本身推得。

量子力学基础量子力学是描述微观世界中物质和能量行为的一门科学，它在20世纪初由物理学家们逐步建立起来。

量子力学是现代物理学的基石，对于理解原子、分子、固体、核反应等现象具有重要意义。

本文将介绍一些量子力学的基础知识。

1. 波粒二象性量子力学将微观粒子既可以表现为粒子，又可以表现为波的特性称为波粒二象性。

这一概念是量子力学的核心之一。

例如，电子不仅可以具有粒子的位置和动量，还可以像波动一样干涉和衍射。

这对于解释实验数据和理解微观效应非常关键。

2. 不确定性原理不确定性原理是量子力学的另一个重要原理，由海森堡于1927年提出。

不确定性原理指出，在某些物理量的测量中，无法同时准确测量其位置和动量，或者能量和时间。

这是因为测量过程会对被测量的系统产生干扰，从而使得同时准确测量两个互相联系的物理量成为不可能。

3. 波函数和波函数坍缩波函数是量子系统在给定时刻的状态描述，它是与量子力学中的各个物理量相对应的一组数学函数。

波函数可以用来计算某个物理量的概率分布，从而预测实验测量结果。

当对一个物理量进行测量时，波函数会发生坍缩，即系统会塌缩到某个确定的状态上。

4. 薛定谔方程薛定谔方程是量子力学的基本方程之一，由奥地利物理学家薛定谔于1925年提出。

薛定谔方程描述了量子系统的演化规律，可用来计算波函数随时间的变化。

薛定谔方程是解释原子、分子、凝聚态物质等现象的重要工具。

5. 超越边界和量子隧穿效应在经典物理学中，粒子的运动受到势能的限制，当粒子的能量低于势垒时，无法跨越势垒。

然而，在量子力学中，由于波粒二象性，粒子可以通过量子隧穿效应，以概率的形式穿越势垒，即使其能量低于势垒。

6. 基态和激发态在量子力学中，系统的能量可以分为不同的离散能级。

基态是系统的最低能量状态，而激发态是高于基态的能量状态。

通过向系统提供能量，可以使系统从基态跃迁到激发态，这在原子和分子的能级转移中起着重要作用。

总结：量子力学作为现代科学的重要分支，为我们理解微观世界提供了重要的工具和理论框架。

量子力学基础引言量子力学是现代物理学的基石之一，它主要研究微观粒子的行为和性质。

与经典力学不同，量子力学在描述微观世界时展现出了一系列独特的现象和规律。

本文将简要介绍量子力学的基本概念、重要实验以及一些常见的误解。

波粒二象性波粒二象性是量子力学的核心概念之一。

微观粒子，如电子和光子，既表现出波动性，又表现出粒子性。

这一现象最早由德布罗意提出，并在后来的实验中得到验证。

双缝干涉实验最著名的演示波粒二象性的实验是双缝干涉实验。

在这个实验中，单个光子或电子通过两个狭缝后，会在屏幕上形成干涉条纹。

这表明它们具有波动性。

然而，当试图探测它们究竟通过哪个缝时，干涉条纹消失，表现出粒子性。

这一结果挑战了经典物理学的直觉。

不确定性原理不确定性原理由海森堡提出，是量子力学的另一个基本原理。

它指出，不可能同时精确测量一个粒子的位置和动量。

这意味着在微观世界中，我们无法完全确定一个粒子的状态，只能得到其概率分布。

超导性和量子纠缠超导性和量子纠缠是量子力学应用的两个重要领域。

超导性是指在低于某个温度时，某些材料的电阻突然变为零。

这一现象在磁悬浮列车和粒子加速器等领域有重要应用。

量子纠缠则是指两个或多个粒子之间存在一种特殊的关联，即使它们相隔很远，也能瞬间影响彼此的状态。

这一现象在量子通信和量子计算中具有巨大的潜力。

常见误解尽管量子力学取得了巨大的成功，但仍然存在一些常见的误解。

例如，有人认为量子力学表明“一切都是不确定的”，或者“观察者的意识决定了现实”。

这些观点都是对量子力学的误读。

量子力学并不否认现实的存在，而是揭示了微观世界的复杂性和不可预测性。

结论总之，量子力学是一门深奥而迷人的学科，它改变了我们对自然界的理解。

虽然它的许多概念和现象与我们的日常经验相悖，但正是这些特性使得量子力学成为了现代科技发展的基石。

随着研究的深入和应用的拓展，量子力学将继续在未来的科学和技术领域发挥重要作用。