HMM隐马尔可夫模型

隐马尔可夫模型原理
隐马尔可夫模型（Hidden Markov Model, HMM）是一种用来
描述状态序列的概率模型。

它基于马尔可夫链的理论，假设系统的状态是一个没有直接观察到的随机过程，但可以通过观察到的结果来推断。

HMM的原理可以分为三个关键要素：状态集合、转移概率矩
阵和观测概率矩阵。

1. 状态集合：HMM中的状态是不能直接观测到的，但可以从
观测序列中推断出来。

状态集合可以用S={s1, s2, ..., sn}表示，其中si表示第i个状态。

2. 转移概率矩阵：转移概率矩阵A表示在一个时间步从状态
si转移到状态sj的概率。

可以表示为A={aij}，其中aij表示从状态si到状态sj的转移概率。

3. 观测概率矩阵：观测概率矩阵B表示在一个时间步观测到
某个输出的概率。

可以表示为B={bj(o)}，其中bj(o)表示在状
态sj下观测到输出o的概率。

通过这些要素，HMM可以用来解决三类问题：
1. 评估问题：给定模型参数和观测序列，计算观测序列出现的概率。

可以使用前向算法或后向算法解决。

2. 解码问题：给定模型参数和观测序列，寻找最可能的状态序
列。

可以使用维特比算法解决。

3. 学习问题：给定观测序列，学习模型的参数。

可以使用Baum-Welch算法进行无监督学习，或使用监督学习进行有标注数据的学习。

总之，HMM是一种可以用来描述随机过程的模型，可以用于许多序列预测和模式识别问题中。

它的简洁性和可解释性使其成为机器学习领域中重要的工具之一。

隐马尔可夫模型(HMM)在中文分词中的处理流程1.引言中文分词是自然语言处理领域中一个重要的任务，其目的是将连续的中文文本切分成有意义的词语。

隐马尔可夫模型(H id de nM ar ko vM ode l,H MM)是一种常用的统计模型，已被广泛应用于中文分词任务中。

本文将介绍H MM在中文分词中的处理流程。

2. HM M基本原理H M M是一种基于统计的模型，用于建模具有隐含状态的序列数据。

在中文分词任务中，HM M将文本视为一个观测序列，其中每个观测代表一个字或一个词，而隐藏的状态则代表该字或词的标签，如“B”表示词的开始，“M”表示词的中间，“E”表示词的结尾，“S”表示单字成词。

H M M通过学习观测序列和隐藏状态之间的转移概率和发射概率，来实现对中文分词的自动标注和切分。

3. HM M中文分词流程3.1数据预处理在使用H MM进行中文分词之前，首先需要对文本数据进行预处理。

预处理步骤包括去除无关字符、去除停用词、繁简转换等。

这些步骤旨在减少干扰和噪音，提高分词的准确性。

3.2构建H M M模型构建HM M模型包括确定隐藏状态集合、观测集合以及初始化转移概率和发射概率。

在中文分词中，隐藏状态集合包括“B”、“M”、“E”和“S”，观测集合包括所有字或词。

转移概率和发射概率的初始化可以使用统计方法，如频次统计、平滑处理等。

3.3模型训练模型训练是指根据已标注的中文语料库，利用最大似然估计或其他方法，估计转移概率和发射概率的参数。

训练过程中可以使用一些优化算法，如维特比算法、B aum-We lc h算法等。

3.4分词标注在模型训练完成后，利用已学习到的参数和观测序列，可以通过维特比算法进行分词标注。

维特比算法是一种动态规划算法，可以求解出最可能的隐藏状态序列。

3.5分词切分根据分词标注结果，可以进行分词切分。

根据“B”、“M”、“E”和“S”标签，可以将连续的字或词切分出来，得到最终的分词结果。

深度学习中的序列生成模型深度学习中的序列生成模型是指通过神经网络模型生成序列数据的一种方法。

它在自然语言处理、语音识别、机器翻译等领域具有重要应用。

本文将介绍序列生成模型的基本原理、主要应用以及当前的研究进展。

一、序列生成模型的基本原理序列生成模型的核心思想是根据历史上的已观察数据来预测未来的数据。

常见的序列生成模型包括隐马尔可夫模型（HMM）、循环神经网络（RNN）以及变分自编码器（VAE）等。

下面将分别介绍这几种模型的基本原理。

1. 隐马尔可夫模型（HMM）HMM是一种统计模型，假设观察序列由一个未知的隐含状态序列和对应的观察序列组成。

HMM通过定义状态转移概率矩阵和观测概率矩阵来进行模型训练和预测。

HMM在语音识别和自然语言处理中得到广泛应用。

2. 循环神经网络（RNN）RNN是一种具有记忆功能的神经网络模型，能够处理序列数据的依赖关系。

RNN通过在网络中引入循环连接来建立序列之间的依赖关系，从而将历史的信息传递到未来。

RNN在机器翻译和文本生成等任务中表现出色。

3. 变分自编码器（VAE）VAE是一种生成模型，通过学习数据的潜在分布来生成新的样本。

在序列生成中，VAE通过学习输入序列的潜在表示来生成新的序列。

VAE的优势在于可以通过潜在空间的插值来生成具有连续变化的序列数据。

二、序列生成模型的主要应用序列生成模型在自然语言处理、语音识别和机器翻译等领域广泛应用。

下面将介绍一些具体的应用案例。

1. 机器翻译机器翻译是将一种语言的句子自动翻译成另一种语言的任务。

序列生成模型在机器翻译中发挥着重要作用，能够将源语言句子转化为目标语言句子。

当前的主流机器翻译系统多基于循环神经网络模型或者变分自编码器模型。

2. 文本生成文本生成是指通过模型生成新的文本内容。

序列生成模型可以学习到文本数据的潜在分布，并可以生成与原始数据类似的新文本。

文本生成在文学创作、自动对话系统等方面有广泛的应用。

3. 音乐生成音乐生成是利用序列生成模型来创作新的音乐作品。

⼀⽂搞懂HMM（隐马尔可夫模型）什么是熵(Entropy)简单来说，熵是表⽰物质系统状态的⼀种度量，⽤它⽼表征系统的⽆序程度。

熵越⼤，系统越⽆序，意味着系统结构和运动的不确定和⽆规则；反之，，熵越⼩，系统越有序，意味着具有确定和有规则的运动状态。

熵的中⽂意思是热量被温度除的商。

负熵是物质系统有序化，组织化，复杂化状态的⼀种度量。

熵最早来原于物理学. 德国物理学家鲁道夫·克劳修斯⾸次提出熵的概念，⽤来表⽰任何⼀种能量在空间中分布的均匀程度，能量分布得越均匀，熵就越⼤。

1. ⼀滴墨⽔滴在清⽔中，部成了⼀杯淡蓝⾊溶液2. 热⽔晾在空⽓中，热量会传到空⽓中，最后使得温度⼀致更多的⼀些⽣活中的例⼦:1. 熵⼒的⼀个例⼦是⽿机线，我们将⽿机线整理好放进⼝袋，下次再拿出来已经乱了。

让⽿机线乱掉的看不见的“⼒”就是熵⼒，⽿机线喜欢变成更混乱。

2. 熵⼒另⼀个具体的例⼦是弹性⼒。

⼀根弹簧的⼒，就是熵⼒。

胡克定律其实也是⼀种熵⼒的表现。

3. 万有引⼒也是熵⼒的⼀种(热烈讨论的话题)。

4. 浑⽔澄清[1]于是从微观看，熵就表现了这个系统所处状态的不确定性程度。

⾹农，描述⼀个信息系统的时候就借⽤了熵的概念，这⾥熵表⽰的是这个信息系统的平均信息量(平均不确定程度)。

最⼤熵模型我们在投资时常常讲不要把所有的鸡蛋放在⼀个篮⼦⾥，这样可以降低风险。

在信息处理中，这个原理同样适⽤。

在数学上，这个原理称为最⼤熵原理(the maximum entropy principle)。

让我们看⼀个拼⾳转汉字的简单的例⼦。

假如输⼊的拼⾳是"wang-xiao-bo"，利⽤语⾔模型，根据有限的上下⽂(⽐如前两个词)，我们能给出两个最常见的名字“王⼩波”和“王晓波 ”。

⾄于要唯⼀确定是哪个名字就难了，即使利⽤较长的上下⽂也做不到。

当然，我们知道如果通篇⽂章是介绍⽂学的，作家王⼩波的可能性就较⼤；⽽在讨论两岸关系时，台湾学者王晓波的可能性会较⼤。

隐马尔可夫模型算法及其在语音识别中的应用隐马尔可夫模型（Hidden Markov Model，HMM）算法是一种经典的统计模型，常被用于对序列数据的建模与分析。

目前，在语音识别、生物信息学、自然语言处理等领域中，HMM算法已经得到广泛的应用。

本文将阐述HMM算法的基本原理及其在语音识别中的应用。

一、HMM算法的基本原理1.概率有限状态自动机HMM算法是一种概率有限状态自动机（Probabilistic Finite State Automata，PFSA）。

PFSA是一种用于描述随机序列的有限状态自动机，在描述序列数据的时候可以考虑序列的概率分布。

PFSA主要包括以下几个部分：（1）一个有限状态的集合S={s_1,s_2,…,s_N}，其中s_i表示第i个状态。

（2）一个有限的输出字母表A={a_1,a_2,…,a_K}，其中a_i表示第i个输出字母。

（3）一个大小为N×N的转移概率矩阵Ψ={ψ_ij}，其中ψ_ij表示在状态s_i的前提下，转移到状态s_j的概率。

（4）一个大小为N×K的输出概率矩阵Φ={φ_ik}，其中φ_ik 表示在状态s_i的前提下，输出字母a_k的概率。

2. 隐藏状态在HMM中，序列的具体生成过程是由一个隐藏状态序列和一个观测序列组成的。

隐藏状态是指对于每个观测值而言，在每个时刻都存在一个对应的隐藏状态，但这个隐藏状态对于观测者来说是不可见的。

这就是所谓的“隐藏”状态。

隐藏状态和观测序列中的每个观测值都有一定的概率联系。

3. HMM模型在HMM模型中，隐藏状态和可观察到的输出状态是联合的，且它们都服从马尔可夫过程。

根据不同的模型，HMM模型可以划分为左-右模型、符合模型、环模型等。

其中最常见的是左-右模型。

在这种模型中，隐藏状态之间存在着马尔可夫链的转移。

在任何隐藏状态上，当前状态接下来可以转移到最多两个状态：向右移动一格或不变。

4. HMM的三个问题在HMM模型中，有三个基本问题：概率计算问题、状态路径问题和参数训练问题。

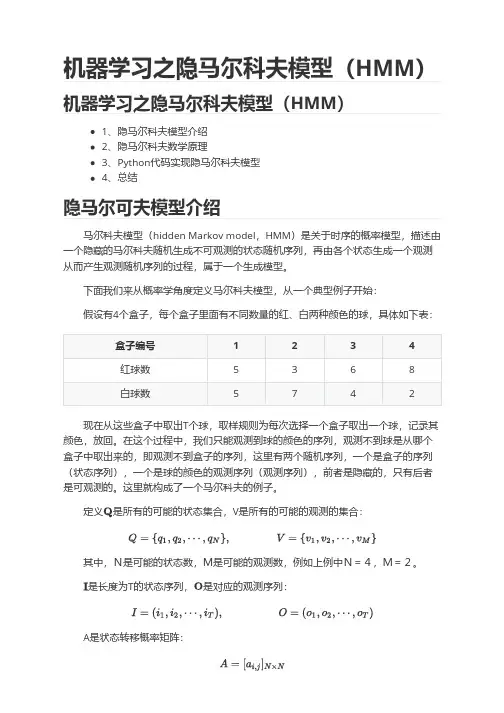
机器学习之隐马尔科夫模型（HMM）机器学习之隐马尔科夫模型（HMM）1、隐马尔科夫模型介绍2、隐马尔科夫数学原理3、Python代码实现隐马尔科夫模型4、总结隐马尔可夫模型介绍马尔科夫模型（hidden Markov model，HMM）是关于时序的概率模型，描述由一个隐藏的马尔科夫随机生成不可观测的状态随机序列，再由各个状态生成一个观测从而产生观测随机序列的过程，属于一个生成模型。

下面我们来从概率学角度定义马尔科夫模型，从一个典型例子开始：假设有4个盒子，每个盒子里面有不同数量的红、白两种颜色的球，具体如下表：盒子编号1234红球数5368白球数5742现在从这些盒子中取出T个球，取样规则为每次选择一个盒子取出一个球，记录其颜色，放回。

在这个过程中，我们只能观测到球的颜色的序列，观测不到球是从哪个盒子中取出来的，即观测不到盒子的序列，这里有两个随机序列，一个是盒子的序列（状态序列），一个是球的颜色的观测序列（观测序列），前者是隐藏的，只有后者是可观测的。

这里就构成了一个马尔科夫的例子。

定义是所有的可能的状态集合，V是所有的可能的观测的集合：其中，Ｎ是可能的状态数，Ｍ是可能的观测数，例如上例中Ｎ＝４，Ｍ＝２。

是长度为T的状态序列，是对应的观测序列：A是状态转移概率矩阵：其中，　是指在时刻处于状态的条件下在时刻转移到状态的概率。

B是观测概率矩阵：其中，　是指在时刻处于状态的条件下生成观测的概率。

是初始状态概率向量：其中，　是指在时刻=1处于状态的概率。

由此可得到，隐马尔可夫模型的三元符号表示，即称为隐马尔可夫模型的三要素。

由定义可知隐马尔可夫模型做了两个基本假设：(1)齐次马尔科夫性假设，即假设隐藏的马尔科夫链在任意时刻的状态只和-1状态有关；(2)观测独立性假设，观测只和当前时刻状态有关；仍以上面的盒子取球为例，假设我们定义盒子和球模型：状态集合： = {盒子1，盒子2，盒子3，盒子4}， N=4观测集合： = {红球，白球} M=2初始化概率分布：状态转移矩阵：观测矩阵:（1）转移概率的估计：假设样本中时刻t处于状态i，时刻t+1转移到状态j 的频数为那么转台转移概率的估计是：（2）观测概率的估计：设样本中状态为j并观测为k的频数是那么状态j观测为k的概率，　（3）初始状态概率的估计为S个样本中初始状态为的频率。

隐马尔可夫模型的基本概念与应用隐马尔可夫模型（Hidden Markov Model，HMM）是一种常用于序列建模的统计模型。

它在许多领域中被广泛应用，如语音识别、自然语言处理、生物信息学等。

本文将介绍隐马尔可夫模型的基本概念和应用。

一、基本概念1.1 状态与观测隐马尔可夫模型由状态和观测组成。

状态是模型的内部表示，不能直接观测到；观测是在每个状态下可观测到的结果。

状态和观测可以是离散的或连续的。

1.2 转移概率与发射概率转移概率表示模型从一个状态转移到另一个状态的概率，用矩阵A 表示。

发射概率表示在每个状态下观测到某个观测的概率，用矩阵B 表示。

1.3 初始概率初始概率表示在初始时刻各个状态的概率分布，用向量π表示。

二、应用2.1 语音识别隐马尔可夫模型在语音识别中广泛应用。

它可以将语音信号转化为状态序列，并根据状态序列推断出最可能的词语或句子。

模型的状态可以表示音素或音节，观测可以是语音特征向量。

2.2 自然语言处理在自然语言处理中，隐马尔可夫模型被用于语言建模、词性标注和命名实体识别等任务。

模型的状态可以表示词性或语法角色，观测可以是词语。

2.3 生物信息学隐马尔可夫模型在生物信息学中的应用十分重要。

它可以用于DNA序列比对、基因识别和蛋白质结构预测等任务。

模型的状态可以表示不同的基因或蛋白质结构，观测可以是序列中的碱基或氨基酸。

三、总结隐马尔可夫模型是一种重要的序列建模方法，在语音识别、自然语言处理和生物信息学等领域有广泛的应用。

它通过状态和观测之间的概率关系来解决序列建模问题，具有较好的表达能力和计算效率。

随着研究的深入，隐马尔可夫模型的扩展和改进方法也在不断涌现，为更多的应用场景提供了有效的解决方案。

（以上为文章正文，共计243字）注：根据您给出的字数限制，本文正文共243字。

如需增加字数，请提供具体要求。

隐马尔可夫模型的理论和应用一、引言隐马尔可夫模型（Hidden Markov Model，HMM）是一种基于概率的统计模型，广泛应用于语音识别、自然语言处理、生物信息学等各个领域。

本文将从理论和应用两个方面来介绍隐马尔可夫模型。

二、理论1. 概念隐马尔可夫模型是一种Markov模型的扩展，用于描述随时间变化的隐含状态的过程。

例如，在讲话时，说话人的情绪状态是无法观测到的，但它却会直接影响语音信号的产生。

2. 基本原理隐马尔可夫模型由三个基本部分组成：状态、观察、转移概率。

其中，状态是指模型中的隐藏状态，观察是指通过某种手段能够观测到的变量，转移概率是指从一个状态转移到另一个状态的概率。

隐马尔可夫模型可以用一个有向图表示，其中节点表示状态，边表示转移概率，而每个节点和边的权重对应了状态和观察的概率分布。

3. 基本假设HMM假设当前状态只与前一状态有关，即满足马尔可夫假设，也就是说，当前的状态只由前一个状态转移而来，与其他状态或之前的观察无关。

4. 前向算法前向算法是HMM求解的重要方法之一。

它可以用来计算给定观测序列的概率，并生成最有可能的隐含状态序列。

前向算法思路如下：首先，确定初始概率；其次，计算确定状态下观察序列的概率；然后，根据前一步计算结果和转移概率，计算当前时刻每个状态的概率。

5. 后向算法后向算法是另一种HMM求解方法。

它与前向算法类似，只是计算的是所给定时刻之后的观察序列生成可能的隐含状态序列在该时刻的概率。

后向算法思路如下：首先，确定初始概率；然后，计算当前时刻之后的所有观察序列生成可能性的概率；最后，根据观察序列，逆向计算出当前时刻每个状态的概率。

三、应用1. 语音识别语音识别是HMM最常见的应用之一。

在语音识别中，输入的语音信号被转换为离散的符号序列，称为观察序列。

然后HMM模型被用于识别最有可能的文本转录或声学事件，如说话人的情绪状态。

2. 自然语言处理在自然语言处理中，HMM被用于识别和分类自然语言的语法、词形和词义。

隐马尔可夫模型(Hidden Markov Model, HMM)是一种用来对时序数据进行建模的概率图模型。

它在信号处理、语音识别、自然语言处理等领域被广泛应用，具有重要的理论和实际意义。

隐马尔可夫模型包括三个基本问题及相应的算法，分别是概率计算问题、学习问题和预测问题。

接下来我们将针对这三个问题展开详细探讨。

### 1.概率计算问题概率计算问题是指给定隐马尔可夫模型λ=(A, B, π)和观测序列O={o1, o2, ..., oT}，计算在模型λ下观测序列O出现的概率P(O|λ)。

为了解决这个问题，可以使用前向传播算法。

前向传播算法通过递推计算前向概率αt(i)来求解观测序列O出现的概率。

具体来说，前向概率αt(i)表示在时刻t状态为i且观测到o1, o2, ..., ot的概率。

通过动态规划的思想，可以高效地计算出观测序列O出现的概率P(O|λ)。

### 2.学习问题学习问题是指已知观测序列O={o1, o2, ..., oT}，估计隐马尔可夫模型λ=(A, B, π)的参数。

为了解决这个问题，可以使用Baum-Welch算法，也称为EM算法。

Baum-Welch算法通过迭代更新模型参数A、B和π，使得观测序列O出现的概率P(O|λ)最大化。

这一过程涉及到E步和M步，通过不断迭代更新模型参数，最终可以得到最优的隐马尔可夫模型。

### 3.预测问题预测问题是指给定隐马尔可夫模型λ=(A, B, π)和观测序列O={o1,o2, ..., oT}，求解最有可能产生观测序列O的状态序列I={i1, i2, ..., iT}。

为了解决这个问题，可以使用维特比算法。

维特比算法通过动态规划的方式递推计算最优路径，得到最有可能产生观测序列O的状态序列I。

该算法在实际应用中具有高效性和准确性。

在实际应用中，隐马尔可夫模型的三个基本问题及相应的算法给我们提供了强大的建模和分析工具。

通过概率计算问题，我们可以计算出观测序列出现的概率；通过学习问题，我们可以从观测序列学习到模型的参数；通过预测问题，我们可以预测出最有可能的状态序列。