下载文档原格式
案例1：一载有石灰和儿童玩具的船舶在航行途中不甚搁浅，情况非常紧急，为脱险，船长下令抛货（石灰）300公吨，并反复开倒车，强行起浮，终于脱险。
但船上轮机受损且船底被划破，致使海水渗进货舱，造成船货部分受损。
该船驶进附近的港口修理并暂卸大部分货物，共花一周时间，增加了各项费用的支出，包括船员的工资。
船修复后装上原货继续起航，不久，A货舱突然起火，火势有蔓延的趋势，船长下令灌水灭火。
灭火后，发现部分儿童玩具和石灰被水浸湿，造成损失。
试分析上述各项损失各属于何种损失？为什么？分析：搁浅是船货遇到的共同危险，为脱险而采取的一系列有意的、合理的行为，并由此造成的损失和费用属于共同海损，包括：抛货损失；反复开倒车造成轮机受损和船底划破的损失；为修船将货卸到岸上等有关卸载费用；增加的船员工资。
另外，启航后A舱起火，为保证船货共同安全，船长命令灌水，灭火时被水浸湿的石灰和儿童玩具的损失也属于共同海损。
案例2：一艘开往新加坡装满棉布的货轮，在航行途中甲舱突然起火，乙舱并未着火，但船长并未调查便认为都已着火，命令对两舱进行灌水施救，结果甲舱棉被大部分被烧毁，剩下一部分，乙舱全部棉布发生严重水渍。
问：甲舱、乙舱所造成的损失各为何种海损？分析：按照海损性质，并参照保险业务的习惯，甲舱棉布大部分被烧毁，属于单独海损，因为这是由“火灾”这一自然灾害直接造成的损失。
甲舱另外一部分因救火灌水遭受水渍，造成的损失属于共同海损。
乙舱棉布未着火，该棉布严重水渍，并非确有危及船货共同安全的危险存在（并未着火），船长命灌水施救的的行为是不合理的，属于判断错误造成的。
因此该项损失不属于共同海损，此项损失只能由船方负责。
案例3：有批玻璃制品出口，由甲乙两轮分别运载，货主投保了平安险。
甲轮在航行途中与他船发生碰撞事故，玻璃制品因此而发生部分损失，而乙轮却在航行途中遭遇暴风雨而使玻璃制品相互碰撞发生部分损失，事后，货主向保险人提出索赔，问保险人该如何处理？分析：对第一种情况，由于造成玻璃制品部分损失的原因是船舶在航行途中与其他船舶相撞，这一碰撞属于意外事故，由其导致的部分损失属于平安险的承保范围，保险人应该赔偿货主；而在第二种情况下，由于造成玻璃制品部分损失的原因是由于暴风雨袭击船舶使之颠簸的结果，而暴风雨属于自然灾害，由其造成的部分损失不属于平安险的承保范围，所以保险人不应该赔偿。
第六章分配理论案例1你愿意加班吗假如你在目前的收入只有400元，这400元连吃、穿、住等基本生活资料都不能满足，你还需要劳动增加工资；当你收入达到2000时，足以满足吃、穿、住等基本生活。
这时老板再让你加班2小时，并支付你加班费20元，你有可能会拒绝。
因为你加班多得的20元是以牺牲休息为代价的，由于货币的边际效用递减，增加的20元不足以弥补你牺牲休息的负效用，劳动供给曲线会呈向后弯曲。
当然如果加班费不是20而是200，我想你一定会加班。
讨论题：1、如何理解劳动的供给曲线向后弯曲？2、如何理解替代效应和收入效应？案例2漂亮的收益美国经济学家丹尼尔·哈莫米斯与杰文·比德尔在1994年第4期《美国经济评论》上发表了一份调查报告。
根据这份调查报告，漂亮的人的收入比长相一般的人高5％左右，长相一般的人又比丑陋一点的人收入高5%一10％左右。
为什么漂亮的人收入高？个人能力包括先天的禀赋和后天培养的能力，长相与人在体育、文艺、科学方面的天才一样是一种先天的禀赋。
漂亮属于天生能力的一个方面，它可以使漂亮的人从事其他人难以从事的职业（如当演员或模特）。
漂亮的人少，供给有限，自然市场价格高，收入高。
漂亮不仅仅是脸蛋和身材，还包括一个人的气质。
在调查中，漂亮由调查者打分，实际是包括外形与内在气质的一种综合。
这种气质是人内在修养与文化的表现。
因此，在漂亮程度上得分高的人实际往往是文化高、受教育高的人。
两个长相接近的人，也会由于受教育不同表现出来的漂亮程度不同。
所以，漂亮是反映人受教育水平的标志之一，而受教育是个人能力的来源，受教育多，文化高，收入水平高就是正常的。
漂亮也可以反映人的勤奋和努力程度。
一个工作勤奋。
勇于上进的人，自然会打扮得体，举止文雅，有一种朝气。
这些都会提高一个人的漂亮得分。
漂亮在某种程度上反映了人的勤奋，与收入相关也就不奇怪了。
最后，漂亮的人机遇更多。
有些工作，只有漂亮的人才能从事，漂亮往往是许多高收入工作的条件之一。
第六章政策执行［案例1］“定心丸”何以变成“闹心丸”第二轮土地承包给广大农民吃了一颗“定心九”，对稳定农民的土地使用权，增加农民长期投入的积极性，保护耕地，都有较大的促进作用，但是在一些地方“定心九”却变成“闹心九”。
据山东省信访部门统计，在山东因土地纠纷引发的农民上访和冲突，已占到农村越级上访量的40％，并呈上升势头。
河南省农调队最近对全省20个县的县、乡主要领导干部的问卷调查表明，土地纠纷与农民负担等成为当前一些农村的热点问题。
强征承包地引发纠纷：1997年，山东省商河县杨庄铺乡政府在没有征得群众同意的情况下，单方将几个村的数千亩土地有偿承包给山东天马置业公司，搞高效农业开发。
村民多次上访，问题始终得不到解决。
村民林富行不平地说：“俺家的两亩地被乡政府强行包给了天马公司，补偿一直都不给，这是啥道理?”去年，河南省洛阳市所属的洛宁、宜阳、新安等县的一些乡镇，以产业结构调整为名，在不给任何经济补偿的情况下，强行让群众在承包地上种植烟叶，否则就收回群众的承包田，结果引发了群众上访。
不少乡村干部对第二轮土地承包存在错误认识，他们认为，“一定30年不变”不过走走形式，以前俺干部能动地，现在还能。
河南、山东两省的农业厅有关负责同志分析说，第一轮土地承包是个“包不包”的问题，而且大多数是口头协议，管理比较松散；而第二轮土地承包十分严格，承包地块、期限都是用书面合同的形式确定的，严格纳入了法制管理的轨道，如果基层干部再延用以前行政强迫命令的办法随便调地，势必引发大量土地纠纷。
中央的土地承包政策在基层得到广泛的拥护，但是在具体操作中会产生矛盾：一家一户承包与土地适度规模经营的矛盾。
陕西省长安县探索出一种叫作“股份田”的新形式，即农民以承包土地入股且参与劳动经营，收益为土地股金和劳动者报酬；投资者以资金入股来经营管理，收益为经营利润和管理者报酬；科技人员以技术入股么技术服务，收益为技术服务指导费，三方皆大欢喜。
第 6 章管理自我情绪做情绪的主人案例一抑郁情绪案例小林以当地第一名的成绩考入北京某重点高校，第一学期期末，本来踌躇满志准备获取奖学金的她未能如愿。
她的情绪从此一落千丈，变得郁郁寡欢，无心学习，也无法处理好与同学的人际关系，还整夜失眠。
最后不得不去医院精神科检查，结果诊断她是患了抑郁症。
分析：据日前一项对大学生抑郁症的抽样调查显示，大学生抑郁障碍疾患率为23.66%，据此推算，北京患有抑郁症的大学生不少于10万人。
在大学生中有抑郁现象的比较多，究其主要原因，是由于自我价值没有得到很好的体现，对自己进行了一些否定。
一般这样的学生情绪都比较低落、不稳定，不爱搭理人，做事情没有兴致，时间长了，容易造成心理情绪积聚，对学习、生活肯定会造成影响，严重的则会患上抑郁症。
如果没有找到正常渠道发泄，可能会沉迷于一些自己觉得是正确的事物上面，比如网络。
这就需要周围的人群关注他们，给他们温暖，生活中有这种情绪的大学生也要多和身边的朋友谈心、交流，释放出自己的压力，以缓解这些症状，从而恢复到正常状态。
案例二焦虑情绪案例钟某某同学为大二男生，身体长得矮小黑瘦，潜意识中接受不了自己身体矮小的现实。
有一次上体育课，身材魁伟的老师一句无意识的揶揄话：“小矮子站我这边来！”引起同学们轰然大笑，钟某某同学自觉很没有脸面，从此陷入对自我否定的激烈恐惧与不安之中，导致后来无法在众人面前抬头，面对异性同学更是诚惶诚恐，学习成绩也不知不觉地下滑。
后来举行班干的换届选举，早有竞选班长念头的他，报名参加了班长一职的竞选演讲，可竞选的日子越临近，他的神经绷得就越紧，到竞选的前一天晚上，他通宵未眠。
待到竞选的时刻来临，他手心冒汗，阵阵心悸，本来已作充分准备的演讲，却连个大概也没有说清楚，当然无法获得同学们的选票，于是落选了。
落选后的他，当然悲观消沉，可就在这个时候，一天走在校园的路上，一个同班女同学主动跟他打招呼，跟他请教一些学习上的问题，还鼓励他说失败是成功之母，相信他只要不泄气，下次一定能够成功等让他感到振奋的话语。
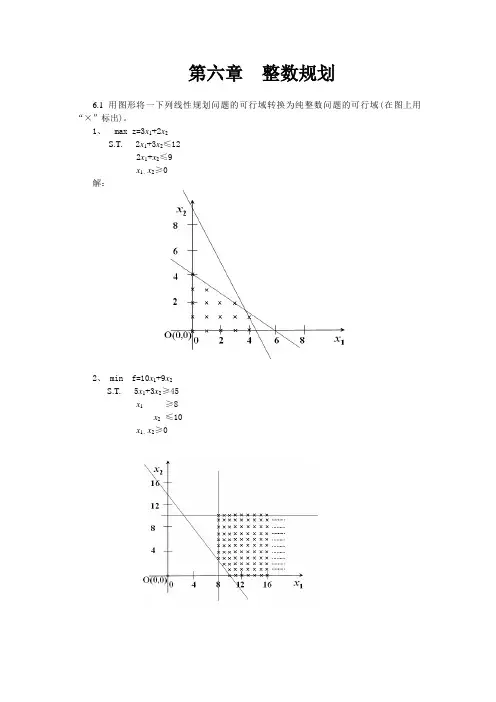
第六章整数规划6.1 用图形将一下列线性规划问题的可行域转换为纯整数问题的可行域(在图上用“×”标出)。
1、 max z=3x1+2x2S.T. 2x1+3x2≤122x1+x2≤9x1、x2≥0解：2、 min f=10x1+9x2S.T. 5x1+3x2≥45x1≥8x2≤10x1、x2≥06.2 求解下列整数规划问题1、 min f=4x1+3x2+2x3S.T. 2x1-5x2+3x3≤44x1+x2+3x3≥3x2+x3≥1x1、x2、x3=0或1解：最优解（0，0，1），最优值：22、 min f=2x1+5x2+3x3+4x3S.T. -4x1+x2+x3+x4≥2-2x1+4x2+2x2+4x2≥4x1+x2-x2+x2≥3x1、x2、x3、x3=0或1解：此模型没有可行解。
3、max Z=2x1+3x2+5x3+6x4S.T. 5x1+3x2+3x3+x4≤302x1+5x2-x2+3x2≤20-x1+3x2+5x2+3x2≤403x1-x2+3x2+5x2≤25x1、x2、x3、x3=正整数解：最优解（0，3，4，3），最优值：474、min z =8x1 +4 x2+3 x3+5 x4+2 x5＋3 x6＋4 x7＋3 x8+4 x9+9 x10+7 x11+5 x12 +10 x13+4 x14+2 x15+175 x16+300 x17+375 x18 +500 x19约束条件x1 + x2+x3≤30x4+ x5＋x6-10 x16≤0x7+ x8＋x9-20 x17≤0x10+ x11＋x12-30 x18≤0x13+ x14＋x15-40 x19≤0x1 + x4+ x7+x10+ x13＝30x2 + x5+ x8+x11+ x14＝20x3 + x6+ x9+x12+ x15＝20x i为非负数（i=1,2…..8）x i为非负整数（i=9,10…..15）x i为为0－1变量（i=16,17…..19）解：最优解（30，0，0，0，0，0，0，0，0，0，0，0，0，20，20，0，0，0，1），最优值：8606.3 一餐饮企业准备在全市范围内扩展业务，将从已拟定的14个点中确定8个点建立分店，由于地理位置、环境条件不同，建每个分店所用的费用将有所不同，现拟定的14个店的费用情况如下表：公司办公会决定选择原则如下：（1）B5、B3和B7只能选择一个。
第六章案例一、基点价格值（一）原理所谓基点，就是利率该变量的计量单位，一个基点等于1个百分点的1%，即0.01%。
基点价格值是指到期收益率变化一个基点，债券价格的变动值。
基点价格值是价格变化的绝对值，价格变化的相对值称作价格变动百分比，它是价格变化的绝对值相对于初始价格的百分比，用式子表示就是：价格变动百分比=基点价格值/初始价格。
（二）事件描述有A、B、C三种债券，半年付息一次，下一次付息在半年后，相关资料如下：（三）分析与思考令收益率上升一个基点，从8％提高到8.01％，可以计算出，新的债券价格分别是：99.9595元、99.9321元和99.9136 元，价格分别变动-0.0405元、-0.0679元和-0.0864元，基点价格值分别是0.0405元、0.0679元和0.0864元。
令收益率下降一个基点，从8％减少到7.99％，新的债券价格分别是：100.0406元、100.0680元和100.0865元，价格分别变动0.0406元、0.0680元和0.0865元，基点价格值分别是0.0406元、0.0680元和0.0865元。
可以看到，收益率上升或下降一个基点时的基点价格值是近似相等的。
由于收益率下降引起价格变动幅度比同等的收益率上升引起的价格变动幅度应该大一些，但是，这里由于收益率的变动很小（仅为一个基点），收益率上升或下降引起的价格波动是大致相等的。
令收益率上升10个基点，从8％提高到8.1％，可以计算出，新的债券价格分别是：99.5955元、99.3235元和99.1406元，价格波动值分别变动0.4045元、0.6765元和0.8594元。
令收益率下降10个基点，从8％减少到7.9％，新的债券价格分别是：100.4066元、100.6825元和100.8699元，价格波动值分别变动0.4066元、0.6825元和0.8699元。
结合上面计算得出的基点价值对应的结果，我们可以总结出一条规律：当收益率变动的幅度较小时（例如10个基点），收益率变动ｎ个基点，价格就近似变动基点价格值的ｎ倍。
由于收益率的变动较小，收益率下降或上升导致的价格波动仍然是大致相等的，价格波动的不对称性可以被忽略。
当收益率上升100个基点，从8％提高到9％，可以计算出，新的债券价格分别是：96.0436元、93.4960元和91.8556元，价格波动值分别变动3.9564元、6.5040元和8.1444元。
再令收益率下降100个基点，从8％减少到7％，新的债券价格分别是：104.1583元、107.1062元和109.1960元，价格波动值分别变动4.1583元、7.1062元和9.1960元。
可以看出，当收益率变动的幅度较大时（例如100个基点），就不能采用前面的近似方法，用基点价格值的ｎ倍来估计价格的波动。
另外，由于收益率的变动较大，价格波动的不对称性也就表现出来，收益率下降或上升带来的价格波动是不等的。
进一步思考：衡量债券利率风险还有哪些指标？二、利率变化与净价格效应（一）原理市场利率变动对债券投资收益的影响来自两个方面：一是利率波动的价格效应，即价格风险；二是利率波动的再投资效应，即再投资风险。
两种效应结合在一起就是利率变化的净价格效应。
价格效应和市场利率的变动是反方向的，当市场利率上升时，债券价格会下跌；而当市场利率下降时，债券价格会上涨。
再投资效应和市场利率的变动则是同方向的。
当市场利率上升时，利息再投资收益增加；而当市场利率下降时，利息再投资收益减少。
可见，市场利率变化时，价格风险和再投资风险对债券价格的影响正好相反，存在抵消现象。
但价格风险和再投资风险究竟哪个更大？或者说在什么情况下两者可以正好抵消，以规避利率变动的影响呢？这是我们以下案例需要探讨的。
（二）事件描述投资者拥有期限为5年，面值1000元，票面利率为8%的债券，每年支付一次利息，当前市场的必要收益率为10%，债券当前市场价格为924.18元。
同时，该投资者的还有一笔期限为4年，现值也等于924.18元的负债。
投资者打算4年后将债券出售来偿还该笔负债。
投资者4年后的债券收入包括销售价格、利息及利息再投资收入。
如果在支付第一期利息前，利率下降到8%或者上升到12%，并且新的利率在将来保持不变。
求利率变化带来的净价格效应。
（三）分析与思考当市场必要收益率为10%时，上述债券久期为4.28年，大于负债久期，因此存在净价格效应。
计算得到下表信息：通过上表计算数据，我们可以得出结论：如果预测利率将会下跌，投资者可以投资于久期超过负债久期的债券，因为此时债券价格的涨幅超过利息收入跌幅，可以通过净价格效应获得更高的回报。
如果预测利率将会上升，投资者可以投资于久期小于负债久期的债券，因为此时债券价格的跌幅小于利息收入涨幅，可以通过净价格效应获得更高的回报。
三、久期的含义和公式（一）原理麦考莱久期：“久期”是对以债券价格波动为主要内容的利率风险的一个严密的表达方式和适当的衡量指标，它能帮助市场参与者有效地实施资产组合策略与套期保值策略。
“久期”这个概念最早是由弗里德里克•麦考莱在1938年发表的一篇研究文章中提出的，他在现值的基础上，衡量了与金融工具（如附息债券）有关的现金流的平均期限。
“久期”是债券的各期支付（包括息票的支付与本金的偿还）所需时间长度的加权平均数。
久期以附息债券价格的函数式01()ntt P PV CF ==∑为基础，在对收益率（r ）求一阶导数之后，再在等式两边同时除以债券价格（P ），得到：11(1)dP D dr P r =-+ 上始终的D 便是久期的概念，它的展开式为：11()()ntt ntt PV CF tPV CF D ==⨯=∑∑公式中的分母是利息和本金支付流的现值，即债券的市场价格；而分子则是指全部利息和本金的现金流用相同的到期收益率(而不是使用预期将来每一次支付发生时的即期利率)来进行折现，然后，将所有经过折现后的现金流的现值用作权重对各次支付所需要的时间进行加权，最后再作加总。
在这里，权重的意义在于它代表着未来的每一次支付占全部债券价值中的特定比重，即每期收到的现金流的现值只代表了债券市场价格的一个部分。
11(1)dP D dr P r =-+由此式可以看出，久期这个概念开创性地将债券收益率的变动和债券的价格变动联系了起来，是对债券价格波动性或对收益率变动的敏感性的衡量：久期越是大，债券价格对收益率变动的反应就越是强烈，这意味着利率风险就越是大；反之则反是。
（二）事件描述××某种债券的到期收益率为10%，面值为$1 000，票面利率为8%，每年付息一次，债券的现行市价为$950.25，存续期还剩3年。
请计算出该债券的久期，并说明含义。
（三）分析与思考根据公式变形得到(1)dP D dr p r =-+，代入D=2.78，r=10%，得到 2.53dPdr p =-。
说明当市场收益率上升1%，债券价格下降2.53%；当市场收益率下降1%，该债券价格上升2.53%。
(1)Dr +也称作修正久期，直接衡量了收益率变动和债券价格变动的关系。
进一步思考：久期最本质的定义是什么？四、凸度的含义和公式 （一）原理债券的价格与其收益率呈反比关系；然而，债券收益率下降抬高债券价格的数额要大于债券收益率发生同等幅度的上升所导致的债券价格下跌的数额。
这种非线性联系在“久期”运用过程中也体现出来：第一，“久期”的预测是对称的，而债券实际价格的变动是不对称的；第二，在收益率发生上升和下跌这两种情况下，“久期”的预测都出现了误差，即都低估了债券价格的实际变动；第三，同样是“久期”的预测出现了偏差，但收益率上升导致债券价格下跌的误差要小于收益率下降导致的债券价格上涨的误差。
为了纠正久期的这种不足，就需要引入凸度的概念。
所谓凸度是指债券收益率的单位变化所引起的债券久期的变化大小，即衡量到期收益率变动所引起的债券价格变动幅度的变动程度。
从图形上看，更直观地说，凸度用来衡量债券价格与收益率关系曲线的曲度。
如果收益率增加相同大小，则凸度大的债券其价格减少幅度较小，凸度小的债券其价格减少幅度较大；如果收益率减少相同大小，则凸性大的债券其价格增加较大，凸度小的债券其价格增加幅度较小。
凸度是债券价格对收益率的二阶导数除以债券价格，公式如下：221d PC P dy =上式中，C 为凸度，P 为债券价格。
凸度对债券价格百分率变动的影响等于凸度的数值乘以收益率的平方，它呈增函数性质，即：2dPC dr P=⨯ （二）事件描述某种债券的息票率为8.4%，每半年付息一次，期限为6年。
债券的面值为$100，由于到期收益率为9%，所以在市场上按$97.26折价出售。
现假定年收益率从9%下降到7%，请分析其对债券价值的影响。
（三）分析与思考936.54==4.8145297.26⨯久期， 4.8145==4.611+0.045修正后久期（）， 211246.34==52.9422 1.04597.26⨯⨯⨯凸性 根据“修正后久期”和“凸度”的公式，假如收益率从9%下降2个百分点至7%，那么预期中的债券价格百分率变动为：期(半年)=629.926.9754.936=，久期(一年)=8145.42629.9=，修正后久期=61.4045.018145.4=+）（。
凸性(半年)= 94.5226.97$045.1234.246112=⨯⨯）（，凸性(一年)=47.26294.52=。
根据“修正后的久期”及“凸性”来预测债券价格百分率的变动： 2dy CV dy MD P dP ⨯+⨯-==(－4.61)(－0.02)+2)02.0)(47.26(-=0.102788=10.28%； 假如收益率从9%上升2个百分点至11%，那么，预期中的债券价格百分率变动为： 2dy CV dy MD P dP ⨯+⨯-==(－4.61)(0.02)+2)02.0)(47.26(=－0.81612=－8.16%。
反过来，假如收益率从9%上升2个百分点至11%，那么预期中的债券价格百分率变动为： 期(半年)=629.926.9754.936=，久期(一年)=8145.42629.9=，修正后久期=61.4045.018145.4=+）（。
凸性(半年)= 94.5226.97$045.1234.246112=⨯⨯）（，凸性(一年)=47.26294.52=。
根据“修正后的久期”及“凸性”来预测债券价格百分率的变动： 2dy CV dy MD P dP ⨯+⨯-==(－4.61)(－0.02)+2)02.0)(47.26(-=0.102788=10.28%； 假如收益率从9%上升2个百分点至11%，那么，预期中的债券价格百分率变动为： 2dy CV dy MD PdP⨯+⨯-==(－4.61)(0.02)+2)02.0)(47.26(=－0.81612=－8.16%。
