小学五年级奥数 立体几何(一)
- 格式:pdf
- 大小:190.67 KB
- 文档页数:3

小学五年级奥数几何长方体和正方体经典例题详解精品学习网为您整理了:五年级奥数几何长方体和正方体经典例题详解欢迎大家阅读愉快!五年级奥数几何长方体和正方体经典例题详解1、一个零件形状大小如下图:算是一算,它的体积就是多少立方厘米,表面积就是多少平方厘米?(1)可以把零件沿虚线分成两部分来求它的体积,左边的长方体体积是10×4×2=80(立方厘米),右边的长方体的体积是10×(6-2)×2=80(立方厘米),整个零件的体积是80+80=160(立方厘米)。
10×4×2+10×(6-2)×2=160(立方厘米)(2)谋这个零件的表面积,看上去比较复杂,其实,朝上的两个面的面积和刚好与朝下的一个面的面积成正比;朝右的两个面的面积和刚好与朝左的一个面的面积成正比。
因此,此零件的表面积就是:(10×6+10×4+4×2×2)×2=232(平方厘米)练习(1)一个长5厘米、宽1厘米、高3厘米的长方体,被切去一块后(如下图),剩下部分的表面积和体积各是多少?练(2)把一根长2米的长方体木料锯成1米短的两段,表面积减少2平方分米,谋这根木料原来的体积。
练习(3)有一个长8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方体(如下图),求切掉正方体后的表面积和体积各是多少?2、存有一个长方体形状的零件。
中间挖去一个正方体的孔(如下图)。
你能算出来它的体积和表面积吗?(单位:厘米)(1)先求出长方体的体积,8×5×6=240(立方厘米),由于挖去一个孔,所以体积减少2×2×2=8(立方厘米),这个零件的体积是240-8=232(立方厘米)(2)长方体完备的表面积就是(8×5+8×6+5×6)×2=236(平方厘米),但由于挖去一个孔,它的表面积增加了一个(2×2)平方厘米的面积,同时又减少了凹陷进来的5个(2×2)平方厘米的面,因此,这个零件的表面积就是236+(2×2)×4=252(平方厘米).练习(1)有一个形状如下图的零件,求它的体积和表面积。

一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、共角定理(鸟头定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.DC BA知识框架专项五 五大模型(一):():()ABC ADE S S AB AC AD AE =⨯⨯△△三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”): ①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”):①2213::S S a b =②221324::::::S S S S a b ab ab =;③S 的对应份数为()2a b +.(1)(2)(3)(4)S 4S 3S 2S 1O DCBA四、相似模型(一)金字塔模型 (二) 沙漏模型①AD AE DE AFAB AC BC AG ===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、共边定理(燕尾定理)有一条公共边的三角形叫做共边三角形。

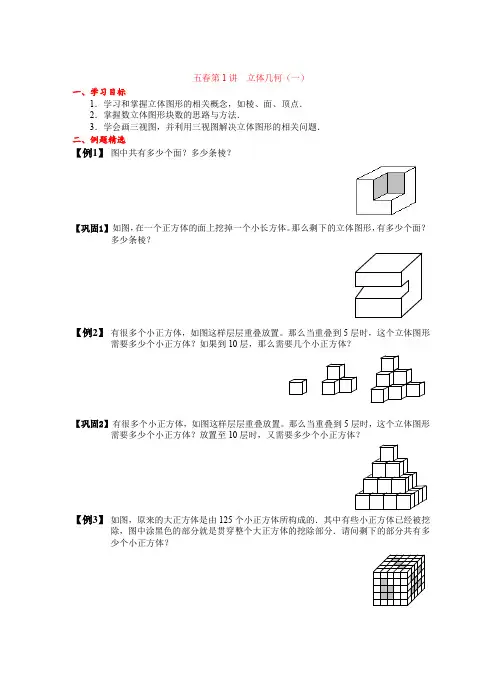
五春第1讲立体几何(一)一、学习目标1.学习和掌握立体图形的相关概念,如棱、面、顶点.2.掌握数立体图形块数的思路与方法.3.学会画三视图,并利用三视图解决立体图形的相关问题.二、例题精选【例1】图中共有多少个面?多少条棱?【巩固1】如图,在一个正方体的面上挖掉一个小长方体。
那么剩下的立体图形,有多少个面?多少条棱?【例2】有很多个小正方体,如图这样层层重叠放置。
那么当重叠到5层时,这个立体图形需要多少个小正方体?如果到10层,那么需要几个小正方体?【巩固2】有很多个小正方体,如图这样层层重叠放置。
那么当重叠到5层时,这个立体图形需要多少个小正方体?放置至10层时,又需要多少个小正方体?【例3】如图,原来的大正方体是由125个小正方体所构成的.其中有些小正方体已经被挖除,图中涂黑色的部分就是贯穿整个大正方体的挖除部分.请问剩下的部分共有多少个小正方体?第8题【巩固3】如图所示,一个5×5×5的立方体,在一个方向上开有1×1×5的孔,在另一个方向上开有2×1×5的孔,在第三个方向上开有3×1×5的孔,剩余部分的小正方体块数是多少?【例4】右图是6×10×12块小正方体堆叠而成,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小长方体各有多少块?【巩固4】如图是4×5×6长方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?【例5】小明用若干个大小相同的正方体木块堆成一个几何体,这个几何体从正面看如下左图所示,从上面看如下右图所示。
那么,这个几何体至少用了多少个木块?三、回家作业【作业1】图中共有多少个面?多少条棱?【作业2】如图层层重叠放置小正方体,那么放置到6层时,总共需要多少个小正方体?【作业3】如图所示,一个5×5×5的立方体,在一个方向上开有1×1×5的孔,在另一个方向上开有2×1×5的孔,剩余部分的小正方体块数有多少个?【作业4】有一个5×6×7的长方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?【作业5】用一些棱长是1的小正方体码放成一个立体,如下图,请画出从上面和正面看到的图形前右左下上。
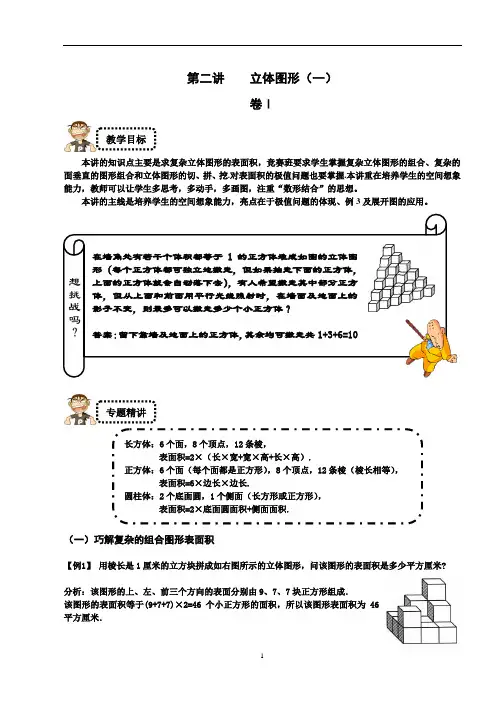
第二讲 立体图形(一)卷Ⅰ本讲的知识点主要是求复杂立体图形的表面积,竞赛班要求学生掌握复杂立体图形的组合、复杂的面垂直的图形组合和立体图形的切、拼、挖.对表面积的极值问题也要掌握.本讲重在培养学生的空间想象能力,教师可以让学生多思考,多动手,多画图,注重“数形结合”的思想。
本讲的主线是培养学生的空间想象能力,亮点在于极值问题的体现、例3及展开图的应用。
(一)巧解复杂的组合图形表面积【例1】 用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?分析:该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形(每个正方体都可独立地搬走,但如果抽走下面的正方体,上面的正方体就会自动落下去),有人希望搬走其中部分正方体,但从上面和前面用平行光线照射时,在墙面及地面上的影子不变,则最多可以搬走多少个小正方体?答案:留下靠墙及地面上的正方体,其余均可搬走共1+3+6=10块.想挑战吗?长方体:6个面,8个顶点,12条棱,表面积=2×(长×宽+宽×高+长×高).正方体:6个面(每个面都是正方形),8个顶点,12条棱(棱长相等),表面积=6×边长×边长.圆柱体:2个底面圆,1个侧面(长方形或正方形),表面积=2×底面圆面积+侧面面积.【例2】边长为1厘米的正方体,如图这样层层重叠放置,那么当重叠到第5层时,这个立体图形的表面积是多少平方厘米?分析:这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米,该图形的总表面积为90立方厘米.[拓展] 如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?分析:当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个3×3×3的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例3】(奥数网原创题)按照上题的堆法一直堆到N层(N>3),要想使总表面积恰好是一个完全平方数,则N的最小值是多少?N N 个小面,总表面积是6个“大面”,所以就增加到分析:每增加一层,每一个“大面”就增加到(1)23N(N+1)个小面,几何题变成数论题,问题转化为“3N(N+1)是一个完全平方数,N的最小值是几(N>3)?”因为N和N+1互质,所以N和N+1必须有一个是完全平方数,一个是平方数的3倍,但N+1不能是平方数的3倍,因为此时N被3除余2,不可能是完全平方数,所以N是平方数的3倍,N+1是完全平方数,开始试验:当N=3×12=3,不符合题意;当N=3×22=12,N+1=13,不是完全平方数;当N=3×32=27,N+1=28,不是完全平方数;当N=3×42=48,N+1=49,是完全平方数,所以N的最小值是48,即堆到第48层时,总表面积是完全平方数,为3×48×49=842.(二)表面积的最值问题【例4】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?分析:截去一个小正方体,表面积不变,只有在截去的小正方体的面相重合时,表面积才会减少,所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.【例5】边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例6】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?分析:教师可以先提问:这个长方体的表面积最大是多少?为使表面积最大,要尽量保证10×2个7×5的面成为表面,想要做到这点很容易,只需将7×5面做底面,而后将10个立方体连排,衔接的面选用3×5的面(衔接的面将不能成为表面积),这样得到的长方体表面积最大.同样要想最小,可把7×5面做衔接的面,可得到10个长方体的连排,但此时我们还可以再制造出衔接面,如图:此时增加了2个5×7的面,减少了10个3×7的面,总体来讲表面积减少了.表面积是:2×(7×15+15×10+10×7)=650(平方厘米),所以这就是最小的表面积.[前铺] 用6块右图所示(单位:cm)的长方体木块拼成一个大长方体,有许多种拼法,其中表面积最小的是多少平方厘米?最大是多少平方厘米?分析:最小:66cm2;最大:(1×2+1×3+2×3)×2×6-1×2×5×2=112.【例7】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?(1)当b=2h时,按图几打包?(2)当b<2h时,按图几打包?(3)当b>2h时,按图几打包?分析:图2和图3正面的面积相同,侧面面积=正面周长×长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b﹤2h时,按图2打包;当b﹥2h时,按图3打包.[前铺] 要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?分析:考虑所有的包装方法,因为6=1×2×3,所以一共有两种拼接方式:第一种按长宽高1×1×6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1×2×3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.卷Ⅱ(三)立体图形的切、拼、挖【例8】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?分析:我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2×2×2=8(平方厘米);左右方向、前后方向:2×2×4=16(平方厘米),1×1×4=4(平方厘米),1/2×1/2×4=1(平方厘米),1/4×1/4×4=1/4 (平方厘米),这个立体图形的表面积为:8+16+4+1+1/4=29又1/4 (平方厘米).【例9】如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析:大立方体的表面积是20×20×6=2400平方厘米.挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3.[拓展1] 图中是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?分析:原正方体的表面积是4×4×6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4×6=120平方厘米.[拓展2] 如右图,一个边长为3a厘米的正方体,分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体(都和对面打通).如果这个镂空的物体的表面积为2592平方厘米,试求正方形截口的边长.分析:原来正方体的表面积为:6×3a×3a=6×9a2(平方厘米),六个边长为a的小正方形的面积为(减少部分):6×a×a=6a2(平方厘米);挖成的每个长方体空洞增加的侧面积为:a×a×4×2=8a2(平方厘米);根据题意可得:54a2-6a2+3×8a2=2592,解得a2=36(平方厘米),故a=6厘米.【例10】有一个棱长为 5 cm的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(右上图),求这个立体图形的内、外表面的总面积.分析:将此带孔的正方体看做由八个8cm3的正方体(8个顶点)和12个1cm3的正方体(12条棱)粘成的.每个正方体有两个面粘接,减少表面积4cm2,所以总的表面积为:(4×6)×8+6×12-4×12=216(cm2).[拓展] 边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例11】如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下侧面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求此立体图形的表面积.分析:外侧表面积为:6×10×10-4×4×4-π×22×2=536-8π.内侧表面积为:16×4×3+2× (4×4-π×2)+2×2π×2×3=192+32-8π+24π=224+16π.总表面积=224+16π+536-8π=760+8π=785.12(平方厘米).【例12】如图,用455个棱长为1 的小正方体粘成一个大的长方体,若拆下沿棱的小正方体,则余下371个小正方体,问:所堆成的大长方体的棱长各是多少?拆下沿棱的小正方体后的多面体的表面积是多少?分析:设长方体棱长为分别为y zx、、.,他们只能取正整数,则有:4554(222)8455371x y zx y z⨯⨯=⎧⎨-+-+-+=-⎩因为4555713=⨯⨯方程组的有序正整数解只有(5,7,13),拆下沿棱的的小正方体后的多面体如图所示,首先计算突出在外面的6个平面,面积是2(11511335)206⨯⨯+⨯+⨯=再计算24个宽都是1的长⨯++=,总面积为358. 条,面积是8(1135)152(三)展开图【例13】在小于16 的自然数中选出6个不同的数,分别写在正方体的6个面上,要求各组相对的两个面上的数的乘积都相等,下图是正方体的展开图,并填上了1,请将其它数填上。
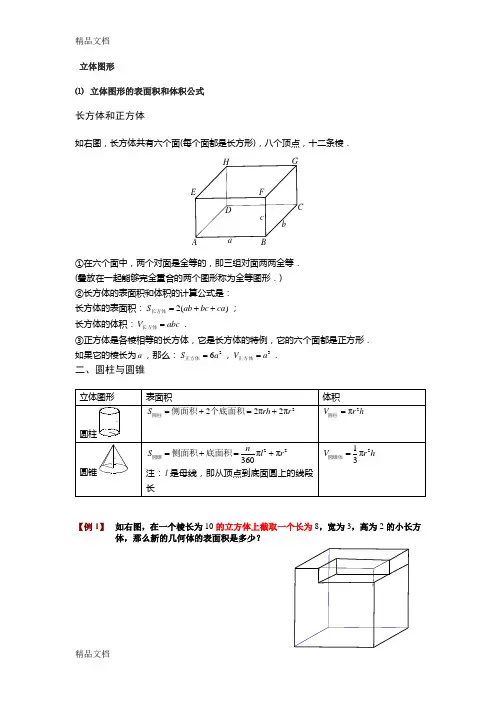
立体图形⑴ 立体图形的表面积和体积公式长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED BA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?改.又是多少?【例 2】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)练习:在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?(锯一次增加两个面)练习.一个表面积为256cm的长方体如图切成27个小长方体,这27个小长方体表面积的和是2cm.表面积最小:互相重合的面最多时表面积最小【例 5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?体积:例1. 如图11-6,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?例2. 某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条如图11-9所示在三个方向上加固.所用尼龙编织条的长分别为365厘米、405厘米、485厘米.若每个尼龙条加固时接头处都重叠5厘米,则这个长方体包装箱的体积是多少立方米?⑵不规则立体图形的表面积整体观照法例1. 如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.例2. 如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.例3.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.例4.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?例5.下图是由18个边长为1厘米的小正方体拼成的,求它的表面积。

五年级几何知识奥数题小学五年级奥数长方体和正方体几何知识经典例题详解:1、一个零件形状大小如下图:算一算,它的体积是多少立方厘米,表面积是多少平方厘米? 【思路导航】(1)可以把零件沿虚线分成两部分来求它的体积,左边的长方体体积是10×10×4×4×4×2=80(2=80(立方厘米),右边的长方体的体积是10×10×(6-2)×(6-2)×(6-2)×2=80(2=80(立方厘米),整个零件的体积是80+80=160(立方厘米)。
10×10×4×4×4×2+10×2+10×2+10×(6-2)×(6-2)×(6-2)×2=160(2=160(立方厘米) (2)求这个零件的表面积,看起来比较复杂,其实,朝上的两个面的面积和正好与朝下的一个面的面积相等;朝右的两个面的面积和正好与朝左的一个面的面积相等。
因此,此零件的表面积就是:(10×(10×6+10×6+10×6+10×4+4×4+4×4+4×2×2×2×2)×2)×2)×2=232(2=232(平方厘米) 练习(1)一个长5厘米、宽1厘米、高3厘米的长方体,被切去一块后(如下图),剩下部分的表面积和体积各是多少? 练习(2)把一根长2米的长方体木料锯成1米长的两段,表面积增加2平方分米,求这根木料原来的体积。
练习(3)有一个长8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方体(如下图),求切掉正方体后的表面积和体积各是多少 2、有一个长方体形状的零件。
中间挖去一个正方体的孔(如下图)。
课程五立体图形问题1。
长方体、正方体表面积的计算2.长方体、正方体的切割问题3.长方体、正方体的体积4.不规则物体的体积计算长方体和正方体的表面积应注意的问题(1)找出必备条件(长、宽、高或棱长),如题中没有直接给出,则先求出必备条件,再求表面积(有盖还是无盖)。
(2)统一计量单位,单位不统一的,一般要通过化、聚,使单位统一后再计算。
(3)求所需用的面积材料时,一般用“进一法“取近似值。
(4)用同样多的立体拼图,由于拼法不同,重叠的次数不同,表面积就会发生变化,每重叠一次,就减少两个面;每切一刀,就增加两个面。
1.长方体和正方体的体积概念及其计算公式(1)长方体体积=长×宽×高V 长方体=abc(2) 正方体体积=棱长×棱长×棱长V 正方体=a 32.求不规则物体的体积水中物体的体积=容器的底面积×水上升或下降的高度。
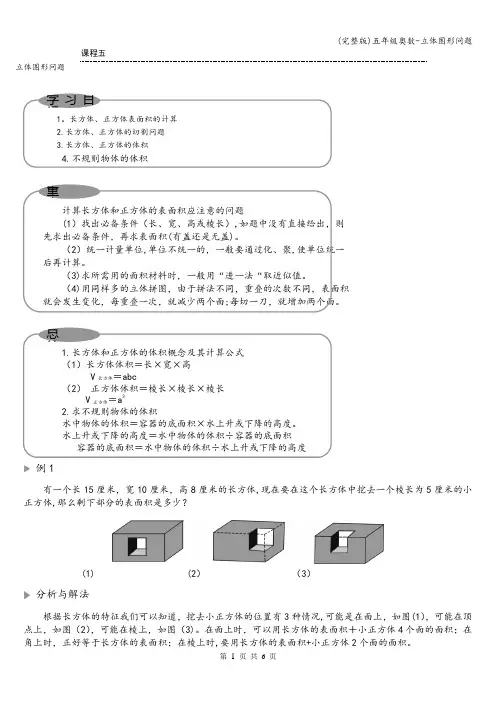
水上升或下降的高度=水中物体的体积÷容器的底面积容器的底面积=水中物体的体积÷水上升或下降的高度例1有一个长15厘米,宽10厘米,高8厘米的长方体,现在要在这个长方体中挖去一个棱长为5厘米的小正方体,那么剩下部分的表面积是多少?(1) (2) (3)分析与解法根据长方体的特征我们可以知道,挖去小正方体的位置有3种情况,可能是在面上,如图(1),可能在顶点上,如图(2),可能在棱上,如图(3)。
在面上时,可以用长方体的表面积+小正方体4个面的面积;在角上时,正好等于长方体的表面积;在棱上时,要用长方体的表面积+小正方体2个面的面积。
学习目标 重 点 总 结解:原长方体表面积为:(15×10+15×8+10×8) ×2=700(平方厘米)在角上时,剩下部分的表面积是700(平方厘米);在面上时,剩下部分的表面积是:700+5×5×4=800(平方厘米)在棱上时,剩下部分的表面积是:700+5×5×2=750(平方厘米)所以剩下部分的表面积是700平方厘米,或800平方厘米,或750平方厘米.说明:本题也是要考虑可能出现的各种情况,要做到不重不漏。
第二讲 立体图形(一)1掌握常见立体图形表面积的求法.2掌握几类典型组合立体图形表面积的求法.3鼓励学生多思考,勤动手,多画图,注重“数形结合以此来培养学生的空间想象能力.对于长、正方体等简单的立方体和其体积、表面积的计算方法,都是相对比较简单的,今天我们一起将这部分内容掌握后着重对其进行拓展研究. 如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.1.在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) 2.长方体的表面积和体积的计算公式是: 长方体的表面积:S 长方体=2(ab +bc +ac ); 长方体的体积:V 长方体=abc .3.正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:S 正方体=6a 2,V 正方体=a 3.专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形(每个正方体都可独立地搬走,但如果抽走下面的正方体,上面的正方体就会自动落下去),有人希望搬走其中部分正方体,但从上面和前面用平行光线照射时,在墙面及地面上的影子不变,则最多可以搬走多少个小正方体?答案:留下靠墙及地面上的正方体,其余均可搬走共1+3+6=10块. 想挑战吗?Ⅰ、涂色与简单的表面积计算:【例1】右图是4×5×6正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?分析:三面涂红色的只有8个顶点处的8个立方体;两面涂红色的在棱长处,共(4-2)×4+(5-2)×4+(6-2)×4=36块;一面涂红的表面中间部分:(4-2)×(5-2)×2+(4-2)×(6-2)×2+(5-2)×(6-2)×2=52块.【例2】(小数报数学竞赛决赛)右图是一个表面被涂上红色的棱长为lO厘米的正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没有被涂上红色的所有表面的面积和是多少平方厘米?分析:10×10×6=600(平方厘米).【例3】(05年清华附培训试题)将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?分析:长:3+1+1=5厘米;宽:1+1+1=3厘米;高:1+1+1=3厘米;所以原长方体的表面积是:(3×5+3×5+3×3)3×2=78平方厘米.[拓展]右图是由27块小正方体构成的 3×3×3的正方体.如果将其表面涂成红色,则在角上的8个小正方体有三面是红色的,最中央的小方块则一点红色也没有,其余18块小方块中,有12个两面是红的,6个一面是红的.这样两面有红色的小方块的数量是一面有红色的小方块的两倍,三面有红色的小方块的数量是一点红色也没有的小方块的八倍.问:由多少块小正方体构成的正方体,表面涂成红色后会出现相反的情况,即一面有红色的小方块的数量是两面有红色的小方块的两倍,一点红色也没有的小方块是三面有红色的小方块的八倍?分析:对于由n3块小正方体构成的n×n×n正方体,三面涂有红色的有8块,两面涂有红色的有12×(n -2)块,一面涂有红色的有6×(n-2)2块,没有涂色的有(n-2)3块.由题设条件,一点红色也没有的小方块是三面涂有红色的小方块的八倍,即(n-2)3=8×8,解得n=6.【例4】如右图,有一个边长是5的立方体,如果它的左上方截去一个边分别是5,3,2的长方体,那么它的表面积减少了多少?分析:原来正方体的表面积为5×5×6=150.现在立体图形的表面积截了两个面向我们的侧面,它们的面积为(3×2)×2=12,所以减少的面积就是12.[前铺]如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?分析:我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10×10×6=600.[拓展] 在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?分析:对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50×50×6=15000(平方厘米).【例5】(北京市第十二届迎春杯)一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?分析:截去一个小正方体,表面积不变,只有在截去的小正方体的面相重合时,表面积才会减少,所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.想想为什么不是15×15×6-7×7-8×8 ?Ⅱ、巧解复杂的组合图形表面积【例6】右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?分析:原正方体的表面积是4×4×6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4×6=120平方厘米.[拓展]:如右图,一个边长为3a厘米的正方体,分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体(都和对面打通).如果这个镂空的物体的表面积为2592平方厘米,试求正方形截口的边长.分析:原来正方体的表面积为:6×3a×3a=6×9a2(平方厘米),六个边长为a的小正方形的面积为(减少部分):6×a×a=6a2(平方厘米);挖成的每个长方体空洞增加的侧面积为:a×a×4×2=8a2(平方厘米);根据题意可得:54a2-6a2+3×8a2=2592,解得a2=36(平方厘米),故a=6厘米.【例7】如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?分析:4×4+(1×1+2×2+4×4)×4=100(平方米).[前铺]如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.分析:我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:5×5×2=50(平方分米);侧面:5×5×4=100(平方分米),4×4×4=64(平方分米).这个立体图形的表面积为:50+100+64=214(平方分米).【例8】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?分析:我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2×2×2=8(平方厘米);左右方向、前后方向:2×2×4=16(平方厘米),1×1×4=4(平方厘米),1/2×1/2×4=1(平方厘米),1/4×1/4×4=1/4 (平方厘米),这个立体图形的表面积为:8+16+4+1+1/4=29又1/4 (平方厘米).【例9】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.求这个立体图形的表面积.分析:从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面+2个左面+2个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(9+8+10)×2=54(平方厘米).[拓展]边长为1厘米的正方体,如图这样层层重叠放置,那么当重叠到第5层时,这个立体图形的表面积是多少平方厘米?分析:这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米,该图形的总表面积为90立方厘米.Ⅲ、立体图形的分割与拼组【例10】(首师大附小升初考试分班试题)一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?分析:锯一次净增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数×2=增加的面数,原正方体表面积:1×1×6=6(平方米)一共据了多少次(2-1)+(3-1)+(4-1)=6次,6+1×1×2×6=18(平方米).【例11】如右图,一个正方体形状的木块,棱长l米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的和是多少平方米?分析:我们知道每切一刀,多出的表面积恰好是原正方体的2个面的面积.现在一共切了(3-1)+(4-1)+(5-1)=9刀,而原正方体一个面的面积1×l=1(平方米),所以表面积增加了9×2×1=18(平方米).原来正方体的表面积为6×1=6(平方米),所以现在的这些小长方体的表积之和为6+18=24(平方米).【例12】用6块右图所示(单位:cm)的长方体木块拼成一个大长方体,有许多种拼法,其中表面积最小的是多少平方厘米?最大是多少平方厘米?分析:最小:66cm2;最大:(1×2+1×3+2×3)×2×6-1×2×5×2=112.[拓展]有一个棱长为 5 cm的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(右上图),求这个立体图形的内、外表面的总面积.分析:将此带孔的正方体看做由八个8cm3的正方体(8个顶点)和12个1cm3的正方体(12条棱)粘成的.每个正方体有两个面粘接,减少表面积4cm2,所以总的表面积为:(4×6)×8+6×12-4×12=216(cm2).[拓展]边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.立体图形的相关知识(表面积、体积等)我们会在五年级春季和六年级继续学习.1. (例1)一个5×6×7正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?分析:三面涂红色的只有8个顶点处的8个立方体;两面涂红色的在棱长处,共(5-2)×4+(6-2)×4+(7-2)×4=48块; 一面涂红的表面中间部分:(5-2)×(6-2)×2+(5-2)×(7-2)×2+(6-2)×(7-2)×2=94块.2. (例6)如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析: 大立方体的表面积是20×20×20×6=2400平方厘米.在角上挖掉一个小正方体后,外面少了3个面,但厘米又多出3个面;在棱上挖掉一个小正方体后,外面少了2个面,但里面多出4个面;在面上挖掉一个小正方体后,外面少了1个面,但里面多出5个面.所以,最后的情况是挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3厘米.3. (例6)一个正方体的棱长为3厘米,在它的前、后、左、右、上、下各面中心各挖去一个棱长为1厘米的正方体做成一种玩具,求这个玩具的表面积.分析:挖去六个小正方体后,大正方体的中心部分即与其主体脱离,这时得到的新玩具是镂空的.把这个玩具分成20部分,8个“角”和12条“梁”,每个“角”为棱长1厘米的小正方体,它外露部分的面积为:12×3=3(平方厘米),则8个“角”外露部分的面积为:3×8=24(平方厘米).每条“梁”为棱长1厘米的小正方体,它外露部分的面积为:12×4=4(平方厘米),则12条“梁”外露部分的面积为: 4×12=48(平方厘米).这个玩具的表面积为:24+48=72(平方厘米). 练习二专题展望4. (例9)用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?分析:该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.5. 有30个边长为1米的正方体,在地面上摆成右上图的形式,然后把露出的表面涂成红色.求被涂成红色的表面积.分析:4×4+(1+2+3+4)×4=56(米2)6. (例12)(我爱数学夏令营活动试题)有三个大小一样的正方体,将接触的面用胶粘接在一起成左图的形状,表面积比原来减少了16平方厘米.求所成形体的体积.分析:三个小正方体拼接成图中的样子,减少了小正方体的4个侧面正方形的面积,表面积减少了16平方厘米,每个正方形侧面为16÷4=4平方厘米,每个正方体棱长为2厘米,三个小正方体体积(即所成形体的体积)是3×23=24立方厘米.蛋型拼板.一种蛋形图板,可以分割成如下图所示的九块板,利用这九块板可以拼成各种各样的图形.国外称之为“魔蛋”.用蛋形拼板拼成的几种动物的造型.你会拼吗?拼拼看.数学知识三角板拼图.用四块形状、大小完全一样的直角三角形纸板(如右图),拼拼搭搭(不能重叠),能出现许多边长不同的正方形.你会拼吗?拼拼看.。
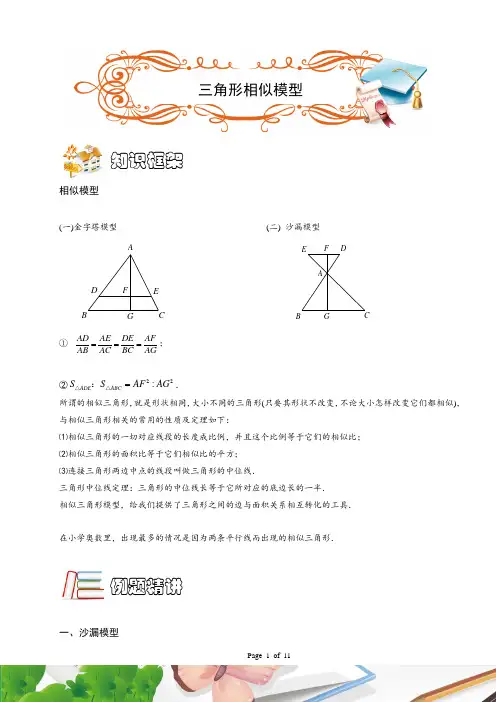
相似模型(一)金字塔模型 (二) 沙漏模型GF E AB CDAB CDEF G①AD AE DE AFAB AC BC AG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.一、沙漏模型知识框架例题精讲三角形相似模型【例 1】 四边形ABCD 被AC 和DB 分成甲乙丙丁4个三角形,已知BE=80,CE=60,DE=40,AE=30,问:丙、丁两个三角形之和是甲乙两个三角形面积之和的多少倍?【巩固】 梯形ABCD 的上底长为3厘米,下底长为9厘米,而三角形ABO 的面积为12平方厘米。
则整个梯形的面积为多少?【例 2】 如图,在平行四边形ABCD 中,AB=16,AD=10,BE=4,那么FC 的长度是多少?【巩固】 如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且DE :EC=1:3,AF 与BE 相交于点G ,求ABG S .【例 3】 如图ABCD 是梯形,BD 是对角线,E 为BD 上一点,EF 是三角形AED 的高,EG 是三角形BCE的高。
如果三角形ABE 和三角形BCE 的面积分别为6和10平方厘米,EF :EG=7:4,那么求梯形ABCD 的面积。
G EFABCDO【巩固】 如图,△ABC 中AE=14AB ,AD=14AC ,ED 与BC 平行,△EOD 的面积是1平方厘米。

第二讲 立体图形(一)卷Ⅰ本讲的知识点主要是求复杂立体图形的表面积,竞赛班要求学生掌握复杂立体图形的组合、复杂的面垂直的图形组合和立体图形的切、拼、挖.对表面积的极值问题也要掌握.本讲重在培养学生的空间想象能力,教师可以让学生多思考,多动手,多画图,注重“数形结合”的思想。
本讲的主线是培养学生的空间想象能力,亮点在于极值问题的体现、例3及展开图的应用。
(一)巧解复杂的组合图形表面积【例1】 用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?分析:该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形(每个正方体都可独立地搬走,但如果抽走下面的正方体,上面的正方体就会自动落下去),有人希望搬走其中部分正方体,但从上面和前面用平行光线照射时,在墙面及地面上的影子不变,则最多可以搬走多少个小正方体?答案:留下靠墙及地面上的正方体,其余均可搬走共1+3+6=10块.想挑战吗?长方体:6个面,8个顶点,12条棱,表面积=2×(长×宽+宽×高+长×高).正方体:6个面(每个面都是正方形),8个顶点,12条棱(棱长相等),表面积=6×边长×边长.圆柱体:2个底面圆,1个侧面(长方形或正方形),表面积=2×底面圆面积+侧面面积.【例2】边长为1厘米的正方体,如图这样层层重叠放置,那么当重叠到第5层时,这个立体图形的表面积是多少平方厘米?分析:这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米,该图形的总表面积为90立方厘米.[拓展] 如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?分析:当小积木互相重合的面最多时表面积最小.设想27块边长为1的正方形积木,当拼成一个3×3×3的正方体时,表面积最小,现在要去掉2块小积木,只有在两个角上各去掉一块小积木,或在同一个角去掉两块相邻的积木时,表面积不会增加,该几何体表面积为54.【例3】(奥数网原创题)按照上题的堆法一直堆到N层(N>3),要想使总表面积恰好是一个完全平方数,则N的最小值是多少?N N 个小面,总表面积是6个“大面”,所以就增加到分析:每增加一层,每一个“大面”就增加到(1)23N(N+1)个小面,几何题变成数论题,问题转化为“3N(N+1)是一个完全平方数,N的最小值是几(N>3)?”因为N和N+1互质,所以N和N+1必须有一个是完全平方数,一个是平方数的3倍,但N+1不能是平方数的3倍,因为此时N被3除余2,不可能是完全平方数,所以N是平方数的3倍,N+1是完全平方数,开始试验:当N=3×12=3,不符合题意;当N=3×22=12,N+1=13,不是完全平方数;当N=3×32=27,N+1=28,不是完全平方数;当N=3×42=48,N+1=49,是完全平方数,所以N的最小值是48,即堆到第48层时,总表面积是完全平方数,为3×48×49=842.(二)表面积的最值问题【例4】一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?分析:截去一个小正方体,表面积不变,只有在截去的小正方体的面相重合时,表面积才会减少,所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.【例5】边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例6】用10块长7厘米,宽5厘米,高3厘米的长方体积木堆成一个长方体,这个长方体的表面积最小是多少?分析:教师可以先提问:这个长方体的表面积最大是多少?为使表面积最大,要尽量保证10×2个7×5的面成为表面,想要做到这点很容易,只需将7×5面做底面,而后将10个立方体连排,衔接的面选用3×5的面(衔接的面将不能成为表面积),这样得到的长方体表面积最大.同样要想最小,可把7×5面做衔接的面,可得到10个长方体的连排,但此时我们还可以再制造出衔接面,如图:此时增加了2个5×7的面,减少了10个3×7的面,总体来讲表面积减少了.表面积是:2×(7×15+15×10+10×7)=650(平方厘米),所以这就是最小的表面积.[前铺] 用6块右图所示(单位:cm)的长方体木块拼成一个大长方体,有许多种拼法,其中表面积最小的是多少平方厘米?最大是多少平方厘米?分析:最小:66cm2;最大:(1×2+1×3+2×3)×2×6-1×2×5×2=112.【例7】要把12件同样的长a、宽b、高h的长方体物品拼装成一件大的长方体,使打包后表面积最小,该如何打包?(1)当b=2h时,按图几打包?(2)当b<2h时,按图几打包?(3)当b>2h时,按图几打包?分析:图2和图3正面的面积相同,侧面面积=正面周长×长方体长,所以正面的周长愈大表面积越大,图2的正面周长是8h+6b,图3的周长是12h+4b.两者的周长之差为2(b-2h).当b=2h时,图2和图3周长相等,可随意打包;当b﹤2h时,按图2打包;当b﹥2h时,按图3打包.[前铺] 要把6件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体,表面积最小是多少?分析:考虑所有的包装方法,因为6=1×2×3,所以一共有两种拼接方式:第一种按长宽高1×1×6拼接,重叠面有三种选择,共3种包装方法.第二种按长宽高1×2×3拼接,有3个长方体并列方向的重叠面有三种选择,有2个长方体并列方向的重叠面剩下2种选择,一共有6种包装方法.其中表面积最小的包装方法如图所示,表面积为1034.卷Ⅱ(三)立体图形的切、拼、挖【例8】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?分析:我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2×2×2=8(平方厘米);左右方向、前后方向:2×2×4=16(平方厘米),1×1×4=4(平方厘米),1/2×1/2×4=1(平方厘米),1/4×1/4×4=1/4 (平方厘米),这个立体图形的表面积为:8+16+4+1+1/4=29又1/4 (平方厘米).【例9】如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析:大立方体的表面积是20×20×6=2400平方厘米.挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3.[拓展1] 图中是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?分析:原正方体的表面积是4×4×6=96(平方厘米).每一个面被挖去一个边长是1厘米的正方形,同时又增加了5个边长是1厘米的正方体作为玩具的表面积的组成部分.总的来看,每一个面都增加了4个边长是1厘米的正方形.从而,它的表面积是:96+4×6=120平方厘米.[拓展2] 如右图,一个边长为3a厘米的正方体,分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体(都和对面打通).如果这个镂空的物体的表面积为2592平方厘米,试求正方形截口的边长.分析:原来正方体的表面积为:6×3a×3a=6×9a2(平方厘米),六个边长为a的小正方形的面积为(减少部分):6×a×a=6a2(平方厘米);挖成的每个长方体空洞增加的侧面积为:a×a×4×2=8a2(平方厘米);根据题意可得:54a2-6a2+3×8a2=2592,解得a2=36(平方厘米),故a=6厘米.【例10】有一个棱长为 5 cm的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(右上图),求这个立体图形的内、外表面的总面积.分析:将此带孔的正方体看做由八个8cm3的正方体(8个顶点)和12个1cm3的正方体(12条棱)粘成的.每个正方体有两个面粘接,减少表面积4cm2,所以总的表面积为:(4×6)×8+6×12-4×12=216(cm2).[拓展] 边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.【例11】如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下侧面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下侧面的洞口是直径为4厘米的圆,求此立体图形的表面积.分析:外侧表面积为:6×10×10-4×4×4-π×22×2=536-8π.内侧表面积为:16×4×3+2× (4×4-π×2)+2×2π×2×3=192+32-8π+24π=224+16π.总表面积=224+16π+536-8π=760+8π=785.12(平方厘米).【例12】如图,用455个棱长为1 的小正方体粘成一个大的长方体,若拆下沿棱的小正方体,则余下371个小正方体,问:所堆成的大长方体的棱长各是多少?拆下沿棱的小正方体后的多面体的表面积是多少?分析:设长方体棱长为分别为y zx、、.,他们只能取正整数,则有:4554(222)8455371x y zx y z⨯⨯=⎧⎨-+-+-+=-⎩因为4555713=⨯⨯方程组的有序正整数解只有(5,7,13),拆下沿棱的的小正方体后的多面体如图所示,首先计算突出在外面的6个平面,面积是2(11511335)206⨯⨯+⨯+⨯=再计算24个宽都是1的长⨯++=,总面积为358. 条,面积是8(1135)152(三)展开图【例13】在小于16 的自然数中选出6个不同的数,分别写在正方体的6个面上,要求各组相对的两个面上的数的乘积都相等,下图是正方体的展开图,并填上了1,请将其它数填上。
第二讲 立体图形(一)1掌握常见立体图形表面积的求法.2掌握几类典型组合立体图形表面积的求法.3鼓励学生多思考,勤动手,多画图,注重“数形结合以此来培养学生的空间想象能力.对于长、正方体等简单的立方体和其体积、表面积的计算方法,都是相对比较简单的,今天我们一起将这部分内容掌握后着重对其进行拓展研究. 如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.1.在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) 2.长方体的表面积和体积的计算公式是: 长方体的表面积:S 长方体=2(ab +bc +ac ); 长方体的体积:V 长方体=abc .3.正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:S 正方体=6a 2,V 正方体=a 3.专题精讲教学目标在墙角处有若干个体积都等于1的正方体堆成如图的立体图形(每个正方体都可独立地搬走,但如果抽走下面的正方体,上面的正方体就会自动落下去),有人希望搬走其中部分正方体,但从上面和前面用平行光线照射时,在墙面及地面上的影子不变,则最多可以搬走多少个小正方体?答案:留下靠墙及地面上的正方体,其余均可搬走共1+3+6=10块. 想挑战吗?Ⅰ、涂色与简单的表面积计算:【例1】右图是4×5×6正方体,如果将其表面涂成红色,那么其中一面、二面、三面被涂成红色的小正方体各有多少块?分析:三面涂红色的只有8个顶点处的8个立方体;两面涂红色的在棱长处,共(4-2)×4+(5-2)×4+(6-2)×4=36块;一面涂红的表面中间部分:(4-2)×(5-2)×2+(4-2)×(6-2)×2+(5-2)×(6-2)×2=52块.【例2】(05年清华附培训试题)将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?分析:长:3+1+1=5厘米;宽:1+1+1=3厘米;高:1+1+1=3厘米;所以原长方体的表面积是:(3×5+3×5+3×3)3×2=78平方厘米.[前铺]如右图,有一个边长是5的立方体,如果它的左上方截去一个边分别是5,3,2的长方体,那么它的表面积减少了多少?分析:原来正方体的表面积为5×5×6=150.现在立体图形的表面积截了两个面向我们的侧面,它们的面积为(3×2)×2=12,所以减少的面积就是12.[拓展]右图是由27块小正方体构成的 3×3×3的正方体.如果将其表面涂成红色,则在角上的8个小正方体有三面是红色的,最中央的小方块则一点红色也没有,其余18块小方块中,有12个两面是红的,6个一面是红的.这样两面有红色的小方块的数量是一面有红色的小方块的两倍,三面有红色的小方块的数量是一点红色也没有的小方块的八倍.问:由多少块小正方体构成的正方体,表面涂成红色后会出现相反的情况,即一面有红色的小方块的数量是两面有红色的小方块的两倍,一点红色也没有的小方块是三面有红色的小方块的八倍?分析:对于由n3块小正方体构成的n×n×n正方体,三面涂有红色的有8块,两面涂有红色的有12×(n -2)块,一面涂有红色的有6×(n-2)2块,没有涂色的有(n-2)3块.由题设条件,一点红色也没有的小方块是三面涂有红色的小方块的八倍,即(n-2)3=8×8,解得n=6.【例3】如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?分析:我们从三个方向(前后、左右、上下)考虑,新几何体的表面积仍为原立方体的表面积:10×10×6=600.[拓展] 在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?分析:对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑.变化前后的表面积不变:50×50×6=15000(平方厘米).【例4】(北京市第十二届迎春杯)一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?分析:截去一个小正方体,表面积不变,只有在截去的小正方体的面相重合时,表面积才会减少,所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.想想为什么不是15×15×6-7×7-8×8 ?Ⅱ、巧解复杂的组合图形表面积【例5】如右图,一个边长为3a厘米的正方体,分别在它的前后、左右、上下各面的中心位置挖去一个截口是边长为a厘米的正方形的长方体(都和对面打通).如果这个镂空的物体的表面积为2592平方厘米,试求正方形截口的边长.分析:原来正方体的表面积为:6×3a×3a=6×9a2(平方厘米),六个边长为a的小正方形的面积为(减少部分):6×a×a=6a2(平方厘米);挖成的每个长方体空洞增加的侧面积为:a×a×4×2=8a2(平方厘米);根据题意可得:54a2-6a2+3×8a2=2592,解得a2=36(平方厘米),故a=6厘米.[前铺]:把大正方形的边长由3a 变成4a,表面积变成4320,其他条件不变再由学生来练习,可得答案a=6.[前铺]如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.分析:我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面.这样这个立体图形的表面积就可以分成这样两部分:上下方向:大正方体的两个底面;四周方向(左右、前后方向):小正方体的四个侧面,大正方体的四个侧面.上下方向:5×5×2=50(平方分米);侧面:5×5×4=100(平方分米),4×4×4=64(平方分米).这个立体图形的表面积为:50+100+64=214(平方分米).【例6】如右图所示,由三个正方体木块粘合而成的模型,它们的棱长分别为1米、2米、4米,要在表面涂刷油漆,如果大正方体的下面不涂油漆,则模型涂刷油漆的面积是多少平方米?分析:4×4+(1×1+2×2+4×4)×4=100(平方米).【例7】下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?分析:我们仍然从3个方向考虑.平行于上下表面的各面面积之和:2×2×2=8(平方厘米);左右方向、前后方向:2×2×4=16(平方厘米),1×1×4=4(平方厘米),1/2×1/2×4=1(平方厘米),1/4×1/4×4=1/4 (平方厘米),这个立体图形的表面积为:8+16+4+1+1/4=29又1/4 (平方厘米).【例8】把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.求这个立体图形的表面积.分析:从上下、左右、前后观察到的的平面图形如下面三图表示.因此,这个立体图形的表面积为:2个上面+2个左面+2个前面.上表面的面积为:9平方厘米,左表面的面积为:8平方厘米,前表面的面积为:10平方厘米.因此,这个立体图形的总表面积为:(9+8+10)×2=54(平方厘米).【例9】边长为1厘米的正方体,如图这样层层重叠放置,那么当重叠到第5层时,这个立体图形的表面积是多少平方厘米?分析:这个图形的表面积是俯视面、左视面、上视面得到的图形面积的2倍. 该立体图形的上下、左右、前后方向的表面面积都是15平方厘米,该图形的总表面积为90立方厘米.Ⅲ、立体图形的分割与拼组【例10】 (首师大附小升初考试分班试题)一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?分析:锯一次净增加两个面,锯的总次数转化为增加的面数的公式为:锯的总次数×2=增加的面数. 原正方体表面积:1×1×6=6(平方米)一共据了多少次(2-1)+(3-1)+(4-1)=6次,6+1×1×2×6=18(平方米).【例11】 如右图,一个正方体形状的木块,棱长l 米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么,这60块长方体表面积的和是多少平方米?分析:我们知道每切一刀,多出的表面积恰好是原正方体的2个面的面积.现在一共切了(3-1)+(4-1)+(5-1)=9刀,而原正方体一个面的面积1×l=1(平方米),所以表面积增加了9×2×1=18(平方米).原来正方体的表面积为6×1=6(平方米),所以现在的这些小长方体的表积之和为6+18=24(平方米).[拓展](我爱数学夏令营活动试题)有三个大小一样的正方体,将接触的面用胶粘接在一起成左图的形状,表面积比原来减少了16平方厘米.求所成形体的体积. 分析:三个小正方体拼接成图中的样子,减少了小正方体的4个侧面正方形的面积,表面积减少了16平方厘米,每个正方形侧面为16÷4=4平方厘米,每个正方体棱长为2厘米,三个小正方体体积(即所成形体的体积)是3×23=24立方厘米.【例12】 有一个棱长为 5 cm 的正方体木块,从它的每个面看都有一个穿透的完全相同的孔(右上图),求这个立体图形的内、外表面的总面积.分析:将此带孔的正方体看做由八个8cm 3的正方体(8个顶点)和12个1cm 3的正方体(12条棱)粘成的.每个正方体有两个面粘接,减少表面积4cm 2,所以总的表面积为:(4×6)×8+6×12-4×12=216(cm 2).[拓展]边长分别是3、5、8的三个正方体拼在一起,在各种拼法中,表面积最小多少?分析:三个正方体两两拼接时,最多重合3个正方形面,其中边长为3的正方体与其它两个正方体重合的面积不超过边长为3的正方形,边长为5和边长为8的正方体的重合面面积不超过边长为5的正方形,三个正方形表面积和为6×3×3+6×5×5+6×8×8-2×2×3×3-2×5×5=502.立体图形的相关知识(表面积、体积等)我们会在五年级春季和六年级继续学习.专题展望1.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?分析:该图形的上、左、前三个方向的表面分别由9、7、7块正方形组成.该图形的表面积等于(9+7+7)×2=46个小正方形的面积,所以该图形表面积为46平方厘米.2. 有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析: 大立方体的表面积是20×20×20×6=2400平方厘米.挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3.3. 如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,那么挖掉的小立方体的边长是多少厘米?分析: 大立方体的表面积是20×20×20×6=2400平方厘米.在角上挖掉一个小正方体后,外面少了3个面,但厘米又多出3个面;在棱上挖掉一个小正方体后,外面少了2个面,但里面多出4个面;在面上挖掉一个小正方体后,外面少了1个面,但里面多出5个面.所以,最后的情况是挖掉了三个小正方体,反而多出了6个面,可以计算出每个面的面积:(2454-2400)÷6=9平方厘米,说明小正方体的棱长是3,它的体积是3×3×3=27,因此剩余的部分体积是20×20×20-27×3=7919.4. 一个正方体的棱长为3厘米,在它的前、后、左、右、上、下各面中心各挖去一个棱长为1厘米的正方体做成一种玩具,求这个玩具的表面积.分析:挖去六个小正方体后,大正方体的中心部分即与其主体脱离,这时得到的新玩具是镂空的.把这个玩具分成20部分,8个“角”和12条“梁”,每个“角”为棱长1厘米的小正方体,它外露部分的面积为:12×3=3(平方厘米),则8个“角”外露部分的面积为:3×8=24(平方厘米).每条“梁”为棱长1厘米的小正方体,它外露部分的面积为:12×4=4(平方厘米),则12条“梁”外露部分的面积为: 4×12=48(平方厘米).这个玩具的表面积为:24+48=72(平方厘米).5. (小数报数学竞赛决赛)右图是一个表面被涂上红色的棱长为lO 厘米的 正方体木块,如果把它沿虚线切成8个正方体,这些小正方体中没有被涂上 红色的所有表面的面积和是多少平方厘米?练习二分析:10×10×6=600(平方厘米).6. 用6块右图所示(单位:cm )的长方体木块拼成一个大长方体,有许多种拼法,其中表面积最小的是多少平方厘米?最大是多少平方厘米?分析:最小:66cm 2;最大:(1×2+1×3+2×3)×2×6-1×2×5×2=112.蛋型拼板.一种蛋形图板,可以分割成如下图所示的九块板,利用这九块板可以拼成各种各样的图形.国外称之为“魔蛋”.用蛋形拼板拼成的几种动物的造型.你会拼吗?拼拼看.三角板拼图.用四块形状、大小完全一样的直角三角形纸板(如右图),拼拼搭搭(不能重叠),能出现许多边长不同的正方形.你会拼吗?拼拼看.数学知识。
五年级几何知识奥数题五年级几何知识奥数题小学五年级奥数长方体和正方体几何知识经典例题详解:1、一个零件形状大小如下图:算一算,它的体积是多少立方厘米,表面积是多少平方厘米?【思路导航】(1)可以把零件沿虚线分成两部分来求它的体积,左边的长方体体积是10×4×2=80(立方厘米),右边的长方体的体积是10×(6-2)×2=80(立方厘米),整个零件的体积是80+80=160(立方厘米)。
10×4×2+10×(6-2)×2=160(立方厘米)(2)求这个零件的表面积,看起来比较复杂,其实,朝上的两个面的面积和正好与朝下的一个面的面积相等;朝右的两个面的面积和正好与朝左的一个面的面积相等。
因此,此零件的表面积就是:(10×6+10×4+4×2×2)×2=232(平方厘米)练习(1)一个长5厘米、宽1厘米、高3厘米的长方体,被切去一块后(如下图),剩下部分的表面积和体积各是多少?练习(2)把一根长2米的长方体木料锯成1米长的两段,表面积增加2平方分米,求这根木料原来的体积。
练习(3)有一个长8厘米,宽1厘米,高3厘米的长方体木块,在它的左右两角各切掉一个正方体(如下图),求切掉正方体后的表面积和体积各是多少?2、有一个长方体形状的零件。
中间挖去一个正方体的孔(如下图)。
你能算出它的体积和表面积吗?(单位:厘米)【思路导航】(1)先求出长方体的体积,8×5×6=240(立方厘米),由于挖去一个孔,所以体积减少2×2×2=8(立方厘米),这个零件的体积是240-8=232(立方厘米)(2)长方体完整的表面积是(8×5+8×6+5×6)×2=236(平方厘米),但由于挖去一个孔,它的表面积减少了一个(2×2)平方厘米的面积,同时又增加了凹进去的5个(2×2)平方厘米的面,因此,这个零件的表面积是236+(2×2)×4=252(平方厘米).练习(1)有一个形状如下图的零件,求它的体积和表面积。
立体图形⑴ 立体图形的表面积和体积公式长方体和正方体如右图,长方体共有六个面(每个面都是长方形),八个顶点,十二条棱.c b aHGFED BA①在六个面中,两个对面是全等的,即三组对面两两全等. (叠放在一起能够完全重合的两个图形称为全等图形.) ②长方体的表面积和体积的计算公式是: 长方体的表面积:2()S ab bc ca =++长方体; 长方体的体积:V abc =长方体.③正方体是各棱相等的长方体,它是长方体的特例,它的六个面都是正方形. 如果它的棱长为a ,那么:26S a =正方体,3V a =正方体.二、圆柱与圆锥【例 1】 如右图,在一个棱长为10的立方体上截取一个长为8,宽为3,高为2的小长方体,那么新的几何体的表面积是多少?改. 又是多少?【例 2】 右图是一个边长为4厘米的正方体,分别在前后、左右、上下各面的中心位置挖去一个边长l 厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?(图中只画出了前面、右面、上面挖去的正方体)练习:在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?【例 3】 下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为12厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同为14厘米,那么最后得到的立体图形的表面积是多少平方厘米?【例 4】 一个正方体木块,棱长是1米,沿着水平方向将它锯成2片,每片又锯成3长条,每条又锯成4小块,共得到大大小小的长方体24块,那么这24块长方体的表面积之和是多少?(锯一 次 增 加 两 个 面)练习.一个表面积为256cm 的长方体如图切成27个小长方体,这27个小长方体表面积的和是 2cm .表面积最小:互相重合的面最多时表面积最小【例5】如图,25块边长为1的正方体积木拼成一个几何体,表面积最小是多少?体积:例1.如图11-6,从长为13厘米,宽为9厘米的长方形硬纸板的四角去掉边长2米的正方形,然后,沿虚线折叠成长方体容器.这个容器的体积是多少立方厘米?例2.某工人用薄木板钉成一个长方体的邮件包装箱,并用尼龙编织条如图11-9所示在三个方向上加固.所用尼龙编织条的长分别为365厘米、405厘米、485厘米.若每个尼龙条加固时接头处都重叠5厘米,则这个长方体包装箱的体积是多少立方米?⑵不规则立体图形的表面积整体观照法例1.如图,在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体,求这个立体图形的表面积.例2.如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_______平方厘米.例3.把19个棱长为1厘米的正方体重叠在一起,按右图中的方式拼成一个立体图形.,求这个立体图形的表面积.例4.用棱长是1厘米的立方块拼成如右图所示的立体图形,问该图形的表面积是多少平方厘米?例5.下图是由18个边长为1厘米的小正方体拼成的,求它的表面积。