当前位置：文档之家 › 第八章位移法

第八章位移法

  • 格式：pdf
  • 大小：2.19 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

第八章位移法

第八章位移法

8
r22
Z2 1
2
M1 图
2 令EI=4
解： n 2
iAB 1.6
iBC 2
iBD iCE 1
50
60 50
60
R1 p
120
R2 P
R1=0 R2=0
r11Z1 r12 Z 2 R1 p 0 r21Z1 r22 Z 2 R2 p 0
M P图
r11 6i
R1 p 24
代入（8-4）式可得
4 Z1 i
4.计算基本未知量
4 Z1 i
（实际为转角 A ）
M M1Z1 M P
5.采用叠加法绘最后内力图 3i r11
A B
120
96
A
Z1 1
R1P
C
C
96
M p图
B
160
3i
M1 图
108
4 M BA 3i 96 108kN m i 4 M BC 3i 120 108kN m i
两端固定的情况
M AB 4i A 2i B M BA
一端固定一端铰支情况
6i F AB M AB l 6i F 2i A 4i B AB M BA l
F F M AB M BA ------固端弯矩
A
B
6i Fl M BA 2i A 4i B AB 0 l 8 1 3i 1 F B ( A AB M BA ) 2 l 2i
基本结构
EI
n4
EI
n3
B A
C
D
G
F
n6 E

位移法位移法(精)

位移法位移法(精)

2i
4i
24
4i
MP
M1
2i 16
M Z1M1 M P
12kN/m 12kN/m 12kN/m 12kN/m
24
24
EEI I
M反对称 EI
EEII
M反对称
72
72
8
8
EI EI
4
4
ME对I称 M对EI称
20
20
16
32
4 M图
(kN.m)
48
92
52
有这样一种刚架，对其左部，用力法较位移法的未知
反对称
对称
24
24
EI
EI
EI
12kN/m 12kN/m 12kN/m
EI
2EI
EI
M反对称
EI
EI
等代结构
72
X 0
11 1
1P
72 4
11

1 EI
43

3

43



256 3EI
4
M1
MP
1P


96 4 3EI
4


512 EI
4
X1
1P
11
6
r22 EI 2 EI 2 EI
系数δ12为单位位移 Z2 1 所引起的
EI
位移，其性质与由支座转动而引起的
位移相当。故可利用第八章的位移公
M2
式 k Rc 计算，即
12 R1c (8 1) 8
Z2 1
0.5EI 0.5EI
0.25EI
系数r21为单位力 X1 1 所引起的反力矩，可由 M1 图根据结点平衡

第八章位移法new

第八章位移法new

1）在B结点增加附加转动约束（附加刚臂）( )。
附加转动约束只能阻止刚结点的转动，不能阻止结
点之间的相对线位移。此时产生固端弯矩
M
F。
BC
q
锁A 住
B 0
B
C
q
M
F BA

0,
M
F BC


ql2 。 8
B
M
F BC
C
2）令B结点产生转角

(
B
)。此时AB、BC杆类似
于B端为固端且产生转角 B 的单跨超静定梁。 4
20
三. 固端弯矩
单跨超静定梁在荷载作用下产生的杆端弯矩称为 固端弯矩。固端弯矩以顺时针方向为正，逆时针方向 为负。
1. 两端固定的梁：
q
ql 2 12
A
ql 2 24
l
ql 2 12 FP l 8
B
A
FP
FP l 8
B
FP l
l/2
8
l/2
M
F AB


ql 2 12
,
M
F BA

ql 2 。 12
增加附加链杆：
B EA C
Z1 BH CH
B EA = 有限值 C
Z1 BH
Z2 CH
A
DA
Z3 D
D
Z1 B
Z2 C
C
Z1 B
Z4 BH B
A
C
Z5 CH
Z2


B
BH
E A
D
当BD杆： EI无限大
D
？
12
§8-2 等截面直杆的刚度（转角位移）方程

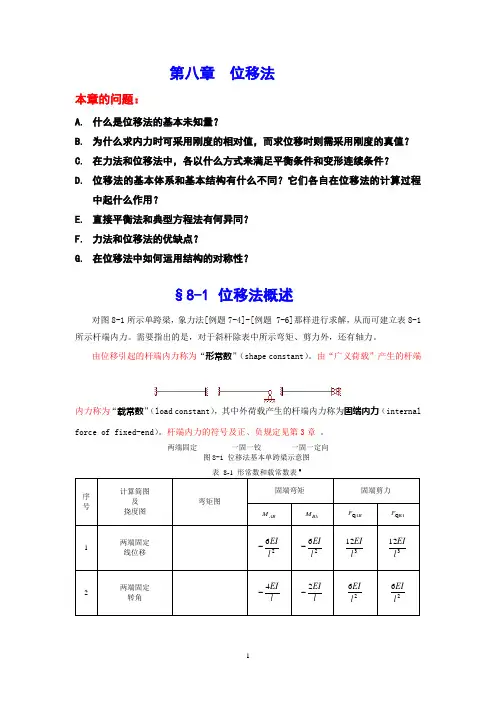
08第八章_位移法

08第八章_位移法

第八章位移法本章的问题：A.什么是位移法的基本未知量？B.为什么求内力时可采用刚度的相对值，而求位移时则需采用刚度的真值？C.在力法和位移法中，各以什么方式来满足平衡条件和变形连续条件？D.位移法的基本体系和基本结构有什么不同？它们各自在位移法的计算过程中起什么作用？E.直接平衡法和典型方程法有何异同？F.力法和位移法的优缺点？G.在位移法中如何运用结构的对称性？§8-1位移法概述对图8-1所示单跨梁，象力法[例题7-4]-[例题 7-6]那样进行求解，从而可建立表8-1所示杆端内力。

需要指出的是，对于斜杆除表中所示弯矩、剪力外，还有轴力。

由位移引起的杆端内力称为“形常数”（shape constant）。

由“广义荷载”产生的杆端内力称为“载常数”（load constant），其中外荷载产生的杆端内力称为固端内力（internal force of fixed-end）。

杆端内力的符号及正、负规定见第3章。

两端固定一固一铰一固一定向图8-1 位移法基本单跨梁示意图*P。

P 。

P 有了表8-1，则图8-2 所示的两端固定单跨梁，利用形、载常数和叠加原理可得杆端内力。

例如A 端杆端弯矩为F4322122646ABAB M l EI lEI l EI l EI M ++-+=∆∆∆∆ （a ） A 端杆端剪力为图8-2单跨梁杆段位移和荷载作用AB3∆4∆2∆1∆FQ 42332213Q 612612AB AB F l EI l EI l EI l EI F ++-+=∆∆∆∆ （b ）式（a ）和式（b ）中FAB M 和F Q AB F 为荷载引起的固端弯矩和固端剪力。

同理，也可叠加得到B 端的杆端内力BA M 和BA F Q 。

这些将杆端位移和杆端内力联系起来的式子，称为两端固定单跨梁的转角位移方程（slope-deflection equation ）或刚度方程（stiffness equation ）。

结构力学第8章位移法

结构力学第8章位移法

结构力学第8章位移法位移法是结构力学中一种常用的分析方法。

它基于结构物由刚性构件组成的假设，通过计算结构在外力作用下产生的位移和变形，进而推导出结构的反力和应力分布。

位移法的基本思想是将结构的局部位移组合成整体位移，通过建立位移和反力之间的关系，解决结构的力学问题。

位移法的分析步骤通常包括以下几个方面：1.建立结构的整体位移函数。

位移函数是位移法分析的基础，通过解结构的运动方程建立结构的位移与自由度之间的关系。

2.应用边界条件。

根据边界条件，确定结构的支座的位移和转角值。

支座的位移和转角值可以由结构的约束条件和外力产生的位移计算得出。

3.构建位移方程组。

将结构的整体位移函数带入到结构的平衡方程中，得到位移方程组。

位移方程组是未知反力系数的线性方程组。

4.解位移方程组。

通过解位移方程组，求解未知反力系数。

可以使用高斯消元法、克拉默法则或矩阵方法等解方程的方法求解。

5.求解反力和应力分布。

通过已知的位移和未知的反力系数，可以计算出结构的反力和应力分布。

这些反力和应力分布可以进一步用于结构的设计和评估。

位移法的优点是适用范围广泛，适合复杂结构的分析。

它可以处理线性和非线性的结构，包括静力学和动力学的分析。

同时，位移法具有较高的精度和准确度，在结构的分析和设计中得到广泛应用。

然而，位移法也存在一些限制。

首先，位移法假设结构是刚性的，忽略了结构的变形和位移过程中的非线性效应。

其次，位移法需要建立适当的位移函数，对于复杂结构来说，这是一个复杂和困难的任务。

此外，位移法在处理大变形和非线性结构时可能会遭遇困难。

综上所述，位移法是结构力学中一种重要的分析方法。

它通过计算结构的位移和变形，推导出结构的反力和应力分布，为结构的设计和评估提供基础。

然而，位移法也存在一些限制，需要在具体的分析问题中谨慎应用。

结构力学上第8章 位移法

结构力学上第8章 位移法

(非独立角位移) l FQBA
M AB M BA
F 3i A 3i M AB l 0
3、一端固 FQAB
A
B1
B
l
F M AB i A i B M AB F M BA i A i B M BA
(非独立线位移)
q B EI C L
Z1
q B
EI C
Z2 4i
Z1=1
EI A 原结构
L
=
Z2=1
EI A qL2 8 基本体系
=
3i
M1图×Z1 2i
+
6EI L2 6EI M2图×Z2 L2
+
qL2 8 MP图
在M1、M2、MP三个 图中的附加刚臂和链杆 中一定有约束反力产生， 而三个图中的反力加起 来应等于零。
M
q
应用以上三组转角位移方程，即可求出三种基本的单跨超 静定梁的杆端弯矩表达式，汇总如下：
F 1）两端固定梁 M AB 4i A 2i B 6i M AB
M BA
l F 2i A 4i B 6i M BA l
2）一端固定另一端铰支梁
F M AB 3i A 3i M AB l M BA 0 3）一端固定另一端定向支承梁 F M AB i A i B M AB
3
2
1
结点转角的数目：7个
独立结点线位移的数目：3个
D
E
A
B
C
C
D
刚架结构，有两个刚结点D、E， 故有两个角位移，结点线位移由铰 结体系来判断，W=3×4－2×6=0， 铰结体系几何不变，无结点线位移。
A
B

位移法


F B 端为铰支座固端弯矩 M AB 由上式得： F M BA F F 铰 支 M AB M AB (c) 2 B 端为滑动支座：q B FQBA 0
P M A 0 FQBAl M AB M BA M A 0
把式(a) 、(b)代入上式，得：
D F F P 6iq A 12i M AB M BA M A P M AB M BA M A l FQBA 0 l l F F P 6iq Al M ABl M BAl M A l 1 l F F P D q Al ( M AB M BA M A ) (d) 12i 2 12i
§8-3 无侧移刚架的计算
1、无侧移刚架基本未知量的判定：
其位移法基本未知量数目
结构上刚结点的独立角位移数 等于结构上的自由刚结点数 。
(a)
1 D E 2 C F
A
(b)
B
D
EA=
C
1 C
B
1 A
2 B
A
(c)
(d)
说明：
1）强调位移法基本未知量是结 构中自由结点上的独立结点位移。 结点上的独立角位移是自由刚结 点上的角位移。
(2) B 端为铰支座
式(8-5)中
M BA 0
，得：
D M AB 4iq A 2iq B 6i L D 0 2iq A 4iq B 6i L
整理上式得：
M AB
D 3iABq A 3i L
(8-9)
(3) B 端为滑动支座
代入(8-5)式，得：
D 1 qA 式(8-6)中 q B FQAB FQBA 0 ，得： L 2
(8-10)

第8章 位移法1

一.位移法基本概念 1. 考察变形情况,AB=AC=
A
EI
EI
B
l/2 P
l/2
C
2. AB杆：相当于一端固定一 端铰支梁在支座A处发生转 角 。 MAB=3i
3. AC杆：相当于两端固 定梁在支座A处发生转角 及荷载共同作用。
MAC=4i+Pl/8 MCA=2i-Pl/8
由上述分析可知，如果能求出 ，则各杆 的内力就可求出。所以可把转角 作为基 本未知量。 4. 如何求 ？
2
基本体系
r11 4i 6i R1P
2i
M1
q
ql 2 / 8 ql 2 / 8
MP
2 ql / 20 位移法求解过程 :
Z1 ql 2 / 80i
M M 1 Z1 M P
q 1)确定基本体系和基本未知量 2)建立位移法方程 3)作单位弯矩图和荷载弯矩图 4)求系数和自由项 ql2 / 40 M 5)解方程 6)作弯矩图
M AB
3i F 3i A AB M AB l
（三）一端固定一端定向杆的转角位移方程
A
B A
P
B
F M BA
A
A
M AB i A M BA －i A
B i
M
F AB
M AB i A M
F AB F BA
M BA i A M
二.单跨超静定梁的形常数与载常数
ql2/8
q D A
C 4i B 3i A 2i
D
C
B
M1图
3) 画出单位弯矩图和荷载弯矩图 4) 求各系数
MP图
5) 画出弯矩图
2 r11 8i R1P ql / 8 R1P ql2 Z1 r11 64i

第8章 位移法

第8章　位移法§8-1　概述§8-2　等截面直杆的转角位移方程§8-3　位移法的基本未知量和基本结构§8-4　位移法的典型方程及计算步骤§8-5　直接由平衡条件建立位移法基本方程§8-6　对称性的应用2021-5-1212021-5-12 1§8-1　位移法的基本概念内力对于线弹性结构位移位移内力两种方法的基本区别之一，在于基本未知量的选取不同：力法是以多余未知力（支反力或内力）为基本未知量，而位移法则是以结点的独立位移（角位移或线位移）为基本未知量。

用位移法分析结构时，先将结构拆分成单个的杆件，进行杆件受力分析（建立杆件的转角位移方程）；再将杆件组装成原结构，利用结点和截面平衡条件建立位移法方程，解出结点位移，再由转角位移方程求出内力。

2021-5-121一、引例1. 确定基本位移未知量图a所示两跨常刚度连续梁，抗弯刚度为EI。

忽略二杆的轴向变形，B结点不会发生线位移，而仅会产生角位移，设此角位移为Z1。

因B结点刚结两梁段于B端，从而保证两梁段在B端有相同的角位移，均为Z1。

2021-5-1212. 分列各组成杆的转角位移方程AB和BC二杆在B端具有相同的角位移和零线位移后，因此可将二杆在B端处分开，单独分析。

2021-5-1211）AB杆2）BC杆2021-5-1213. 通过B结点的平衡条件求出Z1由B结点的平衡可得2021-5-1214. 将Z1代回转角位移方程，求出各杆端弯矩2021-5-1212021-5-121二、其他示例（a）　若略去受弯直杆的轴向变形，并不计由于弯曲而引起杆段两端的接近，则可认为三杆长度不变，因而结点A没有线位移，而只有角位移。

对整个结构来说，求解的关键就是如何确定基本未知量q A的值。

2021-5-1212021-5-121三、位移法计算原理思路小结1. 把结构在非支座结点处拆开，将各杆视为相应的单跨超静定梁。

第8章 位移法

第八章 位移法
§8－1 概述
基本方法——力法、位移法
结构：外因→内力~位移——恒具有一定关系 力 法： 内力 → 位移 位移法：位移 → 内力
基本未知量 力法——多余未知力 位移法——结点位移（线位移，转角位移）
基本概念：（以刚架为例）
n=2 （超静定次数） 忽略轴向变形，
结点位移
Z1（角位移，无线位移） 变形协调条件
§8－2 等截面直杆的转角位移方程
单跨超静定梁——由杆端位移及荷载求杆端力 两端固定等截面梁（两端约束杆） 杆AB有杆端位移φA、φB、ΔAB， 只考虑相对线位移ΔAB
弦转角βAB = ΔAB∕l 顺时针为（＋）
求杆端力 ——力法求支座移动引起的内力
11x1 12 x2 1 A 21x1 22 x2 2 B
1、基本未知量的确定 刚架 —— 除结点角位移外还有结点线位移 假定 ①理想刚结点，铰结点 ②忽略轴力产生的轴向变形 ③小变形（直杆弯曲两端距离不变） 角位移数＝刚结点数
固定端角位移＝0 铰结点、铰支座处杆端转角不独立
线位移数＝独立的结点线位移数
a．观察——φ、Δ
b．独立线位移数——几何构造分析方法确定： （1）将所有刚结点（包括固定支座）变铰结点 （2）铰结体系的自由度数＝独立的线位移数
图8－7 M1：r11=3i + 3i＝6i MP： R1P=96-120=-24kN∙m Z1=-R1P/r11=4kN∙m/i M=MP+Z1M1
无侧移刚架： 【题9－9】2个转角位移 （对称性利用——1个转角位移）
例：（图8－9） （a）有侧移结构
计算步骤 （1）基本未知量 z1（φ1）、z2（Δ2） 刚结点——附加刚臂（只约束转动，不约束移动） 结点——附加支座链杆（独立线位移方向）
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
M 21 0
1
EI l
3
l
M 12 1 3i 5 ql 2 Z1 ql l 2 l 8 M 1 3i 3 FQ 21 12 ql 2 Z1 ql l 2 l 8 FQ12
6i 3 Z1 ql 0 l2 8
于是，可得：
M 34 3i 2 Z1 l l M 34 3i FQ 43 2 Z1 l l FQ 34
原结构
基本体系
Z1 Z1 Z1=1 Z1=1
R1 0
R11 Z1
(d)
R1P
(e)
(f)
r11
从另一方面看，根据前面所述，若线位移Z1确实是原结构中的侧 向线位移，则有
q ql2 8
+
MP图
3i l
21 FQ 21 FQ
M1图
3i l
43 FQ 43 FQ
则同样有
R1 0
退出
退出 退出
等效单跨超静定 梁组合体
结点力矩平衡条件
基本方程 静力平衡条件
结构的剪力平衡条件
四、位移法的第二种基本型式----附加约束法 1 无侧移刚架 (a)
只阻止结点转动，不能 阻止结点移动的附加刚臂
(b) Z1 1 R1 FP 2
(a) 1 M 13
M 12
(b) 1
R1 M'12 M'13
图 8 - 14
Z"1 FP M图
l 2
8F Pl 56
F Q图 3
l/2
3
ቤተ መጻሕፍቲ ባይዱ9F Pl 56
4 l
3 183 F l 552 P
4 486 F 552 P
(b)
图 8-4
(a) Z1 2 EA=∞ Z1 4 (b) 2
图 8-6
2 4 3ql 2 16 4
Z'1
q
ql2 8 1
2
D
+ 3ql 16
M A
B
D
M A
B
1 Z"1
Z"1
l
l/2
F P 1
3
1
Z2 1
Z2 i Z1 2
D
(c)
3
Z"1 4
M A
(d)
B
2 F Q21 4 F Q43
l 2
FP
i
Z1
i
l 2
3 l
4
3
C
退出
图 8-2
超静定结构的弯曲变形示意图
独立的未知结点位移?
图 8-3
2
2014-04-19
Z2
(a) 2 EI Z1 1 Z1
1
Z2 i Z1 2
3
2014-04-19
三、位移法的第一种基本型式----直接平衡法
1 无侧移刚架
(a) 2 EI Z1
M 12
Z'1
3FP l 56
M 13
基本未知量
1 Z1
1
(b) 2
Z'1 FP EI (d) 1 M 12 M 13 (c) 3 1 Z"1
1
M12 3iZ1
M 21 0
退出
图 8 - 17
6
2014-04-19
即
R1 R1P R11 0
式中，R1P表示基本结构在荷载单独作用下附加链杆上将产生的反力， R11表示基本结构上附加链杆移动Z1时，附加链杆上产生的反力。根据比 例关系可得
其中， r11是系数，表示基本结构在Z1=1时，附加链杆中的反力； R1P是自由 项，表示基本结构在荷载单独作用下附加链杆上将产生的反力。
3 40 F Pa 1
结点 1的转角 Z1求得后，可按下式叠加作出最后弯矩图。
M Z1M1 M P
FP 2
23 40 F P 1 FP +
FP
17 40 F P
2
1
9 80 F P
2
M1图
M
3 2EI1 a 1
1
0 : r11
6EI1 a
10 EI1 a
3
M
1 0
1
0 : R1P
1 Z1
Z1 EI 2=2EI1 EI1
原结构
2
附加刚臂
基本体系
M1 0
3
M12 M13 0
M
0 1
M13 R1 M12
a
若基本体系的受力情况与原结构相同，因为原结构中结点1上无集 中力偶作用，所以基本体系上附加刚臂的反力矩应为零，即
3 a/2
(c) R1P 1
a/2
退出
图 8-1
超静定刚架
退出
(1) 、什么样的内力，就对应什么的 位移与变形。
(2) 、什么的位移与变形，就对应什么样的内力。 (b) (a) Z'
1
2 EI Z1
1 Z1
1
2
(a) Z' 12
Z1 1
EA=∞
Z1 4
(b)
Z'1 2
l/2
FP EI (d) 1 3 l M 12 M 13 (c)
q
M图 3ql 16
2
+ 3 13ql 16 1 F Q图 3
1
3
1
5ql 16
M图?
C C
图 8-7
l
退出
(c) 4
图 8-5
Z"1 (d) 2 F Q21 4 F Q43
退出
3
(3)、 研究思路 （a）以独立的未知结点位移为基本未知量。
二、位移法的基本思路 先离散，后组合。即化整为零，积零为整。 基本未知量：独立的未知结点位移 （变形协调条件） 结构离散成杆件，离散的杆件视为等效的单跨超 离散 静定粱，建立等效单跨超静定粱杆端内力与结点 位移的关系。
(b) 2
Z'1
1
1
2 Z'1
1
1
Z"1
l 2
3F Pl 56
1 27 F l 552 P FP
27 F l 552 P
2
27 F 1 552 P FP +
66 F 552 P
-
FP
l/2
i
Z1
i
60 F l 552 P M图 66 F l 552 P (a)
FP EI (d) 1 3 l M 12 M 13 (c) 3
将上述杆端剪力代入剪力平衡方程可得该结构位移法的基本方程为：
基本未知量
(c) 4 Z"1
结点线位移Z1
Z1 Z1 Z1
位移协调
Z1
M 34 3i Z1 l
(d) 2 F Q21 4 F Q43
ql 3 16i
M 43 0
3
剪力平衡 条件
将所求得的Z1代入各杆端内力计算公式可得：
结点 1的转角
l/2
8F Pl 56
图 8 - 10
M图 9F Pl 56
图 8-9
位移法基本方程
从以上所述可知，对于无侧移刚架，位移法是以独立结点角 位移作为基本未知量，根据结点力矩平衡条件，并利用物理条件、 变形谐调条件建立求解结点位移的方程，首先求出位移。然后利用
退出
7iZ1
FP l 0 8
上述解题过程，主要有两步，第一步将结构离散，将离散后的杆 件等效为相应的单跨超静定梁，分析各根杆件的受力情况，用杆端 位移表示各杆件的杆端力；第二步将各杆件联结起来组成结构，利 用变形谐调条件和平衡条件，建立求解结点位移的方程。 侧移刚架
由上结果即可绘出结构的弯矩图及剪力图。
2 4 3ql 2 16 4
（b）应当以力法的计算结果为基础，即以最简 单的超静定结构计算结果为基础。 （c）任何结构的计算必须满足相应的物理条件、静 力平衡条件、变形协调条件。
按照这种研究思路与策略，便形 成了位移法的基本思路。
退出 退出
EI l
图 8-8
EI l
单跨超静定粱
EI l
（静力平衡条件） 组合 杆件组成结构，进行整体分析，得出基本方程。
P
结点的转角均假设以顺时针 方向为正，反之为负。
1
R1 0
从另一方面看，根据前面所述，若转角Z1确实是原结构中结点1的转 角，则有
2
(d)
R11 1
2
附加刚臂中的反力 矩均假设以顺时针 方向为正。
3
M12 M12
则同样有
M13 M13
固定结点
+
R1 R1P R11
3
放松结点
Z1
FP l 56i
将结点 1的转角Z1代入杆件12、13的杆端弯矩方程即得杆件12、13的杆端弯矩。
转角位移方程求出杆端力，绘制内力图。
2 有侧移刚架
(a) Z1 2 EA=∞ Z1 4 (b) Z'1 2
根据杆端弯矩，可求得杆端剪力分别为：
q
EI=常数
i
1
3i ql 2 M 12 Z1 l 8
r11
于是，可得：
10 EI1 a
R1P
3FP a 16
R11 r11Z1
于是，可得位移法的基本方程为
10 EI1 3 Z1 FP a 0 a 16
Z1
3FP a 2 160 EI 1
r11Z1 R1P 0
(a) Z1=1 4EI1 1 r11 a 2EI 3( a 1 ) (b) 2 3 16 F Pa R1P 1 FP 2 5 32 F Pa