荷载的横向分布系数

探讨横向分配系数计算方法桥梁荷载横向分配系数的计算主要有铰接板（梁）法、刚接板（梁）法、偏心压力法、修正偏压法、比拟正交异性板法（G-M法）、弹性支承连续梁法、考虑抗扭的弹性支承连续梁法等[1]。

如何正确选择适用方法是广大设计人员面对的一个重要问题。

1、荷载横向分配系数计算理论在荷载横向分配计算中，结构的横向连接刚度起着至关重要的作用。

横向连接刚度越大，荷载横向分布作用越显著，各主梁所分配的荷载也越趋均匀。

因此需要根据实际的横向结构拟定出较为合理的简化计算模型，从而确定相应的计算方法。

对于城市宽桥，需要用梁格法，通过有限元计算来得到桥梁的横向分配系数[2]。

梁格系理论是将桥梁上部结构用一个等效梁格来代替分析，等效梁格后再将其结果还原到结构中就可得到所需的计算结果。

此法易于理解，便于使用，而且比较精确。

一般说来等效梁格的网格越密，计算结果的精确度就越高。

梁格法主要应用简支梁桥挠度参数跟横向分配系数的关系来求得横向分配系数。

通过最不利荷载的布置求得各片主梁的挠度，再由在单片主梁上跨中加载所得的挠度，从而得出各片主梁的荷载横向分配系数[2]。

2、应用梁格法的实例橄榄河桥位于省道S214线上，原桥为5-15m双曲拱桥，由于该桥病害严重，相关单位对该桥进行了重建。

2014年重建桥梁为4跨预应力混凝土连续梁桥，主梁结构为4片预应力混凝土连续小箱梁。

桥跨布置为19.92m+20m+20m+19.92m。

梁格法采用Midas/civil结构分析软件进行计算，图1为计算模型。

全桥模型在横向最不利汽车荷载布置下各片梁所承受内力值与跨中各片梁内力值之和的比值即为该片梁的横向分配系数。

同时采用刚性梁法计算该桥在最不利汽车荷载作用下的横向分配系数。

主梁从左往右编号为1-4号见图2。

表1为两种方法计算出的1-4号梁的荷载横向分配系数。

3、结语采用刚接梁法及梁格法对一座4片小箱梁构成的主梁的横向分配系数进行了计算。

经过对计算结果比较，可以得到如下结论：1）因刚接梁法主要考虑箱梁翼缘及各片箱梁之间湿接缝的刚接，横隔板的刚度平均分配到梁的纵向，故其横向分配系数计算结果偏大。

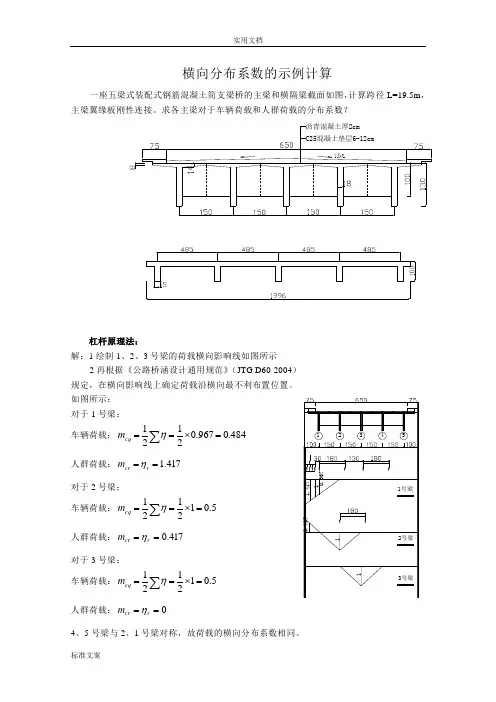
实用文档标准文案横向分布系数的示例计算一座五梁式装配式钢筋混凝土简支梁桥的主梁和横隔梁截面如图，计算跨径L=19.5m ，主梁翼缘板刚性连接。

求各主梁对于车辆荷载和人群荷载的分布系数？杠杆原理法：解：1绘制1、2、3号梁的荷载横向影响线如图所示2再根据《公路桥涵设计通用规范》（JTG D60-2004） 规定，在横向影响线上确定荷载沿横向最不利布置位置。

如图所示： 对于1号梁： 车辆荷载：484.0967.02121=⨯==∑ηcq m 人群荷载：417.1==r cr m η 对于2号梁： 车辆荷载：5.012121=⨯==∑ηcq m 人群荷载：417.0==r cr m η 对于3号梁： 车辆荷载：5.012121=⨯==∑ηcq m 人群荷载：0==r cr m η4、5号梁与2、1号梁对称，故荷载的横向分布系数相同。

偏心压力法（一）假设：荷载位于1号梁 1长宽比为26.25.155.19>=⨯=b l ，故可按偏心压力法来绘制横向影响线并计算横向分布系数c m 。

本桥的各根主梁的横截面积均相等，梁数为5，梁的间距为1.5m ，则：5.220)5.11(2)5.12(2222524232221512=+⨯+⨯=++++=∑=a a a a a ai i2所以1号5号梁的影响线竖标值为：6.0122111=+=∑i a a n η 2.0122115-=-=∑i a a n η由11η和15η绘制荷载作用在1号梁上的影响线如上图所示，图中根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

进而由11η和15η绘制的影响线计算0点得位置，设0点距离1号梁的距离为x ，则：4502.015046.0=⇒-⨯=x xx 0点已知，可求各类荷载相应于各个荷载位置的横向影响线竖标值3计算荷载的横向分布系数 车辆荷载：()533.0060.0180.0353.0593.02121=-++⨯==∑ηcq m 人群荷载：683.0==r cr m η （二）当荷载位于2号梁时 与荷载作用在1号梁的区别以下：4.0122112=+=∑i a a a n η实用文档标准文案0122552=-=∑ia a a n η 其他步骤同荷载作用在1号梁时的计算修正偏心压力法（一）假设：荷载位于1号梁 1计算I 和T I ：2.3813018)2814(150)18150()2814(1301821)(2122221=⨯++⨯-+++⨯⨯=+-++⨯=ch bd c b d ch y8.912.3813012=-=-=y y y[][]43333313132106543)112.38)(18150(2.381508.911831))((31cm d y c b by cy I ⨯=---⨯+⨯⨯=---+⨯=对于翼板1.0073.01501111<==b t ，对于梁肋151.01191822==b t 查下表得所以：311=c ，301.02=c 433331027518119301.01115031cm t b c I i i i T ⨯=⨯⨯+⨯⨯==∑2计算抗扭修正系数β 与主梁根数有关的系数ε则n=5，ε=1.042 G=0.425E875.055.15.1910654310275425.0042.111)(112332=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯+=+=E E B l EI GI T εβ 3计算荷载横向影响线竖标值11η和15η55.0122111=+=∑i a a n βη 15.0122115-=-=∑ia a n βη 由11η和15η绘制荷载作用在1号梁上的影响线如上图所示，图中根据《公路桥涵设计通用规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。

第三章 荷载横向分布计算由于本桥各T 梁之间采用混凝与湿接缝刚性连接，故其荷载横向分布系数，在梁端可按“杠杆原理法”计算（m 0），在跨中按“修正刚性横梁法”计算(m c )。

（一）梁端的横向分布系数m 0根据桥规规定，在横向影响线确定荷载沿横向最不利的布置位置。

例如，对于汽车荷载，规定的汽车横向轮距为1.8m ，两列汽车车轮的横向最小间距为1.30m,车轮距离人行道缘石最少为0.50m 。

求出相应于荷载位置的影响线竖标值后，就可得到横向所有荷载分布给1号梁的最大荷载值为： 式子中：q P —汽车荷载轴重；q η—汽车车轮的影响线竖标。

由此可得：1号梁在汽车荷载作用下最不利荷载横向分布系数为654.001=m 同理有：904.002=m ；904.003=m ；904.004=m ；904.005=m ；654.006=m（二）跨中的横向分布系数m c 1.计算I 和I T求主梁截面中心位置a x (距梁顶)翼板的换算平均厚度 cm h 19224141=+=马蹄形下翼缘换算厚度 cm h 5.34228412=+=S ≈ (260-18)×19×19/2+245×18×245/2=583906cm 3 A ≈(260-18)×19+245×18=9008cm 2 重心距离 a x =S/A=583906/9008=64.82cm 主梁抗弯惯性矩：I ≈1/12×(260-18)×193+(260-18)×19×(64.82-19/2)2+1/12×18×2453 +18×245×(245/2-64.82)2=cm 4=0.5094m 4 翼板主梁抗扭惯性矩b 1/t 1=260/19=13.68＞10, 查表得c 1=0.33梁肋b 2=245-19=226cmb 2/t 2=226/18=12.6＞10, 查表得c 2=0.33 I T =∑c i b i t i 3=0.33×260×193+0.33×226×183=1023452cm 4=0.0102m 42.计算抗扭修正系数β本桥各主梁的横截面均相等，梁数n=6，梁间距为2.6m ，则 其中：E —混凝土弹性模量；G —混凝土剪切模量，E G 43.0=。

横向分布系数荷载横向分布系数：表示某根主梁所承担的最大荷载占各个轴重的倍数。

为使荷载横向分布的计算能更好地适应各种类型的结构特性，就需要按不同的横向结构简化计算模型拟定出相应的计算方法。

目前最常用的几种方法：杠杆原理法：把横向结构（桥面板和横隔梁）视作在主梁上断开而简支在其上的简支梁。

适用于双主梁桥、荷载位于靠近主梁支点处。

偏心压力法：把横隔梁视作刚性极大的梁，故又称刚性横梁法。

当计及主梁抗扭刚度影响时此法又称为修正偏心压力法（修正刚性横梁法）。

适用于窄桥（宽跨比B /l 小于或接近0.5的情况）。

G-M 法：由比拟正交异性板法发展而来，能利用计算机工具或编就的计算图表得出相对来说比较精确的结果。

此法概念明确，计算简捷，对于各种桥面净空宽度和多种荷载组合的情况，可以很快的求出各片主梁的相应内力值。

例：如图所示桥梁横断面，在公路-Ⅰ级荷载作用下，分别用杠杆原理法和偏心压力法求①和②号梁的荷载横向分布系数。

杠杆原理法：首先在①号梁和②号梁横向影响线上，按最不利方式布载，如图所示：①号梁：11900180011219002m −=×+× 11110.0530.521922=×+≈×+ 0.5265= ②号梁：1190018001119001300121900221900m −−=×+×+× 1111611 10.0530.50.316219221922=×+×+×≈×++× 0.6845=偏心压力法：首先画①号梁和②号梁横向影响线，那就要先找到其影响线的两个控制竖标值，由于各主梁的截面均相同，故可按下式计算：()()()()()()422222212341122222221112122114212121 1.5 1.90.5 1.90.5 1.9 1.5 1.918.05m 1.5 1.911=0.250.450.7418.051.5 1.911=0.250.450.2418.051=n ii i i n ii n i i i a a a a a a a n a a n a a a n a ηηη=====+++=×+×+−×+−×=×+=+=+=×−=−=−=−×+∑∑∑∑()()()()212424210.5 1.9 1.5 1.910.250.150.4418.050.5 1.9 1.5 1.911=0.250.150.1418.05n i ni i a a n aη==×××=+=+=××××−=−=−=∑∑然后在①号梁和②号梁横向影响线上，按最不利方式布载，如图所示：①号梁：()10.7160.4320.2260.508=0.6582m =×++− ②号梁：()10.4050.3110.2420.147=0.55252m =×+++ 荷载横向分布系数延桥垮的变化：通常用“杠杆原理法”来计算荷载位于支点处的横向分布系数m 0，其他方法均适用于计算荷载位于跨中的横向分布系数m c 。

人群荷载横向分布系数
摘要：
一、人群荷载与横向分布系数的定义
二、人群荷载与横向分布系数的关系
三、影响人群荷载与横向分布系数的因素
四、如何应用人群荷载与横向分布系数
五、总结
正文：
人群荷载是指在一定时间内，通过某一特定区域的人数。

横向分布系数则是指在同一时间内，某一区域内的行人流量分布情况。

这两个指标在交通规划、城市设计以及安全管理等领域有着广泛的应用。

人群荷载与横向分布系数之间存在密切的关系。

人群荷载的大小会直接影响到横向分布系数，当人群荷载增大时，横向分布系数也会相应增大。

反之，当人群荷载减小时，横向分布系数也会相应减小。

影响人群荷载与横向分布系数的因素有很多，主要包括以下几点：
1.区域特性：如区域的功能、大小、形状等都会对人群荷载与横向分布系数产生影响。

2.时间因素：如高峰时段、平峰时段等不同时段的行人流量差异，也会影响人群荷载与横向分布系数。

3.人群特性：如行人的年龄、性别、行走速度等特性，也会对人群荷载与横向分布系数产生影响。

在实际应用中，人群荷载与横向分布系数可以帮助我们更好地理解行人的流动规律，从而为交通规划、城市设计以及安全管理提供科学的依据。

例如，在交通规划中，可以通过对人群荷载与横向分布系数的分析，合理设置人行道宽度、信号灯配时等参数，以保证行人安全和交通顺畅。

总之，人群荷载与横向分布系数是衡量人群流动特征的重要指标，对于交通规划、城市设计以及安全管理等领域具有重要的指导意义。

荷载的横向分布系数名词解释
荷载的横向分布系数是指在结构设计中，用于描述荷载在结构
横向方向上的分布情况的一个参数。

它反映了荷载在结构宽度方向
上的变化程度，是评估结构在横向方向上受到荷载作用的重要指标。

横向分布系数通常用符号β表示，其定义为荷载在结构宽度方
向上的最大值与最小值之比。

当荷载在结构宽度方向上均匀分布时，横向分布系数为1，表示荷载均匀作用于结构的整个宽度。

而当荷
载在结构宽度方向上不均匀分布时，横向分布系数大于1，表示荷
载在某些区域集中作用，而在其他区域较小。

荷载的横向分布系数在结构设计中起到重要的作用。

它可以影
响结构的受力性能、变形性能和安全性能。

通过合理地确定横向分
布系数，设计人员可以更准确地评估结构在横向方向上的受力情况，避免结构出现局部过载或不均匀变形的问题，确保结构的稳定性和
安全性。

需要注意的是，荷载的横向分布系数是根据具体的设计要求和
实际荷载情况来确定的，不同的结构和荷载类型可能会有不同的横
向分布系数。

因此，在设计过程中，需要根据实际情况对荷载的横向分布系数进行合理选择和计算，以确保结构的设计满足要求。

荷载横向分布影响线及横向分布系数假设各构件处于弹性工作阶段，上部结构由若干个等截面构件组成，铰仅承受竖向剪力（图1）。

图1铰接板受力分析当单位荷载p=1作用在构件i 时，各构件（n i i i ,1,,,2,1+='）均受力，各构件实际受到的作用力称为单位荷载横向分布值。

如p=1作用在构件1时，构件1受到的作用力为，1111Q -=η，由静力平衡可知：5451434132312121Q Q Q Q Q Q Q Q -=-=-=-=ηηηη （1）式中 ηij —单位荷载作用于构件j 时，i 构件的单位荷载横向分布值； i —构件序号； j —荷载所在构件序号；Qi —构件i 与构件i+1间铰接处剪力;由于弹性变位与荷载大小成正比，按照弹性变位互等定理有：,2112ηη= ,3113ηη= 4114ηη=,5115ηη=,则上式又可写成：1111Q -=ηQ Q -=112η3213Q Q -=η (2)4314Q Q -=η 5415Q Q -=η式中的η11、η12、η13、η14、η15 即单位荷载作用于1、2、3、4、5构件时，1号构件在横向分配到的荷载。

如将η11、η12。

按比例画在各构件的基线中心，将各点连成直线，即为构件1的荷载横向分布影响线，如图2。

图2铰接板桥的荷载分布影响线欲求ηij 值需先求出铰接处的剪力Qi 。

Qi 与构件的抗弯刚度和抗扭刚度的比值γ有关。

比值 γ 可用下式表示：21)(8.5l b I I n =γ （ 3）式中 I ——构件截面抗弯惯性矩 In ――构件截面抗扭惯性矩 b1――构件的宽度 l ——构件的计算跨度 对于矩形截面实心板，γ值按下式计：22107.2l b βγ=（4）式中 β――与截面形状有关的系数，可查表8-5。

表8-5 β系数表b /h 1.0 1.2 1.5 1.75 2.0 2.5 3.0 4.0 6.0 8.0 10.0 ≥10 β0.1410.1660.1960.2140.2290.2490.2630.2810.2990.3070.3120.333对于矩形截面空心板，常用的有箱形和开洞矩形截面（图3）。

荷载横向分布系数
荷载横向分布系数是指荷载和梁的宽度的比例关系的系数，它表明梁上的荷载是如何均匀地分布的。

它对于对梁及其抗压力能力的计算非常重要，主要决定着梁弯矩的大小。

另外，它还可以预测梁的变形程度以及梁的整体稳定性和结构安全性。

荷载横向分布系数可以通过梁的中心轴线来计算，可以用梁的节点距离来代表宽度，从而可以得到荷载横向分布系数的计算公式。

「b」和「h」分别代表梁的宽度和高度，而「P」代表点荷载，其公式如下：
荷载横向分布系数= (b/h) × (P/σ)
其中，「σ」是指梁应力，通常为允许应力。

荷载横向分布系数是梁的静健度和强度的重要决定因素。

正确的横向分布系数可以帮助梁承载最大的荷载，从而使梁受更少的变形和破坏。

荷载横向分布系数可以帮助梁充分利用载荷承受能力，可以有效减少结构成本。

最不利荷载横向分布系数名词解释
最不利荷载横向分布系数，也称为最不利横向分布系数，是指在结构设计中用于计算横向荷载作用下的荷载分配系数。

它是用来确定在一定横向荷载作用下，结构上不同部位所受到的最大横向力的分布情况。

在结构设计中，最不利荷载横向分布系数的计算是为了考虑结构在横向荷载作用下的最不利工况，以便确定结构的荷载分配和强度设计。

最不利荷载横向分布系数的值取决于结构的类型、几何形状、边界条件以及应变和应力的分布情况。

最不利荷载横向分布系数的计算通常基于结构的不同弯矩和剪力分
布情况。

通过分析结构在横向荷载作用下的应力和变形分布，可以确定结构上不同部位所受到的最大横向力的分布情况，并计算出对应的最不利荷载横向分布系数。

最不利荷载横向分布系数的值越大，表示结构上某些部位所受到的横向力越大，需要更多的强度设计和支撑。

因此，在结构设计中，确定最不利荷载横向分布系数是非常重要的，可以保证结构在横向荷载作用下的安全性和稳定性。

最不利荷载横向分布系数的计算方法和准则通常由相关的设计规范
和标准提供。

设计人员在进行结构设计时，需要根据具体的结构类型和荷载条件，参考相应的规范，合理选择最不利荷载横向分布系数的值，并进行结构的设计和计算。

双主梁横向分布系数
双主梁横向分布系数是指在双主梁桥设计中，横向荷载作用下，两个主梁之间承受荷载的比例系数。

该系数通常用于确定桥面板和主梁之间的强度连接方式和布置方式。

具体计算方法为，将横向荷载作用下两个主梁之间的最大剪力按照跨径长度分配到每一个桥面板上，再将每个桥面板上的最大剪力按照桥面板宽度分配到主梁上，最终得到每个主梁承受的荷载大小。

两个主梁之间的荷载分配比例即为横向分布系数。

横向分布系数通常在0.5到0.7之间，具体取值取决于桥梁的设计要求和荷载条件。