下载文档原格式
五年级复习（二）“教书先生”唯恐是街市百姓最为熟习的一种称号，从最先的门馆、私塾到晚清的学堂，“教书先生”那一行当怎么说也算是让国人仰慕甚或敬畏的一种社会职业。
不过更早的“先生”观点并不是源于教书，最先出现的“先生”一词也并不是有教授知识那般的含义。
《孟子》中的“先生何为出此言也？” ；《论语》中的“有酒食，先生馔”；《国策》中的“先生坐，何至于此？”等等，均指“先生”为父兄或有学问、有品德的尊长。
其实《国策》中自己就有“先生长辈，有德之称”的说法。
可见“先生”之原意非真实的“教师”之意，倒是与此刻“先生”的称号更接近。
看来，“先生”之根源含义在于礼貌和尊称，并不是具学问者的专称。
称“老师”为“先生”的记录，首见于《礼记 ?曲礼》，有“从于先生，不越礼而与人言” ，此中之“先生”意为“年长、资深之教授知识者”，与教师、老师之意基本一致。
分数（百分数）的乘除法及其应用“师”之观点，大概是从先秦期间的“师长、师傅、先生”而来。
此中“师傅”更早则意指春秋时国君的老师。
《说文解字》中有注曰：“师教人以道者之称也” 。
“师”之含义，此刻泛指从事教育工作或是教授知识技术也或是某方面有专长值得学习者。
“老师”的原意并不是由“老”而形容“师” 。
“老”在旧语义中也是一种尊称，隐喻年长且学问渊博者。
“老”“师”连用最先见于《史记》，有“荀卿最为老师”之说法。
慢慢“老师”之说也不再有年纪的限制，老小皆可合用。
不过司马迁笔下的“老师”自然不是今日意义上的“教师” ，其不过“老”和“师”的复合构词，所表达的含义多指对知识渊博者的一种尊称，虽能从其身上学以“道”，但其不必定是知识的流传者。
今日看来，“教师”的必需条件不但是拥有知识，更重于流传知识。
知识一：分数的乘法与此刻“教师”一称最靠近的“老师”观点，最早也要追忆至宋元期间。
金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟非凡貌，属句有夙性，说字惊老师。
”于是看，宋元期间小学教师被称为“老师”有案可稽。
北师大版小学五年级下册分数加法计算题1. 基本原则在进行分数加法计算题时，我们需要遵循以下基本原则：- 分子相同的分数可以直接相加，分母保持不变。
- 分母相同的分数可以直接相加，分子保持不变。
- 分子和分母都不同的分数需要通过通分运算后再相加。
2. 分数加法的具体步骤下面是解决分数加法计算题的具体步骤：步骤一：确定分母是否相同首先，我们需要判断待相加的分数的分母是否相同。
如果分母相同，则可以直接进行相加，而不需要进行通分运算。
步骤二：分母相同的分数相加如果待相加的分数的分母相同，则可以直接将它们的分子相加，分母保持不变。
例如，对于分母均为3的两个分数$\frac{1}{3}$和$\frac{2}{3}$，可以直接相加得到$\frac{1}{3}+\frac{2}{3}=\frac{3}{3}$。
步骤三：分母不同的分数通分运算后相加如果待相加的分数的分母不同，则需要通过通分运算后再进行相加。
通分运算是指将两个不同分母的分数转化为具有相同分母的等值分数。
具体步骤如下：1. 找到待相加的分数的最小公倍数作为通分的分母。
2. 根据最小公倍数将每个分数的分子进行相应的乘法运算，得到通分后的分数。
3. 将通分后的分数的分子进行相加，分母保持不变。
例如，对于$\frac{1}{2}$和$\frac{2}{3}$这两个分数，我们可以通过通分运算将它们转化为$\frac{3}{6}$和$\frac{4}{6}$，然后进行分子相加得到$\frac{3}{6}+\frac{4}{6}=\frac{7}{6}$。
步骤四：化简结果在得到相加结果后，我们可以对其进行化简，使得分数的分子和分母尽可能地简化。
例如，对于$\frac{7}{6}$这个结果，可以化简为$\frac{1}{1}\frac{1}{6}$。
3. 示例解题下面是一些具体的分数加法计算题的解题示例：示例一：计算$\frac{1}{5}+\frac{2}{5}$。
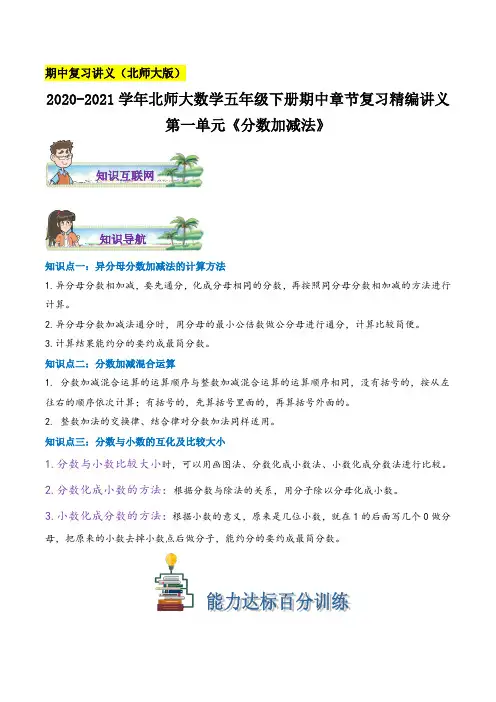
期中复习讲义（北师大版）2020-2021学年北师大数学五年级下册期中章节复习精编讲义第一单元《分数加减法》知识互联网知识导航知识点一：异分母分数加减法的计算方法1.异分母分数相加减，要先通分，化成分母相同的分数，再按照同分母分数相加减的方法进行计算。
2.异分母分数加减法通分时，用分母的最小公倍数做公分母进行通分，计算比较简便。
3.计算结果能约分的要约成最简分数。
知识点二：分数加减混合运算1. 分数加减混合运算的运算顺序与整数加减混合运算的运算顺序相同，没有括号的，按从左往右的顺序依次计算；有括号的，先算括号里面的，再算括号外面的。
2. 整数加法的交换律、结合律对分数加法同样适用。
知识点三：分数与小数的互化及比较大小1.分数与小数比较大小时，可以用画图法、分数化成小数法、小数化成分数法进行比较。
2.分数化成小数的方法：根据分数与除法的关系，用分子除以分母化成小数。
3.小数化成分数的方法：根据小数的意义，原来是几位小数，就在1的后面写几个0做分母，把原来的小数去掉小数点后做分子，能约分的要约成最简分数。
夯实基础一、精挑细选（共5题；每题2分，共10分）1. 在分数加法中，把变成看才能进行计算。
这—过程运用了（）数学思想。
A. 计算B. 转化C. 类比2. 一块蛋糕，淘气吃了它的，笑笑吃了它的，他们一共吃了这块蛋糕的（）。
A. B. C. D.3. 在异分母分数加法计算中，通常把+ 变成+ 才能进行计算。
这一过程运用了（）思想方法。
A. 计算B. 类比C. 想像D. 转化4. 一杯纯牛奶，乐乐喝了杯后，觉得有些凉，就兑满了热水。
他又喝了半杯，就出去玩了。
乐乐喝的牛奶一共是（）杯。
A. B. C. D.5. 两个自然数的倒数和是，这两个数是（）A. 2和4B. 5和6C. 2和3二、判断正误（共5题；每题2分，共10分）6. 一根铁丝，先截去m，然后又截去m，还剩下m，这根铁丝原长2m。
（）7.、和三个分数中，最接近1的分数是。
北师大版小学五年级数学下册全册知识点归纳第一单元《分数加减法》补充知识点：整数加减法运算定律在分数加减法中同样适用，见下图：4、把分数化成小数的方法：通常是利用分数与除法的关系，用分子除以分母来得到。
注意：对于某些分数也可以将它化为分母是10、100、1000之类的分数，然后再直接写成小数形式。
例如：5、常见分数和小数的互化：第二单元《长方体（一）》第一类，中间四连方，两侧各一个，共六种：第二类，中间三连方，两侧各有一、二个，共三种：第四类，两排各三个，只有一种：例如：如图，4个棱长都是10厘米的正方体堆放在墙角处，露在外面的面积是多少？第三单元《分数乘法》约分的最好先约分。
3、打折的含义，例如：九折，是指现价是原价的。
容积单位：升(L) 毫升(ml)补充知识点：冰箱的容积用“升”作单位；我们饮用的自来水用“立方米”作单位。
单位换算：（相邻单位之间的进率为1000）（小单位化成大单位要除以进率，大单位化成小单位要乘以进率。
可以概括为：小化大除一下，大化小乘一下）1米3＝1000分米31分米3＝1000厘米31升＝1000毫升 1升＝1分米31毫升＝1厘米3单名数与复名数之间的互化：单名数：由一个数和一个单位名称组成的名数叫做单名数。
复名数：由两个或两个以上的数及单位名称组成的名数叫做复名数。
分数除以整数的计算方法：分数除以整数（0除外）等于乘这个整数的倒数。
4、整数除以分数等于乘这个分数的倒数。
5、除以一个数（零除外）等于乘这个数的倒数。
孵化期为x天，则：未知的，所以用鸭的孵化期除以它对应的分率，即：例如：下面是一个平面图:是西偏北45°，距离学校1800米。
②以学校为观测点，青青家的位置是东偏北26°，距离学校1500米。
第七单元《用方程解决问题》1、列方程解应用题的步骤：（1）找到题中的等量关系式（2）解设所求量为x（3）根据等量关系式列出相应的方程（4）解答方程，注意计算结果不带单位。
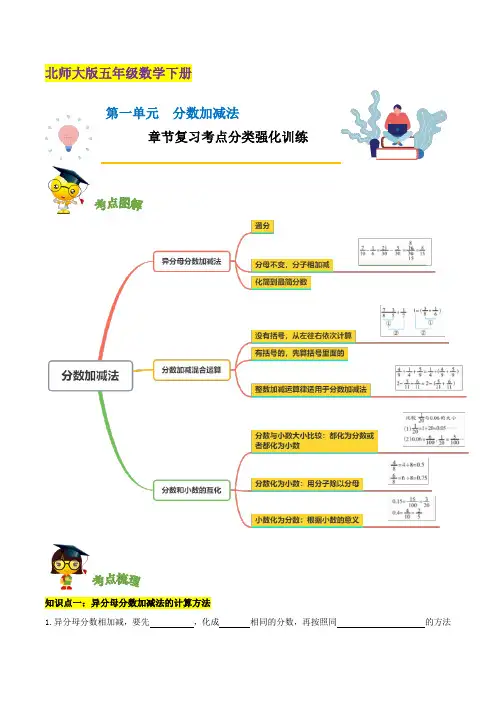
北师大版五年级数学下册第一单元分数加减法章节复习考点分类强化训练知识点一：异分母分数加减法的计算方法1.异分母分数相加减，要先，化成相同的分数，再按照同的方法进行计算。
2.异分母分数加减法通分时，用分母的做进行，计算比较简便。
3.计算结果能约分的要约成。
知识点二：分数加减混合运算1. 分数加减混合运算的与的运算顺序，没有括号的，按从左往右的顺序依次计算；有括号的，先算括号里面的，再算括号外面的。
2. 整数加法的对分数加法同样适用。
知识点三：分数与小数的互化及比较大小1.分数与小数比较大小时，可以用、分数化成小数法、小数化成分数法进行比较。
2.分数化成小数的方法：根据分数与除法的关系，用化成小数。
3.小数化成分数的方法：根据小数的意义，原来是几位小数，就在1的后面写几个0做，把原来的小数去掉小数点后做，能约分的要约成。
【易错典例1】在2、、5、1、这五个分数，能化成有限小数的有2、、．【易错知识点分析】把一个分数化成最简分数，再把分母分解质因数，如果分母中只有因数2、5，此分数就能化成有限小数，如果除2、5外还有其他因数，此分数就不能化成有限小数．【完整解答】：4＝2×650＝2×5×23＝3×615＝3×580＝2×2×2×6×5所以在2、、5、1、这五个分数、、；故答案为：2、、．【思路点拨】此题是考查判断一个分数能否化成有限小数．注意，必须把分数化成最简分数再判断．【易错典例2】小红看一本故事书，第一天看了这本书的，第二天看了这本书的，还剩几分之几没看？【易错知识点分析】据题意可知，小红两天共看了全书的：+＝，将这本书的总页数当做单位“1”，则还剩全书的1﹣（+）＝没有看．【完整解答】1﹣（+），＝5﹣（），＝2﹣，＝．答：还剩全书的没有看．【思路点拨】本题考查了学生解决简单的分数加减法应用题的能力．【易错典例3】某工程队修一条长1000千米的公路，第一周完成了全长的，第二周和第三周各完成了全长的，还剩下全长的几分之几没修？【易错知识点分析】把全长看成单位“1”，用全长减去第一周完成的几分之几，再减去第二周和第三周修的分数就是剩下了几分之几．【完整解答】1﹣﹣，＝﹣（），＝﹣，＝．答：还剩下全长的没修．【思路点拨】本题先找出单位“1”，再根据基本的数量关系求解．【易错典例4】一堂40分钟的体育课，做准备活动用了小时，老师示范用了小时，其余时间学生自由活动，学生自由活动时间是多少小时？【易错知识点分析】根据题意，40分钟＝小时，可用小时减去准备活动用的时间，再减去老师示范用的时间就等于学生自由活动用的时间，列式解答即可得到答案．【完整解答】﹣﹣＝﹣，＝．答：学生自由活动时间是小时．【易错典例5】一捆电线，第一次用去全长的，第二次用去全长的，一共用去全长的几分之几？还剩下几分之几？【易错知识点分析】把这捆电线长度看作单位“1”，第一次用去全长的，第二次用去全长的，所以可用加计算出一共用去全长的几分之几，最后再用单位“1”减去用去的几分之几即可得到剩余全长的几分之几．【完整解答】+＝1﹣＝答：一共用去全长的，还剩下．【思路点拨】解答本题的关键是：找准单位“1”，然后再列式计算即可．【易错典例6】小红和小花共做一批纸花，小红做了，小花做了，他们一共完成了几分之几？还剩几分之几没有完成？【易错知识点分析】根据题意，把这批花的总数量看作单位“1”，可用小红做的数量加小花做的数量即可得到他们共完成总量的几分之几，可用单位“1”减去他们共完成的几分之几即可得到剩余总量的几分之几．【完整解答】+＝1﹣＝答：他们一共完成了，还剩．【思路点拨】解答此题的关键是找准单位“1”，然后再根据分数加减法的计算方法进行计算即可．考点1：同分母分数加减法1．+可以直接相加，是因为两个加数（）A．分子相同B．分母相同C．都是真分数D．都是最简分数2．的结果是（）A．B．C．考点2：异分母分数加减法3．下面算式中的结果不是的是（）A．+B．+C．+D．+4．与的和，加上，结果是（）A．1B．C．D．5．下面各题中，正确的是（）A．+＝B．﹣＝C．﹣＝D．+＝考点3：分数的加法和减法6．+＝（）A．B．7．+的结果是（）A．B．1C．8．在分数加法中要把异分母分数+变成同分母分数+才能进行计算这一过程运用了（）的思想方法．A．计算B．转化C．类比9．甲乙两股长1米的绳子，甲剪去米，乙剪去，余下的绳子（）A．甲比乙短B．甲乙长度相等C．甲比乙长D．不能确定10．表示9个加上6个，和是．11．修一条路，第一天修了全长的，第二天修全长的．两天共修了全长的，第二天比第一天少修全长的，还剩下全长的，已修的比剩下的多．12．一瓶可乐5升，喝了升，还剩升．13．一根铁丝，第一次用去全长的九分之四，第二次用去全长的九分之一，还剩下这根铁丝的几分之几？14．某工程队修一条长1000千米的公路，第一周完成了全长的，第二周和第三周各完成了全长的，还剩下全长的几分之几没修？15．计算：﹣（﹣）16．直接写得数1﹣＝﹣＝++＝﹣0.25＝+＝+＝2﹣＝++＝17．一堂40分钟的体育课，做准备活动用了小时，老师示范用了小时，其余时间学生自由活动，学生自由活动时间是多少小时？18．一根铁丝第一次用去全长的，第二次用去全长的，一共用去这根铁丝的几分之几？这根铁丝还剩几分之几？考点4：分数的加减混合运算19．用你喜欢的方法算﹣（+）﹣+++++（﹣）12.5×32×2.5﹣（﹣）﹣（﹣）﹣1﹣+0.5考点5：小数与分数的互化20．下列各分数，不能化成有限小数的是（）A．B．C．21．下面能化成有限小数的是（）A．B．C．D．22．一个分数，如果分母除了2和5这两个因数之外，还含有其他的因数，那么这个分数不能化成有限小数．．23．的分母含有除素数2和5外还有素数13，所以这个分数不能化成有限小数．．24．下面的分数化成小数，（除不尽的保留两位小数）．345．25．把下面的小数化成分数．0.6 1.95 3.28 5.875 84.125．26．将下列分数化为有限小数，若不能化为有限小数，则将结果保留三位小数：＝＝2＝考点6：分数加减法应用题27．小明和小刚都是爱读书的好孩子，小明图书本数的与小刚的一样多，（）的图书多．A．小刚B．小明C．一样多D．无法确定28．一堆煤有8吨，第一次用去了，第二次用去了吨，还剩下几吨？正确的列式是（）A．8﹣﹣B．8×（1﹣）﹣C．8×（1﹣﹣）29．一根电线长32m，如果用去它的，还剩米，如果再用去m，还剩m．30．一根钢管长米，锯下米，还剩下米；如果锯下它的，还剩下米．31．一个西瓜。
北师大版五年级数学下册概念与公式整理版一、分数乘法、分数除法1. 分数乘法的意义：求几个相同分数的和的简便运算2. 分数除法的意义：已知两个乘数的积和其中一个乘数，求另一个乘数的运算。
如：25÷5=? 已知两个乘数（因数）的积是25，其中的一个因数是5，求另一因数是多少？ 3. 分数乘法的运算法则：1）分数与整数相乘：分子和整数相乘，分母不变；2）分数与分数相乘：分子与分子相乘，分母与分母相乘，能约分的可以先约分。
4. 分数除法的运算法则：1）一个数除以一个整数（0除外）等于这个数乘以这个整数的倒数； 2）一个数除以一个分数等于这个数乘以这个分数的倒数； 3）除以一个数（0除外）等于乘这个数的倒数； 4）当除数<1时，商大于被除数；（商就是得数） 5）当除数=1时，商等于被除数； 6）当除数>1时，商小于被除数。
5. 分数除法的意义：如果两个数的乘积是1，那么这两个数叫做互为倒数，其中一个数叫做另一个数的倒数。
6. 注意：1的倒数是1，而0没有倒数。
7. 分数乘整数的意义：与整数乘法的意义相同，就是求几个相同加数的和的简便运算。
如：12×5表示求5个12的和是多少，或者表示12的5倍是多少。
8. 一个数乘分数的意义：就是求这个数的几分之几是多少。
如：4×13表示求4的13是多少。
3×13表示3的13是多少。
9. 分数乘、除法的实际问题1）求一个数的几分之几是多少，用乘法。
2）已知一个数的几分之几是多少，求这个数，用除法，也可以用解方程。
10. 原价×折扣=现价；现价÷原价=折扣；现价÷折扣=原价。
11. 找单位“1”的方法： ①总数量是单位“1”；例如：小红看完整本书的12，那么单位“1”是整本书的页码。
②原价就是单位“1”；例如：笔记本电脑原价是3000元，现在降价了12，那么单位“1”是原价3000元。
