理论力学2011-2012答案

精选文档理论力学试题及答案一、是非题（每题2分。

正确用√，错误用×，填入括号内。

）1、作用在一个物体上有三个力，当这三个力的作用线汇交于一点时，则此力系必定均衡。

2、力关于一点的矩不因力沿其作用线挪动而改变。

（）3、在自然坐标系中，假如速度υ=常数，则加快度α=0。

（）4、虚位移是偶想的，极细小的位移，它与时间，主动力以及运动的初始条件没关。

5、设一质点的质量为m，其速度与x轴的夹角为α，则其动量在x轴上的投影为mvx=mvcosa。

二、选择题（每题3分。

请将答案的序号填入划线内。

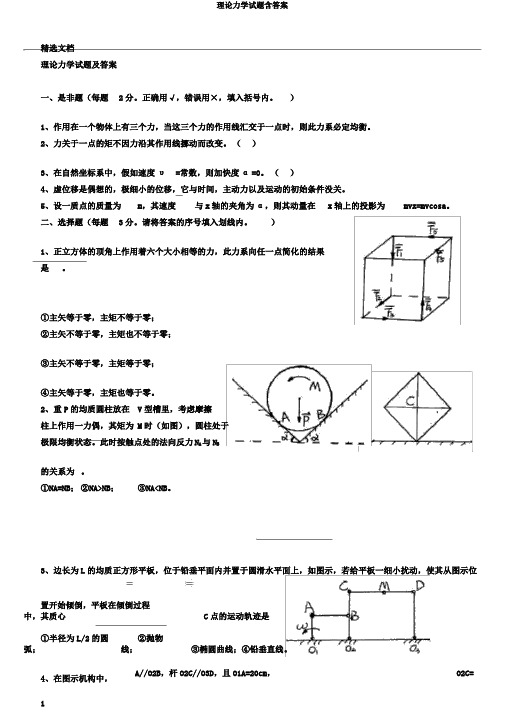
）1、正立方体的顶角上作用着六个大小相等的力，此力系向任一点简化的结果是。

①主矢等于零，主矩不等于零；②主矢不等于零，主矩也不等于零；③主矢不等于零，主矩等于零；④主矢等于零，主矩也等于零。

2、重P的均质圆柱放在V型槽里，考虑摩擦柱上作用一力偶，其矩为 M时（如图），圆柱处于极限均衡状态。

此时按触点处的法向反力N A与N B的关系为。

①N A=NB；②N A>NB；③N A<NB。

3、边长为L的均质正方形平板，位于铅垂平面内并置于圆滑水平面上，如图示，若给平板一细小扰动，使其从图示位置开始倾倒，平板在倾倒过程中，其质心C点的运动轨迹是。

①半径为L/2的圆弧；②抛物线；③椭圆曲线；④铅垂直线。

4、在图示机构中，A//O2B，杆O2C//O3D，且O1A=20cm，O2C=杆O140cm，CM=MD=30cm，若杆AO1以角速度ω=3rad/s匀速转动，则D点的速度的大小为cm/s，M点的加快度的大小为cm/s2。

①60；②120；③150；④360。

.精选文档5、曲柄OA以匀角速度转动，当系统运动到图示地点（OA//O1B。

AB |OA）时，有V A V B，A B，ωAB 0，AB 0。

①等于；②不等于。

三、填空题（每题5分。

请将简要答案填入划线内。

）1、已知A重100kN，B重25kN，A物与地面间摩擦系数为0.2。

1.1 沿水平方向前进的枪弹，通过某一距离s 的时间为t 1，而通过下一等距离s 的时间为2t .试证明枪弹的减速度（假定是常数）为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定，下端悬有m 及m '两质点。

设a 为绳的固有长度，b 为加m 后的伸长，c 为加m '后的伸长。

今将m '任其脱离而下坠，试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前，m 与m '系统平衡.当m '脱离下坠前，m 在拉力T 作用下上升，之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件：0=t 时，,c b a y ++=得0,21==A c A ；故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。

试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。

第11章 动量矩定理一、是非题(正确的在括号内打“√”、错误的打“×”)1. 质点系对某固定点(或固定轴)的动量矩，等于质点系的动量对该点(或轴)的矩。

(×)2. 质点系所受外力对某点(或轴)之矩恒为零，则质点系对该点(或轴)的动量矩不变。

(√)3. 质点系动量矩的变化与外力有关，与内力无关。

(√)4. 质点系对某点动量矩守恒，则对过该点的任意轴也守恒。

(√)5. 定轴转动刚体对转轴的动量矩，等于刚体对该轴的转动惯量与角加速度之积。

(×)6. 在对所有平行于质心轴的转动惯量中，以对质心轴的转动惯量为最大。

(×)7. 质点系对某点的动量矩定理e 1d ()d nOO i i t ==∑L M F 中的点“O ”是固定点或质点系的质心。

(√)8. 如图所示，固结在转盘上的均质杆AB ，对转轴的转动惯量为20A J J mr =+ 2213ml mr =+，式中m 为AB 杆的质量。

(×)9. 当选质点系速度瞬心P 为矩心时，动量矩定理一定有e 1d()d nP P i i t ==∑L M F 的形式，而不需附加任何条件。

(×)10. 平面运动刚体所受外力对质心的主矩等于零，则刚体只能做平动；若所受外力的主矢等于零，刚体只能作绕质心的转动。

(×)图二、填空题1. 绕定轴转动刚体对转轴的动量矩等于刚体对转轴的转动惯量与角速度的乘积。

2. 质量为m ，绕z 轴转动的回旋半径为ρ，则刚体对z 轴的转动惯量为2ρm J z =。

3. 质点系的质量与质心速度的乘积称为质点系的动量。

4. 质点系的动量对某点的矩随时间的变化规律只与系统所受的外力对该点的矩有关，而与系统的内力无关。

5. 质点系对某点动量矩守恒的条件是质点系所受的全部外力对该点之矩的矢量和等于零，质点系的动量对x 轴的动量矩守恒的条件是质点系所受的全部外力对x 轴之矩的代数和等于零。

2010 ～2011 学年度第 二 学期《 理论力学 》试卷（A 卷）一、填空题（每小题 4 分，共 28 分）1、如图1.1所示结构,已知力F ，AC ＝BC ＝AD ＝a ，则CD 杆所受的力F CD ＝（ ），A 点约束反力F Ax =（ ）。

2、如图1.2 所示结构，,不计各构件自重，已知力偶矩M ，AC=CE=a ，A B ∥CD 。

则B 处的约束反力F B =（ ）；CD 杆所受的力F CD =（ ）。

E 1.1 1.23、如图1.3所示，已知杆OA L ，以匀角速度ω绕O 轴转动，如以滑块A 为动点，动系建立在BC 杆上，当BO 铅垂、BC 杆处于水平位置时，滑块A 的相对速度v r =（ ）；科氏加速度a C =（ ）。

4、平面机构在图1.4位置时， AB 杆水平而OA 杆铅直，轮B 在水平面上作纯滚动，已知速度v B ，OA 杆、AB 杆、轮B 的质量均为m 。

则杆AB 的动能T AB =（ ），轮B 的动能T B =（ ）。

1.3 1.45、如图1.5所示均质杆AB 长为L ,质量为m,其A 端用铰链支承,B 端用细绳悬挂。

当B 端细绳突然剪断瞬时, 杆AB 的角加速度 =（ ），当杆AB 转到与水平线成300角时，AB 杆的角速度的平方ω2=（ ）。

6、图1.6所示机构中,当曲柄OA 铅直向上时,BC 杆也铅直向上,且点B 和点O 在同一水平线上；已知OA=0.3m,BC=1m ，AB=1.2m,当曲柄OA具有角速度ω=10rad/s 时,则AB 杆的角速度ωAB =（ ）rad/s,BC 杆的角速度ωBC =（ ）rad/s 。

AB1.57、图1.7所示结构由平板1、平板2及CD 杆、EF 杆在C 、D 、E 、F 处铰接而成，在力偶M 的作用下，在图上画出固定铰支座A 、B 的约束反力F A 、F B 的作用线方位和箭头指向为（ ）（要求保留作图过程）。

1.7二、单项选择题（每小题 4 分，共28 分）1、如图2.1所示，四本相同的书，每本重均为P ，设书与书间的摩擦因数为0.1，书与手间的摩擦因数为0.25，欲将四本书一起抱起，则两侧手应加的压力至少大于（ ）。

第一章静力学基础一、是非题1．力有两种作用效果，即力可以使物体的运动状态发生变化，也可以使物体发生变形。

（）2．在理论力学中只研究力的外效应。

（）3．两端用光滑铰链连接的构件是二力构件。

（）4．作用在一个刚体上的任意两个力成平衡的必要与充分条件是：两个力的作用线相同，大小相等，方向相反。

（）5．作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。

（）6．三力平衡定理指出：三力汇交于一点，则这三个力必然互相平衡。

（）7．平面汇交力系平衡时，力多边形各力应首尾相接，但在作图时力的顺序可以不同。

（）8．约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。

（）二、选择题1．若作用在A点的两个大小不等的力F1和F2，沿同一直线但方向相反。

则其合力可以表示为。

①F1－F2；②F2－F1；③F1＋F2；2．作用在一个刚体上的两个力F A、F B，满足F A=－F B的条件，则该二力可能是。

①作用力和反作用力或一对平衡的力；②一对平衡的力或一个力偶。

③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

3．三力平衡定理是。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡，必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

4．已知F1、F2、F3、F4为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形，由此。

①力系可合成为一个力偶；②力系可合成为一个力；③力系简化为一个力和一个力偶；④力系的合力为零，力系平衡。

5．在下述原理、法则、定理中，只适用于刚体的有。

①二力平衡原理；②力的平行四边形法则；③加减平衡力系原理；④力的可传性原理；⑤作用与反作用定理。

三、填空题1．二力平衡和作用反作用定律中的两个力，都是等值、反向、共线的，所不同的是。

2．已知力F沿直线AB作用，其中一个分力的作用与AB成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为度。

2011-2012第二学期64学时理论力学试卷B 卷参考答案西南林业大学2011—2012学年第02学期 《理论力学》（试卷）（B ）试题答案（64学时）考试形式：闭卷 考试时间：120分钟请使用16K 纸打印一、是非题(对的打√，错的打×，每小题2分，共20分)1、凡是合力都比分力要大。

（×）2、作用力与反作用力同样是一对平衡力，因为它也满足二力平衡条件中所说的两力大小相等、方向相反、作用线沿同一直线。

（×）3、某一平面任意力系向A 点简化简化的主矢为零，而向另一点简化的主矩为零，则该力系一定是平衡力系。

（√）4、应用速度合成定理，在选择动点、动系时，若动点是某刚体上的一点，则动系也固结于这个刚体上。

（×）5、刚体作瞬时平动时，刚体内各点的速度和加速度都相同。

（×）6、两个半径不等的摩擦轮外接触传动，如果不出现打滑现象，两接触点此瞬时的速度相等，切向加速度也相等到。

（√）7、质点系的内力不能改变质点系的动量和动量矩。

（√）8、已知质点的运动方程，就可以确定作用于质点上的力；已知作用于质点上的力，也可以确定质点的运动方程。

（×）9、刚体绕定轴转动时，若它的角速度很大，则作用在它上面的转矩（即力矩或力偶矩）也一定很大。

（×） 10、若质点系所受的外力的主矢等于零，则其质心坐标保持不变。

（×）二、 填空题(每空1分，共20分)1．作用在刚体上的力可沿其作用线任意移动，而不改变力对刚体的作用效果，所以在静力学中力是 滑移 矢量。

2．力对物体的作用效应一般分为 运动（外）效应和 变形（内）效应。

3．对非自由体的运动所预加的限制条件称为 约束 ；约束反力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ；约束反力由 主动力 引起，且随 主动力 改变而改变。

4．平面汇交力系平衡的几何条件是 力多边形自形封闭 ；平面汇交力系平衡的解析条件是力系中各力在任意坐标轴上的投影的代数和等于零。

理论力学课后习题答案1. 第一题题目：一个质点从初始点A沿着一条直线运动到达点A，在此过程中质点受到一个恒定的力A的作用。

求解质点从A 到A的位移A和速度A与时间A的关系。

解答：根据牛顿第二定律A=AA，我们可以得到质点在恒定力作用下的运动方程为 $F = m \\frac{dv}{dt}$。

即：$$F = m \\frac{dx}{dt}$$将方程变形可得：$$dx = \\frac{F}{m} dt$$对上式两边同时积分可得：$$\\int_{x_A}^{x_B} dx = \\frac{1}{m} \\int_0^t F dt$$化简后可得：$$x_B - x_A = \\frac{1}{m} \\int_0^t F dt$$即质点从初始点A移动到达点A时的位移A与时间A的关系为：$$x = x_A + \\frac{1}{m} \\int_0^t F dt$$2. 第二题题目：一个滑块在一个光滑的水平轨道上，质量为A，受到一根拉力为A的绳子的作用。

求解滑块的加速度A。

解答：根据牛顿第二定律A=AA，可以得到滑块的加速度A与拉力A的关系为 $a = \\frac{F}{m}$。

3. 第三题题目：一个质点在一个弹簧的作用下振动，弹簧的劲度系数为A，质量为A。

求解质点的振动周期A。

解答：质点在弹簧的作用下振动，其运动方程为 $m\\frac{d^2x}{dt^2} = -kx$，其中A为质点的位移。

对上式进行变形可得：$$\\frac{d^2x}{dt^2} = -\\frac{k}{m}x$$该微分方程的通解为 $x = A \\sin(\\sqrt{\\frac{k}{m}} t + \\phi)$，其中A为振幅，$\\phi$ 为相位角。

振动周期A可以通过求解动能和势能的平衡关系来得到。

在振动过程中，动能 $K = \\frac{1}{2} m v^2$ 和势能 $U =\\frac{1}{2} k x^2$ 之和保持不变。

《理论力学》——期末考试答案一、单选题1.力对点之矩决定于( )。

A.力的大小B.力臂的长短C.力的大小和力臂的长短D.无法确定正确答案：C2.动点相对于动坐标系的运动称为( )的运动。

A.牵连运动B.相对运动C.绝对运动D.圆周运动正确答案：B3.动点的牵连速度是指该瞬时牵连点的速度，它相对的坐标系是( )。

A.动坐标系B.不必确定的C.静坐标系D.静系或动系都可以正确答案：C4.在质点系动能定理中，应注意外力或内力做的功之和不等于合外力或( )做的功。

A.重力B.浮力C.合内力D.牵引力正确答案：C5.将平面力系向平面内任意两点进行简化，所得主矢量和主矩都相等，且主矩不为零，则该力系简化的最后结果为( )。

A.合力偶B.合力C.平衡力系D.无法进一步合成正确答案：A6.超静定结构的超静定次数等于结构中( )。

A.约束的数目B.多余约束的数目C.结点数D.杆件数正确答案：B7.静不定系统中，多余约束力达到3个，则该系统静不定次数为( )A.3次B.6次C.1次D.不能确定正确答案：A8.关于平面力偶系、平面汇交力系、平面一般力系，最多能够得到的相互独立的平衡方程的个数依次是( )。

A.2、1、3B.2、2、3C.1、2、2D.1、2、3正确答案：D9.平面任意力系向一点简化，应用的是( )。

A.力的平移定理B.力的平衡方程C.杠杆原理D.投影原理正确答案：A10.对于平面力系，一个平衡方程可解( )未知量。

A.1个B.2个C.3个D.不一定正确答案：A11.一平面力系由两组平面平行力系组成(这两组平面平行力系之间互不平行),若力系向某A点简化结果为一合力，下述说法正确的是( )。

A.这两组平面平行力系必然都各自向A点简化为一合力B.这两组平面平行力系可能都各自简化为一力偶C.可能一组平面平行力系向A点简化得到一个力和一个力偶，而另一组平面平行力系向A点简化得到一合力D.可能这两组平面平行力系都各自向A点简化得到一个力和一个力偶正确答案：D12.在任何情况下，在几何可变体系上增加一个二元体后构成的体系是几何( )体系。