理论力学试题及答案
- 格式:docx
- 大小:163.80 KB
- 文档页数:15

精选文档理论力学试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必定均衡。
2、力关于一点的矩不因力沿其作用线挪动而改变。
()3、在自然坐标系中,假如速度υ=常数,则加快度α=0。
()4、虚位移是偶想的,极细小的位移,它与时间,主动力以及运动的初始条件没关。
5、设一质点的质量为m,其速度与x轴的夹角为α,则其动量在x轴上的投影为mvx=mvcosa。
二、选择题(每题3分。
请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为 M时(如图),圆柱处于极限均衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A=NB;②N A>NB;③N A<NB。
3、边长为L的均质正方形平板,位于铅垂平面内并置于圆滑水平面上,如图示,若给平板一细小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C点的运动轨迹是。
①半径为L/2的圆弧;②抛物线;③椭圆曲线;④铅垂直线。
4、在图示机构中,A//O2B,杆O2C//O3D,且O1A=20cm,O2C=杆O140cm,CM=MD=30cm,若杆AO1以角速度ω=3rad/s匀速转动,则D点的速度的大小为cm/s,M点的加快度的大小为cm/s2。
①60;②120;③150;④360。
.精选文档5、曲柄OA以匀角速度转动,当系统运动到图示地点(OA//O1B。
AB |OA)时,有V A V B,A B,ωAB 0,AB 0。
①等于;②不等于。
三、填空题(每题5分。
请将简要答案填入划线内。
)1、已知A重100kN,B重25kN,A物与地面间摩擦系数为0.2。

理论力学试题库及答案(通用篇)一、理论力学试题库(通用篇)试题一:已知一质点在平面直角坐标系中的运动方程为 x = 2t² + 3,y = 4t² - t + 1。
求该质点在t = 2s 时的速度和加速度。
试题二:一质点沿圆周运动,其半径为 r,角速度为ω,角加速度为α。
求质点在任意时刻 t 的速度和加速度。
试题三:一质点从静止开始沿直线运动,受到恒力F 的作用。
求质点在任意时刻 t 的速度和位移。
试题四:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的速度和加速度。
试题五:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移。
试题六:一质点在重力作用下做自由落体运动,求质点在任意时刻 t 的速度和位移。
试题七:一质点在水平地面上受到一斜向上的拉力F,拉力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和加速度。
试题八:一质点在平面内做匀速圆周运动,半径为r,角速度为ω。
求质点在任意时刻 t 的切向加速度和法向加速度。
试题九:一质点在平面内做匀速运动,速度大小为v,方向与水平方向成θ 角。
求质点在任意时刻 t 的位移和速度。
试题十:一质点在水平地面上受到一恒力 F 的作用,力与水平方向的夹角为θ。
求质点在任意时刻 t 的速度和位移。
二、答案答案一:t = 2s 时,速度 v = (4t, 8t - 1) = (8, 15) m/s;加速度 a = (8, 8) m/s²。
答案二:质点在任意时刻 t 的速度v = (rω, 0),加速度a = (0, rα)。
答案三:质点在任意时刻 t 的速度 v = (F/m)t,位移 s = (F/m)t²/2。
答案四:质点在任意时刻 t 的速度 v =(rωcos(ωt), rωsin(ωt)),加速度 a = (-rω²sin(ωt), rω²cos(ωt))。

理论力学大一试题及答案一、选择题(每题5分,共20分)1. 牛顿第一定律描述的是:A. 物体在没有外力作用下将保持静止或匀速直线运动B. 物体在受到外力作用下将改变其运动状态C. 物体在受到外力作用下将保持匀速直线运动D. 物体在受到外力作用下将保持静止答案:A2. 根据动量守恒定律,以下说法正确的是:A. 系统内所有物体的动量之和在没有外力作用下保持不变B. 系统内所有物体的动量之和在有外力作用下保持不变C. 系统内所有物体的动量之和在有外力作用下将增加D. 系统内所有物体的动量之和在有外力作用下将减少答案:A3. 角动量守恒的条件是:A. 系统不受外力矩B. 系统受外力矩C. 系统内力矩之和为零D. 系统内力矩之和不为零答案:A4. 以下哪项不是能量守恒定律的表述:A. 能量既不能被创造,也不能被消灭B. 能量可以以多种形式存在C. 能量可以以多种形式相互转化D. 能量在转化过程中总量会增加答案:D二、填空题(每题5分,共20分)1. 根据牛顿第二定律,物体的加速度与作用力成正比,与物体的质量成________。
答案:反比2. 一个物体在水平面上以初速度v0运动,受到大小为F的恒定摩擦力作用,其加速度为a=________。
答案:-F/m3. 一个质量为m的物体从高度h自由下落,其下落过程中的重力势能变化量为________。
答案:-mgh4. 根据动能定理,一个物体的动能变化量等于外力对物体做的功,即ΔK=________。
答案:W三、计算题(每题15分,共30分)1. 一个质量为2kg的物体从静止开始,受到一个大小为10N的水平拉力作用,求物体在5秒内的位移。
解:根据牛顿第二定律,F=ma,得a=F/m=10/2=5m/s²。
根据位移公式s=1/2at²,得s=1/2*5*5²=62.5m。
答案:62.5m2. 一个质量为5kg的物体从高度10m自由下落,求物体落地时的速度。

理论力学考研试题及答案一、选择题(每题2分,共20分)1. 质点系的动量守恒条件是()。
A. 外力为零B. 外力之和为零C. 外力之和的矩为零D. 外力之和的矩不为零答案:B2. 刚体的转动惯量与()有关。
A. 质量B. 形状C. 质量分布D. 以上都是答案:D3. 牛顿第二定律的数学表达式为()。
A. F = maB. F = m*vC. F = m*aD. F = m*v^2答案:C4. 角动量守恒的条件是()。
A. 外力矩为零B. 内力矩为零C. 外力矩与内力矩之和为零D. 外力矩与内力矩之差为零5. 简谐振动的周期与()无关。
A. 振幅B. 频率C. 质量D. 刚度答案:A6. 达朗贝尔原理的实质是()。
A. 虚功原理B. 虚位移原理C. 虚速度原理D. 虚加速度原理答案:B7. 刚体的平动与转动的区别在于()。
A. 参考系B. 速度C. 加速度D. 角速度答案:D8. 拉格朗日方程的推导基于()。
A. 牛顿运动定律B. 能量守恒定律C. 动量守恒定律D. 虚功原理答案:D9. 刚体转动的角动量方向与()方向相同。
B. 力矩C. 角速度D. 线速度答案:C10. 非惯性参考系中,物体的运动方程中需要加入()。
A. 惯性力B. 重力C. 电磁力D. 摩擦力答案:A二、填空题(每题2分,共20分)1. 质点系的动量守恒定律表明,当质点系所受外力之和为零时,其总动量保持不变。
2. 刚体的转动惯量是刚体对于某一旋转轴的惯性的量度,它与刚体的质量分布和旋转轴的位置有关。
3. 牛顿第二定律表明,物体的加速度与作用在物体上的合外力成正比,与物体的质量成反比。
4. 角动量守恒定律表明,当一个系统不受外力矩作用时,其总角动量保持不变。
5. 简谐振动的周期只与振动系统的固有频率有关,与振幅无关。
6. 达朗贝尔原理是将动力学问题转化为静力学问题的一种方法。
7. 刚体的平动是指刚体上所有点都沿着同一直线运动,而转动则是指刚体绕某一固定轴旋转。

理论力学试题一、填空题1.已知图示正方体边长为a , 在右侧面作用已知力F ,在顶面作用矩为M 的已知力偶矩,如图所示。
求力系对x ,y ,z 轴的力矩。
(6分)xM ∑=( ),y M ∑=( ) zM∑=( )2. 已知:图示机构位于铅垂面内,匀质杆OA 质量为m ,长为l ,且l =4R ,匀质圆盘质量为m ,半径为R ,与杆在A 端固接。
图示瞬时,杆的角速度ω=0,角加速度为α。
求惯性力系向O 点简化结果。
(6分) 主失大小=( ),主矩大小=( ) 方向在图中标出。
二.在图示机构中,已知:OB=OD=DA=20cm ,AC =40cm ,AB ⊥AC ,角θ=30,1F =150N,弹簧的刚度系数k =150N/cm,在图示位置已有压缩变形δ=2cm,不计各构件重量,用虚位移原理求构件在图示位置平衡时,力2F 的大小。
(用其他方法做不给分)(8分)三.已知:图示平面结构,各杆自重不计。
M =10kN ⋅m ,F =20kN ,max q =8kN/m ,2l m =,A ,B ,D 处为铰链连接,E 处为固定端。
求:A,E处的约束力。
(20分)四.已知:平面机构如图:圆轮A沿水平面纯滚动,滑块B上铰链两直杆AB,BD,BD穿过做定轴转动的套筒C,15,45/,0A A R cm v cm s a ===,图示瞬时,45,30,30l cm θϕ===。
求:图示瞬时,AB,BD杆的角速度,AB BD ωω;点B的加速度B a ;BD杆的角加速度BD α。
(20)五.已知:图示系统中,物块A质量为3m ,均质圆盘B与均质圆柱C质量均为m ,半径均为R,弹簧刚度系数为k ,初始时系统静止,弹簧为原长。
系统由静止释放后,圆柱C做纯滚动。
斜面倾角为30,弹簧与绳的倾斜段与斜面平行。
求:当物块A下降距离为s (未达最低位置)时的速度与加速度,两段绳中的拉力。
(20分)理论力学试题答案一、填空题 1、Fa 22 ;0;Fa M 22- 2、ααml mR 236=;22131131696mR ml αα=;二、解:0=F W δ 120c D D B F r F r F r δδδ+-=sin A C r r δδθ= 12A C r r δδ= 1124D A C r r r δδδ== 1124B A C r r r δδδ==1211044C D C C F r F r F r δδδ+-=N 300=D F N 9002=F三、解:分析BD ,受力如图(1)所示。

- - -理论力学---11-1.两个力,它们的大小相等、方向相反和作用线沿同一直线。
这是(A)它们作用在物体系统上,使之处于平衡的必要和充分条件;(B)它们作用在刚体系统上,使之处于平衡的必要和充分条件;(C)它们作用在刚体上,使之处于平衡的必要条件,但不是充分条件;(D)它们作用在变形体上,使之处于平衡的必要条件,但不是充分条件;1-2. 作用在同一刚体上的两个力F1和F2,假设F1 = - F2,则说明这两个力(A)必处于平衡;(B)大小相等,方向一样;(C)大小相等,方向相反,但不一定平衡;(D)必不平衡。
1-3. 假设要在力系上加上或减去一组平衡力系,而不改变原力系的作用效果,则它们所作用的对象必需是(A)同一个刚体系统;(B)同一个变形体;(C)同一个刚体,原力系为任何力系;(D)同一个刚体,且原力系是一个平衡力系。
1-4. 力的平行四边形公理中的两个分力和它们的合力的作用围(A)必须在同一个物体的同一点上;(B)可以在同一物体的不同点上;(C)可以在物体系统的不同物体上;(D)可以在两个刚体的不同点上。
1-5. 假设要将作用力沿其作用线移动到其它点而不改变它的作用,则其移动围(A)必须在同一刚体;(B)可以在不同刚体上;(C)可以在同一刚体系统上;(D)可以在同一个变形体。
1-6. 作用与反作用公理的适用围是(A)只适用于刚体的部;(B)只适用于平衡刚体的部;(C)对任何宏观物体和物体系统都适用;(D)只适用于刚体和刚体系统。
1-7. 作用在刚体的同平面上的三个互不平行的力,它们的作用线汇交于一点,这是刚体平衡的(A)必要条件,但不是充分条件;(B)充分条件,但不是必要条件;(C)必要条件和充分条件;(D)非必要条件,也不是充分条件。
1-8. 刚化公理适用于(A)任何受力情况下的变形体;(B)只适用于处于平衡状态下的变形体;(C)任何受力情况下的物体系统;(D)处于平衡状态下的物体和物体系统都适用。

专升本理论力学试题及答案一、选择题(每题3分,共30分)1. 理论力学的研究对象是什么?A. 物体内部分子运动B. 质点的运动C. 物体在外力作用下的运动D. 物体内部结构答案:C2. 牛顿第一定律又称为A. 惯性定律B. 加速定律C. 作用力与反作用力定律D. 力的独立作用定律答案:A3. 以下哪项不是理论力学中常见的力?A. 重力B. 弹力C. 摩擦力D. 向心力答案:D4. 质点系的动量守恒定律成立的条件是A. 合外力为零B. 合外力和合外力矩都为零C. 只有重力作用D. 质点系在封闭系统内答案:A5. 刚体的转动惯量与以下哪项无关?A. 质量B. 质量分布C. 形状D. 参考点的选择答案:D6. 角速度和线速度的关系是A. 线速度是角速度的两倍B. 线速度是角速度与半径的乘积C. 角速度是线速度的一半D. 线速度与角速度无关答案:B7. 两个物体组成的系统动量守恒,以下哪项一定守恒?A. 机械能B. 内能C. 角动量D. 动能答案:C8. 以下哪项不是达朗贝尔原理的内容?A. 惯性力的概念B. 虚位移原理C. 动静法D. 力的平衡答案:B9. 科里奥利力的方向与物体的运动方向的关系是A. 垂直B. 平行C. 同向D. 反向答案:A10. 以下哪项不是理论力学中常见的稳定性问题?A. 静稳定性B. 动稳定性C. 热稳定性D. 转动稳定性答案:C二、填空题(每题2分,共20分)11. 牛顿第二定律的数学表达式为:________。
答案:F=ma12. 一个物体在水平面上做匀速直线运动,其受到的摩擦力大小等于________。
答案:物体的重力与水平面的摩擦系数的乘积13. 刚体的平面运动可以分解为________和________。
答案:平动、转动14. 一个物体从静止开始自由下落,其在前2秒内的位移与前3秒内的位移之比为________。
答案:4:915. 质点系的动能等于________。

理论力学试题及答案一、选择题(每题2分,共20分)1. 牛顿第一定律描述的是:A. 物体在受力时的运动状态B. 物体在不受力时的运动状态C. 物体在受力时的加速度D. 物体在受力时的位移答案:B2. 根据牛顿第二定律,物体的加速度与作用力和物体质量的关系是:A. 加速度与作用力成正比,与质量成反比B. 加速度与作用力成反比,与质量成正比C. 加速度与作用力成正比,与质量成正比D. 加速度与作用力成反比,与质量成反比答案:A3. 以下哪个不是刚体的运动特性?A. 刚体的质心保持静止或匀速直线运动B. 刚体的各部分相对位置不变C. 刚体的各部分速度相同D. 刚体的各部分加速度相同答案:C4. 角动量守恒定律适用于:A. 只有重力作用的系统B. 只有内力作用的系统C. 外力矩为零的系统D. 外力为零的系统答案:C5. 以下哪个是能量守恒定律的表述?A. 一个封闭系统的总动能是恒定的B. 一个封闭系统的总势能是恒定的C. 一个封闭系统的总能量是恒定的D. 一个封闭系统的总动量是恒定的答案:C二、简答题(每题10分,共20分)6. 简述牛顿第三定律的内容及其在实际中的应用。
答案:牛顿第三定律,又称作用与反作用定律,表述为:对于两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
在实际应用中,例如在推门时,门对人的作用力和人对门的作用力大小相等,方向相反。
7. 描述什么是简谐振动,并给出一个生活中的例子。
答案:简谐振动是一种周期性振动,其回复力与位移成正比,且总是指向平衡位置。
生活中的例子包括弹簧振子,当弹簧被拉伸或压缩后释放,它会在原始平衡位置附近做周期性的往复运动。
三、计算题(每题15分,共30分)8. 一个质量为m的物体,从静止开始,沿着一个斜面下滑,斜面的倾角为θ。
如果斜面的摩擦系数为μ,求物体下滑的加速度。
答案:首先,物体受到重力mg的作用,分解为沿斜面方向的分力mg sinθ和垂直斜面方向的分力mg cosθ。

理论力学试题及答案一、选择题(每题2分,共10分)1. 一个物体在水平面上以速度v匀速直线运动,其动摩擦因数为μ,若物体所受的摩擦力为F,则F等于:A. μvB. μmgC. μND. μ(v^2)答案:B2. 根据牛顿第二定律,物体的加速度与作用在物体上的合外力成正比,与物体的质量成反比。
这一定律的数学表达式为:A. F = maB. F = m/aC. a = F/mD. a = mF答案:A3. 一个物体从静止开始自由下落,其下落的高度h与时间t的关系为:A. h = gt^2B. h = 1/2gt^2C. h = 2gtD. h = gt答案:B4. 两个物体A和B用轻杆连接,A的质量为mA,B的质量为mB,系统在水平面上以共同速度v向右做匀速直线运动。
若杆的力为F,则F的方向是:A. 向左B. 向右C. 不确定D. 无法判断答案:B5. 一个物体在竖直平面内做圆周运动,当物体通过最高点时,其向心力的来源是:A. 重力B. 杆的支持力C. 绳子的张力D. 重力和杆的支持力的合力答案:D二、填空题(每空2分,共10分)1. 一个物体的质量为2kg,受到的合外力为10N,根据牛顿第二定律,其加速度为______ m/s²。
答案:52. 一个物体做匀加速直线运动,初速度为3m/s,加速度为2m/s²,经过4秒后的速度为______ m/s。
答案:153. 在光滑水平面上,一个物体受到一个大小为5N,方向向右的恒定力作用,物体的质量为1kg,其加速度为______ m/s²。
答案:54. 一个物体在竖直上抛运动中,当其上升的最大高度为20m时,其初速度为______ m/s。
答案:205. 根据动能定理,物体的动能变化等于合外力做的功,若一个物体的动能增加了30J,合外力做的功为______ J。
答案:30三、简答题(共20分)1. 解释什么是科里奥利力,并给出其表达式。

理论力学课程试题及答案理论力学是物理学中的一个重要分支,它主要研究宏观物体在力的作用下的运动规律。
理论力学课程通常包括静力学、动力学、运动学、能量守恒定律、动量守恒定律、角动量守恒定律等内容。
以下是一份理论力学课程的试题及答案,供学习者参考。
试题一、选择题(每题2分,共10分)1. 理论力学的研究对象是()A. 微观粒子B. 宏观物体C. 流体D. 热力学系统2. 在国际单位制中,力的单位是()A. 牛顿(N)B. 帕斯卡(Pa)C. 焦耳(J)D. 瓦特(W)3. 一个物体的动量是()A. 物体的质量与速度的乘积B. 物体的动能C. 物体的势能D. 物体的位移4. 根据牛顿第三定律,作用力与反作用力()A. 大小相等,方向相反B. 大小不等,方向相反C. 大小相等,方向相同D. 大小不等,方向相同5. 一个物体在水平面上做匀速直线运动,其受到的摩擦力()A. 等于物体的重力B. 等于物体的动能C. 等于物体的动量D. 与物体的牵引力大小相等,方向相反二、简答题(每题5分,共20分)1. 请简述牛顿运动定律的三个定律。
2. 什么是角动量守恒定律?它在什么条件下成立?3. 简述能量守恒定律,并说明其在实际应用中的重要性。
4. 何为虚功原理?它在解决静力学问题中有何作用?三、计算题(每题10分,共30分)1. 一个质量为2kg的物体在水平面上以3m/s的速度做匀速直线运动,若摩擦系数为0.1,请计算物体受到的摩擦力大小。
2. 一个质量为5kg的物体从静止开始自由下落,忽略空气阻力,求物体在2秒后的速度和位移。
3. 一个质量为3kg的物体在竖直平面内做圆周运动,其半径为1m,角速度为2rad/s,请计算物体在最高点时所需的最小速度。
四、解答题(每题15分,共30分)1. 一个质量为m的物体在竖直方向上受到一个向上的力F作用,物体向上做匀加速直线运动。
若物体的加速度为a,试证明牛顿第二定律在该情况下的表达式,并说明力F与物体质量m和加速度a之间的关系。
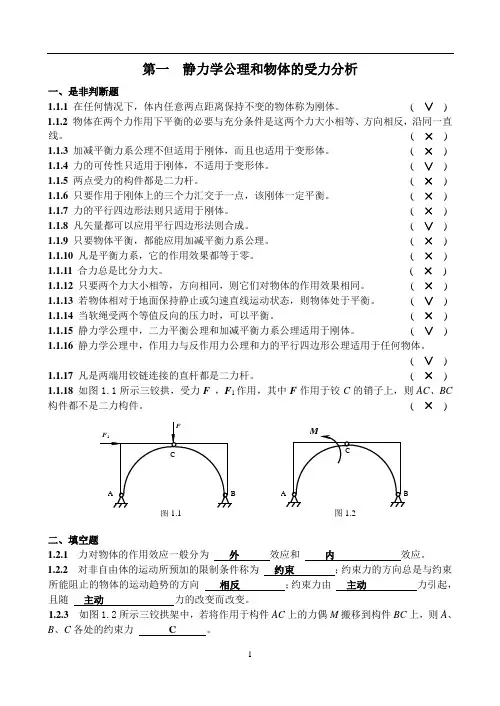
1第一 静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7 力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13 若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14 当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15 静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16 静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图1.1所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
可编辑修改精选全文完整版理论力学题库简答题1-1.简述伽利略相对性原理和牛顿运动定律成立的参考系。
答:(1)内容:不能借助任何力学实验来判断参考系是静止的还是在匀速直线运动;(2)相对与惯性系作匀速直线运动的参考系都是惯性参考系;(3)牛顿运动定理只能在惯性系成立。
1-2. 简述有心力的性质. 并证明质点在有心力作用下只能在一个平面内运动.证明:只要证明角动量是一个常矢量即可.性质:(1)力的作用线始终通过一定点;(角动量是一个常矢量或质点始终在垂直于角动量的平面内运动)(2) 角动量守恒,或掠面速度守恒;(3) 有心力是保守力, 或机械能守恒.1-3.什么情况下质心与几何中心、重心重合?质心系有何特性?(1) 密度均匀物体质心与几何中心重合;(2) 重力加速度为常量时物体质心与重心重合;质心系的特性:(1) 质心系中各质点相对于质心的总动量为零;(2) 质心系的惯性力矩为零;(3) 质心系的惯性力做功为零。
1-4.太阳和地球组成的两体系统中,分别以地球、太阳、质心为参照系,简述地球、太阳的运动情况。
答: (1)质心参照系中地球、太阳的运动:地球,太阳相对于质心作椭圆运动。
(2)地球参照系中太阳运动:太阳相对于地球作椭圆运动。
(3)太阳参照系中地球的运动:地球相对于太阳作椭圆运动。
2-1.分别说明质点组动量守恒定律、动量矩守恒定律、机械能守恒定律成立的条件。
2-2.说明 质点组 对某定点,如原点O ,的动量矩守恒定律成立的条件(要求写出分量式)。
质点组对原点O 的动量矩守恒定律成立的条件为:0)(1=⨯=∑=e i n i i F r M ,分量守恒。
即: 对x 轴:0)()(1=-∑=e iy i e iz n i i F z F y ;对y 轴:0)()(1=-∑=e iz i e ixn i i F x F z ; 对z 轴:0)()(1=-∑=e ixi e iy n i i F y F x 。
理论力学试题题目含参考答案【完整版】(文档可以直接使用,也可根据实际需要修订后使用,可编辑放心下载)理论力学局部第一章 静力学根底一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
〔 〕2.两端用光滑铰链连接的构件是二力构件。
〔 〕3.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
〔 〕4.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
〔 〕5.三力平衡定理指出:三力汇交于一点,那么这三个力必然互相平衡。
〔 〕6.约束反力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
〔 〕二、选择题1.假设作用在A 点的两个大小不等的力1F 和2F ,沿同一直线但方向相反。
那么其合力可以表示为 。
① 1F -2F ;② 2F -1F ;③ 1F +2F ;2.三力平衡定理是 。
① 共面不平行的三个力互相平衡必汇交于一点;② 共面三力假设平衡,必汇交于一点;③ 三力汇交于一点,那么这三个力必互相平衡。
3.在下述原理、法那么、定理中,只适用于刚体的有 。
① 二力平衡原理; ② 力的平行四边形法那么;③ 加减平衡力系原理; ④ 力的可传性原理;⑤ 作用与反作用定理。
4.图示系统只受F 作用而平衡。
欲使A 支座约束力的作用线与AB 成30︒角,那么斜面的倾角应为________。
① 0︒; ② 30︒;③ 45︒; ④ 60︒。
5.二力A F 、B F 作用在刚体上且0=+B A F F ,那么此刚体________。
①一定平衡; ② 一定不平衡;③ 平衡与否不能判断。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.力F沿直线AB作用,其中一个分力的作用与AB成30°角,假设欲使另一个分力的大小在所有分力中为最小,那么此二分力间的夹角为度。
3.作用在刚体上的两个力等效的条件是。
理论力学大一试题及答案理论力学是大学物理专业学生的一门基础课程,它涉及到静力学、动力学、运动学等多个方面。
以下是一份理论力学的大一试题及答案的示例,供参考。
一、选择题(每题3分,共30分)1. 一个物体的惯性仅由以下哪个因素决定?A. 物体的质量B. 物体的形状C. 物体的运动状态D. 物体所处的位置答案:A2. 在国际单位制中,力的单位是以哪位科学家的名字命名的?A. 牛顿B. 爱因斯坦C. 伽利略D. 库仑答案:A3. 根据牛顿第二定律,力与物体的加速度和质量之间的关系是什么?A. F = maB. F = m/aC. F = a/mD. F = a + m答案:A4. 一个物体在水平面上做匀速直线运动,它的机械能是:A. 增加B. 减少C. 不变D. 无法确定答案:C5. 以下哪种情况会导致物体的动量发生变化?A. 物体的速度大小改变B. 物体的质量改变C. 物体的运动方向改变D. 所有以上情况答案:D6. 一个物体在竖直平面内做圆周运动,当它通过最高点时,以下哪个力是必需的?A. 重力B. 向心力C. 摩擦力D. 张力答案:D7. 根据能量守恒定律,一个封闭系统中的总能量是:A. 增加B. 减少C. 不变D. 无法确定答案:C8. 以下哪种力不是保守力?A. 重力B. 摩擦力C. 弹性力D. 电场力答案:B9. 一个物体在水平面上做匀加速直线运动,它的加速度与哪个物理量无关?A. 物体的质量B. 物体所受的合力C. 物体的速度D. 物体的位移答案:D10. 以下哪个选项是正确的动量守恒条件?A. 系统所受合外力为零B. 系统所受合外力不为零C. 系统内部力远大于外部力D. 系统内部力远小于外部力答案:A二、填空题(每空3分,共30分)11. 牛顿第一定律又称为________定律。
答案:惯性12. 一个物体的动量定义为物体的质量与________的乘积。
答案:速度13. 在斜面上静止的物体受到的支持力方向是________。
理论力学试题及答案自考一、选择题(每题2分,共10分)1. 一个物体在水平面上以匀速直线运动,其动摩擦因数为μ,那么该物体所受的摩擦力大小为:A. μmgB. μNC. μN + mgD. μmg + N答案:B2. 在国际单位制中,力的单位是以哪位科学家的名字命名的?A. 牛顿B. 伽利略C. 爱因斯坦D. 阿基米德答案:A3. 如果一个物体的加速度为零,那么它的运动状态是:A. 静止B. 匀速直线运动C. 变速运动D. 以上都是答案:D4. 根据牛顿第三定律,作用力和反作用力:A. 大小相等,方向相反B. 大小不等,方向相反C. 大小相等,方向相同D. 大小不等,方向相同答案:A5. 一个物体从静止开始自由下落,其下落的高度h与时间t的关系为:A. h = gtB. h = 1/2gtC. h = 1/2gt^2D. h = gt^2答案:C二、填空题(每题3分,共15分)6. 牛顿第二定律的数学表达式为:________。
答案:F = ma7. 一个物体的惯性只与物体的________有关。
答案:质量8. 在光滑水平面上,两个相互接触的物体之间不一定有摩擦力,因为摩擦力的产生需要满足两个条件:一是相互接触的粗糙表面,二是________。
答案:有相对运动或相对运动趋势9. 根据能量守恒定律,一个物体的动能和势能之和称为________。
答案:机械能10. 地球表面的重力加速度大约是________m/s²。
答案:9.8三、简答题(每题10分,共20分)11. 什么是动量守恒定律?在什么条件下动量守恒?答案:动量守恒定律指的是在一个封闭系统中,如果没有外力作用,系统内各物体相互作用前后总动量保持不变的物理定律。
在没有外力作用或者外力的合力为零的条件下,动量守恒。
12. 简述牛顿运动定律中的第三定律。
答案:牛顿第三定律又称作用与反作用定律,它指出:对于任意两个相互作用的物体,它们之间的作用力和反作用力大小相等、方向相反,并且在同一直线上。
一、(42分)简要回答与计算下列各题1、如图所示,各杆的自重不计,构件ABC 水平,M=6KN.m ,a=1m 。
求A 处的约束反力。
2、如图所示,力F 通过A (3,4,0)、B (0,4,4)两点(长度单位为m ),若F=100N ,请给出力F 在X 轴上的投影,及F 对X 、Y 轴的矩。
3、刚体做平面运动,其平面图形(未画出)A 、B 两点之间的距离L=0.2m ,两点的加速度垂直与AB 的连线,转向相反、大小均为2/2s m ,求图形该时刻的角加速度的大小,并在图上标明其转向。
4、如图所示AB 杆铅垂,A 点连一滑块可沿水平轨道运动,设B 点速度方向如图所示,其大小不为零,问这种运动是否可能,并说明理由。
5、质量为m 的均质圆盘,平放在光滑的水平面上,其受力情况如图所示,设开始时圆盘静止,图中2Rr =。
试说明圆盘将做何种运动。
6、如图所示,半径为R 的均质圆轮重P ,在水平面上只滚不滑。
通过铰链A 带动一均质细杆AB 运动,杆长为R l 22=,重量也为P 。
在qL LLL2LBEMD CA G 1G 2图示位置瞬时轮心O 的速度为υ。
试确定此时系统的动能和动量的大小和方向。
7、如图所示直角弯杆AC 与直杆BC 在C 点铰接。
BC 中点受力P 作用,各杆重量不计,摩擦不计。
尺寸如图所示。
试用虚位移原理求支座A 的水平方向约束反力。
(用其他方法作不给分)二、(20分)1、图示构架在E 、G 1、G 2处铰接,各杆自重不计。
已知:M=12kN ·m ,q=1 kN/m ,L=2m 。
试求:(1)绳CD 的拉力;(2)固定端B的约束反力。
四、(18分)滑块B, D 分别沿铅直和水平导槽滑动,并借AB 杆和AD 杆与圆轮中心A 点铰接,设圆轮作无滑动滚动。
图所示瞬时滑块D 速度 D = 0.5 m/s ,加速度a D = 0。
己知AB=0.5m , AD=0.4 m 。
试求:(1)杆AD 和杆AB 的角速度;(2) 滑块B 的速度和加速度。
理论力学试题一、单项选择题1. 关于力的概念,错误的有()A.力是物体之间相互机械作用B. 力的三要素:大小、方向、作用点C. 力的单位为:KN或ND. 力是代数量2. 三力平衡汇交定理适用于下列哪一种情况?()A.只适用于变形体B.只适用于刚体C. 只适用于平衡系统D. 物体系统3. F1、F2 、F3及F4是作用在刚体上的平面汇交力系,其力矢之间有如图所示的关系,合力为FR,以下情况中哪几种是正确的?()A. FR= F4B. FR= 2F4C. FR= - F4D. FR= - 2F44. 关于力在直角坐标轴上的投影描述错误的是()A. 力的投影是代数量B.力的投影,从始端到末端的指向与坐标轴正向相同时为正,反之为负。
C.从力的起点和终点作坐标轴的垂线,则垂足之间的线段称为力在该坐标轴上的投影D. 力的投影是矢量5. 如图所示,如果两力偶均作用在杆BC上,铰链A或B的反力方位属于下列哪一种情况?A. 垂直于ACB. 垂直于BCC. 垂直于ABD. AC两点连线6. 关于力对点之矩描述错误的是()A. 力对点之矩是量度力使物体绕点转动效应的物理量B. 平面力对点之矩只取决于力矩的大小及旋转方向C. 平面力对点之矩是一个代数量D. 力对点之矩的大小与矩心的位置选取无关7. 下述说法哪一个正确?()A. 凡是力偶都不能用一个力来平衡B. 凡是力偶都能用一个力来平衡C. 凡是力偶有时能用一个力来平衡8. 判断下图中桁架内力为零的杆件,哪一个答案是正确的?A.一个B.二个C.三个D.四个9. 对于平面一般力系,叙述正确的有()A. 平面一般力系可以简化为主矢和主矩。
B. 主矢和简化中心位置无关,主矩与简化中心位置有关。
C. 主矢和主矩都与简化中心位置有关。
D. 主矢和主矩都与简化中心位置无关。
10. 关于摩擦,下列叙述错误的有()简单(﹡)A.摩擦分为滑动摩擦和滚动摩擦B.静滑动摩擦力等于静滑动摩擦系数与两物体间法向反力的乘积,即F=fNC.摩擦是机械运动中的普遍现象,既有有利的一面,也有不利的一面D.滑动摩擦分为静滑动摩擦和动滑动摩擦11. 关于摩擦角,叙述错误的是()A. 摩擦角的正切等于静摩擦因数B. 摩擦角确定全反力作用线的位置C. 摩擦角是一个范围值D. 摩擦力达到最大值时,与法向反力之间的夹角称为摩擦角12. 关于空间力对轴之矩描述错误的是()A. 力对轴之矩是量度力使物体绕轴转动效应的物理量B. 力对轴之矩只取决于力矩的大小及旋转方向C. 力对轴之矩是一个矢量D. 力对轴之矩的大小等于力在垂直于该轴的平面内的投影与力臂的乘积13. 空间任意力系向两个不同的点简化,下述哪种情况可能?()A. 主矢相等,主矩相等B. 主矢不相等,主矩相等C. 主矢、主矩不相等14. 在某瞬时,若点的切向加速度和法向加速度都等于零,则此点()A. 必定静止不动B. 必作匀速直线运动C. 可能作匀速直线运动D. 可能作匀速曲线运动15. 点作曲线运动时,下述说法哪一个正确?()A. 若切向加速度为正,则点作加速运动B. 若切向加速度与速度符号相同,则点作加速运动C. 若切向加速度与速度符号相反,则点作加速运动D. 若切向加速度为零,则速度为常矢量16. 汽车通过双曲拱桥(桥面曲线为抛物线)时,车厢作()A.平移B.定轴转动C.除平移与转动外的其他运动17. 刚体绕定轴转动时,下述哪一个说法正确?()A. 当转角时,角速度为正B. 当角速度时,角加速度为正C. 当时,必有角加速度D. 当角加速度与角速度同号时为加速转动,当角加速度与角速度异号时为减速转动18. 一平面机构,在图示位置,OA杆的角速度为,若取套管B为动点,动系固结于摇杆OA上,则该瞬时动点的相对速度大小为()A.OBB.0C.BCD.不确定19. 对于点的合成运动,叙述错误的是()A.点的合成运动有三种运动。
2理论力学试题及答案、是非题(每题 2分。
正确用错误用X,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
2、力对于一点的矩不因力沿其作用线移动而改变。
4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。
5、设一质点的质量为 m 其速度—与x 轴的夹角为a,则其动量在x 轴上的投影为 mv =mvcos a o二、选择题(每题 3分。
请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是① 主矢等于零,主矩不等于零; ② 主矢不等于零,主矩也不等于零; ③ 主矢不等于零,主矩等于零; ④ 主矢等于零,主矩也等于零。
2、重P 的均质圆柱放在 V 型槽里,考虑摩擦柱上作用一力偶,其矩为M 时(如图),圆柱处于极限平衡状态。
此时按触点处的法向反力 N A 与N B 的关系为 ① N A = N B ; ② N A > N B ; ③ N A < N B O3、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是①半径为L/2的圆弧; ②抛物线; ③椭圆曲线;④铅垂直线。
4、在图示机构中,杆 0 A //QB,杆 C 2 C //C 3 D,且 O A = 20cm , C 2 C = 40cm , CM = MD = 30cm 若杆 AO 以角速度 w3、在自然坐标系中,如果速度u常数,则加速度a = 0 O=3 rad / s 匀速转动,则D 点的速度的大小为cm/s ,M 点的加速度的大小为 cm/s① 60;② 120;③ 150;④ 360O25、曲柄OA 以匀角速度转动,当系统运动到图 置 (0A | V A V B —A —B J 3 | AB BCB FAB・ABC q F10KN5KNm2mBA2KN/m A CBCA 【M B 0勺A 2Cr_|C_\.M LaV BF c F c4kNF xa AF Bx 2^2F yO sF By q F C0 F ByF xFAxF BX 0 F AX 4kNX A Y A q 1 X B Y B V A aBA a B 1x60—4F y 0FAyFBy0 F Ay10kN0 M A M F 4 0 M A 35kN me [x y]Te[x 1 y]Te 2 cos 45 Sin 45 72/2 72/2sin 45cos 4572/272/2cos( 30 ) sin( 30 ) 43/21/2I 2sin( 30 ) cos( 30 )1/2 A /3/222A i [X 2 A 2 M A y 2]TA iq ir A r oX o y oX AY AA i P iI1/4TX A Y AABsi n (riJs 12U2/2J 2/21/2 2 ABcos 2J02A /2/2 42/2/6T1/2 J3/2V AABACl(十 l sin221 sin id mR 2I1鱼111I2l sinlp/2/2l^j2/2IN2/2I R/2)2 f'1T 11f 22V B舟(“1舟(“1 BCABI 2)ACl sinBC l coslcosl sincota A22r\~~Fl Sincotr 2Isi n 3a Ba AtaBAnaBAa B sin a A cosna BAO 1 O 2O 2O 2O 1 O 1 O 1 O 22TT 1 T 2imR 22) 寸 mR 2(3 12I )2R 1 R 22/22i4mR2(^^4 ;) 押2Q2 d Tdta O i4MR i 7mRO2 L02 M F T R J O2 F T R F TJ s F T 2R F T 4mR3M7Rma i F TL D V D mv o i M D(F) dt(mvo i)丄(mR如2R 7mR4M7mR2)M7RF S0FT2 7mR22 M8M i ——-mRR 2F SF S8M7mR2爲O iM"R4M7R3M7RO i L s F T2RF S2Rma i F T4Mm ---- 27mR23M M7R 7R-mR22ma o i F S 2RF SM 52mR5B 2lcos 5OA AB lxG5B G i 5/D G i5C 0 y B2lsiny c 4 lsiny D 3 I・21sin 5c 号lcos 5 11cos 5M 5 G 2l cos 5 G i 2I cos 5 G i 11 cos 2lcos 2G i l cos 0V s V o r V C V O V co V co 4r L s V s mv c M s (F)2(G G i )lcos F i F 2 e [xz]TF 1 F 2F R F iF R F i F RF oF Rz r iriM O M o (F) M OM 1 M r i F ibFr2F2bF bFriF 2OCbFSF sF Nr2 F2OI / 1/bF bF F iF 1"V COcM O M IM 2bF bF M O bFbF Z F O F RbFbFM O bF y bFb 2 2abcossin (si nV oV c V OV coV COyr2 2 1 2 r zr 2 r 2 2 cos 2 r 2(4 cos ) W mg 1 R(1 cos )T T 0 W 2 mr (-cos ) 3 1mr 2 3 . sin 1 ・ mg 2 r sin V c V o V co V c o T r T 1J 2 2Jc1 mV c 1 [ 12 2 122 mr 2 2 mr 2(1v C v O 2V o V co cos 2 V CO T如1 一mr 2[[丄 mr 2 2 122 2/5mr (4cos )]cos2V ccos )]1 —mr2 2(3 cos 1 -mr 22(4cos ) mg* Rcosmr 2(43 cos )2 mr 2 2sin1 ・mg?r sin(1 cos2(4 1mr 2(^ 2 3 2 Vo 2rcossincos ) 2 T 0mggr(1 cos )V O r2V co 7r2sin2V O V CO cos2 2 2 rg .茹Sin2cosr 2 2(1 cos )dtRcosV O r20o ,其上作用一力Q,且已知P=Q,方向如图,则物块的状态为()第1题图图(a )、(b )为两种结构,则( 图(a )为静不定的,图(b )为为静定的 图(a )、(b )均为静定的 D 填空题(每题3分,共12分) 第2题图图(a )、(b )均为静不定的图(a )为静不定的,图(b )为为静定的向B 点简化的结果为:向D 点简化的结果是什么?第1题图2.图示滚轮,已知 R 2m , r 1m ,30,作用于 B 点的力F 4kN ,求力F 对A 点之矩3.平面力系向O 点简化,主矢F R 与主矩M O 如图。
若已知F R 10kN ,M 。
20kNgm ,求合力大小及 作用线位置,并画在图上。
J s J C m CS 2 1皿"212 mr2 *12 2m(r 4 r r cosG cos )mr 2(42cos )mrLsJs(3 cos )mr 2Lsmr 2 2 sin (4 cos )mr 2V s mV c mr 2 2sinV s mV coV s mV co sin() 4mr 2 2sinM s (F)mgg rsin(4 cos )mr 21mr 2 2sin mg 2r sin(善 cos4 2 sin静止(非临界平衡)状态滑动状态 D 临界平衡状态不能确定1.沿边长为a 2m 的正方形各边分别作用有 F 1, F 2, F 3, F 4,且 F 1 = F 2 = F 3=F 4 =4kN ,该力系 1,厂2,厂3,块重P,与水面的摩擦角2. A C (二) 主矢大小为F R,主矩大小为M B =第2题图V s V o r V C V O V co V co 4rL s V s mv c M s (F)角速度O i A=(三)简单计算题(每小题8分,共24分)1. 梁的尺寸及荷载如图,O 1A O 2B r 0.4m ,O 1O 2 AB ,O 1A 杆的角速度 4rad/s ,角加速度2rad/s 2,求三角板C 点的加速度,并画出其方向。
第3题图 第4题图4.机构如图,O j A 与O 2B 均位于铅直位置,已知 O i A 3m , O 2B 5m ,O2B3rad/s ,则杆 O j A 的求A 、B 处的支座反力。
2. 丁字杆ABC 的A 端固定, 尺寸及荷载如图。
求 A 端支座反力。
3.在图示机构中,已知(四)图示结构的尺寸及载荷如图所示,q= 10kN/m, q o = 20kN/mb 约束反力。
求A、C处(五)多跨静定梁的支撑、荷载及尺寸如图所示。
已知 q= 20kN/m, I = 2m 求支座A D E 处的约束反 力。
(六)复合梁的制成、荷载及尺寸如图所示,杆重不计。
已知 q = 20kN/m, l = 2m,求1、2杆的内力以及 固定端A 处的约束反力。
(七)图示机构中,曲柄 0怎r ,以角速度 4rad/s 绕0轴转动。
O 1C//O 2D , 00= QD= r ,求杆OC 的 角速度。
(一) 单项选择题 1. A 2. B (二) 填空题16kN gm ; F R 0 , M D 16kNgm合力F R 10kN ,合力作用线位置(通过 O i ) d 2m(三)简单计算1.取梁为研究对象,其受力图如图所示。
有X 0,FAX 0M A (F ) 0 , F B F B 5kN Y 0 , J F B F Ay 0kN2. 取丁字杆为研究对1. 02. M A 2.93kNgm3. 4. 4.5rad/s ; 9m/s其受力图如图所示。
有象,X 0, F A P 0F AX 6kN1F Ay —q 0 1.5 0F Ay 4.5kNM A (F) 0, M A M P 4 舟q 0 1.5 1 0M A 32.5kNgm3. 三角板ABC 作平动,同一时刻其上各点速度、加速度均相同。
故a C a A a An a Aa cn a An r 2 0.4 42 6.4m/s 2a c B A OA 0.4 2 0.8m /s 2(四)解:(1)以BC 为研究对象。