3-3二维正态分布
- 格式:ppt
- 大小:939.50 KB
- 文档页数:30
1第三章 二维随机变量及其分布在很多实际问题中,有一些随机试验需要用两个或两个以上的随机变量才能描述, 如, 炮弹着落点的位置必须用两个坐标X 和Y 来描述。
又如气候情况与气温、风力、降水量等多个随机变量有关,为了准确提供气候情况,我们就完全有必要将描述天气情况的多个随机变量作为一个整体来研究。
将n 个随机变量n X X X ,,,21 作为一个整体,记作),,,(21n X X X ,称为n 维随机变量。
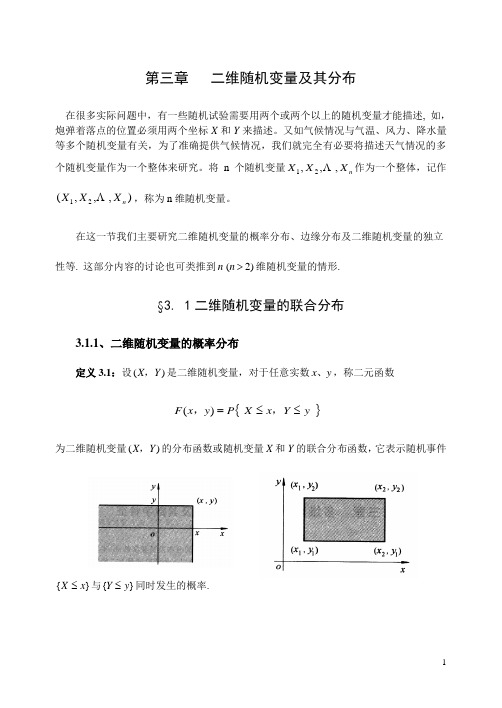
在这一节我们主要研究二维随机变量的概率分布、边缘分布及二维随机变量的独立 性等. 这部分内容的讨论也可类推到)2(>n n 维随机变量的情形.§3. 1二维随机变量的联合分布3.1.1、二维随机变量的概率分布定义3.1:设)(Y X ,是二维随机变量,对于任意实数y x 、,称二元函数{}yY x X P y x F ≤≤=,,)(为二维随机变量)(Y X ,的分布函数或随机变量X 和Y 的联合分布函数,它表示随机事件}{x X ≤与}{y Y ≤同时发生的概率.2图3-1 图3-2将二维随机变量)(Y X ,看成是平面上随机点的坐标,那么分布函数)(y x F ,在点)(y x ,处的函数值就是随机点)(Y X ,落在直线x X =的左侧和直线y Y =的下方的无穷矩形区域内的概率(如图3-1)有了分布函数)(y x F ,,借助于图3-2,容易算出随机点)(Y X ,落在矩形区域 ){(y x D ,=}2121y Y y x X x ≤<≤<,内的概率为:)()(}{21222121y x F y x F y Y y x X x P ,,,-=≤<≤<)()(1112y x F y x F ,,+-.根据概率的定义和二维随机变量的定义,可得:二维分布函数)(y x F ,具有以下基本性质: (1)1)(0≤≤y x F ,;(2))(y x F ,关于变量x 和y 均单调非减,且右连续; (3)对于任意固定的y ,0)(lim )(==-∞-∞→y x F y F x ,,对于任意固定的x ,0)(lim )(==∞--∞→y x F x F y ,,1)(0)(=∞++∞=∞--∞,;,F F ; (4)对于任意2121y y x x <<,恒有:=≤<≤<}{2121y Y y x X x P ,0)()()()(11211222≥+--y x F y x F y x F y x F ,,,,3.3.1.2. 二维离散型随机变量及其分布定义3.2: 如果二维随机变量)(Y X ,可能取的值为有限对或可列无穷对实数,则称)(Y X ,为二维离散型随机变量.显然,)(Y X ,为二维离散型随机变量,当且仅当X 和Y 均为离散型随机变量.设二维离散型随机变量)(Y X ,所有可能的取值为)21()( ,,,,=j i y x j i ,且对应的概率为.,21}( ,,,,====j i p y Y x X P ij j i则称上式为二维随机变量)(Y X ,的概率分布或X 与Y 的联合概率分布.由概率的定义可知:(1) 210,,,=≥j i p ij .(2)∑∑+∞=+∞==111i j ij p .联合分布也常用表格表示,并称为X 与Y 联合概率分布表.4根据定义,离散型随机变量)(Y X ,的联合分布函数∑∑≤≤=≤≤=x x yy iji j py Y x X P y x F },{)(,即对一切满足不等式y y x x j i ≤≤,的ij p 求和.例3.1盒子里有2个黑球、2个红球、2个白球,在其中任取2个球,以X 表示取得的黑球的个数,以Y 表示取得的红球的个数,试写出X 和Y 的联合分布表,并求事件}{1≤+Y X 的概率.解:X 、Y 各自可能的取值均为0、1、2,由题设知,)(Y X ,取(1,2)、(2,1)、(2,2)均不可能. 取其他值的概率可由古典概率计算. 从6个球中任取2个一共有26C =15种取法. )(Y X ,取)00(,表示取得的两个球是白球,其取法只有一种,所以其概率为 }{1510,0===Y X P ,类似地)(Y X ,取其他几对数组的概率为如下: }151}20{}02{,154}11{154152201{}10{==========⨯======Y X P Y X P Y X P Y X P Y X P ,,,,,,)(Y X ,的联合概率分布表为5P {所取两个球中至少有一个白球}=P {所取两个球中黑球和红球的和不超过一个}=}1{≤+Y X P ,由于事件}1{≤+Y X 包含三个基本事件,分别对应着点(0,0)、(0,1)和(1,0),所以:.53154154151}01{}10{}00{}1{=++===+==+===≤+Y X P Y X P y X P Y X P ,,, 3.1.3 二维连续型随机变量及其分布定义3.3:设二维随机变量)(Y X ,的分布函数为)(y x F ,,如果存在非负可积的二元函数)(y x f ,,使得对任意实数y x 、,有}{⎰⎰∞-∞-=≤≤=xydudv v u f y Y x X P y x F )(,)(、,,则称)(Y X ,为二维连续型随机变量,称函数)(y x f ,为二维随机变量)(Y X ,的概率密度函数或随机变量X 和Y 的联合密度函数.由分布函数的定义知,联合密度函数)(y x f ,具有以下性质: (1)0)(≥y x f ,;(2)1)(=⎰⎰∞+∞-∞+∞-dxdy y x f ,;(1)(=∞++∞,即F )反过来,如果一个二元函数)(y x f 、同时满足性质(1)、(2),则它一定是某个二维随机变量的概率密度函数.6 (3)若)(y x f 、在点)(y x 、处连续,则有)()(2y x f yx y x F ,,=∂∂∂; (4)设D 是xoy 平面上任一区域,则点),(y x 落在D 内的概率为{σd y x f D Y X P D)(})(,,⎰⎰=∈.在几何上,{})(D Y X P ∈,的值等于以D 为底,曲面)(y x f Z 、=为顶的曲顶柱体的体积.与一维随机变量相似,有如下常用的二维均匀分布和二维正态分布二维均匀分布:设D 是平面上的有界区域,其面积为A ,若二维随机变量),(Y X 具有概率密度函数⎪⎩⎪⎨⎧∈=其他,0),(,1),(Dy x A y x f则称),(Y X 在D 上服从均匀分布.二维正态分布:若二维随机变量)(Y X ,的概率密度为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-⋅---⋅---=2222221121212221)(2)()1(21exp 121),(σμσμσμρσμρρσσπy y x x y x f(+∞<<∞-+∞<<-∞y x ,)其中参数ρσσμμ,,,,2121均为常数,且10021<>>ρσσ,,,则称)(Y X ,服从参数为2121σσμμ,,,及ρ的二维正态分布,记作);,,,,ρσσμμ222121(~)(N Y X .7如图3-4所示,二维正态分布以),(21μμ为中心,在中心附近具有较高的密度,离中心越远,密度越小,这与实际中很多现象相吻合.图 3-3 二维正态分布密度函数图象例3.2 设二维随机变量)(Y X ,的概率密度函数为⎩⎨⎧≥≥=+-其它,,,,000)()32(y x Ce y x f y x求:(1)常数C ;(2))(Y X ,的分布函数)(y x F ,;(3)}{Y X P <.解:(1)由)(y x f ,的性质2可知:⎰⎰⎰⎰∞+∞++-∞+∞-∞+∞-==)32()(1dxdy Ce dxdy y x f y x ,=⎰⎰∞+∞+--⋅=03261C dy e dx e Cy x所以:6=C (2)⎰⎰∞-∞-=xydxdy y x f y x F )()(,,8 ⎪⎩⎪⎨⎧≥≥--==⎰⎰--+-其它,,,000)1)(1(60032)32(y x e e dxdy e x y y x y x(3).526),(}{00)32(⎰⎰⎰⎰∞++-<===<y y x yx dy e dx dxdy y x f Y X P .例3.3 设二维随机变量)(Y X ,的密度函数为⎩⎨⎧≤≤≤≤=其它,,,,010104)(y x xy y x fD 为xoy 平面内由x 轴、y 轴和不等式1<+y x 所确定的区域,求{}DY X P ∈)(,.解:如图3-4所示: {}⎰⎰=∈Ddxdy y x f D Y X P )(),(,⎰⎰-=xxydy dx 101461=例3.4 设),(Y X 在圆域}{4),(22≤+y x y x 上服从均匀分布,求(1)),(Y X 的概率密度;(2)}{10,10<<<<Y X P解:(1)圆的面积为π4=A ,故),(Y X 的概率密度为9⎪⎩⎪⎨⎧≤+=其他,04,41),(22y x y x f π(2)用G 表示不等式10,10<<<<y x 所确定的区域,由分布函数的性质4有}{10,10<<<<Y X P =⎰⎰=Gdxdy y x f 41),(.(注意概率密度),(y x f 在圆以外的区域都等于零)10 §3.2 边缘分布二维随机变量)(Y X ,作为一个整体,它具有分布函数)(y x F ,.而分量X 和Y 也都是随机变量,也有其各自的分布函数. 记X 和Y 的分布函数为)(x F X 和)(y F Y ,分别称它们为二维随机变量)(Y X ,关于X 和关于Y 的边缘分布函数. 边缘分布函数可以由)(Y X ,的联合分布函数)(y x F ,来确定:{}{})()(∞+=+∞<≤=≤=,,x F Y x X P x X P x F X即:)()(∞+=,x F x F X ;同理)()(y F x F Y ,+∞=. 下面分别讨论二维离散型随机变量和二维连续型随机变量的边缘分布3.2.1 二维离散型随机变量)(Y X ,的边缘分布设)(Y X ,是二维离散型随机变量,设其概率分布为{}.21 ,,,,,====j i p y Y x X P ij j i则X 的边缘分布律为:{}{}{}{}.21121,,,,,==+==++==+====∑∞=i p y Y x X P y Y x X P y Y x X P x X P j ijj i i i i X 的边缘分布函数为 ∑∑≤=+∞=x x jijX i px F x F ),()(.若将{}∑∞===1j iji px X P 记为),.21( =∙i p i ,则X 的边缘分布可写成表格形式且满足1=∑⋅ii p .同理,Y 的边缘分布律为:{}{}{}{}.21121,,,,,===+==++==+====⋅∞=∑j p p y Y x X P y Y x X P y Y x X P y Y P ji ij j i j j j写成表格形式有满足1=∑⋅jj p .Y 的边缘分布函数为∑∑≤=+∞=y y iijY j py F y F ),()(例3.5 设)(Y X ,的概率分布由下表给出,求X 和Y 的边缘分布.解:{}{}000====Y X P X P ,+{}10==Y X P ,+{}20==Y X P , 80.035.030.015.0=++=同理可求得:20.003.012.005.0}1{=++==X P20.0}0{==Y P , 42.0}1{==Y P , 38.0}2{==Y P将X 和Y 的边缘分布列入),(Y X 的联合分布表中通过该例,可以很明显地看出,边缘分布∙i p 和j p ∙分别是联合分布表中第i 行和第j列各元素之和.3.2.2 二维连续型随机变量)(Y X ,的边缘分布设)(Y X ,是二维连续型随机变量,它的概率密度函数为),(y x f ,则X 的边缘分布函数为: ⎰⎰∞-∞+∞-⎢⎣⎡⎥⎦⎤=∞+=x X dx dy y x f x F x F )()()(,, 其密度函数为:⎰∞+∞-=∞+'='=dy y x f x F x F x f XX )()()()(,,同理,Y 的边缘分布函数为⎰⎰∞-∞+∞-⎢⎣⎡⎥⎦⎤=+∞=y Y dy dx y x f y F y F )(),()(,其密度函数为⎰∞+∞-='=dx y x f y F y f Y Y )()()(,通常分别称)(x f X 和)(y f Y 为二维随机变量)(Y X ,关于X 和Y 的边缘密度函数. 例3.6 设随机变量)(Y X ,的密度函数为⎩⎨⎧≤≤≤=其它,,,010)(y x y x k y x f试求参数k 的值及X 和Y 的边缘密度.解:根据联合密度函数的性质,有⎰⎰⎰⎰∞+∞-∞+∞-===101181)(x k ydydx x k dxdy y x f , 所以: 8=kX 的边缘密度函数⎰+∞∞-=dy y x f x f X )()(,当x <0或1>x 时,),(y x f 都等于零,所以此时0)(=x f X当10≤≤x 时,且1≤≤y x 时,xy y x f 8),(=,所以⎰-==12)1(48)(xX x x xydy x f即: ⎩⎨⎧≤≤-=其它,,010)1(4)(2x x x x f X同理可得: ⎩⎨⎧≤≤=其它,,0104)(3y y y f Y例3.7 设随机变量)(Y X ,的密度函数为⎩⎨⎧≤≤≤≤=其它,,,010,104)(y x y x y x f试求X 和Y 的边缘密度.解:关于X 的边缘密度⎰+∞∞-=dy y x f x f X )()(,当x <0或1>x 时,),(y x f 都等于零,所以此时0)(=x f X当10≤≤x 时,且10≤≤y 时,xy y x f 4),(=,所以⎰==124)(x xydy x f X即: ⎩⎨⎧≤≤=其它,,0102)(x x x f X同理可得:⎩⎨⎧≤≤=其它,,0102)(y y y f Y例3.8 求二维正态随机变量)(~)(222121ρσσμμ;,,,,N Y X 的边缘密度.解:记X 和Y 的边缘密度函数分别为)(x f X 和)(y f Y由于222222112121)(2)(σμσμσμρσμ-+-⋅---y y x x=211221122))(1()(σμρσμρσμ--+---x x y所以:dy eedy y x f x f x y x X 211222121)()1(212)(221121)()(σμρσμρσμρσπσ-----∞+∞-∞+∞---∞+∞-⎰⎰⎰⋅-==,令 )(1111222σμρσμρ----=x y t则 )(x f X dt eet x ⎰∞+∞----=22)(1212121σμσπ21212)(121σμσπ--=x e (+∞<<-∞x )可见 )(~211σμ,N X ;同理可得:2222)(221)(σμσπ--=y Y ey f (+∞<<-∞y )即)(~222σμ,N Y .比较联合密度)(y x f ,和边缘密度函数)()(y f x f Y X 、,我们注意到当且仅当0=ρ时,对一切)y x ,(有)()()(y f x f y x f Y X ⋅=,. 以上对二维正态分布的讨论说明:(1)二维正态分布的边缘分布是一维正态分布,由二维联合分布可以唯一确定其每个分量的边缘分布;(2)已知X 与Y 的边缘分布,并不能唯一确定其联合分布,还必须知道参数ρ的值.譬如两个二维正态分布);,,,2/11100(N 和);,,,3/11100(N ,它们的联合分布不同,但其边缘分布都是标准正态分布. 引起这一现象的原因是二维联合分布不仅含有每个分量的概率分布,而且还含有两个变量X 与Y 之间相互关系的信息,而后者正是人们研究多维随机变量的原因. 联合分布中的参数ρ的值,反映了两个变量X 与Y 之间相关关系的密切程度.从以上几个例题可知,联合密度决定边缘密度,但反过来知道边缘密度并不能唯一确定联合密度3.2.3.二维随机变量的独立性在前面我们已经知道,随机事件的独立性在概率计算中起着很大的作用.在多维随机变量中,它们的分量的独立性在概率论和数理统计的研究中占有十分重要的地位。





3.1二维随机变量的概念3.1.1二维随机变量及其分布函数到现在为止,我们只讨论了一维随机变量及其他布,但有些随机现象用一个随机变量来描述还不够,而需要用几个随机变量来描述。
例如,在打靶时,以靶心为原点建立直角坐标系,命中点的位置是由一对随机变量(X,Y)(两个坐标)来确定的。
又如考察某地区的气候,通常要考察气温X,风力Y,这两个随机变量,记写(X,Y)。
定义3.12个随机变量X,Y组成的整体Z=(X,Y)叫二维随机变量或二维随机向量。
定义3.2(1)二元函数F(x,y)=P(X≤x,Y≤y)叫二维随机变量(X,Y)的联合分布函数,简称分布函数。
记作(X,Y)~F(x,y)。
(2)二维随机变量(X,Y)中,各分量X,Y的分布函数叫二维随机变量(X,Y)的边缘分布函数。
因为X<+∞,Y<+∞即-∞<X<+∞,-∞<Y<+∞,分别表示必然事件,所以有X~F x(x)=P(X≤x)=P(X≤x,Y<+∞)=F(x,+∞)Y~F Y(y)=P(Y≤y)=P(x<+∞,Y≤y)=F(+∞,y)公式可见X,Y的边缘分布可由联合分布函数求得。
3.1.2二维离散型随机变量定义3-3若二维随机变量(X,Y)只取有限多对或可列无穷多对(x i,y j),(i,j=1,2,…),则称(X,Y)为二维离散型随机变量。
设二维随机变量(X,Y)的所有可能取值为(x i,y j)(i,j=1,2,…),(X,Y)在各个可能取值的概率为:P{X=x i,Y=y j}=P ij(i,j=1,2,…),称P{X=x i,Y=y j}=P ij(i,j=1,2,…)为(X,Y)的分布律。
(X,Y)的分布律还可以写成如下列表形式:(X,Y)的分布律具有下列性质:(1)p ij≥0(i,j=1,2,…);(2)反之,若数集{P ij}(i,j=1,2,…)具有以上两条性质,则它必可作为某二维离散型随机变量的分布律。