二维正态分布及二维均匀分布

一、习题详解：3.1设二维随机向量(,)X Y 的分布函数为:1222,0,0,(,)0,x y x y x y F x y ----⎧--+≥≥=⎨⎩其他求}{12,35P X Y <≤<≤.解：因为 257(2,5)1222F ---=--+，6512221)5,1(---+--=F5322221)3,2(---+--=F ，4312221)3,1(---+--=F所以 )3,1()3,2()5,1()5,2()53,21(F F F F Y X P +--=≤<≤<==+--=----745672322220.02343.2 盒中装有3个黑球, 2个白球. 现从中任取4个球, 用X 表示取到的黑球的个数, 用Y 表示取到的白球的个数, 求(X , Y ) 的概率分布.解：因为X + Y = 4，所以(X ,Y )的可能取值为(2,2),(3,1)且 0)1,2(===Y X P ，6.053)2,2(452223=====C C C Y X P 4.052)1,3(451233=====C C C Y X P ，0)2,3(===Y X P 故(X ,Y )的概率分布为3.3 将一枚均匀的硬币抛掷3次, 用X 表示在3次中出现正面的次数, 用Y 表示3次中出 现正面次数与出现反面次数之差的绝对值，求(X , Y ) 的概率分布.解：因为|32||)3(|-=--=X X X Y ，又X 的可能取值为0,1,2,3 所以(X ,Y )的可能取值为(0,3),(1,1), (2,1),(3,3)且 81)21()3,0(3====Y X P ，83)21()21()1,1(2113====C Y X P 83)21()21()1,2(1223====C Y X P ，81)21()3,3(3====Y X P故(X ,Y )3.4设二维随机向量(,)X Y 的概率密度函数为:(6),01,02,(,)0,a x y x y f x y --≤≤≤≤⎧=⎨⎩其他 (1) 确定常数a ;(2) 求}{0.5, 1.5P X Y ≤≤(3) 求{(,)}P X Y D ∈,这里D 是由0,0,1x y x y ==+=这三条直线所围成的三角形区域.解：(1)因为dxdy y x a dxdy y x f ⎰⎰⎰⎰--=+∞∞-+∞∞-102)6(),(dx x x a dx y x a ⎰⎰---=---=10221022])4()6[(2])6(21[a dx x a 9)5(210=-=⎰由1),(=⎰⎰+∞∞-+∞∞-dxdy y x f ，得9a =1，故a =1/9.(2) dxdy y x Y X P ⎰⎰--=≤≤5.005.10)6(91)5.1,5.0( dx x dx y y x ⎰⎰--=--=5.005.005.102]89)6(23[91]21)6([91 125)687(5.00=-=⎰dx x (3) 1101{(,)}(,)(6)9xDP X Y D f x y dxdy dx x y dy -∈==--⎰⎰⎰⎰278)1211(181]21)6([9110210102=--=--=⎰⎰-dx x x dx y y x x3.5 设二维随机向量(,)X Y 的概率密度函数为:(2)2,0,0,(,)0,x y e x y f x y -+⎧>>=⎨⎩其他(1) 求分布函数(,)F x y ; (2) 求}{P Y X ≤解：(1) 求分布函数(,)F x y ; 当0,0x y >>，(2)220(,)(,)22(1)(1)yxyxx yu v u v x y F x y f u v dudv e dudv e du e dv e e -+-----∞-∞====--⎰⎰⎰⎰⎰⎰其他情形，由于(,)f x y =0，显然有(,)F x y =0。

1第三章 二维随机变量及其分布在很多实际问题中，有一些随机试验需要用两个或两个以上的随机变量才能描述, 如， 炮弹着落点的位置必须用两个坐标X 和Y 来描述。

又如气候情况与气温、风力、降水量等多个随机变量有关，为了准确提供气候情况，我们就完全有必要将描述天气情况的多个随机变量作为一个整体来研究。

将n 个随机变量n X X X ,,,21 作为一个整体，记作),,,(21n X X X ，称为n 维随机变量。

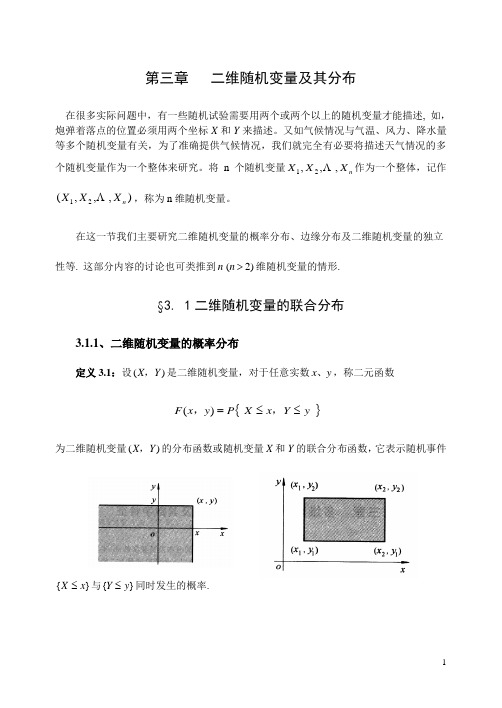
在这一节我们主要研究二维随机变量的概率分布、边缘分布及二维随机变量的独立 性等. 这部分内容的讨论也可类推到)2(>n n 维随机变量的情形.§3. 1二维随机变量的联合分布3.1.1、二维随机变量的概率分布定义3.1：设)(Y X ，是二维随机变量，对于任意实数y x 、，称二元函数{}yY x X P y x F ≤≤=，，)(为二维随机变量)(Y X ，的分布函数或随机变量X 和Y 的联合分布函数，它表示随机事件}{x X ≤与}{y Y ≤同时发生的概率.2图3-1 图3-2将二维随机变量)(Y X ，看成是平面上随机点的坐标，那么分布函数)(y x F ，在点)(y x ，处的函数值就是随机点)(Y X ，落在直线x X =的左侧和直线y Y =的下方的无穷矩形区域内的概率(如图3-1)有了分布函数)(y x F ，，借助于图3-2，容易算出随机点)(Y X ，落在矩形区域 ){(y x D ，=}2121y Y y x X x ≤<≤<，内的概率为：)()(}{21222121y x F y x F y Y y x X x P ，，，-=≤<≤<)()(1112y x F y x F ，，+-.根据概率的定义和二维随机变量的定义，可得：二维分布函数)(y x F ，具有以下基本性质： （1）1)(0≤≤y x F ，；（2）)(y x F ，关于变量x 和y 均单调非减，且右连续； （3）对于任意固定的y ，0)(lim )(==-∞-∞→y x F y F x ，，对于任意固定的x ，0)(lim )(==∞--∞→y x F x F y ，，1)(0)(=∞++∞=∞--∞，；，F F ； （4）对于任意2121y y x x <<，恒有：=≤<≤<}{2121y Y y x X x P ，0)()()()(11211222≥+--y x F y x F y x F y x F ，，，，3.3.1.2. 二维离散型随机变量及其分布定义3.2： 如果二维随机变量)(Y X ，可能取的值为有限对或可列无穷对实数，则称)(Y X ，为二维离散型随机变量.显然，)(Y X ，为二维离散型随机变量，当且仅当X 和Y 均为离散型随机变量.设二维离散型随机变量)(Y X ，所有可能的取值为)21()( ，，，，=j i y x j i ，且对应的概率为.,21}( ，，，，====j i p y Y x X P ij j i则称上式为二维随机变量)(Y X ，的概率分布或X 与Y 的联合概率分布.由概率的定义可知：（1） 210，，，=≥j i p ij .（2）∑∑+∞=+∞==111i j ij p .联合分布也常用表格表示，并称为X 与Y 联合概率分布表.4根据定义，离散型随机变量)(Y X ，的联合分布函数∑∑≤≤=≤≤=x x yy iji j py Y x X P y x F },{)(，即对一切满足不等式y y x x j i ≤≤，的ij p 求和.例3.1盒子里有2个黑球、2个红球、2个白球，在其中任取2个球，以X 表示取得的黑球的个数，以Y 表示取得的红球的个数，试写出X 和Y 的联合分布表，并求事件}{1≤+Y X 的概率.解：X 、Y 各自可能的取值均为0、1、2，由题设知，)(Y X ，取（1，2）、（2，1）、（2，2）均不可能. 取其他值的概率可由古典概率计算. 从6个球中任取2个一共有26C =15种取法. )(Y X ，取)00(，表示取得的两个球是白球，其取法只有一种，所以其概率为 }{1510,0===Y X P ，类似地)(Y X ，取其他几对数组的概率为如下： }151}20{}02{,154}11{154152201{}10{==========⨯======Y X P Y X P Y X P Y X P Y X P ，，，，，，)(Y X ，的联合概率分布表为5P {所取两个球中至少有一个白球}=P {所取两个球中黑球和红球的和不超过一个}=}1{≤+Y X P ，由于事件}1{≤+Y X 包含三个基本事件，分别对应着点（0，0）、（0，1）和（1，0），所以：.53154154151}01{}10{}00{}1{=++===+==+===≤+Y X P Y X P y X P Y X P ，，， 3.1.3 二维连续型随机变量及其分布定义3.3：设二维随机变量)(Y X ，的分布函数为)(y x F ，，如果存在非负可积的二元函数)(y x f ，，使得对任意实数y x 、，有}{⎰⎰∞-∞-=≤≤=xydudv v u f y Y x X P y x F )(,)(、，，则称)(Y X ，为二维连续型随机变量，称函数)(y x f ，为二维随机变量)(Y X ，的概率密度函数或随机变量X 和Y 的联合密度函数.由分布函数的定义知，联合密度函数)(y x f ，具有以下性质： （1）0)(≥y x f ，；（2）1)(=⎰⎰∞+∞-∞+∞-dxdy y x f ，；（1)(=∞++∞，即F ）反过来，如果一个二元函数)(y x f 、同时满足性质（1）、（2），则它一定是某个二维随机变量的概率密度函数.6 （3）若)(y x f 、在点)(y x 、处连续，则有)()(2y x f yx y x F ，，=∂∂∂； （4）设D 是xoy 平面上任一区域，则点),(y x 落在D 内的概率为{σd y x f D Y X P D)(})(，，⎰⎰=∈.在几何上，{})(D Y X P ∈，的值等于以D 为底，曲面)(y x f Z 、=为顶的曲顶柱体的体积.与一维随机变量相似，有如下常用的二维均匀分布和二维正态分布二维均匀分布：设D 是平面上的有界区域，其面积为A ，若二维随机变量),(Y X 具有概率密度函数⎪⎩⎪⎨⎧∈=其他,0),(,1),(Dy x A y x f则称),(Y X 在D 上服从均匀分布.二维正态分布：若二维随机变量)(Y X ，的概率密度为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-+-⋅---⋅---=2222221121212221)(2)()1(21exp 121),(σμσμσμρσμρρσσπy y x x y x f（+∞<<∞-+∞<<-∞y x ,）其中参数ρσσμμ，，，，2121均为常数，且10021<>>ρσσ，，，则称)(Y X ，服从参数为2121σσμμ，，，及ρ的二维正态分布，记作）；，，，，ρσσμμ222121(~)(N Y X .7如图3-4所示，二维正态分布以），（21μμ为中心，在中心附近具有较高的密度，离中心越远，密度越小，这与实际中很多现象相吻合.图 3-3 二维正态分布密度函数图象例3.2 设二维随机变量)(Y X ，的概率密度函数为⎩⎨⎧≥≥=+-其它，，，，000)()32(y x Ce y x f y x求：（1）常数C ；（2）)(Y X ，的分布函数)(y x F ，；（3）}{Y X P <.解：（1）由)(y x f ，的性质2可知：⎰⎰⎰⎰∞+∞++-∞+∞-∞+∞-==)32()(1dxdy Ce dxdy y x f y x ，=⎰⎰∞+∞+--⋅=03261C dy e dx e Cy x所以：6=C （2）⎰⎰∞-∞-=xydxdy y x f y x F )()(，，8 ⎪⎩⎪⎨⎧≥≥--==⎰⎰--+-其它，，，000)1)(1(60032)32(y x e e dxdy e x y y x y x（3）.526),(}{00)32(⎰⎰⎰⎰∞++-<===<y y x yx dy e dx dxdy y x f Y X P .例3.3 设二维随机变量)(Y X ，的密度函数为⎩⎨⎧≤≤≤≤=其它，，，，010104)(y x xy y x fD 为xoy 平面内由x 轴、y 轴和不等式1<+y x 所确定的区域，求{}DY X P ∈)(，.解：如图3-4所示： {}⎰⎰=∈Ddxdy y x f D Y X P )(),(，⎰⎰-=xxydy dx 101461=例3.4 设),(Y X 在圆域}{4),(22≤+y x y x 上服从均匀分布，求（1）),(Y X 的概率密度；（2）}{10,10<<<<Y X P解：（1）圆的面积为π4=A ，故),(Y X 的概率密度为9⎪⎩⎪⎨⎧≤+=其他,04,41),(22y x y x f π（2）用G 表示不等式10,10<<<<y x 所确定的区域，由分布函数的性质4有}{10,10<<<<Y X P =⎰⎰=Gdxdy y x f 41),(.(注意概率密度),(y x f 在圆以外的区域都等于零)10 §3.2 边缘分布二维随机变量)(Y X ，作为一个整体，它具有分布函数)(y x F ，.而分量X 和Y 也都是随机变量，也有其各自的分布函数. 记X 和Y 的分布函数为)(x F X 和)(y F Y ，分别称它们为二维随机变量)(Y X ，关于X 和关于Y 的边缘分布函数. 边缘分布函数可以由)(Y X ，的联合分布函数)(y x F ，来确定：{}{})()(∞+=+∞<≤=≤=，，x F Y x X P x X P x F X即：)()(∞+=，x F x F X ；同理)()(y F x F Y ，+∞=. 下面分别讨论二维离散型随机变量和二维连续型随机变量的边缘分布3.2.1 二维离散型随机变量)(Y X ，的边缘分布设)(Y X ，是二维离散型随机变量，设其概率分布为{}.21 ，，，，，====j i p y Y x X P ij j i则X 的边缘分布律为：{}{}{}{}.21121，，，，，==+==++==+====∑∞=i p y Y x X P y Y x X P y Y x X P x X P j ijj i i i i X 的边缘分布函数为 ∑∑≤=+∞=x x jijX i px F x F ),()(.若将{}∑∞===1j iji px X P 记为），.21( =∙i p i ，则X 的边缘分布可写成表格形式且满足1=∑⋅ii p .同理，Y 的边缘分布律为：{}{}{}{}.21121，，，，，===+==++==+====⋅∞=∑j p p y Y x X P y Y x X P y Y x X P y Y P ji ij j i j j j写成表格形式有满足1=∑⋅jj p .Y 的边缘分布函数为∑∑≤=+∞=y y iijY j py F y F ),()(例3.5 设)(Y X ，的概率分布由下表给出，求X 和Y 的边缘分布.解：{}{}000====Y X P X P ，+{}10==Y X P ，+{}20==Y X P ， 80.035.030.015.0=++=同理可求得：20.003.012.005.0}1{=++==X P20.0}0{==Y P ， 42.0}1{==Y P ， 38.0}2{==Y P将X 和Y 的边缘分布列入),(Y X 的联合分布表中通过该例，可以很明显地看出，边缘分布∙i p 和j p ∙分别是联合分布表中第i 行和第j列各元素之和.3.2.2 二维连续型随机变量)(Y X ，的边缘分布设)(Y X ，是二维连续型随机变量，它的概率密度函数为),(y x f ，则X 的边缘分布函数为： ⎰⎰∞-∞+∞-⎢⎣⎡⎥⎦⎤=∞+=x X dx dy y x f x F x F )()()(，， 其密度函数为：⎰∞+∞-=∞+'='=dy y x f x F x F x f XX )()()()(，，同理，Y 的边缘分布函数为⎰⎰∞-∞+∞-⎢⎣⎡⎥⎦⎤=+∞=y Y dy dx y x f y F y F )(),()(，其密度函数为⎰∞+∞-='=dx y x f y F y f Y Y )()()(，通常分别称)(x f X 和)(y f Y 为二维随机变量)(Y X ，关于X 和Y 的边缘密度函数. 例3.6 设随机变量)(Y X ，的密度函数为⎩⎨⎧≤≤≤=其它，，，010)(y x y x k y x f试求参数k 的值及X 和Y 的边缘密度.解：根据联合密度函数的性质，有⎰⎰⎰⎰∞+∞-∞+∞-===101181)(x k ydydx x k dxdy y x f ， 所以： 8=kX 的边缘密度函数⎰+∞∞-=dy y x f x f X )()(，当x <0或1>x 时，),(y x f 都等于零，所以此时0)(=x f X当10≤≤x 时，且1≤≤y x 时，xy y x f 8),(=，所以⎰-==12)1(48)(xX x x xydy x f即： ⎩⎨⎧≤≤-=其它，，010)1(4)(2x x x x f X同理可得： ⎩⎨⎧≤≤=其它，，0104)(3y y y f Y例3.7 设随机变量)(Y X ，的密度函数为⎩⎨⎧≤≤≤≤=其它，，，010,104)(y x y x y x f试求X 和Y 的边缘密度.解：关于X 的边缘密度⎰+∞∞-=dy y x f x f X )()(，当x <0或1>x 时，),(y x f 都等于零，所以此时0)(=x f X当10≤≤x 时，且10≤≤y 时，xy y x f 4),(=，所以⎰==124)(x xydy x f X即： ⎩⎨⎧≤≤=其它，，0102)(x x x f X同理可得：⎩⎨⎧≤≤=其它，，0102)(y y y f Y例3.8 求二维正态随机变量)(~)(222121ρσσμμ；，，，，N Y X 的边缘密度.解：记X 和Y 的边缘密度函数分别为)(x f X 和)(y f Y由于222222112121)(2)(σμσμσμρσμ-+-⋅---y y x x=211221122))(1()(σμρσμρσμ--+---x x y所以：dy eedy y x f x f x y x X 211222121)()1(212)(221121)()(σμρσμρσμρσπσ-----∞+∞-∞+∞---∞+∞-⎰⎰⎰⋅-==，令 )(1111222σμρσμρ----=x y t则 )(x f X dt eet x ⎰∞+∞----=22)(1212121σμσπ21212)(121σμσπ--=x e （+∞<<-∞x ）可见 )(~211σμ，N X ；同理可得：2222)(221)(σμσπ--=y Y ey f （+∞<<-∞y ）即)(~222σμ，N Y .比较联合密度)(y x f ，和边缘密度函数)()(y f x f Y X 、，我们注意到当且仅当0=ρ时，对一切)y x ，（有)()()(y f x f y x f Y X ⋅=，. 以上对二维正态分布的讨论说明：（1）二维正态分布的边缘分布是一维正态分布，由二维联合分布可以唯一确定其每个分量的边缘分布；（2）已知X 与Y 的边缘分布，并不能唯一确定其联合分布，还必须知道参数ρ的值.譬如两个二维正态分布）；，，，2/11100(N 和）；，，，3/11100(N ，它们的联合分布不同，但其边缘分布都是标准正态分布. 引起这一现象的原因是二维联合分布不仅含有每个分量的概率分布，而且还含有两个变量X 与Y 之间相互关系的信息，而后者正是人们研究多维随机变量的原因. 联合分布中的参数ρ的值，反映了两个变量X 与Y 之间相关关系的密切程度.从以上几个例题可知，联合密度决定边缘密度，但反过来知道边缘密度并不能唯一确定联合密度3.2.3．二维随机变量的独立性在前面我们已经知道，随机事件的独立性在概率计算中起着很大的作用.在多维随机变量中，它们的分量的独立性在概率论和数理统计的研究中占有十分重要的地位。

第三章 多维随机变量及其分布在实际应用中, 有些随机现象需要同时用两个或两个以上的随机变量来描述. 例如, 研究某地区学龄前儿童的发育情况时, 就要同时抽查儿童的身高H 、体重W , 这里, H 和W 是定义在同一个样本空间==}{e S {某地区的全部学龄前儿童}上的两个随机变量. 又如, 考察某次射击中弹着点的位置时，就要同时考察弹着点的横坐标X 和纵坐标Y . 在这种情况下，我们不但要研究多个随机变量各自的统计规律，而且还要研究它们之间的统计相依关系，因而还需考察它们的联合取值的统计规律，即多为随机变量的分布. 由于从二维推广到多维一般无实质性的困难, 故我们重点讨论二维随机变量.第一节 多维随机变量的分布内容分布图示★ 二维随机变量★ 二维随机变量的分布函数 ★ 例1 ★ 二维离散型随机变量及其概率分布★ 例2★ 例3★ 例4 ★ 例5★ 例6★ 二维连续型随机变量及其概率密度★ 例7★ 例8★ 例9★ 二维均匀分布 ★ 例10 ★ 二维正态分布 ★ 例11★ 内容小结 ★ 课堂练习 ★ 习题3-1内容要点：一、 二维随机变量定义1 设随机实验的样本空间为}{e S =, S e ∈为样本点，而)(),(e Y Y e X X ==是定义在S 上的两个随机变量, 称),(Y X 为定义在S 上的二维随机变量或二维随机向量.二、 二维随机变量的分布函数定义2 设),(Y X 是二维随机变量, 对任意实数y x ,, 二元函数},{)}{()}{(),(y Y x X P y Y P x X P y x F ≤≤≤≤=记为称为二维随机变量),(Y X 的分布函数或称为随机变量X 和Y 的联合分布函数.联合分布函数的性质: （1） ,1),(0≤≤y x F 且对任意固定的,y ,0),(=-∞y F 对任意固定的,0),(,=-∞x F x ;1),(,0),(=+∞+∞=-∞-∞F F(2)),(y x F 关于x 和y 均为单调非减函数, 即对任意固定的,y 当),,(),(,1212y x F y x F x x ≥> 对任意固定的,x 当);,(),(,1212y x F y x F y y ≥>(3)),(y x F 关于x 和y 均为右连续, 即 ).0,(),(),,0(),(+=+=y x F y x F y x F y x F三、 二维离散型随机变量及其概率分布定义 3 若二维随机变量),(Y X 只取有限个或可数个值, 则称),(Y X 为二维离散型随机变量.结论：),(Y X 为二维离散型随机变量当且仅当Y X ,均为离散型随机变量.若二维离散型随机变量),(Y X 所有可能的取值为),(j i y x ,,2,1, =j i 则称),2,1,(},{ ====j i p y Y x X P ijj i为二维离散型随机变量),(Y X 的概率分布(分布律), 或Y X 与的联合概率分布(分布律). 与一维情形类似,有时也将联合概率分布用表格形式来表示, 并称为联合概率分布表: 注：对离散型随机变量而言, 联合概率分布不仅比联合分布函数更加直观, 而且能够更加方便地确定),(Y X 取值于任何区域D 上的概率，即∑∈=∈Dy x ijj i pD Y X P ),(}),{(,特别地, 由联合概率分布可以确定联合分布函数:.},{),(,∑≤≤=≤≤=yy x x ijj i p y Y x X P y x F四、二维连续型随机变量及其概率密度定义 设),(Y X 为二维随机变量,),(y x F 为其分布函数, 若存在一个非负可积的二元函数),(y x f , 使对任意实数),(y x , 有,),(),(⎰⎰∞-∞-=xydsdt t s f y x F则称),(Y X 为二维连续型随机变量, 并称),(y x f 为),(Y X 的概率密度(密度函数), 或Y X ,的联合概率密度(联合密度函数).概率密度函数),(y x f 的性质:;0),()1(≥y x f ;1),(),()2(=+∞+∞=⎰⎰∞∞-∞∞-F dxdy y x f(3) 设D 是xOy 平面上的区域,点),(Y X 落入D 内的概率为⎰⎰=∈Ddxdy y x f D y x P ),(}),{(特别地, 边缘分布函数},{}{)(+∞<≤=≤=Y x X P x X P x F X ,),(),(⎰⎰⎰⎰∞-+∞∞-∞-+∞∞-⎥⎦⎤⎢⎣⎡==x x ds dt t s f dsdt t s f上式表明:X 是连续型随机变量, 且其密度函数为:,),()(⎰+∞∞-=dy y x f x f X同理,Y 是连续型随机变量, 且其密度函数为:⎰+∞∞-=dx y x f y f Y ),()(,分别称)(x f X 和)(y f Y 为),(Y X 关于X 和Y 的边缘密度函数. (4) 若),(y x f 在点),(y x 连续, 则有 ).,(),(2y x f yx y x F =∂∂∂进一步, 根据偏导数的定义, 可推得:当y x ∆∆,很小时, 有,),(},{y x y x f y y Y y x x X x P ∆∆≈∆+≤<∆+≤<即,),(Y X 落在区间],(],(y y y x x x ∆+⨯∆+上的概率近似等于.),(y x y x f ∆∆五、二维均匀分布设G 是平面上的有界区域,其面积为A .若二维随机变量),(Y X 具有概率密度函数 ⎪⎩⎪⎨⎧∈=其它,0),(,1),(Gy x Ay x f 则称),(Y X 在G 上服从均匀分布.六、二维正态分布若二维随机变量),(Y X 具有概率密度⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛----=222221121122)1(21221121),(σμσμσμρσμρρσπσy y x x ey x f其中ρσσμμ,,,,2121均为常数,且1||,0,021<>>ρσσ,则称),(Y X 服从参数为ρσσμμ,,,,2121的二维正态分布.注：二维正态随机变量的两个边缘分布都是一维正态分布，且都不依赖于参数ρ，亦即对给定的2121,,,σσμμ，不同的ρ对应不同的二维正态分布，但它们的边缘分布都是相同的，因此仅由关于X 和关于Y 的边缘分布，一般来说是不能确定二维随机变量),(Y X 的联合分布的.例题选讲：二维随机变量的分布函数例1 设二维随机变量),(y x 的分布函数为+∞<<∞-+∞<<∞-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=y x y C x B A y x F ,,3arctan 2arctan ),((1) 试确定常数.,,C B A(2) 求事件}30,2{≤<+∞<<Y X 的概率. 解(1)由二维随机变量的分布函数的性质,可得 ,1)2/)(2/(),(=++=+∞+∞ππC B A F ,0)2/)(2/(),(=+-=+∞-∞ππC B A F ,0)2/)(2/(),(=-+=-∞+∞ππC B A F由这三个等式中的第一个等式知,0≠A ,02/≠+πB ,02/≠+πC 故由第二、三个等式知,02/=-πB ,02/=-πC 于是得,2/π==C B 2/1π=A 故),(Y X 的分布函数为.3arctan 22arctan 21),(2⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+=y x y x F πππ (2)由(1)式得}30,2{<<∞+<Y X P )0,2()3,2()0,()3,(F F F F +-+∞-+∞=.16/1=二维离散型随机变量及其概率分布例2 (讲义例1) 设随机变量X 在1, 2, 3, 4四个整数中等可能地取一个值，另一个随机变量Y 在1~X 中等可能地取一整数值，试求),(Y X 的分布律.解由乘法公式容易求得),(Y X 的分布律.易知},{j Y i X ==的取值情况是:,4,3,2,1=i 取不大于i 的正整数,且}{}|{},{i X P i X j Y P j Y i X P ======,411⋅=i ,4,3,2,1=i i j ≤于是),(Y X 的分布律为例3 (讲义例2) 把一枚均匀硬币抛掷三次, 设X 为三次抛掷中正面出现的次数, 而Y 为正面出现次数与反面出现次数之差的绝对值, 求),(Y X 的概率分布及),(Y X 关于Y X ,的边缘分布.解 ),(Y X 可取值(0,3),(1,1),(2,1),(3,3),8/1)2/1(}3,0{3====Y X P,8/3)2/1(3}1,1{3====Y X P,8/3}1,2{===Y X P ,8/1}3,3{===Y X P故),(Y X 的概率分布如右表.从概率分布表不难求得),(Y X 关于Y X ,的边缘分布.,8/1}0{==X P ,8/3}1{==X P,8/3}2{==X P ,8/1}3{==X P ,8/68/38/3}1{=+==Y P ,8/28/18/1}3{=+==Y P从而得右表例4 设二维随机变量的联合概率分布为求,1{≤Y X P 解}0,1{≥≤Y X P}1,1{}0,1{=-=+=-==Y X P Y X P }1,1{}0,1{==+==+Y X P Y X P.4.002.01.01.0=+++=}0,1{}2,1{)0,0(=-=+-=-==Y X P Y X P F .4.01.03.0=+=二维连续型随机变量及其概率密度例5设),(Y X 的概率分布由下表给出，求 }0,0{},0,0{≤≤=≠Y X P Y X P |}.||{|},{},0{y X P Y X P XY P ===表3—1B解{≠X P ,05.0= }0,0{=≠Y X P }0,0{}1,0{==+-===Y X P Y X P ,3.02.01.0=+=}1,1{}0,0{|}||{|-==+====Y X P Y X P Y X P }1,1{-==+Y X P .6.01.03.02.0=++=例6 一整数N 等可能地在10,,3,2,1 十值中取一个值. 设=D )(N D 是能整除N 的正整数的个数，)(N F F =是能整除N 的素数的个数（注意1不是素数）. 试写出D 和F 的联合分布律.并求分布律.解将实验的样本空间及F D ,取值的情况列表如下:2111211110434242322110987654321F D D 所有可能取值为1,2,3,4。

概率论知识点总结概率论知识点总结「篇一」概率，现实生活中存在着大量的随机事件，而概率正是研究随机事件的一门学科，教学中，首先以一个学生喜闻乐见的摸球游戏为背景，通过试验与分析，使学生体验有些事件的发生是必然的、有些是不确定的、有些是不可能的，引出必然发生的事件、随机事件、不可能发生的事件，然后，通过对不同事件的分析判断，让学生进一步理解必然发生的事件、随机事件、不可能发生的事件的特点，结合具体问题情境，引领学生设计提出必然发生的事件、随机事件、不可能发生的事件，具有相当的开放度，鼓励学生的逆向思维与创新思维，在一定程度上满足了不同层次学生的学习需要。

其次，做游戏是学习数学最好的方法之一，根据课的内容的特点，教师设计了转盘游戏，力求引领学生在游戏中形成新认识，学习新概念，获得新知识，充分调动了学生学习数学的积极性，体现了学生学习的自主性，在游戏中参与数学活动，在游戏中分析、归纳、合作、思考，领悟数学道理，在快乐轻松的学习氛围中，显性目标和隐性目标自然达成,在一定程度上,开创了一个崭新的数学课堂教学模式。

再次，我们教师在上课的时候要理解频率和概率的关系，教材中概率的概念是通过频率建立的，即频率的稳定值及概率，也就是用频率值估计概率的大小。

通过实验，让学生经历“猜测结果一进行实验一分析实验结果”的过程，建立概率的含义。

要建立学生正确的概率含义，必须让他们亲自经历对随机现象的探索过程，引导他们亲自动手实验收集实验数据，分析实验结果，并将所得结果与自己的猜测进行比较，真正树立正确的概率含义。

第四，我们努力让学生在具体情景中体会概率的意义。

由于初中学生的知识水平和理解能力，初中阶段概率教学的基本原则是：从学生熟悉的生活实例出发，创设情境，贴近生活现实的问题情境，不仅易于激发学生的求知欲与探索热情，而且会促进他们面对要解决的问题大胆猜想，主动试验，收集数据，分析结果，为寻求问题解决主动与他人交流合作，在知识的主动建构过程中，促进了教学目标的有效达成，更重要的是，主动参与数学活动的经历会使他们终身受益，在具体情境中体验概率的意义。

2018考研数学概率论的特点及考点分析高等学校概率统计课的教材，内容包括概率论的基本概念、随机变量及其概率分布、数字特征、大数定律与中心极限定理、统计量及其概率分布、参数估计和假设检验、回归分析、方差分析以及用Excel 进行概率统计计算。

下面就是店铺给大家整理的概率论的特点及考点分析，希望对你有用!概率论的特点及考点分析一、首先来谈谈概率论与数理统计这门课的特点：(1)研究对象是随机现象。

高数是研究确定的现象，而概率研究的是不确定的，是随机现象。

对于不确定的，大家感觉比较头疼。

(2)题型比较固定，解法比较单一，计算技巧要求低一些。

比如概率的解答题基本上就围绕在随机变量函数的分布，随机变量的数字特征，参数的矩估计和最大似然估计这几块。

(3)高数和概率相结合。

求随机变量的分布和数字特征运用到高数的理论与方法，这也是考研所要求考生所具备的解决问题的综合能力。

很多考生因为积分计算不过关，导致概率失分。

所以考生应该加强自己的积分计算能力。

二、要针对性的复习概率论与数理统计在掌握考研数学的概率与数理统计的特点后，结合历年考试试题出题规律，概率拿满分不是梦。

下面，跨考教育小编通过概率论与数理统计的各章节来具体分析。

1、随机事件和概率“随机事件”与“概率”是概率论中两个最基本的概念。

“独立性”与“条件概率”是概率论中特有的概念。

条件概率在不具有独立性的场合扮演了一个重要角色，它是一种概率。

正确地理解并会应用这4个概念是学好概率论的基础。

对于公式，大家要熟练掌握并能准确运算。

而大家比较头疼的古典概型与几何概型的计算问题，考纲只要求掌握一些简单的概率计算。

所以在复习的过程中，建议考生们不要陷入古典概型的计算中。

事件、概率与独立性是本章给出的概率论中最基本、最重要的三个概念。

事件关系及其运算是本章的重点和难点，概率计算是本章的重点。

注意事件与概率之间的关系。

本章主要考查随机事件的关系和运算，概率的性质、条件概率和五大公式，注意事件的独立性。