当前位置：文档之家 › 哈工程材料力学 6第六章

哈工程材料力学 6第六章

  • 格式：pdf
  • 大小：1.27 MB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

哈工大 机械学电子教案-第6章

哈工大 机械学电子教案-第6章

应变
5
三. 强度条件 静载常温下延伸率大于5％的材料－－结构钢、硬铝
塑性材料:屈服极限σ 做为破坏的极限应力 ss 脆性材料:强度极限δ b作为破坏的极限应力 b
静载常温下延伸率小于5％的材料－－玻[ ] A
6
四. 受拉（压）杆件的变形
Nl 刚度公式： l EA
3
2
1
13
(习题6-5)：如图所示为一托架，AC是圆杆。许用应力 []AC=160MPa， BC是方杆，其许用应力[]BC=4MPa， F=60KN, 试确定圆钢杆横截面的直径d及木杆方截面的边长b。
14
(习题6-6)：如图所示为一吊架，AB是木杆， 其截面面积 AAB=104mm2，许用应力[]AB=7MPa； BC为钢杆， ABC=600mm2， 许用应力[]BC=160MPa； 试求B处可吊的最大许可载荷F。
54
(习题6-19)：试用叠加法求图示梁A截面的挠度及B截面的转角， 抗弯刚度EI均为常量。
55
(习题6-20)：试用叠加法求图示外伸梁自由端C处的挠度。已知l， F，M=2Fl，抗弯刚度EI为常量。
56
6.6 复杂变形时的强度计算
一. 弯曲与拉伸（压缩）的联合作用
RAx
RAy
压缩正应力
RB
F
RA
RB
48
(习题6-18)：如图所示外伸梁由25a工字钢制成，其跨度l＝6m， 全梁上受均布载荷q作用，为使支座处截面A、B及跨度中央截面 C上的最大正应力均为140MPa，W=401.88cm3。试求外伸部分的 长度a及载荷集度q？
RA
RB
49
三. 梁弯曲时的变形及刚度计算
v
挠曲线 v( x)

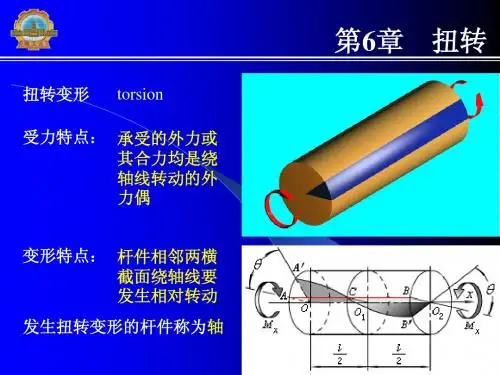
哈工大材料力学第6章

哈工大材料力学第6章

torsion扭转变形受力特点：承受的外力或其合力均是绕轴线转动的外力偶变形特点：杆件相邻两横截面绕轴线要发生相对转动发生扭转变形的杆件称为轴6-1 扭转杆件的内力用截面法可求得该杆任一横截面n—n上只有扭矩一个内力分量，其值为由内力符号的规定，扭矩的正负号正的扭矩矩矢背向截面；负的扭矩矩矢指向截面。

xMT6-1 扭转杆件的内力解：1）求作用在轴上的外力偶nP n P PM kk ⋅⨯===π10330/π10004ωm N 703m N 3001.22π103π10344⋅=⋅⎪⎪⎭⎫⎝⎛⨯⨯=⋅⨯=n P M A A m N 471m N 3008.14π103π10344⋅=⋅⎪⎪⎭⎫⎝⎛⋅⨯=⋅⨯=n P M B B m N 232m N 3003.7π103π10344⋅=⋅⎪⎪⎭⎫ ⎝⎛⋅⨯=⋅⨯=n P M C C 例1 传动轴，转速n =300 rpm ，主动轮A 输入功率P A =22.1kW ，从动轮B 、C 输出功率分别为P B =14.8kW 、P C =7.3kW 。

试求：1）作用在轴上的外力偶矩；2）横截面上的扭矩。

6-1 扭转杆件的内力解：1）求作用在轴上的外力偶矩2）计算横截面上的扭矩OC 与段各截面扭矩均为零CA 段任一截面（图中Ⅰ—Ⅰ截面）AB 段任一截面（图中Ⅱ—Ⅱ截面）3) 作扭矩图1BO N.m232 N.m 471 N.m 703===C B A M M M ，，N.m232 0 011-=-==+=∑C C x M T M T M ，，N.m471 0- 022===+=∑B B x M T M T M ，，例1 传动轴，转速n =300 rpm ，主动轮A 输入功率P A =22.1kW ，从动轮B 、C 输出功率分别为P B =14.8kW 、P C =7.3kW 。

试求：1）作用在轴上的外力偶矩；2）横截面上的扭矩。

1）平面假设6-2 圆轴扭转横截面上的切应力6-2 圆轴扭转横截面上的切应力1）平面假设2）横截面上的切应力公式•几何方程采用柱坐标系ρφx ，取d x 微段6-2 圆轴扭转横截面上的切应力2）横截面上的切应力公式•几何方程•物理方程纯切应力状态)a ( d d d d d tan x x f f x s x x φργγφφ='==≈φφγτx x G =(b)d d xG x φρτφ=切应力沿径向线性分布采用柱坐标系ρφx ，取d x 微段6-2 圆轴扭转横截面上的切应力2）横截面上的切应力公式•几何方程•物理方程•静力平衡方程式(b)代入上式（c ）：式(6-1)代入式(b)：截面的极惯性矩为抗扭刚度(b) d d xG x φρτφ=(c)0d 0=-=∑⎰⎰T A M x Ax φτρ，1)-(6 d d pGI T x =φ2)-(6 d 2A I Ap ⎰⎰=ρp GI 3)-(6 ρτφpx I T=6-2 圆轴扭转横截面上的切应力2）横截面上的切应力公式最大切应力发生在截面外圆周的各个点上令称为抗扭截面系数3)-(6 ρτφpx I T= R I T I T pp x == m ax maxρτφ4)-(6 RI W p t =5)-(6 maxtx W T=φτ6-2 圆轴扭转横截面上的切应力1）平面假设2）横截面上的切应力公式3）截面的极惯性矩与抗扭截面系数•实心圆截面•空心圆截面32πd π2d 42/022DA I D Ap ===⎰⎰⎰ρρρρ16π3DR I W pt ==)(32π44d D I p -=)1(16π43α-=D W t Dd =α例2传动轴，转速n =300 rpm ，主动轮A 输入功率P A =22.1kW ，从动轮B 、C 输出功率分别为P B =14.8kW ，P C =7.3kW 。

第二版《材料力学》第六章至第九章习题解答-(华中科大版-倪樵主编)

第二版《材料力学》第六章至第九章习题解答-(华中科大版-倪樵主编)

2 z
W
M
2 x
W2
[ ]
7-17 图示直角曲拐，C端受铅垂集中力F作用。已知a=160mm，AB杆直径D=40mm，
l=200mm ，E=200GPa， μ=0.3，实验测得D点沿45º方向的线应变 ε45º=0.265 × 10-3。试求：
（1）力F的大小；（2）若AB杆的[σ]=140MPa，试按最大切应力理论校核其强度。
T Wp
16 M 0
D3
16 125 .6
0.023
79.96MPa
单元体可画成平面单元体如图(从上往下观察)
A
6-5 试用求下列各单元体中ab面上的应力（单位MPa） 。
解：(a)
x 70
y 70
xy 0
30
x
y
2
x
y
2
cos(2 30 )
70 1 2
35
(MPa)
x y sin(2 30 ) 70
2
3 60.62 (MPa) 2
(b)
x 70
y 70
xy 0
30
x
y
2
x
y
2
cos(2 30 )
70
(MPa)
x
y
2
sin(2 30 )
0
6-6 各单元体的受力如图所示，试求：（1）主应力大小及方向并在原单元体图上绘出主 单元体；（2）最大切应力（单位MPa） 。
解： (3) My 、Mz、Mx 和F 同时作用，拉弯扭组合，任一截 面D1点是危险点
应力状态：
D1
FN M F
M
2 y
M
2 z
y
AW A

哈工大材料力学

哈工大材料力学

工程中多为梁、杆结构
§1-2 变形固体的基本假设 (The basic assumptions of deformable body )
一、连续性假设 (continuity assumption)
物质密实地充满物体所在空间，毫无空隙。
二、均匀性假设（homogenization assumption)
2. 内力的求法 —— 截面法 (method of sections ) 步骤 (procedures for analysis)
① 截开
在所求内力的截面处，假想
m
地用截面将杆件一分为二.
m
m m
m
m m
m
②代替 任取一部分，其弃去部分对留下部分的作用，用作用在截
面上相应的内力（力或力偶）代替.
2.剪切(shear)
F/2
F/2
F
4.弯曲 (bending)
M
3.扭转(torsion)
Me
Me
M
材料力学是一门很重要的技术基础课，它与机械、土建、航 空、交通水利等工程密切相关，他在基础课和专业课之间起着桥 梁作用.
入门
数学
物理学
理论力学
其他
材料力学
土 木 工 程
土 木 工 程
结 构 力
澳门桥
大型水利工程设施
大量中、外力学专家为力学的发展 作出了突出的贡献，这里只简单介绍部 分力学专家.
达芬奇说：“力学是数学的乐园，因为我们在这里
达
获得了数学的果实.”
芬
奇
伽
利
伽利略创建了材料力学
略
§1-1 材料力学的任务及研究对象
The tasks and research objects

哈工大机械学基础06第6章16春bk

哈工大机械学基础06第6章16春bk

胡克定律


E
强度计算的三类问题：
强度校核 截面设计 许用载荷 计算
N A
A

NF
N
F A
习题6-4：一钢制阶梯形直杆，其受力如图所示，已知
[σ]=260MPa，各段截面面积分别为A1=A3=300mm2， A2=200mm2， E=20×104MPa。试求： （1）各段的轴向力为多少？最大轴向力发生在哪一段内？杆的强 度是否安全？ （2）计算杆的总变形。 3 2 1
RA
3
2
1
例题6-1
图示为一吊架，AB为木杆，其横截面面积为AAB=104mm2，许 用应力[σ] AB =7MPa，BC为钢杆，其横截面面积为ABC=600mm2， 许用应力[σ] BC =160MPa，试求B处可承受的最大许可载荷。
Ⅲ
剪切
工程实例
一、力学模型
受力特征 变形特征
一对平行力 等值、反向、作用线紧靠不重合
Ⅳ
圆轴扭转
工程实例
一、力学模型
受力特征
变形特征
纵向线
变形后
变形前
圆周线 杆件各横截面绕杆件轴线作相对转动 外力偶矩的作用面与 杆件轴线垂直
（1）各纵向线倾斜了同一微小角度γ ， （2）各圆周线围绕轴线旋转一个微小的角度φ， 圆周线长度、形状及相互距离没变
刚体
运动
力
物体
理 论 力 学
可变形 固体
变形 破坏
材 料 力 学
材料力学
１．外力 变形的规律
破坏的规律 内容 ２．材料的力学性质 ３．截面形状和尺寸与承载关系
第6章 构件受力变形及其应力分析
Ⅰ 概述
一、研究的问题

哈工程材料力学--6第六章

哈工程材料力学--6第六章
解：取出图示单元体，依题中条件有：
联立求解，得到
则：
， ，则
题6-9图
6-9试求图示各应力状态的主应力及最大剪应力（应力单位为兆帕）。
解：（ ）
（ ）
，
（ ）
，
注：此类问题中，受力状态是三向的，不再是平面问题，以（ ）为例作详细分析：
在图示坐标系下，
因为 面内应力情况复杂，先进行分析：
则： ， ，
，而 ，又有 ，
第六章应力状态理论和应变状态理论
6-1构件受力如图所示。 确定危险点的位置。 用单元体表示危险点的应力状态。
（ ）不计自重时，危险点为任一横截面上的任意一点
（ ）危险点在 与 之间的任一截面的边缘上任一
（ ）危险点在图示三处
（ ）危险点为任一截面的外边缘上任一点
题6-1图
题6-2图
6-2已知应力状态如图所示，图中应力单位皆为兆帕。试用解析法及图解法求： 主应力大小，主平面位置； 在单元体上绘出主平面位置及主应力方向； 最大剪应力。
（ ）解析法：
斜面与 轴正向夹角为 ，应力图中，
（ ）解析法：
题6-3图
6-4已知矩形截面梁某截面上的弯矩及剪力分别为 ， ，试绘制截面上1、2、3、4各应力点应力状态的单元体，并求其主应力。
解：点1： ,
点2： ，处于纯剪状态,
点3： ，
式中静矩 ,得
,
点4：
题6-4图
6-5薄壁圆筒扭转——拉伸试验的示意图如图所示。若 ， 且 ， 。试求： 点在指定斜截面上的应力； 点主应力的大小及方向（用单元体表示）。
解：求得 处支反力 ， 处支反力为 ，绘出剪力图、弯矩图：
截面上， ， 处，有 ： ，几何数据查型钢表可知，有

哈工程考研总复习提纲解读

哈工程考研总复习提纲解读

第一章平面机构的结构分析一、机构的组成要素1.运动副机构是由许多构件组合而成的。

在机构中，每个构件都以一定的方式与其他构件相互连接。

相互连接的两构件既保持直接接触，又能产生一定的相对运动。

我们把两构件直接接触形成的可动联接称为运动副。

参与接触而构成运动副的点、线、面称为运动副元素。

按组成运动副两构件间的相对运动是平面运动还是空间运动，运动副分为平面运动副和空间运动副。

在此，仅讨论平面运动副。

1)按接触性质分，运动副分为低副和高副①面接触的运动副成为低副，例如滑块与导槽之间则为面接触②点接触或线接触的运动副成为高副，互相啮合的轮齿之间为点或线接触2)按所能产生相对运动的形式分为转动副、移动副、平面滑动副（高副）等①具有一个独立相对转动的运动副成为转动副②具有沿一个方向独立相对移动的运动副成为移动副我们把构件所具有的独立运动的数目成为自由度。

把对独立运动所加的限制成为约束。

每加上一个约束，构件便失去一个自由度。

低副（转动副和移动副）具有两个约束；高副具有一个约束。

2.运动链1)概念两个以上构件以运动副联接而成的系统成为运动链2)分类①闭链和开链如果组成运动链的每个构件至少包含两个运动副元素，则构件形成封闭系统，这种运动链成为闭链。

如果这种链中有的构件只包含一个运动元素，便成为开链如果构件通过运动副联接构成的是相对不可动系统，称为桥架或结构体，即成为一个构件②平面运动链和空间运动链根据运动链中各构件间的相对运动为平面运动还是空间运动，可将运动链分为平面运动链和空间运动链两类3.机构如果将运动链中某一构件固定而成为机架，并有一个或几个构件给定运动规律（原动件），使其余各构件（从动件）具有确定的相对运动，则该运动链便成了机构。

任何机构都包括机架、原动件和从动件三个部分二、平面机构运动简图机构运动简图是用规定的简单线条和符号代表构件和运动副，按比例尺定出各运动副的位置，准确表达机构运动特征的简单图形。

机构运动简图一定要严格按比例尺绘制，否则只能称为机构示意图。

材料力学高教第二版范钦珊第6章习题答案要点

材料力学高教第二版范钦珊第6章习题答案要点

材料力学_高教第二版_范钦珊_第6章习题答案第6章杆件横截面的位移分析6－1 直径d = 36mm的钢杆ABC与铜杆CD在C处连接，杆受力如图所示。

若不考虑杆的自重，试： 1．求C、D二截面的铅垂位移；Fl2．令FP1 = 0，设AC段长度为l1，杆全长为l，杆的总伸长，写出E的表达式。

EA习题6-1图(a) (F)l(F)l解：（1）πdπdEsEs2332(FN)CDlCDπdEc4（2）EAEsAEcAEEsEclEcEs令FP6－2 承受自重和集中载荷作用的柱如图所示，其横截面积沿高度方向按材料的比重。

试作下列量的变化曲线： 1．轴力FNx(x)； 2．应力； 3．位移u(x)。

解：（1），(FN变化，其中为FPFN(x)-FPx习题6-2图(a)FPFPA0FP（2）A(x)A0eFPFP— 89 —（3）A0，当。

∴，则EA0EA0EA06－3 图示连接件由两片宽20mm、厚6mm的铜片与一片同样宽厚的钢片在B处连接而成。

已知钢与铜的弹性模量分别为Es = 200GPa，Ec =105GPa，钢片与铜片之间的摩擦忽略不计。

试求E和B处的位移。

F习题6-3图解：6－4 长为1.2m、横截面面积为的铝制筒放置在固定刚块上，直径为15.0mm的钢杆BC悬挂在铝筒顶端的刚性板上，若二者轴线重合、载荷作用线与轴线一致，且已知钢和铝的弹性模量分别为kNEs = 200Gpa，Ea = 70GPa，FP = 60kN。

试求钢杆上C处位移。

Am EkN(a) 习题6-4图 (b)解：（其中uA = 0） EaAa ∴钢杆6－5 变截面圆锥杆下端B处固定，上端A处承受外力偶矩T作用，如图所示，试证明A端扭转角表达式为解：Mx = T习题6-5图6－6 试比较图示二梁的受力、内力（弯矩）、变形和位移，总结从中所得到的结论。

(a) 解：(b) wmaxFPl3 48EIFlEI— 90 —两者弯矩相同，挠曲线曲率相同，但（b）梁的最大挠度比（a）梁要大，即不相等。

第六章材料力学哈工程

第六章材料力学哈工程

平均线应变
线应变
g
剪应变(或角应变)
与 g 均无量纲。
§6-5 杆件变形的基本形式
一、轴向拉伸或压缩
拉伸 压缩 二、剪切 F F F F F F
三、扭转
Байду номын сангаасMe
Me
四、弯曲 M M
杆件的复杂变形均可由这四种基本变形 组合而成。
缆索 承力柱 拉杆
桥面
3．稳定性
构件在正常工作情况下，要求保持原有的
平衡状态。这就需要构件具有足够的稳定性 —— 构件维持其原有的平衡状态的能力。
P Plj
P Plj
P Plj
干扰力
材料力学的任务：
1）研究构件的强度、刚度和稳定性； 2）研究材料的力学性能； 3）为合理解决工程构件设计中安全性与经济性
§6–3 内力、截面法和应力
一、内力 内力 由于变形引起的物体内部的附加力。
F1 F3 F1 F3
F2
Fn 假想截面
F2
分布内力 Fn
二、截面法
M Q N
X 0, Q 0 Y 0, N P 0 M 0, M Pa 0
O
NP
M Pa
步骤： （1）切开 （2）代力 （3）平衡
之间的矛盾提供力学方面的依据。
§6-2 工程构件的简化模型
一、构件的基本形式
杆件
板件 （壳）
板件 （板）
块件 （或块体）
材料力学主要研究杆件。
二、变形固体及其基本假设 受力后其形状和尺寸发生变化的物体称为 变形固体（简称变形体）。
1. 连续性假设： 认为整个物体所占空间内毫无 空隙地充满物质。
灰口铸铁的显微组织

哈工大《材料力学_-_I_》课程教学大纲

哈工大《材料力学_-_I_》课程教学大纲

《材料力学 - I 》课程教学大纲课程中文名称：材料力学课程英文名称： Mechanics of Materials总学时： 98 讲课学时： 64 习题学时： 8实验学时： 8 上机学时： 18授课对象：机械、建筑、交通、材料、动力、能源等专业本科生先修课程：高等数学，理论力学一、课程教学目的通过本课程学习，要求学生正确理解构件的强度、刚度、稳定性等基本概念以及平衡、几何、物理三类方程在求解力学问题时的重要作用。

能熟练地计算杆件的应力与变形以及分析其强度、刚度与稳定性的能力。

通过实验课教学，培养学生具有一定的创新性、综合性的实验能力。

二、教学内容及基本要求强度、刚度、稳定性；变形固体及其理想化；外力及其分类；变形与位移。

应力状态分析：内力；应力的概念，正应力与切应力；一点的应力状态；切应力互等定律；二向应力状态分析，解析法；二向应力状态分析，图解法；三向应力状态分析；微体平衡。

应变状态分析：应变概念，线应变与切应变；位移与应变的关系；几何方程；应变协调条件，相容方程；平面应变状态分析。

材料的力学性能、应力应变关系：材料的力学性能与基本实验；轴向拉伸和压缩实验；常见工程材料的应力—应变曲线；应力松驰与蠕变；各向同性材料的广义虎克定律；应变能；各向同性材料弹性常数间的关系；各向异性材料应力—应变关系。

轴向拉压：轴向拉压杆的内力；轴向拉压杆的应力；圣文南原理；应力集中；轴向拉压杆的变形，变形能；轴向拉压静不定问题，温度应力，装配应力；构件受慣性力作用时的应力计算。

扭转：扭转杆件的内力；圆轴扭转横截面上切应力；圆轴扭转破坏模式的分析；圆轴扭转变形与变形能；薄壁杆的自由扭转，剪力流。

弯曲：梁的内力，剪力与弯矩；剪力图与弯矩图；载荷、剪力及弯矩间的关系；纯弯曲梁的正应力；有关弯曲的讨论；弯曲切应力；开口薄壁非对称截面梁的弯曲，弯曲中心；梁的弹性弯曲变形，弹性曲线微分方程；直接积分求梁的变形；叠加原理与叠加法求变形；曲杆弯曲。

材料力学(II)第六章PPT课件

材料力学(II)第六章PPT课件

(2 103 N)(3m) 4(2500 108m4 )
6
MPa
材料力学(II)电子教案
动荷载 · 交变应力
30
例题 6-6
2. 求图a梁的最大动应力
C 截面的静位移为
Δst
wC
Pl 3 48EI
(2 103 N)(3m) 48（210 109 Pa)(2 500 108m4 )
0.214 3 103 m 动荷因数为
沿圆环轴线均匀分布的惯性 力的集度（图b）为
qd
1
A
r
w2(D)
2
Arw 2D
2
材料力学(II)电子教案
动荷载 · 交变应力
17
例题 6-4
2. 求sa
由圆环上半部分（图c）的平衡方程得
FNd
1 2
π
0 qd
D d
2
sin
1 2
π Arw 2D D d sin Arw 2D2
022
4
横截面上的正应力为
动荷载 · 交变应力
2
§6-1 概 述
前面各章中研究了在静荷载作用下，构件的强度， 刚度和稳定性问题。本章研究动荷载问题。
动荷载：荷载随时间作急剧的变化，或加载过程 中构件内各质点有较大的加速度。本章研究以下几 种动荷载问题： Ⅰ. 构件作等加速直线运动或等速转动时的动应力
问题； Ⅱ. 构件受冲击荷载作用时的动应力； Ⅲ. 构件在交变应力作用下的疲劳破坏。
Δst
Pl 3 48EI
P/2 2k
0.2143mm
2 103 N 4 300 103 N/m
1.881 0 mm
动荷因数为
Kd 1
1 2 20 5.7 1.881 0

哈工大2010春材料力学11第七章1

哈工大2010春材料力学11第七章1
解： AB 段与BC 段的轴力
FNAB FA10kN F N 3B C ） 变F 形A 能F UB 10kN
UUABUBC2F E N 2A ABAlB2 FE N 2BA CB 2C l
2( 102 00 10 31)029110000110036( 210201003)120 9 2 20 10 00 10 10 63J0.5J11
G T Ip18 08010 7 98 0 1 03 0.430418 00.166/m满足刚度要求。
32
一般来说，200马力的车辆载质量约为8~10吨，车速不大于100公里/小时。
16
第7章 杆件的变形计算
7-3 直接积分法求解梁的弯曲变形 1）梁的变形工程实例 2）梁的挠曲线
17
第7章 杆件的变形计算
a Fb
A
Bx
bF
x 1 xC 2
l
l
aF l
EI1
b 2l
Fx12
C1
EIv16blFx13 C1x1D1
解需：M M 分两21((段xx21积)) 分b l。blFxF2x1(F a(0(xx2x2 1al)a))
边界条件（两端支座）：
x1 0, v1 0 x2 l,v2 0
EI2b 2 F lx2 2F 2(x2a)2C 2
FS A
A为圆环截面面积 3
第六章 杆件横截面上的应力分析
例6-6 图示外伸梁， 截面为22a 工字钢。求梁的最大正应力和最大切应力。
q6kN/m
F30kN
解：1）求支反力
A
C
D
B
2m
3m
3m
2）作内力图
FSmax 17kN Mmax39kNm

哈工大建筑力学课件第6章第68节静定结构的内力计算999欢迎下载.ppt

哈工大建筑力学课件第6章第68节静定结构的内力计算999欢迎下载.ppt

桁架的特点是:
二力杆
(1)所有各结点都是光滑铰结点。
(2)各杆的轴线都是直线并通过铰链中心。
(3)荷载均作用在结点上。
因此杆的横截面上只产生轴力。
符合上述假定条件的桁架称为理想桁架。
桁架结构的优点是：（1）重量轻,受力合理, (2)能承受较大荷载,可做成较大跨度。
27
第七节 静定平面桁架 桁架的杆件布置必须满足几何不变体系的组成规则。 常见的桁架一般是按下列两种方式组成： （1）由一个基本铰接三角形或基础开始,逐次增加二杆结点,组成一个
22
第六节 三铰拱
二、拱和梁的比较·拱的合理轴线 1.拱和梁的比较
(1)在竖向荷载作用下,拱的轴力较大,为主要内力;
拱任一截面K 的弯矩值
M
K
M
0 K
FH yK
,其中水平推力:
FH
M
0 C
f
由于水平推力的存在,三铰拱的弯矩比同跨简支梁相应截面的弯矩值小。
(2)在竖向荷载作用下,梁没有轴力,只承受弯矩和剪力,不如拱受力合理, 拱比梁能更有效地利用材料的抗压性。
得： F13 30kN 由：
Fx 0, F13 cos30o F12 0
得： F12 25.98kN
FBy
31
第七节 静定平面桁架
二、结点法计算桁架内力
[例6-13] 试计算图示桁架各杆内力。
解：
结点2： 由：
Fy 0, 得： F23 0
由： Fx 0,
得： F25 F21 25.98kN
[例 6 – 11]
试绘制图所示三铰拱的内力图。拱的轴线方程为
4f y L2
x(L x)
解: 各截面内力列表如下:
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

120 40 120 40 2 ( ) 30 2 130 MPa, 2 30 MPa 2 2
3 30 MPa ， max
注：此类问题中，受力状态是三向的，不再是平面问题，以（ b ）为例作详细分析： 在图示坐标系下， z 50 MPa, x 20 MPa, y 30 MPa 因为 x y 面内应力情况复杂，先进行分析： 则： x 20 MPa ， y 30 MPa ， xy 40 MPa
50 2 ) 20 2 32 MPa 2
2
（ c ）解析法： 1 0 0 25 25 MPa, 3 25 MPa ，
tg 2 0
2 25 无穷大， 2 0 90, 0 45, max 25 MPa 0
（ d ）解析法： x 40 MPa, y 29 MPa ，
My 140 10 3 9 10 6 79.9 MPa I 15760 10 8 QS 70 103 464 10 6 10 6 20.6 MPa 8 2 Ib 15760 10 1 10
60, 则：
79.9 79.9 cos120 20.6sin120 2.13 MPa 2 2 79.9 sin120 20.6cos120 24.3 MPa 2
1 3 80 MPa 2
式中静矩 S
b h2 ( y 2 ) ,得 2 4
1
x ( x ) 2 xy 2 70.4 MPa, 3 10.4 MPa , 2 0 2 2
点 4： 1 x 120 MPa, 2 3 0
题 6-4 图 6-5 薄壁圆筒扭转——拉伸试验的示意图如图所示。若 P 20kN ， M n 600 N m 且
105 75 105
x y x y cos 210 x sin 210 45 2 2 x y sin150 x cos150 25 3 2
x y sin 210 x cos 210 25 3 2
第六章 应力状态理论和应变状态理论
6-1 构件受力如图所示。①确定危险点的位置。②用单元体表示危险点的应力状态。 （ a ）不计自重时，危险点为任一横截面上的任意一点 （ b ）危险点在 3M 与 2 M 之间的任一截面的边缘上任一 （ c ）危险点在图示三处 （ d ）危险点为任一截面的外边缘上任一点
1 3
40 20 40 20 2 ( ) 40 2 11.2 MPa ， 2 2 40 20 40 20 2 ( ) 40 2 71.2 MPa 2 2 2 ( 40) 4 , 0 3759, max 41.2 MPa 40 20 3
3
tg 2 0
max (
50 2 ) 20 2 32 MPa 2
6-3 在图示应力状态中，试用解析法和图解法求指定斜截面上的应力（应力单位为兆帕） 。 解： （ a ）解析法：
40 0 40 0 cos120 20sin120 27.3 MPa 2 2 40 0 sin120 20cos120 27.3 MPa , 2
50 50 50 50 ( ) 2 20 2 57 MPa ， 3 ( ) 2 20 2 7 MPa 2 2 2 2 2( 20) 4 1 0.8 ，得 0 3840 1920 ， 50 5 2
tg 2 0
max (
主应力计算：
1
79.9 79.9 2 ( ) 20.6 2 84.9 MPa 2 2 79.9 79.9 2 ( ) 20.6 2 5 MPa 2 2
3
tg 2 0
2 20.6 0.516, 0 1356 79.9 80 y 2 80 y 2
6-7 二向应力状态如图所示，应力单元为兆帕。试求主应力并作应力圆。 解： x 80 MPa, 60 ,已知：

cos120 xy sin120 50 MPa

80 y 2
sin120 xy cos120 ,且 xy 0 ,
1 3 50 (50) 50 MPa 2 2
30 20 30 20 2 ( ) 40 2 52.2 MPa, 3 42.2 MPa 2 2
2 50 MPa ， max
（ c ） 1
1 3 47.2 MPa 2
得 1 109.8 MPa, 3 48.8 MPa
题 6-5 图
题 6-6 图
题 6-7 图
6-6 图示简支梁为 36a 工字梁， P 140kN ， l 4m 。 A 点所在截面在集中力 P 的左侧， 且无限接近 P 力作用的截面。试求：① A 点在指定斜截面上的应力；② A 点的主应力及主 平面位置（用单元体表示） 。 解： A 所处截面上弯矩、剪力：
2 x ，则 0 45 x y
题 6-9 图 6-9 试求图示各应力状态的主应力及最大剪应力（应力单位为兆帕） 。 解： （ a ） 1 0 0 50 50 MPa, 3 50 MPa, 2 50 MPa
2
max
（ b ） 1
点 2： x
1 36 MPa, 2 0, 3 36 MPa,
3 10 2 M y 10 10 4 10 60 MPa ， 点 3： x 1 I 3 8 5 10 10 12
QS 120 10 3 46.8 10 6 x 27 MPa 1 I b 5 103 10 8 5 10 2 12
xy 73.2 MPa ， y
所以 x 0, y 61.2 MPa, xy 73.2 MPa 现已知 30,
x 1 x y cos 2 xy sian2 48.1 MPa 2 2

xy x y 1.2, 0 333 sin 2 xy cos 2 10.1 MPa , tg 2 0 x y 2
d 5cm ， 2mm 。试求：① A 点在指定斜截面上的应力；② A 点主应力的大小及方向
（用单元体表示） 。
解： xy
M n M n D 16 M n ，数据代入，得： xy , D d 2 54mm IP IP 2 D 3 (1 4 ) P 2.0 10 4 N 61.2 MPa A (d )
2 20 0.8 50 0
max 32 MPa,1 0 45 2540 得 0 1920 ， 从而 1 57 MPa, 3 7 MPa ，
用图解法，按几何关系可求得 2 0 40, max 32 MPa
（ b ）解析法： 1
tg 2 0
（e）解析法： 1
0 80 0 80 2 ( ) 20 2 4.7 MPa ， 2 2
3
0 80 0 80 2 ( ) 20 2 84.7 MPa 2 2 2 20 0.5 ， 2 0 2634, 0 1317 0 80
联立求解，得到 x y 70 MPa, x 50 MPa 则： 1
70 70 70 70 2 ( ) ( 50) 2 100 MPa 2 2
2
70 70 70 70 2 ( ) ( 50) 2 20 MPa 2 2
3 0 ， tg 2 0
M
查型钢表后， A 点以下表面对中性轴静矩：
1 1 P 140 PL 140 4 140kN .m ， Q 70kN 4 4 2 2
S (13.6 1.58 17.2 1 7.42 12.7) 10 6 464 10 6m 3
正应力、剪应力：
题 6-1 图
题 6-2 图 6-2 已知应力状态如图所示，图中应力单位皆为兆帕。试用解析法及图解法求：①主应力大 小，主平面位置；②在单元体上绘出主平面位置及主应力方向；③最大剪应力。 解： （ a ）解析法 x 50 MPa, y 0, xy 20 MPa, tg 2 0
联立解得： y 40 MPa ，从而 1 80 MPa, 2 40 MPa 注：凡是涉及某斜面上的应力，应从 角定义出发，准确找出 角的值
题 6-8 图 6-8 在通过一点的两个平面上，应力如图所示，单位为兆帕。试求主应力的数值及主平面位 置，并用单元体的草图表示出来。在通过一点的两个平面上，应力如图所示，单位为兆帕。 试求主应力的数值及主平面位置，并用单元体的草图表示出来。 解：取出图示单元体，依题中条件有：
题 6-3 图 6-4 已知矩形截面梁某截面上的弯矩及剪力分别为 M 10kN m ， Q 120kN ，试绘制截 面上 1、2、3、4 各应力点应力状态的单元体，并求其主应力。 解：点 1： x
M 10 1000 120 MPa , 1 2 0, 3 x 120 MPa 1 W 2 6 5 10 10 6 3 Q 3 120 10 3 36 MPa ，处于纯剪状态, 2 bh 2 5 10 10 4

即：
27.3MPa, 27.3MPa
图解法：斜面法线与 x 轴夹角为 60 ，应力图中， 2 60 120 （ b ）解析法：
20 50 30 50 cos 60 (20)sin 60 52.3 MPa 2 2 30 50 sin 60 (20) cos 60 18.7 MPa 2 斜面与 x 轴正向夹角为 30 ，应力图中， 2 30 60 （ c ）解析法： 0 60 0 60 cos90 40sin 90 10 MPa 2 2 0 60 sin 90 40cos90 x (