20170420-实际变压器的等效电路模型
- 格式:pdf
- 大小:127.39 KB
- 文档页数:3


1. 理想变压器理想变压器(ideal transformer)也是一种耦合元件,它是从实际变压器中抽象出来的理想化模型。
理想变压器要同时满足如下三个理想化条件:(1)变压器本身无损耗;这意味着绕制线圈的金属导线无电阻,或者说,绕制线圈的金属导线的导电率为无穷大,其铁芯的导磁率为无穷大。
(2)耦合系数1=k , 121==L L M k 即全耦合;(3)21L L 、和M 均为无限大,但保持n L L =21不变,n 为匝数比。
理想变压器的电路符号如图1所示,图1 理想变压器2. 全耦合变压器全耦合变压器如图2所示,其耦合系数1=k ,但21L L 和是有限值。
由于其耦合系数1=k ,所以全耦合变压器的电压关系与理想变压器的电压关系完全相同。
即2121N N u u =图2 全耦合变压器全耦合变压器初级电流()t i 1由两部分组成,()()()t i t i t i '+=Φ11,一部分()t i Φ称为励磁电流,它是次极开路时电感1L 上的电流,()()ξξΦd u L t i t⎰=111;另一部分()t i '1,()()t i N N t i 2121-=',它与次极电流()t i 2满足理想变压器的电流关系。
根据上述分析可得到图3所示全耦合变压器的模型,图中虚线框部分为理想变压器模型。
u 1-+u 2N 1 N 2图3 全耦合变压器模型3. 实际变压器实际变压器的电感即不能为无限大,耦合系数也往往小于1。
这就是说,它们的磁通除了互磁通外,还有漏磁通,漏磁通所对应的电感称为漏感。
如果从两个线圈的电感中减去各自所具有的漏感,考虑变压器绕组的损耗,我们就可以得到一个利用全耦合变压器表示的变压器的模型,如图4 所示,其中11S M L L L -=称为励磁(或磁化)电感。
图4 实际变压器模型若L M 足够大,则该模型可以等效为图5。
图5。








变压器等效电路变压器是电力系统中常用的重要设备,用于改变交流电压的大小。
在电力系统中,为了进行电路分析和计算,可以采用等效电路模型来表示变压器的工作原理和性能。
本文将介绍变压器等效电路的基本原理和常见模型。
1. 变压器的基本原理变压器是由一个或多个线圈组成的,通过电磁感应的原理来改变电压。
变压器由铁心和绕组组成。
绕组分为初级绕组和次级绕组,通过将电流通过初级绕组,产生的磁场会感应到次级绕组,从而改变输出电压的大小。
变压器的基本原理是基于法拉第电磁感应定律。
2. 变压器的等效电路模型为了简化电路分析和计算,可以采用等效电路模型来代替变压器。
常见的变压器等效电路模型有两种:简化型和精确型。
2.1 简化型等效电路模型简化型等效电路模型将变压器抽象为两个卷绕电感和一个理想变压器,分别代表初级绕组和次级绕组的电感和变压器的变换关系。
在这个模型中,忽略了变压器的内阻和铁芯的磁滞特性。
2.2 精确型等效电路模型精确型等效电路模型更加符合实际变压器的工作原理,考虑了变压器的内阻和铁芯的磁滞特性。
在这个模型中,将变压器抽象为两个卷绕电感、两个卷绕电阻和一个理想变压器。
通过考虑内阻和磁滞特性,可以更加准确地描述变压器的电特性。
3. 变压器等效电路模型的参数无论是简化型还是精确型等效电路模型,都需要知道一些参数来描述变压器的性能。
常见的参数有:3.1 变压器的变比变比是指变压器的输入电压与输出电压的比值。
例如,变比为2:1表示输出电压是输入电压的两倍。
3.2 变压器的电感电感是指变压器的绕组对电流变化的阻抗。
初级绕组和次级绕组的电感分别表示为L1和L2。
3.3 变压器的内阻内阻是指变压器绕组的电阻。
初级绕组和次级绕组的内阻分别表示为R1和R2。
4. 变压器等效电路的应用变压器等效电路模型可以应用于电力系统的分析和计算中。
通过使用等效电路模型,可以更加方便地处理变压器与其他电路元件之间的相互作用。
4.1 电路分析变压器等效电路模型可以与其他电路元件一起进行电路分析,例如,计算电流、电压、功率等参数。
理想变压器的等效电路模型普高(杭州)科技开发有限公司 张兴柱 博士理想变压器,是我们电路中非常熟悉的一个元件。
既然图1是一个实际变压器的物理结构,那么它在理想情况下的等效电路模型又会是怎样呢?假定组成图1磁元件的铁芯具有非常大的导磁率,即μ→无穷,且由外部电流产生的全部磁场均均匀地分布在铁芯内。
(a) 方形铁芯 (b) 环形铁芯图1: 单输出变压器的物理结构因为:→∝µ 所以:01→=cmc A l R µ 所以:02211→+i n i n 或有:2112n n i i −= (1) 再由法拉第电磁感应定律,可得: dt d n v Φ=11 ,dtd n v Φ=22 故有:1212n n v v = (2) 从方程(1)和(2),可得图1变压器在理想情况下的等效电路,如图2(a)所示。
(a) (b)图2: 理想变压器的等效电路模型由于方程(1)中有一个负号,故也可采用图2(b)来表示理想变压器的等效电路模型,它与图2(a)的区别是电流i 2的参考方向,在这种参考方向下,一个理想变压器满足下列电压电流关系:2112//n n i i =1212//n n v v = (3)方程组(3)就是我们在电路中看到的关于变压器元件的电压和电流关系,通过关系,可以看出,由铁芯和两个绕组组成的单输出变压器,其绕组两端的电压之比与绕组的匝数之比成正比,绕组中流过的电流之比与绕组的匝数成反比,如果将两个绕组中的一个看成是输入绕组(或原边绕组),将绕组中的另一个看成是输出绕组(或副边绕组),那么图1的变压器和其等效电路模型就可分别用图3 (a)和图3 (b)来表示,这种变压器的表示方法已被开关电源文献和书籍中所规范,所以本文及后续要介绍的文章,也将以此来表示变压器。
原边或一次侧用下标p 表示,副边或二次侧用下标s 表示。
因此方程组(3)将变成方程组(4):(a) 变压器结构 (b) 等效电路图3: 开关电源中规范化表示的变压器sp p s N N i i //=ps p s N N v v //= (4)当变压器的副边不止一个绕组时,该变压器就是多输出变压器,多输出变压器在理想情况下的电压电流关系可以用方程组(5)表示,其中K 为副边绕组的个数。
变压器的基本方程和等效电路一、变压器的基本方程负载运行时,变压器内部的磁动势、磁通和感应电动势,可列表归纳如下:此外,一次和二次绕组内还有电阻压降i1R1和i2R2。
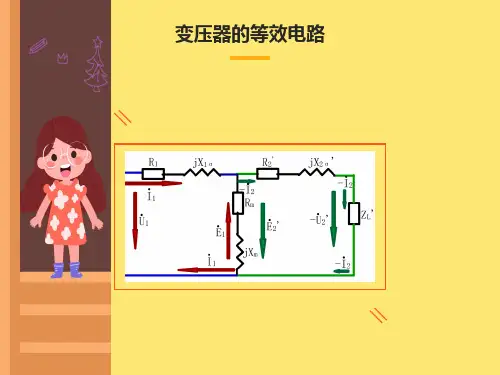
这样,根据基尔霍夫第二定律和图2-8中所示的正方向,即可写出一次和二次侧的电压方程为若一次和二次的电压、电流均随时间正弦变化,则上式可写成相应的复数形式式中,Z1σ和Z2σ分别称为一次和二次绕组的漏阻抗,Z1σ=R1十jX1σ,Z2σ=R2十jX2σ再考虑到式(2—12)和磁动势方程(2—17),可得变压器的基本方程为二、变压器的等效电路在研究变压器的运行问题时,希望有一个既能正确反映变压器内部电磁关系,又便于工程计算的等效电路,来代替具有电路、磁路和电磁感应联系的实际变压器。
下面从变压器的基本方程出发,导出此等效电路。
绕组归算为建立等效电路,除了需要把一次和二次侧漏磁通的效果作为漏抗压降,主磁通和铁心线圈的效果作为激磁阻抗来处理外,还需要进行绕组归算,通常是把二次绕组归算到一次绕组,也就是假想把二次绕组的匝数变换成一次绕组的匝数,而不改变一次和二次绕组原有的电磁关系。
从磁动势平衡关系可知,二次电流对一次侧的影响是通过二次磁动势N2I2起作用,所以只要归算前后二次绕组的磁动势保持不变,一次绕组将从电网吸收同样大小的功率和电流,并有同样大小的功率传递给二次绕组。
归算后.二次侧各物理量的数值称为归算值,用原物理量的符号加“′”来表示。
设二次绕组电流和电动势的归算值为′和′,根据归算前、后二次绕组磁动势不变的原则,可得由此可得二次电流的归算值′为由于归算前、后二次绕组的磁动势未变,因此铁心中的主磁通将保持不变;这样,根据感应电动势与匝数成正比这一关系,便得即二次绕组感应电动势的归算值′为再把二次绕组的电压方程(式(2—22)中的第二式)乘以电压比k,可得式中,R2′和X2σ′分别为二次绕组电阻和漏抗的归算值,R2′=k2R2,X2σ′= k2X2σ;′则是二次电压的归算值,′=k。
(四)、等值电路变压器空载时,从一次绕组看进去的等效阻抗为Z m ,有•-1E =•0I (m m jx r +)=•0I Z m(3-14)Z m =m m jx r +;m r 称励磁电阻,是变压器铁心损耗的等效电阻,即m Fe r I p 20=;m x 为主磁通在铁心中引起的等效电抗,称为励磁电抗,其大小正比于铁心磁路的磁导。
将式(3—14)代入式(3—11)得••-=11E U +•0I Z 1=•0I Z m +•0I Z 1=•0I (Zm +Z 1)相应的等值电路如图3-7所示。
例3-2 一台180kV ·A 的铝线变压器,已知U 1N /U 2N =10000/400V ,Y ,yn 接线,铁心截面积S Fe =160cm 2,铁心中最大磁密度B m =1.445T ,试求一次及二次侧绕组匝数及变压器变比。
图3-7 变压器空载时的等值电路解 变压器变比 k =21U U =253/4003/10000=铁心中磁通 Фm =B m S Fe =1.445 ×160×10-4=231×10—4Wb高压绕组匝数 N 1=1125102315044.431000044.441=-⨯⨯⨯⨯=Φmf U 匝低压绕组匝数 N 2=452511251==k N 匝 第三节 变压器的负载运行当变压器一次绕组加上电源电压•1U ,二次绕组接上负载Z L ,这时变压器就投入了负载运行,如图3—8所示。
图3-8 变压器负载运行 一、变压器负载运行时的电磁关系变压器负载运行时,二次绕组中流过电流•2I ,产生磁动势•2F =•2I N 2,由于二次绕组的磁动势也作用在同一条主磁路上,从而打破了变压器空载运行时的电动势平衡状态。
变压器负载运行时,一次绕组中的电流从空载时的0•I 转变成负载时的•1I 。
变压器负载运行时,铁心中合成磁动势为•2I N 2+•1I N 1,并由此建立主磁通Ф,同时在一次绕组二次绕组中感应电动势•1E 和•2E 。
变压器的3种等效电路变压器是一种常见的电力设备,用于改变交流电的电压。
它可以将高压电能转换为低压电能,或者将低压电能升高为高压电能。
变压器的工作原理是基于电磁感应的原理,通过电磁感应现象来实现电压的转换。
在实际应用中,我们可以用三种等效电路来描述变压器的工作原理。
第一种等效电路是理想变压器等效电路。
理想变压器等效电路是基于理想变压器模型,假设变压器的磁路没有磁阻,变压器的线圈没有电阻,变压器的磁化曲线是线性的。
在理想变压器等效电路中,变压器的主要参数是变比,即输入电压和输出电压之间的比值。
理想变压器等效电路可以用于计算变压器的电压、电流和功率等参数。
但是在实际应用中,变压器的磁路存在磁阻,线圈存在电阻,因此理想变压器等效电路只是一个简化模型,不能完全描述变压器的实际工作情况。
第二种等效电路是短路阻抗等效电路。
短路阻抗等效电路是在理想变压器等效电路的基础上考虑了变压器的短路阻抗。
短路阻抗是指变压器的二次侧短路时,二次侧电压与短路电流之比。
短路阻抗等效电路可以用于计算变压器的短路电流和短路功率损耗等参数。
短路阻抗等效电路在变压器的设计和保护中具有重要的应用价值。
第三种等效电路是电压漏电抗等效电路。
电压漏电抗等效电路是在理想变压器等效电路的基础上考虑了变压器的漏电抗。
漏电抗是指变压器的一次侧电压与一次侧电流之比。
电压漏电抗等效电路可以用于计算变压器的负载电流和负载功率损耗等参数。
电压漏电抗等效电路在变压器的设计和运行中起着重要的作用。
变压器的工作原理可以用三种等效电路来描述。
理想变压器等效电路适用于计算变压器的基本参数,短路阻抗等效电路适用于计算变压器的短路电流和短路功率损耗,电压漏电抗等效电路适用于计算变压器的负载电流和负载功率损耗。
这三种等效电路相互补充,共同构成了对变压器工作原理的全面描述。
在实际应用中,我们可以根据需要选择适合的等效电路进行计算和分析,以确保变压器的安全运行和高效工作。
变压器等效电阻公式推导要推导变压器的等效电阻公式,首先需要了解变压器的基本原理和等效电路模型。
变压器的基本原理是利用电磁感应的原理实现电压的变换。
一个变压器由两个线圈组成,分别为主线圈(Primary coil)和副线圈(Secondary coil)。
当主线圈中通过交流电流时,会在铁芯中产生一个交变磁场,从而感应出在副线圈中产生电动势和电流。
变压器的转变比是指主线圈和副线圈的匝数比,用N1表示主线圈匝数,N2表示副线圈匝数,转变比为N1/N2根据变压器的原理,我们可以将变压器等效为一个理想变压器和一个等效电阻的串联。
这个等效电路模型如下:___________Vp , Primary , VsCoi__________------Rp其中,Vp表示主线圈的电压,Vs表示副线圈的电压,Rp表示变压器的等效电阻。
现在我们来推导变压器等效电阻公式。
根据欧姆定律,在主线圈中的电流Ip为主线圈电压Vp除以主线圈的等效电阻Rp。
即:Ip=Vp/Rp根据变压器的转变比,副线圈中的电压Vs与主线圈中的电压Vp之间有如下的关系:Vs=N2/N1*Vp由于副线圈和主线圈是串联的,所以它们中的电流是相等的,即:Is=Ip将上述等式代入,可以得到:Is=Vp/Rp然后,根据欧姆定律,在副线圈中的电流Is为副线圈电压Vs除以副线圈的等效电阻Rs。
即:Is=Vs/Rs将上述等式代入,可以得到:Vs/Rs=Vp/Rp通过对上述等式进行变形和整理,可以得到变压器的等效电阻公式:Rp=Rs*(N1/N2)²这就是变压器的等效电阻公式,其中Rp表示主线圈的等效电阻,Rs 表示副线圈的等效电阻,N1表示主线圈匝数,N2表示副线圈匝数。
需要说明的是,变压器的等效电阻公式只是一个近似的模型,实际的变压器会受到一些因素的影响,例如涡流损耗和磁滞损耗。
这些因素会使得实际的变压器等效电阻略有偏差。
但是在大多数应用中,可以将变压器近似为一个等效电阻,从而简化电路分析和计算。
实际变压器的等效电路模型
普高(杭州)科技开发有限公司 张兴柱 博士
实际变压器中的铁芯,其导磁率虽然很高,但并不是无限大,另外由外部电流所产生的磁场也并不能全部分布在铁芯内部,而总会有一小部分分布到铁芯周围的空气中。
所以实际的变压器,其等效电路模型与(1)式所表示的会有一些区别。
s p p s N N i i //=p
s p s N N v v //= (1)
下面先来看看在漏磁可以忽略,但铁芯导磁率μ为有限这一情况下的变压器等效电路模型。
图1:变压器结构
当铁芯的导磁率μ有限时,从图1及磁路KVL 定律可得:
s s p p c i N i N R −=Φ
故铁芯中的磁通为:
)(s s p p c
i N i N R −=Φ1 再因为:
dt d N v p p Φ= ,dt
d N v s s Φ= 所以有:
dt
L i N N i dt d R N v p mp s p s p c p p m 2di ][=−= (2) s
p s p N N v v = (3) 其中:m
c p c p mp l A N R N L 22µ==,为变压器原边绕组的电感量,也叫原边的激磁电感。
s p
s p mp i N N i i −=,为变压器原边激磁电感中的电流,称为变压器原边的激磁电流。
观察方程(2)和(3),发现在铁芯导磁率有限且忽略漏磁时的变压器等效电路模型,可用图2表示。
由该等效电路可以看出,此时的变压器模型实际上可以看作是由匝比为Np:Ns 的理想变压器(如红色虚线框所示)和原边激磁电感Lmp 并联所成。
图2: 变压器的实际等效电路(1)
从图2还可以看出,如果变压器的副边开路,即i s =0,那么变压器的原边就等效为一个激磁电感Lmp ,所以变压器原边的激磁电感可以通过电桥进行测试,测试时只要将变压器的副边开路,在变压器的原边测量其电感就可。
事实上,任何变压器在原边都有一个激磁电感。
在开关电源中,其功率变压器所允许的这个激磁电感大小往往与变换器的拓扑有关,在有些拓扑中(如对称驱动的半桥变换器、全桥变换器),其变压器的激磁电感可以非常大,因而在这些拓扑中的变压器可采用高导磁率的铁芯,而且不用加气隙;在有些拓扑中(如反激变换器、不对称半桥变换器),其变压器的激磁电感不能很大,所以在这些拓扑中的变压器要加上一定的气隙或采用导磁率相对低一些的铁芯。
激磁电感虽然是变压器由于铁芯导磁率不是很高而引入的一个等效参数,但在开关电源的不少拓扑中,且可以采用这个激磁电感来实现别的功能,如在不对称半桥变换器和有源去磁正激变换器中,可用这个激磁电感来实现原边MOSFET 的ZVS ;在半桥或全桥LLC 变换器中,可用这个激磁电感来实现谐振工作方式等等。
除了激磁电感外,变压器铁芯中的磁通还会有一小部分漏到铁芯外面,形成所谓的漏磁。
图3 (a)是包含漏磁时的变压器示意图,图3(b)是将原边和副边的漏磁分别用两个小电感表示
v (a) (b)
图3:包含漏磁时的变压器结构示意图
后的变压器等效结构示意图。
由于图3 (b)中的铁芯已经没有漏磁,所以它可用图2的变压器模型等效,因此图3 (b)的变压器,其等效电路模型可用图4表示。
它由理想变压器、原
但由于在推导模型的过程中,采用了B-H的线性近似和铁芯内的均匀磁场分布假定,所以这种变压器的模型也只是一种近似的模型。
包含激磁忽略漏磁的变压器等效电路模型(图2),可在对隔离DC-DC功率变换器进行稳态关系的分析时应用;而变压器的完整等效电路模型(图3),则可在对隔离DC-DC功率变换器进行开关过程波形的分析时应用。