三年级奥数第九讲 剪正方形
- 格式:doc
- 大小:23.50 KB
- 文档页数:2



小学三年级奥数精品讲义目录第一讲加减法的巧算(一)第二讲加减法的巧算(二)第三讲乘法的巧算第四讲配对求和第五讲找简单的数列规律第六讲图形的排列规律第七讲数图形第八讲分类枚举第九讲填符号组算式第十讲填数游戏第十一讲算式谜(一)第十二讲算式谜(二)第十三讲火柴棒游戏(一)第十四讲火柴棒游戏(二)第十五讲从数量的变化中找规律第十六讲数阵中的规律第十七讲时间与日期第十八讲推理第十九讲循环第二十讲最大和最小第二十一讲最短路线第二十二讲图形的分与合第二十三讲格点与面积第二十四讲一笔画第二十五讲移多补少与求平均数第二十六讲上楼梯与植树第二十七讲简单的倍数问题第二十八讲年龄问题第二十九讲鸡兔同笼问题第三十讲盈亏问题第三十一讲还原问题第三十二讲周长的计算第三十三讲等量代换第三十四讲一题多解第三十五讲总复习第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
小熊不禁问:“白兔弟弟,你这么快就算出了答案,有什么决窍吗?”小白兔说:“比如2号选手是93、95、98、96、88、89、87、91、93、91,去掉最高分98,去掉最低分87,剩下的都接近90为基准数,超过90的表示成90+‘零头数’,不足90的表示成90-‘零头数’。
于是(93+95+96+88+89+91+93+91)÷8=90+(3+5+6―2―1+1+3+1)÷8=90+2=92。
你可以试一试。
”小熊照着小白兔说的去做,果然既快又对。

QZ (3)第九讲 找规律求和(一)数列:按照一定次序排列的一列数叫数列。
数列中的每一个数都叫做这个数列的项,各项依次叫做这个数列的第1项、第2项、第3项、……、第n 项、……;我们通常把第1项叫做首项,最后一项叫做末项。
数列的一般形式可以写成: 1a 、2a 、3a 、……、n a 、……;其中n a 是数列的第n 项;这个数列可以简记作}{n a (n 为非0然数)。
等差数列:如果一个数列}{n a ,从第2项起的每一项n a 与它的前一项 1n a - 的差等于同一个数,这个数列就叫做等差数列,这个相同的差叫做等差数列的公差,公差通常用d 表示。
例如:1、3、5、7、9……; d =2。
等差数列的求和公式:和=(首项+末项)×项数÷2。
字母公式: ()12n n S a a n =+⨯÷等差数列的通项公式: 项数=(末项-首项)÷公差+1, 字母公式: ()11n n a a d =-÷+1、在括号里填上合适的数。
(1)4、6、8、10、( )、( )、16; (2)28、( )、20、16、12、8; (3)1、3、5、7、( )、11、13。
2、下面的数列中,哪些是等差数列?若是,请指明公差,若不是,则说明理由。
① 6,10,14,18,22,……,98; ② 1,2,1,2,3,4,5,6; ③ 1,2,4,8,16,32,64; ④ 9,8,7,6,5,4,3,2; ⑤ 3,3,3,3,3,3,3,3; ⑥ 1,0,1,0,1,0,1,03、计算:(1)2 + 4 + 6 + 8 +10 +12 +14(2)5 +10 +15 + 20 + 25 + 30 + 35 + 404、等差数列:5、7、9、11、13、 (95)(1)项数(n)是几?(2)计算这个等差数列的和()S。
n5、等差数列:1、3、5、7、9、……一共有50 项,求末项是多少?6、电影院的第一排有座位35 个,后一排比前一排多6个座位,最后一排有83个座位,那么这个电影院共有多少个座位?7、学校礼堂共有10排座位,已知第一排是15个座位,以后每排比前一排多2个座位,那么共有多少个座位?8、下图三个图形(实线)分别是用4根、10根和16根一样长的小棍围成的。
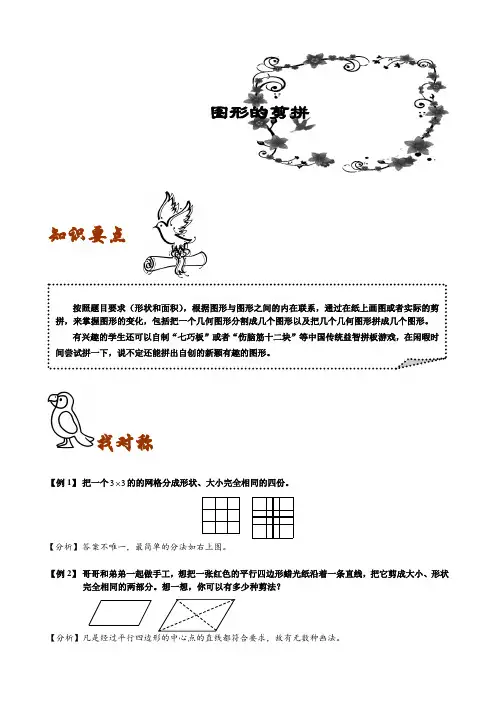
知识要点找对称【例 1】 把一个33 的的网格分成形状、大小完全相同的四份。
【分析】 答案不唯一,最简单的分法如右上图。
【例 2】 哥哥和弟弟一起做手工,想把一张红色的平行四边形蜡光纸沿着一条直线,把它剪成大小、形状完全相同的两部分。
想一想,你可以有多少种剪法?【分析】凡是经过平行四边形的中心点的直线都符合要求,故有无数种画法。
按照题目要求(形状和面积),根据图形与图形之间的内在联系,通过在纸上画图或者实际的剪拼,来掌握图形的变化,包括把一个几何图形分割成几个图形以及把几个几何图形拼成几个图形。
有兴趣的学生还可以自制“七巧板”或者“伤脑筋十二块”等中国传统益智拼板游戏,在闲暇时间尝试拼一下,说不定还能拼出自创的新颖有趣的图形。
图形的剪拼【例 3】要把一个正方形剪成形状相同、大小相等的4个图形,该怎样分?【分析】把一个正方形分成形状、大小相等的4个图形。
可以先把这个正方形分成形状、大小相等的2个图形,然后再把这两个图形继续分成形状、大小相等的4份。
有些方法中我们也可以利用对称图形的特点来分。
本题有很多种解法,这里只列举最常用的几种。
【温馨提示】规则图形或不规则图形的分割成相等的几部分。
第一步:先将原图形平均分成若干个小的规则图形。
第二步:根据题意按要求画分成相等的几部分。
【例 4】你能把下面的图形分割成4个形状相同、大小相等的图形吗?【分析】一共有32个小正方形,分割成4个形状相同、大小相等的图形,每个图形有8小正方形。
答案如图所示。
【例 5】一个长6厘米,宽4厘米的长方形,从中间剪开,如图所示,得到2个大小、形状都相同的长方形,这两个新长方形的周长是多少?【分析】切割开之后,新形成的2个小长方形除了原有长方形的边之外,新产生了两条边,如图虚线所示。
每个新长方形的周长为34214+⨯=()厘米。
两个新长方形的周长是14+14=28厘米或14228⨯=厘米。
图形剪切【例 6】 你能把一个正三角形分成形状相同,大小相等的2个、3个、4个、6个、9个三角形吗?分成分成分成2个三角形分成9个三角形分成6个三角形分成4个三角形分成3个三角形【分析】 通过观察正三角形有3条对称轴,把一个正三角形分成若干份,都可以根据它的对称轴来分。

三年级数学长方形剪正方形题周长练习题1.教室的地板是长方形的,长8米,宽6米。
它的周长是多少?2.将边长20厘米的正方形纸板剪成四个大小相同的小方块。
每个小正方形的周长是多少?3、装裱一幅长50厘米,宽30厘米的画,用一根长150厘米的木条做它的边框够不够?4.从一张长10厘米、宽6厘米的长方形纸上剪出最大的正方形。
这个正方形的周长是多少?5.正方形手帕的边长为2分米。
如果在周围缝上金色蕾丝,那么蕾丝应该有多长?6.一块长方形的菜地,长10米,宽8米。
小方然绕过这片田野的边缘。
他跑了多少米?7.张大爷想用墙围出一个长方形的鸡舍。
如果这个鸡笼长10米,宽8米,需要多少米的塑料网把这个鸡笼围起来?8、一张长方形纸片,长4分米,宽3分米,用这张长方形纸片剪一个最大的正方形,(1)正方形的周长是多少分米?(2)余下部分的周长是多少分米?9.长方形枕套长70厘米,宽50厘米。
你需要在它周围缝多少厘米的花边?10、一个正方形的花坛,边长18米,李叔叔绕着它走一圈,一共走多少米?11.一个长方形的游泳池有40米长。
小刚沿着泳道游了两次泳。
小刚游了几米?12.一根金属丝可以形成一个长8厘米、宽6厘米的长方形。
这根电线有多长?13、一张长32厘米的长方形纸,正好可以剪成两个正方形,你能算出每个正方形的周长吗?14、在一张长是10厘米,宽是8厘米的长方形纸里剪出一个最大的正方形,这个正方形的周长是多少厘米?剩下的图形的周长是多少厘米?15、一个长方形的40米,宽比长少15米,这个长方形的周长是多少米?16、有两个长方形长都是6厘米,宽都是3厘米,(1)把它放入长方形。
这个长方形的周长是多少?(2)把它摆成正方形。
这个正方形的周长是多少?17、用90厘米长的铁丝,做一个边长是14厘米的正方形框子,还余下多少厘米?18.用四个边长为1厘米的小正方形做一个大正方形。
这个大正方形的边长是多少?19.用六个边长为1厘米的小正方形做一个长方形。

剪正方体的剪法正方体是一种非常常见的三维立体几何形体,它的六个面积相等,每个面都是一个正方形。
在制作模型、装饰物品等方面,常常需要对正方体进行剪裁。
因此,学会如何剪正方体是非常有用的。
本文将介绍几种常见的剪正方体的方法。
一、利用模板剪正方体这是最为简单且最为适合初学者的一种剪法。
我们只需要在纸上找到正方体的模板,打印出来,然后用剪刀沿着模板上的实线将正方体剪出来即可。
这种方法需要注意模板的准确性,如果模板不准确,就很难保证剪出来的正方体是完美的。
同时,还需要学会将模板放置在纸的正中心,避免模板歪斜、偏移等不良影响。
二、沿着边缘剪正方体这种方法同样适合初学者,它可以让我们更加清晰地看到正方体的六个面。
具体来说,我们可以利用一把锋利的刀片,沿着正方体的边缘将其剪裁出来。
这种剪法需要我们注意刀片的大小、角度、力度等因素,否则很容易剪出不完美的缺陷或凸出。
三、利用矩形的剪法剪正方体这种方法需要我们将正方体的表面展开为六个矩形,然后在纸上剪下这六个矩形。
具体来说,我们需要将正方体任意一个面竖直放置,将左侧、右侧、下侧三个面按照原始位置展开成一个L形状,然后将上侧面和底侧面展开成两个长方形,再沿着实线将这六个矩形剪下来。
接着,我们需要将这六个矩形按照原来的位置拼合起来,形成一个完整的正方体。
这种方法需要注意矩形的大小、位置、顺序等因素,避免出现矩形宽度不一致、位置歪斜等问题。
四、利用三角形的剪法剪正方体这种方法同样需要将正方体的表面展开为六个形态各异的三角形。
具体来说,我们可以选择将正方体的下侧面竖直放置,再将左侧、右侧、上侧三个面展开成三个形态各异的三角形,接着将正方体顶部和下部的三角形打开,再沿着实线将这六个三角形剪下来。
最后,我们需要将这六个三角形按照原来的位置拼合起来,形成一个完整的正方体。
总之,剪正方体的方法可以有很多种,但无论哪一种方法,都需要我们手法灵活、眼力准确、细心耐心。
只有这样,才能剪出美观完美的正方体。

知识要点找对称【例 1】 把一个33 的的网格分成形状、大小完全相同的四份。
【例 2】 哥哥和弟弟一起做手工,想把一张红色的平行四边形蜡光纸沿着一条直线,把它剪成大小、形状完全相同的两部分。
想一想,你可以有多少种剪法?【例 3】 要把一个正方形剪成形状相同、大小相等的4个图形,该怎样分?图形的剪拼【例4】你能把下面的图形分割成4个形状相同、大小相等的图形吗?【例5】一个长6厘米,宽4厘米的长方形,从中间剪开,如图所示,得到2个大小、形状都相同的长方形,这两个新长方形的周长是多少?图形剪切【例6】你能把一个正三角形分成形状相同,大小相等的2个、3个、4个、6个、9个三角形吗?分成【例7】你能把一个正方形分成6个、7个、8个、9个小正方形吗?(不要求面积相等)【例9】把下图分成5个形状相同、大小相等的图形。
【例10】下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形。
【例11】你能把下面的图形分成7个大小相等的长方形吗?动手画一画。
【例12】如右图所示是由三个正方形组成的图形,请把它分成大小、形状都相同的四个图形。
【例13】阿凡提周游世界,有一天来到一个村庄。
一个地主对他说:“都传说你很聪明,我有一块地,你能把它分成大小相等、形状相同的2份,我就把地送给你。
”聪明的阿凡提不慌不忙,用木棍画了一道线,把这块地分成大小相等、形状相同的2份。
地主傻了眼,只好履行诺言。
后来,阿凡提把地分给了最穷的2户人家,你知道阿凡提是怎么分的吗?图形拼合【例 14】用下面的四块图形能拼成右边的正方形吗?怎样拼?1212124321【例 15】 晚饭后,平平和妈妈玩拼木板游戏。
妈妈拿出5块木板(如下图),要求平平把这5块木板拼成一个正方形。
聪明的平平很快就拼好了。
小朋友,你知道她是怎样拼的吗?试一试。
54321【例 16】用下面的三块图形能拼成右边的正方形吗?怎样拼?121232313321【例 17】下面有5组图形,每个各有5个小正方形,请把这5个图形拼成一个大正方形,可以怎样拼?2354321【例 18】(第九届“中环杯”决赛)“伤脑筋十二块”是中国传统益智拼板游戏。

学而思三年级奥数第九讲长方形与正方形知识点:长方形的面积=长×宽正方形的面积=边长×边长不规则图形面积的计算方法与技巧合理平移、分析、转化等,即转化为标准的图形来进行面积计算。
例1 有一长方形草坪,长31米,宽26米,草坪中间留了1米的路,路把草坪分成4块(如图),求草坪的实有面积是多少?例2如下图,求出阴影部分的面积。
(四角是边长为10厘米的正方形)例3 如图,在一个正方形的水池周围,围绕着宽5米的小花园,小花园的面积为300平方米,水池的面积是多少平方米?例4 如图,求出阴影部分的面积。
(单位:厘米)例5 如图,图中大正方形比小正方形的边长多4厘米,大正方形的面积比小正方形的面积多96平方厘米,大正方形和小正方形的面积各是多少?例6如图,大正方形的面积比小正方形的面积大32平方厘米,求这两个正方形的面积。
(单位:厘米)例7 如图,正方形中套着一个长方形,正方形的边长是12分米,长方形的四个角的顶点恰好把正方形的四条边都分成两段,其中长的一段是短的一段的3倍,这个长方形的面积是多少?例8 用同样大小的长方形小纸片,摆成了如下图的形状,已知小纸片的宽度是12厘米,求阴影部分面积的和。
同步练习1、用长36厘米的一根铁丝围成一个正方形,它的面积是多少?用这根铁丝围成一个长12厘米的长方形,它的面积是多少?2、如图,有一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是一个正方形,周围是花圃,花圃的面积是多少平方米?(单位:米)3、下图是由6个相等的三角形拼成的图形,求这个图形的面积?4、有两个相同的长方形,长13厘米,宽5厘米,如果把它们按如下图叠放在一起,这个图形的面积是多少?5、有一块菜地长16米,宽8米,如下图菜地中间留了2条宽2米的路,把菜地平均分成四块,每一块地的面积是多少?6、一个正方形,如果边长增加2厘米,它的面积增加16平方厘米,求原正方形面积?7、个周长为60分米的长方形,把它的长缩短6分米后,再把它的宽增加6分米,得到的新长方形面积比原来多24平方分米。

正方形的分割知识点总结1. 正方形的基本概念正方形是一种特殊的四边形,具有以下特点:- 四条边相等,且相邻边互相垂直。
- 对角线相等,且互相垂直平分。
- 具有四个直角。
2. 正方形的分割方法正方形的分割方法包括以下几种常见情形:- 将正方形分割为相等的小正方形这是正方形分割问题中最基本的情形。
如果我们希望将一个正方形分割为n个相等的小正方形,则需要满足以下条件:- n必须是一个整数平方;- n的因数必须是奇数;- n的奇数因子必须是一个或多个不同质数的组合。
在实际操作中,我们可以使用方法二或方法三进行分割。
- 将正方形分割为等腰直角三角形如果我们希望将一个正方形分割为若干个等腰直角三角形,则需要满足以下条件:- 三角形的斜边等于正方形的边长;- 三角形的底边是正方形的一条边;- 两个相邻三角形的底边相邻。
- 将正方形分割为菱形如果我们希望将一个正方形分割为若干个菱形,则需要满足以下条件:- 菱形的对角线等于正方形的边长;- 菱形的顶角和顶边与正方形的边平分;- 两个相邻菱形的顶角相邻。
3. 正方形的性质与定理正方形作为一种特殊的四边形,具有一些独特的性质与定理,包括以下几个方面:- 对角线的分割正方形的对角线平分了正方形,并且互相垂直。
定理1:正方形的对角线互相垂直。
证明:设正方形的顶点分别为A、B、C、D,对角线AC与BD相交于O。
由于对角线AC和BD等于,故AO=OC,BO=OD。
又∠AOB=∠BOC=90°,所以△AOB≌△BOC。
同理可得△AOD≌△COD。
故当AC、BD相交于O时,AO=OB=OC=OD,故AC⊥BD。
- 直角三角形的分割正方形的对角线平分了正方形,并且互相垂直。
定理2:正方形的其中一个对角线可以分割正方形为两个相等的直角三角形。
证明:设正方形的顶点分别为A、B、C、D,对角线AC与BD相交于O。
∵AC=BD,∴△AOB≌△BOC(SAS)⇒∠AOB=∠BOC∴△AOB为直角三角形。

第九讲剪正方形
例把一张长18厘米、宽6厘米的长方形,剪成边长为3厘米的小正方形,问能剪多少个这样的小正方形?
画图法:
计算法(一):大长方形的面积÷小正方形的面积=个数
计算法二:
先算横着剪一排能剪几个
再算竖着能剪这样的几排
最后算一共能剪几个
练习
1.把一个长20厘米,宽16厘米的长方形分割成边长为4厘米的小正方形,最
多能分割多少个?
2.一间长16米,宽12米的房间,用边长为4分米的正方形地砖铺地,需工多
少块地砖?
3.一张长26厘米,宽18厘米的长方形彩纸,剪成边长为3厘米的小正方形,
最多能剪多少个完整的小正方形?
4.一张长30厘米,宽25厘米的长方形铁皮,剪成边长为4厘米的小正方形,
最多能剪多少个完整的小正方形?
基础练习
1.把一张长为8,宽为5的长方形木板,锯成一个面积最大的正方形,这个正
方形的面积是多少平方米?剩下木板的面积是多少平方米?
2.一个正方形花坛,花坛的四周种一圈绿篱,绿篱的总长是80米,求花坛的面
积是多少平方米?。
知识要点找对称【例 1】 把一个33 的的网格分成形状、大小完全相同的四份。
【分析】 答案不唯一,最简单的分法如右上图。
【例 2】 哥哥和弟弟一起做手工,想把一张红色的平行四边形蜡光纸沿着一条直线,把它剪成大小、形状完全相同的两部分。
想一想,你可以有多少种剪法?【分析】凡是经过平行四边形的中心点的直线都符合要求,故有无数种画法。
按照题目要求(形状和面积),根据图形与图形之间的内在联系,通过在纸上画图或者实际的剪拼,来掌握图形的变化,包括把一个几何图形分割成几个图形以及把几个几何图形拼成几个图形。
有兴趣的学生还可以自制“七巧板”或者“伤脑筋十二块”等中国传统益智拼板游戏,在闲暇时间尝试拼一下,说不定还能拼出自创的新颖有趣的图形。
图形的剪拼【例 3】要把一个正方形剪成形状相同、大小相等的4个图形,该怎样分?【分析】把一个正方形分成形状、大小相等的4个图形。
可以先把这个正方形分成形状、大小相等的2个图形,然后再把这两个图形继续分成形状、大小相等的4份。
有些方法中我们也可以利用对称图形的特点来分。
本题有很多种解法,这里只列举最常用的几种。
【温馨提示】规则图形或不规则图形的分割成相等的几部分。
第一步:先将原图形平均分成若干个小的规则图形。
第二步:根据题意按要求画分成相等的几部分。
【例 4】你能把下面的图形分割成4个形状相同、大小相等的图形吗?【分析】一共有32个小正方形,分割成4个形状相同、大小相等的图形,每个图形有8小正方形。
答案如图所示。
【例 5】一个长6厘米,宽4厘米的长方形,从中间剪开,如图所示,得到2个大小、形状都相同的长方形,这两个新长方形的周长是多少?【分析】切割开之后,新形成的2个小长方形除了原有长方形的边之外,新产生了两条边,如图虚线所示。
每个新长方形的周长为34214+⨯=()厘米。
两个新长方形的周长是14+14=28厘米或14228⨯=厘米。
图形剪切【例 6】 你能把一个正三角形分成形状相同,大小相等的2个、3个、4个、6个、9个三角形吗?分成分成分成2个三角形分成9个三角形分成6个三角形分成4个三角形分成3个三角形【分析】 通过观察正三角形有3条对称轴,把一个正三角形分成若干份,都可以根据它的对称轴来分。
把一张正方形纸剪一刀数学题全文共四篇示例,供读者参考第一篇示例:把一张正方形纸剪一刀这道数学题看似简单,但其背后蕴含了许多有趣的数学原理和几何概念。
在我们的日常生活中,这样的问题可能并不常见,但通过解决这类问题,我们可以锻炼自己的数学思维和创造力。
本文将通过探讨这个问题的各种解法,让读者对数学的魅力有更深刻的体会。
让我们来思考一下这个问题的基本要求:如何用一刀把一张正方形纸剪成两部分。
一般情况下,我们可能会想到直接将纸对角线剪开,这样就可以得到两个三角形。
如果我们要求分割后的两个部分的形状不同,那么这个问题就有了更多的可能解法。
一种解法是将纸对角线剪开,然后再沿着一条边剪开,这样就可以得到一个三角形和一个梯形。
这种解法利用了对称性,使得两个部分的形状不同。
这也引出了一个有趣的问题:如果将纸对角线剪开后,再将一个三角形割下来,那么余下的部分是什么形状呢?通过解决这个问题,我们可以锻炼自己的几何思维能力和创造力。
在现实生活中,我们也可以将这种抽象的数学问题应用到实际情景中,例如设计艺术品、装饰房间等。
通过不断地挑战自己,我们可以不断地拓展自己的思维边界,发现更多有趣的数学原理和几何概念。
第二篇示例:把一张正方形纸剪一刀的数学题是一道经典的几何题目,通常被用来考察学生对几何形状和面积的理解能力。
这个问题看似简单,但其实蕴含着很深的数学原理。
在这篇文章中,我们将深入探讨如何解答这个问题,并讨论其中的数学原理。
让我们来看一下这个问题的具体描述:有一张正方形纸,给定边长为a。
现在我们要用一刀将这张正方形纸剪成两个部分,要求其中一个部分的面积是另一个部分的2倍。
那么请问,这次剪刀应该怎么切才能满足这个条件呢?这个问题看似简单,但要正确解答却需要一定的数学技巧。
让我们来看一下如何用代数来解决这个问题。
设正方形纸的边长为a,那么正方形的面积就是a²。
我们将这个正方形纸剪成两部分,分别记作x和y,其中x是面积为2y的部分。
剪剪拼拼一位老人在一块正方形的土地上种了四棵树(如图)。
老人有四个儿子,临终前他对四个儿子说:“我死后,你们可以把这块地分成形状、大小完全一样的四块。
每人一块。
这四棵树你们每人必须分一棵,而且不能砍掉也不能移走。
”老人去世后,四个儿子犯愁了:怎样执行父亲的遗嘱呢?图形的剪拼,必须首先根据拼成的图形的特点来考虑如何剪。
比如要拼成正方形,剪出的图形必须有四个相等的边长;如果要拼成长方形,剪开的图形必须有两组相等的对边……当然,图形的剪拼,并不是要你真的用剪刀剪,只要求你把剪的方法通过画线来表示就可以了。
图形的剪拼离不开计算,如通过数数、计算方格数,看能不能拼成正方形或长方形:通过计算,确定把一个图形剪成几等份,每一等份应该占几个方格。
一个图形中有好多方格。
有些方格中写了汉字,使剪开的图形的大小、形状一样,每一部分还要有一个字或两个字。
这种练习,一般先计算每一部分占几格,再把几个字画线隔开,因为两个字不可能在同一块中,再考虑形状来画线。
做这类题目,必须机智、灵活,把图形的特点和计算的结果结合起来考虑。
【例1】把下图剪成四等份,要求剪成的每个小图形形状、大小都一样,应该怎样剪,分析如果将上面的图形向下对折,可以发现上、下两个图形一样,再把右面的图形向左对折,又可以发现左、右两个图形相等。
当然,折的方法不同.答案也不相同。
(备用图)(备用图)〖即学即练1〗下面是一个长方形,请剪出大小相同的长方形和三角形各两个。
(备用图)【例2】如图是一张由20个小正方形组成的硬纸板。
请把它分成四部分,使得每部分都能拼成一个有底无盖的正方体盒子。
在图中用粗线画出分割方法。
(备用图)(备用图)分析一共有20个小正方形,如果分成四部分,每部分都能拼成一个有底无盖的正方体盒子,那么每部分应有5个小正方形。
〖即学即练2〗任意一个三角形,分成三部分后都可以拼成一个长方形,应该怎样分怎样拼?【例 3】用6个拼图,要求边与边完全重合,你能拼出几种图形? 把它们画出来,并指出每个图形中除三角形外,还有哪些基本几何图形。
三年级第一讲:观察法例1:将1~9这九个数字填入图1-6的方框中,使图中所有的不等号均成立。
(适于三年级程度)解:仔细观察图中不等号及方框的排列规律可发现:只有中心的那个方框中的数小于周围的四个数,看来在中心的方框中应填入最小的数1。
再看它周围的方框和不等号,只有左下角的那个方框中的数大于相邻的两个方框中的数,其它方框中的数都是一个比一个大,而且方框中的数是按顺时针方向排列越来越小。
所以,在左下角的那个方框中应填9,在它右邻的方框中应填2,在2右面的方框中填3,在3上面的方框中填4,以后依次填5、6、7、8。
图1-7是填完数字的图形。
例2:从一个长方形上剪去一个角后,它还剩下几个角?(适于三年级程度)解:此题不少学生不加思考就回答:“一个长方形有四个角,剪去一个角剩下三个角。
”我们认真观察一下,从一个长方形的纸上剪去一个角,都怎么剪?都是什么情况?(1)从一个角的顶点向对角的顶点剪去一个角,剩下三个角(图1-8)。
(2)从一个角的顶点向对边上任意一点剪去一个角,剩下四个角(图1-9)。
(3)从一个边上任意一点向邻边上任意一点剪去一个角,剩下五个角(图1-10)。
例3:甲、乙两个人面对面地坐着,两个人中间放着一个三位数。
这个三位数的每个数字都相同,并且两人中一个人看到的这个数比另一个人看到的这个数大一半,这个数是多少?(适于三年级程度)解:首先要确定这个三位数一定是用阿拉伯数字表示的,不然就没法考虑了。
甲看到的数与乙看到的数不同,这就是说,这个三位数正看、倒看都表示数。
在阿拉伯数字中,只有0、1、6、8、9这五个数字正看、倒看都表示数。
这个三位数在正看、倒看时,表示的数值不同,显然这个三位数不能是000,也不能是111和888,只可能是666或999。
如果这个数是666,当其中一个人看到的是666时,另一个人看到的一定是999,999-666=333,333正好是666的一半。
所以这个数是666,也可以是999。
第九讲剪正方形
例把一张长18厘米、宽6厘米的长方形,剪成边长为3厘米的小正方形,问能剪多少个这样的小正方形?
画图法:
计算法(一):大长方形的面积÷小正方形的面积=个数
计算法二:
先算横着剪一排能剪几个
再算竖着能剪这样的几排
最后算一共能剪几个
练习
1.把一个长20厘米,宽16厘米的长方形分割成边长为4厘米的小正方形,最
多能分割多少个?
2.一间长16米,宽12米的房间,用边长为4分米的正方形地砖铺地,需工多
少块地砖?
3.一张长26厘米,宽18厘米的长方形彩纸,剪成边长为3厘米的小正方形,
最多能剪多少个完整的小正方形?
4.一张长30厘米,宽25厘米的长方形铁皮,剪成边长为4厘米的小正方形,
最多能剪多少个完整的小正方形?
基础练习
1.把一张长为8,宽为5的长方形木板,锯成一个面积最大的正方形,这个正
方形的面积是多少平方米?剩下木板的面积是多少平方米?
2.一个正方形花坛,花坛的四周种一圈绿篱,绿篱的总长是80米,求花坛的面
积是多少平方米?。