华侨大学2017年《832信号与系统》考研专业课真题试卷

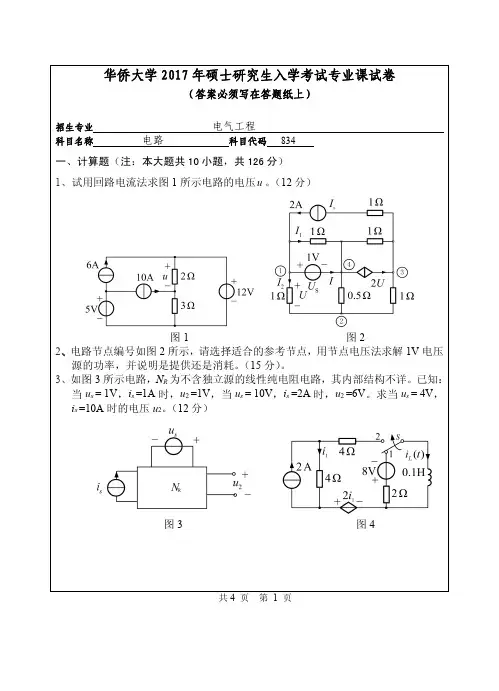
华侨大学2017年硕士研究生入学考试专业课试卷（答案必须写在答题纸上）招生专业电气工程科目名称电路科目代码834一、计算题（注：本大题共10小题，共126分）1、试用回路电流法求图1所示电路的电压u。

（12分）图1图22、电路节点编号如图2所示，请选择适合的参考节点，用节点电压法求解1V电压源的功率，并说明是提供还是消耗。

（15分）。

3、如图3所示电路，N R为不含独立源的线性纯电阻电路，其内部结构不详。

已知：当u s=1V，i s=1A时，u2=1V，当u s=10V，i s=2A时，u2=6V。

求当u s=4V，i s=10A时的电压u2。

（12分）图3图4共4页第1页4、图4所示电路中，开关合在位置1时已达稳定状态，0t =时开关由位置1合向位置2，用三要素法求0t ≥时的()L i t 。

(12分)5、图5所示的正弦稳态电路，已知电源的频率为f 时，电流表A 和A 1的读数分别为0和1A ，若电源的频率变为0.5f 而幅值不变，则电流表A 的读数为多少？(12分)图5图66、已知图6中对称三相电源的相电压为2200A U ︒=∠ ，220120BU ︒=∠- ，220120C U ︒=∠ ，L Z j =Ω，126Z j =+Ω，求1I ，2I ，3I 。

（15分）7、图7所示的电路中，1R =Ω，12L ω=Ω，232L ω=Ω，耦合因数1k =，132Cω=Ω。

求电流1I ，和电压2U 。

（12分）图7图88、已知图8所示二端口的Z 参数矩阵为10 8 5 10Z ⎡⎤=Ω⎢⎥⎣⎦求R 1、R 2、R 3、r 的值。

（12分）共4页第2页9、如图9所示电路原处于零状态。

0t =时刻，开关S 闭合，用运算法（拉普拉斯变换法）求()L i t ，(0)t >。

（12分）图9图1010、图10所示非线性电阻电路中，非线性电阻的伏安特性为32u i i =+，如果()0.1cos V s u t t ω= 时，试用小信号分析法求回路中的电流i 。

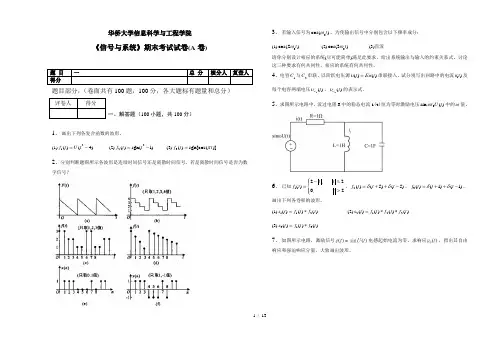
华侨大学信息科学与工程学院《信号与系统》期末考试试卷(A 卷)题 目 一 总 分 核分人 复查人 得分题目部分，（卷面共有100题，100分，各大题标有题量和总分）评卷人 得分一、解答题（100小题，共100分）1．画出下列各复合函数的波形。

(1)21()(4)f t U t =- (2)22()sgn(1)f t t =- (3)3()sgn[cos()]f t t π=2．分别判断题图所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？3．若输入信号为0cos()t ω，为使输出信号中分别包含以下频率成分：(1)0cos(2)t ω (2)0cos(3)t ω (3)直流请你分别设计相应的系统(尽可能简单)满足此要求，给出系统输出与输入的约束关系式。

讨论这三种要求有何共同性、相应的系统有何共同性。

4．电容1C 与2C 串联，以阶跃电压源()()t Eu t υ=串联接入，试分别写出回路中的电流()i t 及每个电容两端电压1()C t υ、2()C t υ的表示式。

5．求图所示电路中，流过电阻R 中的稳态电流i(t)恒为零时激励电压0sin ()t U t ω中的ω值。

6．已知12,2()0,2t t f t t ⎧-≤⎪=⎨>⎪⎩，2()(5)(5)f t t t δδ=++-，3()(1)(1)f t t t δδ=++-，画出下列各卷积的波形。

(1)112()()()s t f t f t =* (2)2122()()()()s t f t f t f t =** (3)313()()()s t f t f t =*7．如图所示电路，激励信号()sin ()e t U t =电感起始电流为零，求响应0()u t ，指出其自由响应和强迫响应分量，大致画出波形。

8．求下图所示系统的单位冲激响应()h t 。

9．已知1()1p H p p-=+，()()te t e U t =-求零状态响应并粗略画出输入输出波形。

2017年招收攻读硕士学位研究生入学考试试题******************************************************************************************** 学科、专业名称：080902电路与系统、080903微电子学与固体电子学、081001 通信与信息系统、081002 信号与信息处理、085208电子与通信工程（专业学位）研究方向：各方向考试科目名称：823 电子技术基础一、简答题（共4小题，每小题5分，共20分）1. 电路如图1所示。

（1）电路实现什么功能？（2）以下三种情况下，输出电压的平均值将分别怎样变化？（a）二极管D1开路；（b）二极管D1短路；（c）负载R L开路。

图12. 现有一个输出电阻为R O的放大电路，正常工作情况下，测得负载开路时的输出电压有效值为U O，接上负载R L后，测得其输出电压有效值为0.5U O，则此电路的输出电阻R O与负载R L之间存在怎样的关系？3. 电路如图2所示。

C1为耦合电容，C2、C3为旁路电容。

其中，T1和T2分别构成了什么接法的放大电路？判断电路是否可能产生正弦波振荡，简述原因。

若能产生正弦波振荡，说明石英晶体在电路中呈容性、感性还是纯阻性？A1u OA27VR1R2R3+15V12V10kΩu IR4200Ω10kΩ10kΩR51kΩD1D2D Z图2 图34. 图3电路中，已知A1、A2均为理想运算放大器，其输出电压的两个极限值为±14V。

说明电路实现什么功能？并画出其电压传输特性曲线。

考试科目：823 电子技术基础共 4 页，第 2 页4. 差分放大电路如图7所示。

设晶体管T 1、T 2特性参数相同，且β＝50，r be ＝1 k Ω。

计算：（1）差模电压放大倍数I2I1Ou u u A ud -=；（2）差模输入电阻R id ； （3）输出电阻R od 。

华侨大学信息科学与工程学院2010-2011学年二学期课程考试试卷答案(A 卷)课程名称：信号与系统 考试时间：120分钟 年级：xxx 级专业： xxx题目部分，（卷面共有50题，100分，各大题标有题量和总分） 一、证明（50小题，共100分）1．证明（1）设12112()nn i i nic c c c H p p p p p λλλλ==+++=++++∑则1()()()i nti i H p t c eu t λδ-==∑又12112()nnii nic c c c H p p p p p ααλαλαλαλ=+=+++=++++++++∑()11()()()()[()()]i nnk ttittiii i H p t c eu t ec eu t H p t e ααλααδδ----==∴+===∑∑（2）设()122()()rrc c c H p p p p λλλ=++++++则112()()()()r kr H p t c c t c t e u t δ-=+++而1221()12()()()()()()()[()()]rrr tr tc c c H p p p p H p t c c t c t eu t eH p t αλαααλαλαλαδδ----+=++++++++++=++=综合（1）（2）故[()()]()()tH p t e H p a t αδδ-=+得证2．证明[()()]()f t t t dt δϕ∞-∞''⎰{}()()[()]()()()()[()()]()[()()()()]()()[()]()()[()]()()()()[()()]()()()()[(f t t d t f t t t t f t t dtt f t t f t t dt f t t d t f t t d t f t t t t f t t dt f t t t t f ϕδϕδδϕδϕϕϕδϕδϕδδϕϕδδ∞∞∞-∞-∞-∞∞-∞∞∞-∞-∞∞∞-∞-∞''''==-'''=-+''=-+''''=--+-⎰⎰⎰⎰⎰{})()]()[()()()()]()[()()()()]t t dtt f t t f t t dt t f t t f t t dtϕδδϕδϕϕ∞∞-∞-∞∞∞-∞-∞''''''''''=+++⎰⎰⎰⎰()[()()2()()()()](0)(0)2(0)(0)(0)(0)t f t t f t t f t t dtf f f δϕϕϕϕϕϕ∞-∞''''''=++''''''=++⎰[(0)()]()[2(0)()]()[(0)()]()f t t dt f t t dt f t t dt δϕδϕδϕ∞∞∞-∞-∞-∞''''''=+-+⎰⎰⎰()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''∴=-+在这里利用了以下公式： ()()()()(0)()()(0)()()(1)(0)k k k t t dt t t dt t t dt ϕδϕδϕϕδϕϕ∞-∞∞-∞∞-∞⎧=⎪⎪''=-⎨⎪⎪=-⎩⎰⎰⎰ 3．证明2()()t t t dt δϕ∞-∞''⎰222()[()]()()()[()]t t d t t t t t t t dt ϕδϕδδϕ∞∞∞-∞-∞-∞''''==-⎰⎰2()2()()()t t t dt t t t dt δϕδϕ∞∞-∞-∞⎡⎤'''=-+⎢⎥⎣⎦⎰⎰22{2()()()[2()]}{()()()[()]}t t t t t t dt t t t t t t dt ϕδδϕδϕδϕ∞∞∞∞-∞-∞-∞-∞''''=----⎰⎰2()[2()]()2()()2()()()t t dt t t t dt t t t dt t t t dt δϕδϕδϕδϕ∞∞∞∞-∞-∞-∞-∞''''=+++⎰⎰⎰⎰2(0)[2()]()t t dt ϕδϕ∞-∞==⎰2()2()t t t δδ''∴=32()[()][2()]t t t t t t t δδδ''''===0证明()()(1)!()n n n t t n t δδ=-用归纳法()()(1)0!()t t t t δδδ==-()()()[()]()()()[()]t t t dt t t d t t t t t t t dt δϕϕδϕδδϕ∞∞∞∞-∞-∞-∞-∞''==-⎰⎰⎰()()()()()()t t t dt t t dt t t dt ϕδϕδϕδ∞∞∞-∞-∞-∞'=---⎰⎰⎰22()()(1)1!()()2()(1)2!()t t t t t t t t δδδδδδ'∴=-=-''==-⋅又33()()()[()]t t t dt t t d t δδϕδ∞∞-∞-∞'''''=⎰⎰33()()()[()]t t t t t t dt ϕδδϕ∞∞-∞-∞'''''=-⎰2()[3()()]t t t t t dt δϕϕ∞3-∞'''=-+⎰233()()()()t t t dt t t t dt δϕδϕ∞∞-∞-∞'''''=--⎰⎰(3)2()()t t dt δϕ∞-∞=-⋅⎰3()(32)()(1)3!()t t t t δδδ3'''∴=-⨯=-由归纳法可得()()(1)!()nn nt t t δδ=-4．证明：()()(3)tk r t e u t t k δ+∞-=-∞=*-∑其波形如下图所示。

2017年华侨大学考研试题832信号与系统
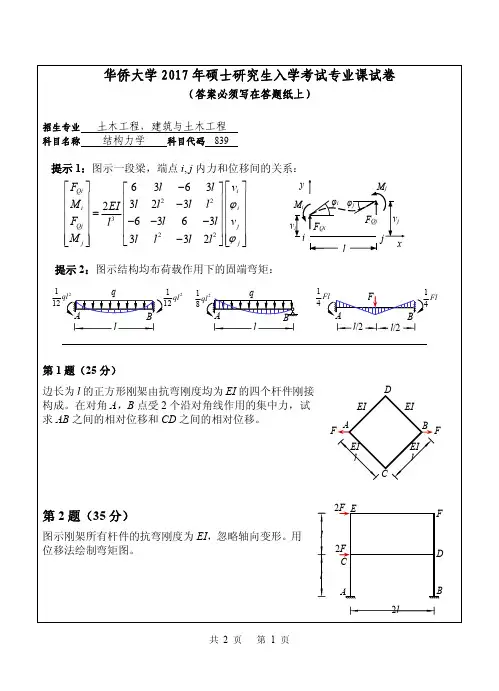
华侨大学2017年硕士研究生入学考试专业课试卷
（答案必须写在答题纸上）
招生专业
信息与通信工程科目名称信号与系统科目代码832第一部分、简答题（共60分）
1、请填入正确答案（共30分，每小题各3分）：（1）积分()()23121t t t dt δ∞
-∞-+-+?=。

（2）信号()0.20.3j k j k x k e e ππ-=+的周期为。

（3）已知冲激序列()()T n t t nT δδ∞
=-∞
=-∑，其三角函数形式的傅里叶级数
为。

（4）设()f t 的频谱函数为()F j ω，则32t f ??-+
的频谱函数等于。

（5）若()()()y t x t h t =*,则()2y t =。

（6）信号()()0f t t d λελλ∞
=-?的单边拉普拉斯变换为。

（7）设()f t 为一有限带宽信号，频带宽度为2k Hz ，试求()2f t 的奈奎斯特抽样率N f =，抽样间隔N T =。

（8）离散信号()x k 的单边Z 变换()21216X z z z z --=+++，()x k 用单位脉冲序列表示，则()x k =。

（9）信号()()()211f k k k ε=--的Z 变换式()F z =。

（10）已知()010 , 1 , 2 , 3 , 4k f k =↑??=，()021 , 1 , 1 , 1 , 0 ,0k f k =↑??=
，则卷积()()12f k f k *=。

共5页第1页。