专题08 立体几何第二十讲 空间点线面的位置关系(原卷版)

空间点、直线、平面之间的位置关系知识梳理： 1．平面的基本性质公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在这个平面内．(公理1的作用是判断直线是否在某个平面内；)公理2：经过不在同一条直线上的三点，有且只有一个平面．(即可以确定一个平面) (公理2及其推论给出了确定一个平面或判断“直线共面”的方法；)公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条通过这个点的公共直线．(公理3的作用是如何寻找两相交平面的交线以及证明“线共点”的理论依据；) 2．直线与直线的位置关系(1)位置关系的分类⎩⎨⎧共面直线⎩⎪⎨⎪⎧平行相交异面直线：不同在任何一个平面内(2)异面直线所成的角①定义：设a ，b 是两条异面直线，经过空间任一点O 作直线a ′∥a ，b ′∥b ，把a ′与b ′所成的锐角(或直角)叫作异面直线a ，b 所成的角(或夹角)．②范围：⎝⎛⎦⎤0，π2. 3．直线与平面平行的判定定理和性质定理∵∴∵＝∴2．如果一条直线和一个平面平行，那么这条直线和这个平面的任意一条直线都平行吗？4．平面与平面平行的判定定理和性质定理∵＝ 提示：不一定．可能平行，也可能相交．4．如果两个平面平行，则一个平面内的直线与另一个平面有什么位置关系？ 5．平行公理平行于同一条直线的两条直线互相平行． 6．定理空间中如果两个角的两边分别对应平行，那么这两个角相等或互补． 突破点 一1.点共线问题,一般转化为证明这些点的某两个平面点公共点,再根据公理3（如果两个不重合的平面有一个公共点，那么它们有且只有一条通过这个点的公共直线．）证明这些点都在这两个平面的交线上.2.线共点问题 ，证明空间三线共点问题，先证明两条直线交于一点，再证明第三条直线也经过这点，把问题转化为证明点再直线上。

3.证明点线共面的常用方法：①纳入平面法：先确定一个平面，再证明有关点、线在此平面内。

②辅助平面法：先证明有关的点、线确定平面α，再证明其他元素确定平面β，最后证明平面α、β重合。

空间向量点线面的位置关系在三维空间中，点、线和面是基本的几何要素。

它们的位置关系在数学和几何学中扮演着重要的角色。

本文将探讨空间向量中点、线和面之间的不同位置关系及其特点。

一、点和线的位置关系在三维空间中，点和线的位置关系主要有以下几种情况。

1. 点在线上：如果一个点位于一条直线上，那么这个点与直线上的任意两点构成的向量都是共线的。

换句话说，点和线的向量共线。

2. 点在线的延长线上：点也可以位于一条线的延长线上，这时点与线上的任意两点构成的向量也是共线的。

3. 点与线相交：在三维空间中，点还可以与一条直线相交。

这时，点与线上的任意两点构成的向量不再共线。

4. 点与线平行：若一点与直线平行，则该点与直线上的任意两点构成的向量平行。

但是，点与线平行并不意味着点在线的延长线上。

二、点和面的位置关系点和面的位置关系也有几种情况，如下所示。

1. 点在面上：如果一个点位于一个平面上，那么这个点与平面上的任意三个点构成的向量都在同一个平面内。

2. 点在面的延长线上：点也可以位于一个平面的延长线上，这时点与平面上的任意三个点构成的向量仍在同一个平面内。

3. 点在平面内但不在平面上：有时，一个点位于一个平面内部但不在平面上。

这时，点与平面上的任意三个点构成的向量不在同一个平面内。

4. 点与平面相交：在三维空间中，点还可以与一个平面相交。

这时，点与平面上的任意三个点构成的向量不在同一个平面内。

三、线和面的位置关系线和面的位置关系主要有以下几种情况。

1. 线在平面上：如果一条直线位于一个平面上，那么直线上的任意两点构成的向量都在同一个平面内。

2. 线与平面相交于一点：一个直线也可以与一个平面相交于一点。

这时，直线上的任意两点构成的向量不在同一个平面内。

3. 线与平面平行：若一条直线与一个平面平行，则直线上的任意两点构成的向量与平面内的向量平行。

但是，直线与平面平行并不意味着直线在平面上。

4. 线在平面的延长线上：一条直线还可以位于一个平面的延长线上，这时直线上的任意两点构成的向量仍在同一个平面内。

专题08 立体几何第二十讲空间点线面的位置关系2019年1.(2019全国III文8）如图，点N为正方形ABCD的中心，△ECD为正三角形，平面ECD⊥平面ABCD，M是线段ED的中点，则A．BM=EN，且直线BM、EN是相交直线B．BM≠EN，且直线BM，EN是相交直线C．BM=EN，且直线BM、EN是异面直线D．BM≠EN，且直线BM，EN是异面直线2.（2019全国1文19）如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点.（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离．3.（2019全国II文7）设α，β为两个平面，则α∥β的充要条件是A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面4.（2019北京文13）已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．5.（2019江苏16）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ． 求证：（1）A 1B 1∥平面DEC 1； （2）BE ⊥C 1E ．6.（2019全国II 文17）如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1.（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，AB =3，求四棱锥11E BB C C -的体积．7.(2019全国III 文19）图1是由矩形ADEB 、Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°.将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2.（1）证明图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ； （2）求图2中的四边形ACGD 的面积.8.（2019北京文18）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底部ABCD 为菱形，E 为CD 的中点． （Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）若∠ABC =60°，求证：平面PAB ⊥平面PAE ；（Ⅲ）棱PB 上是否存在点F ，使得CF ∥平面PAE ？说明理由．9.（2019天津文17）如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD 为等边三角形，平面PAC ⊥平面PCD ，PA CD ⊥，2CD =，3AD =，（Ⅰ）设G H ，分别为PB AC ，的中点，求证：GH ∥平面PAD ； （Ⅱ）求证：PA ⊥平面PCD ；（Ⅲ）求直线AD 与平面PAC 所成角的正弦值.10.（2019江苏16）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ． 求证：（1）A 1B 1∥平面DEC 1； （2）BE ⊥C 1E ．11.（2019浙江19）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点. （1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.12.（2019北京文18）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底部ABCD 为菱形，E 为CD 的中点． （Ⅰ）求证：BD ⊥平面PAC ；（Ⅱ）若∠ABC =60°，求证：平面PAB ⊥平面PAE ；（Ⅲ）棱PB 上是否存在点F ，使得CF ∥平面PAE ？说明理由．13.（2019全国1文16）已知∠ACB=90°，P 为平面ABC 外一点，PC =2，点P 到∠ACB 两边AC ，BC 的距离均为3，那么P 到平面ABC 的距离为___________．14.（2019全国1文19）如图，直四棱柱ABCD –A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点.（1）证明：MN ∥平面C 1DE ； （2）求点C 到平面C 1DE 的距离．15.（2019天津文17）如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD 为等边三角形，平面PAC ⊥平面PCD ，PA CD ⊥，2CD =，3AD =，（Ⅰ）设G H ，分别为PB AC ，的中点，求证：GH ∥平面PAD ；（Ⅱ）求证：PA ⊥平面PCD ；（Ⅲ）求直线AD 与平面PAC 所成角的正弦值.16.（2019浙江8）设三棱锥V -ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点），记直线PB 与直线AC 所成角为α，直线PB 与平面ABC 所成角为β，二面角P -AC -B 的平面角为γ，则 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β17.（2019浙江19）如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A AC AC E F ∠=︒==分别是AC ，A 1B 1的中点. （1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.2015-2018年一、选择题1．(2018全国卷Ⅱ)在正方体1111-ABCD A B C D 中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为A ．22B ．32C ．52D ．722．(2018浙江)已知平面α，直线m ，n 满足m α⊄，n α⊂，则“m ∥n ”是“m ∥α”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．（2017新课标Ⅰ）如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直接AB 与平面MNQ 不平行的是4．（2017新课标Ⅲ）在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥5．（2016年全国I 卷）平面α过正方体ABCDA 1B 1C 1D 1的顶点A ，α∥平面CB 1D 1，α平面ABCD =m ，α平面ABB 1 A 1=n ，则m ，n 所成角的正弦值为A 3B ．22 C3 D ．136．（2016年浙江）已知互相垂直的平面αβ， 交于直线l ．若直线m ，n 满足m ∥α，n ⊥β，则 A ．m ∥l B ．m ∥nC ．n ⊥lD ．m ⊥n三、解答题7．（2018全国卷Ⅱ）如图，在三棱锥-P ABC 中，22==AB BC4====PA PB PC AC ，O 为AC 的中点．O MPCBA(1)证明：PO ⊥平面ABC ；(2)若点M 在棱BC 上，且2=MC MB ，求点C 到平面POM 的距离．8．（2018全国卷Ⅲ）如图，矩形ABCD 所在平面与半圆弧CD 所在平面垂直，M 是CD 上异于C ，D 的点．(1)证明：平面AMD ⊥平面BMC ；(2)在线段AM 上是否存在点P ，使得MC ∥平面PBD ？说明理由．ABCD M9（2018北京）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA =PD ，E ，F 分别为AD ，PB 的中点．PFEDCBA(1)求证：PE ⊥BC ；(2)求证：平面PAB ⊥平面PCD ； (3)求证：EF ∥平面PCD ．10．（2018天津）如图，在四面体ABCD 中，ABC ∆是等边三角形，平面ABC ⊥平面ABD ，点M 为棱AB 的中点，2AB =，AD =90BAD ∠=．(1)求证：AD ⊥BC ；(2)求异面直线BC 与MD 所成角的余弦值； (3)求直线CD 与平面ABD 所成角的正弦值．M A BCD11．(2018江苏)在平行六面体1111ABCD A B C D -中，1AA AB =，111AB B C ⊥．D 11B 1A 1DCBA求证：(1)AB ∥平面11A B C ；(2)平面11ABB A ⊥平面1A BC ．12．(2018浙江)如图，已知多面体111ABCA B C ，1A A ，1B B ，1C C 均垂直于平面ABC ，120ABC ∠=，14A A =，11C C =，12AB BC B B ===．C 1B 1A 1CBA(1)证明：1AB ⊥平面111A B C ；(2)求直线1AC 与平面1ABB 所成的角的正弦值．13．（2017新课标Ⅱ）如图，四棱锥P ABCD -中，侧面PAD 为等边三角形且垂直于底面ABCD ，12AB BC AD ==，90BAD ABC ∠=∠=． DCBA P(1)证明：直线BC ∥平面PAD ；(2)若PCD ∆的面积为P ABCD -的体积。

点线面的位置关系在几何学中，点、线和面是基本的几何元素。

它们之间的位置关系是我们研究几何学的基础。

本文将详细探讨点线面之间的位置关系，并从几何学的角度解释这些关系。

一、点与线的位置关系在平面几何中，点是最简单的几何元素。

它没有长度、面积和方向。

而线则是由无数个点组成的，具有长度但没有宽度。

点与线之间有以下几种位置关系：1. 点在线上：当一个点正好在一条线上时，我们说这个点在这条线上。

这意味着点与线上的所有点重合。

2. 点在线的两侧：如果一个点不在一条线上，并且离线的两侧距离都不为零，则我们说这个点在这条线的两侧。

3. 点在线的延长线上：如果一个点不在一条线上，并且它在这条线的延长线上，则我们说这个点在线的延长线上。

延长线是指将线无限延长的线段。

二、点与面的位置关系与点与线的位置关系类似，点与面之间也有几种不同的位置关系：1. 点在面上：当一个点正好在一个平面上时，我们说这个点在这个平面上。

这意味着点与面上的所有点重合。

2. 点在面的上方或下方：如果一个点不在一个平面上，并且它在这个平面的上方或下方，则我们说这个点在这个平面的上方或下方。

3. 点在面的边界上：如果一个点在一个平面的边界上，则我们说这个点在这个平面的边界上。

三、线与面的位置关系线与面之间的位置关系也是几何学中重要的内容，它们之间有以下几种位置关系：1. 线在面上：当一条线正好在一个平面上时，我们说这条线在这个平面上。

这意味着线上的所有点都在这个平面上。

2. 线与面相交：如果一条线与平面有一个或多个公共点，则我们说这条线与这个平面相交。

3. 线平行于面：如果一条线与平面上的所有点都不相交，则我们说这条线平行于这个平面。

4. 线垂直于面：如果一条线与平面的交点为一点，并且与平面上的所有其他点都垂直，则我们说这条线垂直于这个平面。

综上所述，点线面之间的位置关系是几何学的重要内容，它们的不同位置关系可以通过几何学的方法进行判断和描述。

通过研究这些位置关系，我们可以更好地理解几何学的基本概念，并应用于实际生活和工作中。

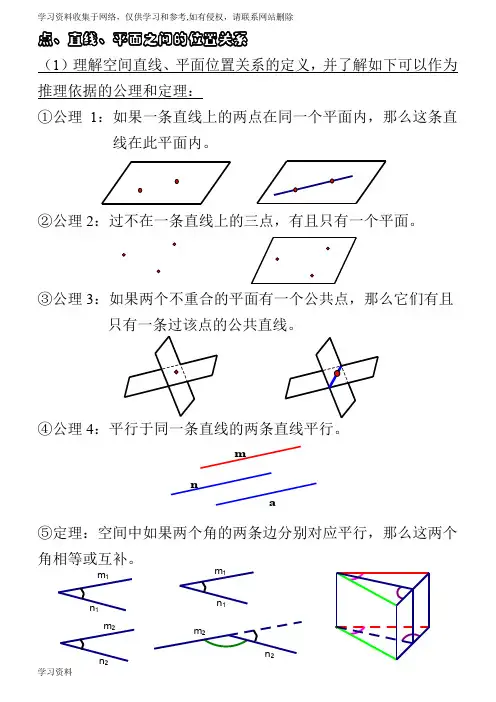
点、直线、平面之间的位置关系
（1）理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理：
①公理1：如果一条直线上的两点在同一个平面内，那么这条直
线在此平面内。

②公理2：过不在一条直线上的三点，有且只有一个平面。

③公理3：如果两个不重合的平面有一个公共点，那么它们有且
只有一条过该点的公共直线。

④公理4：平行于同一条直线的两条直线平行。

⑤定理：空间中如果两个角的两条边分别对应平行，那么这两个角相等或互补。

n m a m 1n 1m 2n 2m 1n 1
m 2n
2
（2）以立体几何的上述定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定定理。

理解以下判定定理：
①平面外一条直线与此平面内的一条直线平行，则该直线与此
平面平行。

②一个平面内的两条相交直线与另一个平面平行，则这两个平
面平行。

③一条直线与一个平面内的两条相交直线垂直，则该直线与此
平面垂直。

④一个平面过另一个平面的垂线，则两个平面垂直。

理解以下性质定理，并能够证明：
①如果一条直线与一个平面平行，那么过该直线的任一个平面与
此平面的交线和该直线平行。

②两个平面平行，则任意一个平面与这两个平面相交所得的交线相互平行。

③垂直于同一个平面的两条直线平行。

④两个平面垂直，则一个平面内垂直于交线的直线与另一个平
面垂直。

(3)能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题。

点线面的位置关系知识点在几何学中，点、线和面是三个基本的几何概念，它们之间存在着一系列的位置关系。

这些位置关系的理解对于解决几何问题以及应用几何知识有着重要的意义。

本文将介绍点线面的位置关系的几个重要知识点。

一、点与直线的位置关系1. 在直线上：当一个点恰好位于一条直线上时，我们可以说这个点在直线上。

例如，点A在直线AB上。

2. 在直线的两侧：如果一个点既不在直线上，也不在直线的延长线上，我们可以说这个点在直线的两侧。

例如，点C在直线AB的两侧。

3. 在直线的延长线上：如果一个点不在直线上，但位于直线的延长线上，我们可以说这个点在直线的延长线上。

例如，点D在直线AB的延长线上。

4. 平行于直线：如果一条直线与给定直线没有任何交点，我们可以说这条直线平行于给定直线。

例如，直线CD平行于直线AB。

二、点与平面的位置关系1. 在平面上：当一个点位于一个平面内部时，我们可以说这个点在平面上。

例如，点A在平面P上。

2. 不在平面上：如果一个点既不在平面上，也不在平面的延长线上，我们可以说这个点不在平面上。

例如，点B不在平面P上。

3. 在平面的延长线上：如果一个点不在平面上，但位于平面的延长线上，我们可以说这个点在平面的延长线上。

例如，点C在平面P的延长线上。

4. 垂直于平面：如果一条直线与给定平面的任意一条线都垂直，我们可以说这条直线垂直于给定平面。

例如，直线EF垂直于平面P。

三、直线与平面的位置关系1. 相交于一点：当一条直线与平面有且仅有一个交点时，我们可以说这条直线与平面相交于一点。

例如，直线L与平面P相交于点A。

2. 平行于平面：如果一条直线与给定平面的任意一条线都平行，我们可以说这条直线平行于给定平面。

例如，直线M平行于平面P。

3. 包含于平面：当一条直线上的所有点都位于给定平面上时，我们可以说这条直线被包含于给定平面中。

例如，直线N被包含于平面P 中。

4. 相交于一条线：当一条直线与平面有无穷多个交点时，我们可以说这条直线与平面相交于一条线。

CBAl 3l 2l 1立体几何之点线面之间的位置关系考试要求：1、 熟练掌握点、线、面的概念；2、 掌握点、线、面的位置关系，以及判定和证明过程；3、掌握点、线、面垂直、平行的性质知识网络：知识要点：1、公理（1）公理 1：对直线 a 和平面α，若点 A 、B ∈a , A 、B ∈α，则（2）公理 2：若两个平面α、β有一个公共点P ，则α、β有且只有一条过点P 的公共直线 a（3）公理 3： 不共线的三点可确定一个平面 推论：① 一条直线和其外一点可确定一个平面②两条相交直线可确定一个平面 ③两条平行直线可确定一个平面（4）公理 4：平行于同一条直线的两条直线平行等角定理：如果一个角的两边和另一个角的两边分别平行且方向相同，那么这两个角相等．2、空间两条不重合的直线有三种位置关系：相交、平行、异面3、异面直线所成角θ的范围是 00<θ≤900例1、已知直线1l 、2l 和3l 两两相交，且三线不共点. 求证：直线1l 、2l 和3l 在同一平面上.空间图形的关系空间基本关系与公理 平行关系 垂直关系 公理 点、线、面的位置关系 判定 性质 应用 应用 性质 判定例2、三个平面将空间分成k 个部分,求k 的可能取值. 分析: 可以根据三个平面的位置情况分类讨论，按条件可将三个平面位置情况分为5种:（1）三个平面相互平行（2）两个平面相互平行且与第三个平面相交 （3）三个平面两两相交且交线重合 （4）三个平面两两相交且交线平行 （5）三个平面两两相交且交线共点例3、已知棱长为a 的正方体中，M 、N 分别为CD 、AD 中点。

求证：四边形是梯形。

例4、如图，A 是平面BCD 外的一点,G H 分别是,ABC ACD ∆∆的重心，求证：//GH BD ．例5、如图，已知不共面的直线,,a b c 相交于O 点，,M P 是直线a 上的两点，,N Q 分别是,b c 上的一点求证：MN 和PQ 是异面直线N MH G D C B Aαc b a Q P N MO例6、已知正方体ABCD －A 1B 1C 1D 1的棱长为a ，则棱A 1B 1所在直线与面对角线BC 1所在直线间的距离是直线与平面平行、平面与平面平行1、 直线与平面的位置关系：平行、相交、在平面内2、 直线和平面平行的判定及性质（1） 判定 如果平面外一条直线和这个平面内的一条直线平行，那么这条直线和这个平面平行。

点线面的位置关系点、线、面是几何学中的基本概念，它们之间存在着重要的位置关系。

通过研究它们的位置关系，我们可以更好地理解和应用几何学知识。

本文将详细探讨点、线、面的位置关系，并对其应用进行讨论。

一、点、线、面的定义1. 点：几何学中最基本的元素，没有大小和形状，只有位置。

可以用坐标表示，例如(x, y)。

2. 线：由无数个点按照一定规律连接而成，具有长度但没有宽度。

可以用两个点的坐标表示，例如(1, 2)和(3, 4)之间的线段。

3. 面：由无数个线按照一定规律连接而成，具有长度和宽度。

可以用多边形的边界来表示，例如三角形、矩形等。

二、点、线、面的位置关系1. 点与线的位置关系：a. 在线上：如果一个点恰好在一条线上，则称该点在线上。

b. 在线内：如果一个点在一条线的两个端点之间，则称该点在线内。

c. 在线外：如果一个点既不在线上，也不在线内，则称该点在线外。

2. 点与面的位置关系：a. 在面上：如果一个点恰好在一个面上，则称该点在面上。

b. 在面内：如果一个点在一个面的边界之内，则称该点在面内。

c. 在面外：如果一个点既不在面上，也不在面内，则称该点在面外。

3. 线与线的位置关系：a. 相交：如果两条线有公共的一个或多个点，则称这两条线相交。

b. 平行：如果两条线的方向相同，但没有公共的点，则称这两条线平行。

c. 重合：如果两条线有无数个公共的点，则称这两条线重合。

4. 线与面的位置关系：a. 相交：如果一条线与一个面有公共的一个或多个点，则称这条线与该面相交。

b. 平行：如果一条线的方向与一个面平行，且线上没有与该面有公共的点，则称这条线与该面平行。

c. 重合：如果一条线与一个面重合，即线上的所有点都在该面上，则称这条线与该面重合。

5. 面与面的位置关系：a. 相交：如果两个面有公共的一条或多条线段，则称这两个面相交。

b. 平行：如果两个面的法向量平行，则称这两个面平行。

c. 重合：如果两个面有无数个公共的点，则称这两个面重合。

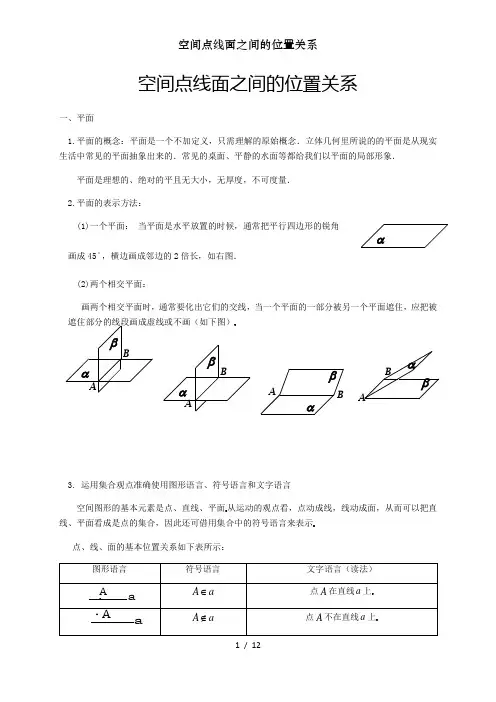
立体几何初步（空间点、线、面的位置关系）一、平面⑴ 平面的概念：（描述性）（描述性）⑵平面的表示：通常用希腊字母a 、β、g 表示，如平面a （通常写在一个锐角内）；也可以用两个相对顶点的字母来表示，如平面A C ⑶点与平面的关系：点A 在平面a 内，记作A a Î；点A 不在平面a 内，记作A a Ï点与直线的关系：点A 的直线l 上，记作A Îl ； 点A 不在直线l 上，记作A Ïl直线与平面的关系：直线l 在平面a 内，记作l Ìa ；直线l 不在平面a 内，记作l Ëa 。

二、几个公理公理1：如果一条直线的两点在一个平面内，那么这条直线上所有的点都在这个平面内。

（即直线在平面内，或者平面经过直线）或者平面经过直线）符号语言：,,,A l B l A B l a a a ÎÎÎÎÞÌ公理2：经过不在同一条直线上的三点，有且只有一个平面。

：经过不在同一条直线上的三点，有且只有一个平面。

推论：推论：⑴一条直线和直线外一点确定一平面；⑴一条直线和直线外一点确定一平面；⑵两条相交直线确定一平面；⑵两条相交直线确定一平面；⑶两条平行直线确定一平面。

⑶两条平行直线确定一平面。

公理3：如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线那么它们有且只有一条过该点的公共直线符号语言：l P l B A B A P Î=ÇÞÇÎ,公理3的作用：①它是判定两个平面相交的方法。

①它是判定两个平面相交的方法。

②它说明两个平面的交线与两个平面公共点之间的关系：交线必过公共点。

②它说明两个平面的交线与两个平面公共点之间的关系：交线必过公共点。

③它可以判断点在直线上，即证若干个点共线的重要依据。

③它可以判断点在直线上，即证若干个点共线的重要依据。

2.1空间中点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系 1、教学重点和难点重点：空间直线、平面的位置关系。

难点：三种语言（文字语言、图形语言、符号语言）的转换 2、三个公理：（1）公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内符号表示为A ∈LB ∈L => L α ，A ∈α ，B ∈α公理1作用：判断直线是否在平面内（2）公理2：过不在一条直线上的三点，有且只有一个平面。

符号表示为：A 、B 、C 三点不共线 => 有且只有一个平面α， 使A ∈α、B ∈α、C ∈α。

公理2作用：确定一个平面的依据。

推论：① 一条直线和其外一点可确定一个平面②两条相交直线可确定一个平面 ③两条平行直线可确定一个平面（3）公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

符号表示为：P ∈α∩β =>α∩β=L ，且P ∈L 公理3作用：判定两个平面是否相交的依据 （4）公理 4：平行于同一条直线的两条直线平行LA ·α C ·B·A· α P· αLβ等角定理：如果一个角的两边和另一个角的两边分别平行且方向相同，那么这两个角相等．2、空间两条不重合的直线有三种位置关系：相交、平行、异面3、异面直线所成角θ的范围是 00<θ≤900 2.1.2 空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系：相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点。

2 公理4：平行于同一条直线的两条直线互相平行。

符号表示为：设a 、b 、c 是三条直线a ∥bc ∥b强调：公理4实质上是说平行具有传递性，在平面、空间这个性质都适用。

公理4作用：判断空间两条直线平行的依据。

3 等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补4 注意点：① a'与b'所成的角的大小只由a 、b 的相互位置来确定，与O 的选择无关，为简便，点O 一般取在两直线中的一条上； ② 两条异面直线所成的角θ∈(0，)；③ 当两条异面直线所成的角是直角时，我们就说这两条异面直线互相垂直，记作a ⊥b ；④ 两条直线互相垂直，有共面垂直与异面垂直两种情形；⑤ 计算中，通常把两条异面直线所成的角转化为两条相交直线所成的角。

空间点线面之间的位置关系一、平面1.平面的概念：平面是一个不加定义，只需理解的原始概念．立体几何里所说的的平面是从现实生活中常见的平面抽象出来的．常见的桌面、平静的水面等都给我们以平面的局部形象．平面是理想的、绝对的平且无大小，无厚度，不可度量． 2.平面的表示方法：(1)一个平面： 当平面是水平放置的时候，通常把平行四边形的锐角画成45，横边画成邻边的2倍长，如右图． (2)两个相交平面：画两个相交平面时，通常要化出它们的交线，当一个平面的一部分被另一个平面遮住，应把被遮住部分的线段画成虚线或不画（如下图）3. 运用集合观点准确使用图形语言、符号语言和文字语言空间图形的基本元素是点、直线、平面线、平面看成是点的集合，因此还可借用集合中的符号语言来表示点、线、面的基本位置关系如下表所示：αBAβαABαβαβBAAβαBA α∈ 点A 在平面α内A α∉ 点A 不在平面α内b a Aa b A =直线a 、b 交于A 点a α⊂直线a 在平面α内a α=∅ 直线a 与平面α无公共点a A α=直线a 与平面α交于点Al αβ= 平面α、β相交于直线l二、平面的基本性质1. 公理1 如果一条直线的两点在一个平面内，那么这条直线在这个平面内推理模式：A AB B ααα∈⎫⇒⊂⎬∈⎭． 如图示：或者：∵,A B αα∈∈，∴AB α⊂ 公理1的作用：①判定直线是否在平面内；②判定点是否在平面内； ③检验面是否是平面．2. 公理2 经过不在同一条直线上的三点，有且只有一个平面推理模式：,, ,,,,A B C A B C A B C ααβ⎫⎪∈⇒⎬⎪∈⎭不共线与β重合或者：∵,,A B C 不共线，∴存在唯一的平面α，使得,,A B C α∈. 推论1：经过一条直线和这条直线外的一点，有且只有一个平面；BA αAαAαaαaαa Aα推论2：经过两条相交直线，有且只有一个平面； 推论3：经过两条平行直线，有且只有一个平面．(1)以上是确定平面的四个不同的条件，是判断两个平面重合的依据，是证明点线共面的依据，也是作截面、辅助面的依据．(2)“有且只有一个”的含义要准确理解．这里的“有”是说图形的存在，“只有一个”是说图形唯一．因此，在证明有关这类语句的命题时，要从“存在性”和“唯一性”两方面来论证． 2. 公理3 如果两个不重合的平面有一个公共点,有且只有一条过该点的公共直线推理模式：A A l A ααββ∈⎫⇒∈=⎬∈⎭如图示：或者：∵,A A αβ∈∈，∴,l A l αβ=∈公理3的作用：(1)判断两个平面是否相交及交线位置； (2)判断点是否在线上 1、证明空间三点共线问题通常证明这些点都在两个平面的交线上，即先确定出某两点在两个平面的交线上，再证明第三点既在第一个平面内，又在第二个平面内。

ABC1D1为平行四边形,所以AD1∥BC1.
因为在正方形A1ADD1中,AD1⊥A1D,所以BC1⊥A1D,故A错误;
因为AD1∥BC1,AD1⊂平面A1ADD1,BC1⊄平面A1ADD1,所以BC1∥平面
A1ADD1,故B正确;
因为AD1∥BC1,AD1与B1D1相交,在等边三角形AB1D1中,∠AD1B1不为直角,所
α互相垂直
l⊥α
直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,
它们唯一的公共点P叫做垂足
图示
画法
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的
一边垂直
(2)直线与平面垂直的判定定理
文字
语言
符号
语言
图形
语言
如果一条直线与一个平面内的两条相交的直线垂直,那么该直线与
此平面垂直
符号语言 a⊂β,b⊂β,a∩b=P,a∥α,b∥α⇒β∥α
图形语言
(2)面面平行的性质定理
两个平面平行,如果另一个平面与这两个平面相交,那么两条交
文字语言
线平行
符号语言 α∥β,γ∩α=a,γ∩β=b⇒)直线与平面垂直的概念
定义
记法
有关
概念
如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面
∵AC⊂平面 ACD,EF⊄平面 ACD,∴EF∥平面 ACD,故 A 正确.
由正方体性质可得 AC⊥BD,故 B 正确.
∵E,F,G,H 分别是棱 AB,BC,CD,AD 的中点,EF∥AC 且
1
GH=2AC,
1
EF=2AC,GH∥AC
且
∴EF∥GH,EF=GH,∴四边形 EFGH 是平行四边形,故 E,F,G,H 四点共面,故

空间点、线、面之间的位置关系一、教材分析教材从长方体出发，观察它的点、线、面之间的位置关系，让学生仔细地观察，从而对点线面有一个直观的感受。

教材举出实例，并给出两幅实物图片，激发学生学习的兴趣，让学生觉得四个公理确实是显而易见的。

本节的等角定理没有给出证明，而是通过从平面到空间的类比，得到和理解这个定理，显得直观且可信。

二、教学目标1、掌握五类位置关系的分裂及其有关概念，掌握平面的基本性质，即公理1,2,3.提高学生的归纳、类比能力。

2、掌握公理4和等角定理，并会运用它们解决问题，培养学生发展空间想象能力、运用图形语言进行交流的能力、几何直观能力。

三、重点难点教学重点：4个公理和等角定理的应用。

教学难点：空间图形的位置关系和公理的归纳。

四、知识要点（一）空间位置关系：I、空间点与线的关系空间点与直线的位置关系有两种：①点P 在直线上：；②点P 在直线外：；II、空间点与平面的关系空间点与平面的位置关系有两种：①点P 在平面上：②点P 在平面外：；（二）平面的基本性质公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

••A B αA B aA Baαα∈⎫⇒⊂⎬∈⎭、、公里1解释了空间“线面关系”，确定线是否属于面。

公理2 ：过不在一条直线上的三点，有且只有一个平面.公理2主要是用来“确定平面”。

公理2有三个推论：推论1： 经过一条直线和这条直线外一点，可以确定一个平面。

推论2： 经过两条相交直线，可以确定一个平面。

推论3：经过两条平行直线，可以确定一个平面。

公理2及其推论主要用于确定平面；证明点线共面公理3 ：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线.••C •B α A 点A 、B 、C 不共线 ⇒ A 、B 、C可以确定一个平面α• • •A B C •αA • •BC •• • A B Cα αβlp• α P =,P P l l l ααββ∈⎫⇒∃∈⎬∈⎭唯一的直线，使得公理3解释了“面面相交”的问题，两个不重合的平面相交，交于一条直线。

空间几何中的点线面的位置关系在空间几何学中，点、线和面是最基本的几何元素。

它们在空间中的位置关系对于理解和解决几何问题至关重要。

本文将讨论点线面在空间中的常见位置关系以及它们之间的相互作用。

一、点与线的位置关系1.1 点在直线上当一个点位于一条直线上时，称该点在直线上。

点在直线上的特点是它与直线上的任意两个点都在同一直线上。

1.2 点在直线上的延长线上当一个点位于直线的延长线上时，称该点在直线上的延长线上。

点在直线延长线上的特点是它与直线上的任意两个点都在同一直线上，包括线的两个端点。

1.3 点在线段上当一个点位于一条线段上时，称该点在线段上。

点在线段上的特点是它位于线段的两个端点之间。

1.4 点在线段的延长线上当一个点位于线段的延长线上时，称该点在线段的延长线上。

点在线段延长线上的特点是它位于线段的两个端点之外。

二、点与面的位置关系2.1 点在平面上当一个点位于一个平面上时，称该点在平面上。

点在平面上的特点是它与平面上的任意两个点都在同一平面上。

2.2 点在平面上的延长线上当一个点位于平面的延长线上时，称该点在平面上的延长线上。

点在平面延长线上的特点是它与平面上的任意两个点都在同一平面上，包括平面的边界和内部点。

2.3 点在平面外当一个点不在平面上时，称该点在平面外。

点在平面外的特点是它无法与平面上的任意两个点构成一条直线。

三、线与面的位置关系3.1 线在平面上当一条线位于平面内时，称该线在平面上。

线在平面上的特点是它与平面上的任意两个点都在同一平面上。

3.2 线平行于平面当一条线与平面上的所有点都不相交时，称该线平行于平面。

平行于平面的特点是线上的所有点与平面上的任意两个点的连线都平行。

3.3 线与平面相交于一点当一条线与平面上的某个点相交时，称该线与平面相交于一点。

线与平面相交于一点的特点是线上的所有点与平面上的任意两个点的连线都相交于同一点。

四、面与面的位置关系4.1 平行面当两个面的法向量平行时，称这两个面为平行面。

点线面的位置关系（1）四个公理公理1:如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

符号语言：A l,B l, 且 A ,B l 。

公理2:过不在一条直线上的三点，有且只有一个平面。

三个推论：① 经过一条直线和这条直线外一点，有且只有一个平面 __________② _________________③ _________________它给出了确定一个平面的依据。

公理3:如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线（两个平面的交线）。

符号语言：P ,且P I l,P l。

公理4：（平行线的传递性）平行与同一直线的两条直线互相平行。

符号语言：a//l,且b//l a//b。

（2）空间中直线与直线之间的位置关系1. 概念异面直线及夹角：把不在任何一个平面内的两条直线叫做异面直线。

已知两条异面直线a,b，经过空间任意一点0作直线a //a,b //b，我们把 a与b 所成的角（或直角）叫异面直线a, b所成的夹角。

（易知：夹角范围0 90）公理4：（平行线的传递性）平行与同一直线的两条直线互相平行。

符号语言：a//l,且b//l a//b。

定理：空间中如果一个角的两边分别与另一个角的两边分别平行，那么这两个角相等或互补。

（注意：会画两个角互补的图形）相交直线：同一平面内，有且只有一个公共点；共面直线2. 位置关系：八‘ 平行直线：同一平面内，没有公共点；异面直线：不同在任何一个平面内，没有公共点（3）空间中直线与平面之间的位置关系直线在平面外直线与平面相交（直线与平面平11I //A）有且只有一个公共点没有公共点直线与平面的位置关系有直线在平面内（I ）有无数个公共点（4）空间中平面与平面之间的位置关系平面与平面之间的位置关系有两种：两个平面平行（// ）没有公共点两个平面相交（I I）有一条公共直线考点1：点，线，面之间的位置关系例1.（2014辽宁,4,5分）已知m,n表示两条不同直线，口表示平面.下列说法正确的是（）A.若m//a ,n //a ,贝U m// nB.若m±a ,n ? a ,贝U m± nC.若m±a ,m± n,贝U n //aD.若m//a ,m± n,贝U n丄a［答案］1.B［解析］1.A选项m n也可以相交或异面,C选项也可以n? a ,D选项也可以n// a或n 与a斜交.根据线面垂直的性质可知选B.例2.（2014山东青岛高三第一次模拟考试，5）设「、’是两条不同的直线，八'是两个不同的平面，则下列命题正确的是（）A.若aUb^aHa.则刃仏B.若口丄0,口〃口,则&丄0C若口丄04丄/〔则D.若心皿丄口上丄八则口丄0［答案］2. D ［解析］2.A选项不正确，因为:、J =是可能的;（ ）（B ）■' -■'（D ）总萨:离苗丄•:心兰获抒二翼,丄凤B 选项不正确，因为’,"时，，’’都是可能的;C 选项不正确，因为’■','时，可能有：■;D 选项正确，可由面面垂直的判定定理证明其是正确的. 故选D例3. （2014广西桂林中学高三2月月考，4）设是两条不同的直线，•、 ■'是两个不同的平面.下列命题中正确的是（A ）小 「. !■；）. J; 一、⑴:-（C ）- - •［答案］3. D［解析］3. 若牛丄二厂二.？*—，•，则平面「与「垂直或相交或平行，故（A ）错误；若芒丄出b 亠疔;炉忌，则直线J 与’相交或平行或异面，故（B ）错误； 若卫丄S ,7丄^，则直线与平面,垂直或相交或平行，故（C ）错误;若’ ’，则直线，故（D ）正确•选D.例4. （2014周宁、政和一中第四次联考，7）设 表示不同的直线， 表示不同的平面，给出下列四个命题： ① 若• //，且 则 ；② 若• // ，且• // .贝U // ;③ 若 cel /? = /.#［ r =皿产 1 口"贝屮 // e // n . ④ 若 a\ = f = a=n.且】〃戏贝” // 刖A. 1B. 2［答案］4. B［解析］4. ①正确；②直线-或，错误；③错误，因为正方体有公共端点的三条棱两两垂直；④正确•故真正确的是①④，共2个.2. 空间几何平行关系转化关系：—J ―X线线平行----------- "钱血平行--------------- 面面平行直线、平面平行的判定及其性质归纳总结1.证明线线平行的方法:CO (平行线的传递性)平行与同一直线的两条直线互相平行。

专题08 立体几何第二十讲 空间点线面的位置关系答案部分2019年1.【解析】如图所示，联结BE ，BD .因为点N 为正方形ABCD 的中心，ECD △为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，所以BM ⊂平面BDE ，EN ⊂平面BDE ，因为BM 是BDE △中DE 边上的中线，EN 是BDE △中BD 边上的中线，直线BM ，EN 是相交直线，设DE a =，则2BD a =，2235244BE a a a =+=， 所以62BM a =，223144EN a a a =+=， 所以BM EN ≠．故选B ．2.【解析】（1）连结1,B C ME .因为M ，E 分别为1,BB BC 的中点，所以1 ME B C ∥，且112ME B C =.又因为N 为1A D 的中点，所以112ND A D =. 由题设知11=AB DC ∥，可得11=BC A D ∥，故=ME ND ∥，因此四边形MNDE 为平行四边形，MN ED ∥.又MN ⊄平面1C DE ，所以MN ∥平面1C DE .（2）过C 作C 1E 的垂线，垂足为H .学习奥数的优点1、激发学生对数学学习的兴趣，更容易让学生体验成功，树立自信。

2、训练学生良好的数学思维习惯和思维品质。

要使经过奥数训练的学生，思维更敏捷，考虑问题比别人更深层次。

3、锻炼学生优良的意志品质。

可以培养持之以恒的耐心和克服困难的信心， 以及战胜难题的勇气。

可以养成坚韧不拔的毅力4、获得扎实的数学基本功，发挥创新精神和创造力的最大空间。

由已知可得DE BC ⊥，1DE C C ⊥，所以DE ⊥平面1C CE ，故DE ⊥CH. 从而CH ⊥平面1C DE ，故CH 的长即为C 到平面1C DE 的距离， 由已知可得CE =1，C 1C =4，所以117C E =，故41717CH =. 从而点C 到平面1C DE 的距离为41717.3.【解析】对于A ，α内有无数条直线与β平行，则α与β相交或βα∥，排除； 对于B ，α内有两条相交直线与β平行，则βα∥；对于C ，α，β平行于同一条直线，则α与β相交或βα∥，排除； 对于D ，α，β垂直于同一平面，则α与β相交或βα∥，排除． 故选B ．4.【解析】若②//m α，过m 作平面m βα'=，则//m m '，又③l α⊥，则l m '⊥，又m ，m '同在β内，所以①l m ⊥，即⇒②③①.5.【解析】证明：（1）因为D ，E 分别为BC ，AC 的中点， 所以ED ∥AB .在直三棱柱ABC-A 1B 1C 1中，AB ∥A 1B 1， 所以A 1B 1∥ED .又因为ED ⊂平面DEC 1，A 1B 1⊄平面DEC 1，所以A 1B 1∥平面DEC 1.（2）因为AB =BC ，E 为AC 的中点，所以BE ⊥AC . 因为三棱柱ABC-A 1B 1C 1是直棱柱，所以CC 1⊥平面ABC . 又因为BE ⊂平面ABC ，所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1，AC ⊂平面A 1ACC 1，C 1C ∩AC =C ， 所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1，所以BE ⊥C 1E .6.【解析】（1）由已知得B 1C 1⊥平面ABB 1A 1，BE ⊂平面ABB 1A 1， 故11B C BE ⊥.又1BE EC ⊥，所以BE ⊥平面11EB C .（2）由（1）知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E ，所以1145AEB A EB ︒∠=∠=，故AE =AB =3，126AA AE ==.作1EF BB ⊥，垂足为F ，则EF ⊥平面11BB C C ，且3EF AB ==. 所以，四棱锥11E BB C C -的体积1363183V =⨯⨯⨯=. F7.【解析】（1）由已知得AD BE ，CG BE ，所以AD CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ⊥BE ，AB ⊥BC ，故AB ⊥平面BCGE ． 又因为AB ⊂平面ABC ，所以平面ABC ⊥平面BCGE ． （2）取CG 的中点M ，联结EM ，DM .因为AB DE ∥，AB ⊥平面BCGE ，所以DE ⊥平面BCGE ，故DE ⊥CG . 由已知，四边形BCGE 是菱形，且60EBC ∠=︒得EM ⊥CG ，故CG ⊥平面DEM . 因此DM ⊥CG .在Rt △DEM 中，1DE =，EM =3，故2DM =.所以四边形ACGD 的面积为4.8.【解析】（Ⅰ）因为PA ⊥平面ABCD ，且BD ⊂平面ABCD ， 所以PA BD ⊥．又因为底面ABCD 为菱形，所以BD AC ⊥． 又PA ⊂平面PAC ，AC ⊂平面PAC ，PA AC A =，所以BD ⊥平面PAC ．（Ⅱ）因为PA ⊥平面ABCD ，AE ⊂平面ABCD ， 所以PA ⊥AE ．因为底面ABCD 为菱形，∠ABC =60°，且E 为CD 的中点， 所以AE ⊥CD ．又//AB CD ，所以AB ⊥AE ．又PA ⊂平面PAB ，AB ⊂平面PAB ，PAAB A =，所以AE ⊥平面PAB ．又AE ⊂平面PAE ，所以平面PAB ⊥平面PAE ．（Ⅲ）棱PB 上存在点F ，且F 为PB 的中点，使得CF ∥平面PAE ． 取F 为PB 的中点，取G 为PA 的中点，连结CF ，FG ，EG ．因为G ，F 分别为PA ，PB 的中点，则FG ∥AB ，且FG =12AB ． 因为底面ABCD 为菱形，且E 为CD 的中点， 所以CE ∥AB ，且CE =12AB ． 所以FG ∥CE ，且FG =CE ． 所以四边形CEGF 为平行四边形， 所以CF ∥EG ．因为CF ⊄平面PAE ，EG ⊂平面PAE ， 所以CF ∥平面PAE ．9.【解析】（Ⅰ）连接BD ，易知ACBD H =，BH DH =.又由BG PG =，故GH PD ∥，又因为GH ⊄平面PAD ，PD ⊂平面PAD ，所以GH ∥平面PAD .（Ⅱ）取棱PC 的中点N ，连接DN .依题意，得DN PC ⊥，又因为平面PAC ⊥平面PCD ，平面PAC平面PCD PC =，所以DN ⊥平面PAC ，又PA ⊂平面PAC ，故DN PA ⊥.又已知PA CD ⊥，CD DN D =，所以PA ⊥平面PCD .（Ⅲ）连接AN ，由（Ⅱ）中DN ⊥平面PAC ，可知DAN ∠为直线AD 与平面PAC 所成的角，因为PCD △为等边三角形，2CD =且N 为PC 的中点，所以DN =又DN AN ⊥，故在Rt AND △中，sin DN DAN AD ∠==所以，直线AD 与平面PAC 10.【解析】（1）因为D ，E 分别为BC ，AC 的中点， 所以ED ∥AB .在直三棱柱ABC-A 1B 1C 1中，AB ∥A 1B 1， 所以A 1B 1∥ED .又因为ED ⊂平面DEC 1，A 1B 1⊄平面DEC 1， 所以A 1B 1∥平面DEC 1.（2）因为AB =BC ，E 为AC 的中点，所以BE ⊥AC . 因为三棱柱ABC-A 1B 1C 1是直棱柱，所以CC 1⊥平面ABC . 又因为BE ⊂平面ABC ，所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1，AC ⊂平面A 1ACC 1，C 1C ∩AC =C ， 所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1，所以BE ⊥C 1E .11.【解析】（I ）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥A C. 又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1， 平面A 1ACC 1∩平面ABC =AC ， 所以，A 1E ⊥平面ABC ，则A 1E ⊥BC . 又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F . 所以BC ⊥平面A 1EF . 因此EF ⊥B C.（Ⅱ）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形． 由于A 1E ⊥平面ABC ，故AE 1⊥EG ，所以平行四边形EGFA 1为矩形． 由（I ）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1， 所以EF 在平面A 1BC 上的射影在直线A 1G 上.连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）. 不妨设AC =4，则在Rt △A 1EG 中，A 1E 3EG 3. 由于O 为A 1G 的中点，故1152A G EO OG ===， 所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35． 12.【解析】（Ⅰ）因为PA ⊥平面ABCD ，且BD ⊂平面ABCD ， 所以PA BD ⊥．又因为底面ABCD为菱形，所以BD AC⊥．又PA⊂平面PAC，AC⊂平面PAC，PA AC A=，所以BD⊥平面PAC．（Ⅱ）因为PA⊥平面ABCD，AE⊂平面ABCD，所以PA⊥AE．因为底面ABCD为菱形，∠ABC=60°，且E为CD的中点，所以AE⊥CD．又//AB CD，所以AB⊥AE．又PA⊂平面PAB，AB⊂平面PAB，PA AB A=，所以AE⊥平面PAB．又AE⊂平面PAE，所以平面PAB⊥平面PAE．（Ⅲ）棱PB上存在点F，且F为PB的中点，使得CF∥平面PAE．取F为PB的中点，取G为PA的中点，连结CF，FG，EG．因为G，F分别为PA，PB的中点，则FG∥AB，且FG=12 AB．因为底面ABCD为菱形，且E为CD的中点，所以CE∥AB，且CE=12 AB．所以FG∥CE，且FG=CE．所以四边形CEGF为平行四边形，所以CF∥EG．因为CF⊄平面PAE，EG⊂平面PAE，所以CF∥平面PAE．13.【解析】过点P作PO⊥平面ABC交平面ABC于点O，过点P作PD⊥AC交AC于点D，作PE⊥BC交BC于点E，联结OD，OC，OE，则,,AC POD BC POE ⊥⊥平面平面 所以,,AC OD BC OE ⊥⊥又90ACB ∠=︒, 故四边形ODCE 为矩形. 有所做辅助线可知3PD PE ==，所以()22231CD CE ==-=，所以矩形ODCE 为边长是1的正方形，则2OC =.在Rt PCO △中，2,2PC OC ==，所以2PO =.PO 即为点P 到平面ABC 的距离，即所求距离为2.14.【解析】（1）连结1,B C ME .因为M ，E 分别为1,BB BC 的中点，所以1 ME B C ∥，且112ME B C =.又因为N 为1A D 的中点，所以112ND A D =. 由题设知11=AB DC ∥，可得11=BC A D ∥，故=ME ND ∥，因此四边形MNDE 为平行四边形，MN ED ∥.又MN ⊄平面1C DE ，所以MN ∥平面1C DE .（2）过C 作C 1E 的垂线，垂足为H .由已知可得DE BC ⊥，1DE C C ⊥，所以DE ⊥平面1C CE ，故DE ⊥CH. 从而CH ⊥平面1C DE ，故CH 的长即为C 到平面1C DE 的距离， 由已知可得CE =1，C 1C =4，所以117C E =，故41717CH =. 从而点C 到平面1C DE 的距离为41717.15.【解析】（Ⅰ）连接BD ，易知ACBD H =，BH DH =.又由BG PG =，故GH PD ∥，又因为GH ⊄平面PAD ，PD ⊂平面PAD ，所以GH ∥平面PAD .（Ⅱ）取棱PC 的中点N ，连接DN .依题意，得DN PC ⊥，又因为平面PAC ⊥平面PCD ，平面PAC平面PCD PC =，所以DN ⊥平面PAC ，又PA ⊂平面PAC ，故DN PA ⊥.又已知PA CD ⊥，CD DN D =，所以PA ⊥平面PCD .（Ⅲ）连接AN ，由（Ⅱ）中DN ⊥平面PAC ，可知DAN ∠为直线AD 与平面PAC 所成的角，因为PCD △为等边三角形，2CD =且N 为PC 的中点，所以3DN =又DN AN ⊥，故在Rt AND △中，3sin DN DAN AD ∠==所以，直线AD 与平面PAC 316.【解析】解法一：如图G 为AC 的中点，V 在底面的射影为O ，则P 在底面上的射影D 在线段AO 上，作DE AC ⊥于E ，易得PE VG ∥，过P 作PF AC ∥于F ， 过D 作DH AC ∥，交BG 于H ，则BPF α=∠，PBD β=∠，PED γ=∠， 则cos cos PF EG DH BDPB PB PB PB αβ===<=，可得βα<； tan tan PD PDED BDγβ===，可得βγ<.解法二：由最小值定理可得βα<，记V AC B --的平面角为γ'(显然γγ'=)， 由最大角定理可得βγγ'<=；解法三特殊图形法：设三棱锥V ABC -为棱长为2的正四面体，P 为VA 的中点，易得132cos 63α==，可得33sin 6α=，623sin 33β==，6223sin 332γ==，故选B ．17.【解析】（I ）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥A C. 又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1， 平面A 1ACC 1∩平面ABC =AC ， 所以，A 1E ⊥平面ABC ，则A 1E ⊥BC . 又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F . 所以BC ⊥平面A 1EF . 因此EF ⊥B C.（Ⅱ）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形． 由于A 1E ⊥平面ABC ，故AE 1⊥EG ，所以平行四边形EGFA 1为矩形． 由（I ）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1，所以EF 在平面A 1BC 上的射影在直线A 1G 上.连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）.不妨设AC =4，则在Rt △A 1EG 中，A 1E EG .由于O 为A 1G 的中点，故12A G EO OG ===， 所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35． 2015-2018年1．C 【解析】如图，连接BE ，因为AB CD ∥，所以异面直线AE 与CD 所成角等于相交直线AE 与AB 所成的角，即EAB ∠．不妨设正方体的棱长为2，则1CE =，2BC =，由勾股定理得BE =AB ⊥平面11BCC B ，可得AB BE ⊥，所以tan 2BE EAB AB ∠==，故选C ． D 1C 1B 1A 1ED C BA2．A 【解析】若m α⊄，n α⊂，m ∥n ，由线面平行的判定定理知m ∥α．若m ∥α，m α⊄，n α⊂，不一定推出m ∥n ，直线m 与n 可能异面，故“m ∥n ”是“m ∥α”的充分不必要条件．故选A ．3．A 【解析】由正方体的线线关系，易知B 、C 、D 中AB MQ ∥，所以AB ∥平面MNQ ， 只有A 不满足．选A ．4．C 【解析】如图，连结1A D ，易知1AD ⊥平面1A DE ，所以11AD A E ⊥，又11BC AD ∥，所以1BC ⊥平面1A DE ，故11A E BC ⊥，选C ．C 111A5．A 【解析】因为过点A 的平面α与平面11CB D 平行，平面ABCD ∥平面1111A B C D ，所以m ∥11B D ∥BD ，又1A B ∥平面11CB D ，所以n ∥1AB ，则BD 与1A B 所成的角为所求角，所以m ，n A ． 6．C 【解析】选项A ，只有当m β∥或m β⊂时，m l ∥；选项B ，只有当m β⊥时m n ∥；选项C ，由于l β⊂，所以n l ⊥；选项D ，只有当m β∥或m β⊂时，m n ⊥，故选C ． 7．【解析】(1)因为4===AP CP AC ，O 为AC 的中点，所以OP ⊥AC ，且=OP 连结OB ．因为2==AB BC AC ，所以∆ABC 为等腰直角三角形， 且OB ⊥AC ，122==OB AC ． 由222OP OB PB +=知，OP ⊥OB ．由OP ⊥OB ，OP ⊥AC 知PO ⊥平面ABC ．HO MPCBA(2)作CH ⊥OM ，垂足为H ．又由(1)可得OP ⊥CH ，所以CH ⊥平面POM ．故CH 的长为点C 到平面POM 的距离． 由题设可知122==OC AC ，24233==CM BC ，45∠=ACB ． 所以253=OM ，sin 455⋅⋅∠==OC MC ACB CH OM ． 所以点C 到平面POM 的距离为455． 8．【解析】(1)由题设知，平面CMD ⊥平面ABCD ，交线为CD ．因为BC ⊥CD ，BC ⊂平面ABCD ，所以BC ⊥平面CMD ，故BC ⊥DM ． 因为M 为CD 上异于C ，D 的点，且DC 为直径，所以 DM ⊥CM ．又BCCM =C ，所以DM ⊥平面BMC ．而DM ⊂平面AMD ，故平面AMD ⊥平面BMC ． (2)当P 为AM 的中点时，MC ∥平面PBD ．证明如下：连结AC 交BD 于O ．因为ABCD 为矩形，所以O 为AC 中点． 连结OP ，因为P 为AM 中点，所以MC ∥OP ．MC ⊄平面PBD ，OP ⊂平面PBD ，所以MC ∥平面PBD ．9．【解析】(1)∵PA PD =，且E 为AD 的中点，∴PE AD ⊥． ∵底面ABCD 为矩形，∴BC AD ∥， ∴PE BC ⊥．(2)∵底面ABCD 为矩形，∴AB AD ⊥．∵平面PAD ⊥平面ABCD ，∴AB ⊥平面PAD ． ∴AB PD ⊥．又PA PD ⊥，∵PD ⊥平面PAB ，∴平面PAB ⊥平面PCD ． (3)如图，取PC 中点G ，连接,FG GD ．G PFED CBA∵,F G 分别为PB 和PC 的中点，∴FG BC ∥，且12FG BC =． ∵四边形ABCD 为矩形，且E 为AD 的中点， ∴1,2ED BC DE BC =∥， ∴ED FG ∥，且ED FG =，∴四边形EFGD 为平行四边形， ∴EF GD ∥．又EF ⊄平面PCD ，GD ⊂平面PCD ， ∴EF ∥平面PCD ．10．【解析】(1)由平面ABC ⊥平面ABD ，平面ABC ∩平面ABD =AB ，AD ⊥AB ，可得AD ⊥平面ABC ，故AD ⊥BC ．(2)取棱AC 的中点N ，连接MN ，ND ．又因为M 为棱AB 的中点，故MN ∥BC ．所以DMN ∠（或其补角）为异面直线BC 与MD 所成的角．NM A BCD在Rt DAM ∆中，1AM =，故DM =因为AD ⊥平面ABC ，故AD ⊥AC ． 在Rt DAN ∆中，1AN =，故DN ．在等腰三角形DMN 中，1MN =，可得12cos MNDMN DM ∠==．所以，异面直线BC 与MD (3)连接CM ．因为ABC ∆为等边三角形，M 为边AB 的中点，故CM ⊥AB ，CM =．又因为平面ABC ⊥平面ABD ，而CM ⊂平面ABC ，故CM ⊥平面ABD ．所以，CDM ∠为直线CD 与平面ABD 所成的角．在Rt CAD ∆中，4CD =．在Rt CMD ∆中，sin 4CM CDM CD ∠==．所以，直线CD 与平面ABD ． 11．【证明】(1)在平行六面体1111ABCD A B C D -中，AB ∥11A B ． 因为AB ⊄平面11A B C ，11A B ⊂平面11A B C ， 所以AB ∥平面11A B C ．D 1C 1B 1A 1DCBA(2)在平行六面体1111ABCD A B C D -中，四边形11ABB A 为平行四边形． 又因为1AA AB =，所以四边形11ABB A 为菱形， 因此1AB ⊥1A B ．又因为1AB ⊥11B C ，BC ∥11B C ， 所以1AB ⊥BC ．又因为1A BBC =B ，1A B ⊂平面1A BC ，BC ⊂平面1A BC ，所以1AB ⊥平面1A BC ． 因为1AB ⊂平面11ABB A ，所以平面11ABB A ⊥平面1A BC ．12．【解析】(1)由2AB =，14AA =，12BB =，1AA AB ⊥，1BB AB ⊥得111AB A B ==，所以2221111A B AB AA +=．故111AB A B ⊥．由2BC =，12BB =，11CC =，1BB BC ⊥，1CC BC ⊥得11B C = 由2AB BC ==，120ABC ∠=得AC =由1CC AC ⊥，得1AC =2221111AB B C AC +=，故111AB B C ⊥．因此1AB ⊥平面111A B C ．(2)如图，过点1C 作111C D A B ⊥，交直线11A B 于点D ，连结AD ．DABCA 1B 1C 1由1AB ⊥平面111A B C 得平面111A B C ⊥平面1ABB ， 由111C D A B ⊥得1C D ⊥平面1ABB ， 所以1C AD ∠是1AC 与平面1ABB 所成的角．由11B C =11A B =，11AC得111cos C A B ∠=，111sin C A B ∠=，所以1C D，故111sin 13C D C AD AC ∠==． 因此，直线1AC 与平面1ABB所成的角的正弦值是13． 13．【解析】（1）在平面ABCD 内，因为90BAD ABC ∠=∠=，所以BC ∥AD ， 又BC ⊄平面PAD ，AD ⊂平面PAD ，故BC ∥平面PAD ． （2）取AD 的中点M ，连结PM ，CM ．由12AB BC AD ==及BC ∥AD ， 90ABC ∠=得四边形ABCM 正方形，则CM AD ⊥．NMDCBA P因为侧面PAD 为等边三角形且垂直于底面ABCD ，平面PAD平面ABCD =AD ，所以PM AD ⊥，PM ⊥底面ABCD ．因为CM ⊂底面ABCD ，所以PM CM ⊥． 设BC x =，则CM x =，CD =，PM =，2PC PD x ==．取CD 的中点N ，连结PN ，则PN CD ⊥，所以2PN x =． 因为PCD ∆的面积为所以122x ⨯=解得2x =-（舍去），2x =．于是2AB BC ==，4AD =，PM = 所以四棱锥P ABCD -的体积12(24)32V +=⨯⨯=． 14．【解析】（1）取AC 的中点O 连结DO ，BO .因为AD CD =，所以AC ⊥DO ． 又由于ABC ∆是正三角形，所以AC ⊥BO .从而AC ⊥平面DOB ，故AC ⊥BD .ABCDEO（2）连结EO ．由（1）及题设知90ADC ∠=，所以DO AO =． 在Rt AOB ∆中，222BO AO AB +=． 又AB BD =，所以222222BO DO BO AO AB BD +=+==，故90DOB ∠=.由题设知AEC ∆为直角三角形，所以12EO AC =． 又ABC ∆是正三角形，且AB BD =，所以12EO BD =．故E 为BD 的中点，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，四面体ABCE 的体积为四面体ABCD 的体积的12，即四面体ABCE 与四面体ACDE 的体积之比 为1:1．15．【解析】（Ⅰ）如图，由已知AD //BC ，故DAP ∠或其补角即为异面直线AP 与BC 所成的角．因为AD ⊥平面PDC ，所以AD ⊥PD ．在Rt △PDA 中，由已知，得AP ==故cos AD DAP AP ∠==． 所以，异面直线AP 与BC．（Ⅱ）证明：因为AD ⊥平面PDC ，直线PD ⊂平面PDC ，所以AD ⊥PD ．又因为BC //AD ，所以PD ⊥BC ，又PD ⊥PB ，所以PD ⊥平面PB C ．（Ⅲ）过点D 作AB 的平行线交BC 于点F ，连结PF ，则DF 与平面PBC 所成的角等于AB 与平面PBC 所成的角．因为PD ⊥平面PBC ，故PF 为DF 在平面PBC 上的射影，所以DFP ∠为直线DF 和平面PBC 所成的角．由于AD //BC ，DF //AB ，故BF =AD =1，由已知，得CF =BC –BF =2．又AD ⊥DC ，故BC ⊥DC ，在Rt △DCF 中，可得2225DF CD CF =+=在Rt △DPF 中，可得 5sin PD DFP DF ∠==． 所以，直线AB 与平面PBC 5． 16．【解析】（Ⅰ）取11B D 中点1O ,连接1CO ，11A O ，O 1ABCDE OM A 1B 1D 1由于1111ABCD A B C D -为四棱柱, 所以11AO OC ∥，11A O OC =， 因此四边形11AOCO 为平行四边形,所以11AO O C ∥,又1O C ⊂面11B CD ,1AO ⊄平面11B CD , 所以1A O ∥平面11B CD ,（Ⅱ）∵AC BD ⊥．E ，M 分别为AD 和OD 的中点， ∴EM BD ⊥，又1A E ⊥平面ABCD ，BD ⊂平面ABCD ， 所以1A E BD ⊥，∵11B D BD ∥，所以11EM B D ⊥，111A E B D ⊥， 又1A E ，EM ⊂平面1,A EM 1A E EM E =，所以11B D ⊥平面1,A EM又11B D ⊂平面11B CD ,所以平面1A EM ⊥平面11B CD ．17．【解析】（Ⅰ）因为PA AB ⊥，PA BC ⊥，所以PA ⊥平面ABC ， 又因为BD ⊂平面ABC ，所以PA BD ⊥．（Ⅱ）因为AB BC =，D 为AC 中点，所以BD AC ⊥， 由（Ⅰ）知，PA BD ⊥，所以BD ⊥平面PAC ． 所以平面BDE ⊥平面PAC ．（Ⅲ）因为PA ∥平面BDE ，平面PAC 平面BDE DE =，所以PA DE ∥．因为D 为AC 的中点，所以112DE PA ==，2BD DC == 由（Ⅰ）知，PA ⊥平面ABC ，所以DE ⊥平面ABC ．所以三棱锥E BCD -的体积111363DBC V S DE BD DC DE ∆=⨯⨯=⋅⋅=． 18．【解析】（Ⅰ）如图，设P A 中点为F ，连结EF ，FB ．FH M NQ E D CB AP因为E ，F 分别为PD ，P A 中点，所以EF ∥AD 且12EF AD =， 又因为BC ∥AD ，12BC AD =，所以 EF ∥BC 且EF =BC ，即四边形BCEF 为平行四边形，所以CE ∥BF ，因此CE ∥平面P AB ． （Ⅱ）分别取BC ，AD 的中点为M ，N ．连结PN 交EF 于点Q ，连结MQ ． 因为E ，F ，N 分别是PD ，P A ，AD 的中点，所以Q 为EF 中点，在平行四边形BCEF 中，MQ ∥CE ．由PAD ∆为等腰直角三角形得PN ⊥AD ．由DC ⊥AD ，N 是AD 的中点得BN ⊥AD ．所以 AD ⊥平面PBN ，由BC ∥AD 得 BC ⊥平面PBN ，那么，平面PBC ⊥平面PBN ．过点Q 作PB 的垂线，垂足为H ，连结MH ．MH 是MQ 在平面PBC 上的射影，所以∠QMH 是直线CE 与平面PBC 所成的角． 设CD =1．在PCD ∆中，由PC =2，CD =1，PD =得CE =，在△PBN 中，由PN =BN =1，PB =得14QH =， 在Rt MQH ∆中，14QH =，MQ =， 所以 2sin 8QMH ∠=， 所以，直线CE 与平面PBC 2 19．【解析】证明：（1）在平面ABD 内，因为AB AD ⊥，EF AD ⊥，所以EF AB ∥. 又因为EF ⊄平面ABC ，AB ⊂平面ABC ，所以EF ∥平面ABC . （2）因为平面ABD ⊥平面BCD ，平面ABD 平面BCD =BD ，BC ⊂平面BCD ，BC BD ⊥，所以BC ⊥平面ABD . 因为AD ⊂平面ABD ，所以BC ⊥AD .又AB AD ⊥，BC AB B =，AB ⊂平面ABC ，BC ⊂平面ABC ， 所以AD ⊥平面ABC ，又因为AC ⊂平面ABC ，所以AD AC ⊥．20．【解析】（1）由正棱柱的定义，1CC ⊥平面ABCD ，所以平面11A ACC ⊥平面ABCD ，1CC AC ⊥．记玻璃棒的另一端落在1CC 上点M 处．因为107AC =40AM =． 所以2240(107)30MN =-=，从而3sin 4MAC ∠=． 记AM 与水平的交点为1P ，过1P 作11PQ AC ⊥，1Q 为垂足，则11PQ ⊥平面ABCD ，故1112PQ=， 从而11116sin PQ AP MAC==∠． 答：玻璃棒l 没入水中部分的长度为16cm.( 如果将“没入水中部分”理解为“水面以上部分”，则结果为24cm)（2）如图，O ，1O 是正棱台的两底面中心.由正棱台的定义，1OO ⊥平面 EFGH ，所以平面11E EGG ⊥平面EFGH ，1OO ⊥EG .同理，平面11E EGG ⊥平面1111E F G H ，1OO ⊥11E G . 记玻璃棒的另一端落在1GG 上点N 处.过G 作GK ⊥11E G ，K 为垂足， 则GK =1OO =32. 因为EG = 14，11E G = 62，所以1KG =6214242-=，从而222211 243240GG KG GK =+=+=. 设1,,EGG ENG αβ==∠∠则114sin sin()cos 25KGG KGG απ=+==∠∠. 因为2απ<<π，所以3cos 5α=-. 在ENG △中，由正弦定理可得4014sin sin αβ=，解得7sin 25β=. 因为02βπ<<，所以24cos 25β=. 于是sin sin()sin()sin cos cos sin NEG αβαβαβαβ=π--=+=+∠ 42473(35)525255=⨯+-⨯=. 记EN 与水面的交点为2P ，过2P 作22P Q EG ⊥，2Q 为垂足，则 22P Q ⊥平面EFGH ，故22P Q =12，从而 2EP =2220sin P NEGQ =∠. 答:玻璃棒l 没入水中部分的长度为20cm.(如果将“没入水中部分”理解为“水面以上部分”，则结果为20cm)。

【母题原题1】【2019年高考全国Ⅲ卷文数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线 【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线．过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，专题08 空间点、直线、平面之间的位置关系5,22MF BF BM ==∴=BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．【母题原题2】【2017年高考全国Ⅲ卷文数】在正方体1111ABCD A B C D -中，E 为棱CD 的中点，则A ．11A E DC ⊥B ．1A E BD ⊥C ．11A E BC ⊥D ．1AE AC ⊥【答案】C【解析】根据三垂线定理的逆定理，可知平面内的线垂直于平面的斜线，则也垂直于斜线在平面内的射影.A.若11A E DC ⊥，那么11D E DC ⊥，很显然不成立；B.若1A E BD ⊥，那么BD AE ⊥，显然不成立；C.若11A E BC ⊥，那么11BC B C ⊥，成立，反过来11BC B C ⊥时，也能推出11BC A E ⊥,所以C 成立；D.若1A E AC ⊥，则AE AC ⊥，显然不成立，故选C ．【名师点睛】垂直、平行关系证明中应用转化与化归思想的常见类型： （1）证明线面、面面平行，需转化为证明线线平行． （2）证明线面垂直，需转化为证明线线垂直． （3）证明线线垂直，需转化为证明线面垂直．【命题意图】考查空间中直线、平面的位置关系的判断，注重对公理、定理的考查，同时考查考生的空间想象能力．【大纲要求】1．空间几何体（1）认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构．（2）能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述三视图所表示的立体模型，会用斜二侧法画出它们的直观图．（3）会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式．（4）会画某些建筑物的视图与直观图（在不影响图形特征的基础上，尺寸、线条等不作严格要求）．（5）了解球、棱柱、棱锥、台的表面积和体积的计算公式．2．点、直线、平面之间的位置关系（1）理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理．公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点都在此平面内．公理2：过不在同一条直线上的三点，有且只有一个平面．公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．公理4：平行于同一条直线的两条直线互相平行．定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补．（2）以立体几何的上述定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定定理．理解以下判定定理．如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行．如果一个平面内的两条相交直线与另一个平面都平行，那么这两个平面平行．如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直．如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直．理解以下性质定理，并能够证明．如果一条直线与一个平面平行，那么经过该直线的任一个平面与此平面的交线和该直线平行．如果两个平行平面同时和第三个平面相交，那么它们的交线相互平行．垂直于同一个平面的两条直线平行．如果两个平面垂直，那么一个平面内垂直于它们交线的直线与另一个平面垂直．3．能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题．4．空间直角坐标系（1）了解空间直角坐标系，会用空间直角坐标表示点的位置．（2）会推导空间两点间的距离公式．【命题规律】通常情况下，在填空选择题中立体几何试题会出现2道试题，命题形式有（1）三视图；（2）几何体的体积和表面积；（3）空间点、线、面之间的位置关系．【方法总结】1．两个平面平行，其中一个平面内的任意一条直线平行于另一个平面．2．夹在两个平行平面之间的平行线段长度相等．3．经过平面外一点有且只有一个平面与已知平面平行．4．两条直线被三个平行平面所截，截得的对应线段成比例．5．同一条直线与两个平行平面所成角相等．6．如果两个平面分别平行于第三个平面，那么这两个平面互相平行．7．如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线，那么这两个平面平行．8．证明直线与平面垂直的方法：（1）利用判定定理（a⊥b，a⊥c，b∩c=M，b⊂α，c⊂α⇒a⊥α）；（2）利用面面平行的性质（a⊥α，α∥β⇒a⊥β）；（3）利用面面垂直的性质定理（α⊥β，α∩β=l，a⊥l，a⊂β⇒a⊥α）；（4）利用面面垂直的性质（α∩β=l，α⊥γ，β⊥γ⇒l⊥γ）．9．证明面面垂直的思路（1）利用面面垂直的定义（作出两平面构成的二面角的平面角，计算平面角为90°）；（2）利用面面垂直的判定定理（a⊥β，a⊂α⇒α⊥β）．1．【广西桂林市2019届高三4月综合能力检测（一模）数学】在直三棱柱111ABC A B C -中，11AB AC AA ===，AB AC ⊥，点E 为棱1AA 的中点，则点1C 到平面1B EC 的距离等于A ．12 B ．2C D ．1【答案】C【解析】连接1C E ，设点1C 到平面1B EC 的距离为d ， 根据三棱锥等体积法得到：三棱锥11111111133C B CE E B CC B CE B CC V V S d S h --=⇒⋅⋅=⋅⋅1AB AC ==，在由AB AC ⊥，得到BC =三角形11B CC 面积为11112B CC =⨯点1A 到11B C的距离即棱锥11E B CC -的高为11122h B C ==；三角形1B EC ，1B E CE ==，1B C =则三=，面积为12，根据等体积公式代入得到11111111133C B CE E B CC B CE B CC V V S d S h --=⇒⋅⋅=⋅⋅，d =．故选C ．【名师点睛】本题涉及到点面距离的求法，点面距可以通过寻找面面垂直，再直接过点做交线的垂线即可；当点面距离不好求时，还可以等体积转化．2．【广西壮族自治区柳州市2019届高三毕业班3月模拟考试数学】设,m n 是两条不同的直线，,αβ是两个不同的平面，下列命题是真命题的是 A ．若mα，m β，则αβ B ．若m α，αβ，则m βC ．若m α⊂，m β⊥，则αβ⊥D ．若m α⊂，αβ⊥，则m β⊥【答案】C【解析】由m ，n 是两条不同的直线，α，β是两个不同的平面，知： 在A 中，若m ∥α，m ∥β，则α与β相交或平行，故A 错误； 在B 中，若m ∥α，α∥β，则m ∥β或m ⊂β，故B 错误；在C 中，若m ⊂α，m ⊥β，则由面面垂直的判定定理得α⊥β，故C 正确； 在D 中，若m ⊂α，α⊥β，则m 与β相交、平行或m ⊂β，故D 错误． 故选C ．【名师点睛】本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．3．【广西南宁市、玉林市、贵港市等2019届高三毕业班摸底考试数学】如图，棱长为a 的正方体1111ABCD A B C D -中，M 为BC 中点，这直线1D M 与平面ABCD 所成角的正切值为A．2 B．5C．5D ．12【答案】C【解析】连接DM ，因为几何体是正方体， 所以∠D 1MD 就是直线D 1M 与平面ABCD 所成角，tan ∠D 1MD=15DD DM ==，故选C ． 【名师点睛】求直线和平面所成角的关键是作出这个平面的垂线进而斜线和射影所成角即为所求，有时当垂线较为难找时也可以借助于三棱锥的等体积法求得垂线长，进而用垂线长比上斜线长可求得所成角的正弦值，当空间关系较为复杂时也可以建立空间直角坐标系，利用向量求解．4．【四川省宜宾市2019届高三第三次诊断性考试数学】如图，边长为2的正方形ABCD 中，,E F 分别是,BC CD 的中点，现在沿,AE AF 及EF 把这个正方形折成一个四面体，使,,B C D 三点重合，重合后的点记为P ，则四面体P AEF -的高为A ．13B ．23C ．34D ．1【答案】B【解析】由题意可知PA PE PF ，，两两垂直， ∴PA ⊥平面PEF ，∴A PEF V -11111123323PEF S PA =⋅=⨯⨯⨯⨯=△， 设P 到平面AEF 的距离为h ，又2111321212112222ABF S =-⨯⨯-⨯⨯-⨯⨯=△， ∴P AEFV -13322h h =⨯⨯=，∴123h =，解得23h =，故选B ．【名师点睛】本题考查了平面几何的折叠问题，空间几何体的体积计算，属于中档题．5．【四川省宜宾市2019届高三第三次诊断性考试数学】设,a b 是空间两条直线，则“,a b 不平行”是“,a b 是异面直线”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】B【解析】由,a b 是异面直线⇒,a b 不平行．反之若直线,a b 不平行，也可能相交． 所以“,a b 不平行”是“,a b 是异面直线”的必要不充分条件．故选B ．【名师点睛】本题考查了异面直线的性质、充分必要条件的判定方法，属于基础题．6．【四川省内江市2019届高三第三次模拟考试数学】在三棱锥A BCD -中，ABD △和BCD ∆是有公共斜边的等腰直角三角形，若三棱锥A BCD -的外接球的半径为2，球心为O ，且三棱锥A BCD -的体积为3，则直线OA 与平面BCD 所成角的正弦值是A ．12 B ．3C ．2D 【答案】D【解析】∵ABD △和BCD △是有公共斜边的等腰直角三角形， ∴线段BD 的中点为球心O ，连接OA ，OB ，易得BD AOC ⊥，∴∠AOC 为二面角A -BD -C 的平面角，且∠AOC 为直线OA 与平面BCD 所成角或其补角，三棱锥A BCD -的体积为11122sin 43323AOC S BD AOC =⨯⨯⨯⨯∠⨯=⨯△，∴sin 2AOC ∠=，故选D ．【名师点睛】本题考查线面角的求法，考查多面体的外接球问题，考查体积的计算，考查空间想象能力与计算能力，属于中档题．7．【四川省攀枝花市2019届高三下学期第三次统考数学】设,m n 是两条不同的直线，,αβ是两个不同的平面，下列命题中正确的是 A ．若mα，m β，则αβB ．若m α⊥，m n ⊥，则n α⊥C ．若m α⊥，m n ，则n α⊥D ．若αβ⊥，m α⊥，则mβ【答案】C【解析】设,m n 是两条不同的直线，,αβ是两个不同的平面，则： 在A 中，若mα，m β，则α与β相交或平行，故A 错误；在B 中，若m α⊥，m n ⊥，则n α或n α⊂，故B 错误；在C 中，若m α⊥，mn ，则由线面垂直的判定定理得n α⊥，故C 正确；在D 中，若αβ⊥，m α⊥，则m 与β平行或m β⊂，故D 错误．故选C ．【名师点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，是中档题．8．【四川省雅安市2019届高三第三次诊断考试数学】如图，圆锥的高PO =底面圆O 的直径2AB =，C 是圆上一点，且30CAB ∠=︒，D 为AC 的中点，则直线OC 和平面PAC 所成角的正弦值为A ．12B ．2C ．3D ．13【答案】C【解析】过点O 作OE PD ⊥于点E ，连接CE ，如下图．在圆O 中，AB 为直径． ∴AC BC ⊥，又D 为AC 中点，PA PC =， ∴AC PD ⊥且AC OD ⊥， 又PD OD D =，∴AC ⊥平面POD ，又AC ⊂平面PAC ， ∴平面POD ⊥平面PAC ， 又平面POD平面PAC PD =，OE PD ⊥，OE ⊂平面POD ，∴OE ⊥平面PAC ．OCE ∴∠就是直线OC 和平面PAC 所成角．由题可得1BC =．在Rt POD △中，可求得：1122OD BC ==，又PO =32PD ==．由13112222POD S OE =⨯⨯=⨯△，得3OE =，所以3sin 13OCE ∠==C ．【名师点睛】本题主要考查了线面角的求法，考查作图及线面、面面垂直证明，还考查计算能力，属于中档题．9．【四川省华文大教育联盟2019届高三第二次质量检测数学】如图，在正方体1111ABCD A B C D -中，,M N 分别是棱111,B C C C 的中点，则异面直线1BD 与MN 所成的角的大小是A ．30°B ．45︒C ．60︒D ．90︒【答案】D【解析】连接11,B C BC ，正方体1111ABCD A B C D -，11D C ⊥面11BB C C ，1B C ⊂面11BB C C ，所以111B C D C ⊥，正方形11BB C C 中，11B C BC ⊥，111,D C BC ⊂面11BD C ，1111D C BC C =，所以1B C ⊥面11BD C ，而1BD ⊂面11BD C ， 所以11BD B C ⊥，又M 为11B C 中点，N 为1CC 中点，可得1MNB C ，所以1BD MN ⊥，即异面直线1BD 与MN 所成的角的大小是90︒． 故选D ．【名师点睛】本题考查正方体内异面直线所成的角，通过线线垂直证明线面垂直，属于中档题． 10．【四川省成都市2019届高三毕业班第二次诊断性检测数学】已知,a b 是两条异面直线，直线c 与,a b 都垂直，则下列说法正确的是 A ．若c ⊂平面α，则a α⊥ B ．若c ⊥平面α，则a α，b aC ．存在平面α，使得c α⊥，a α⊂，b aD ．存在平面α，使得c a ，a α⊥，b a ⊥【答案】C【解析】由a ，b 是两条异面直线，直线c 与a ，b 都垂直，知： 在A 中，若c ⊂平面α，则a 与α相交、平行或a ⊂α，故A 错误；在B 中，若c ⊥平面α，则a ，b 与平面α平行或a ，b 在平面α内，故B 错误； 在C 中，由线面垂直的性质得：存在平面α，使得c ⊥α，a ⊂α，b ∥α，故C 正确；在D 中，若存在平面α，使得c ∥α，a ⊥α，b ⊥α，则a ∥b ，与已知a ，b 是两条异面直线矛盾，故D 错误．故选C ．【名师点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．对于这种题目的判断一般是利用课本中的定理和性质进行排除，判断，还可以画出样图进行判断，利用常见的立体图形，将点线面放入特殊图形，进行直观判断． 11．【四川省攀枝花市2019届高三第二次统一考试数学】如图，在正方体1111ABCD A B C D -中，E 是BC的中点，则异面直线CD 和1D E 所成角的余弦值为A ．23BCD【答案】A【解析】取AD 的中点为F ，连接EF 、1D F ，因为CD //1D F ，所以异面直线CD 和1D E 所成角就是直线EF 和1D E 所成角， 设正方体边长为a ，EF =a ，132a D E ==，所以112cos 3EF D EF D E ∠==，故选A ． 【名师点睛】本题主要考查了空间几何中异面直线的夹角问题，作出异面直线的夹角是解题的关键，属于较为基础题．12．【四川省广安、眉山、内江、遂宁2019届高三第一次诊断性考试数学】下列命题错误的是A ．不在同一直线上的三点确定一个平面B ．两两相交且不共点的三条直线确定一个平面C ．如果两个平面垂直，那么其中一个平面内的直线一定垂直于另一个平面D ．如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面 【答案】C【解析】由公理知直线及直线外一点，确定一个平面，故A 正确； 由公理知两两相交且不共点的三条直线确定一个平面，故B 正确； 由面面垂直的性质定理知错误，故C 不正确； 由面面平行的性质定理知正确，故D 正确．故选C ．【名师点睛】本题考查命题真假的判断，是基础题，解题时要认真审题，注意对概念的理解和定理，性质的应用，属于基础题．13．【贵州省2019届高三普通高等学校招生适应性考试数学】设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出下面四个命题： ①若αβ⊥，βγ⊥，则αγ；②若αβ⊥，m α⊂，n β⊂，则m n ⊥； ③若mα，n α⊂，则m n ；④若αβ，m γα=，n γβ=，则m n ．其中正确命题的序号是 A ．①④ B ．①② C ．④ D ．②③④【答案】C【解析】对于①，若αβ⊥，βγ⊥，则αγ与平行或相交，故错误； 对于②，若αβ⊥，m α⊂，n β⊂，则m n 与平行、相交或异面，错误； 对于③，若m α，n α⊂，则m n 与平行或异面，错误； 对于④，若αβ，m γα=，n γβ=，由面面平行性质定理可知m n ，正确，故选C ．【名师点睛】本题考查命题真假的判断，是基础题，解题时要注意空间思维能力的培养．14．【云南省曲靖市第一中学2018届高三上学期高考复习质量监测卷（四）数学】设,m n 是两条不同的直线，,αβ是两个不同的平面，有下列四个命题： ①若m α⊂，αβ⊥，则m β⊥；②若a β，m β⊂，则m α；③若m α⊥，mn ，αβ，则n β⊥；④若m α，n β，mn ，则αβ其中正确命题的序号是 A ．①② B ．①③ C ．②③ D ．③④【答案】C【解析】①两个面垂直，推不出面中任意直线和另一个面垂直，错误；故排除A 、B 选项，对于②，两个平行平面，其中一个平面内的任意直线都和另一个平面平行，故正确，所以选C ．15．【云南省昆明市2019届高三高考模拟（第四次统测）数学】已知直线l ⊥平面α，直线m ∥平面β，若αβ⊥，则下列结论正确的是A ．l β∥或l β⊂B ．//l mC ．m α⊥D ．l m ⊥【答案】A【解析】对于A ，直线l ⊥平面α，αβ⊥，则l β或l β⊂，A 正确；对于B ，直线l ⊥平面α，直线m 平面β，且αβ⊥，则//l m 或l 与m 相交或l 与m 异面，∴B 错误；对于C ，直线l ⊥平面α，直线m 平面β，且αβ⊥，则m α⊥或m 与α相交或m α⊂或//m α，∴C 错误；对于D ，直线l ⊥平面α，直线m 平面β，且αβ⊥，则//l m 或l 与m 相交或l 与m 异面，∴D 错误．故选A ．【名师点睛】本题考查了空间平面与平面关系的判定及直线与直线关系的确定问题，也考查了几何符号语言的应用问题，是基础题．。